Identification of a PCE Contamination Source in an Intergranular Aquifer Using a Simulation–Optimisation Framework: A Case Study of Ljubljana Polje, Slovenia
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Groundwater Flow and Solute Transport Model
2.3. Simulation–Optimisation Framework
- contamination originates from a single point source, and the observed PCE concentrations in the wells are attributed to this source;
- the source strength remains constant throughout the release period;
- contaminant release occurs directly into the saturated zone of the aquifer, and only transport within the saturated zone is considered;
- the contaminant behaves as a conservative tracer, without degradation or sorption.
3. Results
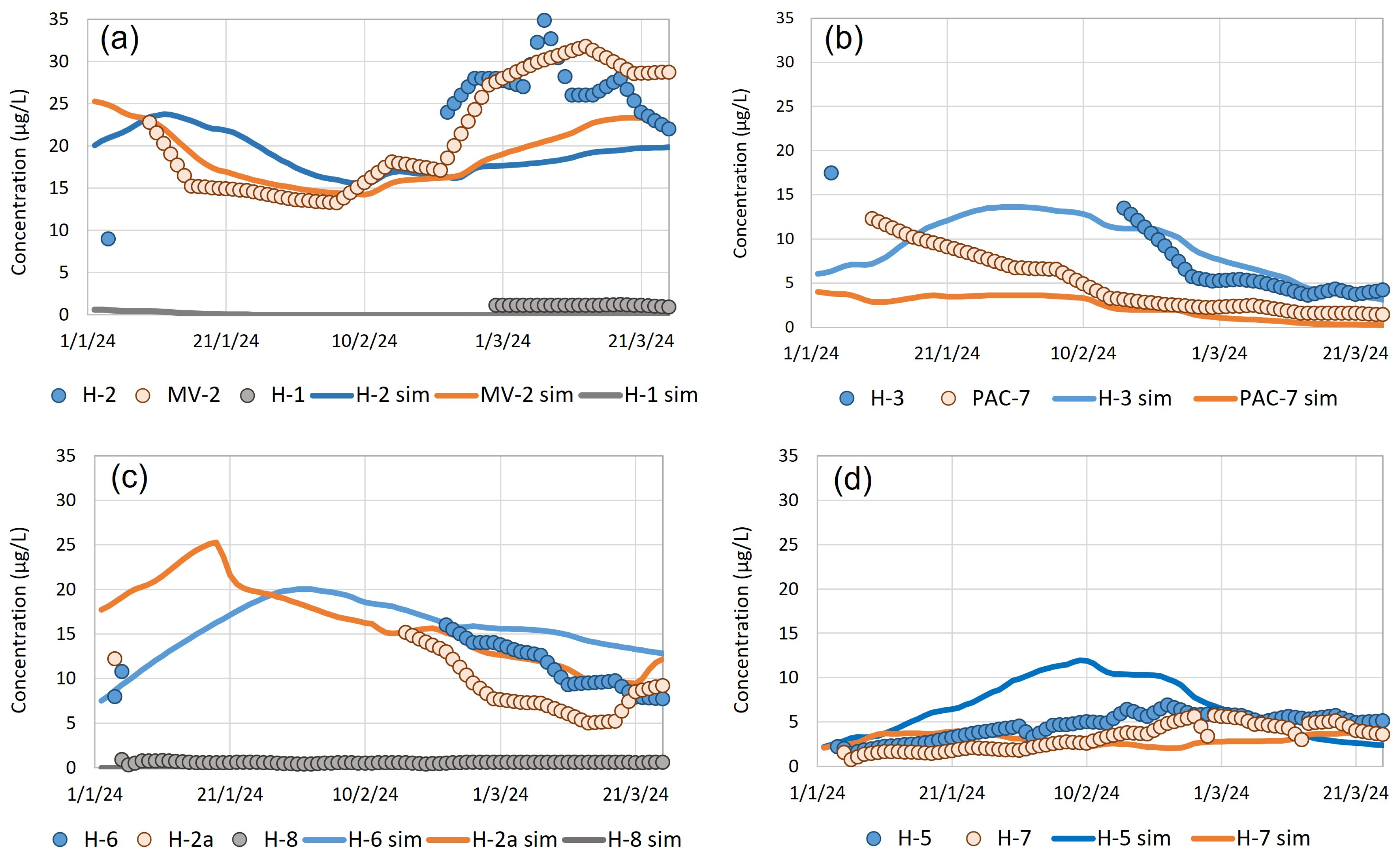
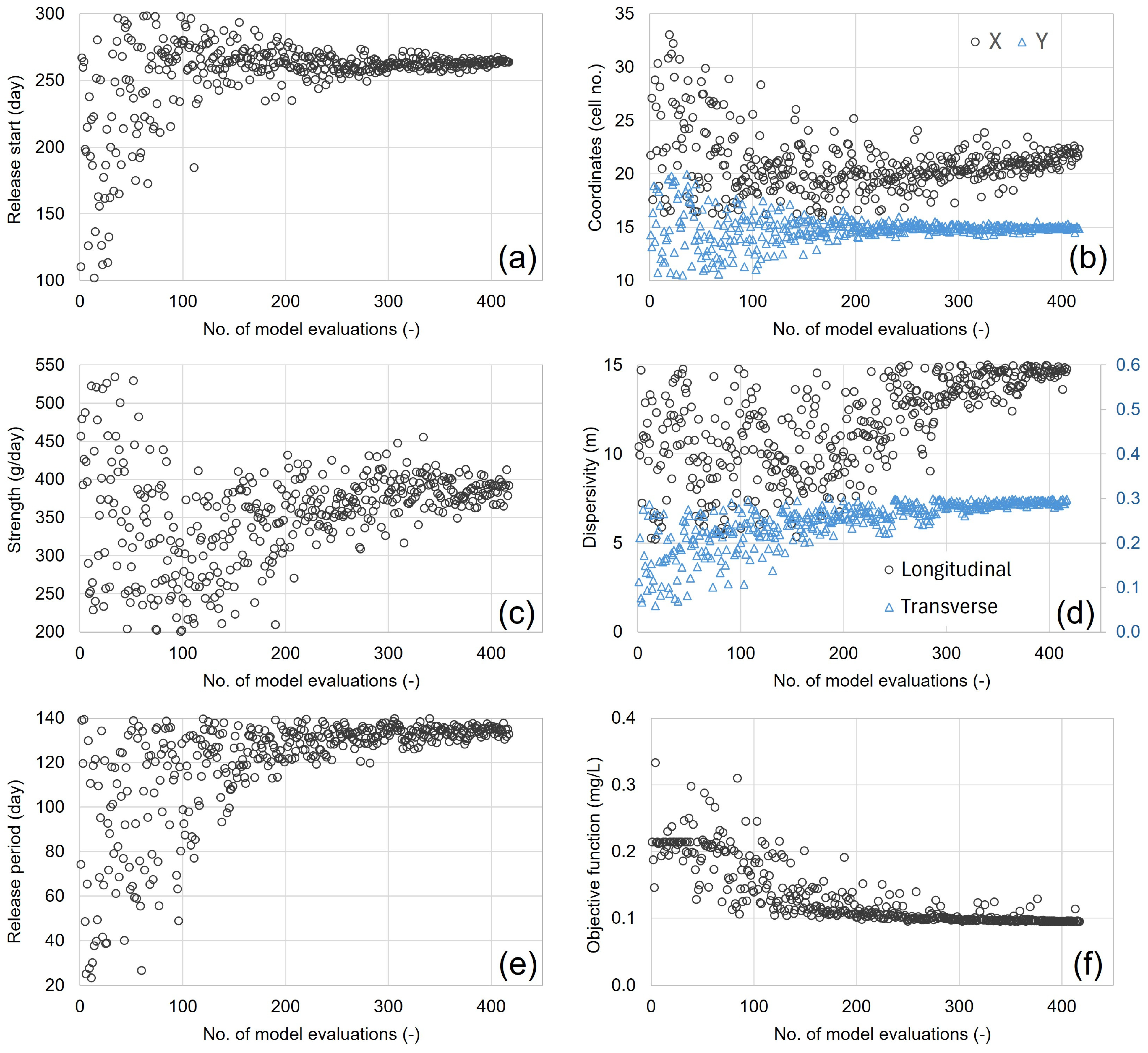
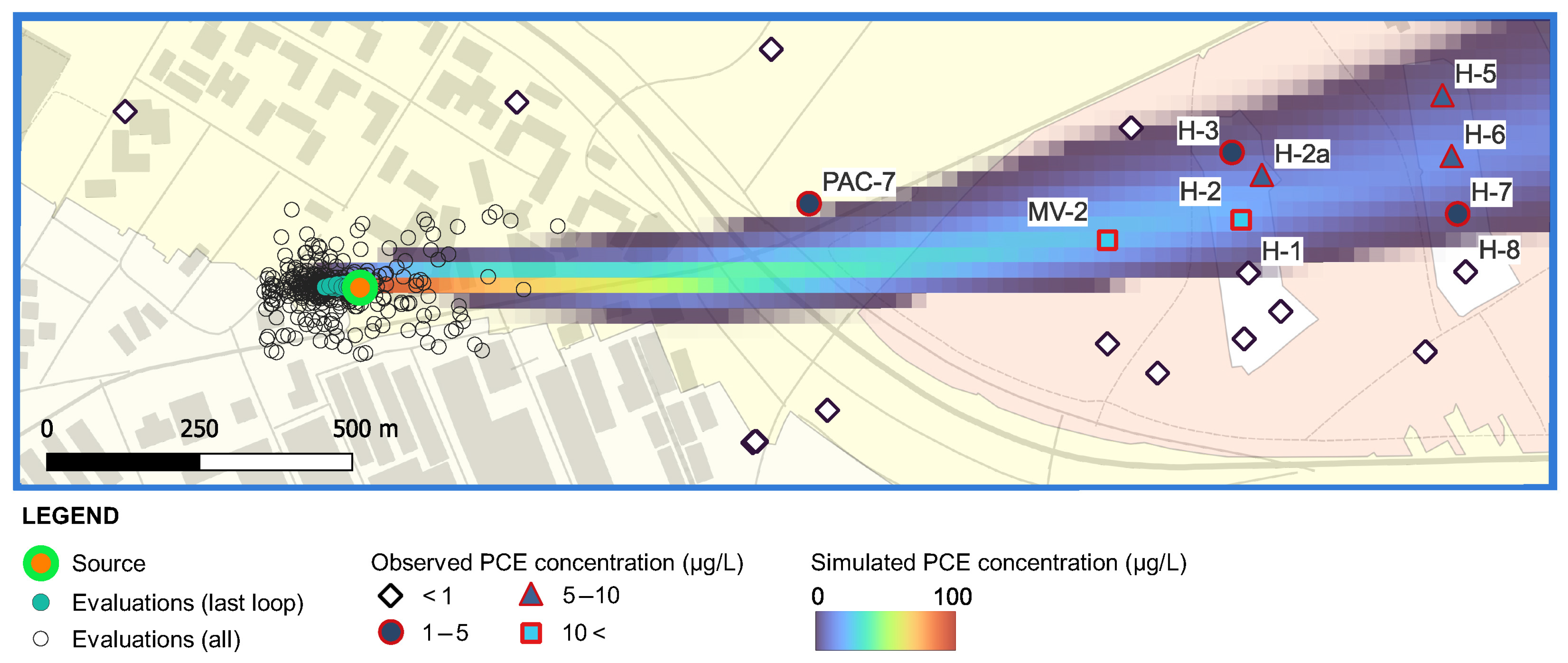
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gómez-Hernández, J.J.; Xu, T. Contaminant Source Identification in Aquifers: A Critical View. Math. Geosci. 2021, 54, 437–458. [Google Scholar] [CrossRef]
- Janža, M. A Decision Support System for Emergency Response to Groundwater Resource Pollution in an Urban Area (Ljubljana, Slovenia). Environ. Earth Sci. 2015, 73, 3763–3774. [Google Scholar] [CrossRef]
- Colombo, L.; Alberti, L.; Mazzon, P.; Antelmi, M. Null-Space Monte Carlo Particle Backtracking to Identify Groundwater Tetrachloroethylene Sources. Front. Environ. Sci. 2020, 8, 142. [Google Scholar] [CrossRef]
- Barati Moghaddam, M.; Mazaheri, M.; Mohammad Vali Samani, J. Inverse Modeling of Contaminant Transport for Pollution Source Identification in Surface and Groundwaters: A Review. Groundw. Sustain. Dev. 2021, 15, 100651. [Google Scholar] [CrossRef]
- Carrera, J.; Alcolea, A.; Medina, A.; Hidalgo, J.; Slooten, L.J. Inverse Problem in Hydrogeology. Hydrogeol. J. 2005, 13, 206–222. [Google Scholar] [CrossRef]
- Michalak, A.M.; Kitanidis, P.K. Estimation of Historical Groundwater Contaminant Distribution Using the Adjoint State Method Applied to Geostatistical Inverse Modeling. Water Resour. Res. 2004, 40, W08302. [Google Scholar] [CrossRef]
- Pollicino, L.C.; Colombo, L.; Alberti, L.; Masetti, M. PCE Point Source Apportionment Using a GIS-Based Statistical Technique Combined with Stochastic Modelling. Sci. Total Environ. 2021, 750, 142366. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Xu, T.; Lu, C.; Xie, Y.; Yang, J. Contaminant Source Identification in an Aquifer Using a Bayesian Framework with Arbitrary Polynomial Chaos Expansion. Stoch. Environ. Res. Risk Assess. 2024, 38, 2007–2018. [Google Scholar] [CrossRef]
- Wang, C.; Dou, Z.; Zhu, Y.; Yang, Z.; Zou, Z. Breaking the Mold of Simulation–Optimization: Direct Forward Machine Learning Methods for Groundwater Contaminant Source Identification. J. Hydrol. 2024, 642, 131759. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A Linked Simulation–Optimization Model for Solving Unknown Groundwater Pollution Source Identification Problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef]
- Ghafouri, H.R.; Mosharaf-Dehkordi, M.; Afzalan, B. Identification of Immiscible NAPL Contaminant Sources in Aquifers by a Modified Two-Level Saturation-Based Imperialist Competitive Algorithm. J. Contam. Hydrol. 2017, 202, 33–46. [Google Scholar] [CrossRef]
- Chakraborty, A.; Prakash, O. Identification of Clandestine Groundwater Pollution Sources Using Heuristic Optimization Algorithms: A Comparison between Simulated Annealing and Particle Swarm Optimization. Environ. Monit. Assess. 2020, 192, 791. [Google Scholar] [CrossRef]
- Gurarslan, G.; Karahan, H. Solving Inverse Problems of Groundwater-Pollution-Source Identification Using a Differential Evolution Algorithm. Hydrogeol. J. 2015, 23, 1109–1119. [Google Scholar] [CrossRef]
- Habiyakare, T.; Zhang, N.; Feng, C.-H.; Ndayisenga, F.; Kayiranga, A.; Sindikubwabo, C.; Muhirwa, F.; Shah, S. Implementation of Genetic Algorithm for the Identification of DNAPL Sources. Groundw. Sustain. Dev. 2022, 16, 100707. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and Efficient Global Optimization for Conceptual Rainfall–Runoff Models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled Complex Evolution Approach for Effective and Efficient Global Minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Rahnamay Naeini, M.; Analui, B.; Gupta, H.V.; Duan, Q.; Sorooshian, S. Three Decades of the Shuffled Complex Evolution (SCE-UA) Optimization Algorithm: Review and Applications. Sci. Iran. 2019, 26, 2015–2031. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L.; Zhang, Y.; Xing, L.; Hao, Q.; Xiao, Y.; Yang, L.; Zhu, H. Identification of Groundwater Pollution Sources by a SCE-UA Algorithm-Based Simulation/Optimization Model. Water 2018, 10, 193. [Google Scholar] [CrossRef]
- Janža, M. Optimization of Well Field Management to Mitigate Groundwater Contamination Using a Simulation Model and Evolutionary Algorithm. Sci. Total Environ. 2022, 807, 150811. [Google Scholar] [CrossRef]
- DHI. Auto Calibration Tool: User Guide; DHI: Hørsholm, Denmark, 2010. [Google Scholar]
- Pollicino, L.C.; Masetti, M.; Stevenazzi, S.; Colombo, L.; Alberti, L. Spatial Statistical Assessment of Groundwater PCE (Tetrachloroethylene) Diffuse Contamination in Urban Areas. Water 2019, 11, 1211. [Google Scholar] [CrossRef]
- Svetina, J.; Prestor, J.; Jamnik, B.; Auersperger, P.; Brenčič, M. Contaminant Trends in Urban Groundwater: Case Study from Ljubljana (Central Slovenia). Water 2024, 16, 890. [Google Scholar] [CrossRef]
- Feo, A.; Pinardi, R.; Artoni, A.; Celico, F. Estimation of Free-Product PCE Distribution in Thick Multilayered Aquifers as Possible Long-Term Pollution Sources for Shallow and Deep Groundwaters Using High-Precision Numerical Simulations. Water 2024, 16, 3053. [Google Scholar] [CrossRef]
- Seyedabbasi, M.A.; Newell, C.J.; Adamson, D.T.; Sale, T.C. Relative Contribution of DNAPL Dissolution and Matrix Diffusion to the Long-Term Persistence of Chlorinated Solvent Source Zones. J. Contam. Hydrol. 2012, 134–135, 69–81. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.; Smit, M.; Grotenhuis, T.; van Gaans, P.; Rijnaarts, H. Effectiveness of Stimulating PCE Reductive Dechlorination: A Stepwise Approach. J. Contam. Hydrol. 2014, 164, 209–218. [Google Scholar] [CrossRef]
- Official Gazette of the Republic of Slovenia (OGRS). Uredba o Pitni Vodi (Drinking Water Regulation). No. 61/23. Available online: https://pisrs.si/pregledPredpisa?id=URED8706 (accessed on 3 November 2025).
- Žlebnik, L. Pleistocen Kranjskega, Sorškega in Ljubljanskega polja (Pleistocene Deposits of the Kranj, Sora and Ljubljana Fields). Geologija 1971, 14, 5–51. [Google Scholar]
- Janža, M.; Lapanje, A.; Šram, D.; Rajver, D.; Novak, M. Research of Geological and Geothermal Conditions for Assessing the Shallow Geothermal Potential in the Area of Ljubljana, Slovenia. Geologija 2017, 60, 309–327. [Google Scholar] [CrossRef]
- Janža, M.; Prestor, J.; Pestotnik, S.; Jamnik, B. Nitrogen Mass Balance and Pressure Impact Model Applied to an Urban Aquifer. Water 2020, 12, 1171. [Google Scholar] [CrossRef]
- Janža, M.; Prestor, J.; Urbanc, J.; Jamnik, B. TCE Contamination Plume Spreading in a Highly Productive Aquifer of Ljubljansko Polje. In Proceedings of the EGU General Assembly; EGU: Vienna, Austria, 2005. [Google Scholar]
- Brenčič, M.; Prestor, J.; Kompare, B.; Matoz, H.; Kranjc, S. Integrated approach to delineation of drinking waterprotection zones. Geologija 2009, 52, 175–182. [Google Scholar] [CrossRef]
- Official Gazette of the Republic of Slovenia (OGRS). Uredba O Vodovarstvenem Območju ZA Vodno Telo Vodonosnika Ljubljanskega Polja (Decree on the Water Protection Area for the Water Body of the Ljubljansko Polje Aquifer). No. 43/15, 181/21, 60/22, 35/23. Available online: https://pisrs.si/pregledPredpisa?id=URED7006 (accessed on 3 November 2025).
- DHI. MIKE SHE: Integrated Catchment Modelling. Available online: https://www.dhigroup.com/technologies/mikepoweredbydhi/mike-she (accessed on 7 October 2025).
- Guilbeault, M.A.; Parker, B.L.; Cherry, J.A. Mass and Flux Distributions from DNAPL Zones in Sandy Aquifers. Ground Water 2005, 43, 70–86. [Google Scholar] [CrossRef]
- Schulze-Makuch, D. Longitudinal Dispersivity Data and Implications for Scaling Behavior. Ground Water 2005, 43, 443–456. [Google Scholar] [CrossRef]
- Neuman, S.P.; Di Federico, V. Multifaceted Nature of Hydrogeologic Scaling and Its Interpretation. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- DHI. MIKE SHE User Manual, Volume 2: Reference Guide; DHI: Hørsholm, Denmark, 2011. [Google Scholar]
| Model Parameter | Initial Value | Lower Bound | Upper Bound |
|---|---|---|---|
| Release start (day) * | 200 | 100 | 300 |
| Strength (g/day) | 400 | 200 | 550 |
| Release period (day) | 100 | 20 | 140 |
| X ** | 26 | 16 | 36 |
| Y ** | 15 | 10 | 20 |
| Longitudinal dispersivity (m) | 10 | 5 | 15 |
| Transverse dispersivity (m) | 0.1 | 0.01 | 0.3 |
| Model Parameter | Optimised Value |
|---|---|
| Release start (day) | 264 |
| Strength (g/day) | 392 |
| Release period (day) | 133 |
| X | 22 |
| Y | 15 |
| Longitudinal dispersivity (m) | 14.80 |
| Transverse dispersivity (m) | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janža, M. Identification of a PCE Contamination Source in an Intergranular Aquifer Using a Simulation–Optimisation Framework: A Case Study of Ljubljana Polje, Slovenia. Water 2025, 17, 3251. https://doi.org/10.3390/w17223251
Janža M. Identification of a PCE Contamination Source in an Intergranular Aquifer Using a Simulation–Optimisation Framework: A Case Study of Ljubljana Polje, Slovenia. Water. 2025; 17(22):3251. https://doi.org/10.3390/w17223251
Chicago/Turabian StyleJanža, Mitja. 2025. "Identification of a PCE Contamination Source in an Intergranular Aquifer Using a Simulation–Optimisation Framework: A Case Study of Ljubljana Polje, Slovenia" Water 17, no. 22: 3251. https://doi.org/10.3390/w17223251
APA StyleJanža, M. (2025). Identification of a PCE Contamination Source in an Intergranular Aquifer Using a Simulation–Optimisation Framework: A Case Study of Ljubljana Polje, Slovenia. Water, 17(22), 3251. https://doi.org/10.3390/w17223251






