Research on Arch Dam Deformation Safety Early Warning Method Based on Effect Separation of Regional Environmental Variables and Knowledge-Driven Approach

Abstract

There are significant differences in the deformation patterns of different parts of arch dams, and there is a common situation of periodic data loss. To accurately analyze the deformation behavior of arch dams, this paper proposes a safety warning and anomaly diagnosis method for arch dam deformation based on the separation of environmental variable effects in different partitions and a knowledge-driven approach. This method combines various techniques such as an optimized ISODATA clustering method, probabilistic principal component analysis (PPCA), square prediction error (SPE) norm control chart, and contribution chart. By defining data forms and rules, existing engineering specifications and experience are transformed into “knowledge” and applied to the operation and management of arch dams, achieving accurate monitoring of arch dam deformation status and timely diagnosis of outliers. Through monitoring data verification of horizontal displacement in a certain arch dam partition, the results show that this method can accurately identify deformation anomalies in the arch dam and effectively separate the influence of environmental variables and noise interference, providing strong support for the safe operation of the arch dam. Accurate deformation monitoring of arch dams is essential for ensuring structural safety and optimizing operational management. However, conventional early warning indicators and empirical models often fail to capture the spatial heterogeneity of deformation and the complex coupling between environmental variables and structural responses. To overcome these limitations, this study proposes a knowledge-driven safety early warning and anomaly diagnosis model for arch dam deformation, based on spatiotemporal clustering and partitioned environmental variable separation. The method integrates the optimized ISODATA clustering algorithm, probabilistic principal component analysis (PPCA), squared prediction error (SPE) control chart, and contribution chart to establish a comprehensive monitoring framework. The optimized ISODATA identifies deformation zones with similar mechanical behavior, PPCA separates environmental influences such as temperature and reservoir level from structural responses, and the SPE and contribution charts quantify abnormal variations and locate potential risk regions. Application of the proposed method to long-term deformation monitoring data demonstrates that the PPCA-based framework effectively separates environmental effects, improves the interpretability of zoned deformation characteristics, and enhances the accuracy and reliability of anomaly identification compared with conventional approaches. These findings indicate that the proposed knowledge-driven model provides a robust and interpretable framework for precise deformation safety evaluation of arch dams.

1. Introduction

Water conservancy projects play a great social benefit in many aspects such as flood control, power generation, water supply, and agricultural irrigation [1]. As a commonly used water-retaining structure in water conservancy projects, the safe and stable operation of arch dams is essential to safeguard these benefits [2]. However, arch dams are subjected to long-term static and dynamic loads such as water level rise and fall, temperature changes, sediment pressure, and earthquakes during operation, and the mechanical properties of the dam materials will deteriorate over time [3]. In addition to conventional displacement monitoring, non-destructive testing (NDT) techniques such as transient electromagnetics (TEM), ground-penetrating radar (GPR), and electrical resistivity tomography (ERT) have been extensively employed in dam engineering to detect internal defects, seepage zones, and material deterioration without causing structural damage [4,5,6,7,8,9]. These NDT techniques provide valuable subsurface diagnostic information that cannot be obtained through conventional instrumentation and play an essential role in assessing dam integrity and serviceability. However, traditional NDT applications often produce only instantaneous “snapshot” measurements of internal material properties and are highly sensitive to environmental and operational factors, which limits their capability for long-term and continuous safety monitoring [4]. Recent research has highlighted the potential of time-lapse ERT and advanced acoustic or radar-based NDT for capturing the temporal evolution of seepage and deterioration processes in large hydraulic structures [5,6], while integrated physics-based and hybrid modeling frameworks have been proposed to enhance data interpretation and structural health assessment [7]. Nevertheless, developing an efficient methodology to perform continuous, real-time, and large-scale monitoring using NDT remains a key challenge in dam safety evaluation. Therefore, to ensure the safety and engineering effectiveness of arch dams, it is necessary to establish a dam safety monitoring system and to identify information on the structural safety state by analyzing the monitoring data [10]. Among the various monitoring programs, displacement monitoring is a key indicator for assessing the structural integrity and serviceability of arch dams [11]. By analyzing the arch dam deformation monitoring data based on a data-driven safety monitoring model, it is possible to determine whether there is a trend change or anomaly in the structural state of the dam [12,13].

However, the deformation characteristics of arch dams are complicated, and the two systems of horizontal arch and vertical beam bear loads together, which makes different regions show different deformation laws under the same external conditions [14]. This inconsistency in deformation patterns increases the difficulty of comprehensive and accurate monitoring of arch dams [1] such as by introducing a coordinate factor for the measurement points [14], principal component extraction methods [15], panel data models [16], defining the geometric centers of multiple measurement points [1], spatial correlation functions [17], or joint monitoring based on multipoint clustering [18] and relevance [19]. Therefore, it is necessary to divide the deformation partitions of the arch dam based on existing monitoring data and carry out safety monitoring separately.

From a temporal perspective, traditional data-driven models cannot continuously track displacement behavior with dynamic evolution patterns in time-varying environments by establishing offline models through regression of historical displacement and related influencing factors [20]. In addition, due to instrument failures, engineering accidents, and other reasons [21], there is often missing monitoring data for arch dams, which further increases the difficulty of accurately evaluating the deformation status of arch dams [22]. For this reason, Li et al. [23] identified key features affecting the stress of high arch dams by introducing interpretable machine learning methods. Zhang et al. [24] used a finite-element-based forward analysis method to quantify the uncertainty of water pressure components. Ren et al. [15] used kernel principal component analysis to fuse multisensor data, extract more important contextual components, and remove deformation correlations from multiple monitoring points from the original monitoring data to conduct anomaly monitoring separately. Rong et al. [25] constructed a progressive diagnostic criterion based on probability principles, combined with an improved local outlier factor (LOF) and mutual verification considering spatiotemporal correlation, and established a multipoint anomaly recognition model. Cheng et al. [26] successfully separated environmental impact and noise interference from monitoring data by analyzing the covariance matrix of dam response multivariate monitoring data. Yang et al. [27] used mixed model analysis results and information entropy to characterize the degree of danger of single-point deformation and multipoint deformation. Zhan et al. [28] considered the structural state of the dam before and after reinforcement and linked the structural strength criterion with the deformation evolution mechanism, providing a theoretical basis and decision support for the long-term service and operation management of reinforced dams. Chen et al. [29] extracted spatial principal components of arch dam deformation and embedded concept transformation and fusion rules into cloud models to develop and update deformation warning indicators that consider randomness and fuzziness.

Although these new models have improved the accuracy of arch dam deformation monitoring to a certain extent, they still face the problems of missing data series and large gaps between the deformation characteristics of multiple measurement points in practical application [30]. To overcome these problems, it is particularly important to apply the knowledge and experience of previous safety monitoring of arch dams of the same type to the operation and management of new arch dams [31]. By integrating engineering specifications, engineering experience, data types, thresholds, and relative components of multiple measurement points, a knowledge-driven safety warning and anomaly diagnosis method for arch dam deformation can be developed [31], thereby further improving the accuracy and reliability of arch dam deformation monitoring [29].

Aiming at the above problems, this paper proposes an arch dam deformation safety early warning and outlier causation diagnosis method based on partitioned environmental variable effect separation and knowledge-driven model. The method integrates the optimized ISODATA clustering method, probabilistic principal component analysis (PPCA), control charts of squared prediction error (SPE), paradigm contribution charts, and other technical means. By defining the data forms and rules, the existing engineering specifications and engineering experience can be transformed into “knowledge” and applied to the operation and management of arch dams to realize the precise monitoring of the deformation state of arch dams and the timely diagnosis of abnormal values. In the following sections, the principle, characteristics, and application effect of this method are introduced in detail, and its effectiveness is verified by the monitoring data of horizontal displacement of an arch dam.

In summary, despite the progress of existing data-driven and statistical models, accurately characterizing the deformation behavior of arch dams remains challenging due to spatial heterogeneity, incomplete data, and the complex coupling between environmental variables and structural responses. Conventional early warning indicators are typically defined empirically, lacking adaptability to region-specific deformation characteristics. Therefore, it is crucial to establish a zoned monitoring framework that separates environmental effects while incorporating prior engineering knowledge. To address these challenges, this study develops a knowledge-driven safety early warning and anomaly diagnosis model for arch dam deformation based on spatiotemporal clustering and partitioned environmental variable separation. The proposed approach transforms engineering codes and accumulates operational experience into explicit knowledge rules and integrates them with advanced statistical techniques such as optimized ISODATA clustering and probabilistic principal component analysis (PPCA). By doing so, the method bridges the gap between empirical engineering judgment and intelligent data analysis, providing a novel and reliable framework for precise deformation monitoring and safety evaluation of arch dams.

2. Deformation Partitioning of Arch Dams Based on Optimized ISODATA Clustering

The Iterative Self-Organizing Data Analysis Techniques Algorithm (ISODATA) dynamically adjusts the number of clusters according to the actual situation of each cluster during the runtime, which can effectively solve the problem of traditional K-means clustering algorithms and other clustering algorithms that cannot be determined in advance [32]. However, ISODATA still has certain drawbacks: for example, random selection of initial clustering centers may lead to slower convergence of the clustering algorithm, poorer results, and also increase the chance of clustering results. And the selection of the Euclidean distance as the distance metric in the input space of the original arch dam deformation monitoring curve cannot capture the high-dimensional characteristics of the arch dam deformation monitoring curve, which is the main reason why ISODATA is not suitable to be used in the arch dam deformation monitoring curve [33].

To this end, this paper optimizes the traditional ISODATA for spatial clustering of arch dam deformation measurement points through the selection of initial clustering centers and high-dimensional feature extraction of arch dam deformation monitoring curves based on the kernel method, respectively.

2.1. Selection of Initial Clustering Centers

Assuming that the monitoring sequence of the i-th deformation measurement point of the arch dam is ${\mathit{x}}_i$, ${\mathit{x}}_i$ is a one-dimensional vector composed of multiple real numbers. By randomly selecting the first initial cluster center, assuming that n initial cluster centers have already been selected (0 < n < k), when selecting the n + 1th cluster center, points farther away from the current n cluster centers have a higher probability of being selected.

The steps of the optimization algorithm for selecting the initial clustering center are as follows:

(1)

Randomly select a sample from the sample set as the first initial cluster center;

(2)

For each remaining sample ${\mathit{x}}_i$, first calculate the distance between it and the existing cluster centers, record the shortest distance, and represent it as $d\left({\mathit{x}}_i\right)$;

(3)

For each sample ${\mathit{x}}_i$, its probability of being selected as the next cluster center is ${\displaystyle \frac{d{\left({\mathit{x}}_i\right)}^2}{{\sum }_{x\in D}d{\left({\mathit{x}}_i\right)}^2}}$. Based on this probability, the cluster center for this round is selected. The larger the sample. $d\left({\mathit{x}}_i\right)$, the higher its probability of being selected;

(4)

Return to step (2) until the selection of $k$ initial clustering centers is made.

Through this initial clustering center selection strategy, the initial clustering centers that are selected are farther away from each other, and the possibility that they belong to different clusters is also greater, and it is easier to converge.

2.2. High-Dimensional Feature Extraction of Arch Dam Deformation Monitoring Curves Based on the Kernel Method

Aiming at the traditional Euclidean distance, which makes it difficult to obtain the high-dimensional features of the arch dam deformation monitoring curve, the kernel method is introduced for optimization. The core idea is to map the original arch deformation monitoring curve into a high-dimensional feature space through non-linear mapping and then perform clustering in the new high-dimensional feature space. The non-linear mapping improves the probability of linear separability of data points, and the clustering algorithm can calculate the distance between samples according to the high-dimensional features of the arch dam deformation monitoring curves to carry out clustering, and the effect of clustering is also improved accordingly.

Assuming $\mathit{X}$ is the input space and $\mathit{H}$ is a high-dimensional space, there exists a mapping function $\varphi \left({\mathit{x}}_i\right)$ that maps the samples ${\mathit{x}}_i$ in $\mathit{X}$ space to space $\mathit{H}$. If there exists a function $K({\mathit{x}}_i,{\mathit{x}}_j)$ that satisfies the condition $K({\mathit{x}}_i,{\mathit{x}}_j)=\varphi \left({\mathit{x}}_i\right)•\varphi \left({\mathit{x}}_j\right)$ for all ${\mathit{x}}_i,{\mathit{x}}_j\in \mathit{X}$, then $K({\mathit{x}}_i,{\mathit{x}}_j)$ is called a kernel function, where $\varphi \left({\mathit{x}}_i\right)•\varphi \left({\mathit{x}}_j\right)$ is the inner product of $\varphi \left({\mathit{x}}_i\right)$ and $\varphi \left({\mathit{z}}_i\right)$. The kernel method can bypass the mapping function $\varphi \left(\mathit{x}\right)$ and solve through the kernel function $K({\mathit{x}}_i,{\mathit{x}}_j)$.

The distance between two samples in high-dimensional space can be represented by a kernel function:

$$\begin{array}{c}d\left({\mathit{x}}_i,{\mathit{x}}_j\right)={‖\varphi \left({\mathit{x}}_i\right)-\varphi \left({\mathit{x}}_j\right)‖}^2\\ =\varphi {\left({\mathit{x}}_i\right)}^2-2\varphi \left({\mathit{x}}_i\right)\varphi \left(x_j\right)+\varphi {\left({\mathit{x}}_j\right)}^2\\ =K\left({\mathit{x}}_i,{\mathit{x}}_i\right)-2K\left({\mathit{x}}_i,{\mathit{x}}_j\right)+K\left({\mathit{x}}_j,{\mathit{x}}_j\right)\end{array}$$

(1)

In addition, we also need to calculate the distance between each sample ${\mathit{x}}_i$ and each cluster center ${\mathit{\mu }}_j$. In high-dimensional space, the distance is:

$$\begin{array}{c}d\left({\mathit{x}}_i,{\mathit{\mu }}_j\right)={‖\varphi \left({\mathit{x}}_i\right)-\varphi \left({\mathit{\mu }}_j\right)‖}^2\\ =\varphi {\left({\mathit{x}}_i\right)}^2-2\varphi \left({\mathit{x}}_i\right)\varphi \left({\mathit{\mu }}_j\right)+\varphi {\left({\mathit{\mu }}_j\right)}^2\end{array}$$

(2)

In high-dimensional space, the cluster centers of class $C_j$ can be represented as:

$$\varphi \left({\mathit{\mu }}_j\right)={\displaystyle \frac{1}{\left|C_j\right|}}\sum _{\varphi \left(\mathit{x}\right)\in C_j}\varphi (\mathit{x})$$

(3)

By substituting Equation (3) into Equation (2), the distance between the sample ${\mathit{x}}_i$ and cluster center ${\mathit{\mu }}_j$ can be further solved as:

$$\begin{array}{c}d\left({\mathit{x}}_i,{\mathit{\mu }}_j\right)=\varphi {\left({\mathit{x}}_i\right)}^2-{\displaystyle \frac{2}{\left|C_j\right|}}{\displaystyle \sum _{\varphi \left(\mathit{x}\right)\in C_j}}\varphi \left({\mathit{x}}_i\right)\varphi (\mathit{x})+{\displaystyle \frac{1}{{\left|C_j\right|}^2}}{\displaystyle \sum _{\varphi \left({\mathit{x}}_1\right)\in C_j}}{\displaystyle \sum _{\varphi \left({\mathit{x}}_2\right)\in C_j}}\varphi \left({\mathit{x}}_1\right)\varphi \left({\mathit{x}}_2\right)\\ =K\left({\mathit{x}}_i,{\mathit{x}}_i\right)-{\displaystyle \frac{2}{\left|C_j\right|}}{\displaystyle \sum _{\varphi \left(\mathit{x}\right)\in C_j}}K\left({\mathit{x}}_i,\mathit{x}\right)+{\displaystyle \frac{1}{{\left|C_j\right|}^2}}{\displaystyle \sum _{\varphi \left({\mathit{x}}_1\right)\in C_j}}{\displaystyle \sum _{\varphi \left({\mathit{x}}_2\right)\in C_j}}K\left({\mathit{x}}_1,{\mathit{x}}_2\right)\end{array}$$

(4)

From the above derivation process, it can also be seen that, in the clustering process, the distance between samples can be calculated entirely using kernel functions. Commonly used kernel functions include the linear kernel function $K(\mathit{x},\mathit{z})={\mathit{x}}^T\mathit{z}+c$, polynomial kernel function, and Gaussian kernel function $K(\mathit{x},\mathit{z})=\mathit{exp}\left(-\gamma \Vert \mathit{x}-\mathit{z}{\Vert }^2\right)$, where $c$, $a$, and $\gamma$ are the coefficients of the kernel function. Represent the monitoring time series of two measurement points, both of which are one-dimensional vectors.

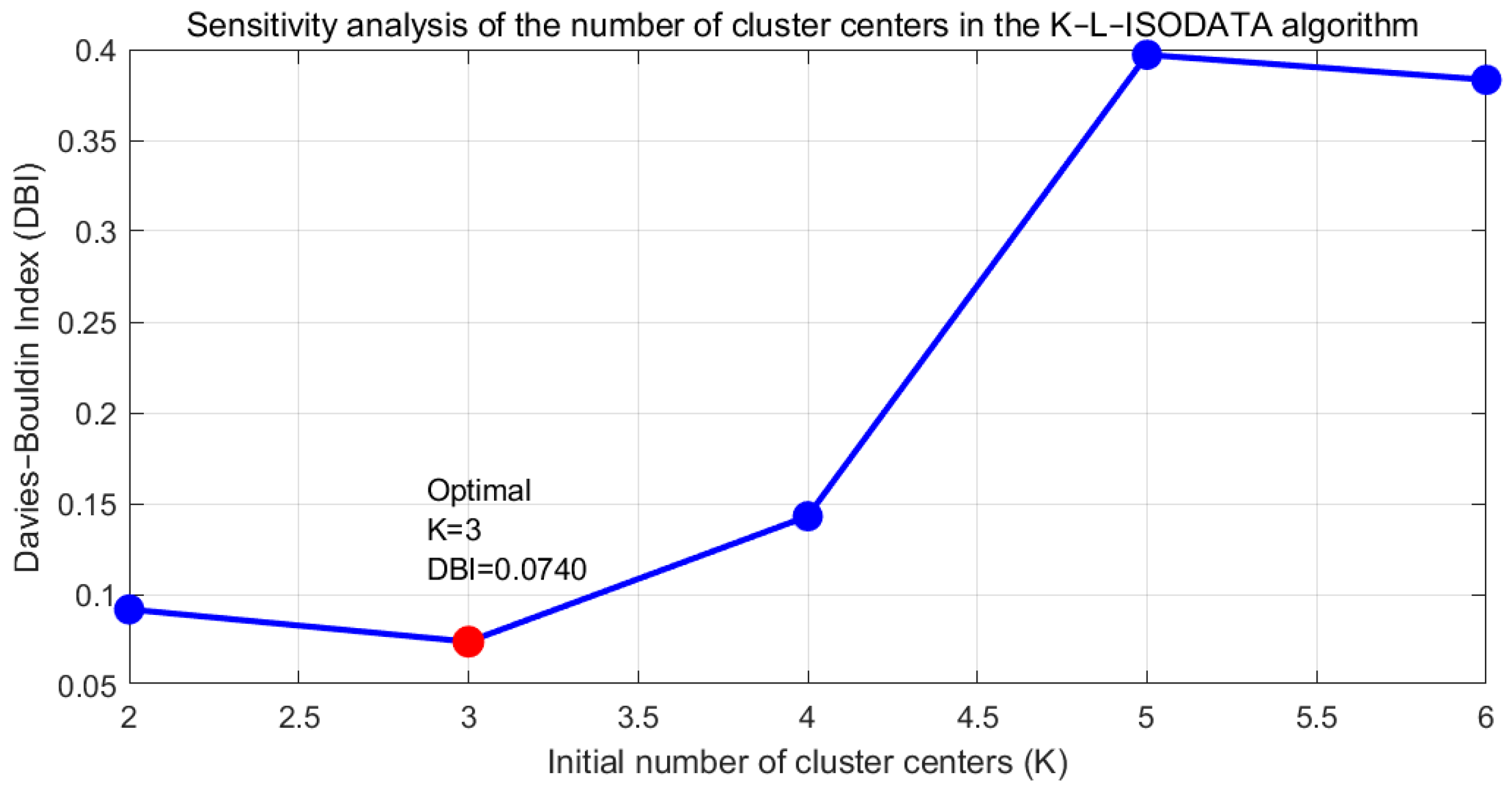
2.3. Sensitivity Analysis of the Initial Cluster Number K in the K–L–ISODATA

To evaluate the robustness of the optimized K–L–ISODATA clustering algorithm, a sensitivity analysis was conducted by varying the initial number of cluster centers K from 2 to 6. For each configuration, the Davies–Bouldin index (DBI) was calculated to assess clustering compactness and separability. As shown in Figure 1, the DBI value first decreases and then increases with increasing K, reaching its minimum of 0.0740 at K = 3. This indicates that dividing the deformation zone into three clusters yields the most compact and well-separated configuration. Therefore, the selection of K = 3 is validated as the optimal setting for the K–L–ISODATA procedure.

3. PPCA-Based Expression and Isolation of Environmental Impacts

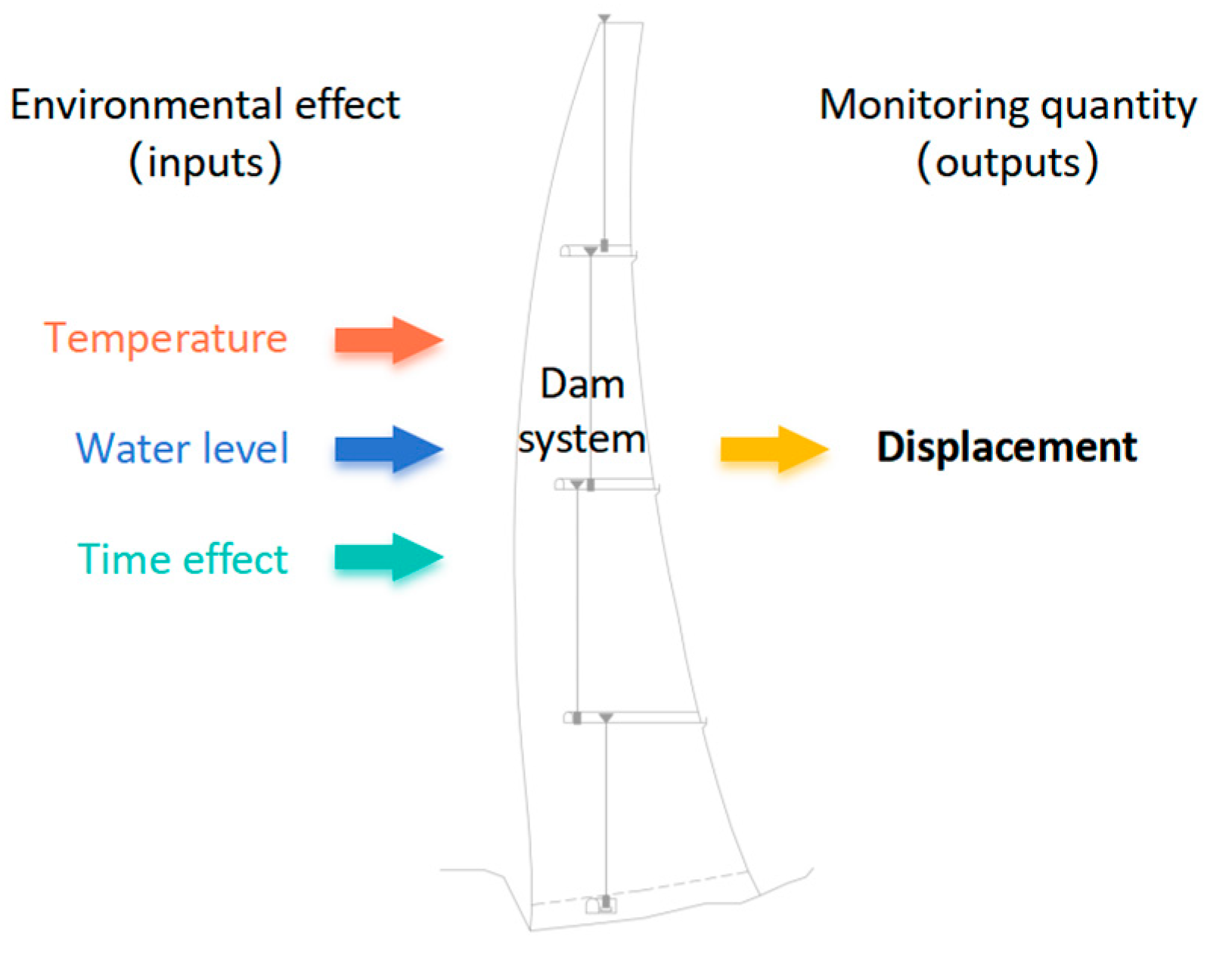
3.1. The Relationship Between Environmental Variables and Dam Effect Quantities

If the dam shown in Figure 2 is regarded as a system, then various environmental variables (such as temperature, water level, etc.) are the inputs of the system, while monitoring values such as displacement, uplift pressure, and seepage flow are the outputs of the system. Assuming $\mathit{X}$ is a random vector formed by the monitoring data of $q$ monitoring points for a certain monitoring project of the dam, generally speaking, the random vector can be represented in the following form:

$$\mathit{X}=\mathit{f}\left(\mathit{v}\right)+\mathit{g}\left(\mathit{\eta }\right)$$

(5)

where $\mathit{f}\left(\mathit{v}\right)$ is the effect generated by environmental variables such as temperature T, reservoir water level H, and time S, and $\mathit{g}\left(\mathit{\eta }\right)$ is the impact of other factors $\mathit{\eta }$ besides environmental variables, including changes in dam structure materials and monitoring noise, on monitoring data.

3.2. PPCA-Based Expression and Separation of the Effects of Environmental Variables in Arch Dams

In the dam safety automation monitoring system, due to instrument damage and other reasons, some measuring points often have small amounts of data missing at different periods, resulting in the inability to synchronize monitoring data from each measuring point. If the traditional PCA method is directly used [34], it is necessary to delete all data with missing dates and extract the PC, which will inevitably result in a loss of a large amount of monitoring information and is not conducive to monitoring and diagnosing the overall performance of the dam [35].

PPCA is based on the correlation relationship between measurement points, and through this correlation relationship, the missing data in the monitoring information are deduced, and the PPC that characterizes the overall state of the dam is extracted, to achieve the purpose of extracting the key information in the multimeasurement point monitoring data [36].

If there are measurement points for a certain effect quantity, and each measurement point contains measurements, then these measurement points form a matrix:

$$\mathit{X}=\left. [\begin{array}{c}{\mathit{X}}_1\\ {\mathit{X}}_2\\ \cdots \\ {\mathit{X}}_i\\ \cdots \\ {\mathit{X}}_q\end{array}\right]=\left. [\begin{array}{cccccc}{x}_{11}& x_{12}& \cdots & x_{1i}& \cdots & x_{1n}\\ x_{21}& x_{22}& \cdots & x_{2i}& \cdots & x_{2n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{i1}& x_{i2}& \cdots & x_{ij}& \cdots & x_{in}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{q1}& x_{q2}& \cdots & x_{qj}& \cdots & x_{qn}\end{array}\right]$$

(6)

In the formula, ${\mathit{X}}_i$ is the row vector, representing the observation data sequence of the $i$ measurement point; $x_{ij}$ represents the $j$ observation value of the measurement point $i$. If there exists an $r$-dimensional $(r<q)$ latent variable $\mathit{Y}={\left. [{\mathit{Y}}_1,{\mathit{Y}}_2,\cdots ,{\mathit{Y}}_{\mathit{i}},\cdots ,{\mathit{Y}}_{\mathit{r}}\right]}^T$, the matrix $\mathit{X}$ can be expressed as:

$$\mathit{X}=\mathit{W}\mathit{Y}+\mathit{\mu }+\epsilon$$

(7)

In the formula, $\mathit{W}$ is a $q\times r$-order matrix, reflecting the correlation between the original variable $\mathit{X}$ and $\mathit{Y}$ the latent variable, $\mathit{\mu }$ is the sample mean vector, $\mathit{\mu }={\left. [u_1,u_2,\cdots ,u_q\right]}^T$, and $u_j$ is the average monitoring data of the $j$ measurement point; $\epsilon$ is the observation noise, following a normal distribution, denoted as $\epsilon ~N\left(0,{\sigma }^2\mathit{I}\right)$, where $\mathit{I}$ is the identity matrix and ${\sigma }^2$ is the variance of the observation noise. According to statistical principles, it can be concluded that:

$$\mathit{X}~N\left(\mathit{\mu },\mathit{W}{\mathit{W}}^T+{\sigma }^2\mathit{I}\right)$$

(8)

If the information of $\mathit{X}$ is complete, $\mathit{W}$ can be directly calculated by performing singular value decomposition on the covariance matrix of $\mathit{X}$, and the corresponding $\mathit{Y}$ is the PC. If the information of $\mathit{X}$ is incomplete, the missing columns should be separated from $\mathit{X}$ first, and the columns with complete information should be combined into a matrix ${\mathit{X}}_{\mathrm{exist} }$. Perform singular value decomposition on it and calculate ${\mathit{W}}_{\mathrm{exist}}$. As $\mathit{X}~\mathit{N}\left(\mathit{\mu },\mathit{W}{\mathit{W}}^T+{\sigma }^2\mathit{I}\right)$, the likelihood function of $\mathit{X}$ can be constructed as follows:

$$\mathit{L}=\mathit{ln}\left\{p\left(\mathit{Y}\mid \mathit{X},\mathit{W},\mathit{\mu },{\sigma }^2\right)\right\}$$

(9)

Construct the error function:

$$\mathit{Err}={‖{\mathit{X}}_{\mathrm{exist} }-{\mathit{W}}_{\mathrm{exist} }\tilde{\mathit{Y}}‖}^2$$

(10)

In the equation, $\tilde{\mathit{Y}}$ is the estimated value of $\mathit{Y}$. Use the maximum expected algorithm to iteratively solve Equation (9), and substitute the estimated values XS and WS of $\mathit{X}$ and $\mathit{W}$ obtained each time into Equation (10). Stop the iteration when Err reaches its minimum value, and the resulting $\tilde{\mathit{X}}$ is the reconstructed sequence; $\tilde{\mathit{Y}}$ stands for PPC, expressed as:

$$\tilde{\mathit{Y}}={\left({\tilde{\mathit{W}}}^T\tilde{\mathit{W}}\right)}^{-1}{\tilde{\mathit{W}}}^T\tilde{\mathit{X}}$$

(11)

The above equation can be written as:

$$\tilde{\mathit{Y}}=\left. [\begin{array}{c}{\tilde{\mathit{Y}}}_1\\ {\tilde{\mathit{Y}}}_2\\ \cdots \\ {\tilde{\mathit{Y}}}_i\\ \cdots \\ {\tilde{\mathit{Y}}}_r\end{array}\right]=\left. [\begin{array}{cccccc}{k}_{11}& k_{12}& \cdots & k_{1j}& \cdots & k_{1q}\\ k_{21}& k_{22}& \cdots & k_{2j}& \cdots & k_{2q}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{i1}& k_{i2}& \cdots & k_{ij}& \cdots & k_{iq}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{r,1}& k_{r,2}& \cdots & k_{r,j}& \cdots & k_{r,q}\end{array}\right]\left. [\begin{array}{c}{\tilde{\mathit{X}}}_1\\ {\tilde{\mathit{X}}}_2\\ \cdots \\ {\tilde{\mathit{X}}}_i\\ \cdots \\ {\tilde{\mathit{X}}}_q\end{array}\right]$$

(12)

In the formula, $k_{ij}$ is the coefficient of the original variable $j$ in the PPC $j$. The larger the absolute value of $k_{ij}$, the higher the correlation between ${\mathit{Y}}_i$ and ${\mathit{X}}_j$, and the more ${\mathit{X}}_j$ can be explained by ${\mathit{Y}}_i$. When $k_{ij}$ is positive, ${\mathit{Y}}_i$ is positively correlated with ${\mathit{X}}_j$, otherwise it is negatively correlated.

When the number of original variables is $q$, a maximum of $q-1$ PPCs can be reconstructed, but the explanatory power of these $q-1$ PPCs on the original variables varies. The contribution of environmental variables to the displacement of arch dams is much greater than the influence of other factors. Therefore, it is necessary to extract $z$ PPCs from $q-1$ that best describe the impact of environmental variables on arch dam displacement. Reasonably determining the value of $z$ is crucial, as it directly determines the separation of the impact of environmental variables $\mathit{f}\left(\mathit{v}\right)$ and the impact of noise $g\left(\mathit{\eta }\right)$. At present, there are mainly the following methods [15]:

(1)

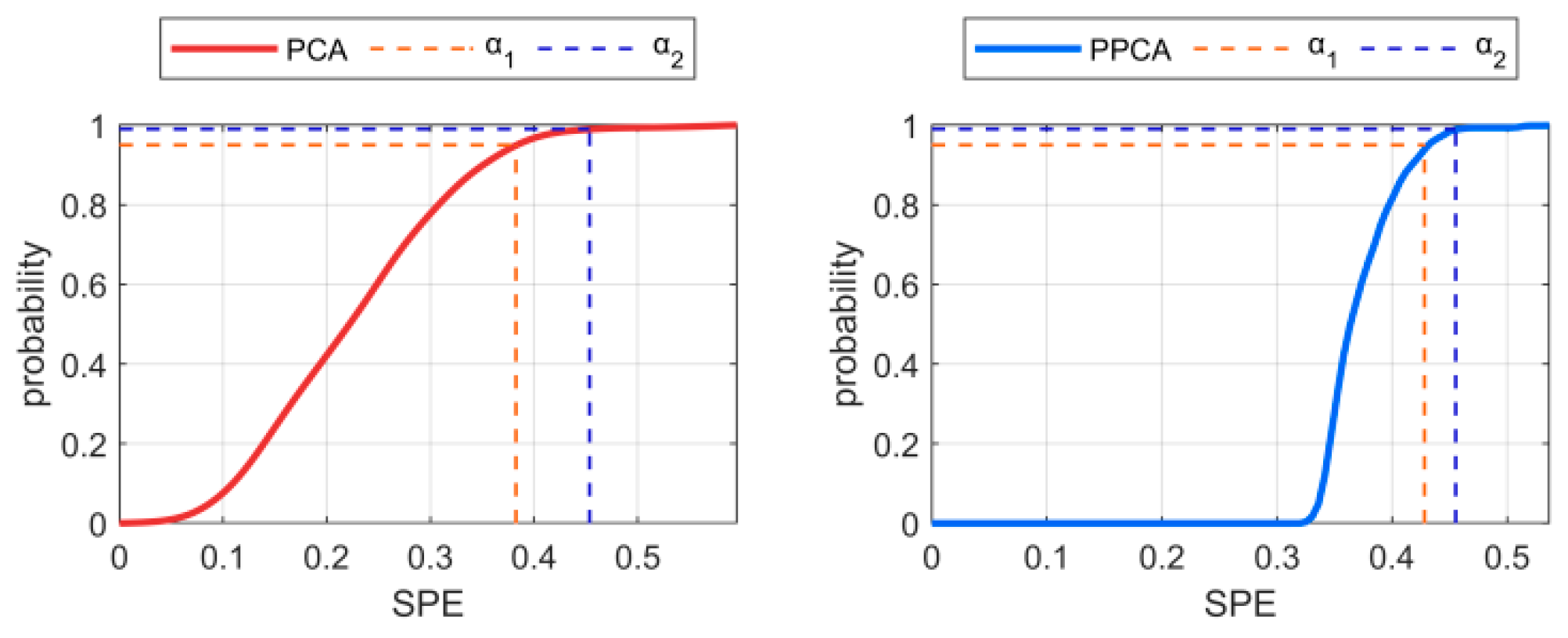
Sort all feature values in descending order and plot them on the x-axis and y-axis with numbers. The number of the feature value corresponding to the location of the mutation point in the graph is the value of z. This method is mainly based on the understanding that the effects of noise and environmental variables are fundamentally different, and sudden changes occur in the eigenvalue spectrum;

(2)

Calculate the cumulative contribution of each PPC by arranging all eigenvalues in descending order.

$$\eta \left(z\right)=\sum _{i=1}^z{\beta }_i/\sum _{i=1}^{q-1}{\beta }_i\times 100\%, \left({\beta }_1>{\beta }_2>\cdots >{\beta }_i>\cdots >{\beta }_{q-1}\right)$$

(13)

where ${\beta }_i$ is eigenvalues of the covariance matrix $\tilde{\mathit{X}}$.

The specified limit value is $e=0.95$. When $\eta \left(z\right)<e$ and e ≥ 0.95, the corresponding $z$ is obtained. The premise of this method is to assume that factors other than environmental variables have little impact on monitoring data under normal circumstances [37].

The impact of noise and other factors $\mathit{\epsilon }$ can be obtained by removing the influence of environmental variables from the monitoring data:

$$\mathit{\epsilon }=\mathit{x}-\mathit{f}\left(\mathit{v}\right)$$

(14)

The above analyses are mostly conducted on reference data from normal dam operation, and to fully reflect the influence of each environmental variable on the dam effect, the range of variation of the environmental quantities corresponding to the selected data should be as large as possible. In order to reflect the time-varying pattern of the dam, the reference data should be updated periodically by removing older data and adding new observations to the reference data series.

4. Knowledge-Driven Knowledge-Based Monitoring of Deformation Properties of Arch Dams

The proposed knowledge-driven monitoring framework integrates four complementary techniques to ensure both accuracy and interpretability in arch dam deformation analysis. Specifically, the optimized ISODATA is used to identify deformation zones with similar mechanical behavior, while PPCA separates environmental influences such as temperature and reservoir level from the intrinsic structural responses within each zone. The SPE control chart establishes quantitative thresholds for early warning identification, and the contribution chart locates the monitoring points responsible for abnormal variations. The combination of these techniques forms a complete workflow—from deformation zoning and environmental effect separation to abnormality detection and diagnosis—enhancing the precision and reliability of dam safety evaluation.

Following this conceptual framework, the main technical steps and procedures are described in detail below.

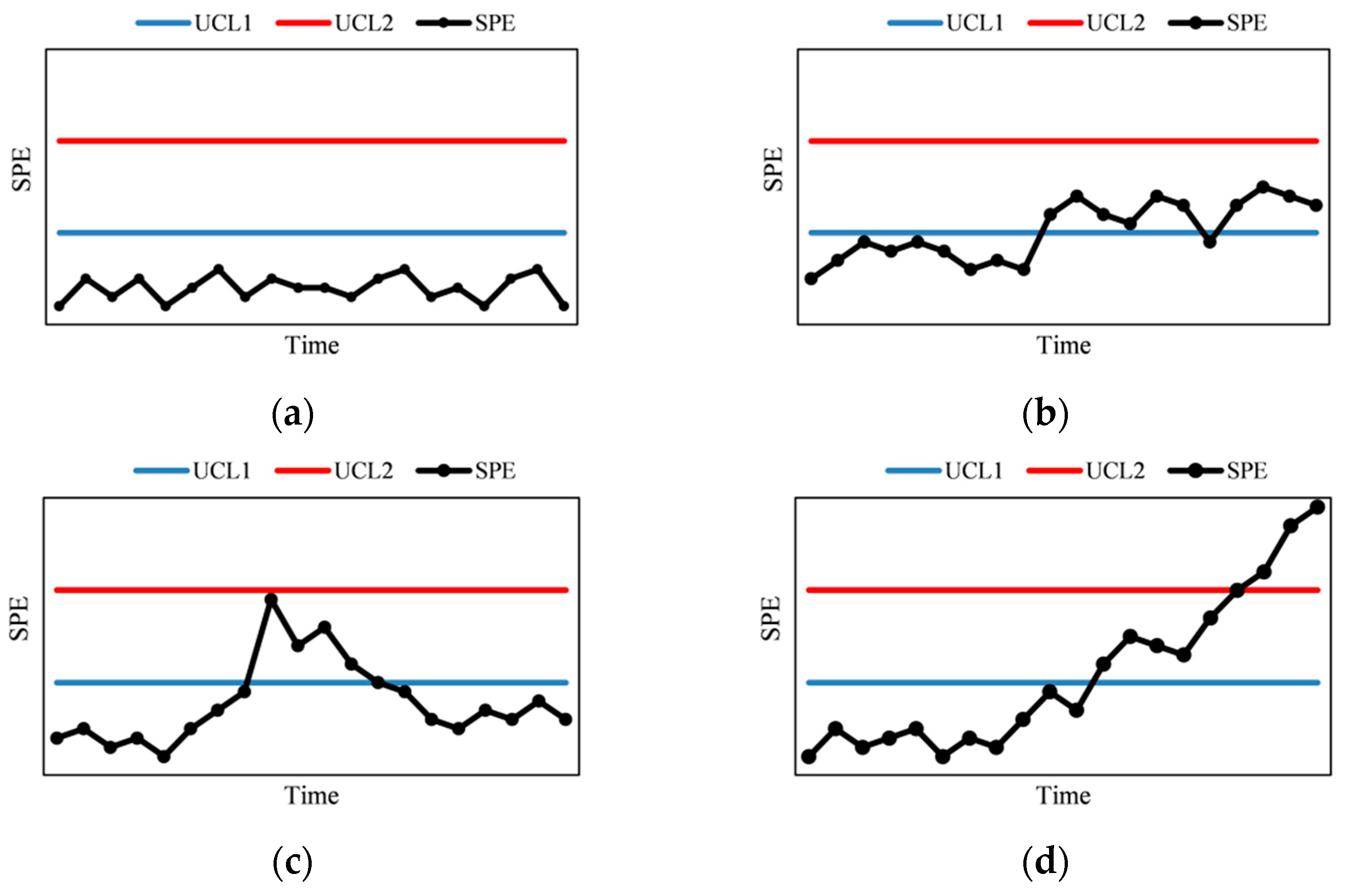
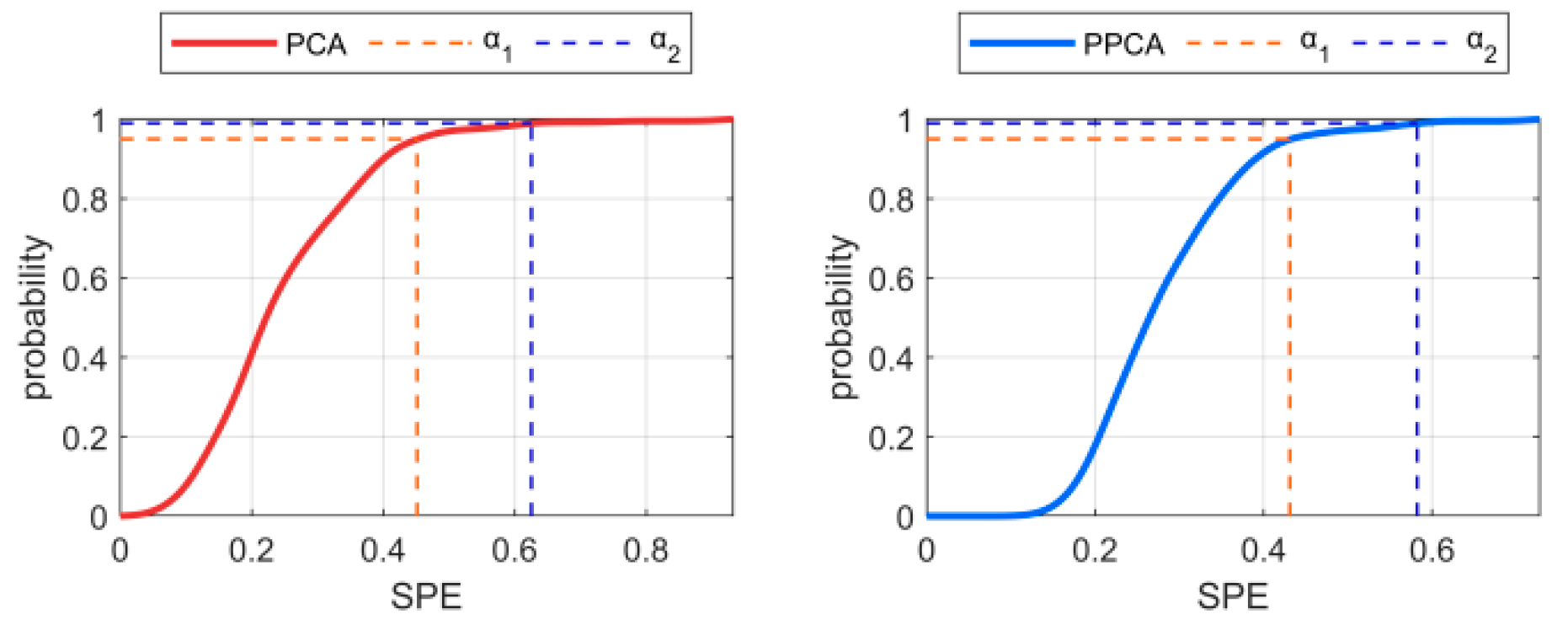
4.1. Using KDE to Determine the Form of Distribution and Control Limits of the SPE

Assuming that the effects are caused by the environmental variables $\tilde{\mathit{x}}=\mathit{f}\left(\mathit{v}\right)$, define the squared prediction error ($\mathrm{S}\mathrm{P}\mathrm{E}$) parameters.

$$\mathrm{S}\mathrm{P}\mathrm{E}={‖\mathit{x}-\tilde{\mathit{x}}‖}^2$$

(15)

For any observed value at any time, a norm can be calculated according to the above formula to quantitatively reflect the magnitude of the influence of factors other than environmental variables. Under normal operation of the dam, the $\mathrm{S}\mathrm{P}\mathrm{E}$ norm should be within the control limit range. However, when there are abnormalities in the dam structure or malfunctions in the monitoring instruments, factors other than environmental variables will significantly increase the impact on the monitoring data, and the $\mathrm{S}\mathrm{P}\mathrm{E}$ norm of the measured data will exceed the control limit.

The distribution form of $\mathrm{S}\mathrm{P}\mathrm{E}$ is directly related to the calculation of control limits for its monitoring and control. Generally, it can be assumed that $\mathrm{S}\mathrm{P}\mathrm{E}$ follows a normal distribution, and the corresponding control limits can be calculated using a normal distribution function. A more accurate method is to use the KDE method proposed by Martin and Morris to calculate the distribution form of $\mathrm{S}\mathrm{P}\mathrm{E}$. The KDE method uses a kernel function K (usually a Gaussian function) to fit the distribution function of the data. The distribution function of a one-dimensional random variable can be estimated using Equation (16):

$$\tilde{f}\left(x\right)={\displaystyle \frac{1}{nh}}\sum _{i=1}^{n}K\left({\displaystyle \frac{x-X_i}{h}}\right)$$

(16)

where $n$ is the number of samples; $h$ is the time window width, also known as the smoothness parameter or bandwidth; $K$ is the kernel function; $X_i$ is the $i$ monitoring data.

After estimating the probability density function of $\mathrm{S}\mathrm{P}\mathrm{E}$ using Equation (16), the corresponding control limit can be calculated. Following the method of formulating control limits based on normal distribution, the second-level control limits UCL1 and UCL2 are formulated based on the percentile values corresponding to probabilities ${\alpha }_1$ and ${\alpha }_2$ in the probability density function of $\mathrm{S}\mathrm{P}\mathrm{E}$. Generally, ${\alpha }_1=0.95$ and ${\alpha }_2=0.99$ are set [38].

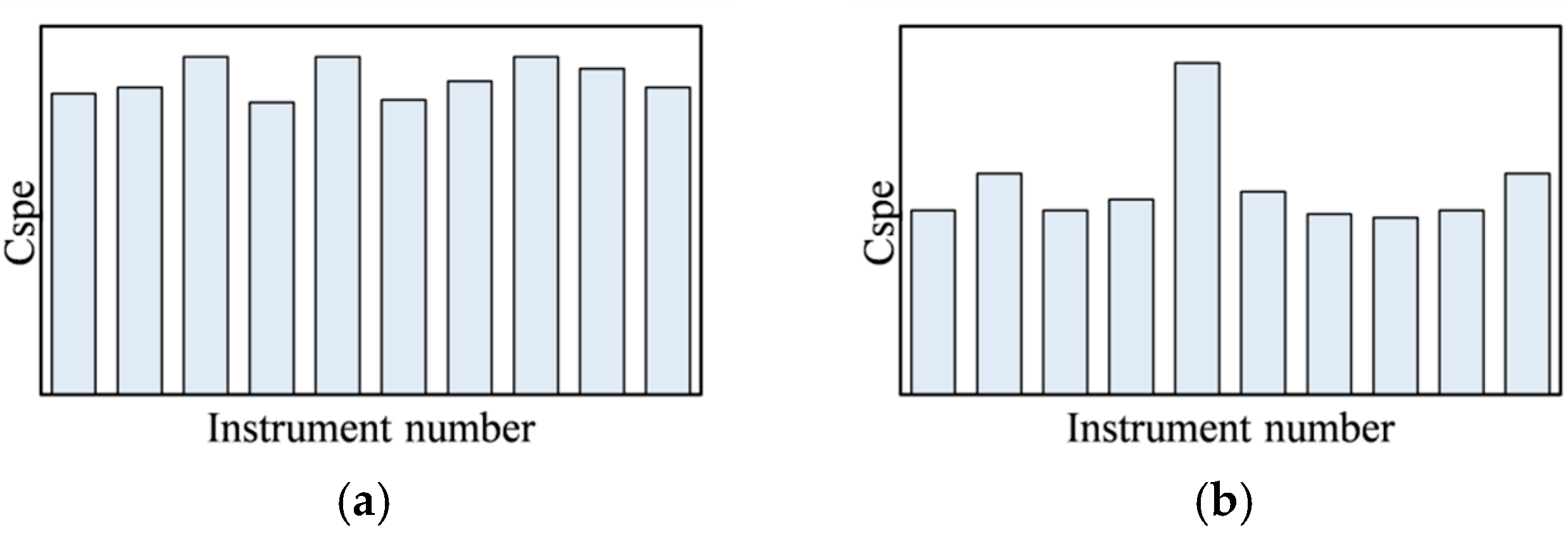
4.2. Anomaly Diagnosis Using Contribution Maps

When monitoring data are abnormal, in addition to timely alarms, it is important to locate the abnormal measurement points to diagnose the abnormality, detect potential dam safety hazards, and analyze the cause of the data abnormality promptly. This can be achieved through the contribution diagram of the multivariate statistical process to realize this process. Rephrase $\mathrm{S}\mathrm{P}\mathrm{E}$ in the following form:

$$\mathrm{S}\mathrm{P}\mathrm{E}={‖\mathit{x}-\tilde{\mathit{x}}‖}^2=\sum _{i=1}^M(x_i-{\tilde{x}}_i{)}^2=\sum _{i=1}^{M}Csp{e}_i$$

(17)

where $Csp{e}_i=(x_i-{\tilde{x}}_i)$ represents the contribution of the measurement point $i$ to $\mathrm{S}\mathrm{P}\mathrm{E}$.

For monitoring data at different times, a series of $Cspe$ can be obtained by substituting them, and the spatial and temporal distribution of $Cspe$ indicates the distribution of different measurement points at different times.

4.3. Knowledge-Driven Arch Dam Deformation Safety Warning and Outlier Causation Diagnosis

By summarizing the deformation monitoring data of verticals, levels, inclinometers, and control charts of multiple arch dams such as Laxiwa, Longyangxia, Lijiahe, Lijiaxia, Liuxihe, Jinshuitan, and Xiangshui, as well as the qualitative analysis results of the SPE control chart, four typical cases of the control chart are shown in Figure 3. Among them, the control charts corresponding to situation (c) and situation (d) both have alarms, but situation (c) shows a V-shaped curve after briefly exceeding UCL2 and then decreases to the normal range, while situation (d) shows a trend of growth in the control chart.

The contribution graph at a certain moment is shown in Figure 4. There are two basic patterns for contribution maps. In pattern I, the distribution of components corresponding to each measurement point is relatively uniform, while in pattern II, the components of individual measurement points are significantly higher than those of other measurement points, with obvious peaks.

By combining the four scenarios of the control chart of the observation data with the two modes of the contribution chart, the following six combinations can be obtained:

(1)

The control chart is in mode (a), indicating normal monitoring data.

(2)

The control chart is model (b), and the monitoring data are normal.

(3)

The control chart is for mode (c), the contribution chart is for mode I, and the monitoring data is anomalous for a short period, possibly due to extreme environmental quantities.

(4)

The control chart is for mode (c), and the contribution chart is for mode II, which may be the result of a malfunction of an individual instrument that returns to normal.

(5)

The control chart is for mode (d), and the contribution chart is for mode I. The monitoring data is abnormal and shows a trend of growth. If there are no extreme environmental variables, it may be due to significant temporal changes in the dam structure, which should be noted.

(6)

The control chart is for mode (d), and the contribution chart for mode II has shown a trend of growth, and monitoring data anomalies may be caused by individual instrument failures.

When it is possible to eliminate data errors caused by human factors, qualitative inference of the monitoring project’s condition can be made based on the combination of control chart and contribution chart of the measured data.

Based on the qualitative analysis and experience summary above, the “knowledge” formed can be used to classify and analyze the squared prediction error norm of the impact of environmental variables on the separation of different partitions of the arch dam to evaluate the current safety status of the arch.

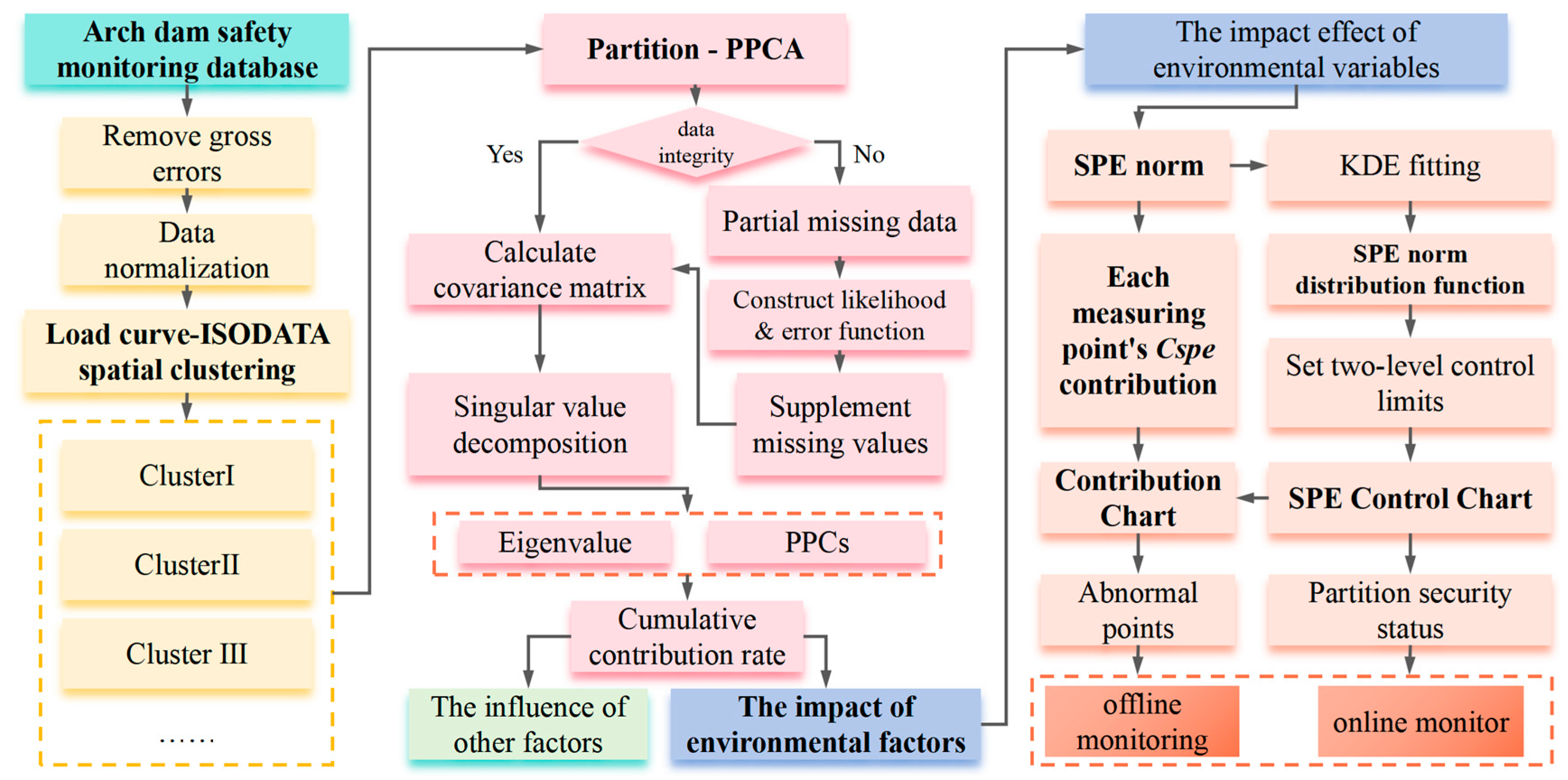
5. A Method for Deformation Safety Warning and Anomaly Diagnosis of Arch Dams Based on the Separation of Environmental Variable Effects and Knowledge-Driven Approach

The proposed deformation safety early warning and anomaly diagnosis framework for arch dams integrates four major components: (1) optimized ISODATA clustering for deformation partitioning, (2) PPCA-based environmental effect separation, (3) SPE control chart construction for anomaly identification, and (4) contribution chart analysis for fault localization. These components are sequentially combined to form a systematic and interpretable workflow that effectively separates environmental influences, identifies abnormal behavior, and provides early warnings for dam operation management. Compared with conventional empirical or purely statistical models, the proposed method enhances interpretability, adaptability, and engineering applicability in real-world dam safety monitoring.

The flow of arch dam deformation safety monitoring modeling Is shown In Figure 5. The method proposed in this paper is mainly divided into the following steps.

(1)

Data acquisition: Extract all the monitoring data of the deformation monitoring program from the arch dam safety monitoring database.

(2)

Coarse error removal and data normalization: Remove erroneous extreme value points, count the dates of all monitoring data for all measurement points, organize the monitoring data for each measurement point on this basis, and replace them with null values if they are missing.

(3)

Spatial clustering: Optimized ISODATA clustering was used to classify measurement points into multiple categories, which in turn classified the dam into multiple regions.

(4)

Partition PPCA: The maximum expectation algorithm was used to reconstruct the missing sequences, and the PPCA was used to calculate the PPCs of multiple measurement points in each partition.

(5)

Separation of influence of environmental quantity and noise: According to the inflection point or cumulative contribution rate of eigenvalue sequence, z PPCs that can best describe the influence of environmental variables on arch dam displacement are obtained. The residual component is noise impact or abnormal monitoring.

(6)

Offline monitoring: Use reference data to calculate the $\mathrm{SPE}$ norm, and use the KDE estimated $\mathrm{SPE}$ probability density function to calculate diagnostic criteria for monitoring quantity.

(7)

Online monitoring: Standardize new monitoring data using the mean and variance of reference data, calculate the corresponding $\mathrm{SPE}$ norm of the data, and compare it with diagnostic criteria.

(8)

Outlier location: If the $\mathrm{SPE}$ norm of the measured data exceeds the control limit, a contribution graph is used to locate the outlier and analyze the cause of the anomaly.

6. Engineering Examples

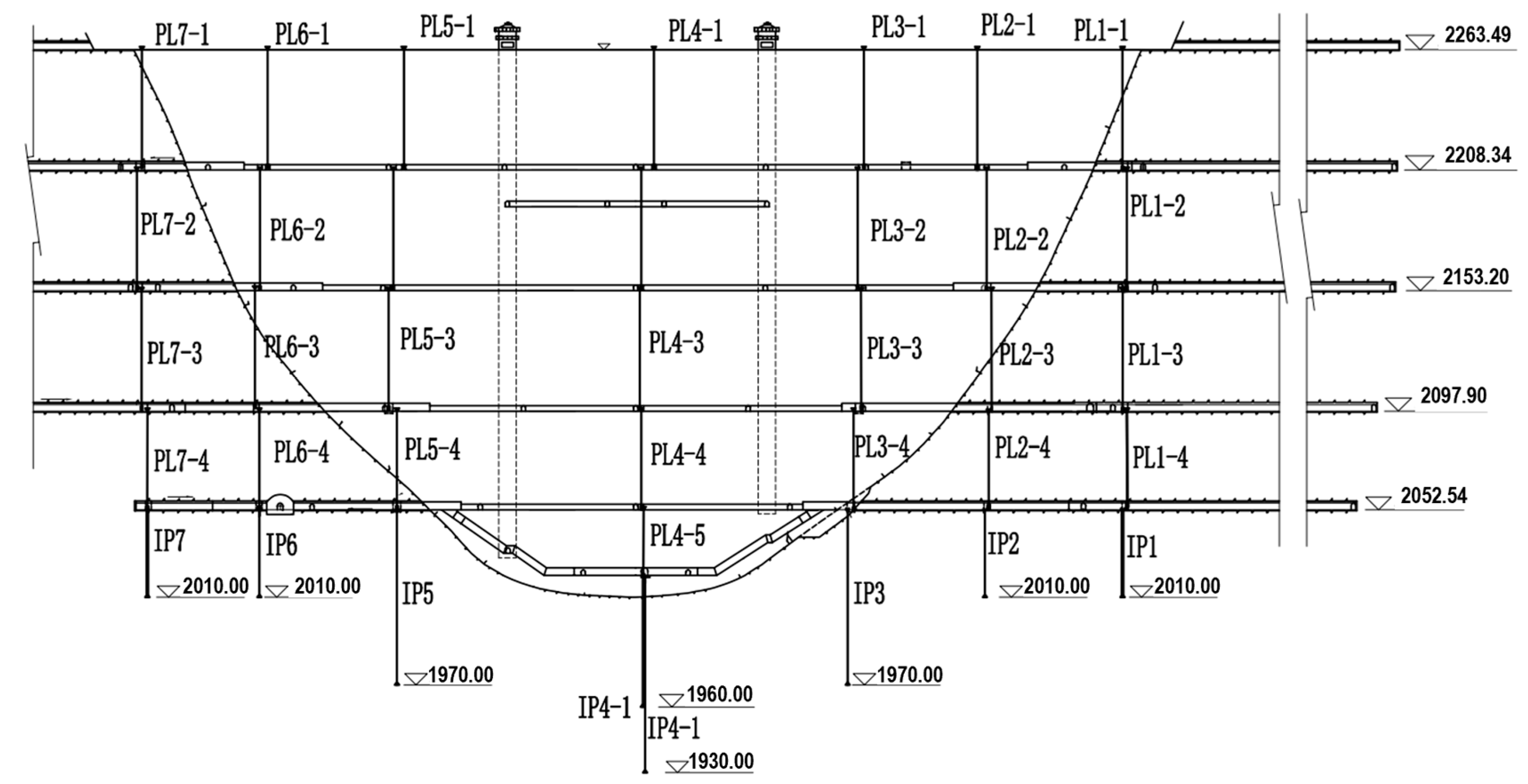
6.1. Project Overview

A hydroelectric power station water-retaining building for a double curved thin arch dam has a base surface elevation of 2010.0 m and the crest elevation of the dam is 2260.0 m. The arch dam vertical line monitoring data are used to verify the arch dam deformation safety monitoring model proposed in this paper. The layout of the vertical monitoring system is shown in Figure 6.

The water level and the ambient temperature in the reservoir area are shown in Figure 7, and it can be seen from Figure 8 that the upstream water level of the arch dam was maintained at a high level in 2011 and then increased gradually from 2011 to 2013, but the increase was small, and it stabilized after 2013. The ambient temperature in the reservoir area fluctuates seasonally from −10~30 °C.

The distribution of radial displacement of the dam body on typical low-temperature and high-temperature days is shown in Figure 8. From Figure 8, it can be seen that the radial displacement of the base and shoulder of the arch dam is small, and the radial displacement of the crown and top of the dam is large, and the displacement on the left bank is slightly smaller than that on the right bank but left–right symmetric.

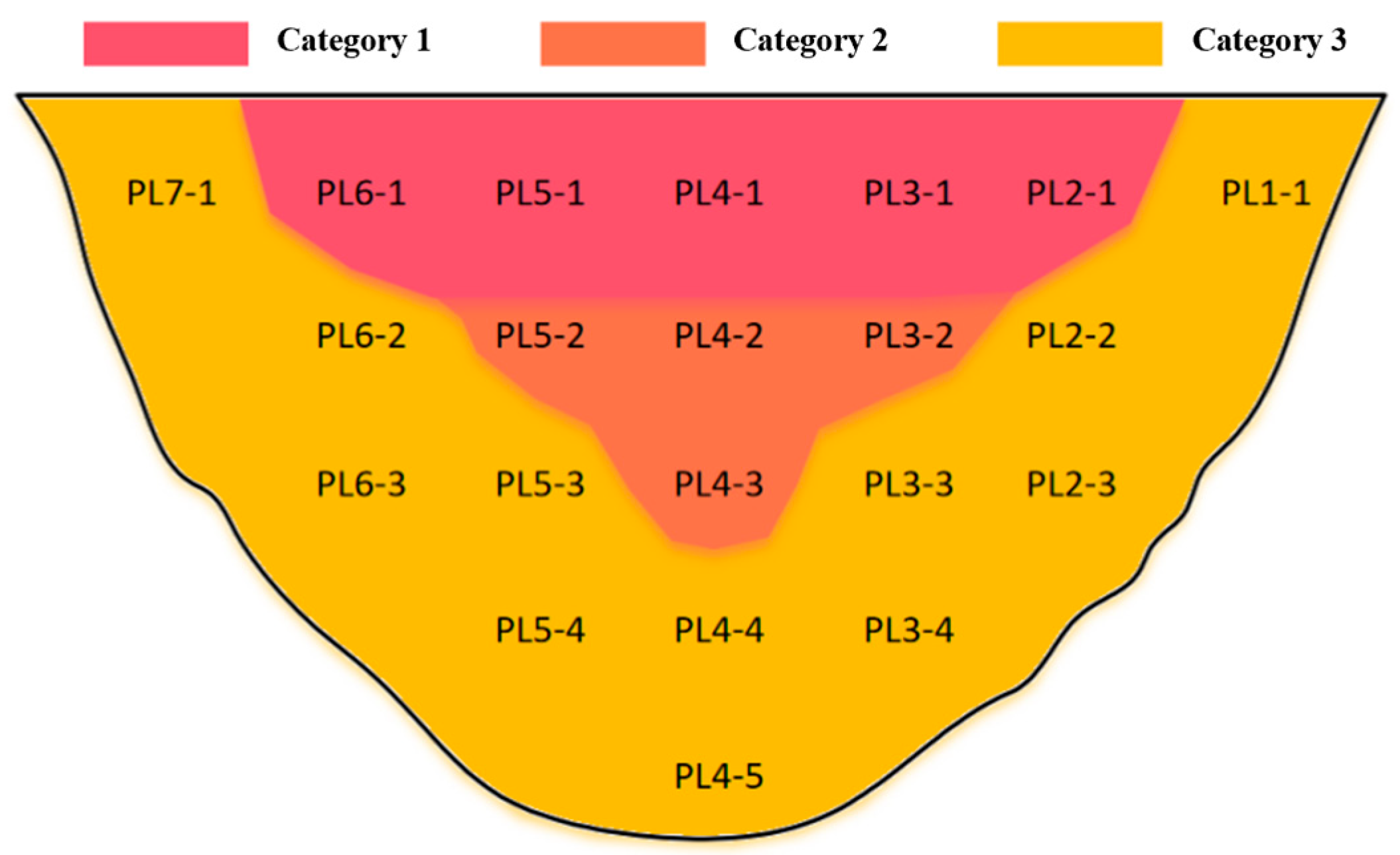
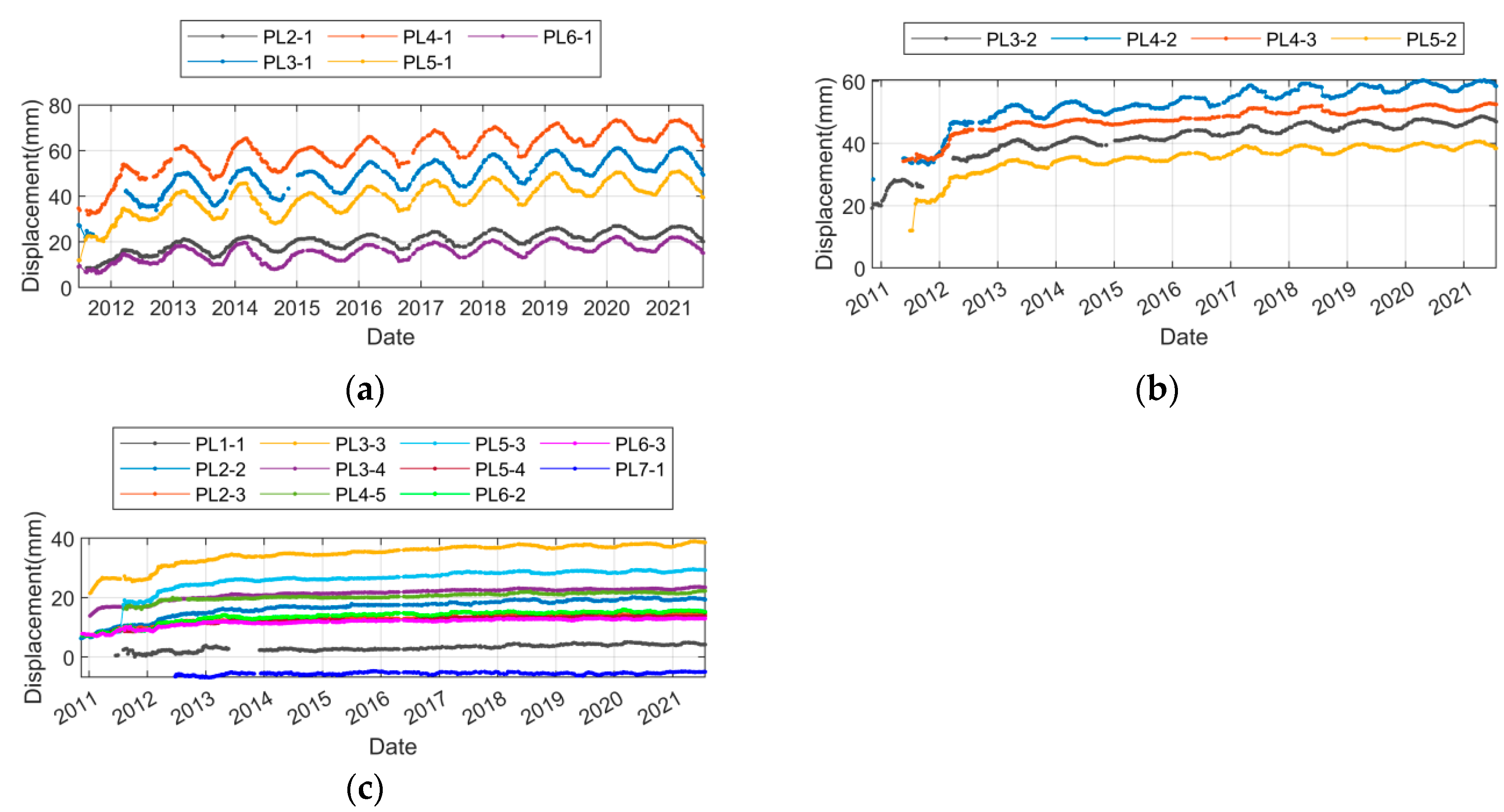
6.2. Spatial Clustering of Deformation Monitoring Points of a Concrete Arch Dam

Although the number of categories $K$ varies during the ISODATA clustering process, an initial expected number of clusters still needs to be given before use. Once given, the subsequent number of clusters can only vary within the range of $[0.5K,2K]$. Referring to relevant papers, if the initial number of categories $K=4$ the subsequent number of clusters can vary between [2, 8], fully meeting the requirements of spatial clustering analysis of arch dam deformation measurement points. Using the Gaussian kernel function to calculate the distance between samples, the radial displacement measurement points of the arch dam vertical system are finally divided into three categories, that is, the dam body is divided into three regions, as shown in Figure 9. The radial displacement process lines of the three types of measuring points are shown in Figure 10.

From Figure 9 and Figure 10, it can be seen that the measurement points within each partition exhibit a high correlation in time and space. If the first type of measuring point is located in the middle of the arch dam crest, it is greatly affected by temperature, and it shows an increasing trend with the rise of water level. At the same time, it generates significant periodic displacement with temperature fluctuations every year. The second type of measuring point is located in the middle of the arch dam, and its displacement is still affected by temperature fluctuations. Compared with the first type of measuring point, the monitoring sequence is longer, and the displacement changes significantly during the period of water level rise. The third type of measuring point is close to the dam foundation and is less affected by temperature, with a slight increase as the water level rises.

The clustering results show that the monitoring points on the dam surface can be divided into several zones with distinct deformation characteristics. Points located near the arch crown exhibit relatively large fluctuation ranges due to higher flexibility and temperature sensitivity, while those near the arch foot and abutments show smaller deformation amplitudes as a result of stronger foundation constraints. This spatial distribution pattern reflects the mechanical heterogeneity of the arch dam structure. The optimized ISODATA effectively captures these spatial differences, ensuring that points with similar deformation responses are grouped together. Such partitioning provides a more accurate basis for subsequent environmental effect separation and safety evaluation.

It should be noted that a small portion of the monitoring data was missing for some measurement points due to short-term sensor malfunction and maintenance during reservoir regulation periods. To minimize the impact of missing data, the probabilistic principal component analysis (PPCA) method was applied to reconstruct incomplete sequences based on inter-point correlations before clustering. As a result, the optimized ISODATA could still accurately identify zones with consistent deformation behavior, and the data loss had negligible effect on the spatial clustering outcomes.

6.3. Partitioned Principal Component Analysis

For a hydroelectric power station water-retaining building for a double curved thin arch dam, the maximum height of the dam is 250 m, the base surface elevation is 2210.0 m, and the crest elevation of the dam is 2460.0 m. The arch dam vertical line monitoring data are used to verify the arch dam deformation safety monitoring model proposed in this paper. The layout of the vertical monitoring system is shown in Figure 6.

PCA and PPCA were used to extract the PCs and PPCs of all the measured values of the public data of all the measuring points in each sub-district, respectively, and the cumulative contribution of the first two PCs or PPCs to the overall information was obtained as shown in

Table 1. Cumulative contribution of the top 2 PCs or PPCs to the overall information for each sub-district.

Number of PCs	Partition 1		Partition 2		Partition 3		All Measurement Points
	PPC	PC	PPC	PC	PPC	PC	PPC	PC
1	0.9645	0.9508	0.9955	0.9872	0.9861	0.9839	0.9463	0.9276
2	0.9869	0.9706	0.9983	0.9942	0.9954	0.9956	0.9897	0.9898

.

According to Table 1, the first PC or PPC of the three partitions can represent over 95% of the information from all measurement points in that partition. The first two PCs or PPCs can represent over 97% of the information from all measurement points in the partition. Therefore, using the first PC or PPC can meet the requirement of $\eta \left(1\right)$ ≥ 95%.

According to the theory in Section 3, PC₁ or PPC₁ can be further regarded as the effects of environmental variables such as temperature T, reservoir water level H, and aging, while the components after PC₂ or PPC₂ can be regarded as the impact of changes in dam structural materials and monitoring noise on monitoring data, which is a manifestation of non-linear changes or anomalies in dam safety status.

Meanwhile, as shown in Table 1, the cumulative contribution rate of PPC₁ to the overall information is higher than that of PC₁ in all three partitions. And except for the third type of measurement point PPC₂, whose cumulative contribution rate is slightly lower than PC₂, the cumulative contribution rate of PPC₂ at the first and second type of measurement points is also significantly higher than PC₂. This indicates that PPCA has a significant effect on expressing and reducing the overall information of multiple measurement points.

The cumulative contribution rates of PPC₁ and PC₁ at all measurement points are all below 0.95, significantly lower than those in each partition. The cumulative contribution rates of PPC₂ and PC₂ are only slightly higher than that of partition 1. Compared to the principal components calculated by partitioning, the displacement patterns of all measurement points are more complex and difficult to characterize with fewer PCs or PPCs.

6.4. Offline Analysis

6.4.1. Partitioned Offline Analysis

The dam was damaged by the downstream insulation board in July 2013, and the management unit completed the repair work in December 2014, which lasted 18 months. During the loss of the insulation board, the downstream surface of the dam body was exposed to the air for a long time, resulting in a significant increase in the periodic displacement affected by temperature. The impact range is part of the left bank of the dam crest, including PL2-1, PL3-1, PL4-1, and PL5-1 measuring points in Figure 7, which belong to partition 1. Therefore, in this section, the monitoring data of the five measuring points in partition 1 during the loss of the insulation board are taken as the pathological offline data to be diagnosed, and the remaining data are taken as the reference data for offline monitoring verification.

To observe the abnormal displacement caused by the damage of the insulation board, set the initial value of five measuring points in partition 1 to 0 and redraw the process line as shown in Figure 11. Refer to Figure 12 for the reference data and PC and probability principal component (PPC) de-meaned process lines of five measuring points in partition 1. Refer to Figure 13 for SPE distribution and control limits drawn based on the reference data. Refer to

Table 2. Secondary control limits.

UCL	PCA	PPCA
$\mathrm{UCL}1 (\alpha =0.95$)	0.4517	0.4311
$\mathrm{UCL}2 (\alpha =0.99$)	0.6255	0.5822

for the secondary control limit index values.

It can be seen from the above figures and tables that:

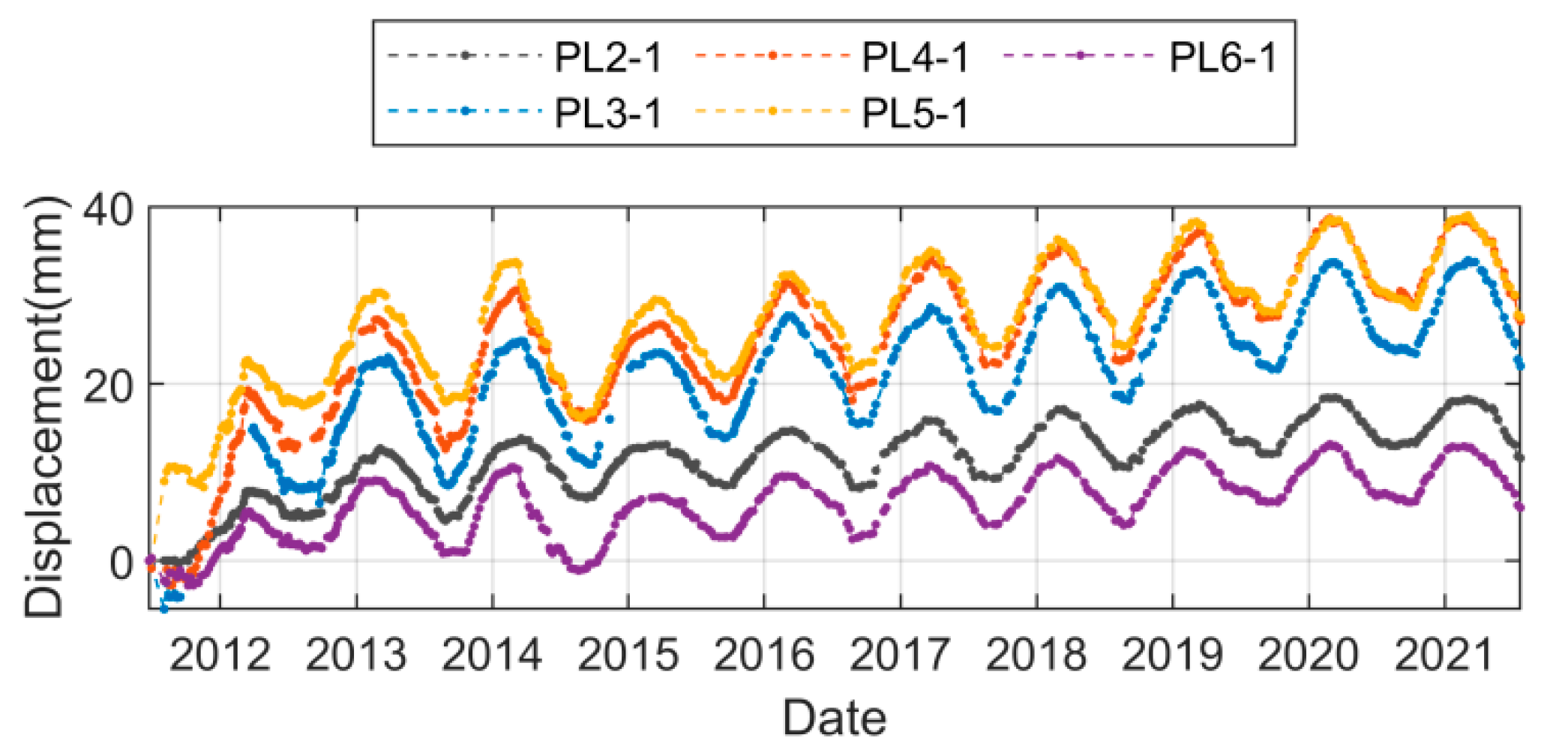
(1)

Affected by the lack of insulation board on the downstream surface, the seasonal variation amplitude of the five measuring points in partition 1 increased significantly from July 2013 to December 2014. Among them, PL2-1, PL3-1, PL4-1, and PL5-1 are also accompanied by an obvious growth trend, while PL6-1 is stable, and only the phenomenon of seasonal displacement increases. After the insulation board was repaired in 2015, the seasonal displacement of each measuring point decreased significantly.

(2)

Due to the lack of monitoring data for about 4 months at the PL3-1 measuring point during the water level rise in 2012, when using the traditional PCA method to extract the main city, only the measured values at the corresponding time of the other four measuring points can be deleted, resulting in a large number of missing monitoring information. The PPCA method can extract the PPCs of multiple measurement points with partial missing data, and well retain the monitoring information during water level rise.

(3)

The SPE distribution of reference data extracted by the PPCA method is more concentrated, and its control limits UCL1 and UCL2 are slightly smaller than the results of the PCA method.

The SPE control chart of the offline data to be diagnosed is shown in Figure 14. Because the offline data to be diagnosed has a long period, only the SPE contribution hydrograph of each measuring point is drawn in Figure 15.

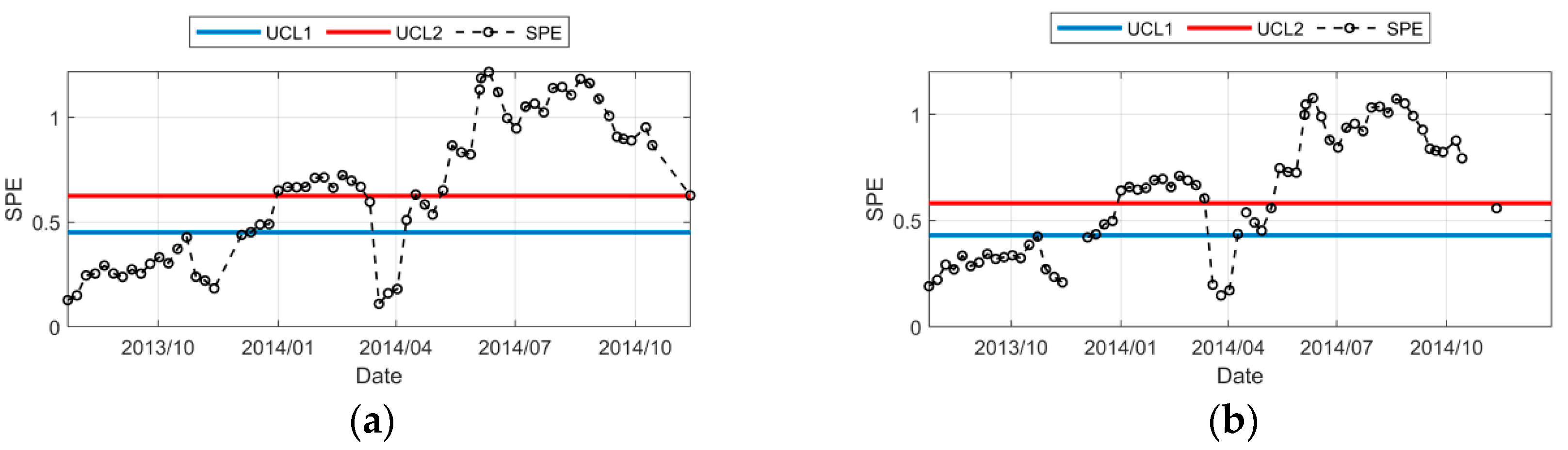
(1)

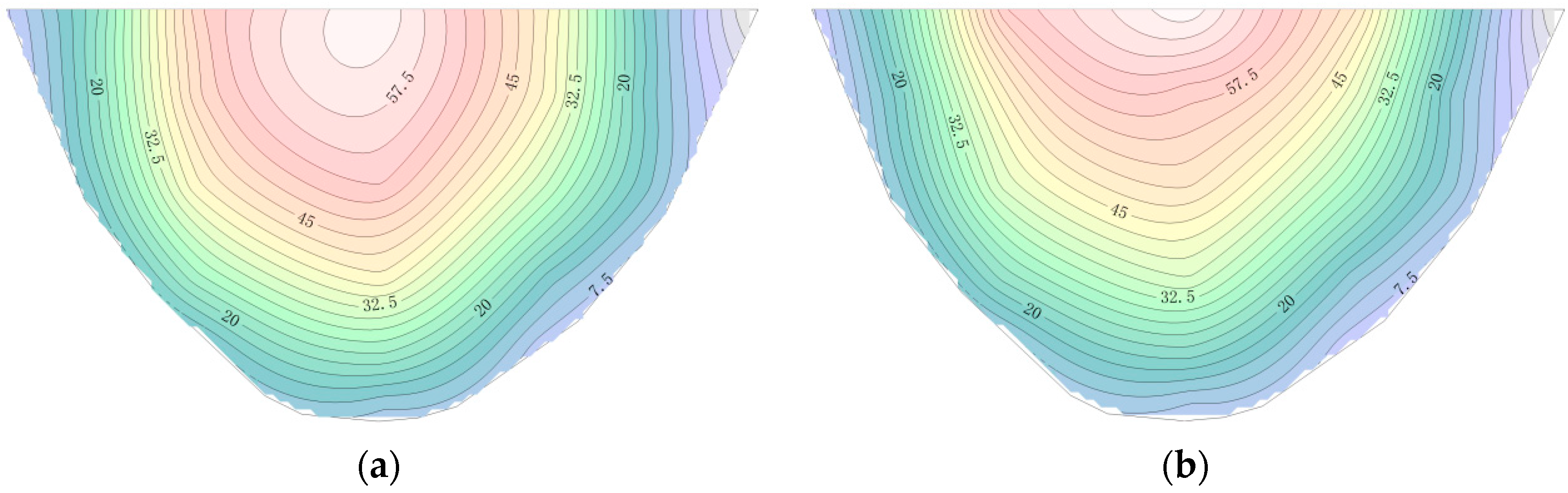
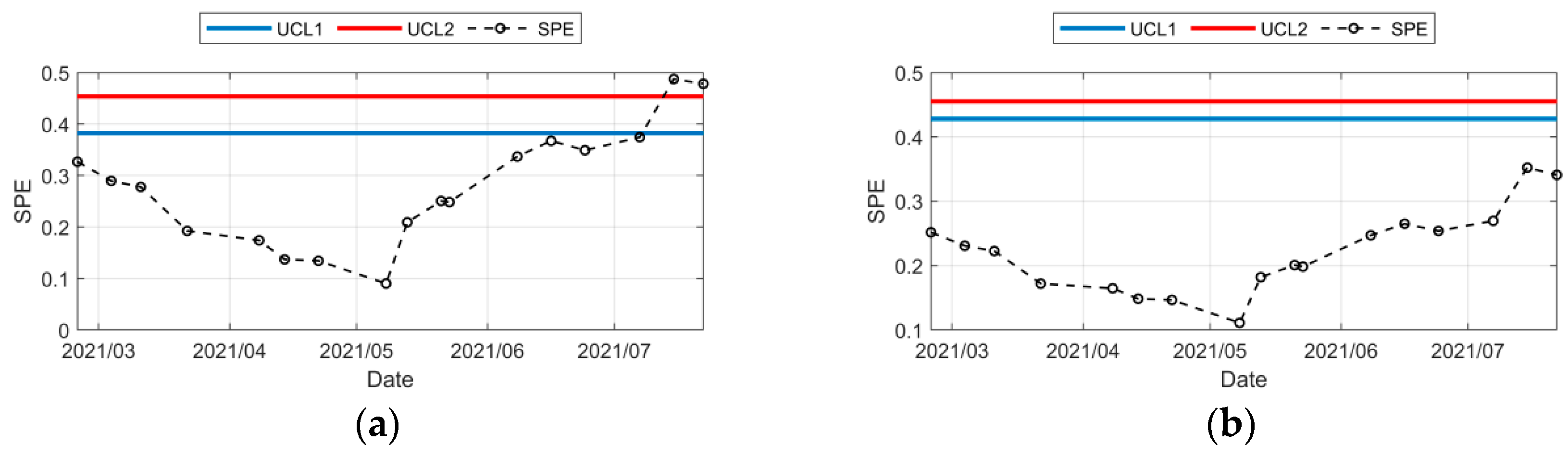
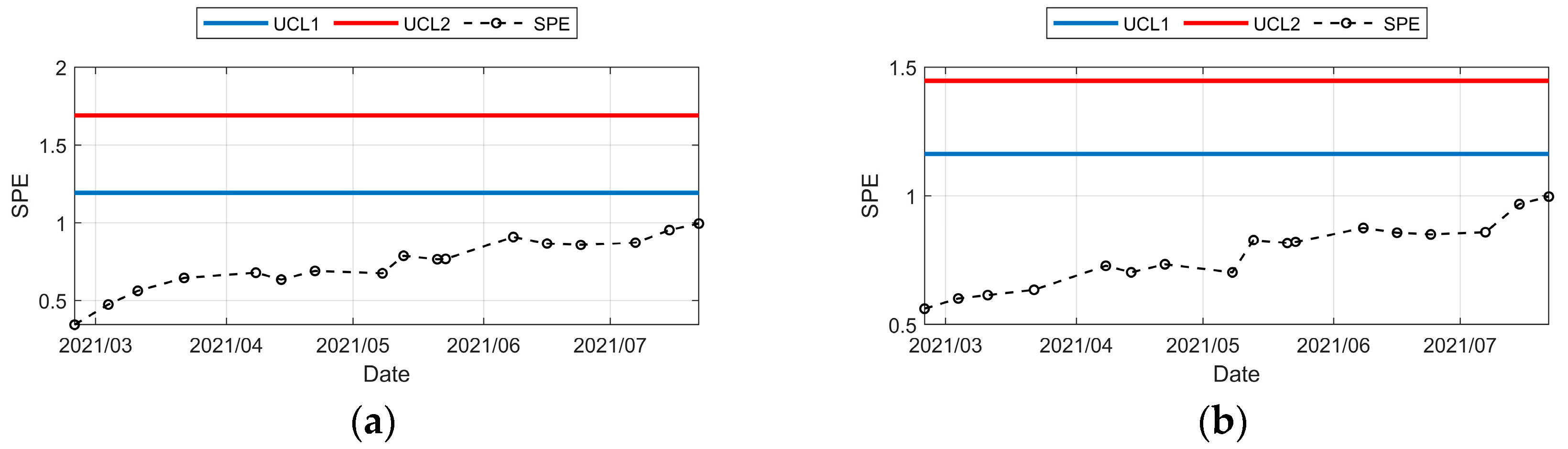
From the control chart, it can be seen that the dam crest displacement was gradually affected by the failure of the insulation board and increased significantly in November 2013, February to April 2014, and June to September 2014, respectively. It can be seen that the abnormal displacement of the arch dam affected by temperature can be divided into three stages in the 18 months of aging of the insulation board, and the abnormal displacement in the three stages is getting larger and larger.

(2)

From July 2013 to November 2013, the insulation board just failed and the temperature gradually decreased. At this time, the dam crest still did not show obvious abnormalities. The control diagram of the dam crest area belongs to class (c) in Figure 4, and the system does not need to alarm, but the SPE value of the PPCA method is closer to UCL1 and more sensitive. The period from November 2013 to March 2014 belongs to category (d) in Figure 4, that is, the system should alarm in November 2013, and the SPE value of the PPCA method is higher and also more sensitive. From April 2014 to December 2014, the repair of the insulation board was gradually completed, but the dam deformation was still affected by the failure of the insulation board in the early stages. At this time, the SPE value of the PPCA method was slightly less than that of the PCA method, which reflected the role of insulation board repair construction.

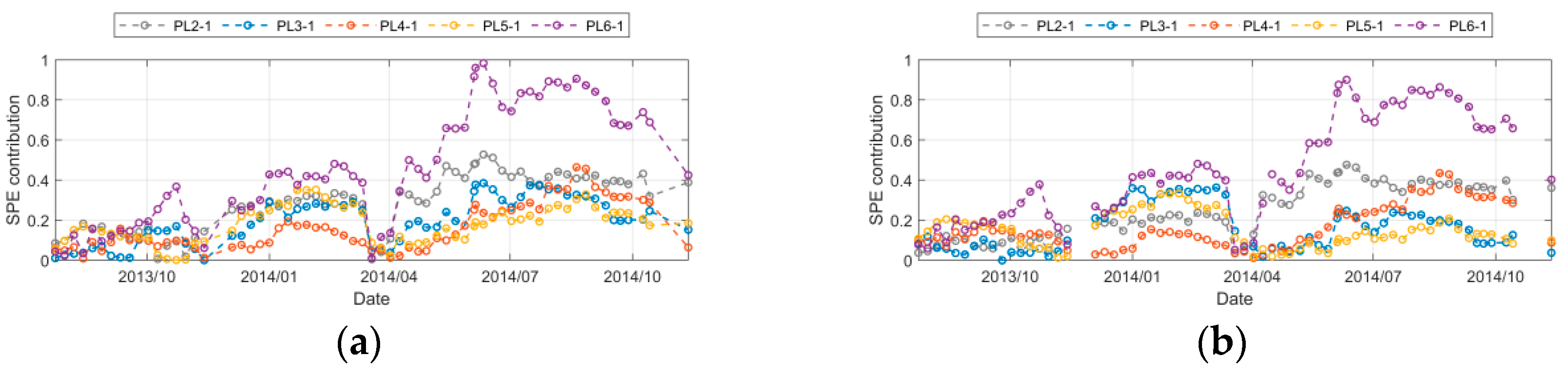
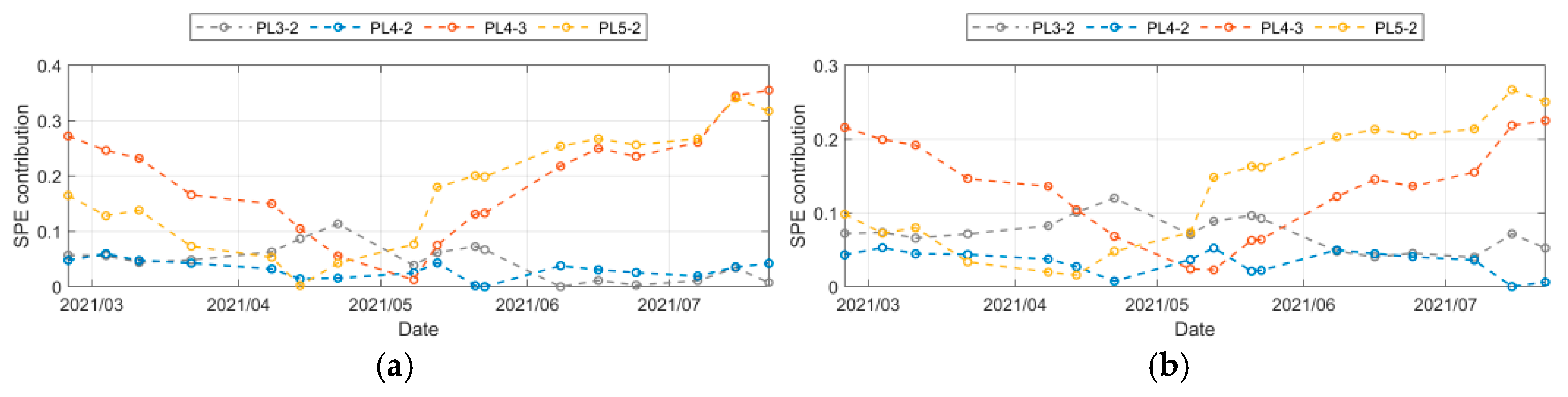
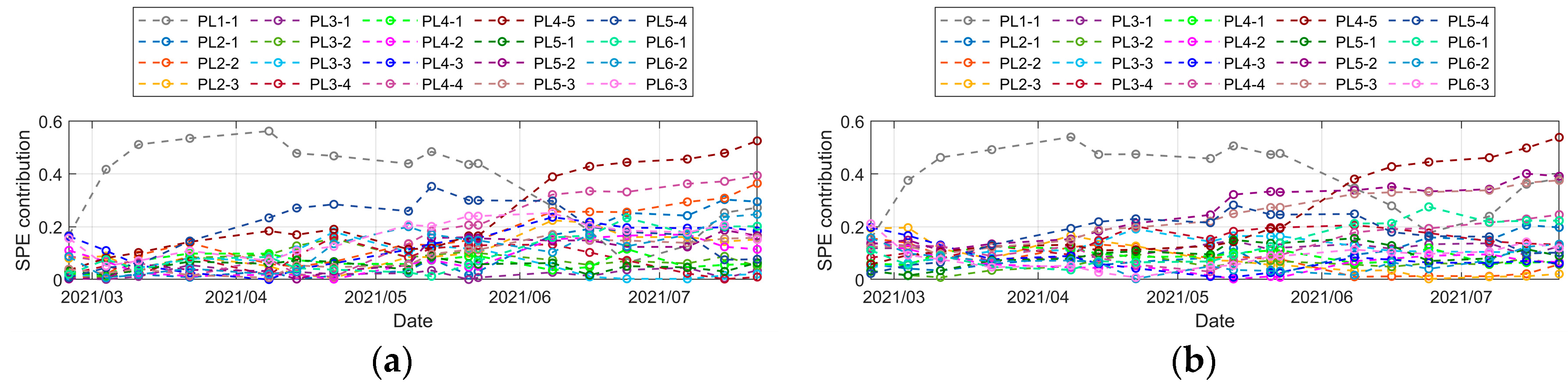
(3)

From the contribution diagram, the two methods are quite different. Since the PL6-1 measuring point is not within the influence range of the loss of insulation board, both methods show that the SPE contribution of the PL6-1 measuring point is the most obvious, indicating that there is a large gap between the deformation law of this measuring point and other measuring points, which is consistent with the above analysis.

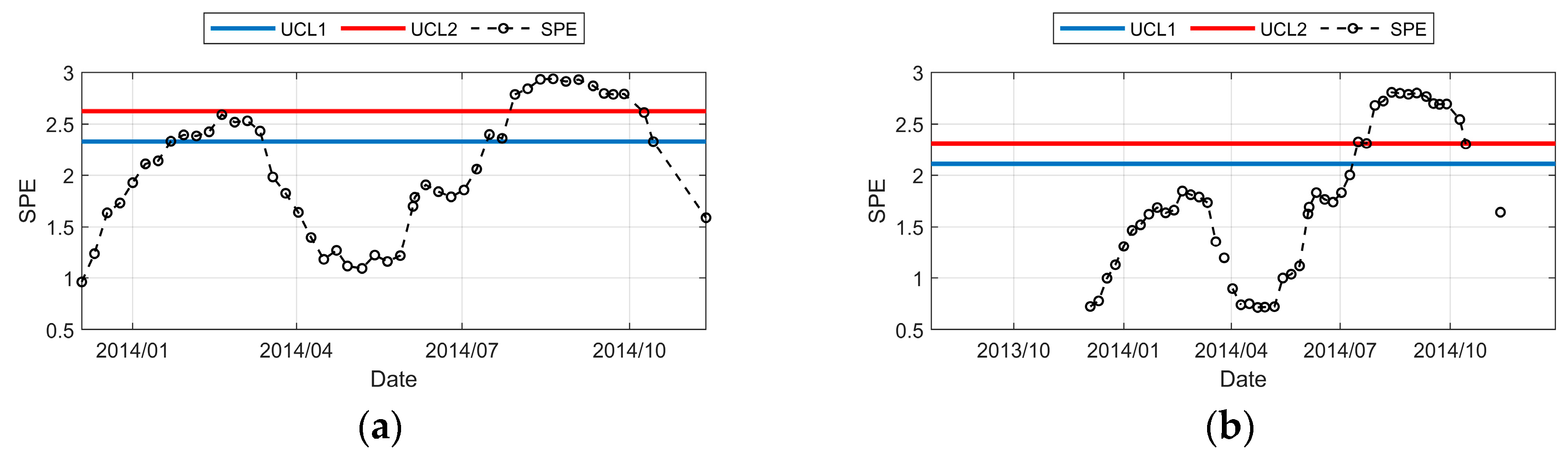
6.4.2. Offline Analysis for All Monitoring Points

In contrast, the offline data to be diagnosed are shown using all the data for offline data diagnosis SPE. The SPE control chart is shown in Figure 16 for each measurement point. The contributing process lines are shown in Figure 17.

Because the displacement laws in different regions of the arch dam, especially the displacement, are very different, if the monitoring data of all measuring points are directly used for offline diagnosis, UCL1 and UCL2 will be significantly improved. The PPCA method did not reach UCL1 in 2014, and the PCA method did not reach UCL2.

From the contribution diagram, the SPE contribution of PL6-1 and PL5-1 is significantly greater than that of other measurement points, while the SPE contribution diagram of partition 1 mainly reflects the anomaly of PL6-1 measurement points. Although the SPE contribution value of the PL5-1 measurement point is also significantly greater than that of other measurement points, the SPE contribution of the PL5-1 measurement point tends to be flat after July 2014. From the actual operation of the dam, PL6-1 is the main measuring point affected by the failure of the temperature plate. PL5-1 is closer to the arch crown, so the abnormal deformation is smaller and tends to be stable in the later stage.

By comparing the offline diagnosis results of the zoning and all the measuring points, it can be seen that, due to the large difference in the displacement laws, especially the displacement amount, in different regions of the arch dam, UCL1 and UCL2 will be significantly improved, and it will further lead to the difficulty of timely early warning of dam anomalies using all the measuring points.

6.5. Online Monitoring

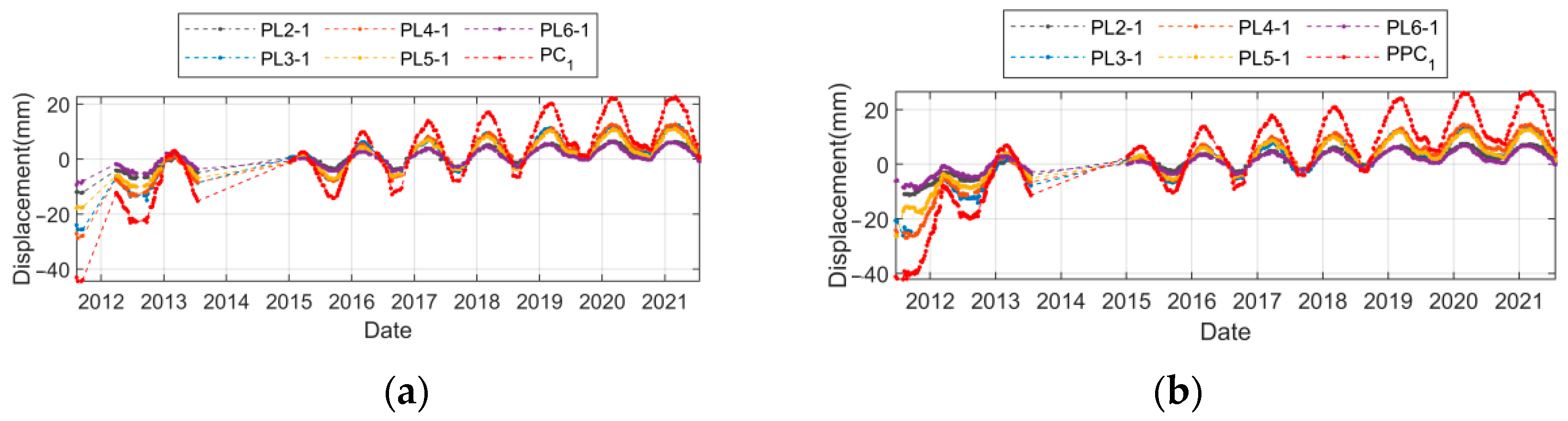
6.5.1. Online Monitoring of Partitions

For the four measuring points in the second division, the monitoring data before 23 February 2021 is used as the historical reference monitoring data, and the data after 23 February 2021 is used as the online data, and PCA and PPCA are respectively used to exclude the effects caused by environmental variables. See Figure 18 for the radial displacement de-averaging hydrograph and PC and PPC hydrograph of the four measuring points. KDE is used to estimate the probability density of SPE and the secondary control limit is shown in Figure 19, and the index values are shown in

Table 3. Secondary control limit.

	PCA	4PPCA
UCL1	0.3826	0.4282
UCL2	0.4536	0.4553

.

According to Figure 18:

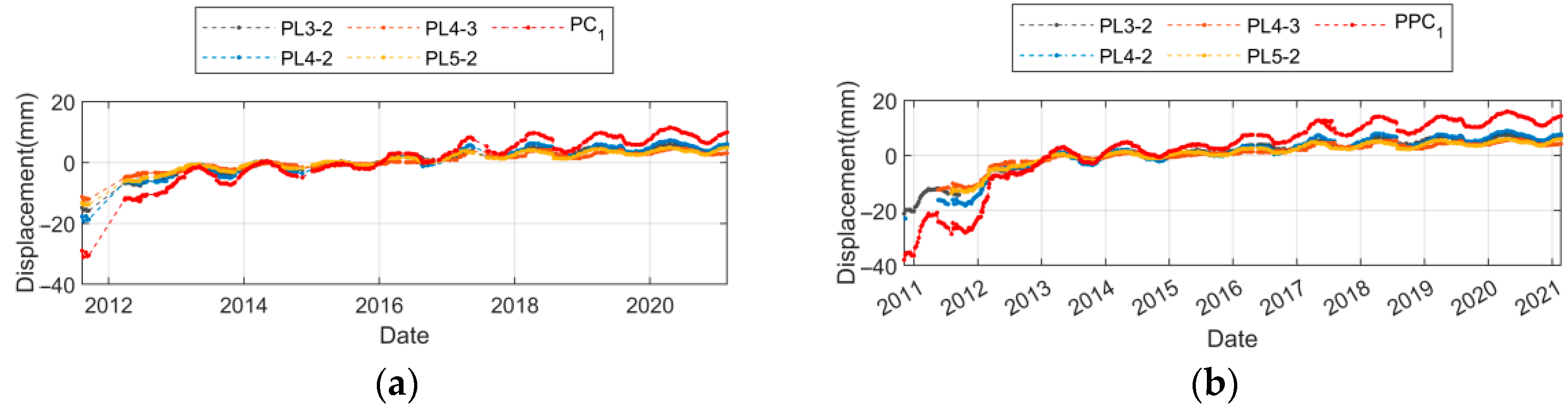
(1)

Both PPC₁ and PC₁ can completely encompass the maximum and minimum values of each measurement point over the years, and the growth trend and the amplitude of cyclic displacement are greater.

(2)

PPCA can fully utilize the available information to extract the effects of environmental variables. Since PCA needs to extract PCs based on the data of the public date of each measurement point, only 418 sets of data are available. In contrast, PPCA can estimate the PPCs of the missing segments based on the probability distribution of the original data, so that 540 sets of partially missing monitoring data can be used.

(3)

Because the PPCA utilizes a portion of the monitoring data from the 2011 water level rise period, the overall trend shows a more pronounced increase in the PPC₁ than in the PC₁.

The control charts of the two methods are the same. PPCA considers all monitoring data, but the monitoring time of each measuring point is different, so the control chart using PPCA is partially missing. At the same time, as shown in Figure 12, the data used by PPCA contains a lot of monitoring information about the water level rise period. Therefore, after using PPCA to exclude the effects caused by environmental variables, the SPE of the remaining components of the public data is above 0.33. The SPE of the PCA residual component has a normal distribution between 0 and 0.6.

Because the historical monitoring data are not fully aligned, PCA cannot consider the impact of water level rise on dam displacement. Therefore, compared with PPCA, the control limit UCL1 extracted by PCA is significantly smaller, that is, it will alarm in advance.

See Figure 20 for the SPE control chart and Figure 21 for the contribution.

The control charts using PCA belong to the case 6 type in Table 1, that is, they have entered the alarm state, while the control charts using PPCA are all under the control limit UCL1, without alarm.

From the contribution diagram, the contributions of the measurement points near 8 May 2021 are low, while the contributions of PL4-3 and PL5-2 measurement points are significantly increased before 1 May 2021 and after 13 May 2021.

It can be seen from Figure 14 that the displacement laws of measuring points PL3-2 and PL4-2 are consistent. Compared with the PL3-2 and PL4-2 measuring points, the displacement of the PL4-3 measuring point has a lag of about 2 months. While the displacement of the PL5-2 measuring point is about one month ahead of 1 May 2021, after 13 May 2021, it is only about seven days ahead of PL3-2 and PL4-2 measuring points. This shows that the displacement law of the PL5-2 measuring point has changed before and after 8 May 2021. In the contribution diagram using PPCA, the contribution of PL5-2 is significantly greater than that of PL4-3, which also shows that the PPCA method is more suitable for arch dam deformation monitoring.

According to Figure 21a, the system alarm was caused by abnormal deformation of PL4-3 and PL5-2 between May 2021 and August 2021. However, during this period, there was no abnormal event in the arch dam, and the reservoir water level remained within 1m below the normal pool level for a long time. The reason for the alarm may be that the temperature between May 2021 and August 2021 is higher than that in previous years, and the left bank dam section where the PL5-2 measuring point is located is exposed to sunshine for a long time, resulting in thermal expansion of the left bank dam body, which affects the PL4-3 measuring point. However, the above analysis shows that the arch dam has no abnormal phenomenon at this time, so it is a false alarm, which further proves that PPCA is more suitable for arch dam deformation monitoring than traditional PCA.

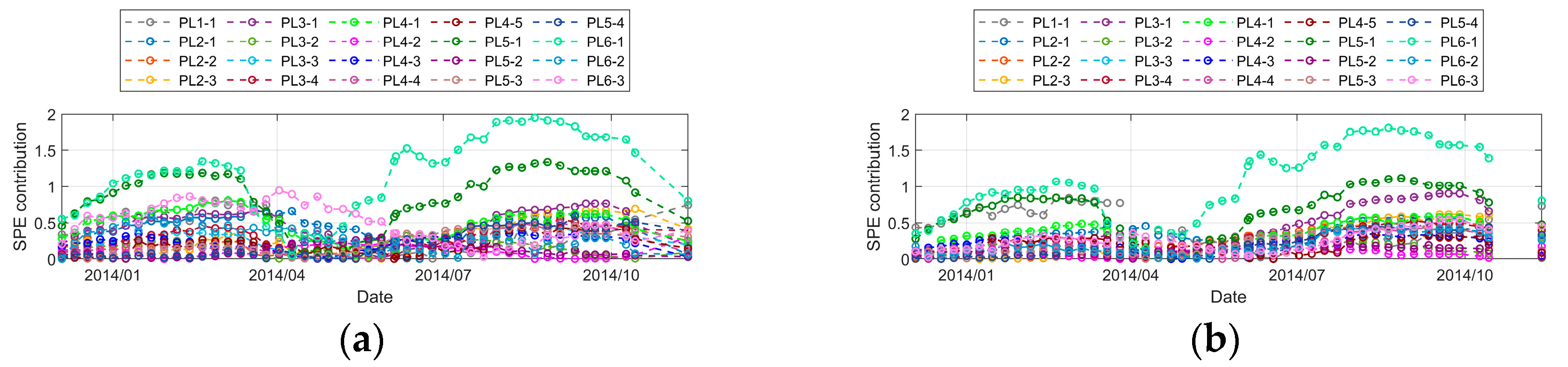
6.5.2. Online Monitoring for All Measuring Points

In contrast, all data are used for offline data diagnosis. The offline data control chart to be diagnosed is shown in Figure 22, and the SPE contribution chart of online data of all measuring points is shown in Figure 23.

Using all measuring points for online diagnosis, UCL1 and UCL2 exceeded 1, about four times the control limit of partition 2 in Figure 20. From the SPE control chart, PCA and PPCA methods did not exceed the SPE control limit. During the online monitoring, the SPE value of the online data of all measuring points showed an increasing trend, reflecting that the overall safety of the arch dam was gradually approaching the control limit. It is inconsistent with the law that the value of online data in partition 2 decreases first, then increases, and then decreases.

The main factors affecting the deformation of different parts of the arch dam are different: the deformation of the dam foundation is limited by the foundation, and the deformation value is small, while the deformation value of the dam crest is significantly larger than that of other areas and is greatly affected by temperature, and the periodic variation amplitude is also significantly larger. Therefore, there are great differences in the expression of the impact of arch dam environmental variables in each region of the arch dam. Including all measuring points in the analysis will seriously affect the separation results of the impact of environmental variables, and it is easy to misjudge the safety state of the arch dam.

6.6. Discussion

The comparative analysis between PCA and PPCA indicates that the proposed knowledge-driven framework significantly enhances the accuracy and robustness of deformation monitoring. By effectively estimating missing data and separating environmental influences from structural responses, PPCA reduces the interference of temperature and reservoir level fluctuations, thereby improving the stability of the early warning results. The application of optimized ISODATA clustering further highlights the spatial heterogeneity of the arch dam, enabling independent characterization and diagnosis of deformation behavior in different zones.

Compared with conventional statistical or machine-learning-based approaches, the proposed model emphasizes interpretability and knowledge integration rather than relying solely on data fitting. By transforming engineering specifications and accumulated operational experience into explicit knowledge rules, the model provides a more transparent and reliable tool for long-term dam safety assessment. This approach ensures that deformation analysis is both data-driven and physically meaningful.

The results obtained from offline and online monitoring confirm that the knowledge-driven model can distinguish abnormal deformation patterns from normal environmental responses. Overall, the study presents a comprehensive and interpretable analytical framework that bridges the gap between empirical monitoring methods and intelligent data-driven techniques in dam safety evaluation.

7. Conclusions

Based on the optimized ISODATA clustering method, PPCA, the control chart, and contribution chart of the SPE norm, this paper proposes an arch dam deformation safety early warning and abnormal value cause diagnosis method based on the effect separation of regional environmental variables and knowledge-driven approach, which is verified by the monitoring data of the horizontal displacement of an arch dam.

(1)

By optimizing the selection of initial cluster centers and extracting high-dimensional features of arch dam deformation monitoring curves based on the kernel method, the traditional ISODATA is optimized, which effectively solves the problems of uncertain cluster number and difficult-to-capture high-dimensional features of data. The deformation monitoring points of the arch dam are divided into multiple categories, and then the dam body is divided into multiple regions, which provides the basis for the subsequent zoning monitoring.

(2)

PPCA can deal with the missing problem in the monitoring data of multiple monitoring points, calculate the missing data through the correlation relationship, and extract the PPCs representing the overall performance of the dam, which effectively retains the monitoring information and can better separate the impact of environmental variables and noise interference.

(3)

The displacement law of all measuring points is more complex, which is difficult to characterize by fewer PCs or PPCs. The SPE control limit of all measuring points is significantly higher than that of the partition. Moreover, there are great differences in the expression of the impact of arch dam environmental variables in each region of the arch dam. Including all measuring points in the analysis will seriously affect the separation results of the impact of environmental variables, and it is easy to misjudge the safety state of the arch dam.

(4)

By analyzing the different mode combinations of the control chart and contribution chart of the SPE norm, we can analyze the anomalies of offline data and online data. The control chart can quickly analyze the overall safety status of each area of the dam, and the contribution chart can more accurately analyze the abnormal conditions of different measuring points in the area.

The method proposed in this paper is not only applicable to the deformation monitoring of arch dams but also can be extended to the safety monitoring of other hydraulic engineering structures. The accuracy and reliability of structural safety monitoring of water conservancy projects can be further improved by integrating engineering specifications, engineering experience, data types, thresholds, and relative components of multiple measurement points.