Assessing the Applicability of the LTSF Algorithm for Streamflow Time Series Prediction: Case Studies of Dam Basins in South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Time Series Forecasting Algorithms
2.2.1. Long-Term Series Forecasting Linear Algorithms
2.2.2. Long Short-Term Memory
2.2.3. Extreme Gradient Boosting
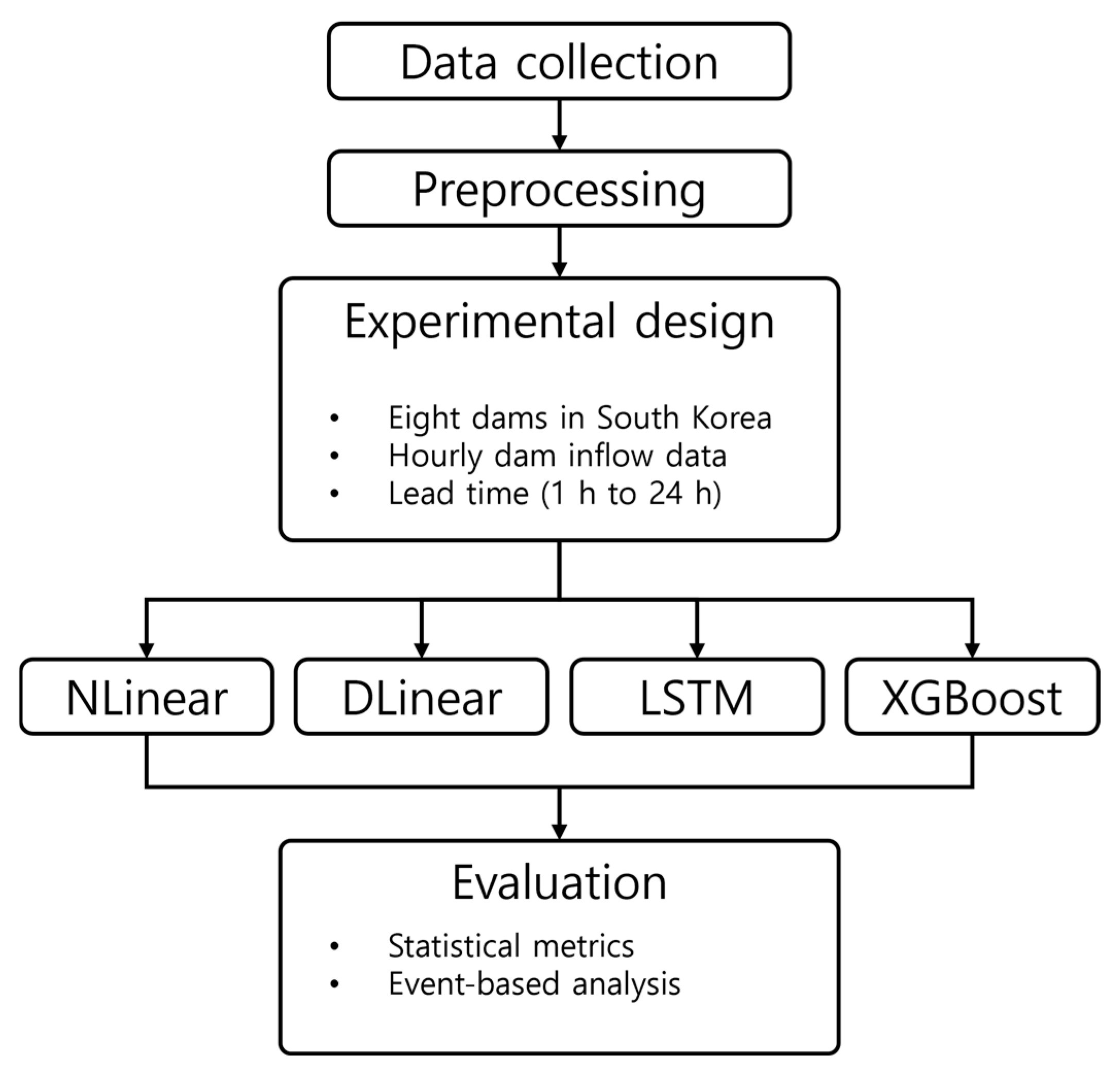
2.3. Experimental Design
2.3.1. Input Window Size and Data Partitioning
2.3.2. LTSF-Linear Models
2.3.3. LSTM Model
2.3.4. XGBoost
2.4. Performance Metrics
2.4.1. Normalized Root Mean Square Error (nRMSE)
2.4.2. Normalized Mean Absolute Error (nMAE)
2.4.3. Coefficient of Determination (R2)
2.4.4. Mean Bias (mBias)
2.4.5. Kling–Gupta Efficiency (KGE)
3. Results
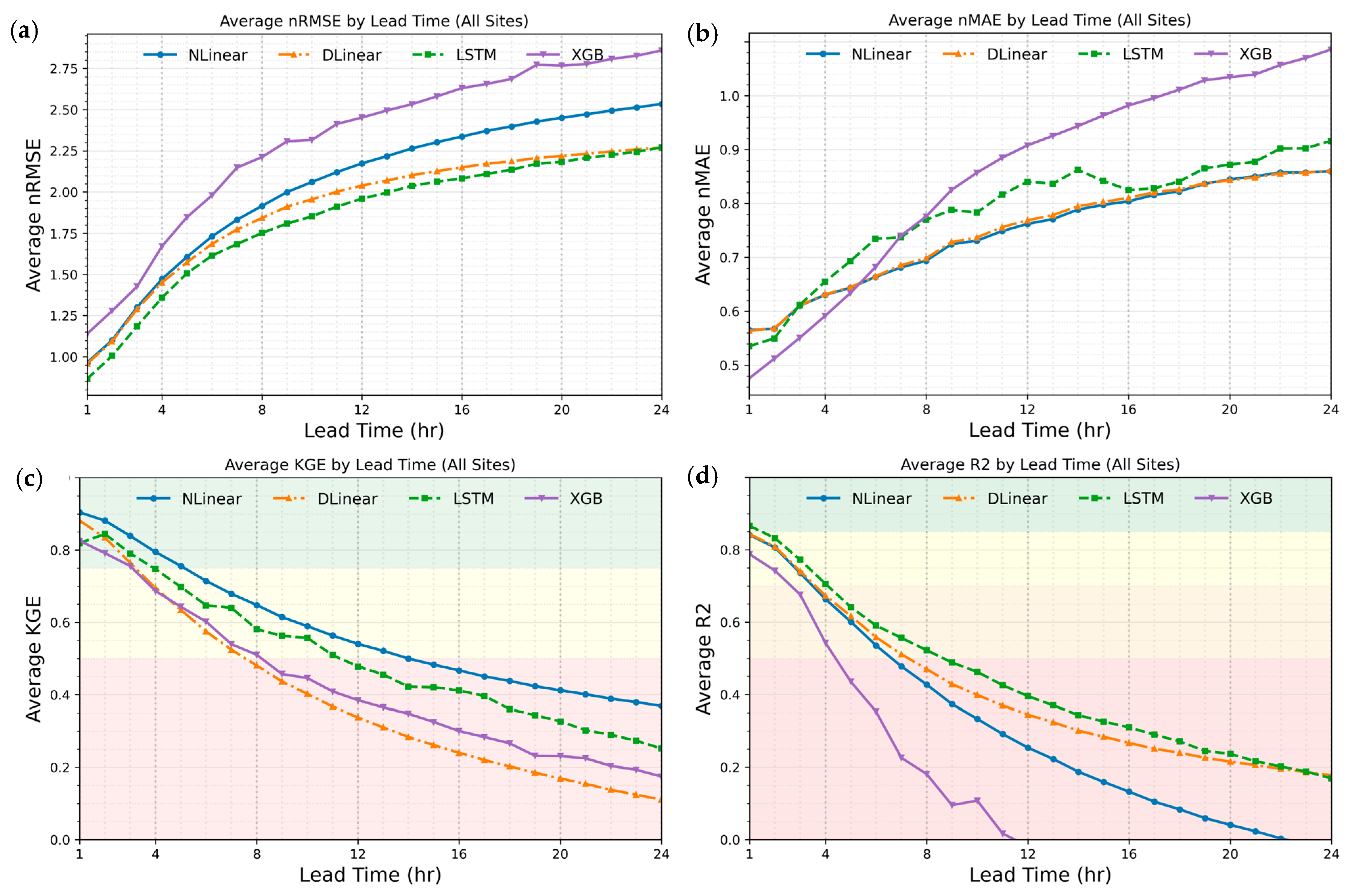
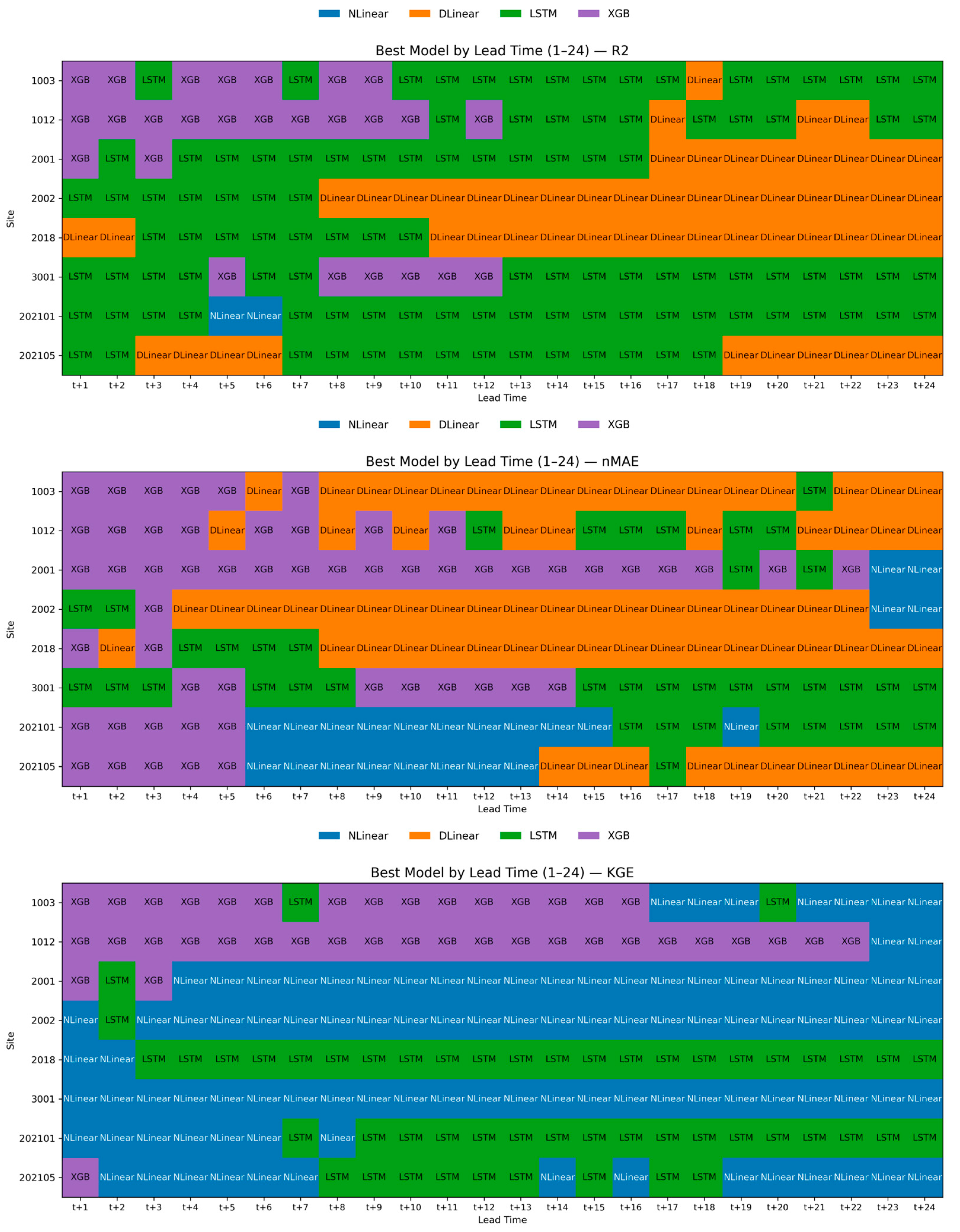
3.1. Lead Time Dependence and Reliability
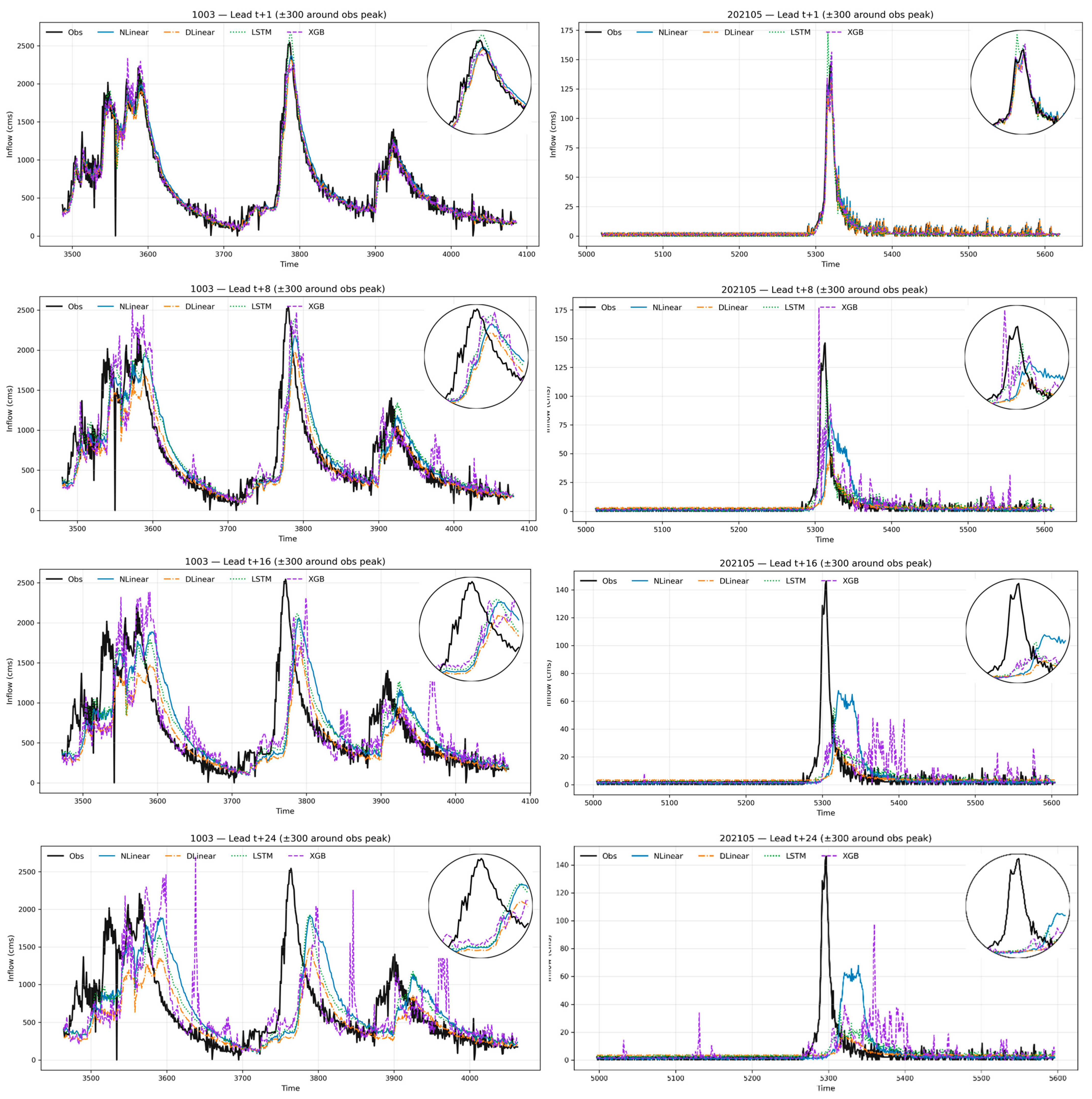
3.2. Per-Site Boxplots of Model Performance Across Lead Times (1–24 h), Site Grouping, and Peak Reproduction
4. Discussion
4.1. Main Findings and Implications
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Zarei, M.; Bozorg-Haddad, O.; Baghban, S.; Delpasand, M.; Goharian, E.; Loáiciga, H.A. Machine-Learning Algorithms for Forecast-Informed Reservoir Operation (FIRO) to Reduce Flood Damages. Sci. Rep. 2022, 12, 346. [Google Scholar] [CrossRef] [PubMed]
- Delaney, C.J.; Hartman, R.K.; Mendoza, J.; Dettinger, M.; Delle Monache, L.; Jasperse, J.; Ralph, F.M.; Talbot, C.; Brown, J.; Reynolds, D.; et al. Forecast-Informed Reservoir Operations Using Ensemble Streamflow Predictions for a Multipurpose Reservoir in Northern California. Water Resour. Res. 2020, 56, e2019WR026604. [Google Scholar] [CrossRef]
- Anghileri, D.; Voisin, N.; Castelletti, A.; Nijssen, B.; Lettenmaier, D.P. Value of Long-Term Streamflow Forecasts to Reservoir Operations. Water Resour. Res. 2016, 52, 4209–4225. [Google Scholar] [CrossRef]
- Wang, Q.J.; Bennett, J.C.; Robertson, D.E.; Shrestha, D.L.; Hapuarachchi, H.A.P. Improving Real-Time Reservoir Operation During Floods Using Inflow Forecasts. J. Hydrol. 2021, 598, 126017. [Google Scholar] [CrossRef]
- Ficchì, A.; Perrin, C.; Andréassian, V. Impact of Temporal Resolution of Inputs on Hydrological Model Performance: An Analysis Based on 2400 Flood Events. J. Hydrol. 2016, 538, 454–470. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Salas, J.D. Analysis and Modeling of Hydrologic Time Series. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; pp. 19.1–19.72. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Zhang, G.P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Montanari, A.; Brath, A. A Stochastic Approach for Assessing the Uncertainty of Rainfall–Runoff Simulations. Water Resour. Res. 2004, 40, W01106. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L. Comparing Neural Network and Autoregressive Moving Average Techniques for the Provision of Continuous River Flow Forecasts in Two Contrasting Catchments. Hydrol. Process. 2000, 14, 2157–2172. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A Comparative Study of Artificial Neural Networks and Support Vector Machines for Predicting Groundwater Levels in a Coastal Aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support Vector Regression for Rainfall–Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Kim, T.; Shin, J.-Y.; Kim, H.; Kim, S.; Heo, J.-H. The use of Large-Scale Climate Indices in Monthly Reservoir Inflow Forecasting and Its Application on Time Series and Artificial Intelligence Models. Water 2019, 11, 374. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods Used for the Development of Neural Networks for the Prediction of Water Resource Variables in River Systems: Current Status and Future Directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Kim, T.; Shin, J.-Y.; Kim, H.; Heo, J.-H. Ensemble-based neural network modeling for hydrologic forecasts uncertainty in the model structure and input variable selection. Water Res. Res. 2020, 56, e2019WR026262. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Mok, J.Y.; Choi, J.H.; Moon, Y.I. Prediction of Multipurpose Dam Inflow Using Deep Learning. J. Korea Water Resour. Assoc. 2020, 53, 881–892. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Lee, T.; Shin, J.-Y.; Kim, J.-S.; Singh, V.P. Stochastic Simulation on Reproducing Long-term Memory of Hydroclimatological Variables using Deep Learning Model. J. Hydrol. 2020, 582, 124540. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall–Runoff Model with LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Kratzert, F.; Herrnegger, M.; Klotz, D.; Hochreiter, S.; Klambauer, G. NeuralHydrology—Interpreting LSTMs in Hydrology. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Samek, W., Montavon, G., Vedaldi, A., Hansen, L., Muller, K.R., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11700. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.J.; Ganguly, S.; Hsu, K.; Kifer, D.; Fang, K.; et al. HESS Opinions: Incubating Deep-Learning-Powered Hydrologic Science Advances as a Community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Giorgio, A.; Del Buono, N.; Berardi, M.; Vurro, M.; Vivaldi, G.A. Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework. Sensors 2022, 22, 8062. [Google Scholar] [CrossRef]
- Gegenleithner, S.; Pirker, M.; Dorfmann, C.; Kern, R.; Schneider, J. Long Short-Term Memory Networks for Enhancing Real-Time Flood Forecasts: A Case Study for an Underperforming Hydrologic Model. Hydrol. Earth Syst. Sci. 2025, 29, 1939–1962. [Google Scholar] [CrossRef]
- Li, Z.; Qi, S.; Li, Y.; Xu, Z. Revisiting Long-Term Time Series Forecasting: An Investigation on Linear Mapping. arXiv 2023, arXiv:2305.10721. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q.; Sun, Q. Are Transformers Effective for Time Series Forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time Series Forecasting with Deep Learning: A Survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Environment, Republic of Korea. Master Plan for National Water Management; Ministry of Environment: Sejong, Republic of Korea, 2021. Available online: https://water.go.kr/eng/515 (accessed on 15 September 2025).
- Water Resources Management Information System (WAMIS). Available online: http://www.wamis.go.kr (accessed on 15 September 2025).
- UNESCO IHP. South Korea Hydrometeorological Data from WAMIS. 2025. Available online: https://ihp-wins.unesco.org/en/dataset/south-korea-hydrometeorological-data-from-wamis (accessed on 16 September 2025).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE/KGE Implications. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Vrugt, J.A.; de Oliveira, D.Y. Confidence Intervals of the Kling–Gupta Efficiency. J. Hydrol. 2022, 612, 127968. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical Note: Inherent Benchmark or Not? Comparing Nash–Sutcliffe and Kling–Gupta Efficiency Scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Laiti, L.; Mallucci, S.; Piccolroaz, S.; Bellin, A.; Zardi, D.; Fiori, A.; Nikulin, G.; Majone, B. Testing the Hydrological Coherence of High-Resolution Simulations: On KGE Use and Thresholds. Water Resour. Res. 2018, 54, 1618–1637. [Google Scholar] [CrossRef]
- Abdalla, E.M.H.; Alfredsen, K.; Muthanna, T.M. Towards Improving the Calibration Practice of Conceptual Hydrological Models of Extensive Green Roofs. J. Hydrol. 2022, 607, 127548. [Google Scholar] [CrossRef]
- Kim, H.R.; Moon, M.; Yun, J.; Ha, K.J. Trends and Spatio-Temporal Variability of Summer Mean and Extreme Precipitation across South Korea for 1973–2022. Asia-Pac. J. Atmos. Sci. 2023, 59, 385–398. [Google Scholar] [CrossRef]
- Seo, G.Y.; Min, S.K.; Lee, D.; Son, S.W.; Park, C.; Cha, D.H. Hourly Extreme Rainfall Projections over South Korea Using Convection Permitting Climate Simulations. npj Clim. Atmos. Sci. 2025, 8, 209. [Google Scholar] [CrossRef]
- Cinkus, G.; Mazzilli, N.; Jourde, H.; Wunsch, A.; Liesch, T.; Ravbar, N.; Chen, Z.; Goldscheider, N. When Best Is the Enemy of Good—Critical Evaluation of Performance Criteria in Hydrological Models. Hydrol. Earth Syst. Sci. 2023, 27, 2397–2411. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 55, e2019WR026065. [Google Scholar] [CrossRef]
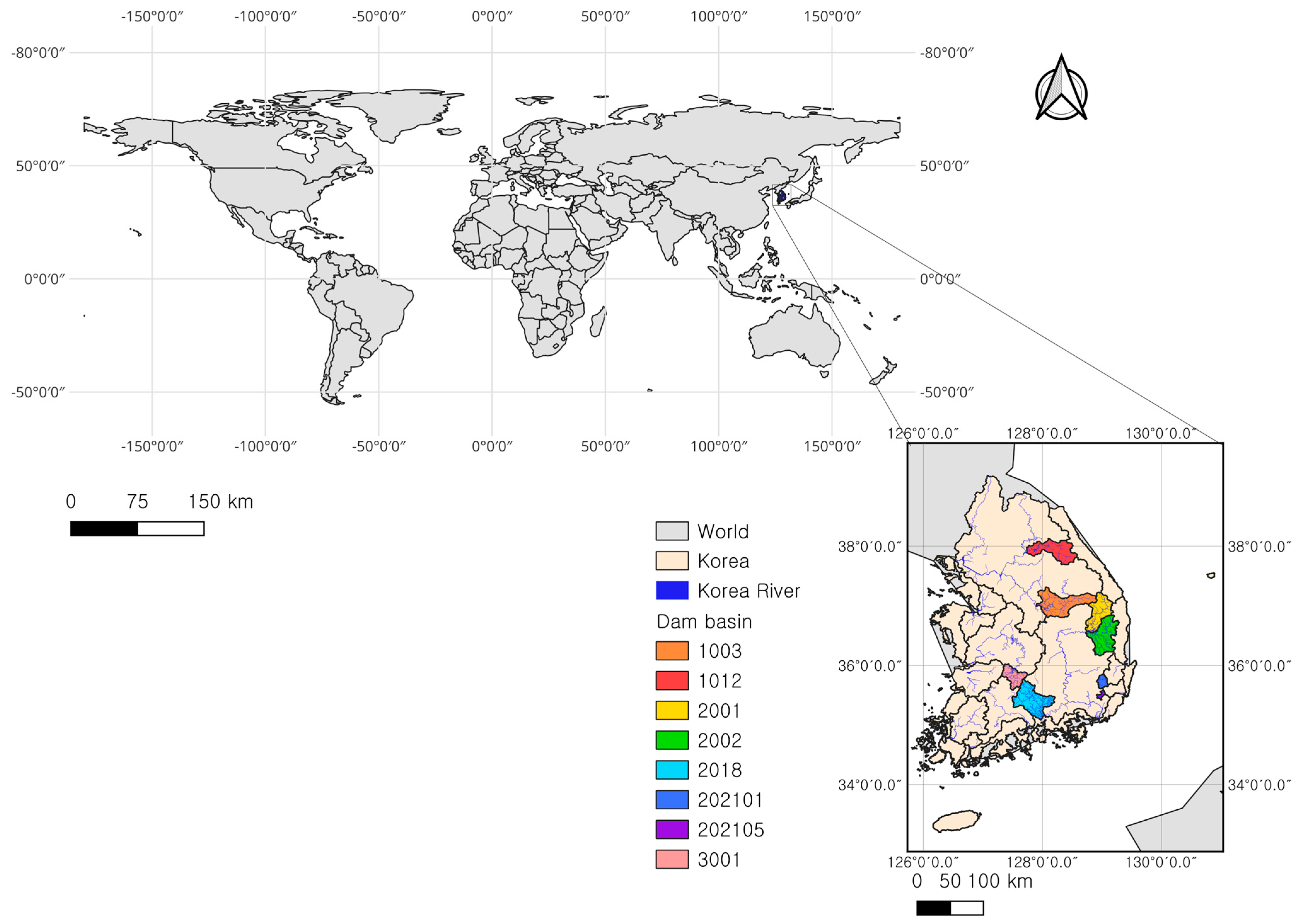



| Name | Code | Area (km2) | MeanCatchment Slope (%) | MainStreamLength (km) | Total Stream Length (km) | Drainage Density (km/km2) | Observation Period (YYYYMMDD) | Number of Samples |
|---|---|---|---|---|---|---|---|---|
| Andong | 2001 | 1628.7 | 50.7 | 170.1 | 5381.3 | 3.3 | 20190212–20241231 | 51,607 |
| Chungju | 1003 | 2483.8 | 50.1 | 115.3 | 4347.3 | 1.8 | 20190208–20241231 | 51,649 |
| Imha | 2002 | 1975.8 | 48.7 | 112.8 | 5740.9 | 2.9 | 20190212–20241231 | 51,623 |
| Milyang | 202105 | 103.5 | 54.3 | 28.1 | 191.0 | 1.8 | 20190212–20241231 | 51,571 |
| Namgang | 2018 | 2281.7 | 41.8 | 110.8 | 6841.3 | 3.0 | 20190212–20241231 | 51,568 |
| Soyang | 1012 | 1852.0 | 56.5 | 156.5 | 2840.9 | 1.5 | 20190208–20241231 | 51,457 |
| Unmun | 202101 | 302.0 | 49.4 | 37.9 | 674.8 | 2.2 | 20190212–20241231 | 51,600 |
| Yongdam | 3001 | 930.4 | 42.8 | 62.6 | 2130.5 | 2.3 | 20190216–20241231 | 51,457 |
| Metric | Nlinear | Dlinear | LSTM | XGBoost |
|---|---|---|---|---|
| RMSE | 79.2 | 74.9 | 73.5 | 82.1 |
| nRMSE | 2.0 | 1.9 | 1.8 | 2.3 |
| MAE | 35.3 | 34.3 | 35.8 | 36.4 |
| nMAE | 0.75 | 0.75 | 0.79 | 0.86 |
| mBias | −0.07 | 0.8 | −5.53 | −6.01 |
| R2 | 0.3 | 0.4 | 0.43 | 0.04 |
| R | 0.60 | 0.62 | 0.66 | 0.66 |
| KGE | 0.57 | 0.39 | 0.51 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Shin, J.-Y.; Kim, S.; Kwon, J. Assessing the Applicability of the LTSF Algorithm for Streamflow Time Series Prediction: Case Studies of Dam Basins in South Korea. Water 2025, 17, 3214. https://doi.org/10.3390/w17223214
Park J, Shin J-Y, Kim S, Kwon J. Assessing the Applicability of the LTSF Algorithm for Streamflow Time Series Prediction: Case Studies of Dam Basins in South Korea. Water. 2025; 17(22):3214. https://doi.org/10.3390/w17223214
Chicago/Turabian StylePark, Jiyeon, Ju-Young Shin, Sunghun Kim, and Jihye Kwon. 2025. "Assessing the Applicability of the LTSF Algorithm for Streamflow Time Series Prediction: Case Studies of Dam Basins in South Korea" Water 17, no. 22: 3214. https://doi.org/10.3390/w17223214
APA StylePark, J., Shin, J.-Y., Kim, S., & Kwon, J. (2025). Assessing the Applicability of the LTSF Algorithm for Streamflow Time Series Prediction: Case Studies of Dam Basins in South Korea. Water, 17(22), 3214. https://doi.org/10.3390/w17223214






