Prototype-Scale Experimental Investigation of Manhole Cover Bounce and Critical Overpressure in Urban Drainage Shafts

Abstract

Manhole shafts in urban drainage systems are prone to accumulating trapped air pockets during intense rainfall, which can lead to sudden bounce of hinged covers and pose significant near-field risks. However, threshold criteria at the prototype scale remain unavailable. To obtain quantitative evidence of cover bounce under full-scale conditions and to clarify the effects of counterweight, dual-shaft coupling, and pressure–displacement phase lag, a series of experiments have been conducted on a prototype platform consisting of two shafts with hinged covers. Tests have been repeated under various counterweight conditions ranging from 0 to 30 kg. Pressure data from multiple transducers and high-speed video recordings have been synchronously acquired, filtered, and temporally aligned. Based on these, the critical overpressure at initial lift-off was identified, and oscillation characteristics and coupling effects have been analyzed. The critical overpressure was found to increase monotonically with added counterweight. When the counterweight was large, the system transitioned into a decaying response, with negligible subsequent bounce. The single-peak “rise–fall” pattern observed in single-shaft conditions no longer appeared when both covers lifted simultaneously. Notably, the critical overpressure did not coincide with the pressure peak, and a significant phase lag was observed between the pressure maximum and the moment of maximum displacement. These findings provide actionable support for the identification, modeling, and rapid mitigation of manhole cover bounce risks in urban drainage systems.

1. Introduction

A large amount of air was released from urban drainage pipelines during the rapid filling process by water, and retained air pockets have been prone to form within inspection shafts—under conditions of heavy rainfall. Geysering and manhole cover displacement frequently occurred, posing safety risks to vehicles and pedestrians, damaging municipal infrastructure, and causing secondary urban flooding, as a result of the rapid pressure rise inside inspection shafts. As indicated by field monitoring, high-energy water–air mixtures have been frequently observed surging upward in the shaft region during heavy rainfall events, which often led to the forceful ejection of manhole covers. Figure 1 presents the corresponding monitoring imagery. Researchers had repeatedly validated and reproduced the underlying mechanisms through physical experiments and numerical simulations in both drainage pipelines and experimental shafts [1,2].

Mainstream approaches have been predominantly based on the two-dimensional shallow water equations, focusing on surface-scale water depth and velocity to produce inundation depth maps, velocity hazard maps, and further derive pedestrian stability criteria [3,4,5], particularly in the context of flood risk mapping. In contrast, one-dimensional drainage network models have been mainly employed to assess system discharge capacity and node surcharge, often serving as boundary inputs or auxiliary modules for surface models. However, such one-dimensional models have not yet been able to directly capture the complex transient gas–liquid dynamics and pressure variations within manholes, which makes it difficult to incorporate manhole cover displacement into the graded risk classification and threshold determination systems for urban flooding [6,7]. Nevertheless, manhole cover displacement constitutes a near-field, high-risk hazard that directly affects pedestrians and vehicles, with its potential consequences far exceeding those associated with traditional indicators such as inundation depth or surface flow velocity.

More importantly, even under moderate rainfall conditions, severe fluctuations in air–water mixture pressure and rapid transitions in flow regime may still be triggered in sewer systems due to gas generation from in-pipe biochemical reactions, sediment accumulation, and sudden increases in diurnal discharge, ultimately inducing overpressure in manholes and resulting in manhole cover displacement [8,9,10]. Meanwhile, the rapidly evolving urban flood modeling frameworks based on GIS platforms and deep learning algorithms have generally failed to incorporate the identification and response mechanisms associated with manhole-related hazards [11,12,13,14,15,16]. In summary, the current flood risk assessment frameworks remain severely inadequate in terms of identifying, quantifying, and visually representing manhole cover displacement as a critical risk factor.

As a critical hazard source in urban flood processes, manhole cover displacement has received limited attention in existing research, particularly with respect to influencing factors such as cover type, mass, and orifice area. In earlier work, Yamamoto [17] proposed the basic mechanism of manhole ejection based on engineering observations and had summarized a regulatory framework of “venting–reinforcement-monitoring” which laid the foundation for subsequent experimental studies and modeling analyses. In recent years, Wang et al. [18,19] had conducted transient numerical simulations using the OpenFOAM platform, revealing that the rapid release of trapped air pockets could induce significant pressure fluctuations sufficient to cause cover displacement. They had further identified a typical fluctuation pattern characterized by “shock–attenuation-secondary peak” and analyzed the effects of venting area and air pocket volume on the resulting pressure dynamics. Although three-dimensional CFD simulations have provided preliminary insights into the fluid responses during ejection events, a simplified modeling framework suitable for city-scale risk analysis has remained lacking.

Against this backdrop, Tijsseling [20] proposed a two-degree-of-freedom nonlinear “manhole–air-water” coupled model based on the rigid water-plug assumption, initially establishing a simplified theoretical framework for manhole cover displacement. Subsequently, the research team had incorporated the boundary condition of a venting orifice and developed a coupled “venting–pressure-displacement” model capable of effectively describing the ejection response of unhinged covers [21]. Building upon this, van de Meulenhof et al. [22] had extended the model to a four-degree-of-freedom system by introducing the rotational degree of freedom of the cover, and reproduced the complete process of hinged manhole “ejection-rebound-re-ejection” based on impulse-momentum equations. Although the aforementioned models have become relatively comprehensive in simulating the dynamic response of manhole covers, equal attention must be paid to the underlying air–water processes that initiate such displacements. For example, Zhou et al. [23,24] had systematically analyzed the influence of cover orifice size on air pocket accumulation and shaft pressure fluctuations, and further explored the coupled effects of in-pipe convective heat transfer and unsteady friction on peak pressure dynamics. Similarly, Fang et al. [1] employed three-dimensional transient simulations of T-junction pipelines to reveal a characteristic “compression–splitting-release” process of air pockets within confined spaces, providing an important supplement to the understanding of manhole displacement phenomena.

In summary, although current urban flood research has largely achieved its fundamental goal of safeguarding lives and property, there remains a lack of systematic investigation into manhole cover displacement—a near-field, high-risk phenomenon that poses a direct threat to pedestrian safety. In particular, due to the severe scarcity of prototype experimental data, existing studies have yet to provide sufficient support for the identification, modeling, and evaluation of this specific risk. To bridge this research gap, the present study has established a prototype experimental platform tailored for hinged manhole covers and conducted comparative dual-shaft experiments under varying counterweight conditions. The aim is to obtain quantifiable and reproducible datasets that can serve as a solid foundation for revealing the underlying mechanisms of manhole ejection, developing predictive models, and improving urban flood risk assessment frameworks.

2. Experimental Investigation

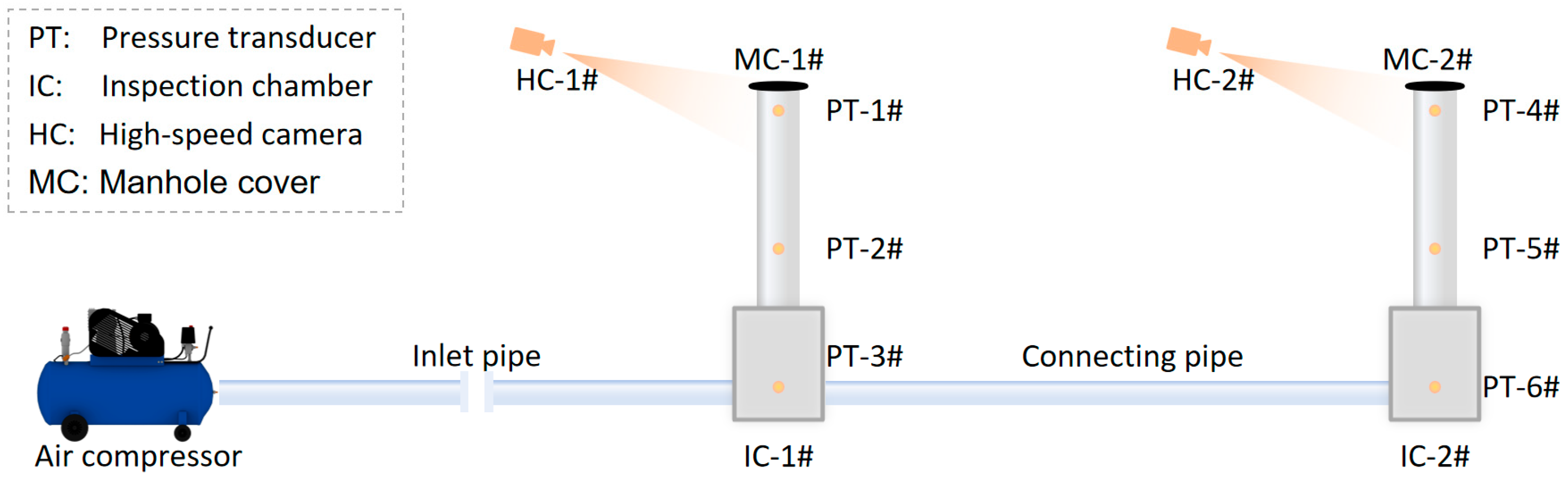
2.1. Experimental Apparatus

A prototype double-shaft experimental platform was constructed in the laboratory for this study. It is composed of an air supply system, two inspection chambers, a connecting pipe, and a data acquisition system (see Figure 2). The two inspection chambers had been designated as IC-1# and IC-2#; the pressure transducers had been labeled PT-1# through PT-6#; the two hinged manhole covers had been designated MC-1# and MC-2#; and the two high-speed cameras had been labeled HC-1# and HC-2#. The rotation angle of each manhole cover had been defined as positive when opening upward.

(1)

Air supply system: A screw-type air compressor (model JAC30B-8) had been employed, with a rated discharge capacity of 5.0 m³/min, a maximum discharge pressure of 0.8 MPa, a drive power of 36.8 kW, and a rated rotational speed of 2500 rpm. Compressed air had been delivered from the compressor to the downstream inspection chamber through the inlet pipe, which had been 5.0 m in length and 0.5 m in internal diameter.

(2)

Single-chamber structure: Each inspection chamber had been composed of a chamber body, a vertical shaft, and a hinged manhole cover. The internal dimensions of the chamber body had been 2.0 m × 1.9 m × 2.4 m; the vertical shaft had an internal diameter of 0.7 m and a height of 4.6 m; and the manhole cover had a diameter of 0.7 m and a self-weight of 25.0 kg. A single vent orifice had been installed on each manhole cover, with an orifice diameter of 0.04 m. Three pressure transducers (PT-1# to PT-3#) had been installed at equal vertical intervals from top to bottom, with a measurement range of 0–200 kPa, a sampling frequency ≥ 1 kHz, and an accuracy of 0.1%, in order to record the transient air pressure evolution within the shaft. The bouncing motion of the manhole cover had been recorded by high-speed cameras in two imaging formats: 1920 × 1080 at 100 fps and 2560 × 1600 at 50 fps, for back-calculating the rotation angle and the lift-off moment.

(3)

Dual-chamber connection: The center-to-center distance between the two inspection chambers in the actual engineering prototype had been approximately 80 m. Considering that this study had focused on the critical overpressure triggering and manhole cover response induced by localized air injection—and given that the speed of sound in air is relatively high (approximately 340 m/s)—a 10.0 m-long connecting pipe with an internal diameter of 0.5 m had been adopted to link the two chambers in the experiment, so as to accommodate laboratory space constraints while preserving the key time scales as closely as possible. Under this setup, the acoustic transmission time had been reduced from approximately 0.234 s in the prototype to 0.029 s in the experiment (about 1/8), but it still remained significantly smaller than the characteristic time of a single charge–release cycle. Given the high sampling frequency and temporal resolution of the pressure transducers and high-speed cameras used in the test, the response variations caused by this distance scaling had been considered adequately detectable, thereby ensuring the accuracy of experimental observations.

2.2. Experimental Conditions and Procedures

To account for potential slight variations in the gap between the manhole cover and the frame during repeated bouncing, which may affect the air release rate and the cover’s response, industrial grease is applied to seal the ring gap prior to each test. This treatment is intended to enhance the overall air-tightness and to ensure consistent initial boundary conditions across all trials, thereby maintaining the stability and repeatability of the experimental results.

A small amount of compressed air is injected into the system before each round of testing, and the readings of pressure transducers PT-1# to PT-6# are monitored over time under non-bouncing conditions. The overall air-tightness is considered sufficient for the experimental requirements if the system pressure drop does not exceed 50 Pa over a 3 min period.

Counterweights of 0, 5, 10, 15, 20, 25, and 30 kg are installed on each manhole cover to construct different initial anti-ejection test conditions in order to investigate the influence of counterweight mass on critical overpressure triggering and bouncing response. No fewer than three repeated tests are conducted under each test condition to verify the stability and repeatability of the experimental data.

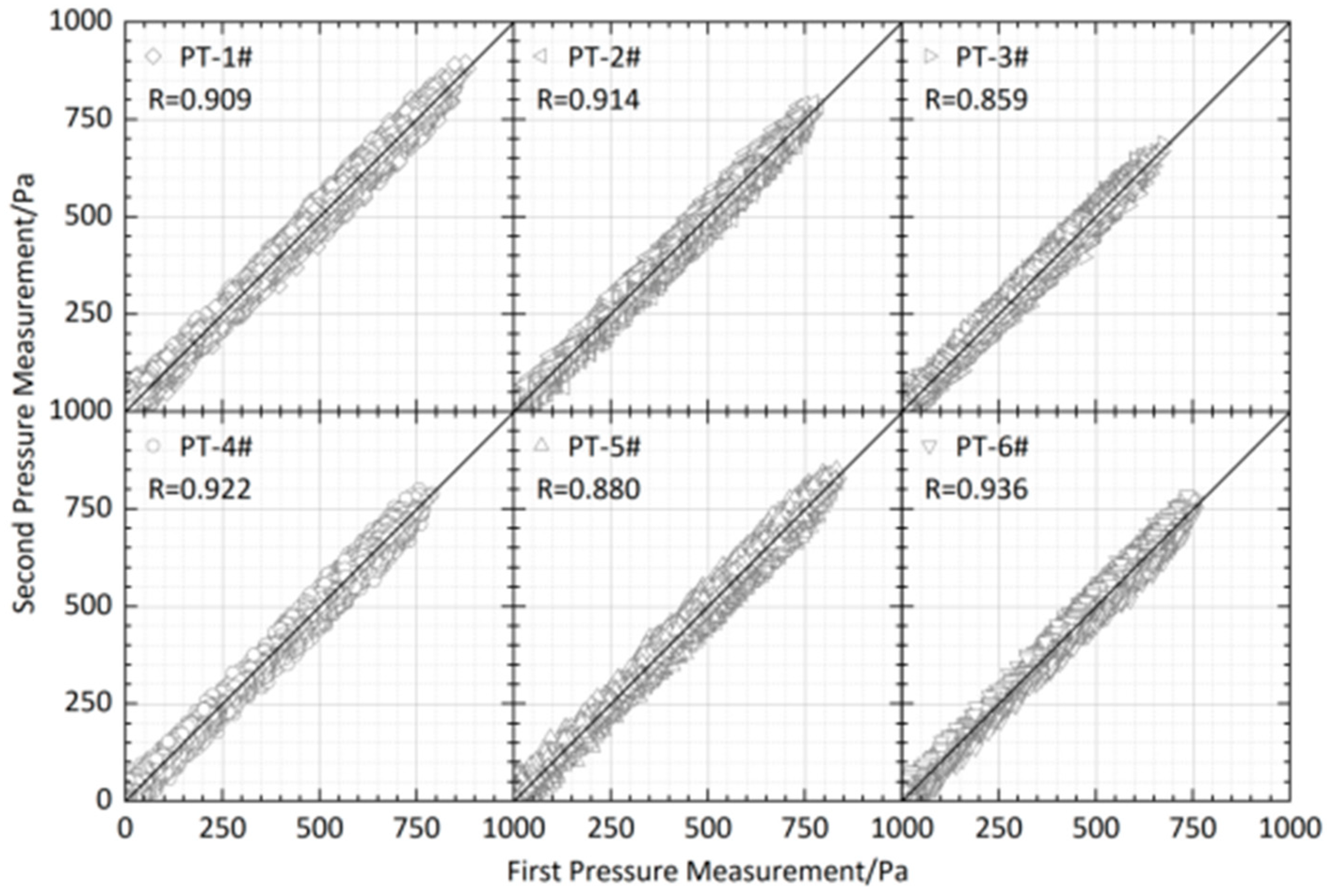
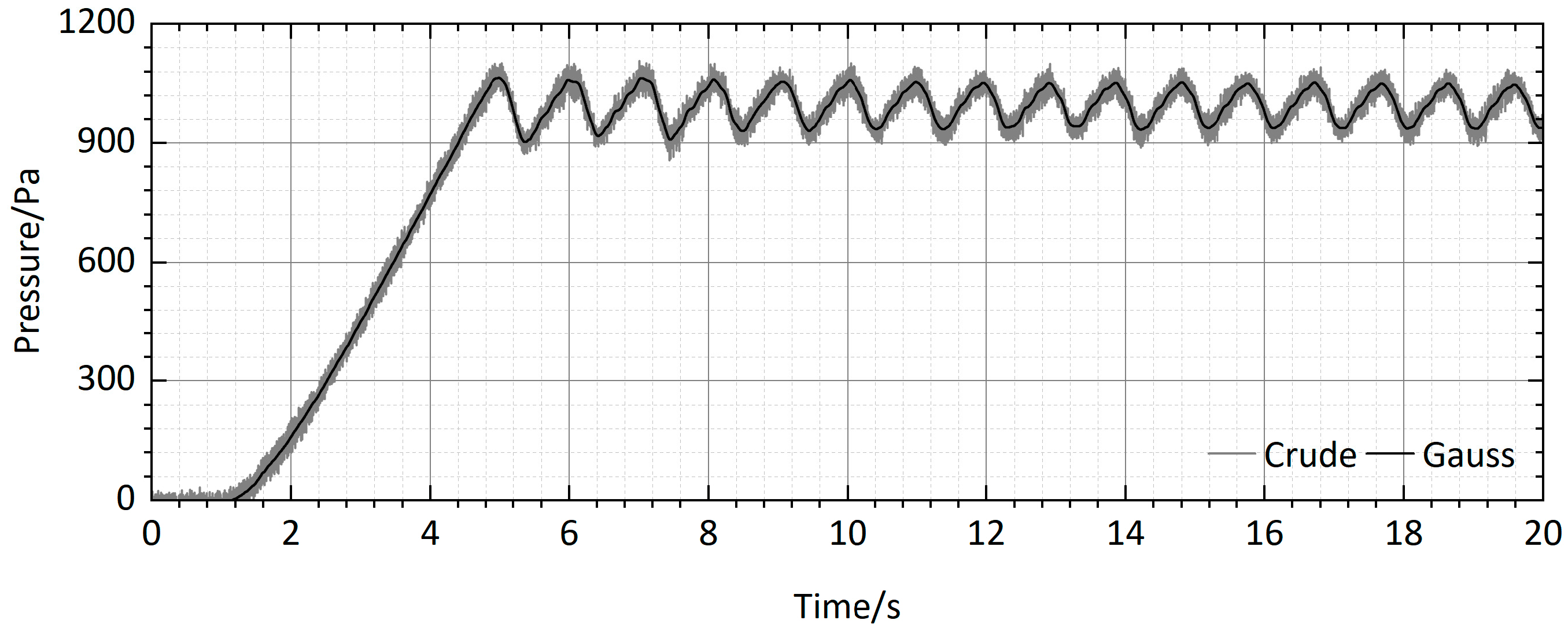
2.3. Comparison of Repeatability Tests

Figure 3 presents the measured pressures obtained from multiple repeated tests, in which the horizontal axis represents the data from the first trial, while the vertical axis corresponds to the data from the second trial. In addition, the correlation between repeated trials is analyzed by calculating the Pearson correlation coefficient, which is defined as follows [25]:

$$R={\displaystyle \frac{\sum _{i = 1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum _{i = 1}^n{(X_i-\overline{X})}^2}\sqrt{\sum _{i = 1}^n{(Y_i-\overline{Y})}^2}}}$$

(1)

where n represents the number of data points in sample X or Y; $\overline{X}$ and $\overline{Y}$ represent the mean values of sample X and Y, respectively; and X_i and Y_i represent the measured data indexed by i in sample X and Y, respectively.

For the repeated trials without counterweights on the manhole covers, the Pearson correlation coefficients of the measured pressure range from 0.859 to 0.936. These correlation data indicate that the test conditions in the generalized model experiments are precisely controlled, the procedures are repeatable, and the results are reliable and valid.

3. Simulation Results Analysis

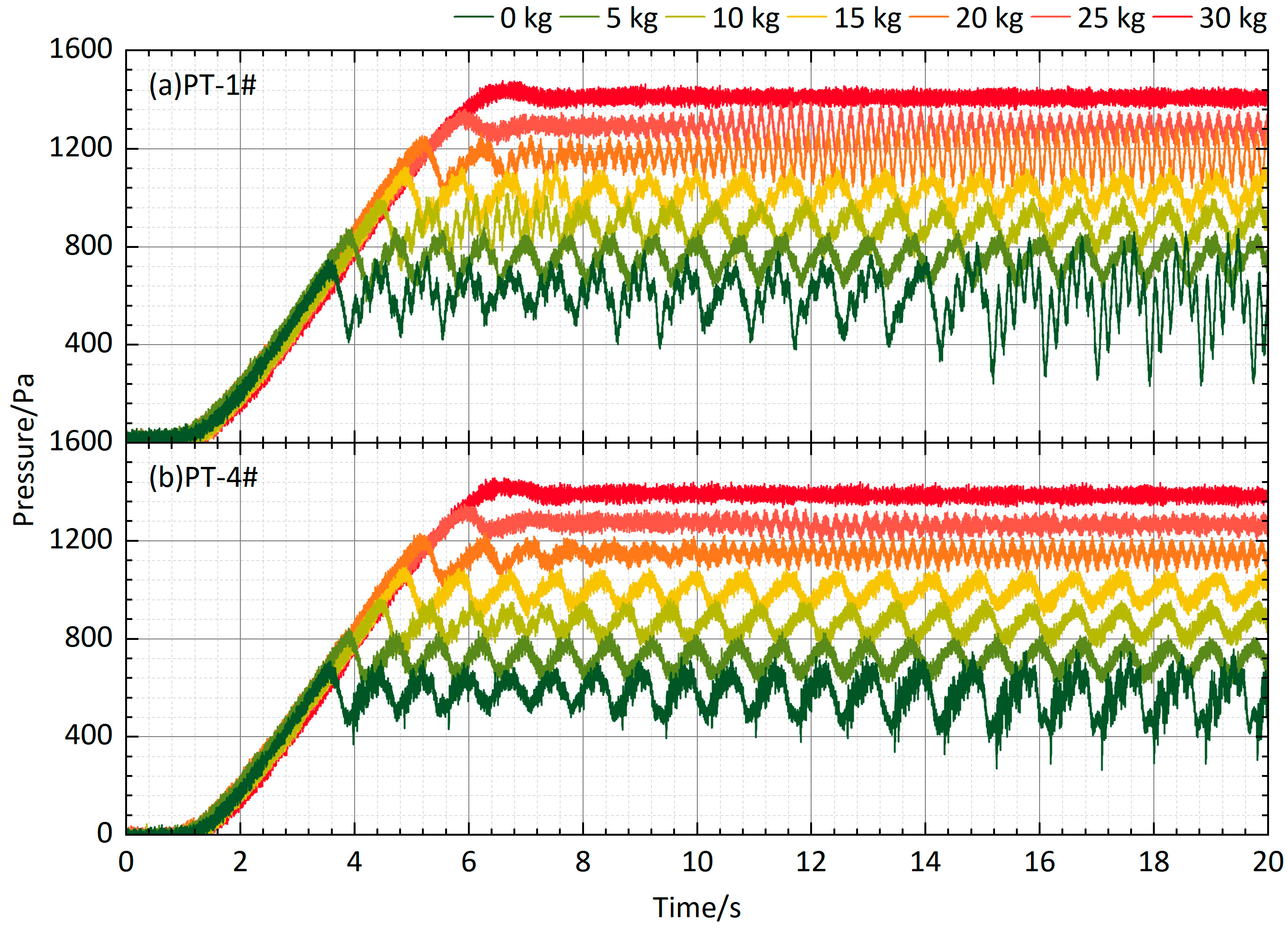
3.1. Bounce Response of a Single Manhole Cover

To investigate the bounce behavior of a single hinged manhole cover, this test series was conducted by sealing MC-1# and applying various counterweights (0, 5, 10, 15, 20, 25, and 30 kg) to MC-2#. The pressure fluctuations recorded by transducers PT-4# to PT-6# under different counterweight conditions are presented in Figure 4.

As shown in Figure 4, pressure peaks measured at multiple locations within the shaft exhibit comparable magnitudes, confirming the feasibility of using a 10 m connecting pipe. This indicates that the acoustic transmission time is much shorter than the characteristic timescale of the pressurization–venting process. The peak pressure associated with the initial lift-off increases with the counterweight, reaching 737, 814, 943, 1099, and 1241 Pa under 0, 5, 10, 15, and 20 kg, respectively. The second peak, although slightly lower, remains close in value—measured at 717, 798, 939, 1092, and 1223 Pa, respectively. It is worth noting that when the counterweight was increased to 25 and 30 kg, the first pressure peaks rose further to 1339 and 1454 Pa. However, due to incomplete reseating of the cover after bounce—which resulted in a gap forming between the cover and the rim—gas leakage persisted, preventing further significant bouncing. In these cases, the pressure gradually stabilized at approximately 1266 and 1394 Pa, respectively.

To further reveal the coupling between displacement and pressure during single-cover bounce, Figure 5 presents the sequential motion of the hinged cover under a counterweight of 15 kg for both the first and second bounce events.

During the first bounce, it took 0.30 s for the cover to reach its maximum deflection after lift-off, during which the edge displacement reached 0.030 m and the rotation angle was approximately 2.48°. The cover then settled back onto the rim over a period of 0.18 s. After approximately 0.47 s, a second lift-off occurred, requiring 0.39 s to reach the peak position; both the maximum displacement and angle have been similar to those of the first event, again measuring 0.030 m and 2.48°, respectively. As shown in Figure 4, the critical overpressure that triggered the initial bounce corresponds approximately to the first pressure peak. However, when the cover reached its maximum displacement, the pressure recorded by PT-4# was about 957 Pa, which is not the minimum of that pressure fluctuation cycle. The lowest pressure, approximately 900 Pa, occurred after the cover had fully reseated, indicating that the sequence of “cover bounce–gas release–resealing” spans more than half of one pressure fluctuation cycle.

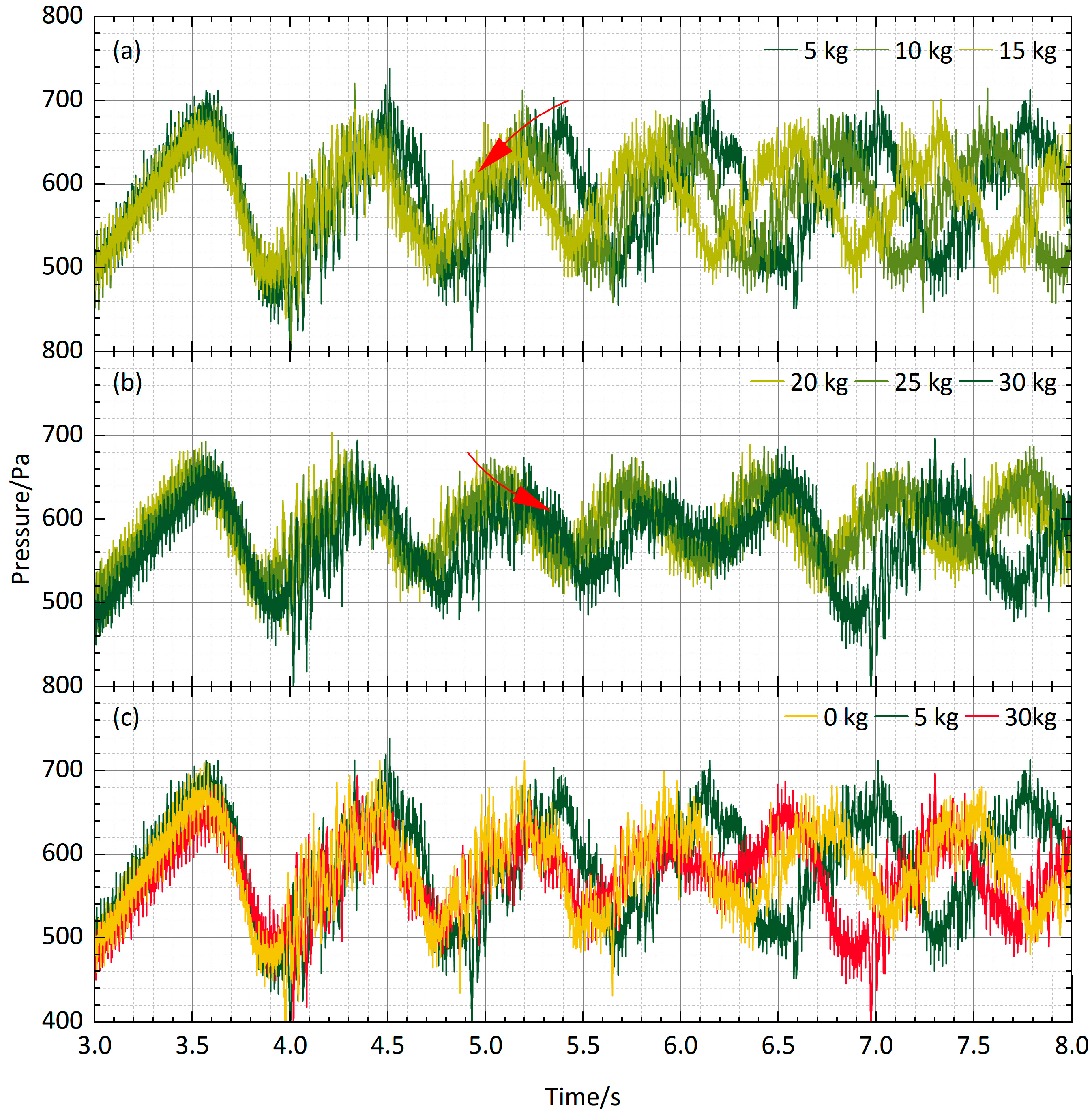
3.2. Bounce Response of Dual Manhole Covers

The preceding subsection established the characteristic pattern of pressure fluctuations associated with the bounce of a single manhole cover. To further investigate the influence of varying counterweights on MC-1# upon the bounce behavior of MC-2#, Figure 6 presents the pressure fluctuations recorded by PT-4# under the condition that MC-2# was held at a fixed counterweight of 0 kg, while the counterweight on MC-1# was systematically varied. Emphasis is placed on the evolution of pressure oscillations following the initial lift-off event.

Compared with the single-cover cases shown in Figure 4, the results in Figure 6 indicate that the critical overpressure required for bounce is not directly influenced by changes in the counterweight of the other cover, provided the cover’s own counterweight remains constant. However, due to the presence of a venting pathway through the adjacent shaft, the air pressure within the cavity is locally reduced at the critical moment, resulting in a measured overpressure at lift-off that is lower than in the single-shaft condition. The overall critical overpressure stabilizes at approximately 700 Pa, reflecting a coupling effect induced by orifice-mediated venting during the cover bounce process.

Further analysis of Figure 6a,b shows that the frequency of pressure fluctuations at MC-2# gradually increases when the counterweight on the adjacent MC-1# is set to 5, 10, or 15 kg, but decreases significantly as the counterweight is increased to 20, 25, or 30 kg. This “rise–then-fall” trend predominantly occurs under asymmetric conditions, where MC-1# remains stationary while MC-2# undergoes independent bounce. In contrast, synchronized or near-synchronized oscillatory responses between the two shafts are only observed when equal counterweights are applied to both covers, allowing simultaneous bounce conditions to be met. Additionally, the case shown in Figure 6c, where MC-1# = MC-2# = 0 kg, exhibits a fluctuation pattern that deviates from the previously observed trend. This suggests that under extremely light loading, the system’s bounce behavior may be constrained by the phase offset and nonlinear interference associated with dual-shaft venting, rather than by the counterweight effect alone.

To further investigate the overall system response under dual-shaft coupling, Figure 7 plots the pressure time histories recorded at two sensor locations—PT-1# and PT-4#—under conditions where identical counterweights (ranging from 0 to 30 kg) have been applied to both MC-1# and MC-2#. The results show that the pressure fluctuations recorded at the two measurement points are highly consistent, with the waveforms nearly overlapping. This indicates that, given the much higher speed of sound in air relative to the characteristic transmission time of the system, both shaft openings respond almost simultaneously to pressure variations within the cavity. In other words, localized events such as cover bounce, reseating, and leakage can be transmitted across the system in an extremely short time, significantly enhancing the dynamic coupling between the two shafts.

Using the data from PT-4# as an example, the critical overpressures corresponding to the initial bounce under equal counterweight conditions for MC-1# and MC-2# have been measured as 682, 808, 939, 1057, 1195, 1310, and 1429 Pa for counterweights of 0, 5, 10, 15, 20, 25, and 30 kg, respectively—exhibiting a typical trend in which greater counterweights correspond to higher bounce thresholds. However, under loading conditions of no less than 20 kg, the amplitude of subsequent pressure fluctuations is noticeably reduced, indicating a transition to decaying-mode bounce behavior. This outcome is consistent with the earlier analysis: excessive counterweight prevents the manhole cover from fully reseating after bounce, resulting in the formation of a gap between the cover and the rim. This gap induces a continuous depressurization process, which inhibits the accumulation of pressure energy within the system necessary to trigger a secondary bounce. As a result, both the frequency and amplitude of pressure oscillations decrease concurrently.

It can thus be concluded that the bounce response of the dual-shaft system depends not only on the applied counterweights, but also on the combined effects of inter-shaft venting behavior, pressure transmission speed, and overall system synchrony.

3.3. Temporal Correspondence and Amplitude Relationship Between Pressure and Displacement

To suppress high-frequency noise in the pressure sequence and improve the stability of subsequent time-alignment, a Gaussian filter was applied to the raw pressure data from PT-4# [26]. Taking the case of “MC-1# sealed, MC-2# loaded with 15 kg” as an example, Figure 8 compares the pressure signals before and after filtering. The noise was effectively attenuated, providing a reliable basis for subsequent temporal analysis.

$$G[x]={\displaystyle \frac{1}{S}}\mathit{exp}\left(-{\displaystyle \frac{(x-\frac{k}{2}{)}^2}{2{\sigma }^2}}\right)$$

(2)

where x represents the index of the kernel; k represents the size of the kernel; $\sigma$ represents the standard deviation; and S represents the normalization factor.

As the displacement of the manhole cover was extracted from 1920 × 1080 @ 100 fps high-speed video, the pressure data have been resampled to ensure a unified time scale, with the moment of initial lift-off used as the alignment reference. Based on this, a synchronized time–history relationship between the pressure at PT-4# and the rotation angle of MC-2# was established, as shown in Figure 9.

The typical temporal sequence reveals that, prior to lift-off, the pressure within the shaft is primarily governed by static pressure. At the onset of bounce, a brief pressure rise is observed, attributed to the rapid outward airflow induced by the slight opening of the cover, which increases the contribution of dynamic pressure. This is followed by a combined phase of substantial air discharge and progressive reseating of the cover, during which the pressure first drops and then rises. Notably, the maximum displacement does not coincide with the pressure minimum; instead, the minimum pressure typically occurs after the cover has fully reseated and re-sealed the shaft. This reflects a distinct phase lag and periodicity characterized by “pressure leading displacement”. Because the manhole cover returns to its fully seated position after each bounce, this reset mechanism ensures that every lift-off event starts from identical initial conditions. Consequently, the relationship between the critical overpressure and the lift-off angle remains consistent for both the first and subsequent lift-offs.

In terms of amplitude, an increase in counterweight leads to a higher critical overpressure required to trigger bounce, while the maximum rotation angle of the cover exhibits a monotonic decreasing trend. For example, when the counterweight was set to 25, 30, 35, 40, and 45 kg (Total mass), the corresponding critical overpressures have been measured as 675, 750, 915, 1064, and 1199 Pa, respectively, with maximum rotation angles of 2.82°, 2.71°, 2.48°, 2.26°, and 1.80°. This is consistent with the mechanical equilibrium of a nonlinear bounce model: a higher-pressure driving force is required to overcome damping and the restoring torque when the rotational inertia and gravitational torque are larger; as pressure decays, the angular amplitude correspondingly converges toward zero.

In summary, the pressure–displacement relationship exhibits a clear phase lag in time and a paired amplitude pattern in which heavier loading corresponds to higher critical overpressure and smaller maximum angles. These results provide solid temporal evidence to support the development of quantitative fitting and classification criteria based on critical overpressure and displacement amplitude.

4. Discussion

This study demonstrates that increasing the manhole cover mass significantly raises the critical overpressure required for initial lift-off, while simultaneously reducing the bounce angle and height. Under heavier loading, the system is also prone to a response mode characterized by incomplete reseating after the first bounce, continuous air leakage, and rapid attenuation of pressure fluctuations (see Figure 4 and Figure 7). This is consistent with general understanding in nonlinear bounce dynamics: greater gravitational torque and rotational inertia raise the threshold required to overcome damping and restoring torque, thereby leading to smoother pressure fluctuations and a relatively prolonged oscillation period. Relevant dynamic models—covering both free vertical motion and hinged rotational motion—have been established and applied to explain phenomena such as initial lift-off, rebound, and secondary bounce, thereby providing a mechanical framework for interpreting the experimental trends observed in this study [20,21,22].

When the two vertical shafts are connected by a short horizontal pipe, pressure disturbances within the cavity propagate back and forth through the “shaft–pipe–shaft” system on a timescale close to the speed of sound in air. As a result, the pressure time histories in adjacent shafts exhibit near-synchronous characteristics. If one shaft forms an effective venting pathway at the critical moment, the pressure peak in the other shaft is suppressed. Even if bounce occurs, the resulting bounce height remains minimal. As shown in Figure 10, this effect is illustrated by comparing the before-and-after response of MC-1# under the condition where both covers have been loaded with 15 kg. The red box highlights the comparison between pre- and post-bounce states. Due to the minimal motion involved, the cover did not rotate about its hinge axis but exhibited only a slight local lift. At this moment, gas release from the system was primarily achieved through the bounce of MC-2#. Combined with the findings of Allasia and Molina et al. [27,28], the above observations suggest that during the stages of air-pocket rise and release, spatially non-uniform gas–liquid interfaces and velocity fields are prone to develop, which can induce various cover motion patterns such as hovering, fluttering, and brief unseating.

Based on the experimental results of this study and prior research, the prevention and control of manhole cover bounce can be summarized as a closed-loop strategy comprising “source mitigation–process regulation–terminal protection–monitoring and early-warning”:

(1)

Source mitigation: Large trapped air pockets caused by rapid filling should be avoided as much as possible. This can be achieved through operational scheduling, controlled overflow, and pre-venting measures, all of which help reduce the risk of transient overpressure at its origin.

(2)

Process regulation: Ventilation structures should be optimized in terms of orifice size, layout, and the use of one-way or two-way valves. Pressure-relief or discharge devices should be installed in critical sections. Both experimental and numerical results confirm that venting boundaries are key levers in controlling overpressure magnitude.

(3)

Terminal protection: Without compromising maintenance safety, anti-lift structures (such as locking or limiting mechanisms) should be implemented, and the hinged cover structure and seat-ring sealing should be reinforced or weighted appropriately. This ensures a balanced capacity for both resisting bounce and allowing controllable venting under transient overpressure.

(4)

Monitoring and early-warning: Real-time monitoring of water level and transient pressure should be established with multi-level alert thresholds. Triggered warnings should link to operational protocols such as flow control or traffic restriction to enable proactive intervention.

5. Conclusions

Based on a full-scale twin-shaft experimental platform, this study investigated the bounce response of hinged manhole covers under counterweights ranging from 0 to 30 kg. Multiple operating conditions and repeated trials have been conducted. Multi-point pressure measurements and high-speed video recordings have been synchronously collected and used to perform pressure–displacement time alignment, identify the critical overpressure for initial lift-off, compare dual-shaft coupling effects, and assess experimental repeatability. The influence of counterweight on critical thresholds, amplitude, and frequency was analyzed, and an engineering-oriented criterion linking counterweight and critical overpressure was proposed. The main findings are summarized as follows:

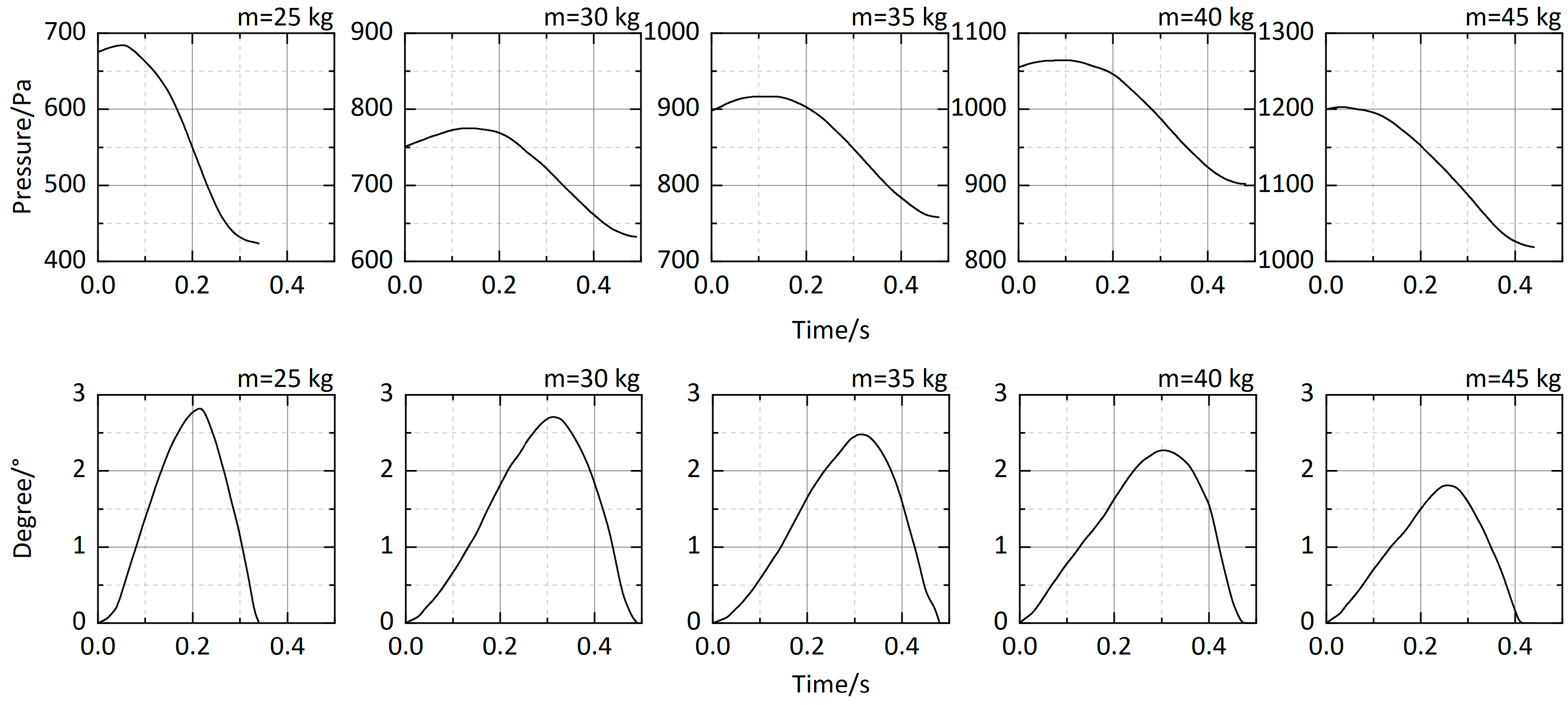
• The critical overpressure required for initial bounce increases monotonically with counterweight. In this study, the lowest observed threshold was approximately 700 Pa. When the counterweight exceeded 25 kg, the cover failed to fully reseat after the first bounce, resulting in continuous air leakage and the absence of subsequent significant rebounds. Under such conditions, the system stabilized at an overpressure of approximately 1300 Pa.
• The trend observed in single-shaft cases—where the pressure fluctuation period initially increases and then decreases with increasing cover mass—no longer holds when both shafts undergo simultaneous bounce. In the dual-shaft configuration, the phase difference in venting and the coupled propagation effects dominate the subsequent fluctuation pattern and frequency, masking the mass–period relationship observed in single-shaft scenarios.
• The critical overpressure does not coincide with the peak of the pressure waveform. For counterweights of 25, 30, 35, 40, and 45 kg, the corresponding critical overpressures have been 675, 750, 915, 1064, and 1199 Pa, respectively, while the maximum rotation angles have been 2.82°, 2.71°, 2.48°, 2.26°, and 1.80°. In all cases, the pressure waveform reached a maximum value greater than the critical overpressure, indicating a pronounced phase lag in which the pressure peak precedes the peak displacement.