Comparative Analysis on the DMA Partitioning Methods Whether Trunk Mains Participated
Abstract
:1. Introduction
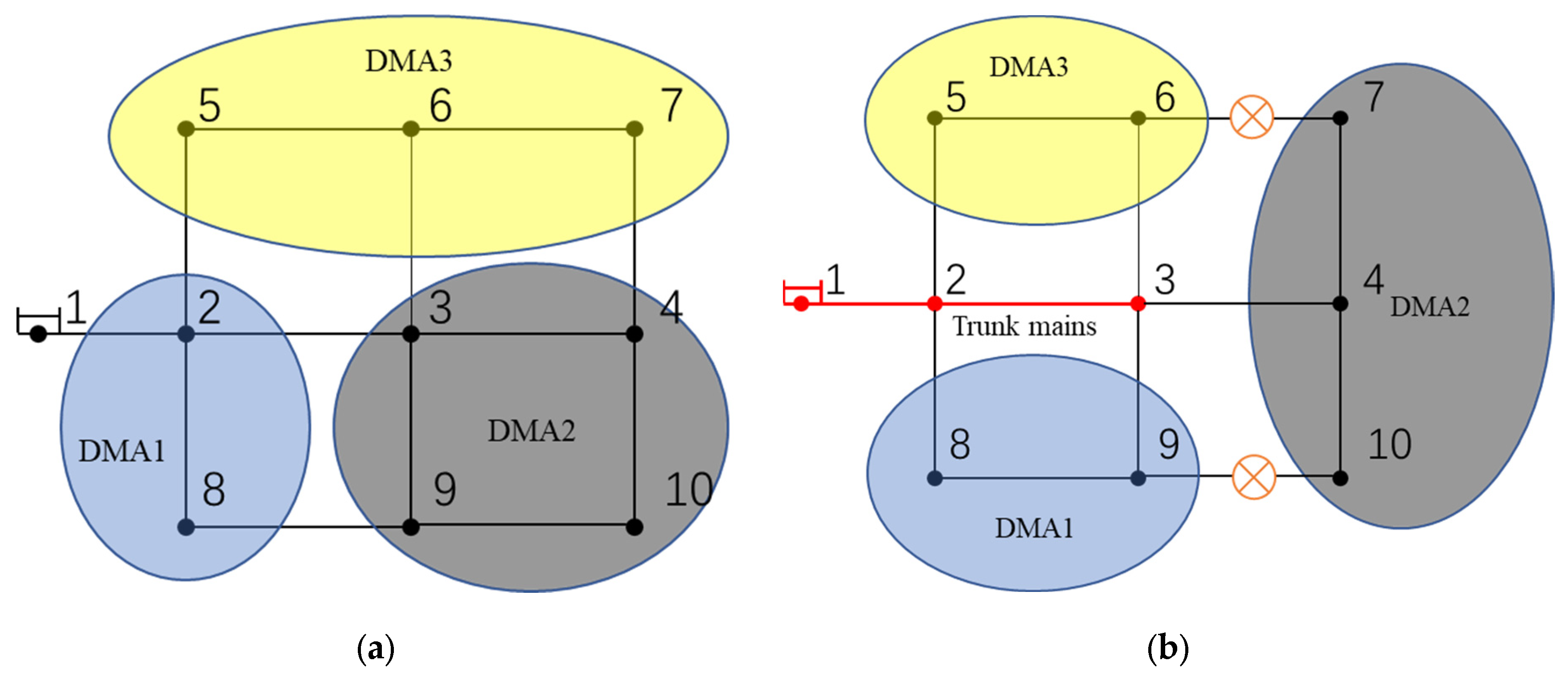
2. Brief Introduction to Two Partitioning Methods
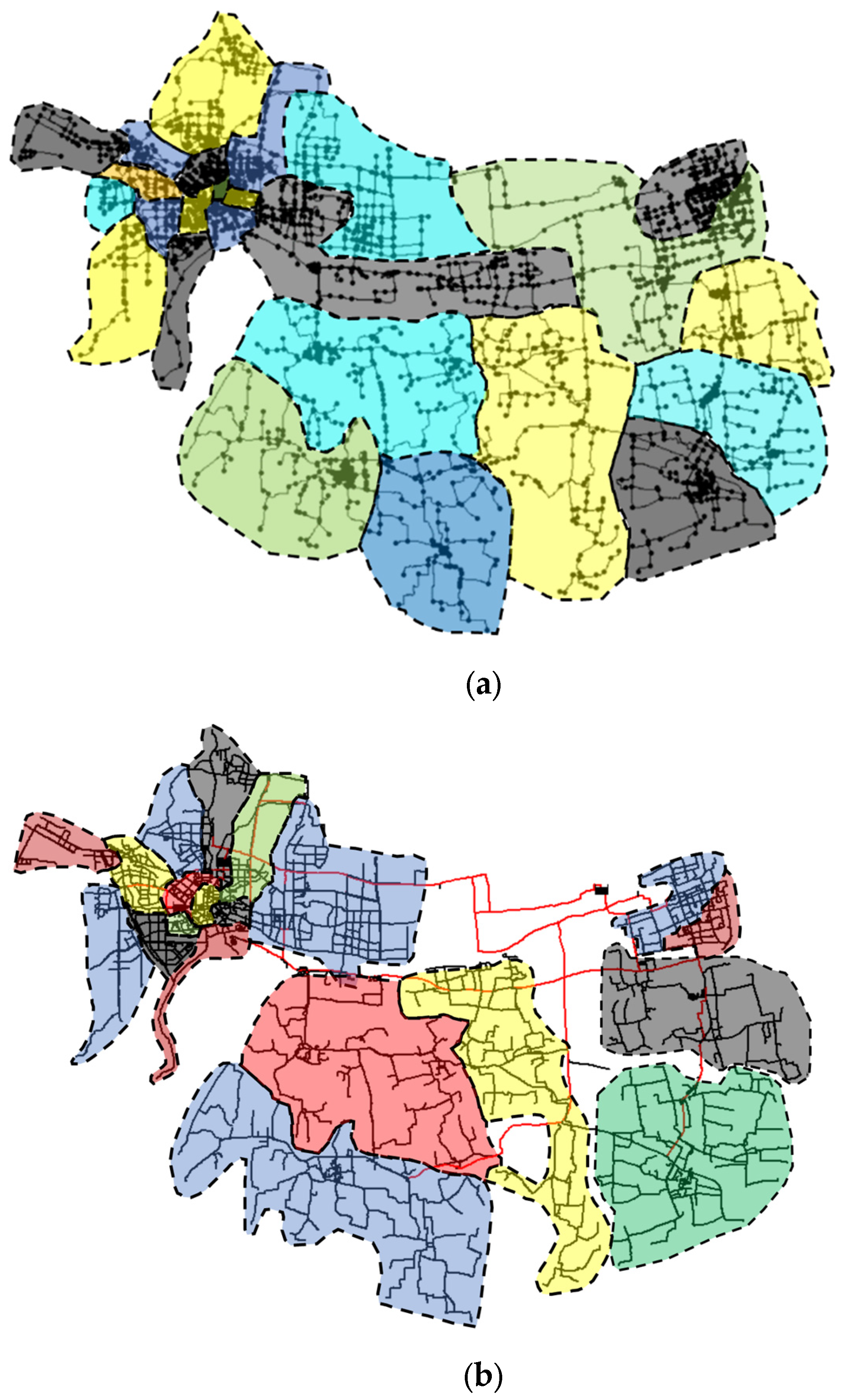
3. Introduction to Case Network
4. Performance Comparison
4.1. Economy
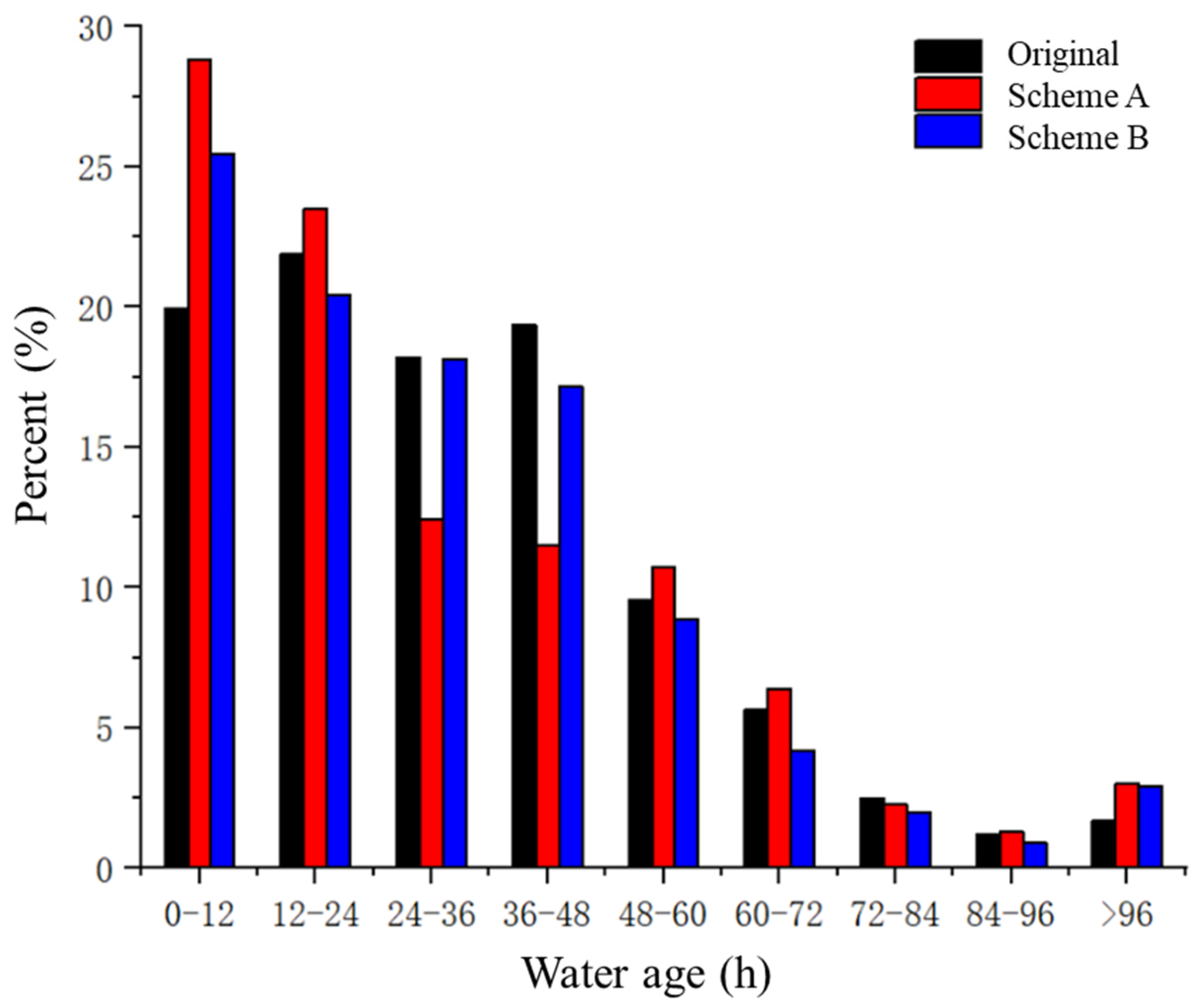
4.2. Water Age
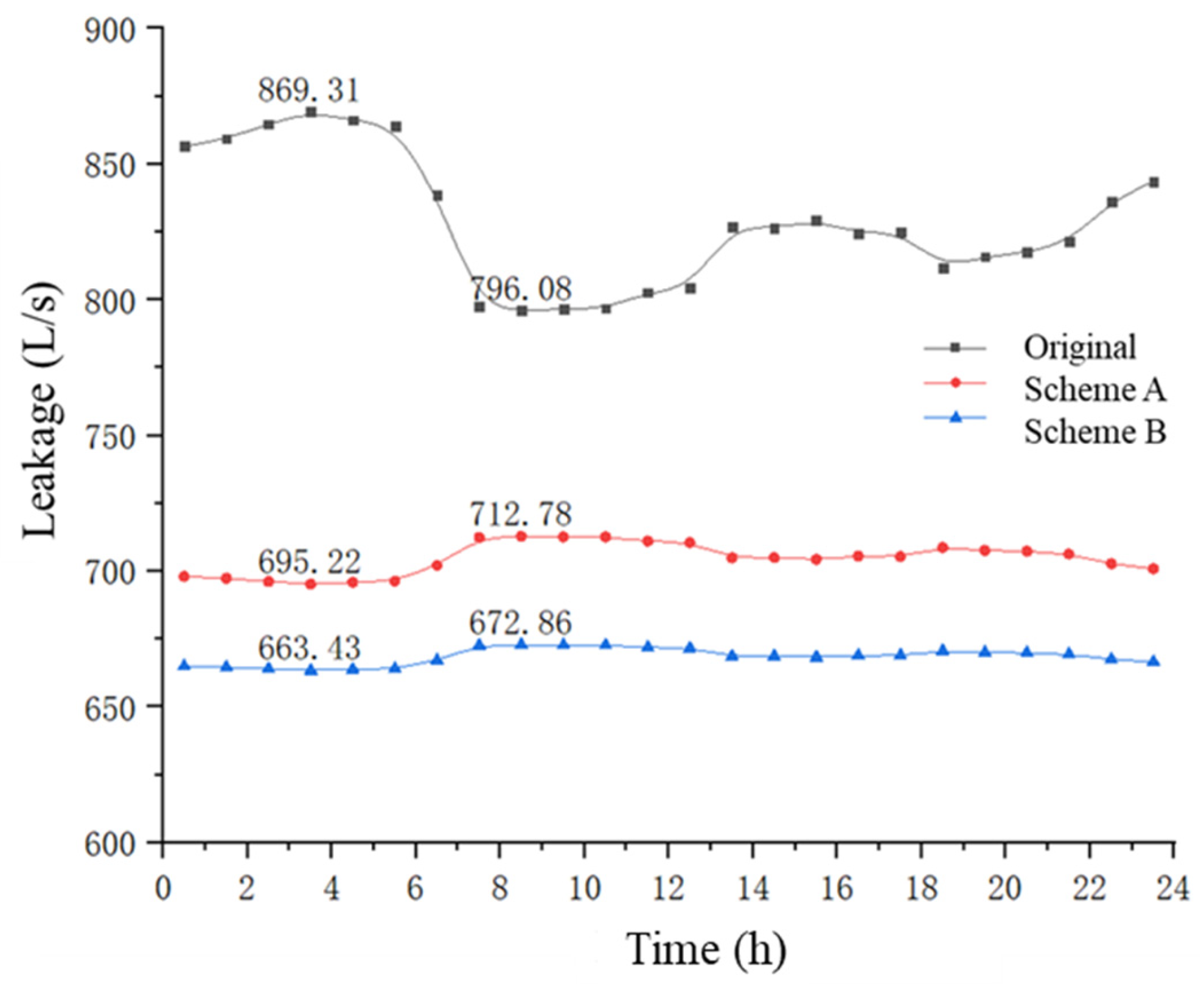
4.3. Leakage Control
5. Conclusions
- (1)
- For economy, the method in which the trunk mains participates in the partitioning process (Scheme A) is better than the method in which the trunk mains does not participate in the partitioning process (Scheme B). In Scheme B, when the trunk mains are separated from the WDN, many boundary pipes are generated within the remaining pipe system, increasing the cost of the DMA partition. In the case study, even though Scheme B has eight fewer DMA partitions than Scheme A, the overall project cost is 15.34% higher than Scheme A. Therefore, for cities with tight budgets, it is recommended to choose the method wherein the trunk mains participate in the partitioning process.
- (2)
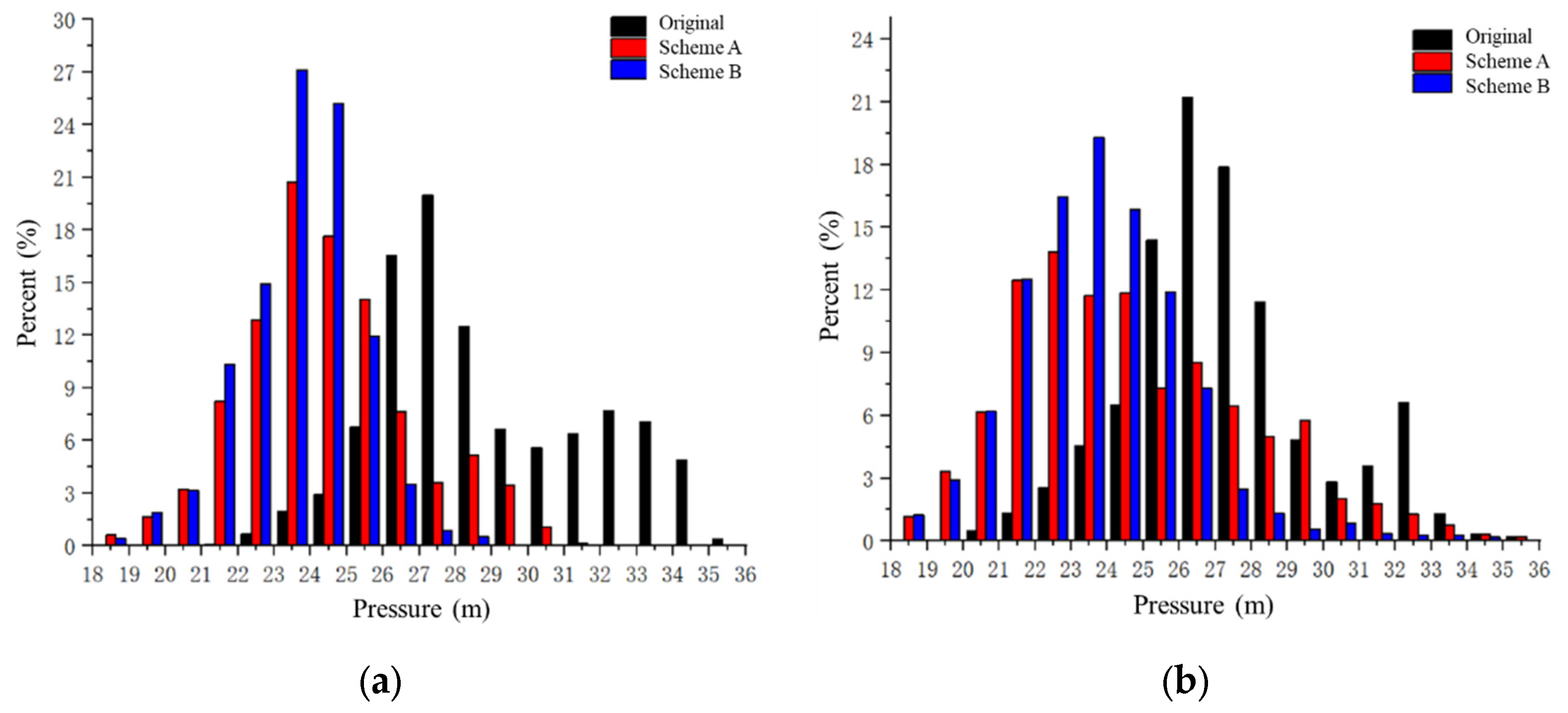
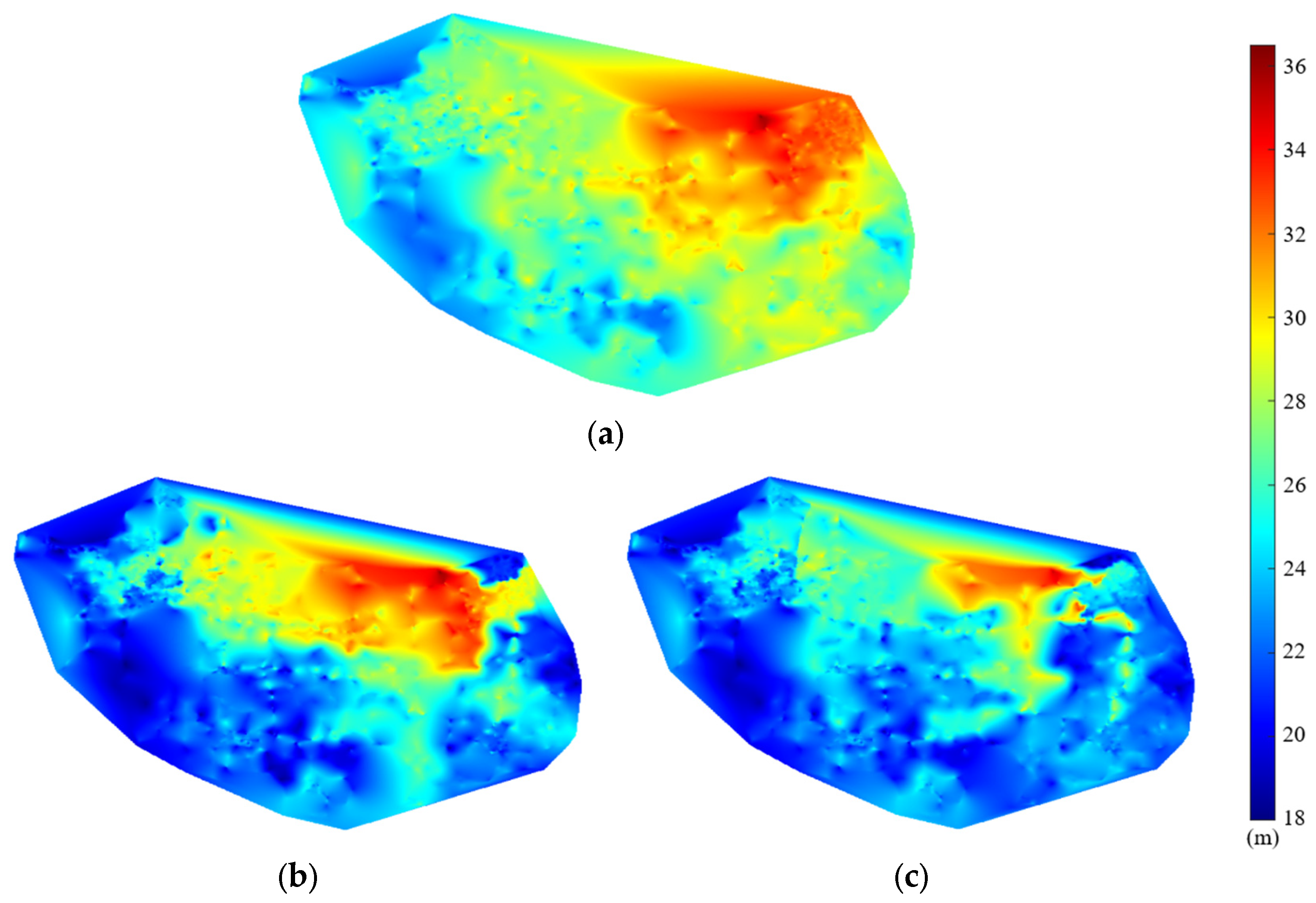
- For water quality, Scheme B is a better choice than Scheme A. In the case study, Scheme B has less high-age water than Scheme A. Even the percentage of water in age 12–96 h of Scheme B is slightly lower than the original WDN. Therefore, if water quality protection needs to be considered when partitioning the WDN, it is recommended to choose the method in which the trunk mains do not participate in the partitioning process.
- (3)
- For leakage control, Scheme B is better than Scheme A. There is an obvious upstream and downstream relationship between DMAs in Scheme A. The impact on downstream DMAs needs to be considered when managing the pressure of upstream partitions. In contrast, the trunk mains supply water to DMAs directly in Scheme B. The DMAs are relatively independent. Therefore, in terms of its long-term leakage control objectives, it is recommended to choose the method wherein the trunk mains do not participate in the partitioning process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ozdemir, O. Water leakage management by district metered areas at water distribution networks. Environ. Monit. Assess. 2018, 190, 182. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.F.; Tzatchkov, V.; Alcocer-Yamanaka, V.H. Dual-use value of network partitioning for water system management and protection from malicious contamination. J. Hydroinformatics 2015, 17, 361–376. [Google Scholar] [CrossRef]
- Liu, J.; Kang, Y. Segment-based resilience response and intervention evaluation of water distribution systems. J. Water Supply Res. Technol.-Aqua 2022, 71, 100–119. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, F.; Kapelan, Z.; Savic, D.; Duan, H.F.; Zhang, Q. Efficient leak localization in water distribution systems using multistage optimal valve operations and smart demand metering. Water Resour. Res. 2020, 56, e2020WR028285. [Google Scholar] [CrossRef]
- Shao, Y.; Yao, H.; Zhang, T.; Chu, S.; Liu, X. An Improved Genetic Algorithm for Optimal Layout of Flow Meters and Valves in Water Network Partitioning. Water 2019, 11, 1087. [Google Scholar] [CrossRef] [Green Version]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social Network Community Detection for DMA Creation: Criteria Analysis through Multilevel Optimization. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A practical multi-objective optimization sectorization method for water distribution network. Sci. Total Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef]
- Han, R.; Liu, J. Spectral Clustering and Genetic Algorithm for Design of District Metered Areas in Water Distribution Systems. Procedia Eng. 2017, 186, 152–159. [Google Scholar] [CrossRef]
- Diao, K.; Zhou, Y.; Rauch, W. Automated Creation of District Metered Area Boundaries in Water Distribution Systems. J. Water Resour. Plan. Manag. 2013, 139, 184–190. [Google Scholar] [CrossRef]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-Based Procedure for Partitioning Water Distribution Systems into Independent Districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An Automated Tool for Smart Water Network Partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M. A heuristic design support methodology based on graph theory for district metering of water supply networks. Eng. Optim. 2011, 43, 193–211. [Google Scholar] [CrossRef]
- Gomes, R.; Sá Marques, A.; Sousa, J. Identification of the optimal entry points at District Metered Areas and implementation of pressure management. Urban Water J. 2012, 9, 365–384. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Fuertes-Miquel, V.S. Design of Water Distribution Networks using a Pseudo-Genetic Algorithm and Sensitivity of Genetic Operators. Water Resour. Manag. 2013, 27, 4149–4162. [Google Scholar] [CrossRef]
- Liu, J.; Lansey, K.E. Multiphase DMA Design Methodology Based on Graph Theory and Many-Objective Optimization. J. Water Resour. Plan. Manag. 2020, 146, 04020068. [Google Scholar] [CrossRef]
- Ferrari, G.; Savic, D.; Becciu, G. Graph-Theoretic Approach and Sound Engineering Principles for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2014, 140. [Google Scholar] [CrossRef] [Green Version]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Pérez-García, R. A Novel Water Supply Network Sectorization Methodology Based on a Complete Economic Analysis, Including Uncertainties. Water 2016, 8, 179. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Yao, H.; Chu, S.; Yu, T.; Shao, Y. Optimized DMA Partition to Reduce Background Leakage Rate in Water Distribution Networks. J. Water Resour. Plan. Manag. 2021, 147. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Galdiero, E.; Giugni, M.; Savic, D.; Uberti, G.S.d. Automatic Multi-objective Sectorization of a Water Distribution Network. Procedia Eng. 2014, 89, 1200–1207. [Google Scholar] [CrossRef] [Green Version]
- De Paola, F.; Fontana, N.; Galdiero, E.; Giugni, M.; Uberti, G.S.d.; Vitaletti, M. Optimal Design of District Metered Areas in Water Distribution Networks. Procedia Eng. 2014, 70, 449–457. [Google Scholar] [CrossRef] [Green Version]
- Nicolini, M.; Zovatto, L. Optimal Location and Control of Pressure Reducing Valves in Water Networks. J. Water Resour. Plan. Manag. 2009, 135. [Google Scholar] [CrossRef]

| Diameter (mm) | Gate Valve ($) | Flowmeter ($) |
|---|---|---|
| 150 | 95 | 177 |
| 200 | 134 | 256 |
| 250 | 186 | 356 |
| 300 | 250 | 535 |
| 400 | 373 | 891 |
| 450 | 481 | 1117 |
| 500 | 506 | 1160 |
| 600 | 835 | 2023 |
| 700 | 1196 | 2903 |
| 800 | 1535 | 3953 |
| 850 | 1874 | 4066 |
| 900 | 2214 | 4842 |
| 1000 | 3191 | 7122 |
| 1200 | 5693 | 12,355 |
| 1400 | 8986 | 18,458 |
| Schemes | A | B |
|---|---|---|
| Flowmeters | 100,230 | 91,398 |
| gate valves | 55,364 | 88,060 |
| Sum | 155,594 | 179,459 |
| Percent (%) | Water Age (h) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0–12 | 12–24 | 24–36 | 36–48 | 48–60 | 60–72 | 72–84 | 84–94 | >96 | |
| Original | 19.6 | 21.9 | 18.1 | 19.7 | 9.0 | 5.3 | 2.5 | 1.2 | 1.6 |
| Scheme A | 28.5 | 23.4 | 12.3 | 11.9 | 10.6 | 6.2 | 2.4 | 1.3 | 2.7 |
| Scheme B | 25.6 | 20.8 | 18.0 | 17.3 | 8.7 | 4.1 | 2.3 | 1.0 | 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Liu, Y.; Yao, H.; Yu, T.; Shao, Y. Comparative Analysis on the DMA Partitioning Methods Whether Trunk Mains Participated. Water 2022, 14, 3876. https://doi.org/10.3390/w14233876
Zhou H, Liu Y, Yao H, Yu T, Shao Y. Comparative Analysis on the DMA Partitioning Methods Whether Trunk Mains Participated. Water. 2022; 14(23):3876. https://doi.org/10.3390/w14233876
Chicago/Turabian StyleZhou, Hua, Youfei Liu, Huaqi Yao, Tingchao Yu, and Yu Shao. 2022. "Comparative Analysis on the DMA Partitioning Methods Whether Trunk Mains Participated" Water 14, no. 23: 3876. https://doi.org/10.3390/w14233876





