Modeling Investigation of Thermal Circulations of a Large and Shallow Subtropical Lake
Abstract
:1. Introduction
2. Study Area and Observation Data
2.1. Study Area
2.2. Data
3. Model Simulations
3.1. Simulation Domains
3.2. Model Description
4. Determining Lake Breeze Occurrence from Observational Data and Model Output
4.1. From Observational Data
4.2. From Model Output
5. Model Evaluation
5.1. Surface Fluxes
5.2. Surface Air Temperature and Wind
6. Results and Discussion
6.1. Lake Breeze Frequency
6.2. Onset Time, Ending Time and Duration of Lake Breeze
6.3. Penetration Distance
6.4. A Case Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deoli, V.; Kumar, D.; Kuriqi, A. Detection of Water Spread Area Changes in Eutrophic Lake Using Landsat Data. Sensors 2022, 22, 6827. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Gao, Z.; Wang, X.; Chen, Y. Modeling the impact of urbanization on the local and regional climate in Yangtze River Delta, China. J. Theor. Appl. Climatol. 2010, 102, 331–342. [Google Scholar] [CrossRef]
- Zhang, N.; Zhu, L.; Zhu, Y. Urban heat island and boundary layer structures under hot weather synoptic conditions: A case study of Suzhou City, China. J. Adv. Atmos. Sci. 2011, 28, 855. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, B.; Gao, J.; Kang, H. Impact of Taihu Lake on city ozone in the Yangtze River Delta. J. Adv. Atmos. Sci. 2017, 34, 226–234. [Google Scholar] [CrossRef]
- Yang, M.; Yu, J.; Li, Z.; Guo, Z.; Burch, M.; Lin, T.-F. Taihu Lake Not to Blame for Wuxi’s Woes. J. Sci. 2008, 319, 158. [Google Scholar] [CrossRef]
- Kristovich, D.A.R.; Laird, N.F. Observations of widespread lake-effect cloudiness: Influences of lake surface temperature and upwind conditions. J. Weather Forecast. 1998, 13, 1029–1045. [Google Scholar] [CrossRef]
- Kristovich, D.A.R.; Steve, R.A., III. A satellite study of cloud-band frequencies over the Great Lakes. J. Appl. Meteor. 1995, 34, 2083–2090. [Google Scholar] [CrossRef]
- Laird, N.F.; Metz, N.D.; Gaudet, L.; Grasmick, C.; Higgins, L.; Loeser, C.; Zelinsky, D.A. Climatology of cold season lake-effect cloud bands for the North American Great Lakes. J. Int. J. Clim. 2016, 37, 2111–2121. [Google Scholar] [CrossRef]
- Rodriguez, Y.; Kristovich, D.A.R.; Hjelmfelt, M.R. Lake-to-Lake Cloud Bands: Frequencies and Locations. J. Mon. Weather Rev. 2007, 135, 4202–4213. [Google Scholar] [CrossRef]
- Laird, N.; Bentley, A.M.; Ganetis, S.A.; Stieneke, A.; Tushaus, S.A. Climatology of Lake-Effect Precipitation Events over Lake Tahoe and Pyramid Lake. J. Appl. Meteorol. Clim. 2016, 55, 297–312. [Google Scholar] [CrossRef]
- Laird, N.; Sobash, R.; Hodas, N. The Frequency and Characteristics of Lake-Effect Precipitation Events Associated with the New York State Finger Lakes. J. Appl. Meteorol. Clim. 2009, 48, 873–886. [Google Scholar] [CrossRef] [Green Version]
- Bergmaier, P.T.; Geerts, B.; Campbell, L.S.; Steenburgh, W.J. The OWLeS IOP2b Lake-Effect Snowstorm: Dynamics of the Secondary Circulation. J. Mon. Weather Rev. 2017, 145, 2437–2459. [Google Scholar] [CrossRef]
- Kristovich, D.A.R.; Clark, R.D.; Frame, J.; Geerts, B.; Knupp, K.R.; Kosiba, K.A.; Laird, N.F.; Metz, N.D.; Minder, J.R.; Sikora, T.D.; et al. The Ontario Winter Lake-Effect Systems Field Campaign: Scientific and Educational Adventures to Further Our Knowledge and Prediction of Lake-Effect Storms. J. Bull. Am. Meteorol. Soc. 2017, 98, 315–332. [Google Scholar] [CrossRef]
- Owens, N.D.; Rauber, R.M.; Jewett, B.F.; McFarquhar, G.M. The Contribution of Lake Enhancement to Extreme Snowfall within the Chicago–Milwaukee Urban Corridor during the 2011 Groundhog Day Blizzard. J. Mon. Weather Rev. 2017, 145, 2405–2420. [Google Scholar] [CrossRef]
- King, P.W.S.; LeDuc, M.J.; Sills, D.M.L.; Donaldson, N.R.; Hudak, D.R.; Joe, P.; Murphy, B.P. Lake Breezes in Southern Ontario and Their Relation to Tornado Climatology. J. Weather Forecast. 2003, 18, 795–807. [Google Scholar] [CrossRef]
- Levy, I.; Makar, P.A.; Sills, D.; Zhang, J.; Hayden, K.L.; Mihele, C.; Narayan, J.; Moran, M.D.; Sjostedt, S.; Brook, J. Unraveling the complex local-scale flows influencing ozone patterns in the southern Great Lakes of North America. J. Atmos. Chem. Phys. 2010, 10, 10895–10915. [Google Scholar] [CrossRef] [Green Version]
- Makar, P.A.; Zhang, J.; Gong, W.; Stroud, C.; Sills, D.; Hayden, K.L.; Brook, J.; Levy, I.; Mihele, C.; Moran, M.D.; et al. Mass tracking for chemical analysis: The causes of ozone formation in southern Ontario during BAQS-Met 2007. J. Atmos. Chem. Phys. 2010, 10, 11151–11173. [Google Scholar] [CrossRef] [Green Version]
- Hayden, K.L.; Sills, D.M.L.; Brook, J.R.; Li, S.-M.; Makar, P.A.; Markovic, M.Z.; Liu, P.; Anlauf, K.G.; O’Brien, J.M.; Li, Q.; et al. Aircraft study of the impact of lake-breeze circulations on trace gases and particles during BAQS-Met 2007. J. Atmos. Chem. Phys. 2011, 11, 10173–10192. [Google Scholar] [CrossRef] [Green Version]
- Ellis, R.A.; Murphy, J.G.; Markovic, M.Z.; VandenBoer, T.C.; Makar, P.A.; Brook, J.; Mihele, C. The influence of gas-particle partitioning and surface-atmosphere exchange on ammonia during BAQS-Met. J. Atmos. Chem. Phys. 2011, 11, 133–145. [Google Scholar] [CrossRef] [Green Version]
- Wentworth, G.; Murphy, J.; Sills, D. Impact of lake breezes on ozone and nitrogen oxides in the Greater Toronto Area. J. Atmos. Environ. 2015, 109, 52–60. [Google Scholar] [CrossRef]
- Garratt, J.R.; Physick, W.L. The inland boundary layer at low latitudes: II Sea-breeze influences. J. Bound. Layer Meteorol. 1985, 33, 209–231. [Google Scholar] [CrossRef]
- Yan, H.; Anthes, R.A. The Effect of Latitude on the Sea Breeze. J. Mon. Weather Rev. 1987, 115, 936–956. [Google Scholar] [CrossRef]
- Antonelli, M.; Rotunno, R. Large-Eddy Simulation of the Onset of the Sea Breeze. J. Atmos. Sci. 2007, 64, 4445–4457. [Google Scholar] [CrossRef] [Green Version]
- Tsujimoto, K.; Koike, T. Land-lake breezes at low latitudes: The case of Tonle Sap Lake in Cambodia. J. Geophys. Res. Atmos. 2013, 118, 6970–6980. [Google Scholar] [CrossRef]
- Zumpfe, D.E.; Horel, J.D. Lake-Breeze Fronts in the Salt Lake Valley. J. Appl. Meteorol. Clim. 2007, 46, 196–211. [Google Scholar] [CrossRef]
- Sills, D.M.L.; Brook, J.R.; Levy, I.; Makar, P.A.; Zhang, J.; Taylor, P.A. Lake breezes in the southern Great Lakes region and their influence during BAQS-Met 2007. J. Atmos. Chem. Phys. 2011, 11, 7955–7973. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gao, Y.; Qin, H.; Huang, J.; Liu, C.; Hu, C.; Wang, W.; Liu, S.; Lee, X. Spatiotemporal Characteristics of Lake Breezes over Lake Taihu, China. J. Appl. Meteorol. Clim. 2017, 56, 2053–2065. [Google Scholar] [CrossRef]
- Porson, A.; Steyn, D.G.; Schayes, G. Sea-breeze scaling from numerical model simulations, part II: Interaction between the sea breeze and slope flows. Bound. Layer Meteorol. 2007, 122, 31–41. Available online: https://rdcu.be/cH3Cw (accessed on 8 November 2022). [CrossRef]
- Freitas, E.D.; Rozoff, C.M.; Cotton, W.R.; Dias, P.L.S. Interactions of an urban heat island and sea-breeze circulations during winter over the metropolitan area of São Paulo, Brazil. J. Bound. Layer Meteorol. 2007, 122, 43–65. [Google Scholar] [CrossRef]
- Crosman, E.T.; Horel, J.D. Idealized large-eddy simulations of sea and lake breezes: Sensitivity to lake diameter, heat flux and stability. Bound. Layer Meteorol. 2012, 144, 309–328. Available online: https://rdcu.be/cH3yb (accessed on 8 November 2022). [CrossRef]
- Yamato, H.; Mikami, T.; Takahashi, H. Impact of sea breeze penetration over urban areas on midsummer temperature distributions in the Tokyo Metropolitan area. J. Int. J. Clim. 2017, 37, 5154–5169. [Google Scholar] [CrossRef]
- Segal, M.; Leuthold, M.; Arritt, R.W.; Anderson, C.; Shen, J. Small Lake Daytime Breezes: Some Observational and Conceptual Evaluations. J. Bull. Am. Meteorol. Soc. 1997, 78, 1135–1147. [Google Scholar] [CrossRef]
- Miller, S.T.K.; Keim, B.D.; Talbot, R.W.; Mao, H. Sea breeze: Structure, forecasting, and impacts. J. Rev. Geophys. 2003, 41, 124. [Google Scholar] [CrossRef] [Green Version]
- Crosman, E.T.; Horel, J.D. Sea and Lake Breezes: A Review of Numerical Studies. Bound. Layer Meteorol. 2010, 137, 1–29. Available online: https://rdcu.be/cH3yv (accessed on 8 November 2022). [CrossRef] [Green Version]
- Xiao, C.; Lofgren, B.M.; Wang, J.; Chu, P.Y. Improving the lake scheme within a coupled WRF-lake model in the Laurentian Great Lakes. J. Adv. Model. Earth Syst. 2016, 8, 1969–1985. [Google Scholar] [CrossRef]
- Curry, M.; Hanesiak, J.; Sills, D. A Radar-Based Investigation of Lake Breezes in Southern Manitoba, Canada. J. Atmos. Ocean 2015, 53, 237–250. [Google Scholar] [CrossRef]
- Lombardo, K.; Sinsky, E.; Jia, Y.; Whitney, M.M.; Edson, J. Sensitivity of Simulated Sea Breezes to Initial Conditions in Complex Coastal Regions. J. Mon. Weather Rev. 2016, 144, 1299–1320. [Google Scholar] [CrossRef]
- Xu, L.; Liu, H.; Du, Q.; Wang, L. Evaluation of the WRF-lake model over a highland freshwater lake in southwest China. J. Geophys. Res. Atmos. 2017, 121, 13989–14005. [Google Scholar] [CrossRef]
- Lombardo, K.; Sinsky, E.; Edson, J.; Whitney, M.M.; Jia, Y. Sensitivity of Offshore Surface Fluxes and Sea Breezes to the Spatial Distribution of Sea-Surface Temperature. J. Bound. Layer Meteorol. 2018, 166, 475–502. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Q.; Gao, Y.; Hao, X.; Liu, S. Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models. Water 2019, 11, 1026. [Google Scholar] [CrossRef]
- Wu, T.; Qin, B.; Huang, A.; Sheng, Y.; Feng, S.; Casenave, C. Reconsideration of wind stress, wind waves, and turbulence in simulating wind-driven currents of shallow lakes in the Wave and Current Coupled Model (WCCM) version 1.0. Geosci. Model Dev. 2022, 15, 745–769. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, A.; Lu, Y.; Lazhu; Yang, X.; Qiu, B.; Zhang, Z.; Zhang, X. Numerical Study of the Thermal Structure and Circulation in a Large and Deep Dimictic Lake Over Tibetan Plateau. J. Geophys. Res. Oceans 2021, 126, e2021JC017517. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, J.; Li, G.; Wang, Y.; Liu, C.; Zhao, K.; Tao, X.; Hu, X.-M.; Lee, X. Improving Lake-Breeze Simulation with WRF Nested LES and Lake Model over a Large Shallow Lake. J. Appl. Meteorol. Clim. 2019, 58, 1689–1708. [Google Scholar] [CrossRef]
- Wang, F.; Li, Q.; Wang, Y. Lake-atmosphere exchange impacts ozone simulation around a large shallow lake with large cities. Atmos. Environ. 2021, 246, 118086. [Google Scholar] [CrossRef]
- Subin, Z.M.; Murphy, L.N.; Li, F.; Bonfils, C.; Riley, W.J. Boreal lakes moderate seasonal and diurnal temperature variation and perturb atmospheric circulation: Analyses in the Community Earth System Model 1 (CESM1). J. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 15639. [Google Scholar] [CrossRef]
- Deng, B.; Liu, S.; Xiao, W.; Wang, W.; Jin, J.; Lee, X. Evaluation of the CLM4 Lake Model at a Large and Shallow Freshwater Lake. J. Hydrometeorol. 2013, 14, 636–649. [Google Scholar] [CrossRef] [Green Version]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Qin, B.; Xu, P.; Wu, Q.; Luo, L.; Zhang, Y. Environmental issues of Lake Taihu, China. J. Hydrobiol. 2007, 581, 3–14. [Google Scholar] [CrossRef]
- Lee, X.; Liu, S.; Xiao, W.; Wang, W.; Gao, Z.; Cao, C.; Hu, C.; Hu, Z.; Shen, S.; Wang, Y.; et al. The Taihu Eddy Flux Network: An Observational Program on Energy, Water, and Greenhouse Gas Fluxes of a Large Freshwater Lake. J. Bull. Am. Meteorol. Soc. 2014, 95, 1583–1594. [Google Scholar] [CrossRef]
- Wang, W.; Xiao, W.; Cao, C.; Gao, Z.; Hu, Z.; Liu, S.; Shen, S.; Wang, L.; Xiao, Q.; Xu, J.; et al. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J. Hydrol. 2014, 511, 811–824. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, N. Urban Heat Island Mitigation Effectiveness under Extreme Heat Conditions in the Suzhou–Wuxi–Changzhou Metropolitan Area, China. J. Appl. Meteorol. Clim. 2018, 57, 235–253. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.-L.; Koren, V.; Duan, Q.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Earth Surf. 1996, 101, 7251–7268. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. J. Mon. Weather. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A Simple Single-Layer Urban Canopy Model For Atmospheric Models: Comparison with Multi-Layer And Slab Models. J. Bound. Layer Meteorol. 2001, 101, 329–358. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, S.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. J. Int. J. Clim. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Lim, K.-S.S.; Hong, S.-Y. Development of an Effective Double-Moment Cloud Microphysics Scheme with Prognostic Cloud Condensation Nuclei (CCN) for Weather and Climate Models. J. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4, M02001. [Google Scholar] [CrossRef]
- Gu, H.; Jin, J.; Wu, Y.; Ek, M.B.; Subin, Z.M. Calibration and validation of lake surface temperature simulations with the coupled WRF-lake model. J. Clim. Chang. 2015, 129, 471–483. [Google Scholar] [CrossRef]
- Henderson-Sellers, B. New formulation of eddy diffusion thermocline models. J. Appl. Math. Model. 1985, 9, 441–446. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhang, Z.; Wang, W.; Ren, X.; Gao, Y.; Liu, S.; Lee, X. Diurnal and Seasonal Variations of Thermal Stratification and Vertical Mixing in a Shallow Fresh Water Lake. J. Meteorol. Res. 2018, 32, 219–232. [Google Scholar] [CrossRef]
- Biggs, W.G.; Graves, M.E. A Lake breeze index. J. Appl. Meteorol. Climatol. 1962, 1, 474–480. [Google Scholar] [CrossRef]
- Comer, N.T.; McKendry, I.G. Observations and numerical modelling of Lake Ontario breezes. J. Atmos. Ocean. 1993, 31, 481–499. [Google Scholar] [CrossRef]
- Borne, K.; Chen, D.; Nunez, M. A method for finding sea breeze days under stable synoptic conditions and its application to the Swedish west coast. J. Int. J. Climatol. 1998, 18, 901–914. [Google Scholar] [CrossRef]
- Laird, N.F.; Kristovich, D.A.R.; Liang, X.Z. Lake michigan lake breezes: Climatology, local forcing, and synoptic environment. J. Appl. Meteorol. 2001, 40, 409–424. [Google Scholar] [CrossRef]
- Keeler, J.M.; Kristovich, D.A.R. Observations of Urban Heat Island Influence on Lake-Breeze Frontal Movement. J. Appl. Meteorol. Clim. 2012, 51, 702–710. [Google Scholar] [CrossRef]
- Curry, M.; Hanesiak, J.; Kehler, S.; Sills, D.M.L.; Taylor, N.M. Ground-Based Observations of the Thermodynamic and Kinematic Properties of Lake-Breeze Fronts in Southern Manitoba, Canada. J. Bound. Layer Meteorol. 2017, 163, 143–159. [Google Scholar] [CrossRef]
- Mariani, Z.; Dehghan, A.; Joe, P.; Sills, D. Observations of Lake-Breeze Events During the Toronto 2015 Pan-American Games. J. Bound. Layer Meteorol. 2018, 166, 113–135. [Google Scholar] [CrossRef]
- Huang, M.; Gao, Z.; Miao, S.; Xu, X. Characteristics of sea breezes over the Jiangsu coastal area, China. J. Int. J. Clim. 2016, 36, 3908–3916. [Google Scholar] [CrossRef]
- Keen, C.S.; Lyons, W.A. Lake/Land Breeze Circulations on the Western Shore of Lake Michigan. J. Appl. Meteorol. 1978, 17, 1843–1855. [Google Scholar] [CrossRef]
- Dimou, K. 3-D Hybrid Eulerian-Lagrangian/Particle Tracking Model for Simulating Mass Transport in Coastal Water Bodies. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. Available online: http://dspace.mit.edu/handle/1721.1/28011 (accessed on 8 November 2022).
- Deoli, V.; Kumar, D.; Kumar, M.; Kuriqi, A.; Elbeltagi, A. Water spread mapping of multiple lakes using remote sensing and satellite data. Arab. J. Geosci. 2021, 14, 2213. [Google Scholar] [CrossRef]
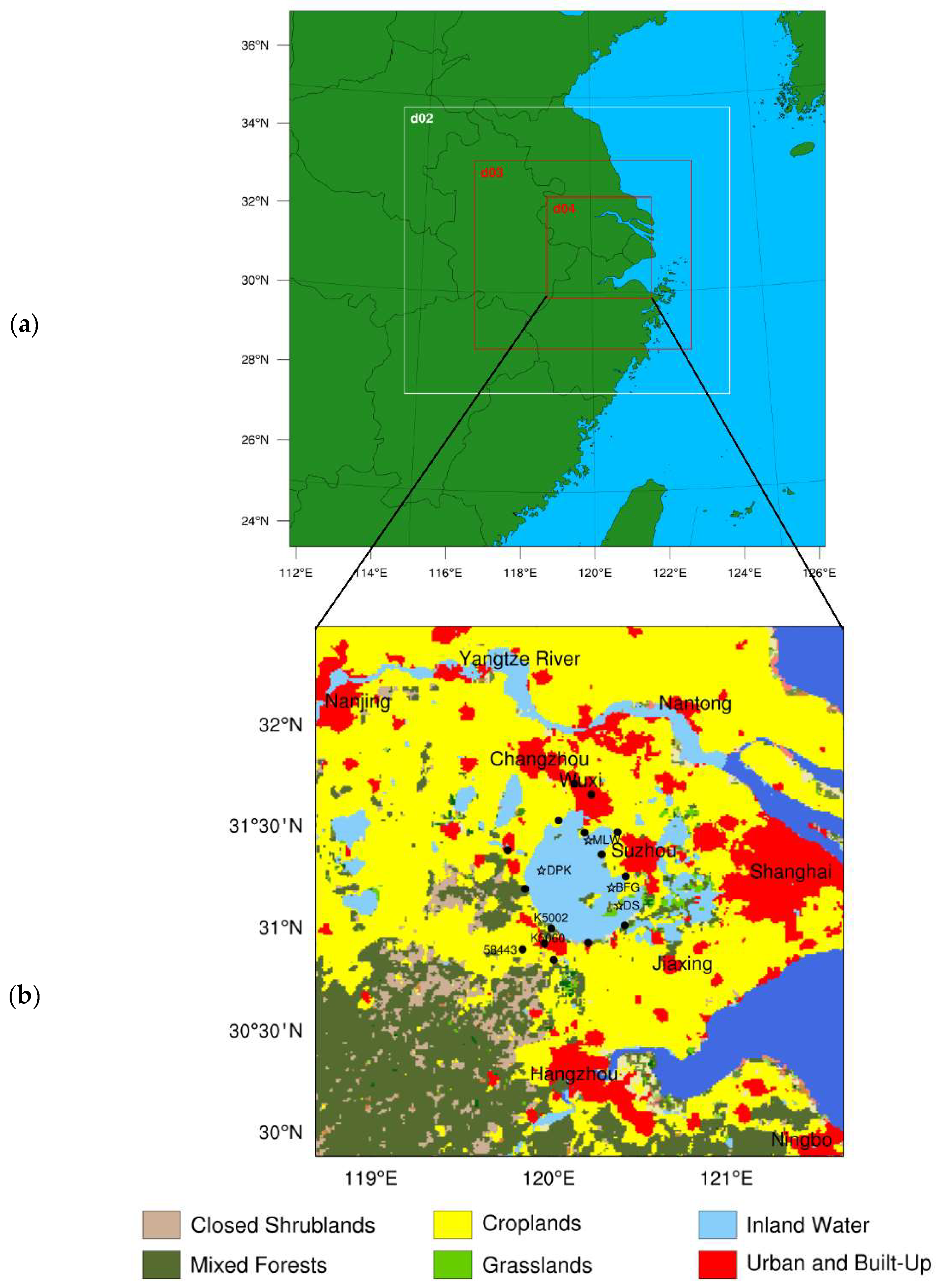
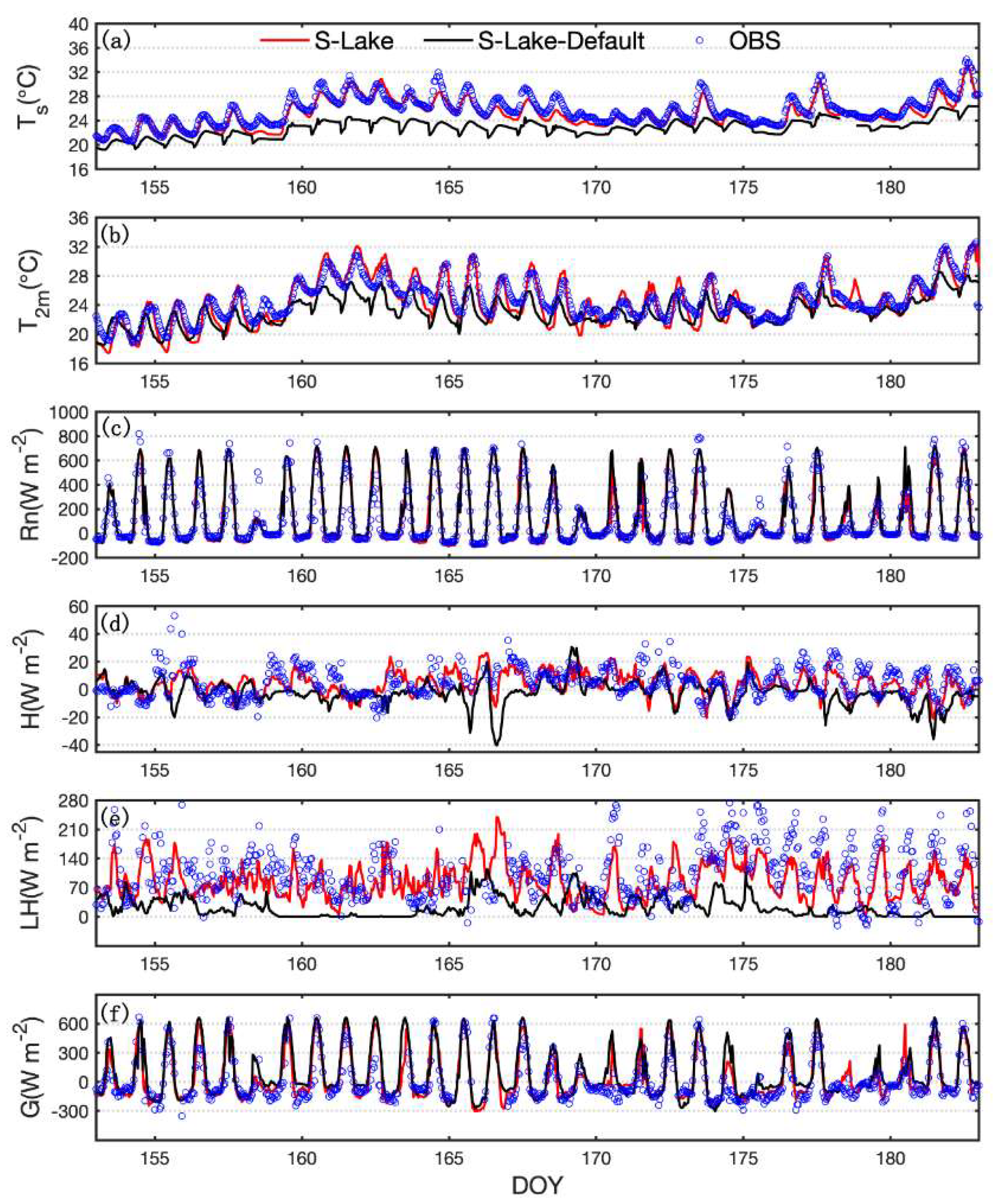
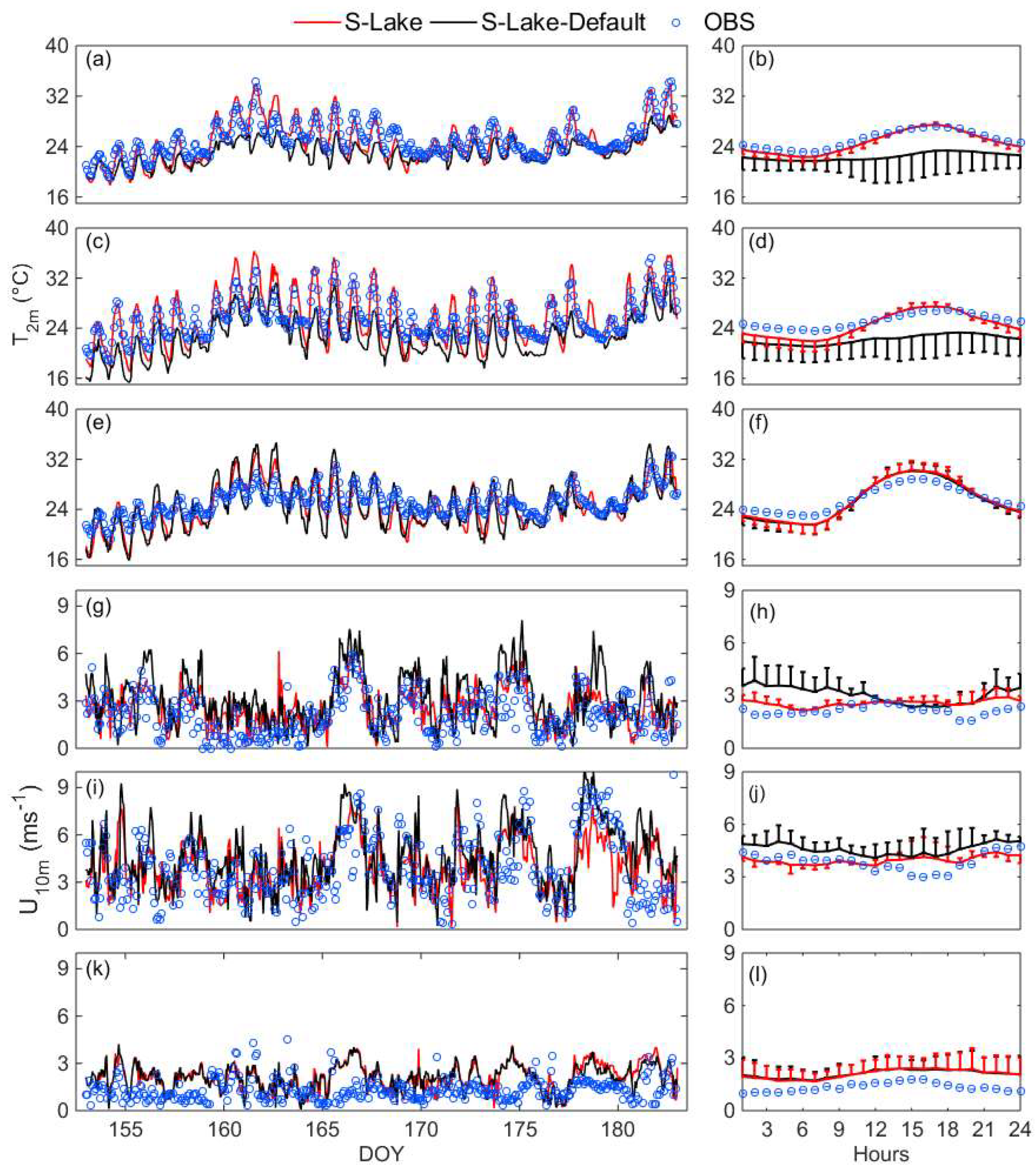
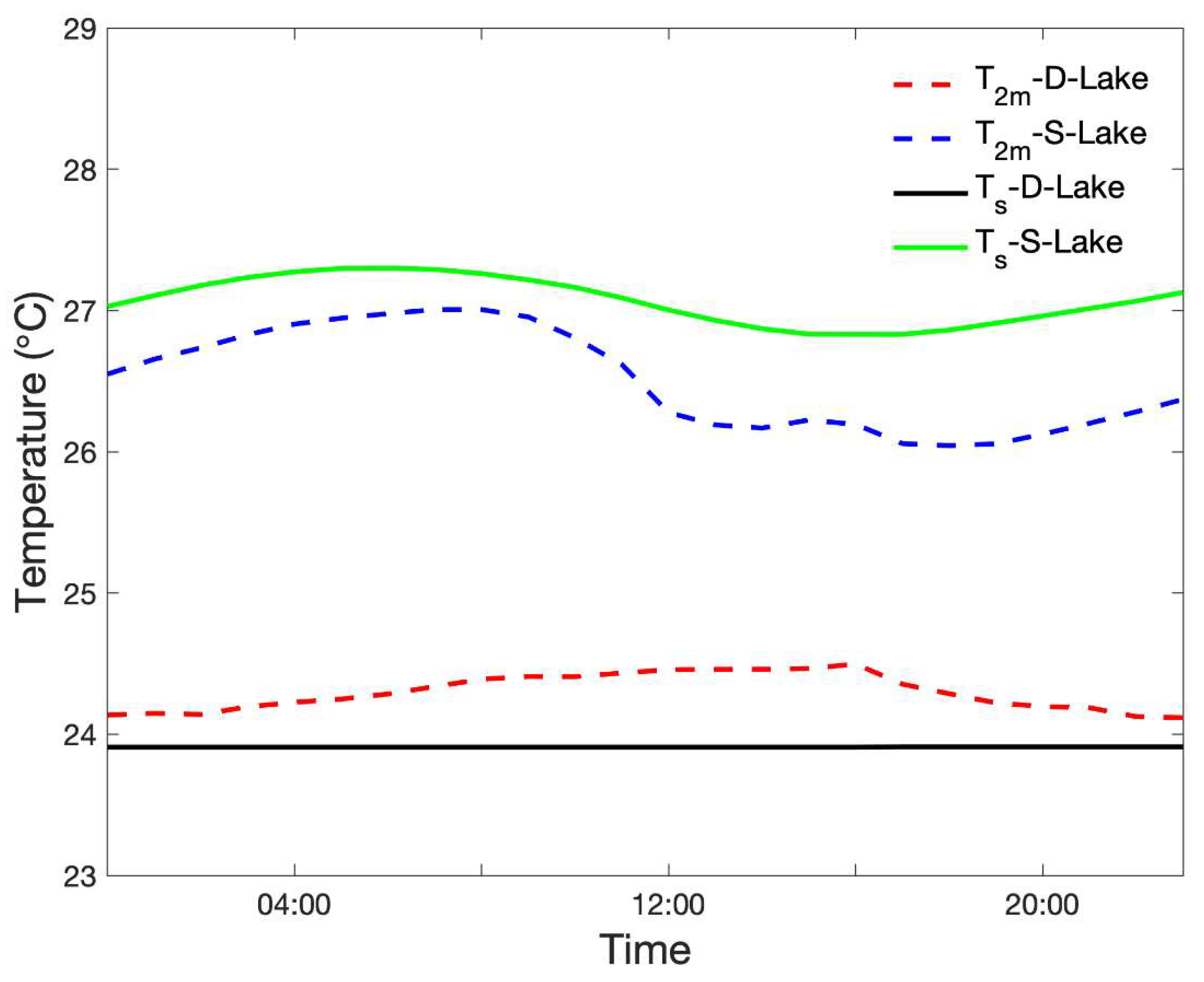

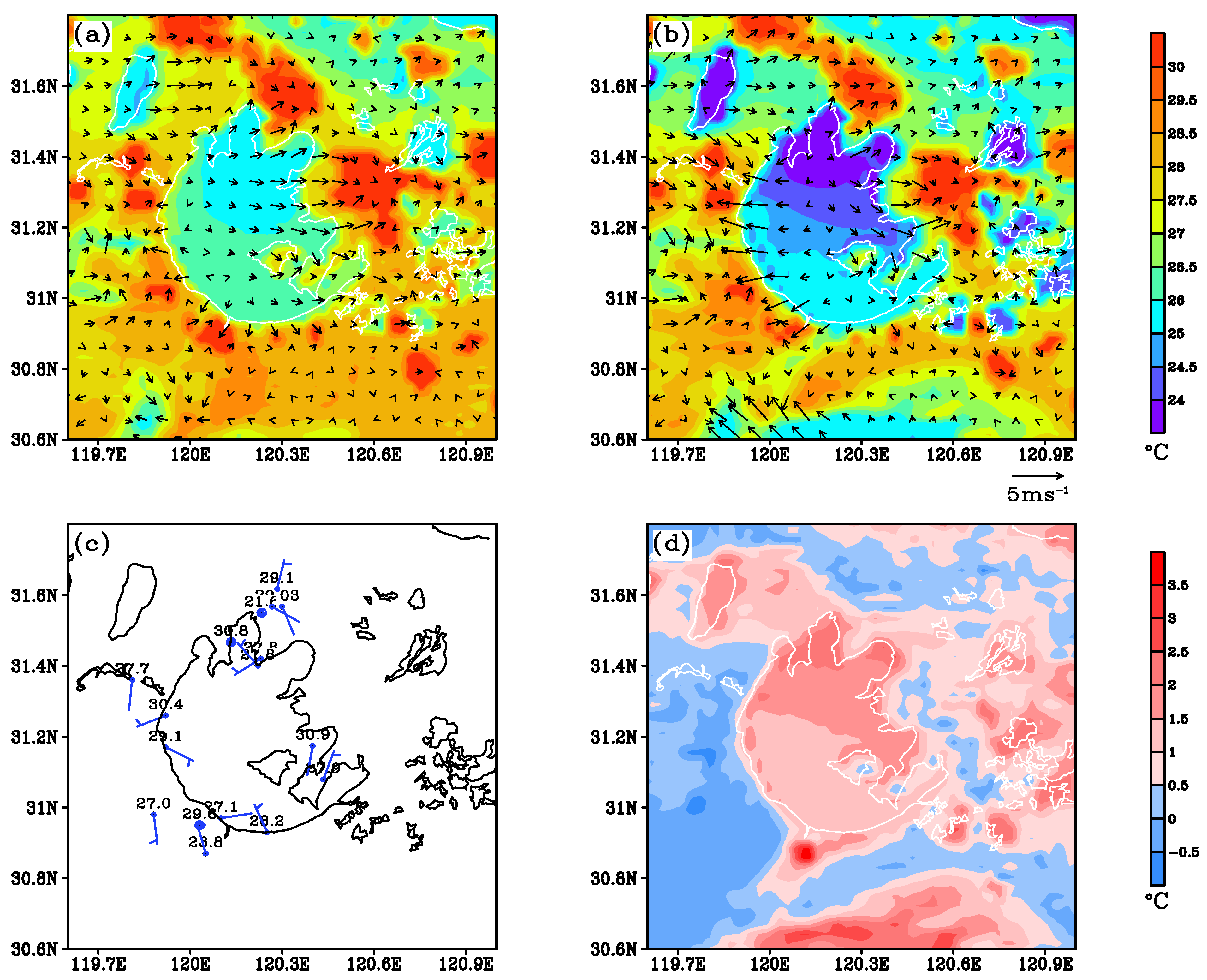
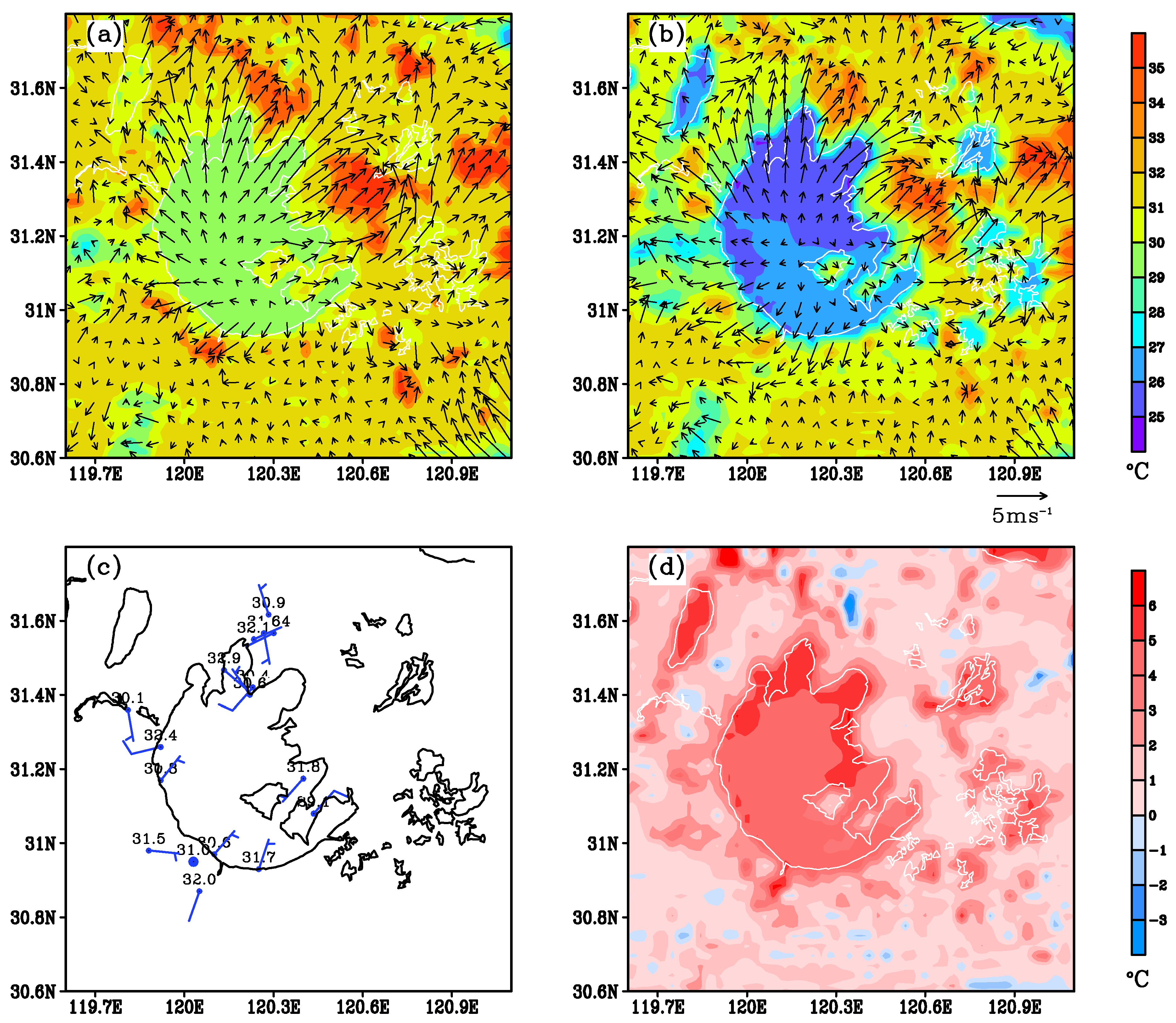

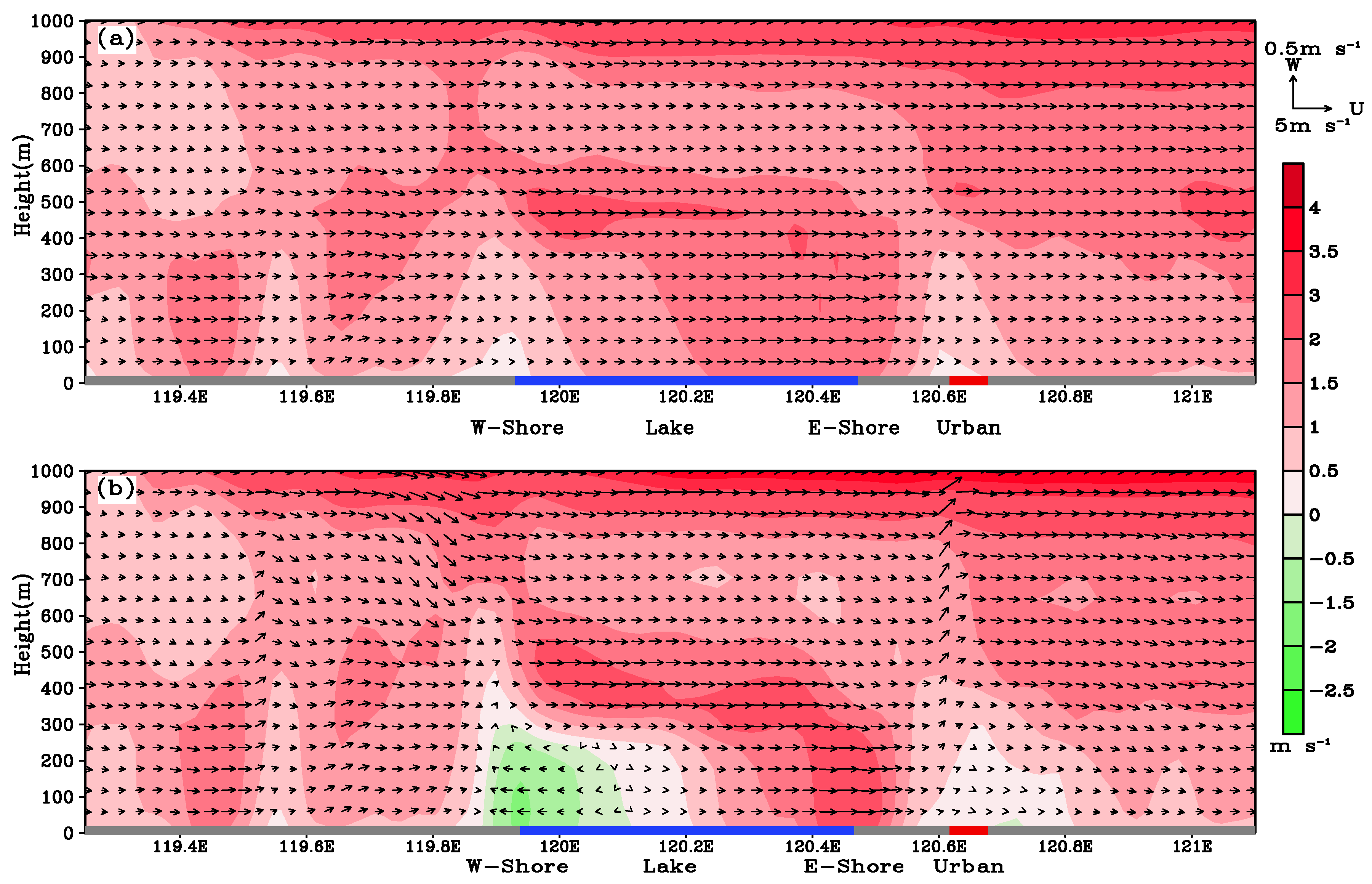

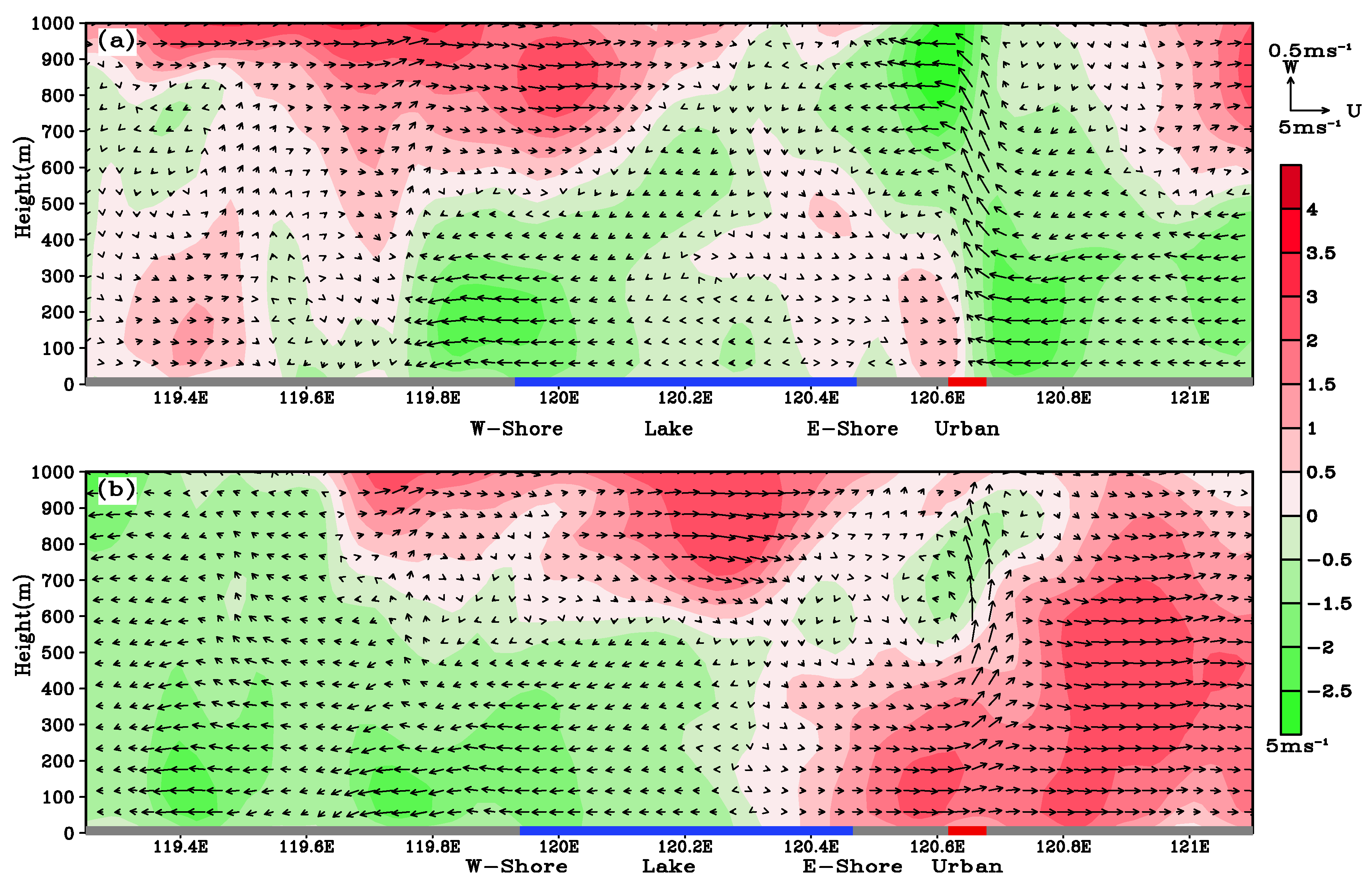
| Station | Longitude | Latitude | Distance |
|---|---|---|---|
| 1. BFG | 31.40 | 120.22 | on lake |
| 2. DPK | 31.26 | 119.92 | on lake |
| 3. MLW | 31.17 | 120.40 | on lake |
| 4. K5027 | 31.17 | 119.92 | onshore |
| 5. K5002 | 30.97 | 120.10 | onshore |
| 6. K5001 | 30.93 | 120.25 | onshore |
| 7. M3848 | 31.42 | 120.23 | onshore |
| 8. M3852 | 31.47 | 120.13 | onshore |
| 9. M3908 | 31.22 | 120.46 | onshore |
| 10. M3911 | 31.33 | 120.33 | onshore |
| 11. M3921 | 30.98 | 120.47 | near shore |
| 12. DS | 31.08 | 120.43 | near shore |
| 13. K5060 | 30.95 | 120.03 | near shore |
| 14. M3903 | 31.44 | 120.44 | near shore |
| 15. 58443 | 30.98 | 119.88 | far shore |
| 16. 58450 | 30.87 | 120.05 | far shore |
| 17. M3850 | 31.57 | 120.30 | far shore |
| 18. M3855 | 31.62 | 120.28 | far shore |
| 19. 58346 | 31.36 | 119.81 | far shore |
| Tskin (°C) | Sense Heat Flux (W·m−2) | Latent Heat Flux (W·m−2) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Lake-Default | S-Lake | S-Lake-Default | S-Lake | S-Lake-Default | S-Lake | |||||||
| RMSE | RC | RMSE | RC | RMSE | RC | RMSE | RC | RMSE | RC | RMSE | RC | |
| 1. BFG | 3.24 | 0.81 | 1.59 | 0.92 | 15.71 | 0.28 | 10.12 | 0.67 | 90.87 | −0.04 | 44.81 | 0.71 |
| 2. MLW | 3.63 | 0.78 | 1.93 | 0.88 | 18.27 | 0.22 | 14.37 | 0.62 | 96.35 | 0.17 | 53.84 | 0.68 |
| 3. DPK | 3.46 | 0.80 | 1.81 | 0.91 | 19.23 | 0.27 | 13.21 | 0.64 | 114.67 | 0.14 | 50.97 | 0.69 |
| 4. DS | 2.72 | 0.90 | 2.62 | 0.92 | 71.42 | 0.80 | 43.62 | 0.83 | 54.14 | 0.89 | 21.49 | 0.92 |
| Average | 3.26 | 0.82 | 1.98 | 0.90 | 31.15 | 0.39 | 20.33 | 0.69 | 89.00 | 0.29 | 42.77 | 0.75 |
| Air Temperature (°C) | Wind Speed (m‧s−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| S-Lake-Default | S-Lake | S-Lake-Default | S-Lake | |||||
| Station | RMSE | RC | RMSE | RC | RMSE | RC | RMSE | RC |
| 1. BFG | 4.89 | 0.58 | 1.34 | 0.94 | 2.58 | 0.48 | 1.57 | 0.71 |
| 2. DPK | 4.75 | 0.59 | 1.52 | 0.93 | 2.25 | 0.51 | 1.53 | 0.70 |
| 3. MLW | 4.83 | 0.64 | 1.48 | 0.92 | 1.98 | 0.68 | 1.40 | 0.75 |
| 4. K5027 | 3.27 | 0.79 | 1.39 | 0.93 | 1.75 | 0.51 | 1.54 | 0.70 |
| 5. K5002 | 2.99 | 0.77 | 1.37 | 0.93 | 1.76 | 0.62 | 1.12 | 0.69 |
| 6. K5001 | 3.18 | 0.80 | 1.45 | 0.94 | 1.85 | 0.45 | 1.82 | 0.68 |
| 7. M3848 | 3.32 | 0.77 | 1.83 | 0.91 | 1.79 | 0.52 | 1.71 | 0.71 |
| 8. M3852 | 3.53 | 0.75 | 1.50 | 0.92 | 2.56 | 0.38 | 1.67 | 0.62 |
| 9. M3908 | 3.37 | 0.71 | 1.33 | 0.93 | 1.56 | 0.43 | 1.47 | 0.63 |
| 10. M3911 | 3.29 | 0.70 | 1.33 | 0.91 | 1.38 | 0.46 | 1.55 | 0.64 |
| 11. M3921 | 3.54 | 0.69 | 1.28 | 0.90 | 1.29 | 0.55 | 1.68 | 0.67 |
| 12. DS | 1.68 | 0.91 | 1.54 | 0.92 | 1.48 | 0.51 | 1.42 | 0.68 |
| 13. K5060 | 1.94 | 0.92 | 1.86 | 0.93 | 2.80 | 0.59 | 1.62 | 0.64 |
| 14. M3903 | 2.02 | 0.90 | 2.01 | 0.90 | 1.33 | 0.62 | 1.55 | 0.62 |
| 15. 58443 | 2.17 | 0.89 | 2.06 | 0.89 | 1.46 | 0.67 | 1.67 | 0.67 |
| 16. 58450 | 1.94 | 0.91 | 1.84 | 0.91 | 1.29 | 0.74 | 1.51 | 0.73 |
| 17. M3850 | 1.97 | 0.90 | 1.95 | 0.91 | 2.08 | 0.63 | 1.42 | 0.62 |
| 18. M3855 | 1.91 | 0.91 | 1.87 | 0.91 | 0.88 | 0.64 | 1.25 | 0.64 |
| 19. 58346 | 1.88 | 0.90 | 1.87 | 0.90 | 0.99 | 0.63 | 1.81 | 0.65 |
| Average | 2.97 | 0.79 | 1.62 | 0.91 | 1.73 | 0.56 | 1.51 | 0.67 |
| June | July | August | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D-Lake | S-Lake | OBS | D-Lake | S-Lake | OBS | D-Lake | S-Lake | OBS | D-Lake | S-Lake | OBS | |
| East Shore | 56.7 | 33.3 | 26.7 | 48.4 | 12.9 | 12.9 | 45.2 | 32.3 | 22.6 | 50 | 26 | 20.7 |
| West Shore | 46.7 | 30.0 | 33.3 | 41.9 | 12.9 | 9.67 | 41.9 | 29.0 | 25.8 | 44.6 | 23.9 | 22.8 |
| South Shore | 46.7 | 26.7 | 30.0 | 54.8 | 12.9 | 12.9 | 41.9 | 25.8 | 25.8 | 47.8 | 21.7 | 22.8 |
| North Shore | 56.7 | 30.0 | 40.0 | 48.4 | 16.1 | 9.67 | 45.2 | 35.5 | 28.6 | 50 | 27.1 | 26 |
| Any of Shore | 56.7 | 33.3 | 40.0 | 54.8 | 16.1 | 12.9 | 45.2 | 35.5 | 28.6 | 52.2 | 28.3 | 38 |
| All of Shore | 46.7 | 26.7 | 26.7 | 35.5 | 9.67 | 9.67 | 32.3 | 19.4 | 19.4 | 38 | 18.5 | 18.5 |
| East Shore | West Shore | South Shore | North Shore | |||||
|---|---|---|---|---|---|---|---|---|
| S-Lake | D-Lake | S-Lake | D-Lake | S-Lake | D-Lake | S-Lake | D-Lake | |
| Maxi distance | 33 | 35 | 23 | 26 | 21 | 30 | 32 | 33 |
| Mini distance | 6 | 8 | 0 | 4 | 0 | 6 | 8 | 12 |
| Mean distance | 10 | 14 | 6 | 11 | 7 | 12 | 10 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhuo, M. Modeling Investigation of Thermal Circulations of a Large and Shallow Subtropical Lake. Water 2022, 14, 3719. https://doi.org/10.3390/w14223719
Wang Y, Zhuo M. Modeling Investigation of Thermal Circulations of a Large and Shallow Subtropical Lake. Water. 2022; 14(22):3719. https://doi.org/10.3390/w14223719
Chicago/Turabian StyleWang, Yongwei, and Meitong Zhuo. 2022. "Modeling Investigation of Thermal Circulations of a Large and Shallow Subtropical Lake" Water 14, no. 22: 3719. https://doi.org/10.3390/w14223719





