Evaluating Three Supervised Machine Learning Algorithms (LM, BR, and SCG) for Daily Pan Evaporation Estimation in a Semi-Arid Region
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region and the Data
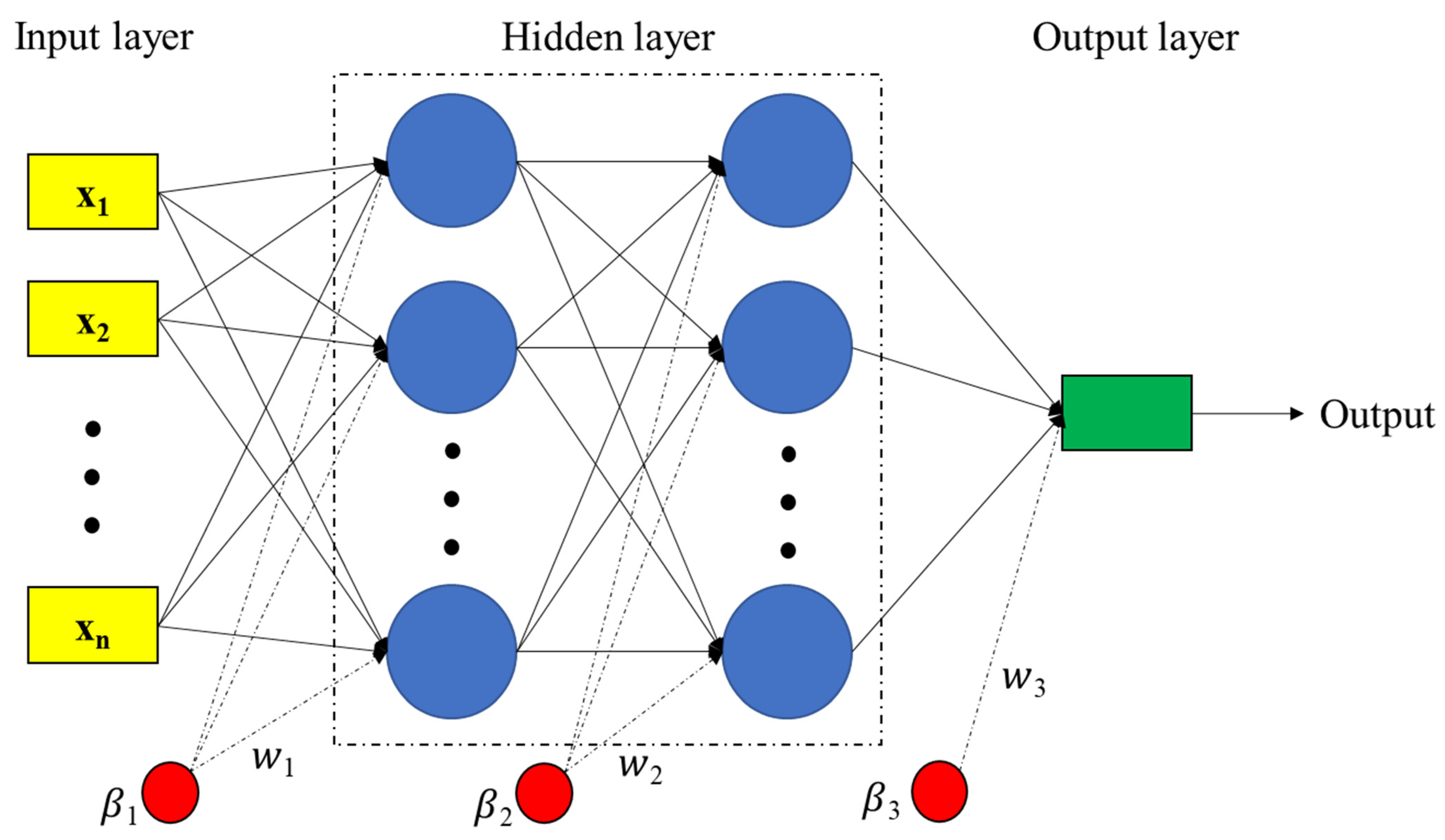
2.2. Multilayer Perceptron (MLP) Neural Network
2.3. Learning Algorithms for MLP Neural Network
2.3.1. Levenberg–Marquardt (LM)
2.3.2. Bayesian Regularization
2.3.3. Scaled Conjugate Gradient
2.4. Evaluating the Estimations
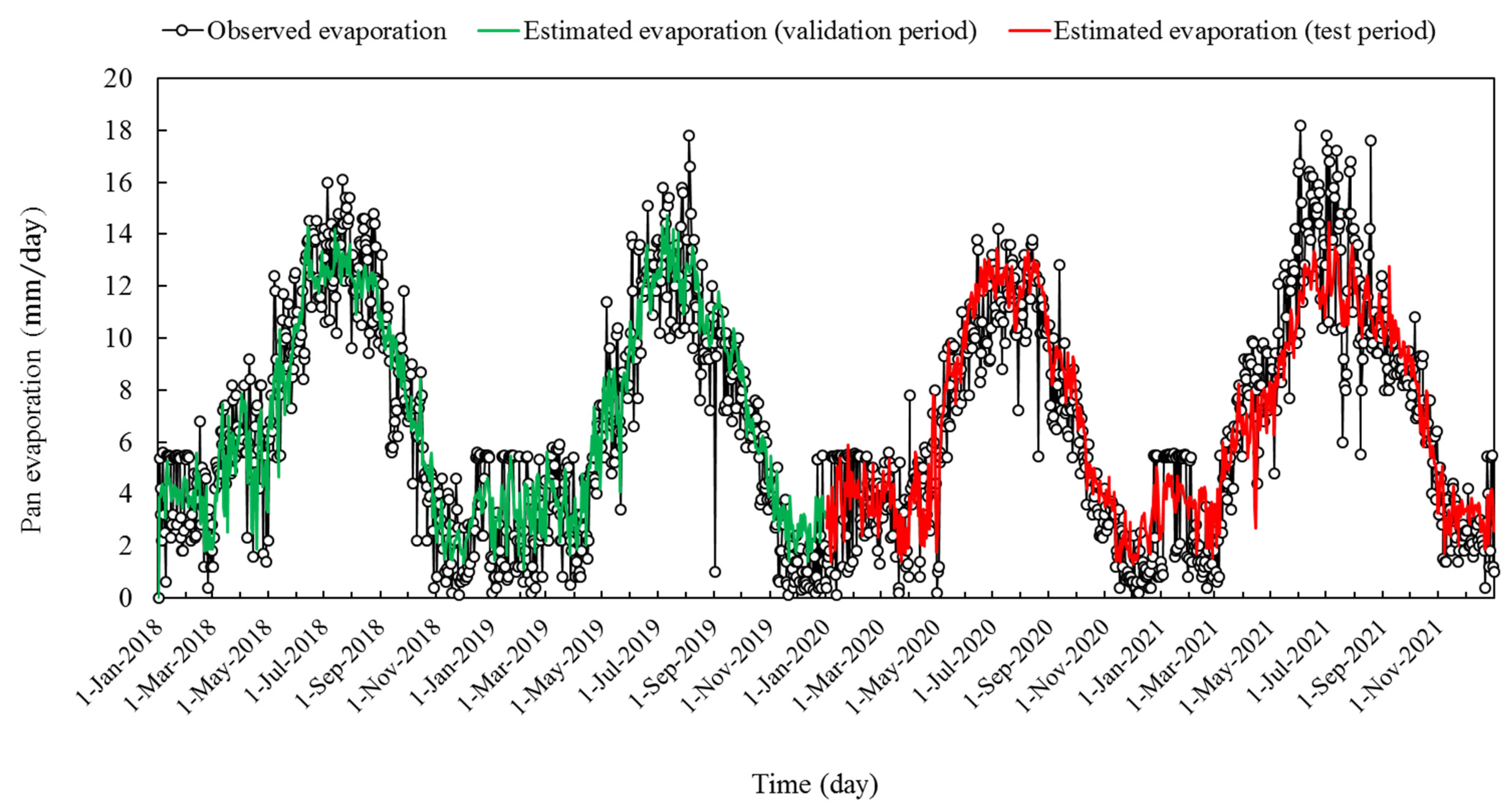
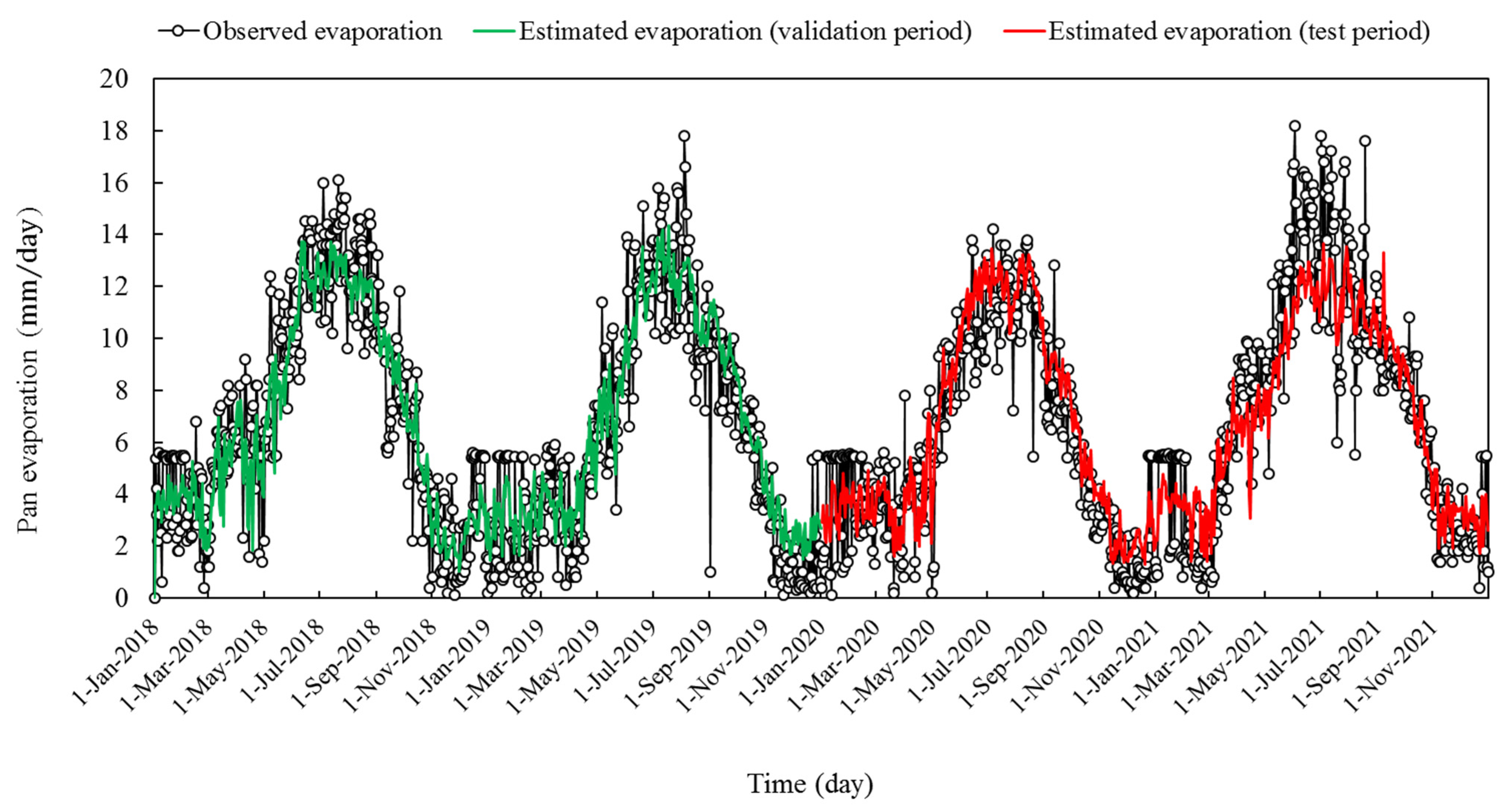
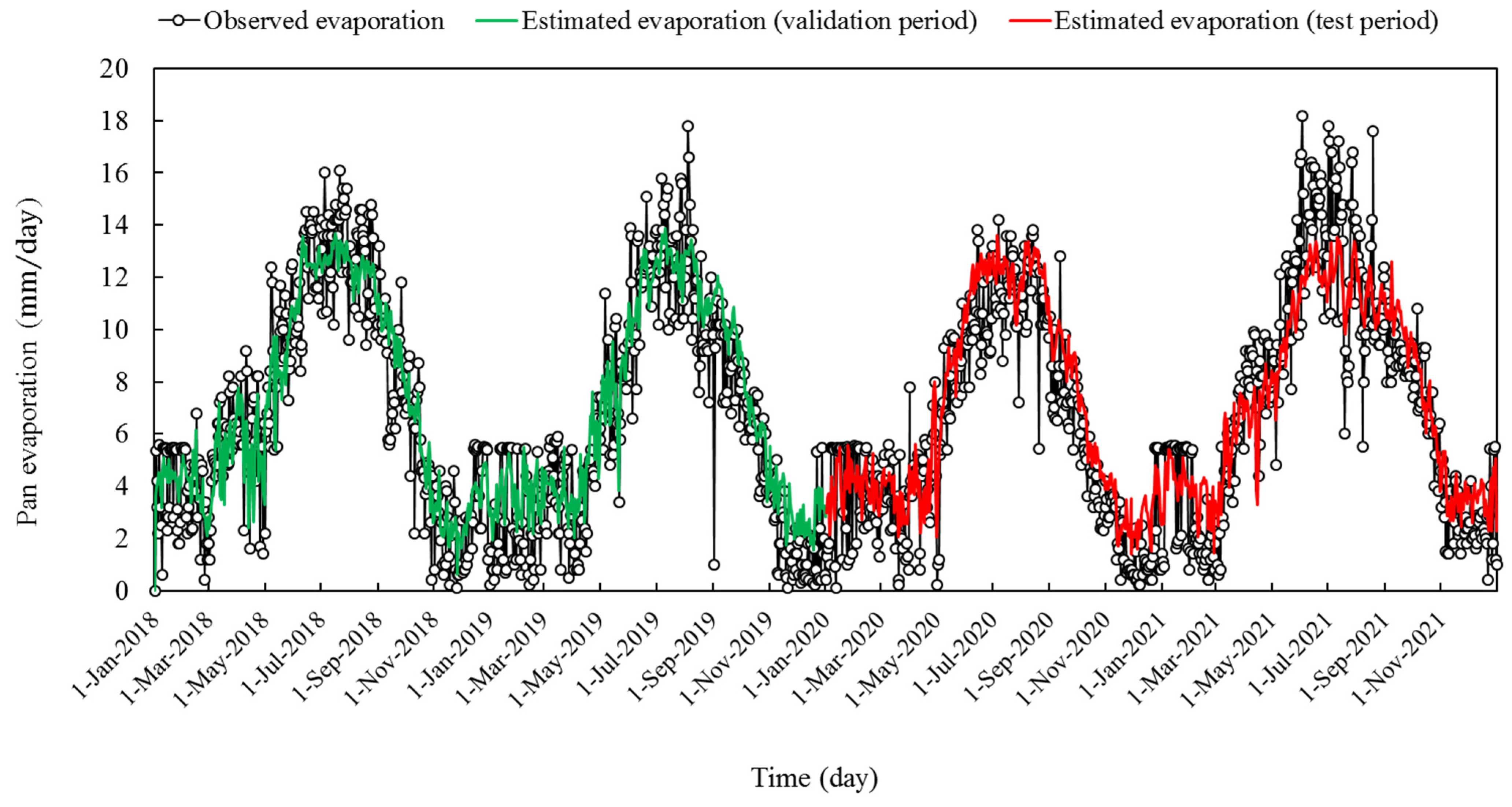
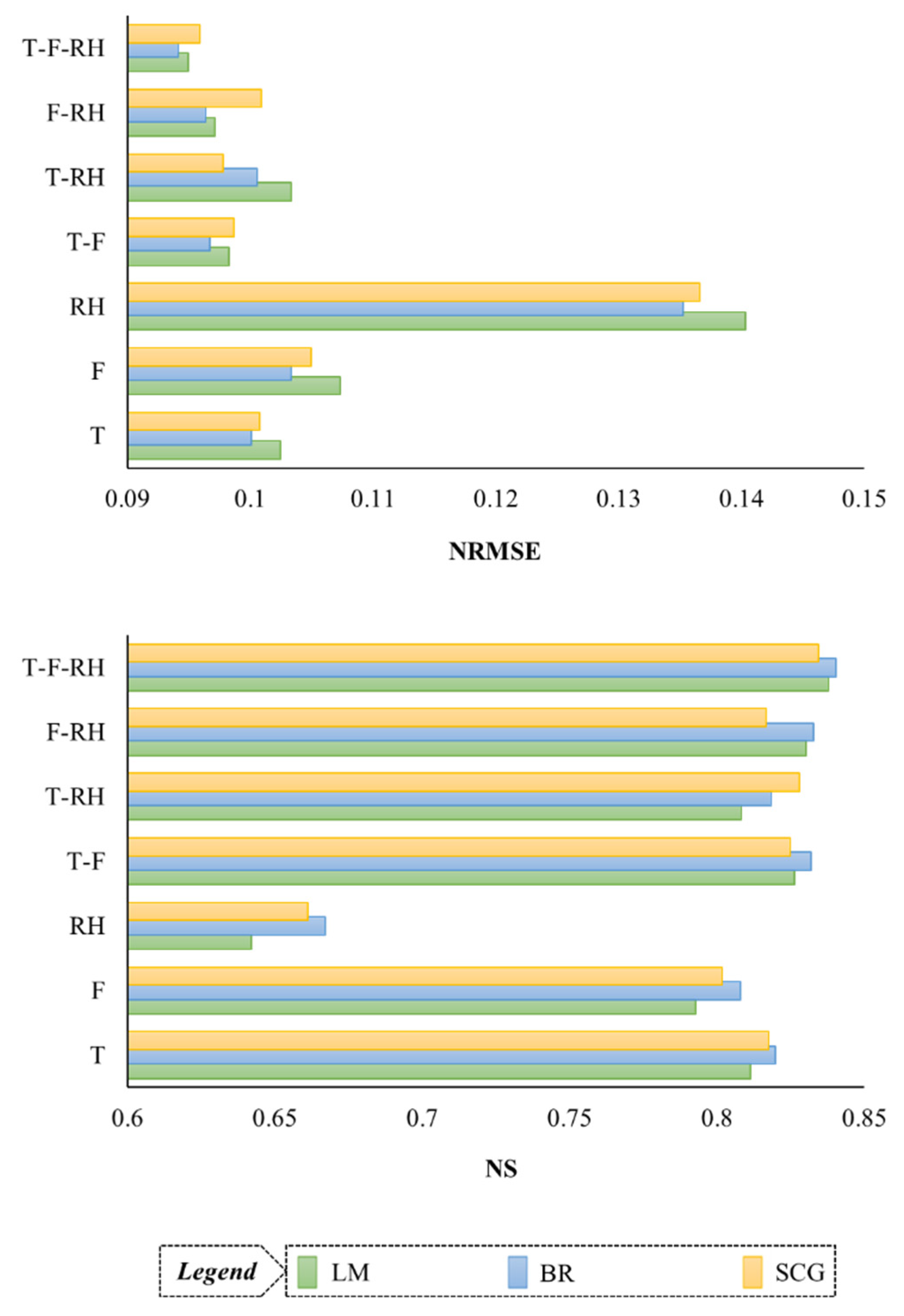
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| ANFIS | Adaptive neuro-fuzzy inference system |
| T | Mean air temperature |
| BR | Bayesian regularization |
| R2 | Coefficient of determination |
| Tdew | Dew point temperature |
| ELM | Extreme learning machine |
| FG | Fuzzy genetic |
| GEP | Gene expression programming |
| GRNN | Generalized regression neural network |
| GDX | Gradient descent with variable learning rate backpropagation |
| KSOFM | Kohonen self-organizing feature maps |
| LSSVM | Least square support vector machine |
| LM | levenberg marquardt |
| Tmax | Maximum air temperature |
| Fmax | Maximum pressure |
| RHmax | Maximum relative humidity |
| F | Mean pressure |
| Tmin | Minimum air temperature |
| Fmin | Minimum pressure |
| RHmin | Minimum relative humidity |
| MLP | Multilayer perceptron |
| MLR | Multiple linear regression |
| MARS | Multivariate adaptive regression spline |
| NS | Nash Sutcliff |
| NNARX | Neural network autoregressive with exogenous input |
| Epan | Pan evaporation |
| P | Precipitation |
| QRF | Quantile regression forests |
| RBNN | Radial basis neural networks |
| RF | Random forests |
| RH | Relative humidity |
| RH03 | Relative humidity at 03:00 |
| RH09 | Relative humidity at 09:00 |
| RH15 | Relative humidity at 15:00 |
| RVM | Relevance vector machine |
| RP | Resilient backpropagation |
| RMSE | Root Mean Square Error |
| SCG | Scaled conjugate gradient |
| SOMNN | self-organizing feature map neural network |
| RS | Solar radiation |
| SS | Stephens and Stewart |
| S | Sunshine |
| SVM | Support vector machine |
| VP | Vapor pressure |
| Twet | Wet-bulb temperature |
| WI | Willmott’s index of agreement |
| WS | Wind speed |
Appendix A
| Reference | Study Region | Models | Input Variables |
|---|---|---|---|
| Ashrafzadeh et al. [3] | Iran | MLP, SVM, SOMNN | Tmin, Tmax, T, RH, P, WS, S |
| Kişi [7] | USA | MLP, RBNN, MLR, SS | T, RS, WS, RH |
| Ali Ghorbani et al. [30] | Iran | MLP | Tmin, Tmax, WS, RH, S |
| Ghorbani et al. [36] | Iran | MLP, SVM | Tmin, Tmax, WS, RH, S |
| Kim et al. [33] | Iran | MLP, KSOFM, GEP, MLR | T, WS, RH, S, RS |
| Wang et al. [34] | China | MLP, GRNN, FG, LSSVM, MARS, ANFIS, MLR, SS | T, RS, S, RH, WS |
| Ashrafzadeh et al. [21] | Iran | MLP, SVM | Tmax, RHmax, RHmin, WS, S |
| Ehteram et al. [35] | Malaysia | MLP | T, WS, RH, RS |
| Al-Mukhtar [6] | Iraq | RF, QRF, SVM, MLR, ANN | Tmax, Tmin, RH, WS |
| Zounemat-Kermani et al. [28] | Turkey | NNARX, GEP, ANFIS | T, RS, RH, WS |
| Deo et al. [29] | Australia | RVM, ELM, MARS | Tmax, Tmin, RS, VP, P |
References
- Ghazvinian, H.; Karami, H.; Farzin, S.; Mousavi, S.F. Experimental study of evaporation reduction using polystyrene coating, wood and wax and its estimation by intelligent algorithms. Irrig. Water Eng. 2020, 11, 147–165. [Google Scholar]
- Singh, A.; Singh, R.; Kumar, A.; Kumar, A.; Hanwat, S.; Tripathi, V. Evaluation of soft computing and regression-based techniques for the estimation of evaporation. J. Water Clim. Chang. 2021, 12, 32–43. [Google Scholar] [CrossRef]
- Ashrafzadeh, A.; Malik, A.; Jothiprakash, V.; Ghorbani, M.A.; Biazar, S.M. Estimation of daily pan evaporation using neural networks and meta-heuristic approaches. ISH J. Hydraul. Eng. 2020, 26, 421–429. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D. Pan evaporation modeling in different agroclimatic zones using functional link artificial neural network. Inf. Process. Agric. 2021, 8, 134–147. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Z.; Kisi, O.; Yu, D. Pan evaporation modeling using four different heuristic approaches. Comput. Electron. Agric. 2017, 140, 203–213. [Google Scholar] [CrossRef]
- Al-Mukhtar, M. Modeling the monthly pan evaporation rates using artificial intelligence methods: A case study in Iraq. Env. Earth Sci. 2021, 80, 39. [Google Scholar] [CrossRef]
- Kişi, Ö. Modeling monthly evaporation using two different neural computing techniques. Irrig. Sci. 2009, 27, 417–430. [Google Scholar] [CrossRef]
- Lim, W.H.; Roderick, M.L.; Farquhar, G.D. A mathematical model of pan evaporation under steady state conditions. J. Hydrol. 2016, 540, 641–658. [Google Scholar] [CrossRef]
- Martínez, J.M.; Alvarez, V.M.; González-Real, M.; Baille, A. A simulation model for predicting hourly pan evaporation from meteorological data. J. Hydrol. 2006, 318, 250–261. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Roderick, M.L.; Farquhar, G.D. A simple pan-evaporation model for analysis of climate simulations: Evaluation over Australia. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Christiansen, J.E. Pan evaporation and evapotranspiration from climatic data. J. Irrig. Drain. Div. 1968, 94, 243–266. [Google Scholar] [CrossRef]
- Griffiths, J. Another evaporation formula. Agric. Meteorol. 1966, 3, 257–261. [Google Scholar] [CrossRef]
- Kohler, M.A.; Nordenson, T.J.; Fox, W. Evaporation from Pans and Lakes; US Government Printing Office: Washington, DC, USA, 1955; Volume 30.
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Stephens, J.C.; Stewart, E.H. A comparison of procedures for computing evaporation and evapotranspiration. Publication 1963, 62, 123–133. [Google Scholar]
- Qasem, S.N.; Samadianfard, S.; Kheshtgar, S.; Jarhan, S.; Kisi, O.; Shamshirband, S.; Chau, K.-W. Modeling monthly pan evaporation using wavelet support vector regression and wavelet artificial neural networks in arid and humid climates. Eng. Appl. Comput. Fluid Mech. 2019, 13, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Moghaddamnia, A.; Gousheh, M.G.; Piri, J.; Amin, S.; Han, D. Evaporation estimation using artificial neural networks and adaptive neuro-fuzzy inference system techniques. Adv. Water Resour. 2009, 32, 88–97. [Google Scholar] [CrossRef]
- Alsumaiei, A.A. Utility of artificial neural networks in modeling pan evaporation in hyper-arid climates. Water 2020, 12, 1508. [Google Scholar] [CrossRef]
- Ashrafzadeh, A.; Ghorbani, M.A.; Biazar, S.M.; Yaseen, Z.M. Evaporation process modelling over northern Iran: Application of an integrative data-intelligence model with the krill herd optimization algorithm. Hydrol. Sci. J. 2019, 64, 1843–1856. [Google Scholar] [CrossRef]
- Dehghanipour, M.H.; Karami, H.; Ghazvinian, H.; Kalantari, Z.; Dehghanipour, A.H. Two comprehensive and practical methods for simulating pan evaporation under different climatic conditions in iran. Water 2021, 13, 2814. [Google Scholar] [CrossRef]
- Kişi, Ö. Daily pan evaporation modelling using multi-layer perceptrons and radial basis neural networks. Hydrol. Process. Int. J. 2009, 23, 213–223. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Pan evaporation simulation based on daily meteorological data using soft computing techniques and multiple linear regression. Water Resour. Manag. 2015, 29, 1859–1872. [Google Scholar] [CrossRef]
- Patle, G.; Chettri, M.; Jhajharia, D. Monthly pan evaporation modelling using multiple linear regression and artificial neural network techniques. Water Supply 2020, 20, 800–808. [Google Scholar] [CrossRef]
- Kim, S.; Shiri, J.; Kisi, O. Pan evaporation modeling using neural computing approach for different climatic zones. Water Resour. Manag. 2012, 26, 3231–3249. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Hu, B.; Bilal, M.; Zounemat-Kermani, M.; Li, H. Evaporation modelling using different machine learning techniques. Int. J. Clim. 2017, 37, 1076–1092. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Kisi, O.; Piri, J.; Mahdavi-Meymand, A. Assessment of artificial intelligence–based models and metaheuristic algorithms in modeling evaporation. J. Hydrol. Eng. 2019, 24, 04019033. [Google Scholar] [CrossRef]
- Deo, R.C.; Samui, P.; Kim, D. Estimation of monthly evaporative loss using relevance vector machine, extreme learning machine and multivariate adaptive regression spline models. Stoch. Env. Res. Risk Assess. 2016, 30, 1769–1784. [Google Scholar] [CrossRef]
- Ali Ghorbani, M.; Kazempour, R.; Chau, K.-W.; Shamshirband, S.; Taherei Ghazvinei, P. Forecasting pan evaporation with an integrated artificial neural network quantum-behaved particle swarm optimization model: A case study in Talesh, Northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 724–737. [Google Scholar] [CrossRef]
- Lakmini Prarthana Jayasinghe, W.J.M.; Deo, R.C.; Ghahramani, A.; Ghimire, S.; Raj, N. Development and evaluation of hybrid deep learning long short-term memory network model for pan evaporation estimation trained with satellite and ground-based data. J. Hydrol. 2022, 607, 127534. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the artificial neural network model for prediction of monthly standardized precipitation and evapotranspiration index using hydrometeorological parameters and climate indices in eastern Australia. Atmos. Res. 2015, 161, 65–81. [Google Scholar] [CrossRef]
- Kim, S.; Shiri, J.; Singh, V.P.; Kisi, O.; Landeras, G. Predicting daily pan evaporation by soft computing models with limited climatic data. Hydrol. Sci. J. 2015, 60, 1120–1136. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Li, H. Pan evaporation modeling using six different heuristic computing methods in different climates of China. J. Hydrol. 2017, 544, 407–427. [Google Scholar] [CrossRef]
- Ehteram, M.; Panahi, F.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Elshafie, A. Predicting evaporation with optimized artificial neural network using multi-objective salp swarm algorithm. Env. Sci. Pollut. Res. 2022, 29, 10675–10701. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, M.; Deo, R.C.; Yaseen, Z.M.; H Kashani, M.; Mohammadi, B. Pan evaporation prediction using a hybrid multilayer perceptron-firefly algorithm (MLP-FFA) model: Case study in North Iran. Theor. Appl. Clim. 2018, 133, 1119–1131. [Google Scholar] [CrossRef]
- Pakdaman, M. The Effect of the type of training algorithm for multi-layer perceptron neural network on the accuracy of monthly forecast of precipitation over Iran, case study: ECMWF model. J. Earth Space Phys. 2022, 48, 213–226. [Google Scholar] [CrossRef]
- Abghari, H.; Ahmadi, H.; Besharat, S.; Rezaverdinejad, V. Prediction of Daily Pan Evaporation using Wavelet Neural Networks. Water Resour. Manag. 2012, 26, 3639–3652. [Google Scholar] [CrossRef] [Green Version]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K.-w. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef] [Green Version]
- Torabi Haghighi, A.; Abou Zaki, N.; Rossi, P.M.; Noori, R.; Hekmatzadeh, A.A.; Saremi, H.; Kløve, B. Unsustainability syndrome—from meteorological to agricultural drought in arid and semi-arid regions. Water 2020, 12, 838. [Google Scholar] [CrossRef] [Green Version]
- Moghadassi, A.; Parvizian, F.; Hosseini, S. A new approach based on artificial neural networks for prediction of high pressure vapor-liquid equilibrium. Aust. J. Basic Appl. Sci. 2009, 3, 1851–1862. [Google Scholar]
- Heidari, E.; Sobati, M.A.; Movahedirad, S. Accurate prediction of nanofluid viscosity using a multilayer perceptron artificial neural network (MLP-ANN). Chemom. Intell. Lab. Syst. 2016, 155, 73–85. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms and Applications; Pearson Education India: Noida, India, 2006. [Google Scholar]
- Burden, F.; Winkler, D. Bayesian regularization of neural networks. Artif. Neural Netw. 2008, 458, 23–42. [Google Scholar]
- Ghoreishi, S.; Heidari, E. Extraction of Epigallocatechin-3-gallate from green tea via supercritical fluid technology: Neural network modeling and response surface optimization. J. Supercrit. Fluids 2013, 74, 128–136. [Google Scholar] [CrossRef]
- Moghadassi, A.; Hosseini, S.M.; Parvizian, F.; Al-Hajri, I.; Talebbeigi, M. Predicting the supercritical carbon dioxide extraction of oregano bract essential oil. Songklanakarin J. Sci. Technol. 2011, 33, 531–538. [Google Scholar]
- Yetilmezsoy, K.; Ozkaya, B.; Cakmakci, M. Artificial intelligence-based prediction models for environmental engineering. Neural Netw. World 2011, 21, 193–218. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. Ieee Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; pp. 1930–1935. [Google Scholar]
- Wali, A.S.; Tyagi, A. Comparative study of advance smart strain approximation method using levenberg-marquardt and bayesian regularization backpropagation algorithm. Mater. Today: Proc. 2020, 21, 1380–1395. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Schraudolph, N.N.; Graepel, T. Towards stochastic conjugate gradient methods. In Proceedings of the 9th International Conference on Neural Information Processing, ICONIP’02. Singapore, 18–22 November 2002; pp. 853–856. [Google Scholar]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-fuzzy and soft computing-a computational approach to learning and machine intelligence [Book Review]. Ieee Trans. Autom. Control 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Karimpour, F. Estimating Daily Rice Crop Evapotranspiration in Limited Climatic Data and Utilizing the Soft Computing Algorithms MLP, RBF, GRNN, and GMDH. Complexity 2022, 2022, 4534822. [Google Scholar] [CrossRef]
- Kim, S.; Shiri, J.; Kisi, O.; Singh, V.P. Estimating daily pan evaporation using different data-driven methods and lag-time patterns. Water Resour. Manag. 2013, 27, 2267–2286. [Google Scholar] [CrossRef]
- Malik, A.; Rai, P.; Heddam, S.; Kisi, O.; Sharafati, A.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Pan evaporation estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an integrative data intelligence model. Atmosphere 2020, 11, 553. [Google Scholar] [CrossRef]
- Shahi, S.; Mousavi, S.F.; Hosseini, K. Simulation of Pan Evaporation Rate by ANN Artificial Intelligence Model in Damghan Region. J. Soft Comput. Civ. Eng. 2021, 5, 75–87. [Google Scholar]
- Aghelpour, P.; Singh, V.P.; Varshavian, V. Time series prediction of seasonal precipitation in Iran, using data-driven models: A comparison under different climatic conditions. Arab. J. Geosci. 2021, 14, 551. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumar, N.; Chandel, A.; Arshad, A.; Pande, C.B.; Islam, A.R.M. Modelling the reference crop evapotranspiration in the Beas-Sutlej basin (India): An artificial neural network approach based on different combinations of meteorological data. Env. Monit. Assess. 2022, 194, 1–20. [Google Scholar] [CrossRef]
- Chand, A.; Nand, R. Rainfall prediction using artificial neural network in the south pacific region. In Proceedings of the 2019 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Melbourne, VIC, Australia, 9–11 December 2019; pp. 1–7. [Google Scholar]
- Aghelpour, P.; Varshavian, V. Evaluation of stochastic and artificial intelligence models in modeling and predicting of river daily flow time series. Stoch. Env. Res. Risk Assess. 2020, 34, 33–50. [Google Scholar] [CrossRef]
- Rabehi, A.; Guermoui, M.; Lalmi, D. Hybrid models for global solar radiation prediction: A case study. Int. J. Ambient Energy 2020, 41, 31–40. [Google Scholar] [CrossRef]
- Aghelpour, P.; Guan, Y.; Bahrami-Pichaghchi, H.; Mohammadi, B.; Kisi, O.; Zhang, D. Using the MODIS sensor for snow cover modeling and the assessment of drought effects on snow cover in a mountainous area. Remote Sens. 2020, 12, 3437. [Google Scholar] [CrossRef]
- Sihag, P.; Esmaeilbeiki, F.; Singh, B.; Pandhiani, S.M. Model-based soil temperature estimation using climatic parameters: The case of Azerbaijan Province, Iran. Geol. Ecol. Landsc. 2020, 4, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Tezel, G.; Buyukyildiz, M. Monthly evaporation forecasting using artificial neural networks and support vector machines. Theor. Appl. Clim. 2016, 124, 69–80. [Google Scholar] [CrossRef]
- Mustafa, M.; Rezaur, R.; Saiedi, S.; Rahardjo, H.; Isa, M. Evaluation of MLP-ANN training algorithms for modeling soil pore-water pressure responses to rainfall. J. Hydrol. Eng. 2013, 18, 50–57. [Google Scholar] [CrossRef]





| Variable | Training Period (2006–2017) * | Validation Period (2018–2019) | Validation Period (2020–2021) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Average | STD. | Min. | Max. | Average | STD. | Min. | Max. | Average | STD. | |
| Tmax (°C) | 2.0 | 42.6 | 26.7 | 9.4 | 9.0 | 42.4 | 27.1 | 9.5 | 5.2 | 42.4 | 27.6 | 9.2 |
| Tmin (°C) | −8.1 | 26.6 | 10.2 | 7.9 | −6.0 | 27.8 | 10.5 | 7.9 | −5.8 | 25.0 | 10.2 | 7.8 |
| T (°C) | −1.1 | 34.7 | 19.0 | 9.0 | 0.9 | 35.5 | 19.3 | 9.2 | 1.5 | 34.0 | 19.4 | 9.0 |
| Tdew (°C) | −16.7 | 16.7 | 0.8 | 4.9 | −16.4 | 12.6 | −0.1 | 5.0 | −18.8 | 15.1 | −1.1 | 5.4 |
| Twet (°C) | −4.1 | 21.4 | 10.1 | 5.0 | −1.5 | 18.4 | 10.0 | 4.7 | −1.8 | 20.0 | 9.8 | 4.7 |
| Fmax (mbar) | 840.9 | 865.6 | 852.7 | 4.1 | 841.6 | 862.7 | 852.9 | 4.2 | 842.0 | 864.3 | 853.1 | 4.1 |
| Fmin (mbar) | 837.7 | 861.1 | 849.5 | 3.9 | 838.8 | 859.2 | 849.5 | 4.1 | 838.8 | 860.4 | 849.7 | 4.0 |
| F (mbar) | 839.9 | 862.8 | 851.0 | 3.9 | 840.5 | 860.6 | 851.2 | 4.1 | 840.7 | 861.7 | 851.3 | 3.9 |
| VP (mbar) | 5.7 | 56.9 | 26.2 | 13.5 | 7.8 | 58.9 | 26.7 | 14.4 | 7.0 | 55.5 | 26.8 | 13.9 |
| RHmax (%) | 14.0 | 100.0 | 60.1 | 20.6 | 11.0 | 100.0 | 59.1 | 24.2 | 14.0 | 100.0 | 56.5 | 24.8 |
| RHmin (%) | 2.0 | 93.0 | 19.4 | 14.6 | 2.0 | 97.0 | 18.5 | 16.3 | 1.0 | 98.0 | 16.1 | 14.9 |
| RH (%) | 7.3 | 98.3 | 36.8 | 18.2 | 6.6 | 98.9 | 36.4 | 20.6 | 7.3 | 99.3 | 33.8 | 20.0 |
| RH03 (%) | 12.0 | 100.0 | 58.0 | 19.9 | 11.0 | 100.0 | 56.3 | 23.5 | 13.0 | 100.0 | 53.8 | 23.7 |
| RH09 (%) | 2.0 | 100.0 | 23.9 | 17.4 | 2.0 | 100.0 | 23.3 | 19.0 | 2.0 | 100.0 | 20.5 | 18.3 |
| RH15 (%) | 2.0 | 100.0 | 28.9 | 19.7 | 2.0 | 100.0 | 28.3 | 21.6 | 1.0 | 100.0 | 26.1 | 21.2 |
| Epan (mm) | 0.0 | 18.8 | 7.0 | 3.9 | 0.1 | 17.8 | 6.7 | 4.2 | 0.1 | 18.2 | 6.8 | 4.2 |
| Components | Scenario | Inputs | R2 |
|---|---|---|---|
| Temperature (T) | S1 | T | 67.1% |
| S2 | T, Tmax | 67.1% | |
| S3 | T, Tmax, Tmin | 67.4% | |
| S4 | T, Tmax, Tmin, Twet | 72.4% | |
| S5 * | T, Tmax, Tmin, Twet, Tdew | 74.4% | |
| Pressure (F) | S6 | VP | 72.4% |
| S7 | VP, F | 73.4% | |
| S8 | VP, F, Fmax | 73.5% | |
| S9 | VP, F, Fmax, Fmin | 73.5% | |
| Relative humidity (RH) | S10 | RHmax | 57.7% |
| S11 | RHmax, RH03 | 57.7% | |
| S12 | RHmax, RH03, RH | 57.8% | |
| S13 | RHmax, RH03, RH, RH15 | 57.8% | |
| S14 | RHmax, RH03, RH, RH15, RH09 | 58.9% | |
| S15 | RHmax, RH03, RH, RH15, RH09, RHmin | 59.1% | |
| Temperature and pressure (T–F) | S16 | VP, T | 73.2% |
| S17 | VP, T, Tmax | 73.2% | |
| S18 | VP, T, Tmax, Tmin | 73.4% | |
| S19 | VP, T, Tmax, Tmin, Twet | 75.4% | |
| S20 | VP, T, Tmax, Tmin, Twet, F | 76.1% | |
| S21 | VP, T, Tmax, Tmin, Twet, F, Fmax | 76.3% | |
| S22 | VP, T, Tmax, Tmin, Twet, F, Fmax, Fmin | 76.3% | |
| S23 | VP, T, Tmax, Tmin, Twet, F, Fmax, Fmin, Tdew | 76.5% | |
| Temperature and relative humidity (T–RH) | S24 | T, Tmax, Tmin, RHmax | 70.4% |
| S25 | T, Tmax, Tmin, RHmax, RH03 | 70.4% | |
| S26 | T, Tmax, Tmin, RHmax, RH03, RH | 70.5% | |
| S27 | T, Tmax, Tmin, RHmax, RH03, RH, Twet | 73.6% | |
| S28 | T, Tmax, Tmin, RHmax, RH03, RH, Twet, RH15 | 73.6% | |
| S29 | T, Tmax, Tmin, RHmax, RH03, RH, Twet, RH15, RH09 | 73.6% | |
| S30 | T, Tmax, Tmin, RHmax, RH03, RH, Twet, RH15, RH09, RHmin | 73.7% | |
| S31 | T, Tmax, Tmin, RHmax, RH03, RH, Twet, RH15, RH09, RHmin, Tdew | 75.1% | |
| Pressure and relative humidity (F–RH) | S32 | VP, RHmax | 74.3% |
| S33 | VP, RHmax, RH03 | 74.4% | |
| S34 | VP, RHmax, RH03, RH | 74.4% | |
| S35 | VP, RHmax, RH03, RH, F | 75.6% | |
| S36 | VP, RHmax, RH03, RH, F, Fmax | 75.7% | |
| S37 | VP, RHmax, RH03, RH, F, Fmax, Fmin | 75.7% | |
| S38 | VP, RHmax, RH03, RH, F, Fmax, Fmin, RH15 | 75.8% | |
| S39 | VP, RHmax, RH03, RH, F, Fmax, Fmin, RH15, RH09 | 75.8% | |
| S40 | VP, RHmax, RH03, RH, F, Fmax, Fmin, RH15, RH09, RHmin | 75.8% | |
| Temperature, pressure and relative humidity (T–F–RH) | S41 | VP, T, Tmax, Tmin, RHmax | 75.6% |
| S42 | VP, T, Tmax, Tmin, RHmax, RH03 | 75.7% | |
| S43 | VP, T, Tmax, Tmin, RHmax, RH03, RH | 75.8% | |
| S44 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet | 75.9% | |
| S45 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F | 76.7% | |
| S46 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax | 76.7% | |
| S47 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax, Fmin | 76.7% | |
| S48 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax, Fmin, RH15 | 76.8% | |
| S49 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax, Fmin, RH15, RH09 | 76.8% | |
| S50 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax, Fmin, RH15, RH09, RHmin | 76.8% | |
| S51 | VP, T, Tmax, Tmin, RHmax, RH03, RH, Twet, F, Fmax, Fmin, RH15, RH09, RHmin, Tdew | 76.8% |
| Input Scenario | Transfer Function | Network Makeup * | Train | Validation | Test | |||
|---|---|---|---|---|---|---|---|---|
| RMSE | WI | RMSE | WI | RMSE | WI | |||
| T | satlin | 12-10-1 | 1.853 | 0.932 | 1.836 | 0.945 | 1.832 | 0.944 |
| F | satlin | 15-10-1 | 1.939 | 0.924 | 1.879 | 0.939 | 1.962 | 0.931 |
| RH | satlin | 12-12-1 | 2.395 | 0.871 | 2.295 | 0.907 | 2.733 | 0.866 |
| T-F | satlin | 15-10-1 | 1.773 | 0.939 | 1.739 | 0.951 | 1.779 | 0.947 |
| T-RH | satlin | 18-12-1 | 1.844 | 0.934 | 1.838 | 0.945 | 1.861 | 0.942 |
| F-RH | tansig | 18-18-1 | 1.799 | 0.935 | 1.686 | 0.953 | 1.791 | 0.945 |
| T-F-RH ** | tansig | 12-12-1 | 1.797 | 0.936 | 1.652 | 0.956 | 1.747 | 0.949 |
| Input Scenario | Transfer Function | Network Makeup * | Train | Validation | Test | |||
|---|---|---|---|---|---|---|---|---|
| RMSE | WI | RMSE | WI | RMSE | WI | |||
| T | tansig | 12-10-1 | 1.887 | 0.928 | 1.777 | 0.948 | 1.807 | 0.943 |
| F | satlin | 12-12-1 | 1.892 | 0.928 | 1.821 | 0.943 | 1.880 | 0.937 |
| RH | satlin | 10-10-1 | 2.410 | 0.872 | 2.199 | 0.916 | 2.646 | 0.874 |
| T-F | satlin | 15-10-1 | 1.815 | 0.934 | 1.697 | 0.953 | 1.765 | 0.946 |
| T-RH | tansig | 12-10-1 | 1.810 | 0.935 | 1.778 | 0.949 | 1.821 | 0.945 |
| F-RH | tansig | 18-15-1 | 1.832 | 0.934 | 1.660 | 0.956 | 1.790 | 0.947 |
| T-F-RH ** | tansig | 12-12-1 | 1.836 | 0.934 | 1.629 | 0.957 | 1.742 | 0.949 |
| Input Scenario | Transfer Function | Network Makeup * | Train | Validation | Test | |||
|---|---|---|---|---|---|---|---|---|
| RMSE | WI | RMSE | WI | RMSE | WI | |||
| T | tansig | 12-10-1 | 1.879 | 0.929 | 1.792 | 0.948 | 1.816 | 0.944 |
| F | tansig | 12-12-1 | 1.915 | 0.926 | 1.832 | 0.941 | 1.927 | 0.933 |
| RH | tansig | 10-10-1 | 2.394 | 0.867 | 2.245 | 0.909 | 2.648 | 0.869 |
| T-F | satlin | 12-10-1 | 1.823 | 0.934 | 1.738 | 0.951 | 1.796 | 0.945 |
| T-RH | satlin | 18-15-1 | 1.853 | 0.932 | 1.722 | 0.953 | 1.778 | 0.947 |
| F-RH | satlin | 10-10-1 | 1.874 | 0.930 | 1.747 | 0.950 | 1.865 | 0.941 |
| T-F-RH ** | satlin | 12-12-1 | 1.814 | 0.935 | 1.668 | 0.955 | 1.766 | 0.947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghelpour, P.; Bagheri-Khalili, Z.; Varshavian, V.; Mohammadi, B. Evaluating Three Supervised Machine Learning Algorithms (LM, BR, and SCG) for Daily Pan Evaporation Estimation in a Semi-Arid Region. Water 2022, 14, 3435. https://doi.org/10.3390/w14213435
Aghelpour P, Bagheri-Khalili Z, Varshavian V, Mohammadi B. Evaluating Three Supervised Machine Learning Algorithms (LM, BR, and SCG) for Daily Pan Evaporation Estimation in a Semi-Arid Region. Water. 2022; 14(21):3435. https://doi.org/10.3390/w14213435
Chicago/Turabian StyleAghelpour, Pouya, Zahra Bagheri-Khalili, Vahid Varshavian, and Babak Mohammadi. 2022. "Evaluating Three Supervised Machine Learning Algorithms (LM, BR, and SCG) for Daily Pan Evaporation Estimation in a Semi-Arid Region" Water 14, no. 21: 3435. https://doi.org/10.3390/w14213435






