Study of the Effect of Leucine on Calcium Carbonate Precipitation in a Circular Economy Perspective
Abstract
:1. Introduction
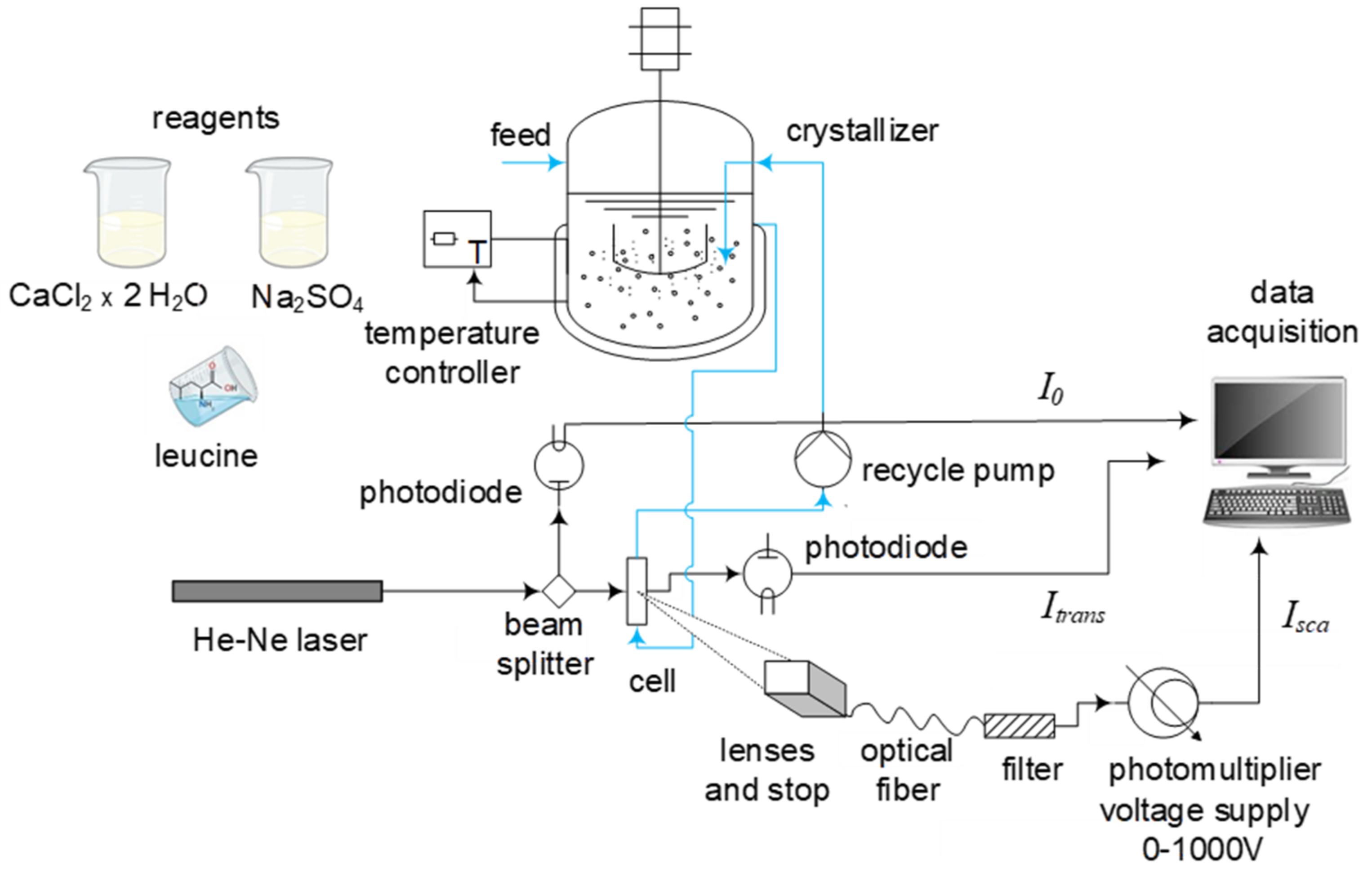
2. Materials and Methods
- calcium ion activity
- carbonate ion activity
- solubility product of calcium carbonate.
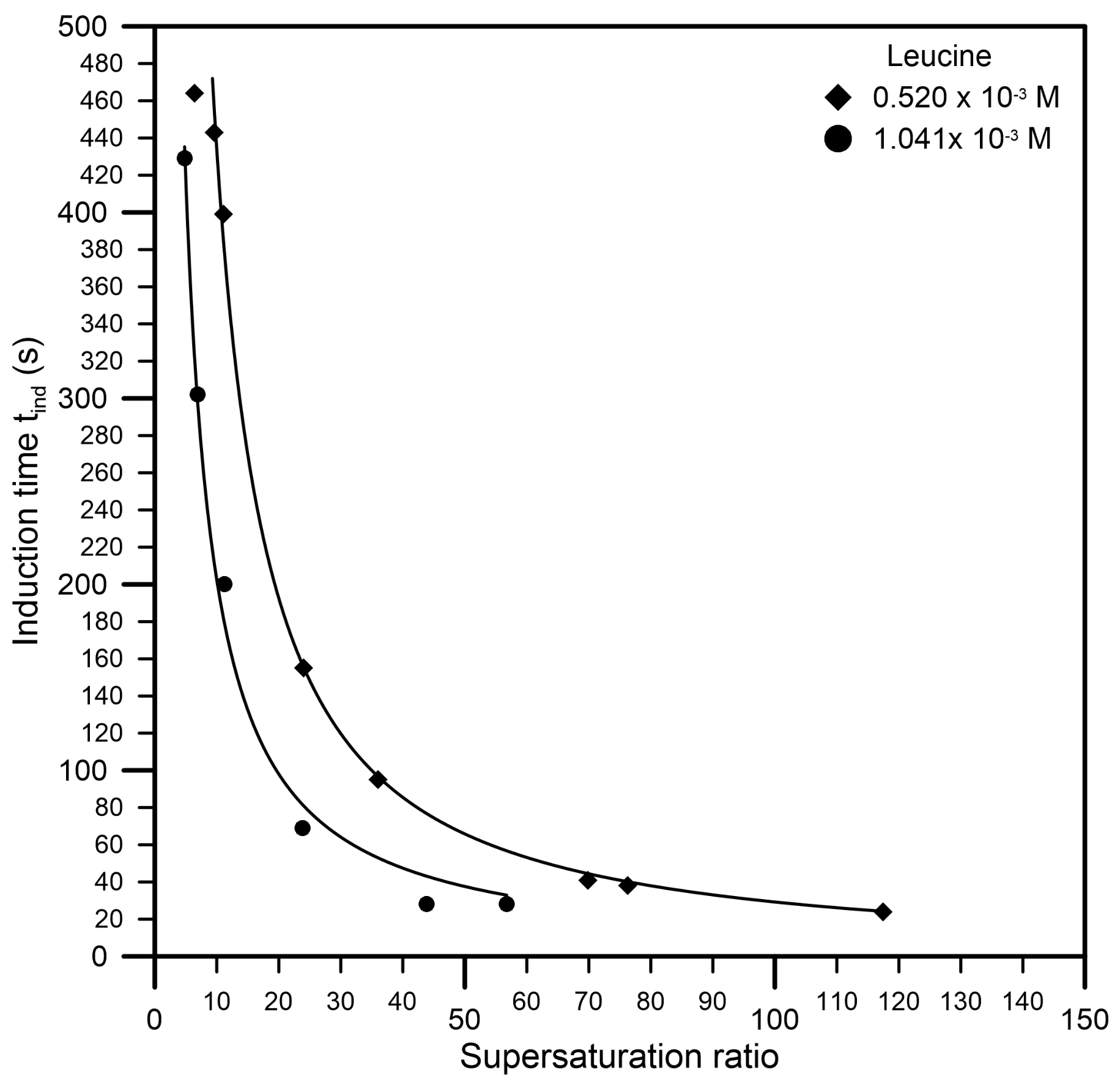
3. Results and Discussion
- empirical constant
- absolute temperature,
- supersaturation ratio
- shape factor.
- interfacial tension, .
- molar volume, .
- Avogadro number, .
- correction factor ( heterog. nucl. homog. nucl.).
- gas constant, .
- number of ions.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| K1 | K2 | KW | KL1 | KL2 |
|---|---|---|---|---|
| 4.45 × 10−7 | 4.69 × 10−11 | 1 × 10−14 | 7.41 × 10−4 | 1.75 × 10−5 |
| Salts (M) | Ca2+ (M) | CO32− (M) | S | |||
|---|---|---|---|---|---|---|
| 0.01150 | 0.01150 | 2.29 × 10−5 | 0.4369 | 0.4369 | 5.22 × 10−9 | 9.62 |
| 0.01598 | 0.01598 | 4.53 × 10−5 | 0.3886 | 0.3886 | 4.54 × 10−9 | 24.04 |
| 0.02870 | 0.02870 | 1.29 × 10−4 | 0.3063 | 0.3063 | 4.57 × 10−9 | 76.26 |
- are the dissociation constants of carbonic acid
- , is the dissociation constant of water
- are the dissociation constants of leucine
- is the solubility product, evaluated using Equation (3)
- are the activity coefficients of and .
- the charge of species,
- ionic strength () of the solution
- , constant ()
- constant ()
- constant () which is a function of the temperature
- absolute temperature ()
- dielectric constant of water
- By means of the following equation, the ionic strength can be calculated:
- concentration of species ().
References
- Zhao, J.; Wang, M.; Lababidi, H.M.; Al-Adwani, H.; Gleason, K.K. A review of heterogeneous nucleation of calcium carbonate and control strategies for scale formation in multi-stage flash (MSF) desalination plants. Desalination 2018, 442, 75–88. [Google Scholar] [CrossRef]
- Hoek, E.M.; Jassby, D.; Kaner, R.B.; Wu, J.; Wang, J.; Liu, Y.; Rao, U. Sustainable Desalination and Water Reuse; Morgan & Claypool Publishers: Williston, VT, USA, 2021. [Google Scholar]
- Erdogan, N.; Eken, H.A. Precipitated calcium carbonate production, synthesis and properties. Phys. Probl. Min. Process. 2017, 53, 57–68. [Google Scholar]
- Jimoh, O.A.; Ariffin, K.S.; Bin Hussin, H.; Temitope, A.E. Synthesis of precipitated calcium carbonate: A review. Carbonates Evaporites 2018, 33, 331–346. [Google Scholar] [CrossRef]
- Xu, Y.; Ye, J.; Zhou, D.; Su, L. Research progress on applications of calcium derived from marine organisms. Sci. Rep. 2020, 10, 18425. [Google Scholar] [CrossRef]
- Declet, A.; Reyes, E.; Suarez, O.M. Calcium carbonate precipitation: A review of the carbonate crystallization process and applications in bioinspired composites. Rev. Adv. Mater. Sci. 2016, 44, 87–107. [Google Scholar]
- Yadav, V.K.; Yadav, K.K.; Cabral-Pinto, M.M.S.; Choudhary, N.; Gnanamoorthy, G.; Tirth, V.; Prasad, S.; Khan, A.H.; Islam, S.; Khan, N.A. The Processing of Calcium Rich Agricultural and Industrial Waste for Recovery of Calcium Carbonate and Calcium Oxide and Their Application for Environmental Cleanup: A Review. Appl. Sci. 2021, 11, 4212. [Google Scholar] [CrossRef]
- Czaplicka, N.; Konopacka-Łyskawa, D. Utilization of Gaseous Carbon Dioxide and Industrial Ca-Rich Waste for Calcium Carbonate Precipitation: A Review. Energies 2020, 13, 6239. [Google Scholar] [CrossRef]
- Czaplicka, N.; Konopacka-Łyskawa, D.; Lewandowska, P.; Łapiński, M.; Bray, R. Influence of selected CO2 absorption promoters on the characteristics of calcium carbonate particles produced by carbonation of the post-distillation liquid from the Solvay process. Powder Technol. 2021, 391, 432–441. [Google Scholar] [CrossRef]
- Chang, R.; Kim, S.; Lee, S.; Choi, S.; Kim, M.; Park, Y. Calcium Carbonate Precipitation for CO2 Storage and Utilization: A Review of the Carbonate Crystallization and Polymorphism. Front. Energy Res. 2017, 10, 5–17. [Google Scholar] [CrossRef] [Green Version]
- Bang, J.-H.; Yoo, Y.; Lee, S.-W.; Song, K.; Chae, S. CO2 Mineralization Using Brine Discharged from a Seawater Desalination Plant. Minerals 2017, 7, 207. [Google Scholar] [CrossRef] [Green Version]
- Ogunbiyi, O.; Saththasivam, J.; Al-Masri, D.; Manawi, Y.; Lawler, J.; Zhang, X.; Liu, Z. Sustainable brine management from the perspectives of water, energy and mineral recovery: A comprehensive review. Desalination 2021, 513, 115055. [Google Scholar] [CrossRef]
- Bang, J.H.; Chae, S.C.; Lee, S.W.; Kim, J.W.; Song, K.; Kim, J.; Kim, W. Sequential carbonate mineralization of desalination brine for CO2 emission reduction. J. CO2 Util. 2019, 33, 427–433. [Google Scholar] [CrossRef]
- Amjad, Z. Scale inhibition in desalination applications: An overview. In Corrosion 96; NACE-96-230; OnePetro: Richardson, TX, USA, 1996. [Google Scholar]
- Xiang, L.; Xiang, Y.; Wang, Z.G.; Jin, Y. Influence of chemical additives on the formation of super-fine calcium carbonate. Powder Technol. 2002, 126, 129–133. [Google Scholar] [CrossRef]
- Mantilaka, M.M.; Karunaratne, D.G.; Rajapakse, R.M.; Pitawala, H.M. Precipitated calcium carbonate/poly(methyl methacrylate) nanocomposite using dolomite. Synth. Charact. Prop. 2013, 235, 628–632. [Google Scholar]
- Cai, G.-B.; Zhao, G.-X.; Wang, X.-K.; Yu, S.-H. Synthesis of polyacrylic acid stabilized amorphous calcium carbonate nanoparticles and their application for removal of toxic heavy metal ions in water. J. Phys. Chem. C 2010, 114, 12948–12954. [Google Scholar] [CrossRef]
- Hwang, D.J.; Yu, Y.H.; Baek, C.S.; Lee, G.M.; Cho, K.H.; Ahn, J.W.; Han, C.; Lee, J.D. Preparation of high purity PCC from medium- and low-grade limestones using the strongly acidic cation exchange resin. J. Ind. Eng. Chem. 2015, 30, 309–321. [Google Scholar] [CrossRef]
- Szczes, A.; Chibowski, E.; Hołysz, L. Influence of ionic surfactants on the properties of freshly precipitated calcium carbonate. Colloids Surf A 2007, 297, 14–18. [Google Scholar] [CrossRef]
- Euliss, L.E.; Bartl, M.H.; Stucky, G.D. Control of calcium carbonate crystallization utilizing amphiphilic block copolypeptides. J. Cryst. Growth 2006, 286, 424–430. [Google Scholar] [CrossRef]
- Picker, A.; Kellermeier, M.; Seto, J.; Gebauer, D.; Cölfen, H. The multiple effect of amino acids on the early stages of calcium carbonate crystallization. Z. Krist. Cryst. Miner. 2012, 227, 744–757. [Google Scholar] [CrossRef] [Green Version]
- Thompson, S.P.; Parker, J.E.; Street, S.R.; Tang, C.C. Morphological templating of metastable calcium carbonates by the amino acid leucine. J. Phys. Conf. Ser. 2010, 286, 012030. [Google Scholar] [CrossRef]
- Borukhin, S.; Bloch, L.; Radlauer, T.; Hill, A.H.; Fitch, A.N.; Pokroy, B. Screening the incorporation of amino acids an inorganic crystalline host: The case of calcite. Adv. Funct. Mater. 2012, 22, 4216–4224. [Google Scholar] [CrossRef]
- Christoph, B.; Seto, J. Single amino acids as additives modulating CaCO3 mineralization. Adv. Top. Biominer. 2012, 17, 33–48. [Google Scholar]
- Malkaj, P.; Kanakis, I.; Dalas, E. The effect of leucine on the crystal growth of calcium carbonate. J. Cryst. Growth 2004, 266, 533–538. [Google Scholar] [CrossRef]
- Dalas, E.; Malkaj, P.; Vasileiou, Z.; Kanellopoulou, D.G. The effect of Leucine on the crystal growth of calcium phosphate. J. Mater. Sci. Mater. Med. 2008, 19, 277–282. [Google Scholar] [CrossRef]
- Chaussemier, M.; Pourmohtasham, E.; Gelus, D.; Pécoul, N.; Perrot, H.; Lédion, J.; Cheap-Charpentier, H.; Horner, H.O. State of art of natural inhibitors of calcium carbonate scaling. A review article. Desalination 2015, 356, 47–55. [Google Scholar] [CrossRef]
- Hasson, D.; Shemer, H.; Sher, A. State of the art of friendly “green” scale control inhibitors: A review article. Ind. Eng. Chem. Res. 2011, 50, 7601–7607. [Google Scholar] [CrossRef]
- Mersmann, A. Crystallization Technology Handbook; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Prisciandaro, M.; Olivieri, E.; Lancia, A.D. PBTC as an Antiscalant for Gypsum Precipitation: Interfacial Tension and Activation Energy Estimation. Ind. Eng. Chem. Res. 2012, 51, 12844–12851. [Google Scholar] [CrossRef]
- Söhnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Coll. Int. Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- Lancia, A.; Musmarra, D.; Prisciandaro, M. Measuring induction period for calcium sulfate dihydrate precipitation. AIChE J. 1999, 45, 390–397. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann, Ltd.: Oxford, UK, 2001. [Google Scholar]
- Söhnel, O.; Garside, J. Precipitation; Butterworth-Heinemann, Ltd.: Oxford, UK, 1992. [Google Scholar]
- Stumm, W.; Morgan, J.J. Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, 3rd ed.; Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Larson, T.E.; Buswell, A.M. Calcium Carbonate Saturation Index and Alkalinity Interpretations. J. Am. Water Works Ass. 1942, 34, 1667. [Google Scholar] [CrossRef]
- Di Celso, G.M.; Prisciandaro, M.; Karatza, D.; Lancia, A.; Musmarra, D. Salt scales on process equipment: Measurement of the induction time for calcium carbonate nucleation. Can. J. Chem. Eng. 2017, 95, 1671–1675. [Google Scholar] [CrossRef]
- Di Celso, G.M.; Prisciandaro, M.; Karatza, D.; Lancia, A.; Musmarra, D. Calcium carbonate scales on process equipment: A measure of the induction time for nucleation. Desalination Water Treat. 2017, 69, 173–177. [Google Scholar] [CrossRef] [Green Version]
- Prisciandaro, M.; Di Celso, G.M.; Lancia, A.; Musmarra, D.; Karatza, D. Citric acid as a green additive to retard calcium carbonate scales on process equipment. Can. J. Chem. Eng. 2020, 98, 1973–1979. [Google Scholar] [CrossRef]

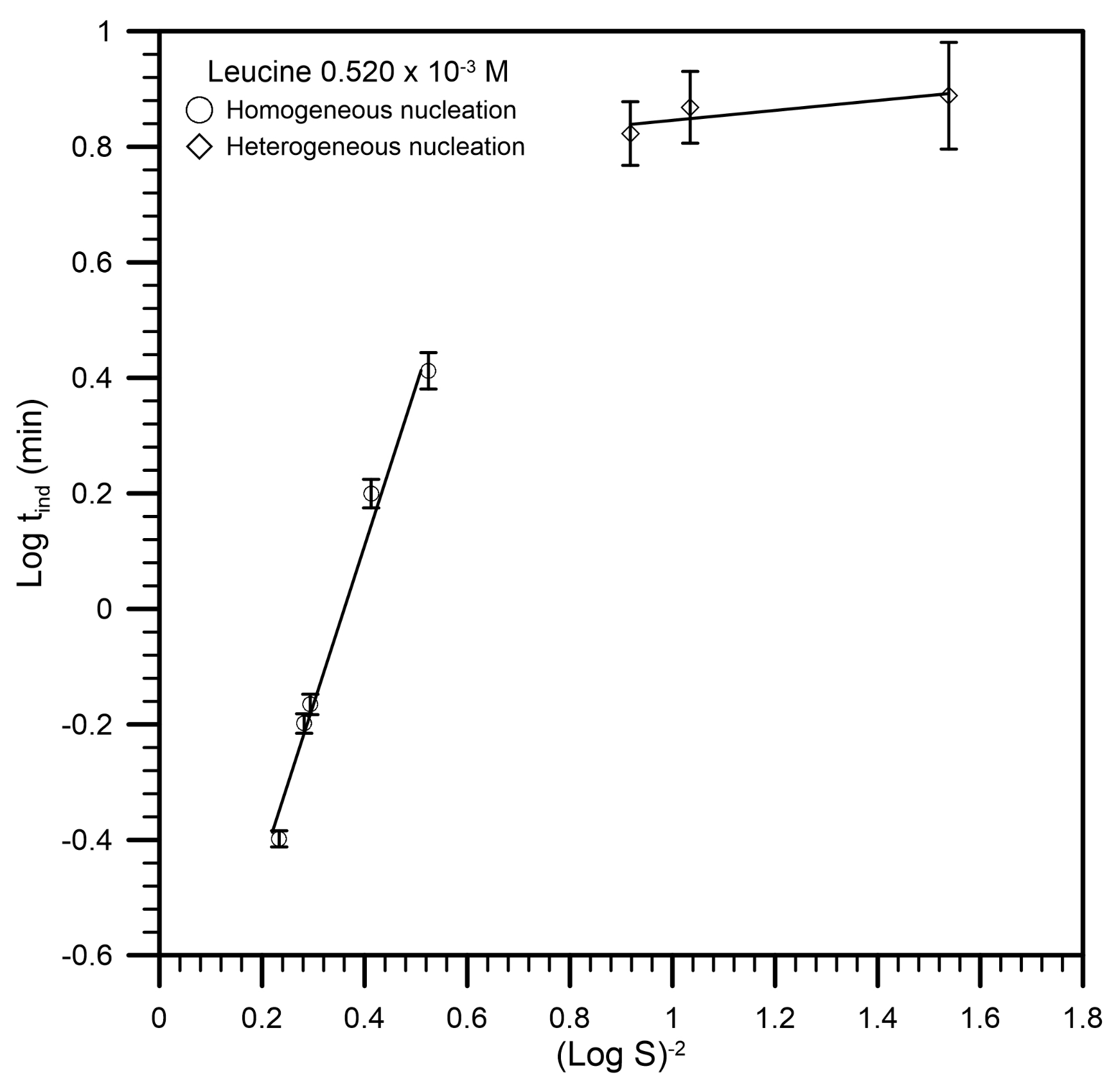
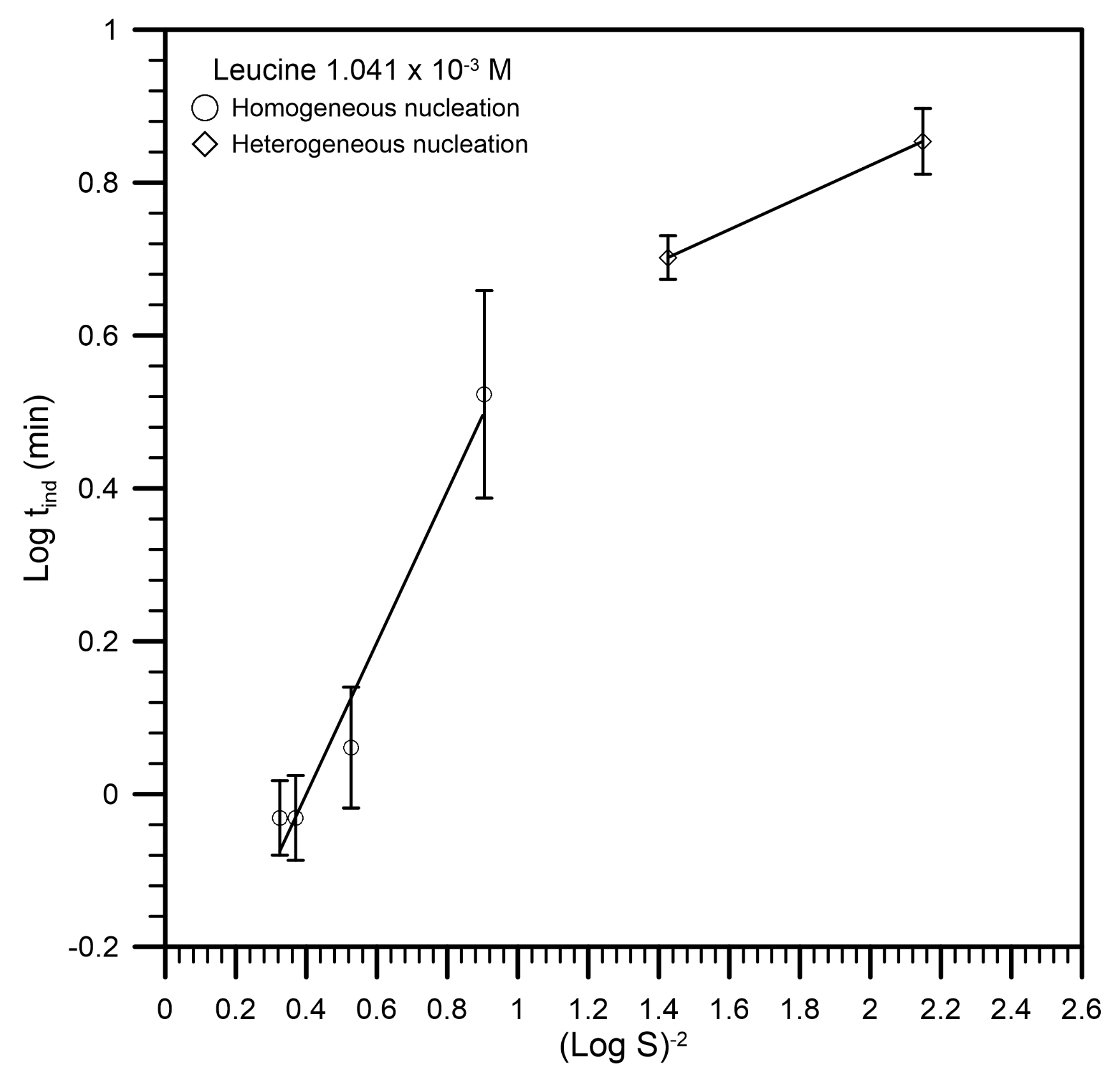
| Leucine (M) | R2 | ||
|---|---|---|---|
| 0 | 1.08 × 106 | 2.11 | 0.991 |
| 0.520 × 10−3 | 6.43 × 103 | 1.17 | 0.998 |
| 1.041 × 10−3 | 2.25 × 103 | 1.05 | 0.993 |
| Additive Concentration (M) | Interfacial Tension |
|---|---|
| 0 | 109.3 |
| 0.520 × 10−3 | 84.05 |
| 1.041 × 10−3 | 68.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazziotti di Celso, G.; Prisciandaro, M.; Karatza, D.; Musmarra, D.; Lancia, A. Study of the Effect of Leucine on Calcium Carbonate Precipitation in a Circular Economy Perspective. Water 2022, 14, 270. https://doi.org/10.3390/w14020270
Mazziotti di Celso G, Prisciandaro M, Karatza D, Musmarra D, Lancia A. Study of the Effect of Leucine on Calcium Carbonate Precipitation in a Circular Economy Perspective. Water. 2022; 14(2):270. https://doi.org/10.3390/w14020270
Chicago/Turabian StyleMazziotti di Celso, Giuseppe, Marina Prisciandaro, Despina Karatza, Dino Musmarra, and Amedeo Lancia. 2022. "Study of the Effect of Leucine on Calcium Carbonate Precipitation in a Circular Economy Perspective" Water 14, no. 2: 270. https://doi.org/10.3390/w14020270






