Hydrological Forecasting under Climate Variability Using Modeling and Earth Observations in the Naryn River Basin, Kyrgyzstan
Abstract
:1. Introduction
2. Materials and Methods
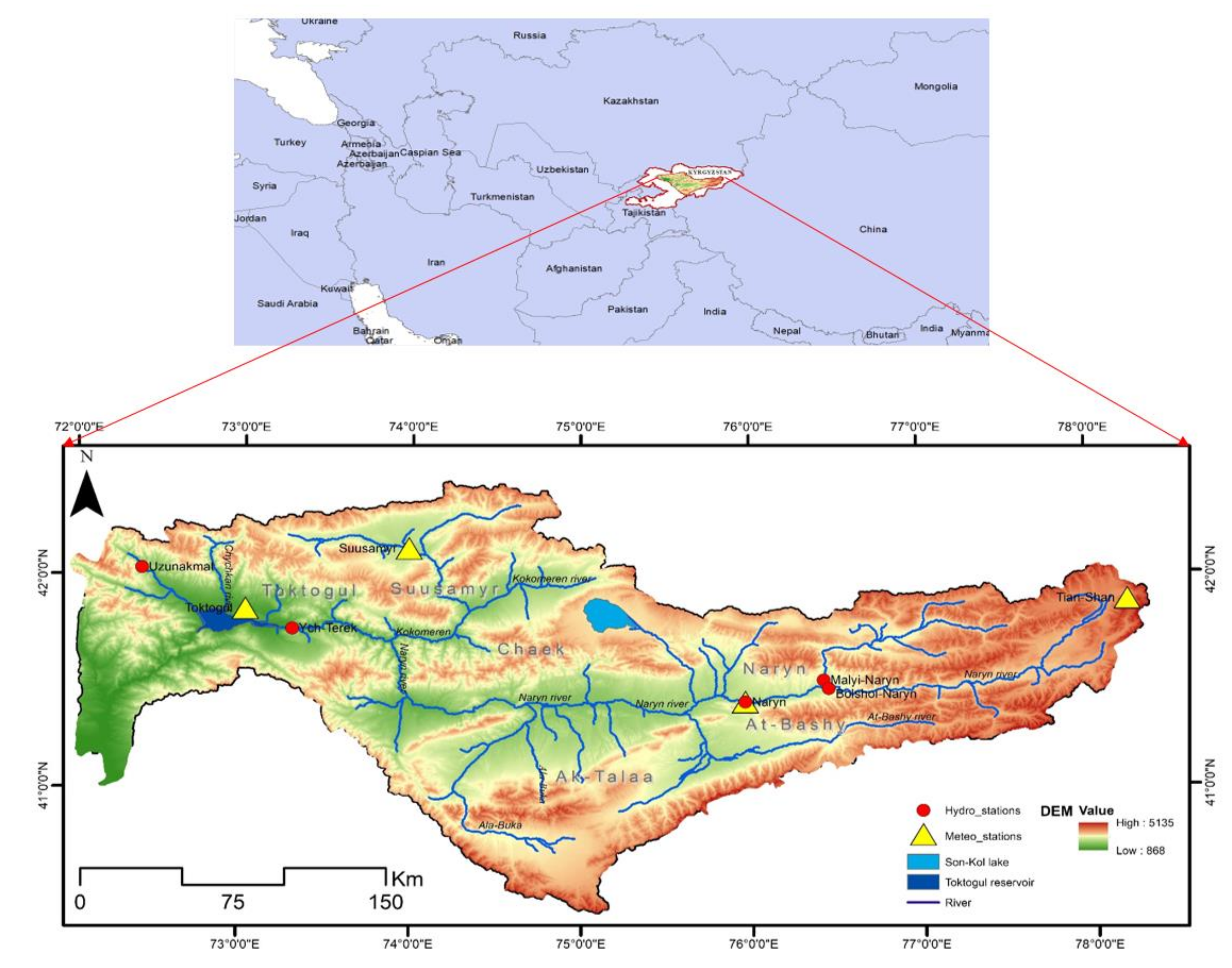
2.1. Study Area
2.2. Data Used
2.3. Methodology
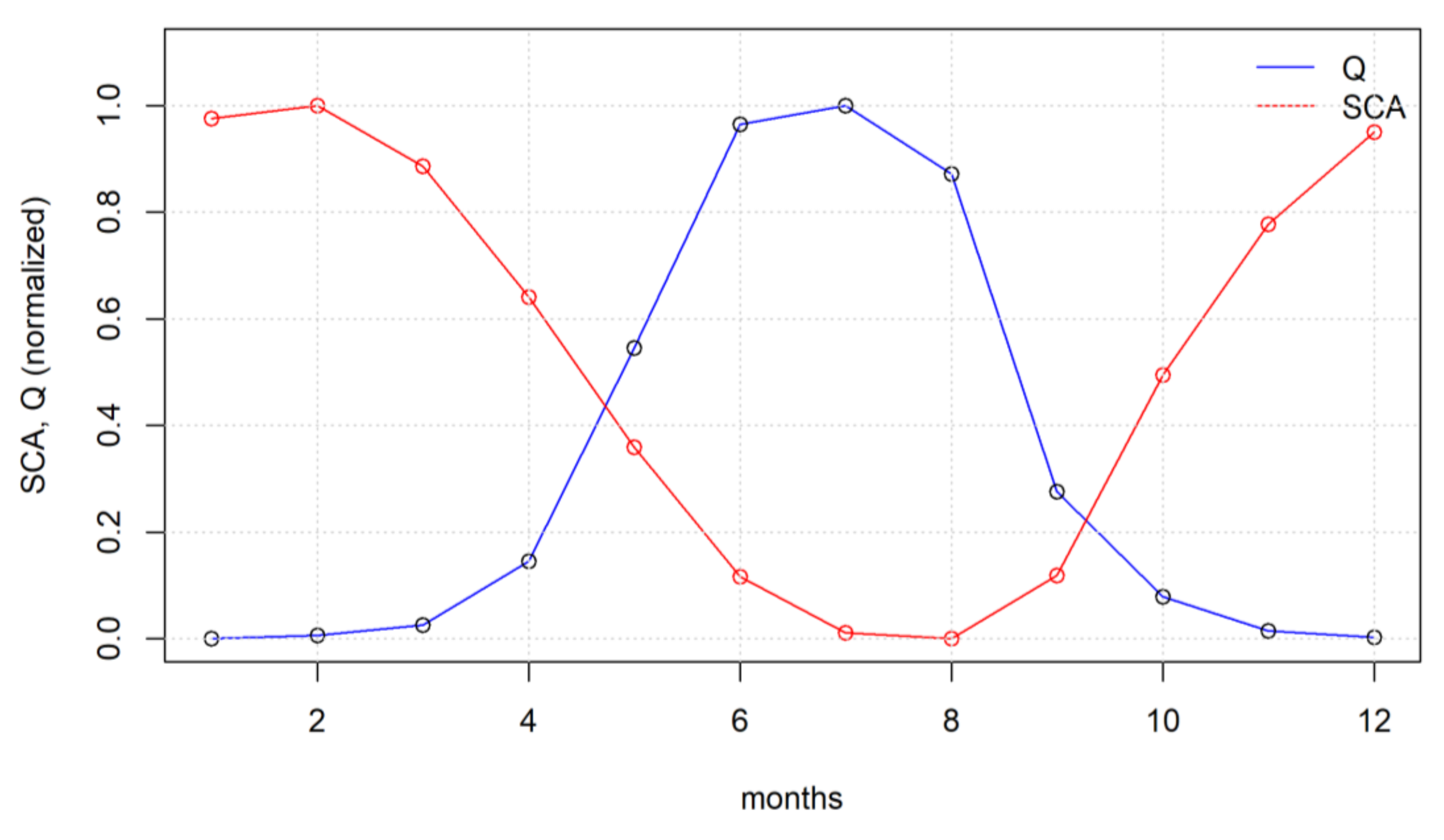
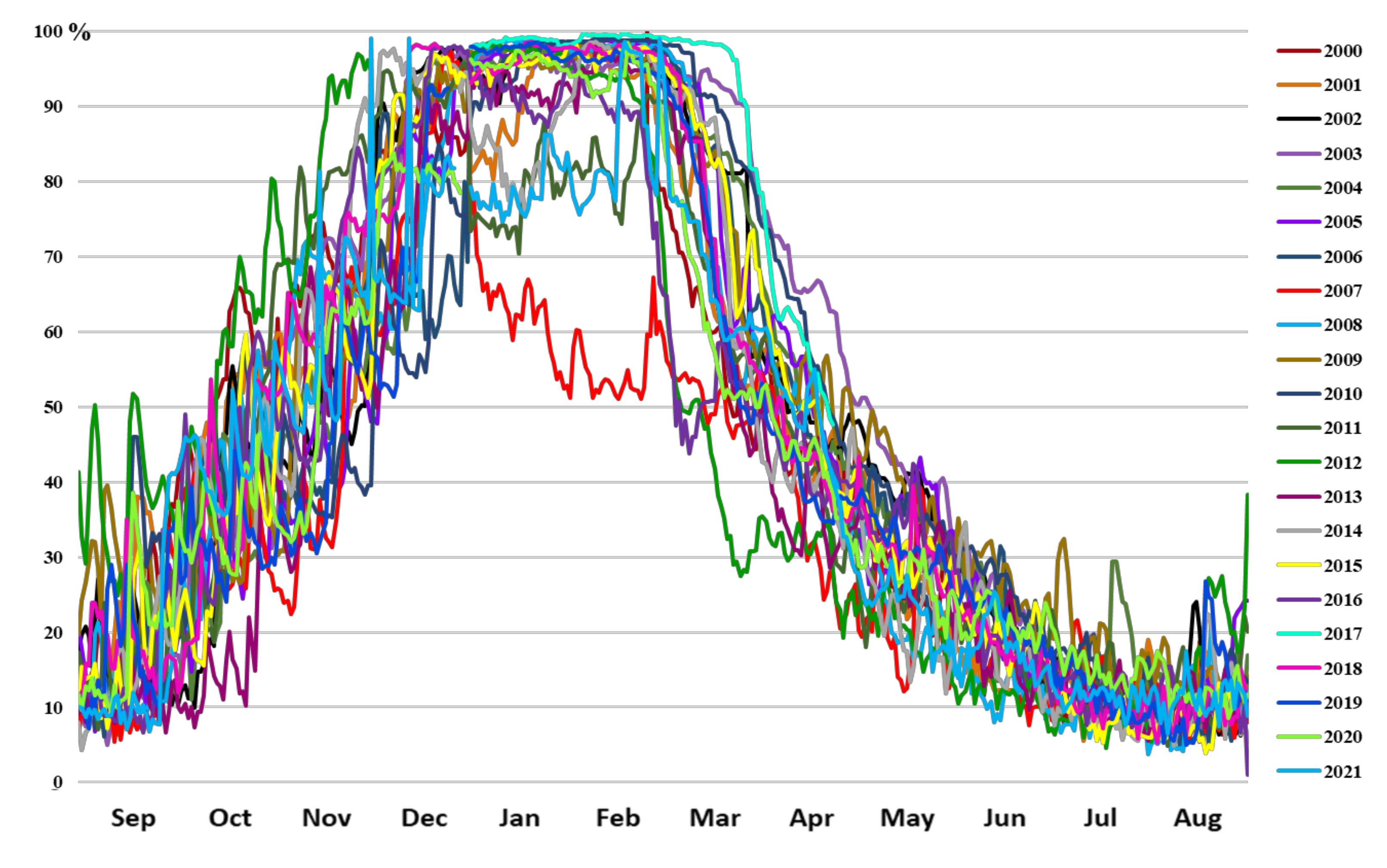
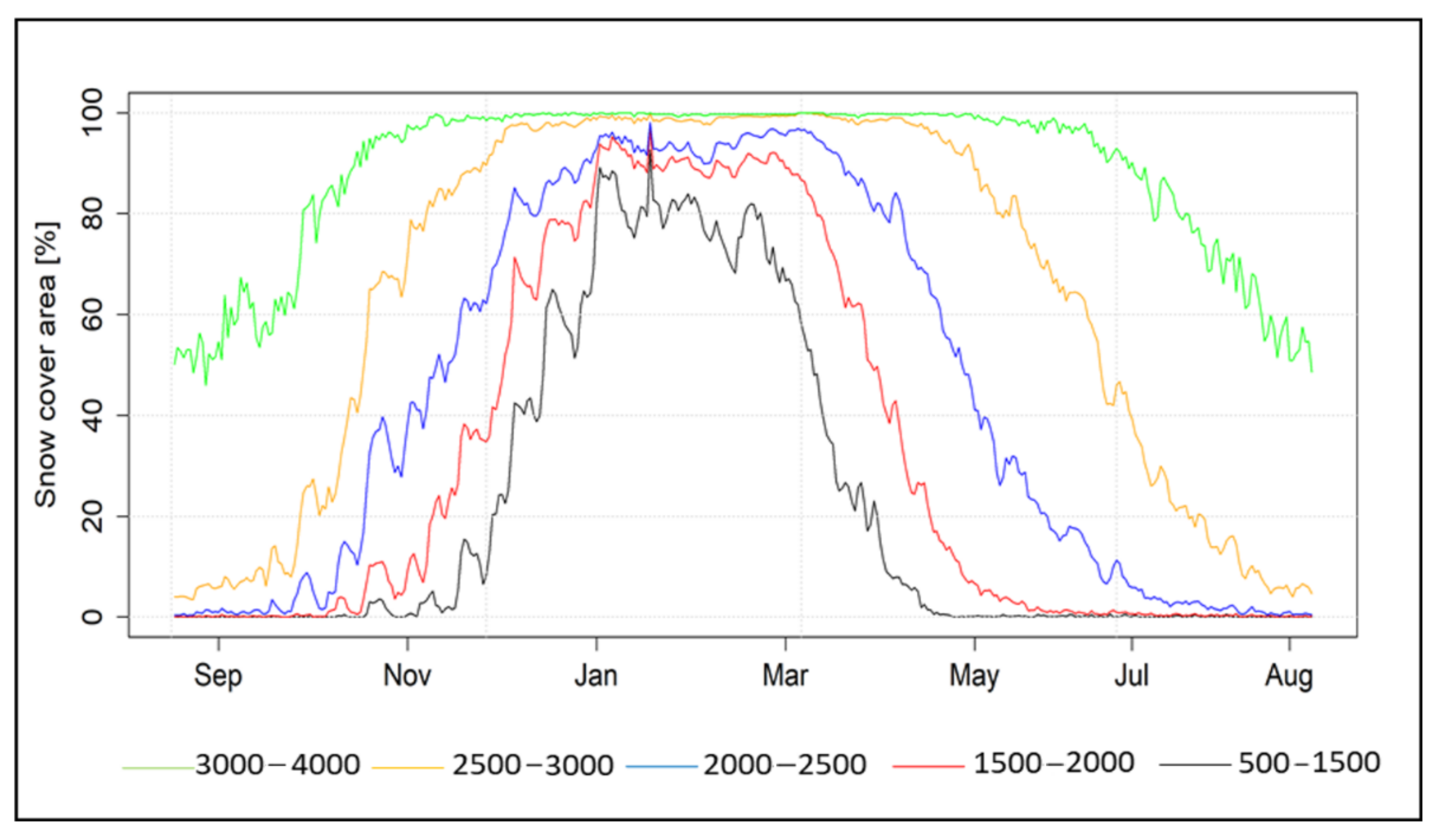
3. Results
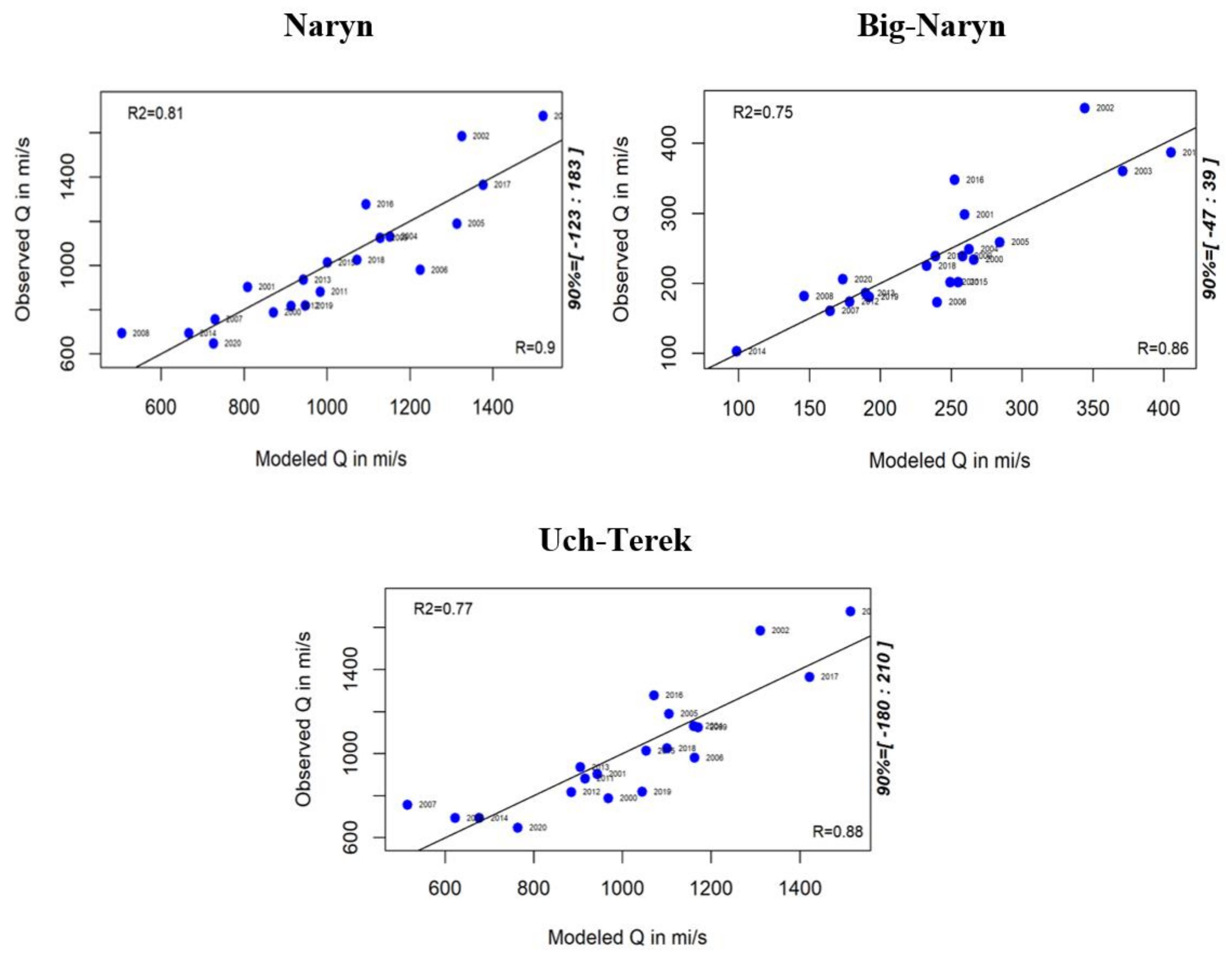
3.1. Simulation Results of MODSNOW
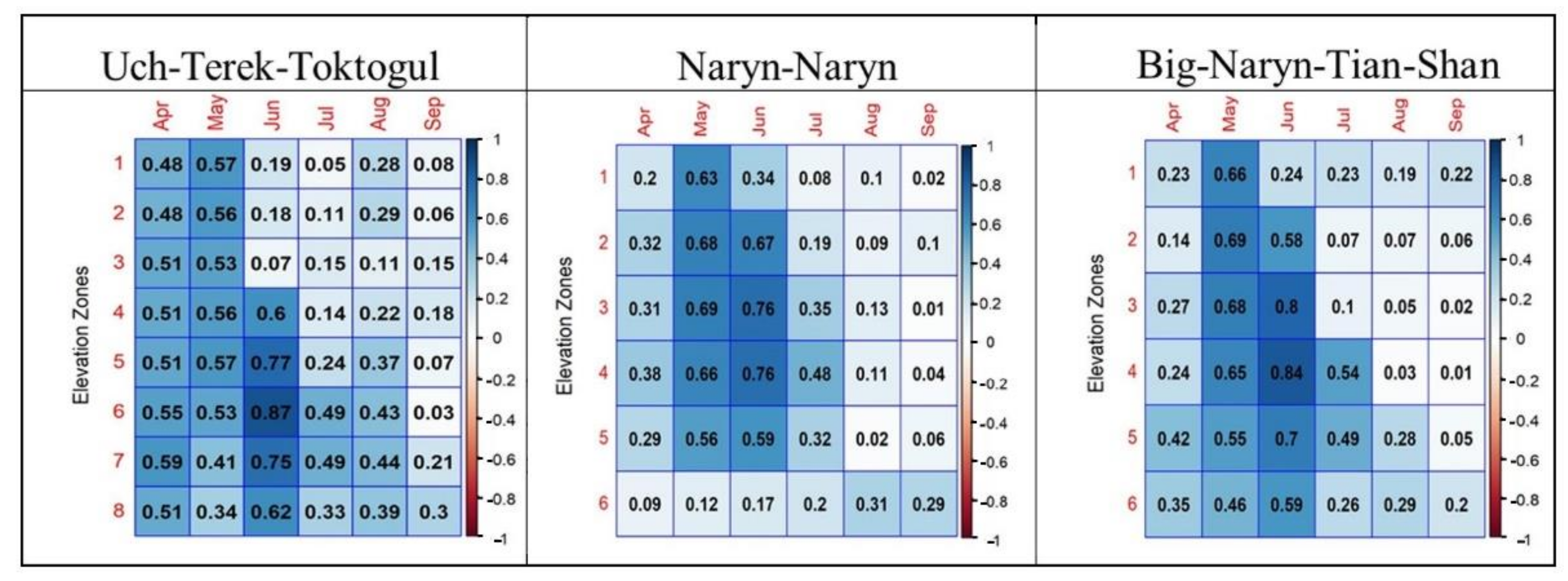
3.2. Snow Cover-Runoff Model Set Up
3.3. Runoff Distribution Forecast for the Growing Season
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aizen, V.B. Pamir glaciers. In Encyclopedia of Snow, Ice and Glaciers; Sigh, V.P., Singh, P., Eds.; Haritashya Springer Publisher: Wallingford, UK, 2011; pp. 813–815. [Google Scholar]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M. Precipitation, melt and runoff in the northern Tien Shan. J. Hydrol. 1996, 186, 229–251. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Gong, G.; Entekhabi, D.; Cohen, J.; Robinson, D. Sensitivity of atmospheric response to modeled snow anomaly characteristics. J. Geophys. Res. Atmos. 2004, 109, D06107. [Google Scholar] [CrossRef]
- Hill, A.; Minbaeva, C.; Wilson, A.; Satylkanov, R. Hydrologic Controls and Water Vulnerabilities in the Naryn river basin, Kyrgyzstan: A Socio-Hydro Case Study of Water Stressors in Central Asia. Water 2017, 9, 325. [Google Scholar] [CrossRef]
- Notarnicola, C. Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 2020, 243, 111781. [Google Scholar] [CrossRef]
- Xenarios, S.; Gafurov, A.; Schmidt-Vogt, D.; Sehring, J.; Manandhar, S.; Hergarten, C.; Shigaeva, J.; Foggin, M. Climate change and adaptation of mountain societies in Central Asia: Uncertainties, knowledge gaps, and data constraints. Reg. Environ. Chang. 2019, 19, 1339–1352. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Karl, T.R.; Knight, R.W.; Stenchikov, G.L. Changes of snow cover, temperature, and radiative heat balance over the Northern Hemisphere. J. Clim. 1994, 7, 1633–1656. [Google Scholar] [CrossRef]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.; Walker, J.P.; Pauwels, V.R.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Memon, A.A.; Muhammad, S.; Rahman, S.; Haq, M. Flood monitoring and damage assessment using water indices: A case study of Pakistan flood-2012. Egypt. J. Remote Sens. Space Sci. 2015, 18, 99–106. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P.; De Jong, S.; Bierkens, M. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Xu, C.; Halldin, S. The Effect of Climate Change on River Flow and Snow Cover in the NOPEX Area Simulated by a Simple Water Balance Model: Paper presented at the Nordic Hydrological Conference (Akureyri, Iceland–August 1996). Hydrol. Res. 1997, 28, 273–282. [Google Scholar] [CrossRef]
- Lee, S.; Klein, A.G.; Over, T.M. A comparison of MODIS and NOHRSC snow-cover products for simulating streamflow using the Snowmelt Runoff Model. Hydrol. Processes Int. J. 2005, 19, 2951–2972. [Google Scholar] [CrossRef]
- Zakharova, E.; Kouraev, A.; Biancamaria, S.; Kolmakova, M.; Mognard, N.; Zemtsov, V.; Kirpotin, S.; Decharme, B. Snow cover and spring flood flow in the Northern Part of Western Siberia (the Poluy, Nadym, Pur, and Taz Rivers). J. Hydrometeorol. 2011, 12, 1498–1511. [Google Scholar] [CrossRef]
- Terekhov, A.; Abayev, N.; Vitkovskaya, I. The effect of changing stratification in the atmosphere in central zone of Eurasia according to vegetation data of Tien Shan mountains during 2002–2019. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2020. [Google Scholar]
- Niyazov, J.; Kalashnikova, O.Y.; Gafurov, A. MODIS Imagery Based Water Content Forecasting Methodology for Mountain Rivers in Central Asia. Cent. Asian J. Water Res. 2020, 6, 66–78. [Google Scholar]
- Liguori, S.; Rico-Ramirez, M.; Cluckie, I. Uncertainty propagation in hydrological forecasting using ensemble rainfall forecasts. IAHS Publ. 2009, 331, 30. [Google Scholar]
- Gafurov, A.; Lüdtke, S.; Unger-Shayesteh, K.; Vorogushyn, S.; Schöne, T.; Schmidt, S.; Kalashnikova, O.; Merz, B. MODSNOW-Tool: An operational tool for daily snow cover monitoring using MODIS data. Environ. Earth Sci. 2016, 75, 1078. [Google Scholar] [CrossRef]
- Wang, R.; Ding, Y.; Shangguan, D.; Guo, W.; Zhao, Q.; Li, Y.; Song, M. Influence of Topographic Shading on the Mass Balance of the High Mountain Asia Glaciers. Remote Sens. 2022, 14, 1576. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Wang, J.; Wang, X.; Li, H.; Jiang, Z. Spatiotemporal variation of snow cover in Tianshan Mountains, Central Asia, based on cloud-free MODIS fractional snow cover product, 2001–2015. Remote Sens. 2017, 9, 1045. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Liu, T. Monitoring recent changes in snow cover in Central Asia using improved MODIS snow-cover products. J. Arid Land 2017, 9, 763–777. [Google Scholar] [CrossRef]
- Alamanov, S.; Sakiev, K.; Akhmedov, S. Physical Geography of Kyrgyzstan; Turar: Bishkek, Kyrgyzstan, 2013. (In Russian) [Google Scholar]
- He, M.; Lee, H. Advances in Hydrological Forecasting. Forecasting 2021, 3, 517–519. [Google Scholar] [CrossRef]
- Dietz, A.J.; Conrad, C.; Kuenzer, C.; Gesell, G.; Dech, S. Identifying changing snow cover characteristics in central Asia between 1986 and 2014 from remote sensing data. Remote Sens. 2014, 6, 12752–12775. [Google Scholar] [CrossRef] [Green Version]
- Gafurov, A.; Bárdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef]
- Barrett, A.; Leavesley, G.; Hay, L. Integrating Satellite-Derived Snow Covered Area Information with a Hydrologic Forecast Model. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2001. [Google Scholar]
- Aouissi, J.; Benabdallah, S.; Chabaane, Z.L.; Cudennec, C. Evaluation of potential evapotranspiration assessment methods for hydrological modelling with SWAT—Application in data-scarce rural Tunisia. Agric. Water Manag. 2016, 174, 39–51. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Duethmann, D.; Peters, J.; Blume, T.; Vorogushyn, S.; Güntner, A. The value of satellite-derived snow cover images for calibrating a hydrological model in snow-dominated catchments in Central Asia. Water Resour. Res. 2014, 50, 2002–2021. [Google Scholar] [CrossRef]
- Heuvelmans, G.; Muys, B.; Feyen, J. Regionalisation of the parameters of a hydrological model: Comparison of linear regression models with artificial neural nets. J. Hydrol. 2006, 319, 245–265. [Google Scholar] [CrossRef]
- Ritter, A.; Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Borovikova, L.; Konovalov, U.; Myagkov, S. Automatized System of Runoff Forecasting for the Amudarya River Basin. In North American Water and Environment Congress & Destructive Water; ASCE: New York, NY, USA, 1996; p. 454. [Google Scholar]
- Krajčí, P.; Holko, L.; Perdigão, R.A.; Parajka, J. Estimation of regional snowline elevation (RSLE) from MODIS images for seasonally snow covered mountain basins. J. Hydrol. 2014, 519, 1769–1778. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Cheng, Q.; Wu, P.; Gan, W.; Fang, L. Cloud removal in remote sensing images using nonnegative matrix factorization and error correction. ISPRS J. Photogramm. Remote Sens. 2019, 148, 103–113. [Google Scholar] [CrossRef]
- Apel, H.; Abdykerimova, Z.; Agalhanova, M.; Baimaganbetov, A.; Gavrilenko, N.; Gerlitz, L.; Kalashnikova, O.; Unger-Shayesteh, K.; Vorogushyn, S.; Gafurov, A. Statistical forecast of seasonal discharge in Central Asia using observational records: Development of a generic linear modelling tool for operational water resource management. Hydrol. Earth Syst. Sci. 2018, 22, 2225–2254. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Conrad, C. Snow-cover variability in central Asia between 2000 and 2011 derived from improved MODIS daily snow-cover products. Int. J. Remote Sens. 2013, 34, 3879–3902. [Google Scholar] [CrossRef]
- Konovalov, V. Automated system of runoff forecasting for the Amudarya River basin. In Destructive Water: Water-Caused Natural Disasters, Their Abatement and Control; IAHS Press: Wallingford, UK, 1997; p. 193. [Google Scholar]
- Tang, Z.; Wang, J.; Li, H.; Liang, J.; Li, C.; Wang, X. Extraction and assessment of snowline altitude over the Tibetan plateau using MODIS fractional snow cover data (2001 to 2013). J. Appl. Remote Sens. 2014, 8, 084689. [Google Scholar] [CrossRef]
- Deng, G.; Tang, Z.; Hu, G.; Wang, J.; Sang, G.; Li, J. Spatiotemporal dynamics of snowline altitude and their responses to climate change in the Tienshan Mountains, Central Asia, During 2001–2019. Sustainability 2021, 13, 3992. [Google Scholar] [CrossRef]
- Gerlitz, L.; Vorogushyn, S.; Gafurov, A. Climate informed seasonal forecast of water availability in Central Asia: State-of-the-art and decision making context. Water Secur. 2020, 10, 100061. [Google Scholar] [CrossRef]


| Period | Equation | R2 | SimQ (m3) 2021 | ObsQ (m3) 2021 | Forecast,% | Proved Forecast | Unproved Forecast | Forecast Accuracy 2000–2021 in % |
|---|---|---|---|---|---|---|---|---|
| Stations Naryn-Naryn | ||||||||
| Apr. | Apr. = 4.9*SCA − 0.072*Qprev = 0.17*Prec + 1.2*Temp − 434 | 0.70 | 39.3 | 46.2 | 85 | 15 | 5 | 75 |
| May | May = 2.3*SCA + 0.51*Qprev + 0.04*Prec − 0.82*Temp − 78 | 0.60 | 119 | 122 | 98 | 12 | 8 | 60 |
| June | June = 2.9*SCA + 0.88*Qprev − 12*Temp + 70 | 0.62 | 124 | 143 | 98 | 15 | 6 | 71 |
| July | July = 1.7*SCA + 0.29*Qprev + 0.027*Prec + 11*Temp − 95 | 0.54 | 219 | 225 | 97 | 15 | 5 | 75 |
| Aug. | Aug. = −0.66*SCA + 0.37*Qprev − 0.22*Prec − 27*Temp + 674 | 0.25 | 153 | 160 | 96 | 10 | 11 | 47.6 |
| Sep. | Sep. = −13*SCA + 0.54*Qprev + 0.099*Prec − 21 | 0.41 | 78 | 81.6 | 95.5 | 14 | 6 | 70 |
| Apr.–Sep. | Apr._Sep. = 0.018*SCA + 5.5*Qprev + 0.38*Prec + 1.2*Temp − 40 | 0.47 | 129 | 130 | 100 | 13 | 8 | 61 |
| Stations Big-Naryn-Tian-Shan | ||||||||
| Apr. | Q_apr = 0.14*SCA_zone_2 + 0.65*Qprev − 0.15*Prec + 0.81*Temp + 30 | 0.34 | 33 | 24.1 | 137 | 13 | 8 | 33 |
| May | Q_apr = 0.31*SCA_zone_2 + 0.61*Qprev − 0.15*Prec + 0.99*Temp + 15 | 0.39 | 50.1 | 62.9 | 80 | 14 | 7 | 33 |
| June | Q_may = 0.15*SCA_zone_2 + 0.87*Qprev + 0.29*Prec − 6.2*Temp − 22 | 0.69 | 68. | 64.3 | 106 | 14 | 7 | 70 |
| July | Q_may = 0.29*SCA_zone_2 + 0.78*Qprev + 0.26*Prec − 5.7*Temp − 27 | 0.71 | 107 | 111 | 96 | 11 | 10 | 55 |
| Aug. | Q_jun = 1.9*SCA_zone_3 + 0.54*Qprev + 0.13*Prec + 4.4 | 0.64 | 71.6 | 72.4 | 96 | 6 | 15 | 65 |
| Sept. | Q_jun = 1.5*SCA_zone_2 + 0.67*Qprev + 0.1*Prec − 4.7*Temp − 15 | 0.67 | 34.5 | 38.2 | 90 | 7 | 14 | 60 |
| Apr.– Sep. | Q_jul = 0.63*SCA_zone_4 + 0.28*Qprev − 0.005*Prec + 61 | 0.43 | 70.4 | 61 | 87 | 12 | 9 | 52 |
| Stations Uch-Terek-Toktogul | ||||||||
| Apr. | Apr. = 21*SCA + 1.4*Qprev − 0.14*Prec − 1988 | 0.51 | 296 | 241 | 123 | 15 | 6 | 71 |
| May | May = 9.4*SCA + 1*Qprev − 1.9*Prec − 5.6*Temp + 1 | 0.65 | 665 | 650 | 102 | 12 | 8 | 60 |
| June | June = 9.1*SCA + 0.44*Qprev + 1.1*Prec − 6.3*Temp − 305 | 0.68 | 607 | 580 | 105 | 14 | 6 | 70 |
| July | July = 1.7*SCA + 0.29*Qprev + 0.027*Prec + 11*Temp − 95 | 0.42 | 629 | 625 | 96 | 12 | 8 | 60 |
| Aug. | Aug. = −0.66*SCA + 0.37*Qprev − 0.22*Prec − 27*Temp + 674 | 0.62 | 461 | 415 | 111 | 12 | 8 | 60 |
| Sept. | Sep. = −13*SCA + 0.54*Qprev + 0.099*Prec − 21 | 0.65 | 298 | 310 | 96 | 12 | 8 | 60 |
| Apr.– Sep. | Apr._Sep. = 3.9*SCA + 1.5*Qprev + 0.73*Prec + 16*Temp − 272 | 0.53 | 507 | 473 | 93 | 15 | 6 | 71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pamirbek kyzy, M.; Chen, X.; Liu, T.; Duulatov, E.; Gafurov, A.; Omorova, E.; Gafurov, A. Hydrological Forecasting under Climate Variability Using Modeling and Earth Observations in the Naryn River Basin, Kyrgyzstan. Water 2022, 14, 2733. https://doi.org/10.3390/w14172733
Pamirbek kyzy M, Chen X, Liu T, Duulatov E, Gafurov A, Omorova E, Gafurov A. Hydrological Forecasting under Climate Variability Using Modeling and Earth Observations in the Naryn River Basin, Kyrgyzstan. Water. 2022; 14(17):2733. https://doi.org/10.3390/w14172733
Chicago/Turabian StylePamirbek kyzy, Merim, Xi Chen, Tie Liu, Eldiiar Duulatov, Akmal Gafurov, Elvira Omorova, and Abror Gafurov. 2022. "Hydrological Forecasting under Climate Variability Using Modeling and Earth Observations in the Naryn River Basin, Kyrgyzstan" Water 14, no. 17: 2733. https://doi.org/10.3390/w14172733







