1. Introduction
One of the most crucial natural resources, without which life cannot exist, is water. According to the studies, approximately 66% of the Earth is made up of water with the availability of fresh or usable water being only 1%, while the rest of the water is saline or salt water. Water is an integral part of the prosperity and wealth of a nation. However, the level of water has been falling considerably during the last few decades, which is one of the emerging problems in the modern world. Due to the ever-increasing population of the world, water resources are under pressure to provide basic functions to such a big population due to the water pollution on and under the surface, which is a threatening situation, keeping in mind the depleting water resources. As the population of the world is growing at a rapid pace, it affects its demand, as well as its cost [
1]. It can result in the decline of per capita water used at higher population rates. It is proven that a deficiency of clean water can increase the likelihood that people live in poverty. Water is unevenly distributed among the countries. About 60% of the world’s water is accessible, which suggests that even though water is abundant on Earth, its accessibility for drinking, agricultural, and commercial use is unevenly distributed geographically [
2].
Water quality and abundant water supply are of key importance when it comes to preserving the ecosystem [
3]. The availability of clean, fresh water supports social and economic well-being [
4]. According to the United Nations Environment Program (2000), 20% of people worldwide lack access to clean drinking water, while around 50% of the population of the world is denied access to safe sanitation systems, which is posing a serious threat to water shortages and waterborne-related diseases. With the increase of approximately 60 million people yearly, an estimated 64 billion m
of water is needed to be added annually to the water reservoirs.
The availability of a safe and sufficient quantity of drinking water is a crucial part of basic healthcare since drinking water quality has a significant effect on the health of people. The level of components in potable water must not threaten consumer health or reduce its usefulness [
5]. The following characteristics of good water quality should be met by water.
Free of harmful organisms.
Clean and clear (low turbidity).
Lack of saline.
Devoid of substances that provide an unpleasant flavor or smell.
Devoid of substances that might have harmful effects on human health.
Low levels of substances such as lead that are immediately hazardous or have negative long-term effects.
Free of chemicals that could damage the water supply system or taint washed-in clothing.
1.1. Elements in Water
There are a variety of water quality standards that can be followed depending on the region or country. The World Health Organization (WHO) has created guidelines for the lower and upper limits of several inorganic chemicals that are typically present in drinking water, making them one of the most commonly used standards. The World Health Organization’s maximum permissible concentration of elements is described in
Table 1.
1.2. Problem Statement
The public requires access to safe, easily accessible water for drinking, household usage, food production, and recreational activities. A country’s economic development may be considerably boosted by better water supply and resource management. Water that is sufficient for personal and household use, constantly available, safe, accessible, and reasonably priced is a right that belongs to everyone. Due to contaminated water every year, lots of people experience kidney failure, cancer, etc. [
7]. Contaminated water can lead to diarrhea, cholera, typhoid, etc. [
6]. Laboratory methods for water quality classification are time-consuming procedures and need lots of resources. Presently, lots of systems are available for water quality classification but they lack accuracy. Thus, it is the need of the hour to have an automated system that can automatically classify the quality of water with less effort.
1.3. Research Aims and Objectives
Drinking water quality surveillance is the continuous, vigilant evaluation and acceptability of drinking water supplies by the public health community. A perfect distribution system will not keep the public healthy if the water it distributes receives insufficient treatment, and flawless treatment is useless if the system’s design or cross-connections allow for contamination. Due to the prevalent problems of water contamination over the past decade, water quality prediction has emerged as a topic of great importance for the survival of life on Earth. Consequently, a large body of automatic water quality prediction approaches can be found in the literature. Predominantly, such works provide comparatively low accuracy. Furthermore, the datasets available for experiments have a large number of missing attributes needed to predict water quality, and the resulting accuracy is low. This study aims to solve these problems by making the following contributions. Firstly, a KNN imputer is used to deal with the missing values problem. Using this technique, the water quality prediction accuracy is distinctly improved compared to deleting the missing values. Secondly, a multilayer perceptron (MLP) is used for water quality prediction. Experiments are performed using different architectures for MLP, including three, six, and nine layers, where the best results are obtained using the customized nine-layered architecture. In addition, a range of machine learning models is used for comparison for the prediction of water quality with and without the KNN imputer.
This study is further divided into four sections. Starting with a description of studies related to current work in
Section 2, the proposed methodology, dataset, and machine learning models are presented in
Section 3.
Section 4 discusses the results while the conclusion is given in
Section 5.
2. Related Work
Water is essential to human life since it is used in so many daily activities such as drinking, cooking, maintaining personal cleanliness, farming, and industrial processes [
8]. Other processes, such as biotransformation and the creation of electricity, also depend on water [
9]. Because human existence depends on the availability of water, both sources (surface and groundwater) are subject to varying degrees of pollution from numerous pollutants [
10].
There has been a greater demand for reliable, accurate, and adaptable prediction models as surface water pollution has been acknowledged as a problem and there is growing interest in water quality assessment [
11]. Numerous researchers have used neural networks and other machine learning algorithms to forecast water quality in recent years, with promising prediction outcomes [
12]. Machine learning models have shown limitations in generalizing complex and highly nonlinear connections between the modeling parameters [
13].
Although research has shown that various machine learning models, including deep neural networks, kernel models, fuzzy logic, genetic programming, neuro-inference models, and others, have been utilized to design surface water quality phenomena [
14], there are still a number of new classifiers that have not yet been investigated. For the conservation of the water environment, water quality prediction is very important. Authors developed a water quality assessment approach based on long short-term memory (LSTM) and IGRA, taking into account the multivariate correlation and temporal sequence of the water quality data [
15]. The first suggestion made by IGRA was to choose features that have a higher absolute correlation being predicted. Second, an LSTM-based prediction model was created, with the indicators collected by IGRA serving as its inputs. Results show promising output for water quality prediction.
Traditional water quality prediction approaches used machine learning and statistical characteristics (normal distribution) and techniques and has not achieved good results. Contrarily, artificial intelligence-based approaches have shown better results as there is no need to determine the relation of dependent variables with independent ones [
16]. The authors applied a neural network model to determine the quality of groundwater [
17], and provide an improved water quality monitoring system for drinking purposes. Authors investigated quality indicators for potability by applying explainable artificial intelligence [
18]. Many researchers have concentrated their efforts on using many variables as a function model after the realization of the significance of monitoring and forecasting the changing water quality. Artificial neural networks (ANNs) such as MLP and radial bias have been employed by researchers for water quality prediction and have achieved satisfactory results [
19]. A water quality index was also produced using an ANN and five significant and widely accepted water quality indicators [
20]. The literature includes studies on using artificial intelligence systems to predict the water quality index [
21].
The recurrent neural network (RNN) is the most widely used deep learning model for the analysis of time-series data. An improved RNN with a significant capacity for information acquisition and archival is LSTM, which has been used extensively for predicting water quality [
22,
23]. In order to perform a thorough predictive study of the water quality in the next time period, the authors developed a prediction technique based on the bidirectional LSTM that takes into account the reliance at many time scales [
24].
For accurate real-time water quality prediction, the researchers introduced a novel feature selection and classification approach in [
25]. The complexity of the suggested approach is decreased by using a learning-based model and quantum teaching to choose the best possible collection of characteristics. The authors proposed two tree-based hybrid models, namely, XGBoost and RF, to provide more precise short-term water quality prediction and they also introduced a novel data denoising technique (CEEMDAN) [
26].
Numerous versions of models have been utilized by researchers to determine water quality; they are still facing challenges in the process. The literature review indicates that there is a limited number of studies using deep neural networks in predicting water quality, especially for drinking purposes. In addition, models that can adapt to the complex character of the majority of environmental engineering challenges are required.
3. Materials and Methods
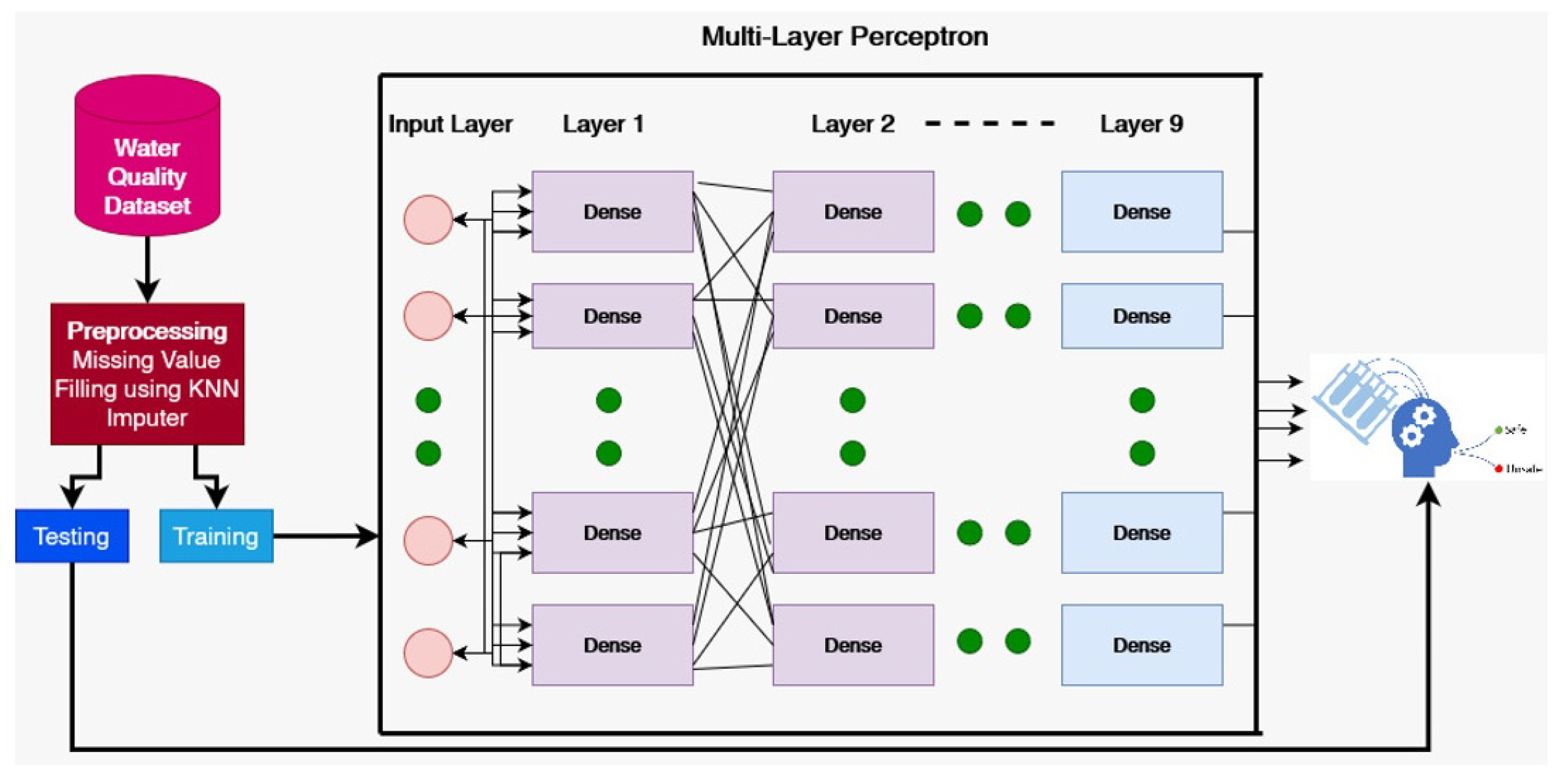
This section presents the proposed approach for water quality prediction, machine learning models, and the dataset used for experiments. The data flow of the proposed approach is depicted in
Figure 1. First, the dataset is collected, which contains the electronic health records for different features of water. Since the dataset contains missing values, data preprocessing is needed to deal with this problem. This study leverages the KNN imputer in this regard. Afterward, different machine learning models are applied in addition to the MLP model. For training and testing these models, the data are split into training and testing sets. The classifiers are applied to determine the water quality as potable and not safe for humans.
3.1. Dataset
The dataset utilized in this research is taken from Kaggle. Kaggle is a renowned and free data repository from which we can obtain a dataset without any hassle. The dataset used in this study is available with the name of ‘Water Quality’ [
27]. The dataset consists of 10 columns and it has 935 instances. The target class is potable. It has two values, ‘0’ or ‘1’, where ‘0’ denotes that the water is not safe for drinking and ‘1’ denotes that it is safe for drinking. A detailed dataset description is presented in
Table 2.
Data visualization helps researchers find the hidden patterns and relationships among the data attributes [
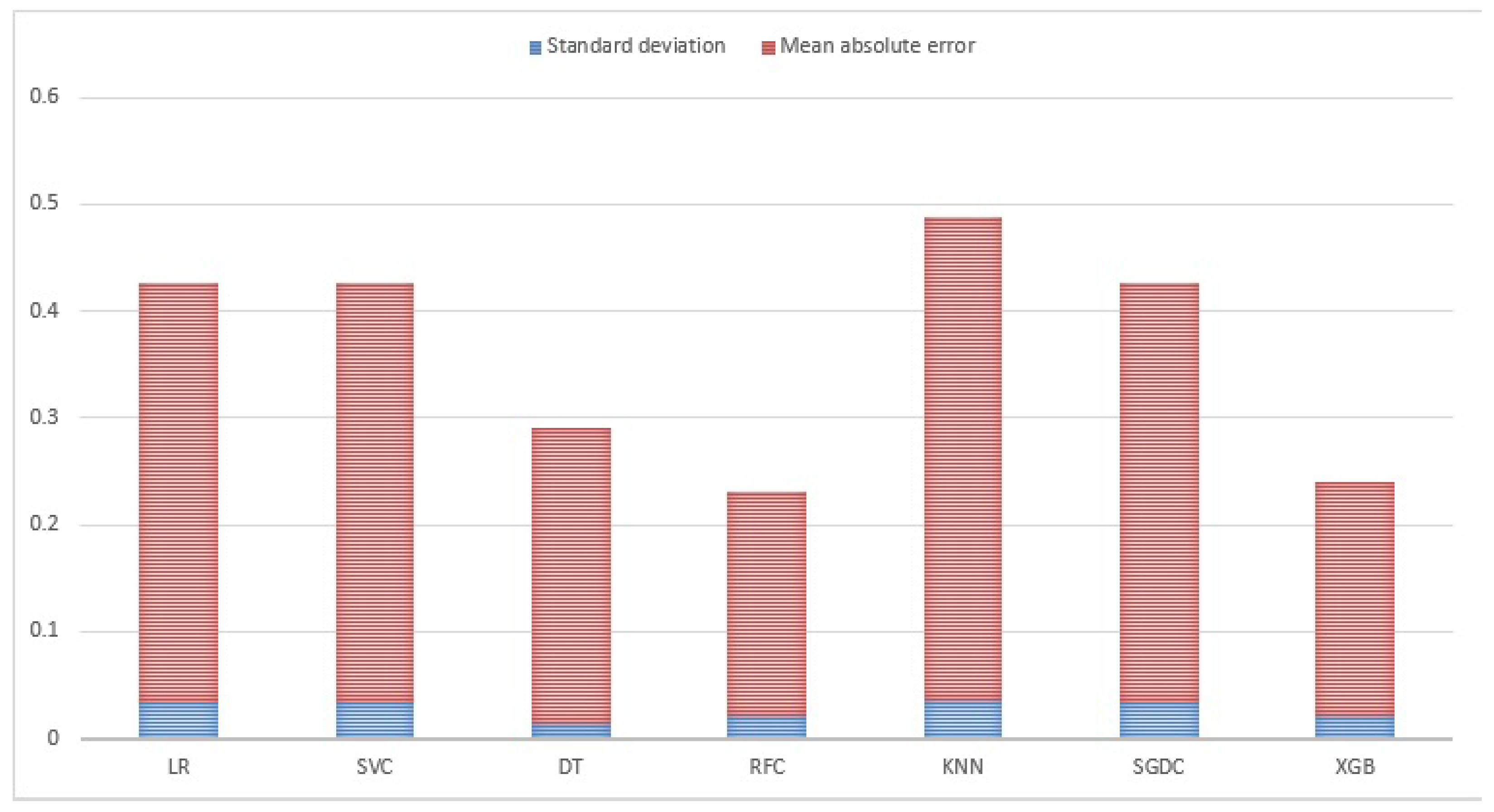
28]. The goal of data visualization is to efficiently and concisely present facts or information to readers. A chart, map, or infographic is frequently used to visually convey data. Data visualization helps transform data into a more understandable format and shows patterns and outliers. The dataset contains two classes, where 61% of the data belong to the ‘not potable’ class, and 39% of the data belong to the ‘potable’ class. The potable class indicates that the water is clean and safe for human use.
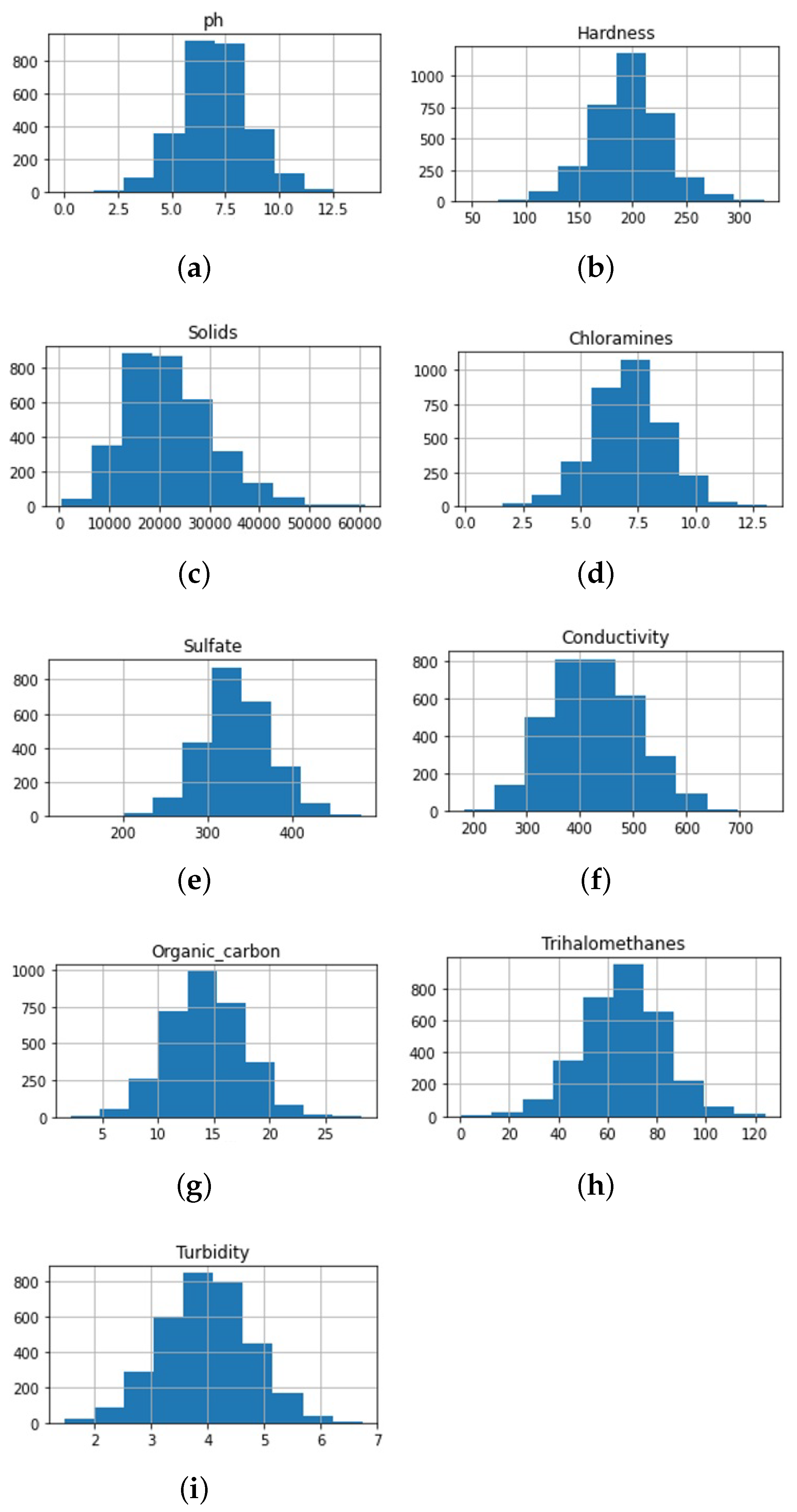
Figure 2 shows the histogram distribution of the nine features used for training the machine learning models. The tenth attribute is the target class with potable and not potable values. The histogram helps to understand the distribution of each feature in the dataset. It shows how frequently a value/feature appears in a relatively unbiased way.
Figure 2 shows that the given features have a normal distribution and they are not skewed. Moreover, the distribution is unimodal and symmetric. The given range of these features is different, and the occurrence of each feature is helpful to determine the center of a particular feature. For example,
Figure 2a shows that the majority of pH values lie between 5.0 and 8.0.
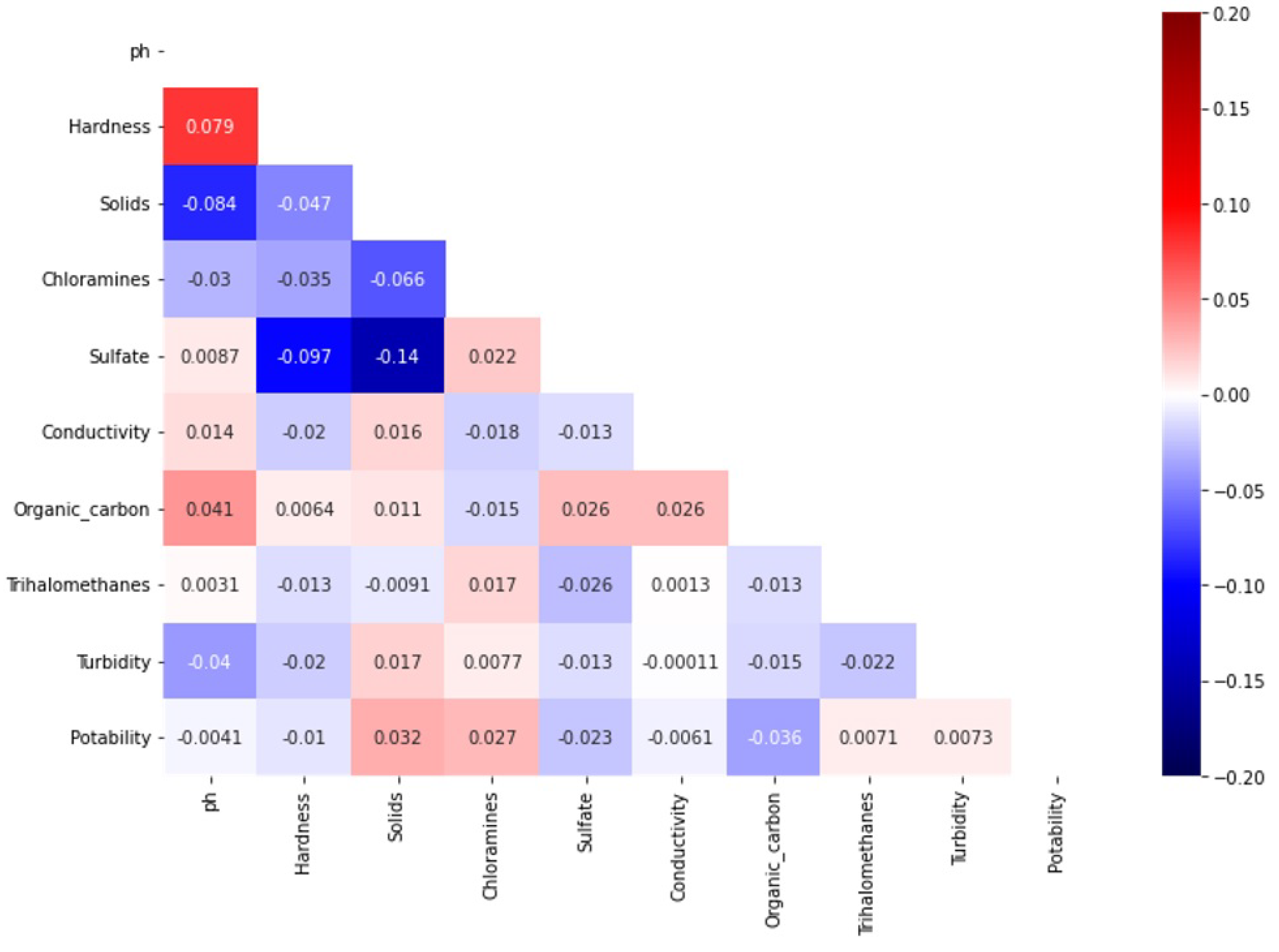
Dataset attributes have a different level of correlation for water quality prediction.
Figure 3 shows the relationship of the features using the heatmap for dataset attributes, which indicates the importance of each attribute with respect to the target class. It indicates that ‘solids’ and ‘chloramines’ attributes have a strong linear relationship with potability, while ‘organic_carbon’ and ‘sulfate’ have an inverse relationship with potability. This relationship helps to understand which features are important to determine the target class for water quality.
3.2. Data Preprocessing
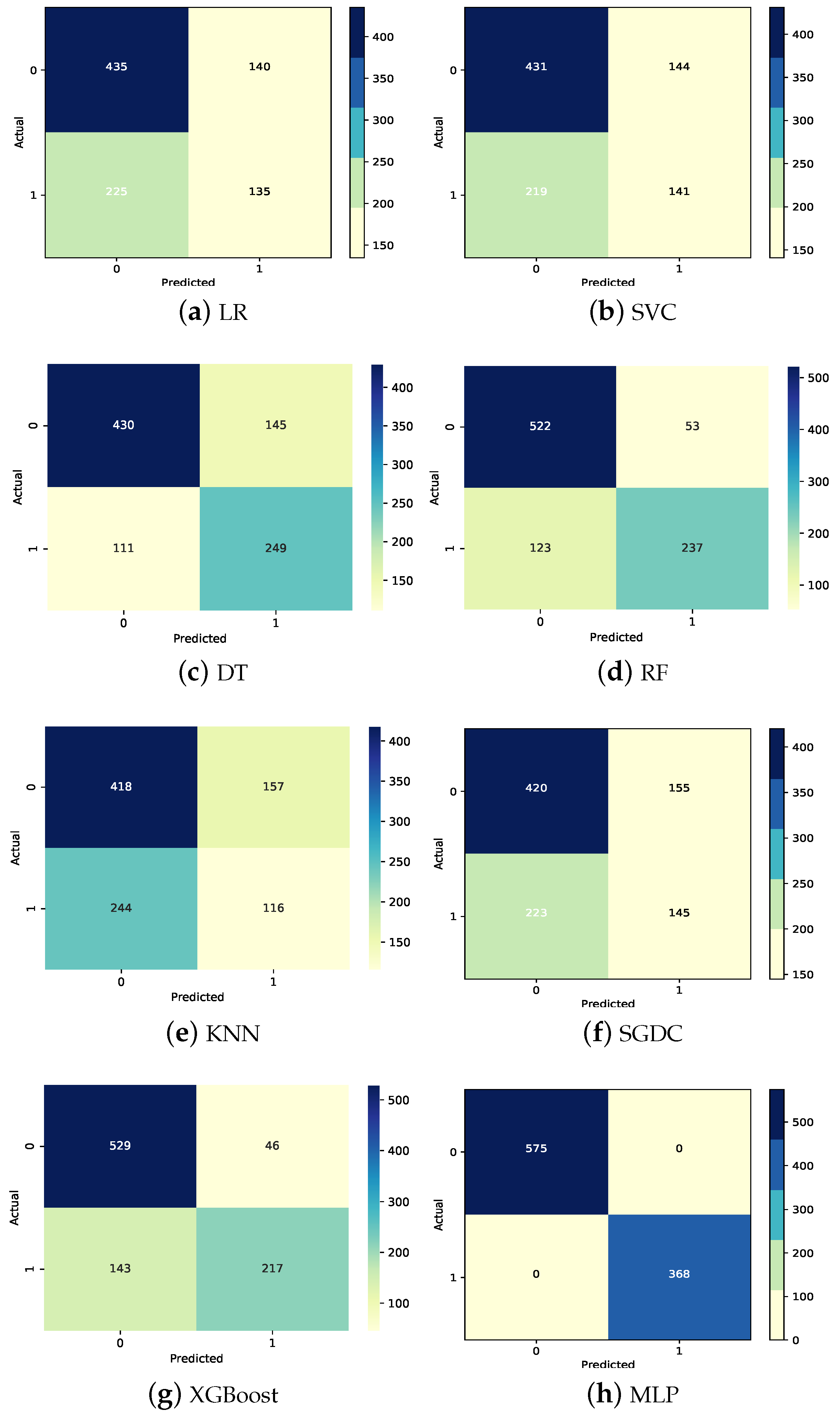
Data preprocessing is an important step to obtain better performance from the models. In this step, the unnecessary or redundant data are removed from the dataset. These data have no meaning for the machine learning models. Preprocessing helps to enhance the efficacy of the learning models. Not only does preprocessing help to enhance the performance of the model, it also helps to reduce the computational time. In this research, during the data preprocessing, we came to learn that there are several missing values in the dataset. Missing values present in the dataset, according to the class, are presented in
Table 3.
It is clear from the table that there are a large number of missing values. As the dataset is categorical, the missing values can be handled with two different methods:
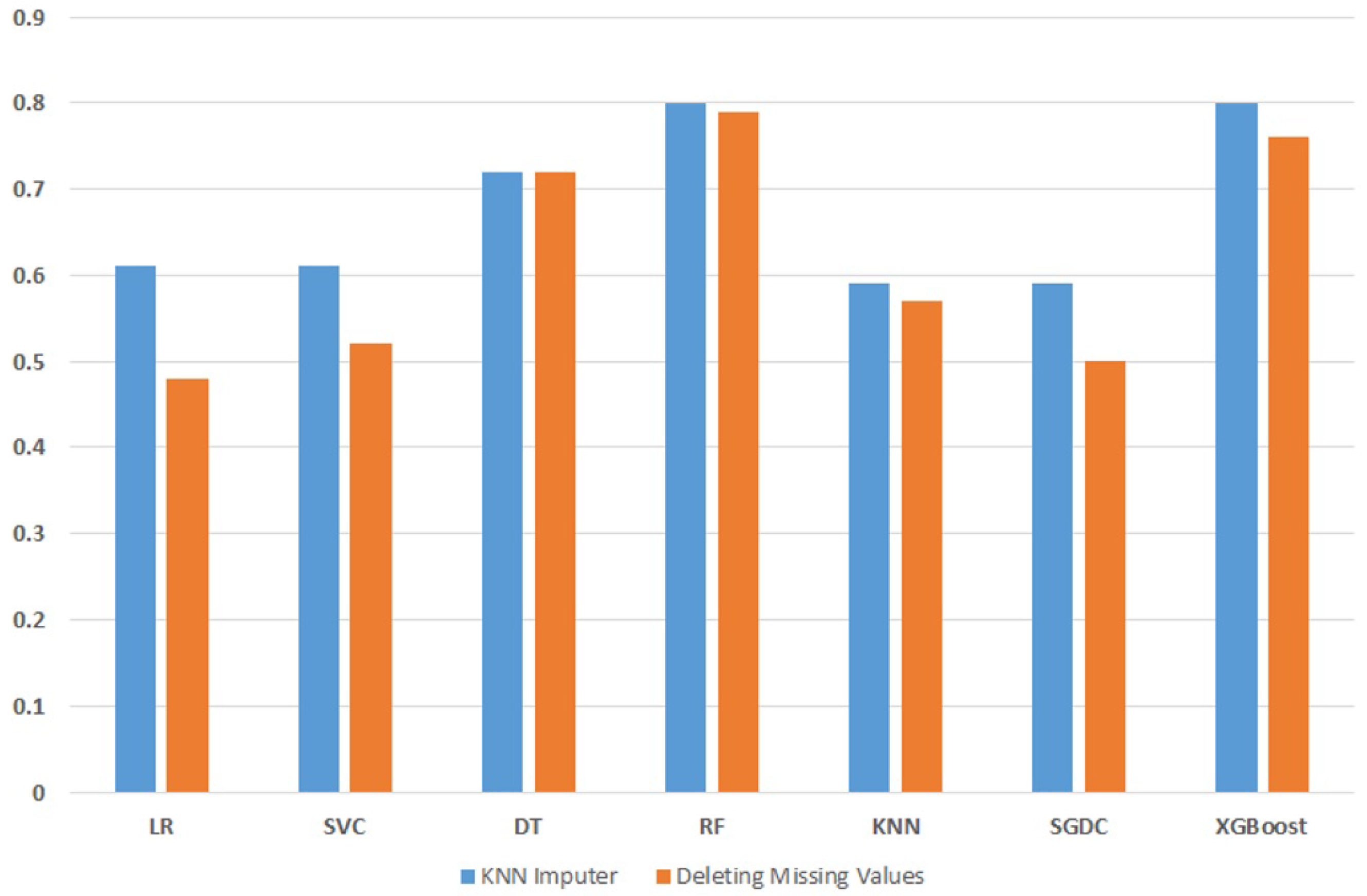
3.2.1. KNN Imputer
In the modern world, data are collected from various sources and used for analysis, insight generation, theory validation, and other purposes. There may frequently be some information missing from these data which is gathered from various sources. This can be the result of an issue with data extraction or collection caused by human error. Thus, dealing with these missing values becomes a crucial step in the preprocessing of data. The choice of imputation method is important because it can have a big impact on the models’ performance. A popular technique for imputing missing values is KNN imputer by sci-kit-learn. It is frequently used as an alternative to conventional imputation methods [
29]. By using the Euclidean distance matrix to find the nearest neighbors, the KNN imputer aids in the impute of missing values that are present in the observations. By ignoring the missing values and increasing the weight of the non-missing coordinates, the Euclidean distance is determined. Mathematically, Euclidean distance can be calculated as:
where
3.2.2. Removing Missing Values from Dataset
The second option for handling the data is to remove the missing values from the data. The second set of experiments is performed using this approach where all the fields with the missing values are removed.
3.3. Machine Learning Models Used in Study
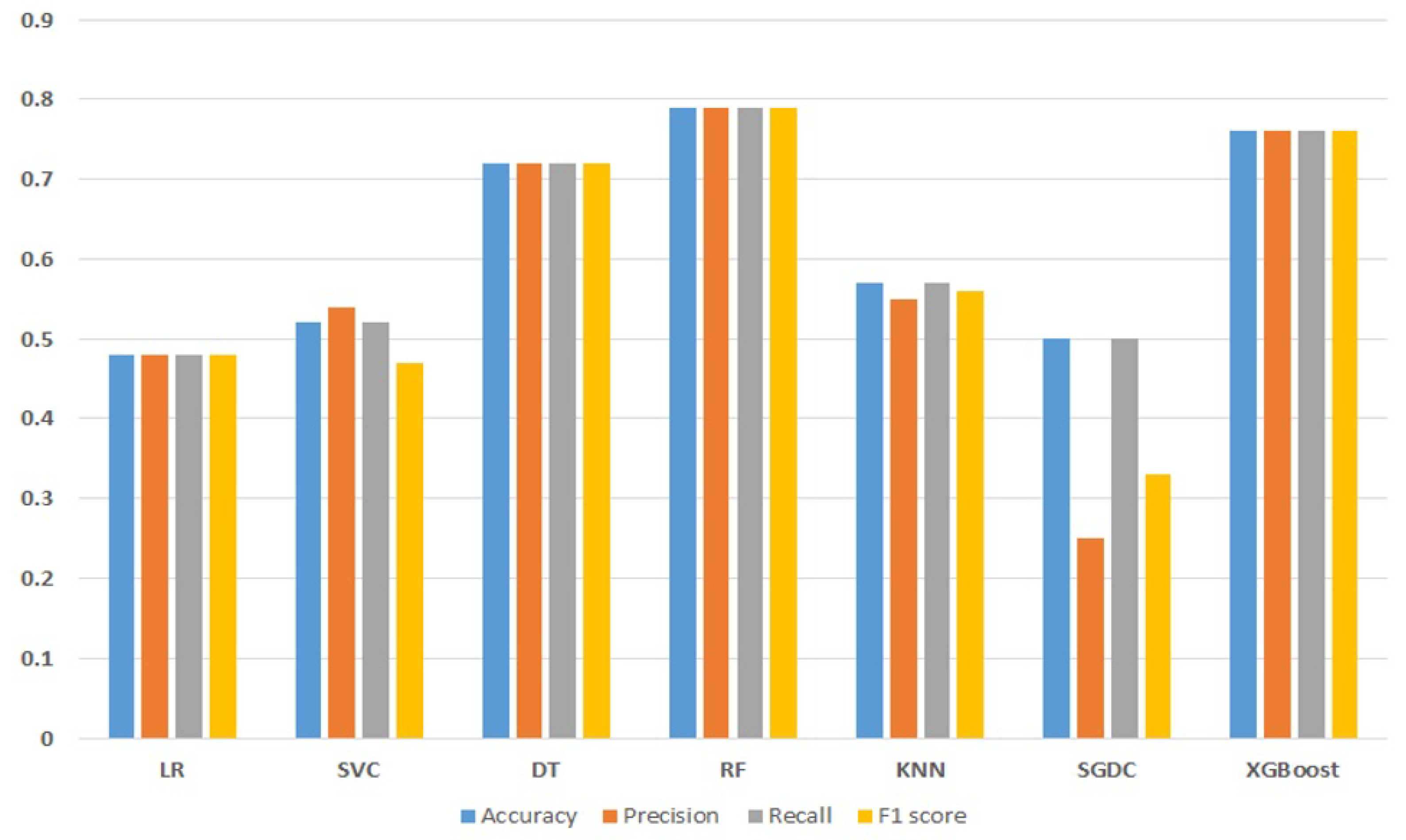
Machine learning plays a significant role in enhancing the accuracy and efficacy of water quality classification. To classify water quality, there exists a variety of machine learning algorithms. The Scikit-learn library of Python has a variety of machine learning classifiers. This library is open source and has a sizeable user base; it largely contributes to the research community. This study uses the Scikit-learn library to implement LR, SVC, DT, RF, KNN, SGDC, and XGBoost.
3.3.1. Logistic Regression
For solving the binary classification problem, LR is one of the widely used methods. The logistic equation, often known as the sigmoid function, is the technique that makes LR so popular [
30]. Any evaluated number may be given to the sigmoid function (S-shaped curve) that converts it to a number between 0 and 1.
where
e represents the base of algorithms. The real numerical values are to be transformed. The logistic functions value also ranges between 0 and 1.
where
y presents the expected performance,
is the bias or intercept, and
presents the coefficient for
x which is an input value.
In the input data, each column has a coefficient that is correlated with the training data. To achieve a higher value of accuracy, LR uses ‘max_iter’ for solving converge.
3.3.2. Support Vector Classifier
SVC is also known as a support vector machine. It is a famous supervised machine learning algorithm. SVC performs classification problems by developing the best line in two dimensions [
31]. SVC uses the RBC kernel and can be used to find the regression line. The general equation is:
where
k is the kernel function, and
is the distance between
and
. The kernel function
k can be written as
where
is the hyperparameter.
3.3.3. Decision Tree
DT is a renowned machine learning algorithm extensively utilized for regression and classification problems. The selection of the root node at each level is a problem in the decision tree [
32]. This process is termed ‘attribute selection’. For attribute selection, there are two renowned techniques: the ‘Gini index’ and ‘information gain’. The Gini index can be computed by the following equation:
The Gini index helps to compute the impurity of data in the dataset. Another attribute selection technique is information gain. Information gain tells about the purity of data. Information gain can be calculated when we have the entropy of the target class and entropy of the each attribute. Entropy
D can be calculated as:
where
presents the probability,
presents the class, and
D presents the dataset.
The entropy of attribute
is utilized as the current root and can be calculated as:
Finally, the following information is gained when attribute
is chosen to branch or split data:
3.3.4. Random Forest
A tree-based classifier RF combines several poor apprentices (poor learners) to generate very accurate predictions. To train different decision trees utilizing diverse bootstrap samples, RF uses bootstrap bagging [
33]. A bootstrap sample is generated using the sub-sampling of the training dataset, where the size of the training and test sample dataset is the same. Similar to other ensemble classifiers, RF uses decision trees for making predictions. At each stage, the identification of the root node is a challenging task for the development of decision trees.
The number of decision trees participating in the prediction process is , , , and p is the decision made by the decision trees by a majority vote.
In RF, the term “random state” is used during training to regulate the unpredictability of the sample.
3.3.5. K-Nearest Neighbor
KNN is a simple supervised classification technique. The KNN locates the similarity between the previous examples and new data and then places the new data in the group with high similarity [
34]. Distance calculations between the existing samples and new data are used to determine similarity. Different distance estimation techniques, such as Euclidean, Manhattan, and Minkowski, are used for measuring distance. The KNN technique can be applied to classification and regression problems. Due to the fact that KNN is a nonparametric method, it does not evaluate any inferences about the underlying data.
3.3.6. Stochastic Gradient Decent Classifier
The working principle of SGDC relies on the working of LR and SVM. SGDC uses the LR convex loss function and proves to be a powerful classifier. It is an excellent option for multiclass categorization. SGDC aggregates multiple classifiers in the OvA (one-versus-all) method [
35]. The quality of SGDC is that it handles large datasets efficiently. It uses a single example per iteration. As SGDC uses the regression technique, it is very easy to implement and easy to understand. For better results, SGDC must be correctly valued. SGDC has a high value of sensitivity in terms of feature scaling.
3.3.7. XGBoost
XGBoost is a fast supervised learning algorithm. For the accurate and precise classification of water quality, XGBoost is used in this study. Due to the availability of regularized learning features, it helps in smoothing the final weights and it avoids the overfitting phenomenon [
36]. The specific algorithm is as follows:
where
d is the loss function,
is the regularization term,
is the predicting value,
n is the instance number in training, and
k is the number of trees.
3.4. Deep Learning Models Used in Study
Due to promising results and high accuracy values, deep neural networks are in the eye of many researchers. Water quality classification is also performed using the deep learning model MLP in this study. A brief description of MLP is given in this section.
Multilayer Perceptron
An input vector and the associated output vector are nonlinearly mapped by the deep learning neural network known as MLP. MLP constitutes a hidden layer, input layer, and output layer. For the activation of neurons, MLP uses nonlinear activation function except for the input node [
37]. Due to the availability of a nonlinear function for activation, MLP can handle data that cannot be linearly separated [
38]. The connection weights are modified, and the calculation takes into account both the desired and actual output. The output node is presented by
y at the
nth data point. The error can be computed by the following equation:
where
p is the output of perceptron and
t presents the target value.
Node weights are changed following the adjustment to lessen the inaccuracy of the overall output.
Any change in the weight is given using gradient descent.
where
represents the learning rate and
is the output of the previous neuron.
Derivation calculation is calculated with the help of
, which is an induced local field. This derivative is calculated as
is a derivative of the constant activation function.
3.5. Proposed Approach for Water Quality Prediction
The dataset for this study was taken from Kaggle, a well-known data source. After obtaining the dataset, the preprocessing was carried out to resolve the problem of missing values. These missing values had a strong impact on the efficacy of the learning models. To handle the missing values, KNN imputer was used. After that, the data splitting was performed in 70:30, with 70% for the training of the model and 30% of the data used for testing purposes. The proposed MLP system is used for water quality classification. It is a feedforward deep learning network that gives a mapping between the matching output vector and an input vector. The proposed MLP system consists of nine layers with each layer of 250 neurons. MLP is used with the “binary_crossentropy” loss function while “Adam” is used as the optimizer. The learning rate is set to 0.001, while a batch size of 100 is used with 20 epochs for training the model.