1. Introduction
Groundwater that supplies phreatic aquifers is one of the most important freshwater resources. However, one of the supposed dramatic consequences of global climate change points to a scarcity in the “near” future of this resource across the world. It, therefore, becomes urgent to take up this challenge and propose plans for the development, use, and protection of groundwater in a healthy, sustainable, and responsible manner. Given the importance and the interest of these developments, the development of these plans must be based on a quality scientific approach. In other words, the management of water resources must involve a good understanding of the complex physical phenomena involved in the transformation cycle of groundwater. Among these phenomena, we evoke the mass transport by advection–diffusion in porous media which is present in many sectors of socio-economic activity in relation to flows. Examples include medicine (flow of fluid through organs), geology (thermal rock, thermal energy management), environment (contamination of the water table, radioactive waste), chemistry (catalytic reactors, filtration…), petroleum (production of natural gas, flow of petroleum), mechanics (nuclear reactors, insulation, combustion…), and many others. The phenomena of dispersion can be of various origins. We talk about mass diffusion which is due to the mixing processes between two miscible fluids. This dispersion is estimated from the determination of the concentration fields of a passive tracer traveling from its point of injection. If, in addition, these fields present a gradient, we then see a new dispersion appear (even in the absence of flow). This is called molecular diffusion. It should be noted that the timescales associated with molecular diffusion are sufficiently large so that the latter can induce dispersion at the macroscopic scale. Finally, comes turbulent diffusion as its name suggests characterizing the turbulent flow in the porous media studied. It acts in the same way as molecular diffusion. Other phenomena can also be at the origin of diffusion by mixing processes. Mention is made, for example, of the mixture due to the various obstructions that a porous media may contain. This type of mixing is then caused by the tortuosity of the porous media studied. Likewise, the geometry of the porous media produces recirculation of the flow which in turn can induce the dispersion process. Furthermore, the connectivity of the porous media is likely to force the flow to borrow certain parts and not others of the media, thus creating a mixing zone from which the diffusion phenomenon can result. Finally, comes the hydrodynamic dispersion which is due to the existence of a speed gradient of the fluid phase. In a porous media, this speed gradient is consequent on the non-slip condition at the level of the solid wall of the pores. In summary, all these diffusion process types described above show that the mixing process in porous media is very difficult to apprehend since it is the consequence of the combination of a large number of phenomena of different time and space scales. This difficulty thus makes the determination of the dispersion coefficient extremely difficult.
From the previous paragraphs, we also understand that the dispersion coefficient is considered an important parameter in the knowledge of solute transport in the hydrogeological system. Therefore, its estimation with good precision is inevitable to guarantee a fine and successful description of the studied porous media. As illustrated above, the identification of the dispersion coefficient concerns most of the socio-economic sectors.
Indeed, the identification of the diffusion has been studied for industrial activities, such as the technical aspect of battery systems [
1] and especially on sulfuric acid. Likewise, analytical experiments have made it possible to determine the dispersion coefficients by implementing scanning fluorescence correlation spectroscopy, in particular for molecules in solution [
2]. In terms of transport in environmental media, Monteith and Unsworth [
3] identified the dispersion coefficient for mass and heat transfer (water vapor and CO
2 transfer). In atmospheric engineering, Schnelle [
4] carried out experiments to determine the dispersion coefficient of the study media with the aim of performing simulations for the prediction of accidental atmospheric pollution. In hydrogeology, the use of passive tracers, particularly in understanding the transfer of solutes, provides relevant information on hydrodynamic groundwater resources and to complete hydro–dispersive systems. In fact, passive tracers provide more detailed information on the dispersion coefficients, but the measurement campaigns require serious preparation on the fields and analysis protocols. The success will depend on the duration of the campaign, the choice of tracers, and the mass injected into the hydrogeological systems [
5]. But with the spectacular progress of computing powers, the identification of the dispersion coefficient can be processed by numerical modeling which constitutes a reliable and inexpensive alternative to identification by experimentation. So this problem has been formulated as an optimization problem subject to constraints. Indeed, as specified above, the use of numerical simulations becomes essential for estimating mass transfer in groundwater. These models (called direct model) require the data of a set of parameters (called input), such as diffusivity, source/sink terms, and boundary and initial conditions. However, in practice, we only have a limited amount of these data to carry out reliable simulations to characterize the studied hydrogeological system. To remedy this difficulty, we resort to inverse modeling. Parameter identification occurs in many engineering disciplines: oceanography, meteorology, medicine, mechanical, and thermal industry, environment, hydrogeology, and many more.
Inverse models are used to identify the input parameters of the direct model by incorporating in-situ or laboratory observations. Of course, solving the inverse problems (IP) may also encounter difficulties related to the quality of the in-situ measurements that will be incorporated into the model. Indeed, the uncertainties (noise) attached to the measurements are at the origin of the unstable solutions thus rendering the IP ill-posed. In addition to unstable solutions, it is well known that inverse problems also suffer from the non-uniqueness of the solution. It is then necessary to find a precise mathematical framework to apply the methods of solving inverse problems. It means choosing the right approximation spaces and adopting the right regularization methods. It is for these reasons that the IP have been extensively studied both on theoretical and applied aspects [
6,
7,
8,
9,
10,
11]. In addition, several research works have been published in the field of hydrogeology and, in particular, for the determination of the transmissivity and/or dispersion coefficients necessary for the study of the propagation of accidental pollution. Obviously, we cannot list all of the work on IP, but we can cite some relevant references on the subject. These are the excellent book of Sun [
12], the review of Zhou [
13,
14].
The aim of this paper is the application of the inverse problem techniques solution in hydrogeology and more particularly for the identification of the isotropic HDT of the experimental site “Beauvais LaSalle (North of France)”. Indeed, this identification will be based on the numerical solution of the inverse problem. This step will be accomplished by the direct problem (DP) solution by LBM, followed by a step of numerical optimization based on a metaheuristic algorithm called CMA-ES. For the direct model, we solve the anisotropic advection diffusion type transport equation. Several methods of solving this type of equation based on classical discretization methods (finite differences, finite elements, finite volumes) have been proposed in the literature. In recent years, we have seen the proposal of several algorithms for solving ADE by LBM and its variants [
15,
16,
17,
18,
19]. These investigations have shown that LBM provides excellent results in terms of precision, efficiency, and applicability (highly parallelizable in a natural way). As far as we are concerned to solve the ADE constituting the direct problem, our choice fell on the use of the LBM because of its high simplicity of implementation and its easy parallelization. Thus, the final objective of this paper is the presentation of an integrated optimization algorithm for the identification of an anisotropic HDT (noted HYDRODISP-LBM/CMA-ES). This algorithm combines a hydro–dispersive calculation code by LBM (HYDRODISP-LBM) and an optimization code by the metaheuristic method CMA-ES.
This paper is organized as follows.
Section 1 is an introduction presenting the state of the art on the numerical solution of ADE and its interest in the various engineering sciences. The second section presents the different mathematical tools that lead to the integrated optimization code HYDRODISP-LBM/ CMA-ES.
Section 3 is devoted to the application of the HYDRODISP-LBM/CMA-ES algorithm to the realistic case of the Beauvais LaSalle site to identify the anisotropic HDT characterizing this site in the North of France. Finally,
Section 4 discusses the results obtained, presents a general conclusion of the paper, and proposes some perspectives for possible improvements of the proposed integrated optimization algorithm HYDRODISP-LBM/CMA-ES.
2. Mathematical Formulation of the Model
2.1. Governing Equations
The mixing processes by dispersion in a media (also porous) denoted by
characterized by a HDT
and crossed by a flow of velocity
are governed by a scalar equation of the convection-diffusion type formulated by:
where
is the diffused concentration,
t is the time,
and
are respectively the divergence and the gradient operators and
is the term source or sink term. It should be noted that the velocity field
denotes the velocity of the fluid flow carrying the concentration
through the studied porous medium. This velocity was calculated beforehand by the numerical solution of Darcy’s law by the LBM method implemented in the computer code of HYSFLO-LBM [
20]. As specified in the introductory section, here, we are interested in the isotropic HDT, therefore in the 2D modeling, the tensor
will be of the form:
To maintain isotropy, the diffusion coefficient
must be taken in the directions of the flow direction, by considering the following expression of the
where
is the molecular diffusion,
is the transversal diffusivity and is the
modulus of the flow velocity. It should also be noted that the coefficient
is dependent on space and time through the parameters
(transversal dispersivity) and
. Therefore, the identification of
is equivalent to identifying
(variable in space). Thus, the optimization algorithm implemented for this study is based on the identification of the coefficient D deduced from the Expression (3). Equation (1) expresses the partial differential equation (PDE) to be solved to estimate the concentration
. This PDE is not complete without the specification of the boundary and initial conditions. By introducing these conditions on an arbitrary domain
of the boundary
such as
and
, the complete mathematical model is given by:
where
is a known function for imposing the Dirichlet condition
,
is also a known function for imposing the Neuman condition on the domain boundary
and the vector
denotes the normalized normal vector to
oriented towards the outside of the domain.
For a given HDT , the mathematical Model (4) describes the spatio-temporal evolution of a concentration field transported by the advection and diffusion processes. In this case, we agree to say that we solve the direct problem (DP). Conversely, if the concentration is known at a few points in the (from the measured values, for example), the Model (4) allows, in this case, determining the HDT . In this case, we talk about the solution of the inverse problem noted (IP).
It is well known that the numerical resolution of the inverse problem supposes certain conditions of regularity. In this context, Ciarlet [
21] studied this problem from a mathematical point of view and proposed certain conditions which ensure the existence and uniqueness of the problem formulated by the system of Equation (4). The reader interested in the mathematical analysis aspect of the inverse problem will find rich information in Ramm’s [
22] and Kirsch’s [
23] books. Other authors are also interested in solving the inverse problem and have shown that in hydrogeology, this problem is poorly posed. To obtain physical solutions a step of regularization is necessary before starting the numerical resolution. In practice, this step consists of, among other things, modifying the objective function so that the optimization phase tends towards a physical solution (existence, uniqueness, and stability). We come back to this part in the section which describes the DP/optimization coupling.
2.2. Lattice Boltzmann Method
The numerical resolution of the transport by the advection–diffusion equation (ADE) constitutes a major stake in environmental engineering. Classical discretization methods, such as the finite differences method (FDM), the finite elements method (FEM), and the finite volumes method (FVM), have been and are still widely used to solve this type of equation. However, for two decades now, LBM has started to establish itself as a serious alternative to the classic methods (FDM, FEM, FVM). LBM’s mathematical formalism is based on the kinetic theory of gases. Unlike the concept of continuous media, LBM considers the medium as a discrete space of particles in perpetual reaction with each other. LBM is also based on the principles of statistical physics since it is interested in a distribution function (DF) of the velocities
rather than the average velocity of the representative elementary volume (REV) on which are based the equations of the mechanics of continuous media. Therefore, LBM solves the Boltzmann equation (BE) that governs the advection of
in the presence of a source term. This equation which describes the macroscopic behavior of the fluid via the DF
is expressed by the following equation [
24,
25]:
where the function
is the probability that at the time
a particle is at position
with velocity
.
is an operator that models collisions between particles. We can understand that LBM solves the scalar Equation (5) for the DF
instead of the ADE Equation (4) for the concentration
. To deduce the macroscopic variable
, we go through the calculation of different orders of the DF moments. For example, if we use LBM for Navier–Stokes, the density variable is deduced from the DF moment of order zero, the fluid velocity is deduced from the DF moment of order one, and finally the kinetic energy is deduced from the DF moment of order two, and so on.
The simplest collision operator is undoubtedly proposed by Bhatnagar–Gross–Krook (BGK) [
26]. However, several authors have shown that this operator may prove insufficient to correctly cover the macroscopic variables from the resolution by BE. In this paper, we have used the BGK collision operator which is largely sufficient to cover the macroscopic variables when solving the ADE by LBM. This operator is written by:
where
is the relaxation time,
is the thermodynamic equilibrium distribution function (EDF). All the basic books that introduce the LBM describe the entire approximation steps to obtain an analytical form of this function. Zouhri et al. [
20] proposed a synthetic presentation of the expression of
.
2.3. Solution of the ADE by LBM
Like any PDE, the resolution of the BE (5) begins with a discretization of the variables of the equation (here it is the space
and speed
). In 2D spatial discretization, we use a Cartesian computing grid of size
. For the speeds, the discretization indicates that at a point
of the lattice, a speed is allowed to take a predefined number of directions. Thus in 2D, if we choose a discretization of 9 directions, one speaks about the ”D2Q9 lattice”.
Figure 1 shows the layout of this type of lattice.
This configuration indicates that after a collision the particle at the point can only move in one of the nine directions (staying at the point is considered as a direction of velocity ). For the space discretization, several schemes have been proposed for this PDE type, but LBM uses a particular characteristic scheme. In fact, characteristic schemes are always accompanied by an interpolation step to estimate the speed when the endpoint of the characteristic does not exactly coincide with a node of the lattice. LBM then chooses a time step so as to avoid this interpolation. With this particularity, the LBM algorithm consists of two stages: the collision and the propagation (called also streaming). These two stages make LBM highly parallelizable.
The discretization of BE must reproduce the collision and propagation stages as well as possible. After the collision, begins the propagation at which a fictitious particle is allowed to orient itself in the lattice only towards one of the 8 direct neighbors with a predefined speed
. Thus, the discretization of the propagation step (streaming) is expressed by:
where
is the value of
before the streaming and the 9 speeds are given explicitly by the expressions below
At the end of the propagation, the particles settle in the lattice to interact with the other particles (this is the collision) and start again in other directions and at other speeds according to diffusion rules. Thus, the discretization of the collision step is expressed by:
Finally, by combining expressions (8) and (9), we find the most popular form of discretization of BE used for fluid flow simulations based on the LBM.
To complete the solution of BE, the algorithm of LBM needs to specify the ED and the relaxation time . It should be noted that the is defined as the integral of the Maxwell–Boltzmann distribution over the entire velocity space. As the exact calculation of such an integral is difficult, it is customary to approach it numerically using high-order quadrature formulas. Thus, the approximation of used for LBM is estimated by the Gauss–Hermite quadrature formula which is found to have excellent accuracy.
It is quite clear that the expression of
depends on the type of the PDE to be solved. Indeed, any PDE is formulated for a specific physical phenomenon. This phenomenon is a combination of several other phenomena of different physical magnitudes. On the other hand, we remind that the
expression was derived from a Taylor expansion of the Maxwell–Boltzmann distribution in the neighborhood of
, where
is the isothermal sound velocity (for details of derivation, see [
27]). One deduces that it is the order of this development which allows expressing the analytical expression of
. This expression must cover and represent all orders of the physical quantities included in the phenomenon that we wish to model. For example, to solve the Navier–Stokes PDEs, we have to perform the two-order Taylor expansion to obtain a
which will correctly reproduce the velocities and the pressure of the studied flow. On the other hand, to solve ADE by LBM, a Taylor development of order 1 is sufficient to find the expression of
which will reproduce the phenomena of advection and diffusion. As mentioned above, in this paper, we used the LBM D2Q9 model to solve Equation (4). In this case, the ED
is given by:
where
and
are the weight coefficients resulting from the Gauss–Hermite type quadrature formula which was adopted to approximate the calculation of the integral. These coefficients are given by:
Details on how to compute the weighting coefficients
can be found in Succi [
25].
As mentioned previously, the relaxation time
must be also specified. In fact, the multi-scale Chapman–Enskog Expansion allows proposing a constraint linking the dispersion coefficient
and the relaxation time
. Therefore, during the execution of the LBM algorithm, this parameter will be calculated explicitly from the
coefficient by:
is the dimensionless relaxation time .
At this stage, we have defined all parameters necessary for the execution of the D2Q9 LBM algorithm which can be summarized in the following two steps:
It should be noted that the different types of boundary conditions are imposed on the unknown
of the PDE (4). However, the LBM method solves the PDE (5) of unknown the DF
. It is then necessary to transform the boundary conditions relating to
variables to new ones which will be imposed on the DF
. In [
28,
29] one can find various transformations which make it possible to impose the various types of boundary conditions (Dirichlet, Neuman, Robin, etc.). To finish this subsection, we give the LBM algorithm which was implemented to solve the PDE (4) to build the computation code HYDRODISP-LBM (Algorithm 1).
| Algorithm 1: The pseudo-code of LBM |
| set numerical parameters |
| initialization
|
| initialize by the measured values
|
| Compute associated to from (Equation (11))
|
| loop: |
| | compute from (Equation (13)) |
| | compute from (Equation (11)) |
| | collision from (Equation (14a)) |
| | streaming from (Equation (14b)) (after 14a and 14b we have ) |
| | set boundary condition |
| | compute |
| | test exit |
| | set |
| go to the next time step |
One can remark that the velocity field
is a datum for the DP algorithm. This velocity field can come from any numerical model solving the Darcy’s equation in the concerned study area. For the application presented in this paper, we used the HYSFLO-LBM model already presented in a published paper in this journal [
20].
2.4. CMA-ES Algorithm
For the optimization step that constitutes the numerical resolution of an inverse problem, we have chosen to adopt a method in the category of metaheuristic algorithms. It is more precisely the evolution strategy algorithm commonly called CMA-ES (Covariance Matrix Adaptation–Evolution Strategy) [
30] (Hanssen, 2016). This choice was motivated by several reasons, namely that this algorithm is very well adapted to the cases of objective functions which are not known in an explicit way (this is our case in this study, since the values of our objective functions are calculated by the resolution of the direct problem). Based on stochastic processes, CMA-ES is particularly suited to the optimization of non-convex functions whose values are noisy. This algorithm is even recommended for poorly conditioned problems. Contrary to the algorithms with a gradient that converges towards the local optimums, CMA-ES ensures a convergence towards the global optimum. Finally, this algorithm is qualified as robust since it has been used successfully in various disciplines of engineering and environmental sciences.
As mentioned previously, CMA-ES is an evolutionary strategy type algorithm with a functioning similar to that of genetic algorithms. That is to say, this algorithm acts on a population of individuals in four stages: initialization, selection, recombination, and mutation. During its execution, the CMA-ES algorithm connects the 4 steps to produce “the best individuals” for the next iteration (also called generation). If we denote by the number of individuals (also called parents) in the population, at each generation, CMA-ES operates on these individuals (also called children) to produce “best individual” among the individuals. This particular CMA-ES algorithm is then called CMA-ES ().
Mutation is arguably the main step in the CMA-ES algorithm. The parameters of this step (called strategy parameters) direct this algorithm for the covariance matrix transformations and their adaptation according to the generated population. Strategy parameters are automatically adapted (without user intervention) based on information from the previous generation [
31,
32]. This advantage makes the CMA-ES algorithm more and more attractive for the most complex optimization problems. In order not to overload the presentation, we will not give here more details on CMA-ES, but the interested reader will consult our previous work [
20,
33,
34]. To finish this subsection, we give the flowchart of the operation of the CMA-ES algorithm (Algorithm 2).
| Algorithm 2: The pseudo-code of CMA-ES () |
| set numerical parameters () |
| initialization …, with |
| generation: |
| | selection …, with |
| | mutation |
| | evaluation |
| | test exit exit |
| | adaptation |
| go to the next generation |
where
is the size of the optimization variable,
is the size of the population. Hansen [
35] suggests
,
is a real positive parameter,
is the covariance matrix (symmetric and positive definite).
is the individual’s population,
is the number of the “best individual” according to the fitness value (i.e.,
),
is the objective function,
is the weighted average of
vectors on these
individuals,
denotes a vector of independent normal random numbers with zero mean and covariance matrix
. Finally, we remind that
and
are the strategy parameters that the algorithm CMA-ES self-adapts during each generation.
2.5. The Integrated Optimization Algorithm (HYDRODISP-LBM/CMA-ES)
For transport phenomena in porous media by advection–diffusion mixing processes, the HDT is a main parameter for the hydro–dispersive groundwater modeling. It is, therefore, necessary to know this tensor with high accuracy in order to obtain correct results: for example, for a groundwater front pollution propagation. However, this tensor is an intrinsic parameter of the studied porous medium and it is generally unknown. Several techniques have been proposed for its determination and they are essentially experimental. In fact, to determine the tensor experimentally, a passive tracer is injected at a point in the domain (called a well), and we follow during the time its movement by taking concentrations of the tracer at another point distant from the injection point. By using the basic statistical tools applied to the restored curve, we can then deduce the dispersion coefficient of the studied porous media. However, this technique requires prior knowledge of the direction of flow which will guide the choice of sampling point, but generally, this information is difficult to obtain without going through the hydrodynamic study of the study area. In addition, this method has also been proven ineffective when the medium is characterized by anisotropy.
In this paper, we propose to identify the HDT
of a porous medium in a numerical way. Indeed, to identify
, we formulated the problem from a mathematical point of view as a solution to an inverse problem with constraints. In another way, if one has the measurements of concentrations in the field denoted by
, this problem is then equivalent to finding the tensor
which minimizes the difference between the observed concentrations and those computed by solving the DP that we denote
. In this case the IP that must be resolved can be formulated by:
where
is the objective function defined by
and
is the admissible set values of
.
The inverse problem (15) is the formulation of the integrated optimization algorithm (IOA) which will be implemented to build the HYDRODISP-LBM/CMA-ES computation code. It is an iterative algorithm that couples the step of solving the DP and the step of optimization by CMA-ES. At convergence, this algorithm provides the HDT that we wish to identify
such that:
Obviously and like any numerical method, the numerical resolution of the IP is also confronted with certain difficulties, such as the stability, the uniqueness of the solution, and the convergence of the optimization algorithms, and, in particular, if it is the methods with gradients which have been adopted. All these difficulties have been massively studied by various researchers around the world from both a mathematical and numerical point of view. Several techniques have been proposed to circumvent these difficulties. In order to not repeat all of these techniques here, the interested reader will find a summary in the Reference [
20], but for more information, the reader may also consult the reference books on inverse problem topics. Par example [
7,
12,
36,
37,
38,
39].
It should be noted that in hydrogeology, if one has the measurements of the hydraulic potential
, the problem of identifying the transmissivity tensor
(Darcy’s equation) is formulated in a similar way to problem (15) [
20]. It is considered as an ill-posed problem in the sense of Hadamard [
40]. Consequently, the various techniques of numerical solution of this IP do not ensure the uniqueness of the solution (denoted
). To overcome this difficulty, it is then necessary to make additional hypotheses called a regularization strategy [
39,
41,
42]. In practice, the most used regularization method for this type of problem consists in introducing a priori information on the tensor
(for example, all kinds of measurements of
available on the study domain). This strategy is called the Tikhonov regularization method [
43] which consists of modifying the objective function
of the IP to become:
where
is the tensor containing a priori information (values of measurements), and
is the non-negative regularization parameter. In the book of Vogel [
7], one can find the different choices of the regularization parameter
that can significantly improve the efficiency (in the sense of convergence) of the IOA formulated by (15). All the choices for this parameter have been made in order to preserve the consistency with the inaccuracy of the input data of the problem. Finally, let us note that in the absence of a priori information, the tensor
must be taken equal to zero.
As far as we are concerned, for the identification of the HDT
, we do not have the a priori information
. On the other hand, the fact of writing
in a precise form according to the flow velocity via expression (3) is then equivalent to a priori information. Therefore, in our case, we do not need to specify the value of the tensor
. In addition, and for more regularity, during the optimization step of the IOA, we will use the objective function
modified by the Tikhonov regularization method, such as
where
is non-negative regularization parameter.
To finish this section, we describe the successive operations of the computer code HYDRODISP-LBM/CMA-ES implemented for the IOA. The code starts with an initial HDT that the CMA-ES algorithm also uses as the tensor value at generation . CMA-ES performs the selection and mutation steps to provide a new HDT . With this tensor, it is the computer code HYDRODISP-LBM of the direct problem in (15) which runs in turn to provide the value of the concentration . At this stage of the IOA, the objective function is constructed according to expression (18), then CMA-ES proceeds to the evaluation step (fitness) in order to be able to test the convergence. If the converge is obtained, CMA-ES returns the optimal HDT . Otherwise, CMA-ES goes to the step of adapting the strategy parameters to propose the new generation (). Thus, if necessary, these steps will be repeated until the convergence of the IOA towards the optimal value . Algorithm 3 summarizes the different steps of the IOA implemented by the HYDRODISP-LBM/CMA-ES computer code in this study to solve numerically the IP formulated by (15).
| Algorithm 3: The pseudo-code of HYDRODISP-LBM/CMA-ES |
| set the observations values vector |
| generation: |
| initialization |
| generation: |
| | selection from mutation |
| | solve the (DP) by HYDRODISP-LBM |
| | construct the objective function according (18) |
| | evaluation |
| | test if then convergence to the and exit |
| | adaptation |
| go to the next generation |
4. Discussion of the Modeling Results
Before starting the interpretation and discussion of the simulation results of the IOA, we give a description of the conditions of these simulations. The IOA was applied to the Beauvais site (North of France) which has been described in detail in our article published in this journal [
20]. It is an unconfined aquifer-type site with continuous instrumentation since 2015. The site is rectangular in shape with a length of 133 m and a width of 123 m. For a high spatial resolution, we adopted a computational grid of
, that is to say a computational lattice for the DP of 123 × 133. On this site, several sensors have been deployed to measure the various parameters of the aquifer. Thus, we had 20 points of measuring the concentration of different chemical substances. Among the ions analyzed, we chose for our simulations in this paper to use the chloride ion (
) concentration as the tracer. From these 20 concentration values, we deducted the concentration fields over the entire computational domain by Kriging type interpolation.
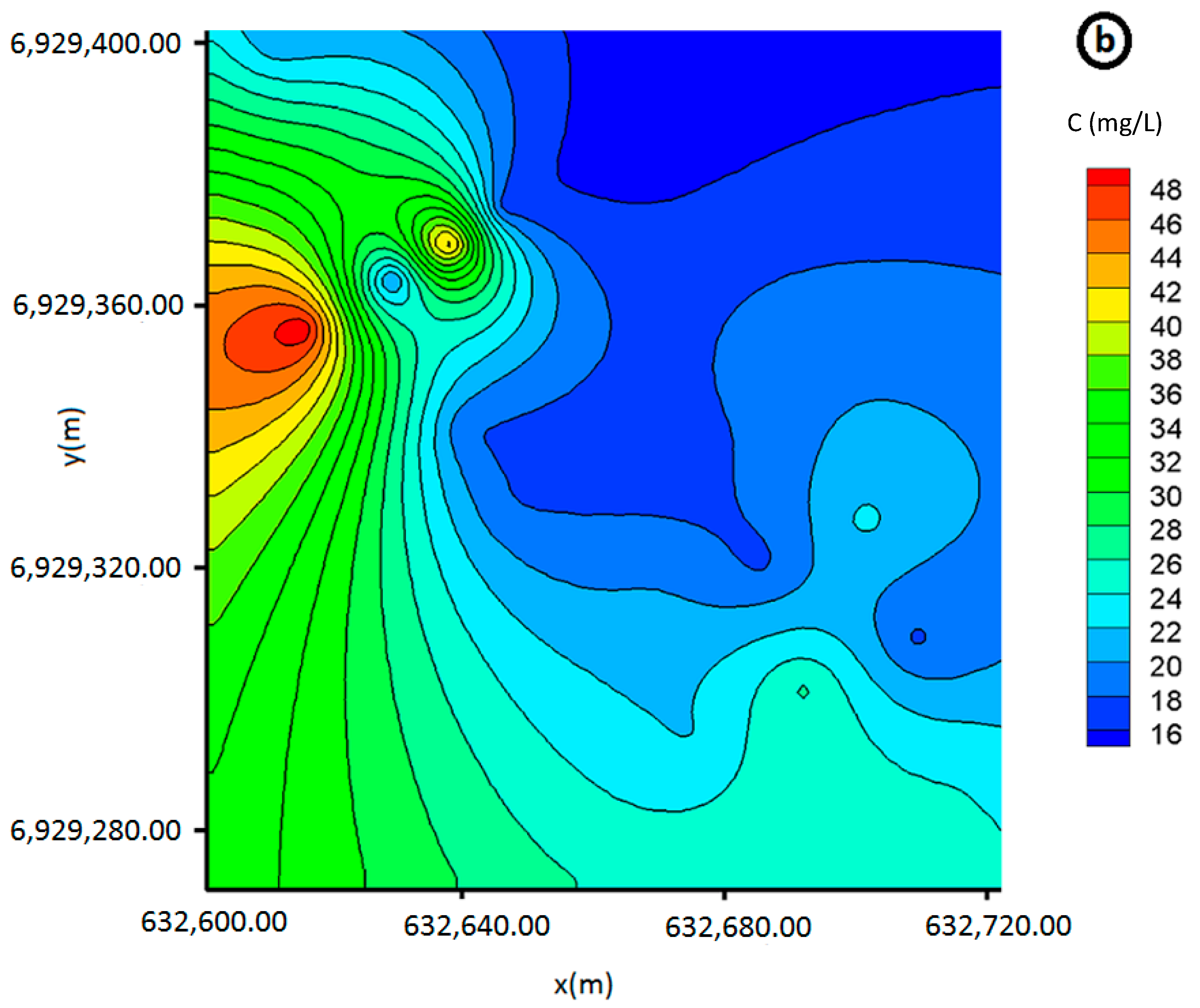
Figure 2 shows the concentration obtained; the interpolated concentration is denoted
which was used as the reference field necessary to the IOA for the construction of the objective function
expression (18). Finally, we note that the numerical solution of the DP required the knowledge of the values of the concentration on the four edges of the computational domain. For all the simulations presented in this study, we imposed the DP Dirichlet type boundary conditions. The values of the
function were extracted from those of
on the four edges. Thus, if we denoted by
the set of the four edges, then we have
.
As specified previously, the direct problem-solving ADE require knowledge of the velocity field
necessary of for the advective transport phase of the chlorine concentration. In fact, before proposing this paper which studies the hydro–dispersive aspect of HESB, we presented a purely hydrodynamic study of this site [
20]. Indeed, since we have 20 hydraulic head measurement points (
Figure 2), we then proposed a similar approach (IOA: HYSFLO-LBM/CMA-ES) in order to identify the transmissivity tensor
of the water table [
20]. Once the tensor
was identified, by using Darcy’s law we were able to estimate the velocity field of the studied site (
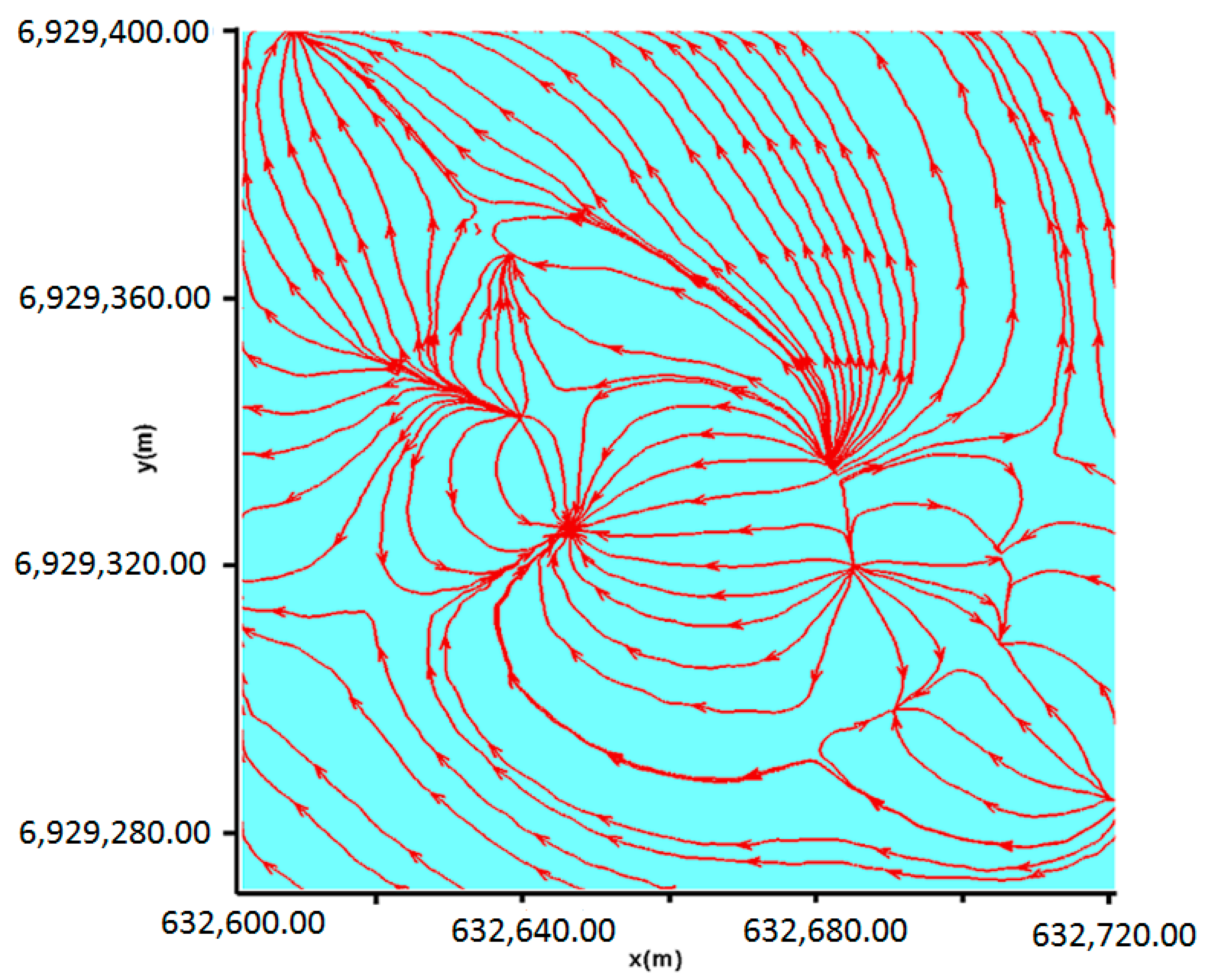
Figure 3). This figure shows a complex structure of the underground flow of the HESB but highlights several wells and sources in the field consistent with the measurements of the hydraulic head taken on the HESB.
The IOA HYDRODISP-LBM/CMA-ES developed in this study was applied to the HESB site to identify the HDT
. As explained by algorithm 3, a simulation by IOA begins with the first step by solving the DP by HYDRODISP-LBM, then performs the optimization by the CMA-ES algorithm in the second step. The computational time of the DP is insignificant (12 s on an Intel Xeon E5520 @ 2.27 GHz CPU with 32 GB of RAM). On the other hand, it is the optimization stage that consumes the most computing time. In fact, in the CMA-ES algorithm, the individual mutation stage explores all the elements of the research space to hope to propose the “best” population of
individuals among the
parents. The other steps of CMA-ES, such as selection, recombination, and adaptation, do not consume much time compared to the mutation. For information, a complete simulation until convergence by HYDRODISP-LBM/CMA-ES consumes a little more than 2 days in calculation time for a tolerance
. Moreover, it is important to note that the CMA-ES algorithm is based on stochastic processes for the research stage and consequently, the individuals of the populations proposed for each generation may be affected by certain errors. To reduce the impact of the propagation of these errors in the final results of the identified tensor, we carried out about fifteen successive simulations, and we considered the optimal HDT
as the arithmetic mean of these fifteen simulations. Before starting the interpretation of the modeling results, it is useful to define the numerical quantity which helps us to quantify the errors. These are the absolute error
and the relative error
defined by:
It is interesting to note that the application of the IOA to a site can meet the double objectives: it allows both the calibration of the model of the DP (we speak about the automatic calibration) and the identification of the HDT of the studied site.
Figure 4a,b respectively show the field of the measured
concentration field and the simulated one by the model HYDRODISP- LBM by considering the identified HDT
as data of the DP. In a visual comparison of these two figures, one can conclude an excellent agreement between these two fields of concentration. Moreover, to quantify the small remaining errors, we must examine
Figure 5a, b. From these two figures, we read that the relative error did not exceed 4% while the absolute error hardly reached
.
If we refer to
Figure 2 which references the 20 measurement points, we observe that the most important errors were located at the piezometric points Pz8 Pz12, Pz13 and at the well point F4. In fact, this observation is not surprising, since, in our previous study of the hydrodynamics of the same area [
20], we showed that these parts of the site are characterized by a complex geological and flow structure. These remarks are confirmed if we examine in addition
Figure 3, which presents the flow streamlines. This figure shows that in the vicinity of these points, we observe the presence of a succession of sources (divergent streamlines) and of wells (converging streamlines) which induces a hydrodynamic difficulty to apprehend. Finally, if we admit the complexity of the geology of the site and the errors made on the measurements (either by the accuracy of the deployed sensors or by the difficulty of access to the measurement point), we can then conclude that the proposed coupling in this work (HYDRODISP-LBM/CMA-ES provides an excellent result for the calibration of models solved by the DP.
As mentioned above, the application of the HYDRODISP-LBM/CMA-ES coupling to the site also makes it possible to identify the HDT of the
tracer.
Figure 6 shows the spatial distribution of the HDT. The analysis and the interpretation of the dispersion map (
Figure 6) revealed higher dispersion in especially in the central and the north sectors of the HESB (about
). In parallel, these sectors were characterized by the spatial distribution of the dispersion coefficients which varied between
and
. This variation shows the complexity of the chalk formation and its heterogeneity according to the groundwater flow, hydrogeological characteristics (permeability and transmissivity), porosity, and the presence of fractures.
Figure 6 shows also that the maximum dispersion was obtained at points Pz8 and Pz14. This remark is not surprising since from a hydrodynamic point of view these two points behave like wells with maximum velocity (
Figure 2). In view of Expression (3) which linearly links the dispersion to the velocity magnitude, we can then predict that the maximum dispersion will also be obtained at these two points.
We specify that there are no references on the HDT concerning our study site HESB. The investigations presented in this paper are the first and new hydro–dispersive investigation results for this site. Consequently, we have no means of verifying the orders of magnitude of the values that we announce. Nevertheless, we believe that the approach of the identification of the tensor
is commendable. Of course, there are a number of investigations [
45,
46,
47,
48] (most of them are experimental in the laboratory) that determine the diffusion coefficient of chloride. However, not the transverse dispersivity which we are interested in in this paper, and consequently, these works cannot inform us about the range of expected values of the dispersivity
. On the other hand, all these authors agree on the fact that the determination of this coefficient is a difficult exercise to carry out since it strongly depends on several parameters controlling the mixing processes in a given medium. Indeed, these mixing processes result from the two different transport mechanisms. The first is due to matrix diffusion and the second is governed by the transfer of solutes by the permeable environment flux which is characterized by fractures. According to [
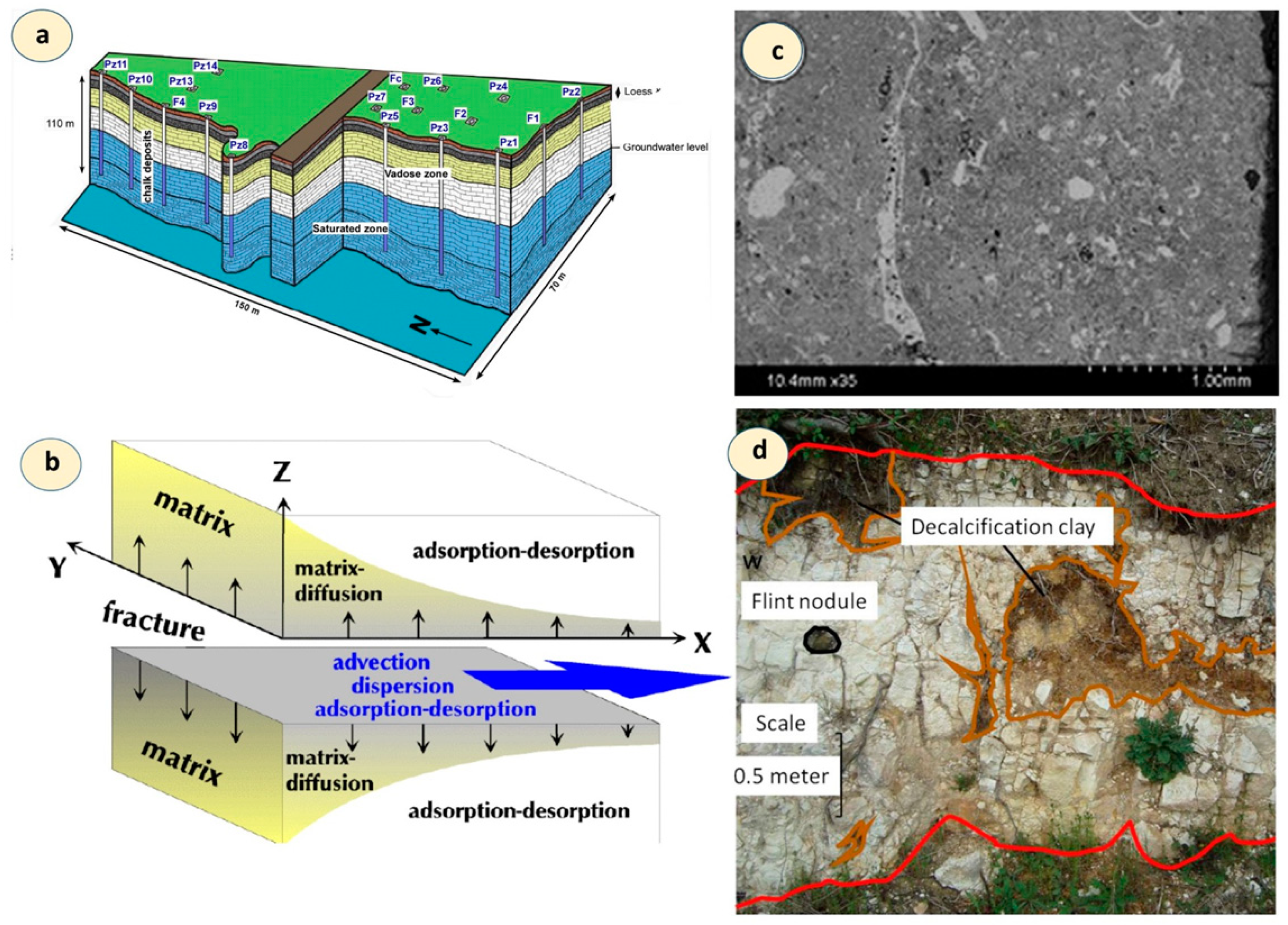
49], these solutes are transferred by the concentration gradient from the fluid parts contained in the permeable support (fractures) to the non-fluid parts (matrix) (
Figure 7b). In the chalk environment (
Figure 7a), the transport media required the first time for the characterization of the petrophysical characteristics of the chalk formation. Indeed, the use of the Scanning Electron Microscopy (SEM) (
Figure 7c) analysis of the chalk samples coming from outcrops which are located near to our site HESB allows defining the porosity of the chalk. The carbonate matrix is characterized by a sedimentological wackstone texture. The SEM (
Figure 7d) method provided an intra-granular porosity that varied between 25 and 30% [
50]. This porosity could be classified according to the degrees of fissuration and to the vertical distribution allowing to deduce the primary and secondary porosity with 0.15–45% and 0.005–0.02, respectively [
51]. The variation of diffusion coefficient could be related to the relationship between geometrical properties of fractures and matrix [
52]. This complexity of the chalk aquifer and especially the variation of diffusion coefficients have been evaluated in the Negev Desert [
47] as a function of the porosity, permeability, the depth (Eocene section of the 285 m), and mineralogy characteristics of this formation. The estimated diffusion coefficient of the Negev Desert is very low (orders of magnitude about
), but the most important results reveal that the diffusion coefficients of Eocene chalk depend especially on the porosity.
To assess the degree of importance of the heterogeneity of the dispersion tensor
, we performed a new simulation, but with a constant dispersion coefficient
. This coefficient was obtained by the spatial mean of the identified tensor
(
).
Figure 8 shows the concentration field obtained by adopting the constant dispensation coefficient (in this study we find
=
. By comparing it with the
Figure 4b, which was obtained by the heterogeneous tensor, we observe a quasi-perfect similarity except in the vicinity of the point Pz8 and the point Pz13 where the isocontours were, this time, off-center compared to the position of the source. This finding is not surprising since we mentioned previously that these zones of the studied area are characterized by a complex geological formation inducing a flow that is difficult to apprehend. In view of these results, we can conclude that the heterogeneity of the dispersion tensor does not play an important role in the dispersion of the tracers in this study area.