A Review of Numerical Simulations of Secondary Flows in River Bends
Abstract
:1. Introduction
2. Secondary Flow in River Bends
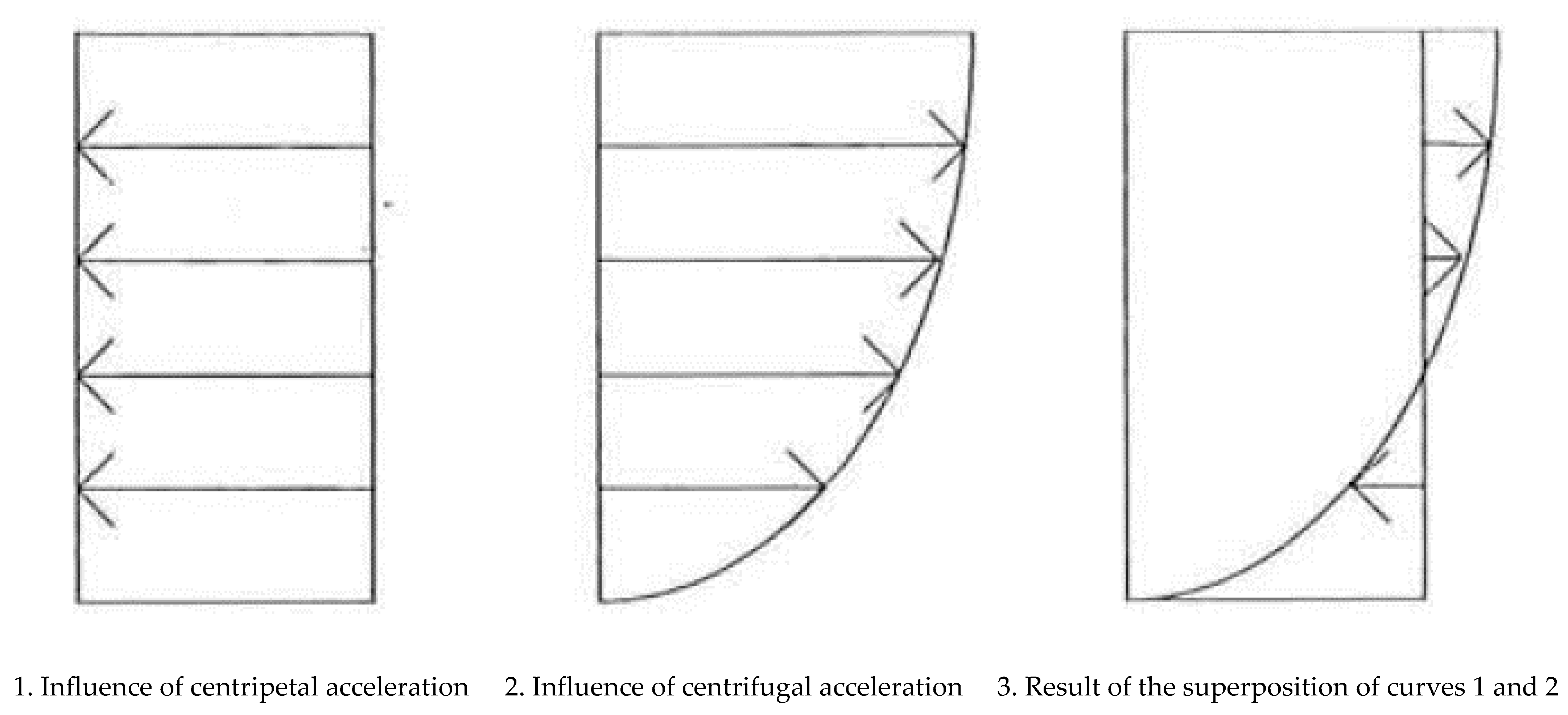
2.1. Mechanism of Secondary Flow
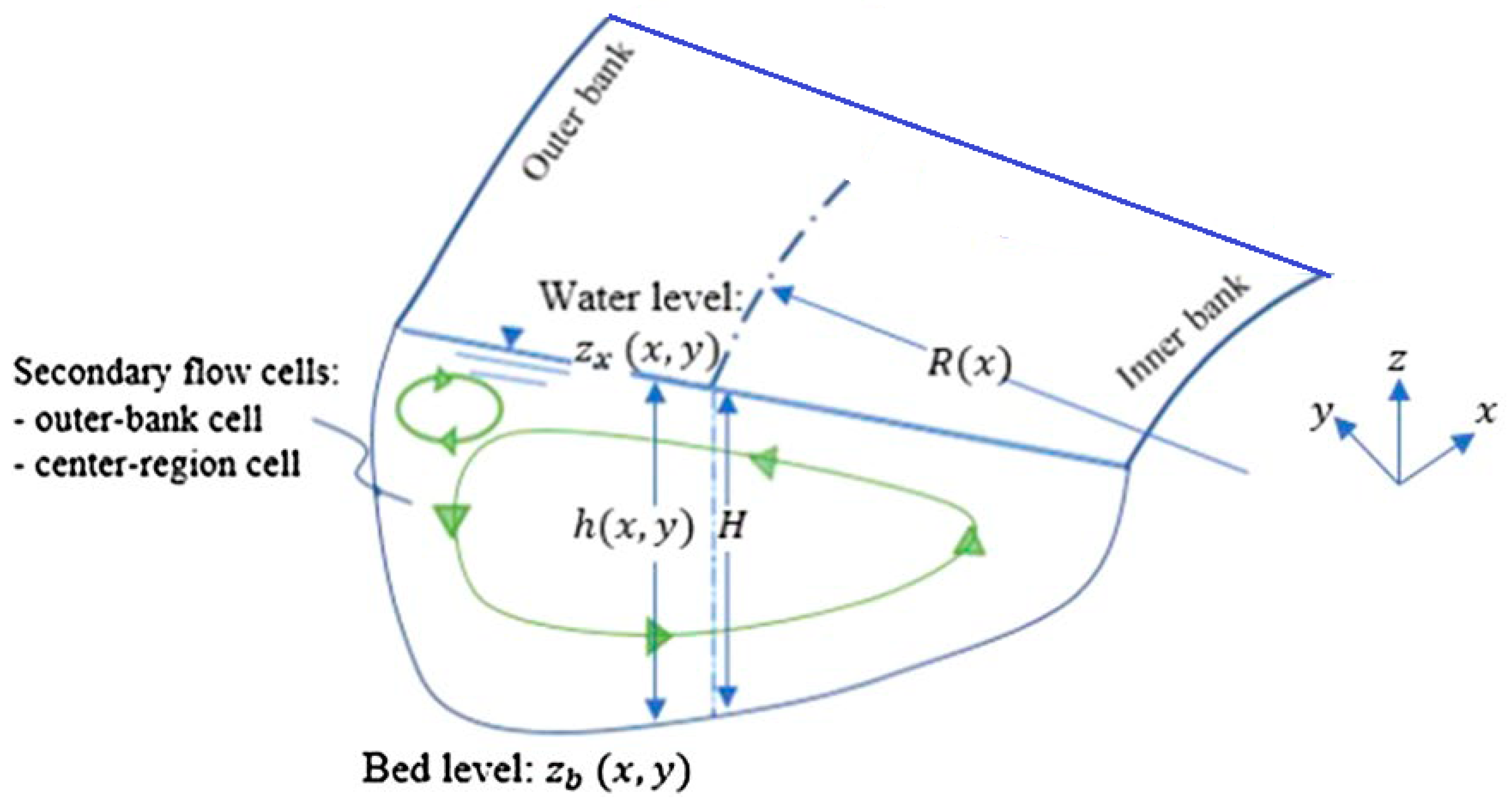
2.2. Secondary Flow Cells
2.3. Velocity Redistribution
2.4. Mathematical Description of the Main Flow and Secondary Circulation
3. Boundary Conditions
3.1. Wall Boundaries
3.2. Free Surface
- Vertical velocities are zero;
- The derivative in the vertical direction of the radial and longitudinal velocities are zero.
3.3. Inlet
3.4. Outlet
4. Advantages and Disadvantages of Various Numerical Methods
4.1. RANS Modeling
4.2. RSM Modeling
4.3. LES Modeling
4.4. DES Modeling
5. Research on River Bends Flows and Key Findings
5.1. Secondary Flow in a Curved Channel
5.2. Secondary Flow and Pollutant Dispersion
5.3. Secondary Flow and Sediment Transport
5.4. Secondary Flow in Bend over Topography
6. Discussion
7. Future Research Needs
8. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Compliance with Ethics Requirements
References
- Ghobadian, R.; Mohammadi, K. Simulation of subcritical flow pattern in 180° uniform and convergent open-channel bends using SSIIM 3-D model. Water Sci. Eng. 2011, 4, 270–283. [Google Scholar] [CrossRef]
- Rozovskii, I. Flow of Water in Bends of Open Channels; Academy of Sciences of the Ukrainian SSR, Israel Program for Scientific Translations: Jerusalem, Israel, 1961. [Google Scholar]
- De Vriend, H. Flow Measurements in a Curved Rectangular Channel; Delft University of Technology: Delft, The Netherlands, 1979. [Google Scholar]
- De Vriend, H. Velocity redistribution in curved rectangular channels. J. Fluid Mech. 1980, 107, 423–439. [Google Scholar] [CrossRef]
- Engelund, F.; Skovgaard, O. On the origin of meandering and braiding in alluvial streams. J. Fluid Mech. 1973, 57, 289–302. [Google Scholar] [CrossRef]
- Blanckaert, K.; Graf, W.H. Mean flow and turbulence in open-channel bend. J. Hydraul. Eng. 2001, 127, 835–847. [Google Scholar] [CrossRef]
- Booij, R. Measurements and large eddy simulations of the flows in some curved flumes. J. Turbul. 2003, 4, 1–17. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Supercritical bend flow. J. Hydraul. Eng. 1997, 123, 208–218. [Google Scholar] [CrossRef]
- Roca, M.; Martin Vide, J.P.; Blanckaert, K. Reduction of bend scour by an outer bank footing: Footing design and bed topography. J. Hydraul. Eng. 2007, 133, 139–147. [Google Scholar] [CrossRef]
- Tominaga, A.; Nagao, M. Secondary Flow Structure in Bends of Narrow Open Channels with Various Cross Sections. In Proceedings of the 4th International Conference on Hydroscience and Engineering, Seoul, Korea, 26–29 September 2000. [Google Scholar]
- Shimizu, Y.; Yamaguchi, H.; Itakura, T. Three-dimensional computation of flow and bed deformation. J. Hydraul. Eng. 1990, 116, 1090–1108. [Google Scholar] [CrossRef]
- Wang, S.S.; Hu, K. Improved methodology for formulating finite element hydrodynamic models. Finite Elem. Fluids 1990, 8, 457–478. [Google Scholar]
- Hsieh, T.Y.; Yang, J.C. Investigation on the suitability of two-dimensional depth-averaged models for bend-flow simulation. J. Hydraul. Eng. 2003, 129, 597–612. [Google Scholar] [CrossRef]
- Ikeda, S.; Nishimura, T. Flow and bed profile in meandering sand-silt rivers. J. Hydraul. Eng. 1986, 112, 562–579. [Google Scholar] [CrossRef]
- Molls, T.; Chaudhry, M.H. Depth-averaged open-channel flow model. J. Hydraul. Eng. 1995, 121, 453–465. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Cheng, N.S. Time-mean structure of secondary flows in open channel with longitudinal bedforms. Adv. Water Resour. 2006, 29, 1634–1649. [Google Scholar] [CrossRef]
- Chang, Y.C. Lateral Mixing in Meandering Channels; University of Iowa: Iowa City, IA, USA, 1971. [Google Scholar]
- Fischer, H.B. The effects of bends on dispersion in streams. Water Resour. Res. 1969, 5, 496–506. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S. Reynolds stress modelling of rectangular open-channel flow. Int. J. Num. Meth. Fluids 2006, 51, 1319–1334. [Google Scholar] [CrossRef]
- Khosronejad, A.; Rennie, C.D.; Neyshabouri, S.A.A.S.; Townsend, R.D. 3D numerical modeling of flow and sediment transport in laboratory channel bends. J. Hydraul. Eng. 2007, 133, 1123–1134. [Google Scholar] [CrossRef]
- Luo, J.; Razinsky, E.H. Analysis of turbulent flow in 180 deg turning ducts with and without guide vanes. J. Turbomach. 2009, 131, 021011. [Google Scholar] [CrossRef]
- van Balen, W.; Uijttewaal, W.S.J.; Blanckaert, K. Large eddy simulation of a mildly curved open-channel flow. J. Fluid Mech. 2009, 630, 413–442. [Google Scholar] [CrossRef] [Green Version]
- Marriott, M.J. The Effect of Overbank Flow on the Conveyance of the Inbank Zone in Meandering Compound Channels. In Proceedings of the 28th IAHR Congress, Graz, Austria, 22–27 August 1999. [Google Scholar]
- Zeng, J.; Constantinescu, G.; Blanckaert, K.; Weber, L. Flow and bathymetry in sharp open-channel bends: Experiments and predictions. Water Res. 2008, 44, W09401. [Google Scholar] [CrossRef]
- Mosonyi, E.; Gotz, W. Secondary Currents in Subsequent Model Bends. In Proceedings of the International Association for Hydraulic Research International Symposium on River Mechanics, Bangkok, Thailand, 9–12 January 1973; pp. 191–201. [Google Scholar]
- Leschziner, M.A.; Rodi, W. Calculation of strongly curved open channel flow. J. Hydraul. Div. 1979, 105, 1297–1314. [Google Scholar] [CrossRef]
- Jansen, P.P. Principles of River Engineering; VSSD: Delft, The Netherlands, 1994. [Google Scholar]
- Jongbloed, J. Three-Dimensional Modelling of Secondary Flow in River Bends; Delft University of Technology: Delft, The Netherlands, 1996. [Google Scholar]
- Bathurst, J.; Thorne, C.; Hey, R.D. Direct measurements of secondary currents in river bends. Nature 1977, 269, 504–506. [Google Scholar] [CrossRef]
- Blanckaert, K. Saturation of curvature-induced secondary flow, energy losses, and turbulence in sharp open-channel bends: Laboratory experiments, analysis, and modeling. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K. Hydrodynamic processes in sharp meander bends and their morphological implications. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Graf, W.H.; Blanckaert, K. Flow Around Bends in Rivers. In Proceedings of the 2th International Conference, New Trends in Water and Environmental Engineering for Safety and Life: Eco-Compatible Solutions for Aquatic Environments, Capri, Italy, 24–28 June 2002. [Google Scholar]
- Booij, R.; Tukker, J. 3-Dimensional Laser-Doppler Measurements in a Curved Flume. In Developments in Laser Techniques and Applications to Fluid Mechanics; Adrian, R.J., Durão, D.F.G., Durst, F., Heitor, M.V., Maeda, M., Whitelaw, J.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Booij, R. Turbulentie in de Waterloopkunde: Handleiding; Department of Hydraulic Engineering: Delft, The Netherlands, 1992. [Google Scholar]
- Pezzinga, G. Applicazione del Modello K-e non Lineare Alio Studio di Circolazioni Secondarie. Atti del XXII Convegno di Idraulica e Costruzioni Idrauliche, Cosenza 1990, 2, 125–139. Available online: http://www.dica.unict.it/users/gpezzing/english.htm (accessed on 20 January 2021).
- Rodi, W. Turbulence Models and Their Application in Hydraulics a State of Art Review, 2nd ed.; International Association for Hydraulic Research: Delft, The Netherlands, 1984. [Google Scholar]
- Jian, Y.; McCorquadale, J.A. Simulation of curved open channel flows by 3D hydrodynamic model. J. Hydraul. Eng. 1998, 124, 687–698. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Melaaen, M.C. Analysis of Curvilinear Non-Orthogonal Coordinate for Numerical Calculation of Fluid Flow in Complex Geometries; The Norwegian Institute of Technology: Trondheim, Norway, 1990. [Google Scholar]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layer; Hemisphere: Washington, DC, USA, 1977. [Google Scholar]
- Mcguirk, J.J.; Rodi, W. The Calculation of Three-Dimensional Turbulent Free Jets; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Rodi, W. Turbulence Models and their Applications in Hydraulics; IAHR MonographL; CRC Press; Taylor & Francis Group: Abingdon, UK, 1993. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Gildeh, H.K. Numerical Modeling of Thermal/Saline Discharges in Coastal Waters; University of Ottawa: Ottawa, ON, Canada, 2013. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 8. [Google Scholar] [CrossRef] [Green Version]
- Davidson, L. An Introduction to Turbulence Models; Chalmers University of Technology: Göteborg, Sweden, 2011. [Google Scholar]
- Cable, M. An Evaluation of Turbulence Models for the Numerical Study of Forced and Natural Convective Flow in Atria; Queen’s University: Kingston, ON, Canada, 2009. [Google Scholar]
- Shur, M.; Strelets, P.R.; Spalart, M.; Travin, A. Detached-eddy simulation of an airfoil at high angle of attack. Engineering Turbulence Modelling and Experiments 4. In Proceedings of the 4th International Symposium on Engineering Turbulence Modelling and Measurements, Ajaccio, Corsica, France, 24–26 May 1999; pp. 669–678. [Google Scholar]
- Duan, J.G. Simulation of Flow and Mass Dispersion in Meandering Channels. J. Hydraul. Eng. 2004, 130, 964–976. [Google Scholar] [CrossRef]
- Ghaneeizad, S.M.; Jovein, E.B.; Abrishami, J. An Investigation of Turbulence Models in Flow Treatment Simulation in Strongly Curved Bends. In Proceedings of the 9th International Conference on Hydroinformatics HIC, Tianjin, China, 7–11 September 2010. [Google Scholar]
- Gholami, A.; Akhtari, A.A.; Minatour, Y.; Hossein, B.; Javadi, A.A. Experimental and Numerical Study on Velocity Fields and Water Surface Profile in a Strongly- Curved 90° Open Channel Bend. Eng. Appl. of Comput. Fluid Mech. 2014, 8, 447–461. [Google Scholar] [CrossRef] [Green Version]
- Stoesser, T.; Ruether, N.; Olsen, N.R.B. Calculation of primary and secondary flow and boundary shear stresses in a meandering channel. Adv. Water Resour. 2010, 33, 158–170. [Google Scholar] [CrossRef]
- Fraga, B.; Cea, L.; Peña, E. Comparison between standard and non-linear k-ε turbulence models for three-dimensional simulation of turbulent flow in a meandering open channel. In Proceedings of the River Flow 2012—Proceedings of the International Conference on Fluvial Hydraulics, San Jos, Costa Rica, 5–7 September 2012; pp. 1161–1168. [Google Scholar]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2018, 19, 543–568. [Google Scholar] [CrossRef]
- Yan, X.; Rennie, C.D.; Mohammadian, A. A three-dimensional numerical study of flow characteristics in strongly curved channel bends with different side slopes. Environ. Fluid Mech. 2020, 20, 1491–1510. [Google Scholar] [CrossRef]
- Ghanmi, A. Modeling of flows between two consecutive reverse curves. J. Hydraul. Res. 1999, 37, 121–135. [Google Scholar] [CrossRef]
- Falcon, M. Secondary flow in curved open channels. Ann. Rev. Fluid Mech. 1984, 16, 179–193. [Google Scholar] [CrossRef]
- Duan, G.; Wang, S.S.Y.; Jia, Y. The applications of the enhanced CCHE2D model to study the alluvial channel migration processes. J. Hydraul. Res. 2001, 39, 469–480. [Google Scholar] [CrossRef]
- Siebert, W. Stroemungscharakteristiken in Einen Kanal Mit 180-Kruemmungen, Mitteilungen 168; Theodor-Rehbock Flusslaboratorium: Karlsruhe, Germany, 1982. [Google Scholar]
- Lien, H.C.; Hsieh, T.Y.; Yang, J.C.; Yeh, K.C. Bend-flow simulation using 2D depth-averaged model. J. Hydraul. Eng. 1999, 125, 1097–1108. [Google Scholar] [CrossRef] [Green Version]
- Safarzadeh Gandoshmin, A.; Salehi Neishbouri, A. Numerical Simulation of Flow Structure in Lateral Intake on 180-Degree Bend; Tarbiat Modarres University: Tehran, Iran, 2005. [Google Scholar]
- Lu, W.; Zhang, W.; Cui, C.; Leung, A. A numerical analysis of free-surface flow in curved open channel with velocity-pressure-free-surface correction. Comput. Mech. 2004, 33, 215–224. [Google Scholar] [CrossRef]
- Bodnar, T.; Prihoda, J. Numerical simulation of turbulent free-surface flow in curved channel. Flow Turbul. Combust 2006, 76, 429–442. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, H.; Shao, X.; Jia, D. 2-D numerical simulation of flow in a curved open channel. Adv. Water Resour. Hydraul. Eng. 2009, 871–876. [Google Scholar]
- Constantinescu, G.; Koken, M.; Zeng, J. Simulation of flow in an open channel bend of strong curvature using Detached Eddy Simulation. River Flow 2010, 2010, 1527–1534. [Google Scholar]
- van Balen, W.; Blanckaert, K.; Uijttewaal, W.S.J. Analysis of the role of turbulence in curved open-channel flow at different water depths by means of experiments, LES and RANS. J. Turbul. 2010, 11, 1–34. [Google Scholar] [CrossRef]
- Jing, H.; Guo, Y.; Li, C.; Zhang, J. Three-dimensional numerical simulation of compound meandering open channel flow by the Reynolds stress model. Int. J. Numer. Meth. Fluids 2009, 59, 927–943. [Google Scholar] [CrossRef]
- Jing, H.; Li, C.; Guo, Y.; Xu, W. Numerical simulation of turbulent flows in trapezoidal meandering compound open channels. Int. J. Numer. Meth. Fluids 2011, 65, 1071–1083. [Google Scholar] [CrossRef]
- Holley, E.R.; Abraham, G. Field tests of transverse mixing in rivers. J. Hydraul. Div. Am. Soc. Civ. Eng. 1973, 99, 2313–2331. [Google Scholar]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering and Straight; Geological Survey Professional Paper 282-B; U.S. Geologic S.; U.S. Government Printing Office: Washington, DC, USA, 1957; pp. 37–86.
- Demuren, A.O.; Rodi, W. Calculation of flow and pollutant dispersion in meandering channels. J. Fluid Mech. 1986, 172, 63–92. [Google Scholar] [CrossRef]
- Matsuura, T. Stream-Bank Protection in Narrow Channel Bends Using ‘Barbs’—A Laboratory Study; University of Ottawa: Ottawa, ON, Canada, 2004. [Google Scholar]
- Dietrich, W.E.; Whiting, P.J. Boundary Shear Stress and Sediment Transport in River Meanders of Sand and Gravel; River Meandering, Water Resources Monograph Series; Ikeda, S., Parker, G., Eds.; American Geophysical Union (AGU): Washington, DC, USA, 1989; Volume 12, pp. 1–50. [Google Scholar]
- Wu, W.; Rodi, W.; Wenka, T. 3D numerical modeling of flow and sediment transport in open channels. J. Hydraul. Eng. ASCE 2000, 126, 4–15. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Bergs, M.A. Flow processes in a curved alluvial channel. Water Resour. Res. 1988, 24, 45–56. [Google Scholar] [CrossRef]
- Jamieson, E.C.; Post, G.; Rennie, C.D. Spatial variability of three-dimensional Reynolds stresses in a developing channel bend. Earth Surf. Process. Landforms 2010, 35, 1029–1043. [Google Scholar] [CrossRef]
- van Balen, W.; Uijttewaal, W.S.J.; Blanckaert, K. Large-Eddy Simulation of a Curved Open-Channel Flow over Topography. Phys. Fluids 2010, 22, 075108. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K. Flow and Turbulence in Sharp Open-Channel Bends. [Nr 2545, Ecole Polytechnique Fe’de´rale Lausanne, Switzerland.]. Ph.D. Thesis, Ecole Polytechnique Federale Lausanne, Lausanne, Switzerland, 2003. Available online: https://core.ac.uk/download/pdf/147899832.pdf (accessed on 20 January 2021).
- Blanckaert, K.; De Vriend, H.J. Secondary flow in sharp open-channel bends. J. Fluid Mech. 2004, 498, 353–380. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K. Topographic steering, flow circulation, velocity redistribution and bed topography in sharp meander bends. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Church, M.; Biron, P.M.; Roy, A.G. Gravel Bed Rivers: Processes, Tools, Environments; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; CRC Press; Taylor & Francis Group: Abingdon, UK, 1993. [Google Scholar]
- De Almeida, J.R.M.; Ota, J.J. Comparative study between turbulence models in curved channels. Braz. J. Water Resour. 2020, 25, 21. [Google Scholar] [CrossRef]
- Demuren, A.; Rodi, W. Calculation of turbulence-driven secondary motion in non-circular ducts. J. Fluid Mech. 1984, 140, 189–222. [Google Scholar] [CrossRef]
- Iliescu, T.; Fischer, P. Backscatter in the rational LES model. Comput. Fluids 2004, 33, 783–790. [Google Scholar] [CrossRef]
- Kean, J.W.; Kuhnle, R.A.; Smith, J.D.; Alonso, C.V.; Langendoen, E.J. Test of a method to calculate nearbank velocity and boundary shear stress. J. Hydraul. Eng. 2009, 135, 591–601. [Google Scholar] [CrossRef]
- Vanoni, V.A. Transportation of suspended sediment by water. Trans. Am. Soc. Civ. Eng. 1946, 111, 67–133. [Google Scholar] [CrossRef]
- Rutherford, J.C. River Mixing; John Wiley & Sons: Hoboken, NJ, USA; Chichester, UK, 1994. [Google Scholar]
- Boxall, J.B.; Guymer, I.; Marion, A. Transverse mixing in sinuous natural open channel flows. J. Hydraul. Res. 2003, 41, 153–165. [Google Scholar] [CrossRef]
- Marion, A.; Zaramella, M. Effects of velocity gradients and secondary flow on the dispersion of solutes in curved channels. J. Environ. Eng. 2006, 132, 1295–1302. [Google Scholar]
- Rowinski, P.; Guymer, I.; Kwiatkowski, K. Response to the slug injection of a tracer—Large scale experiment in a natural river. Hydrol. Sci. J. 2008, 53, 1300–1309. [Google Scholar] [CrossRef] [Green Version]
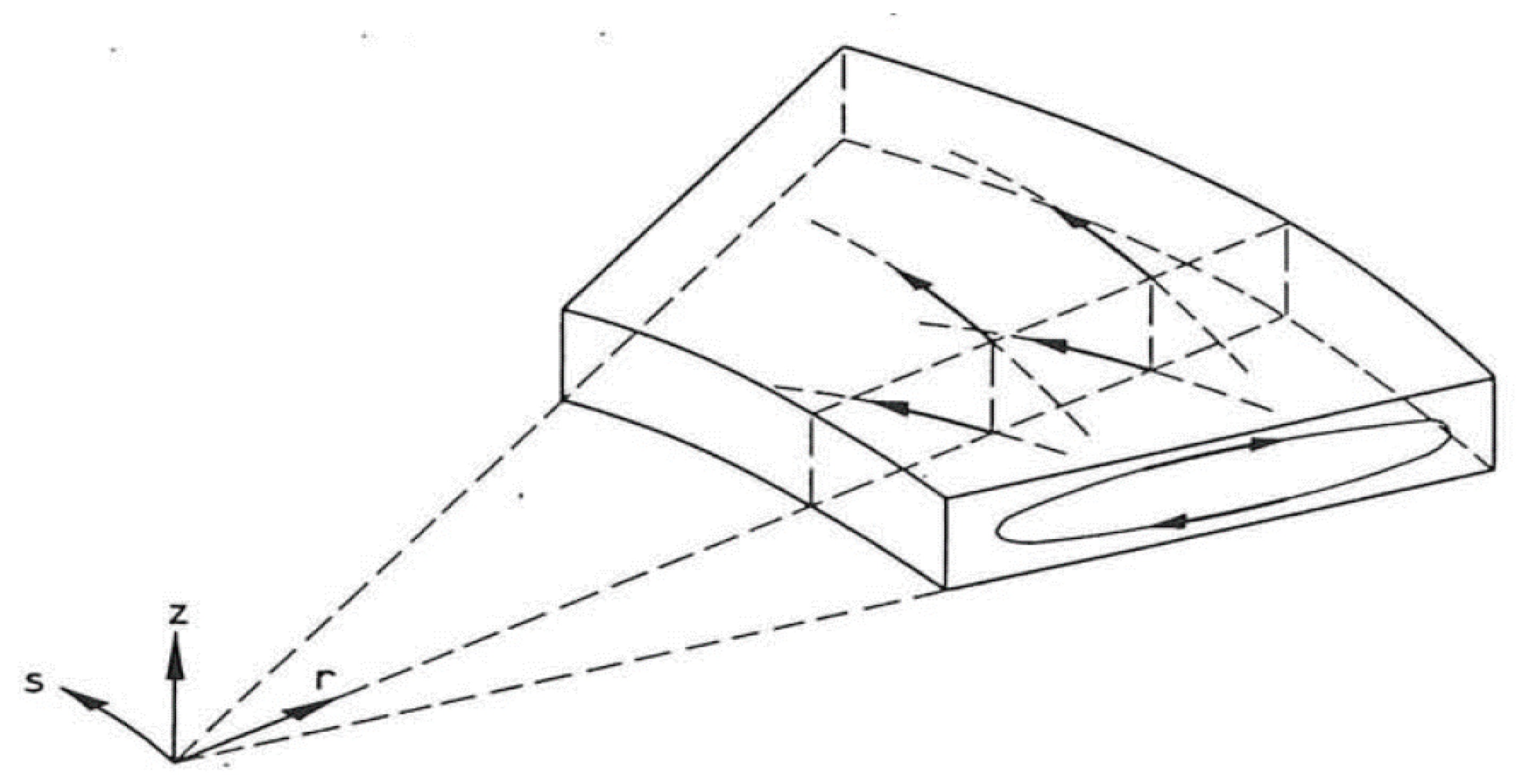
 ) and secondary-flow streamlines (
) and secondary-flow streamlines (  ) in the inner wall region of a shallow channel (d/B = 0.1) (De Vriend, 1980) [4].
) in the inner wall region of a shallow channel (d/B = 0.1) (De Vriend, 1980) [4].
 ) and secondary-flow streamlines (
) and secondary-flow streamlines (  ) in the inner wall region of a shallow channel (d/B = 0.1) (De Vriend, 1980) [4].
) in the inner wall region of a shallow channel (d/B = 0.1) (De Vriend, 1980) [4].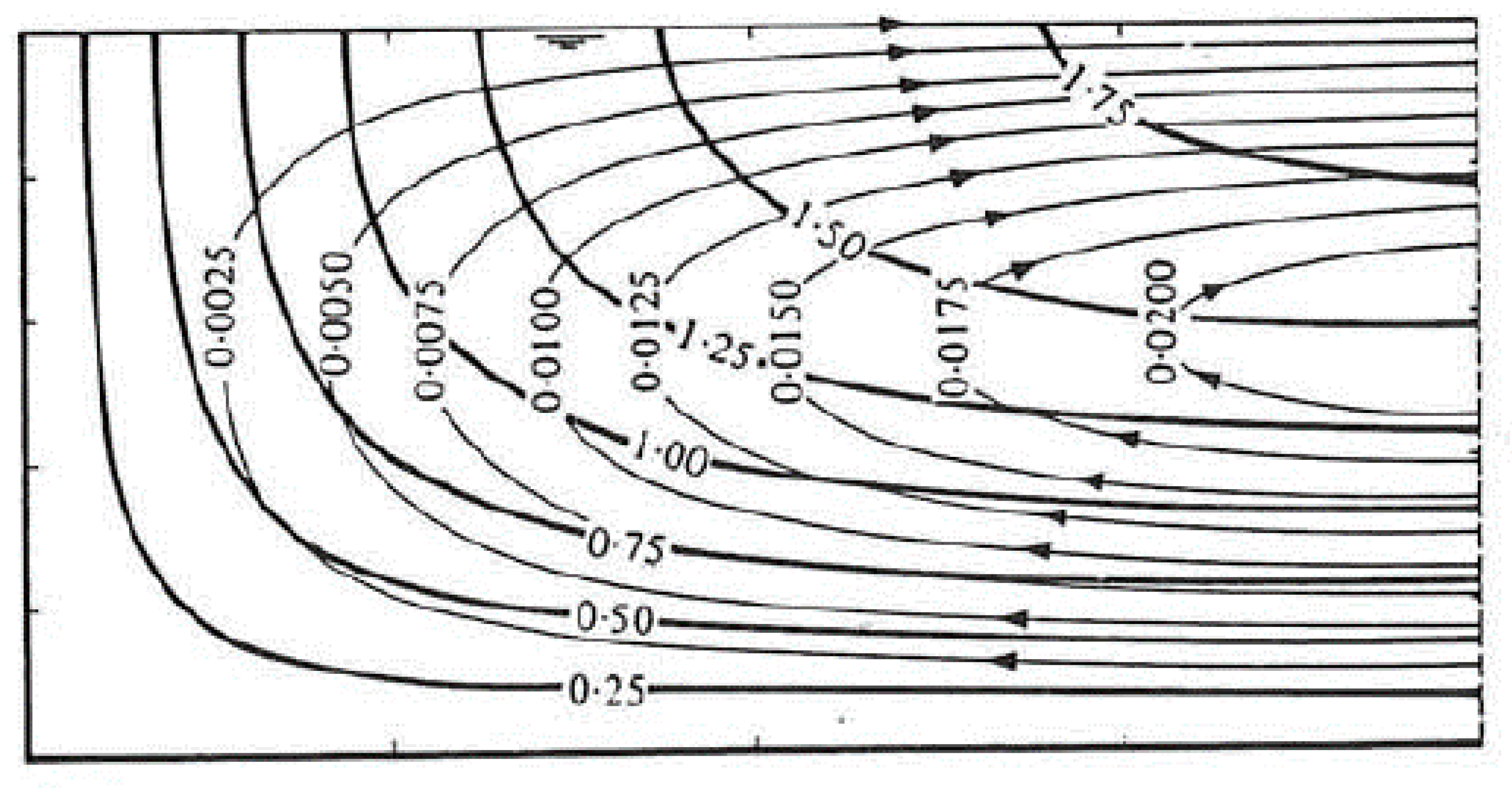
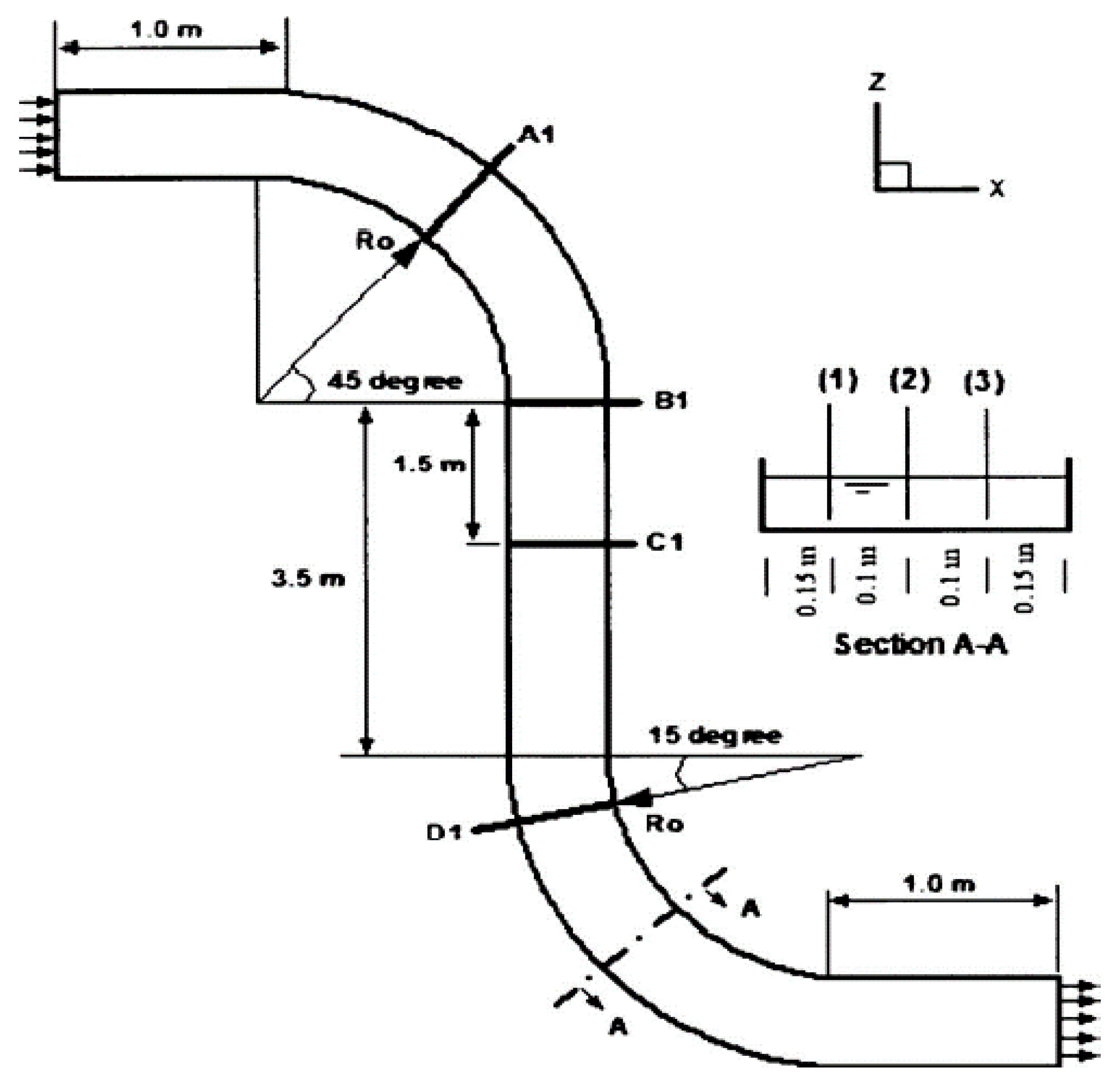
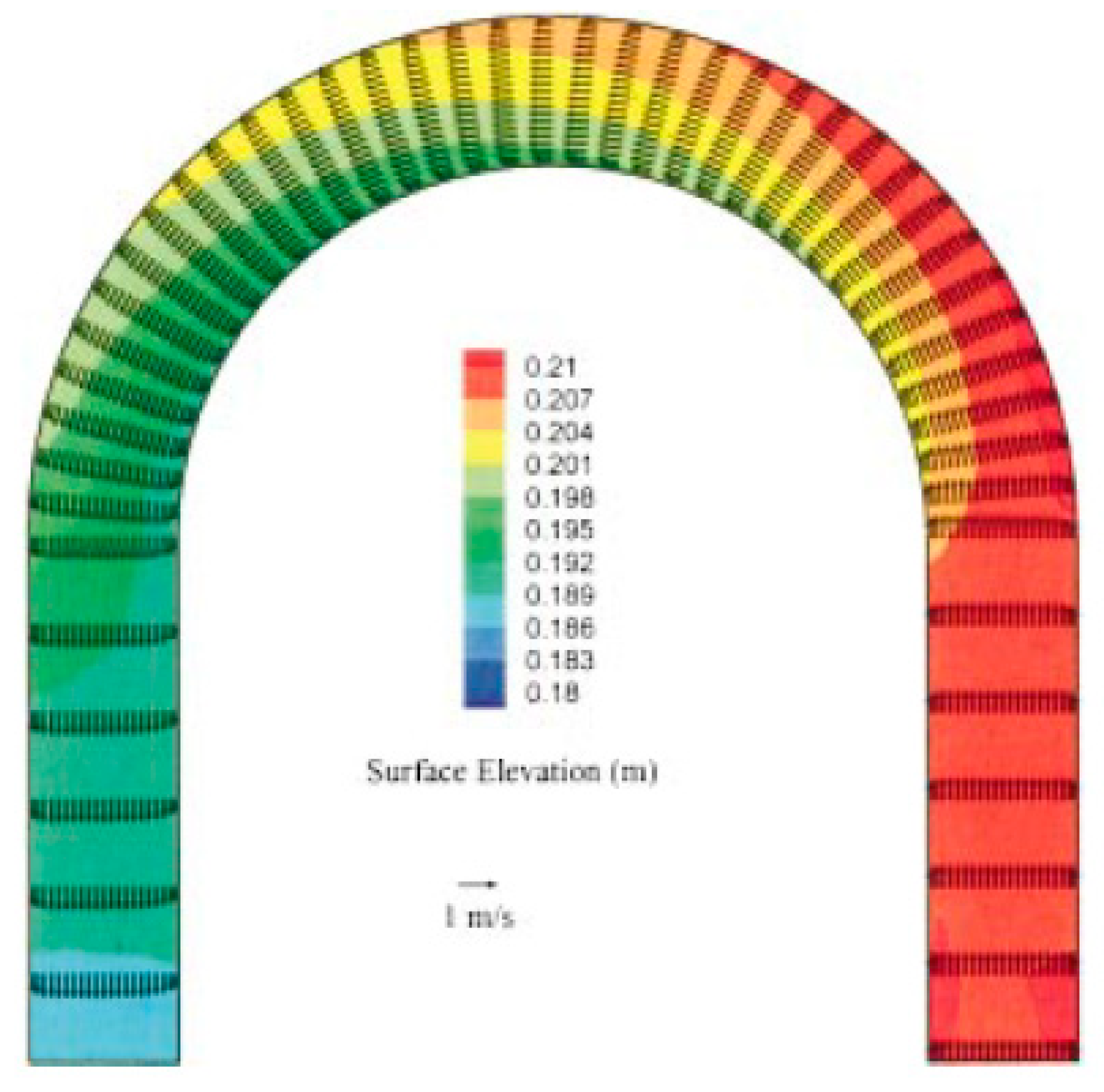
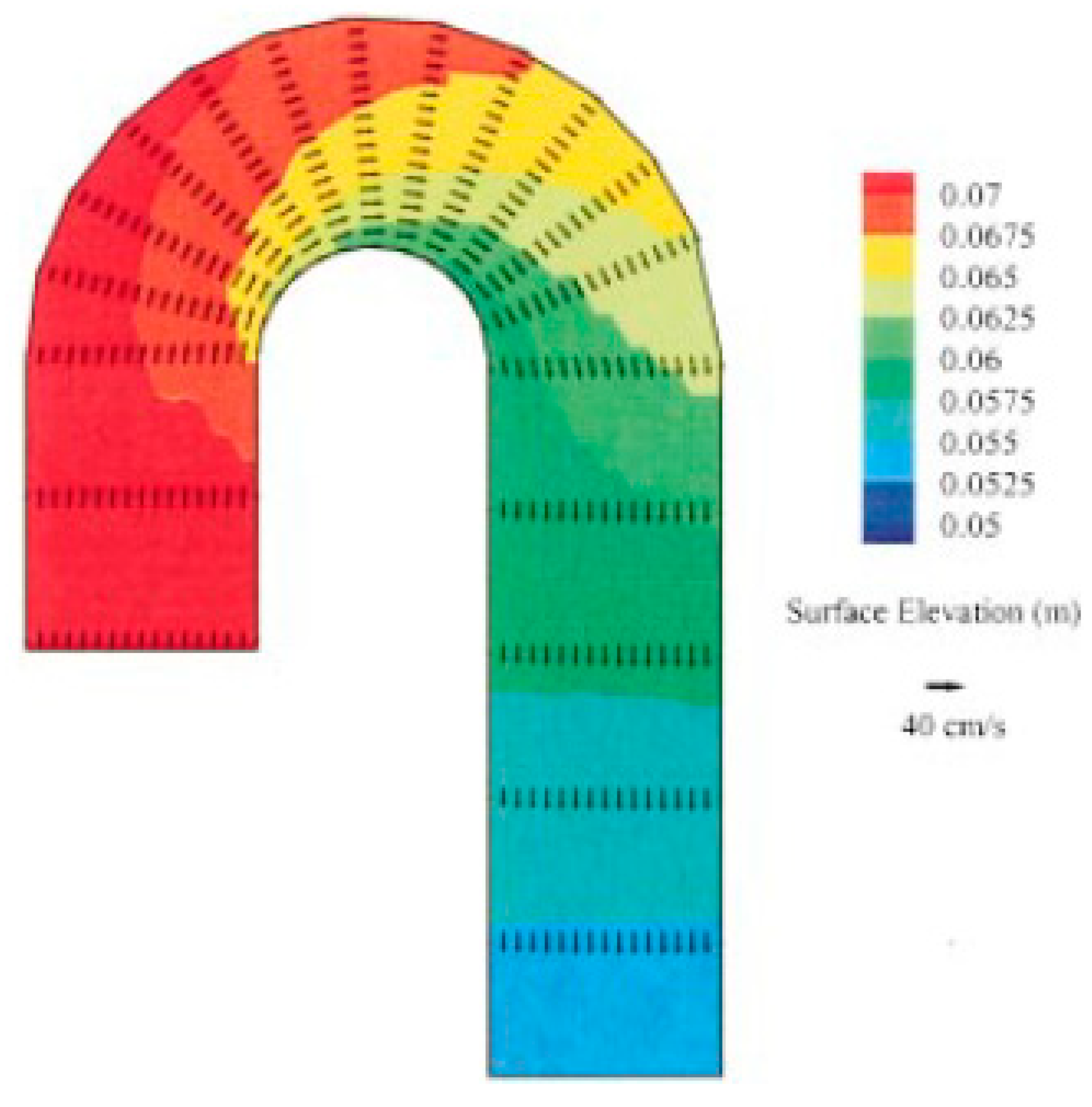

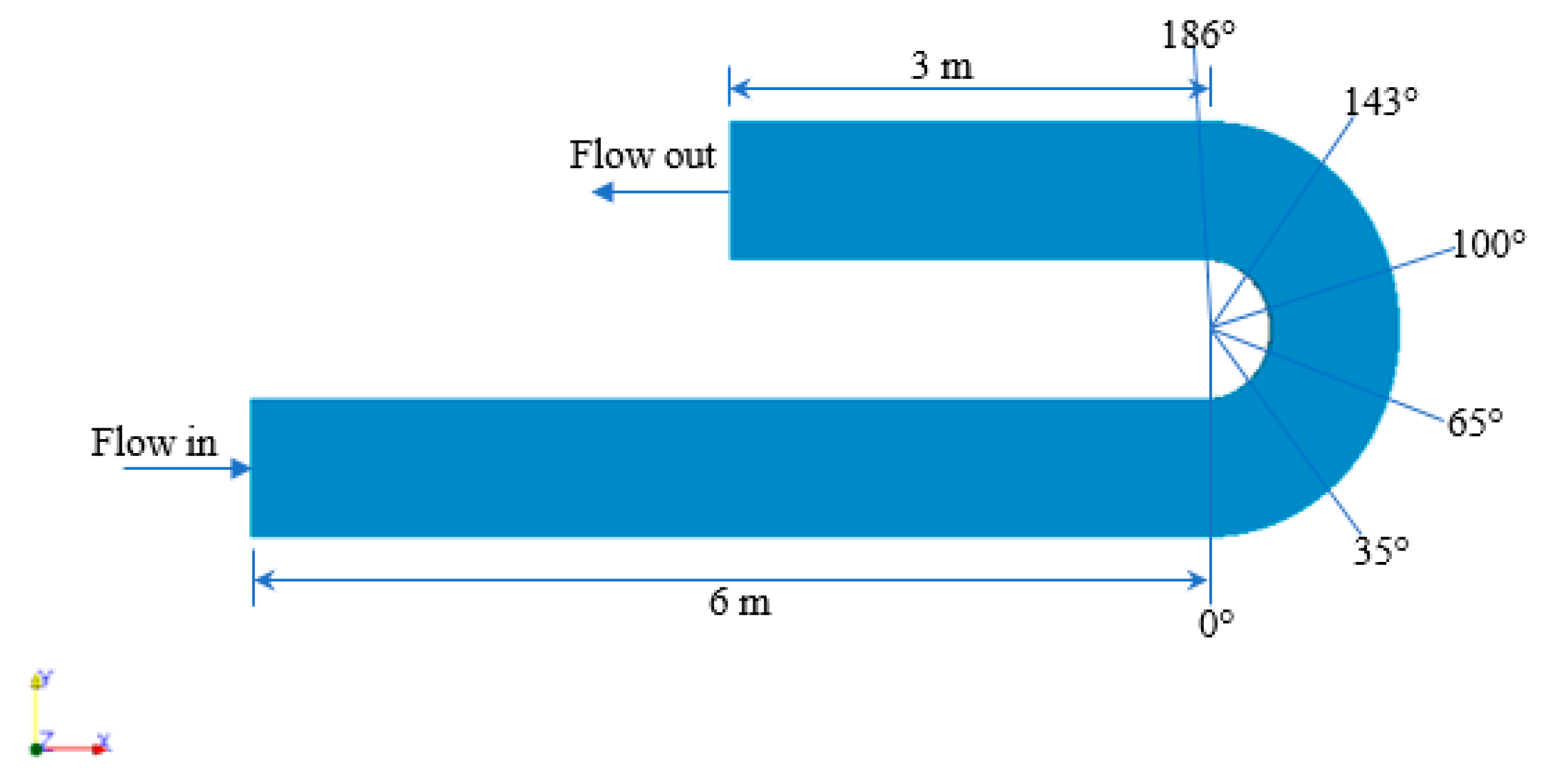

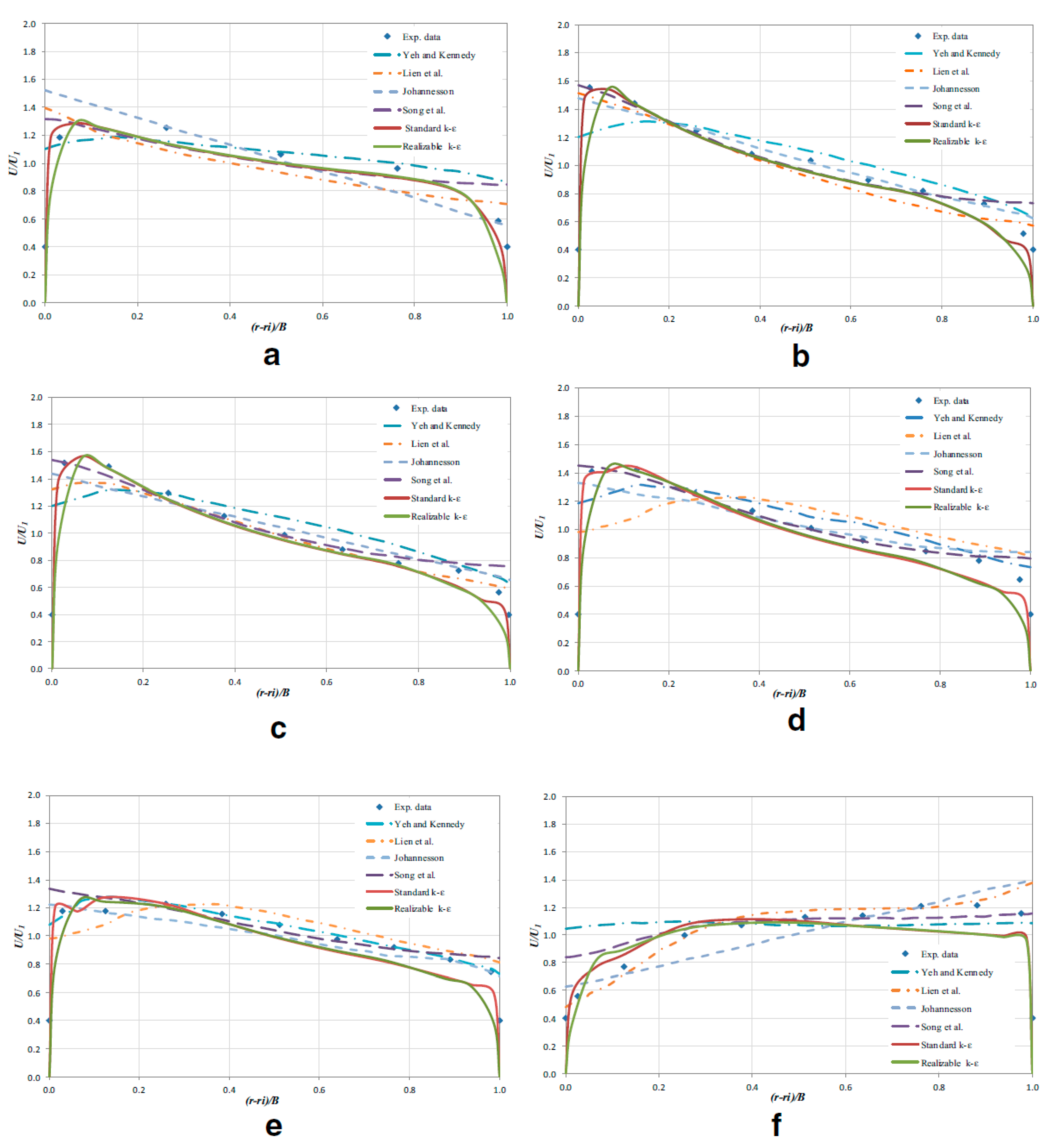

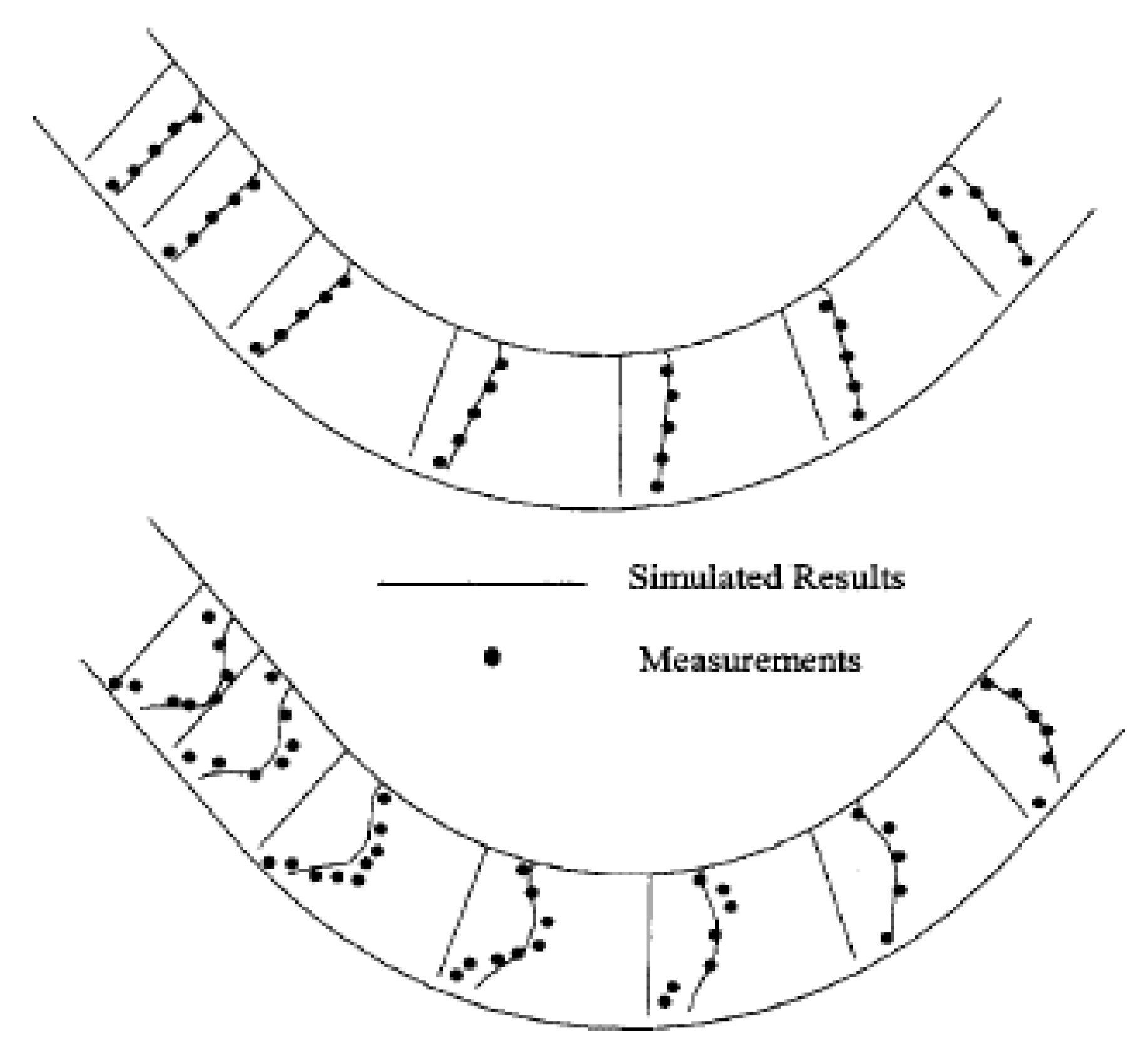
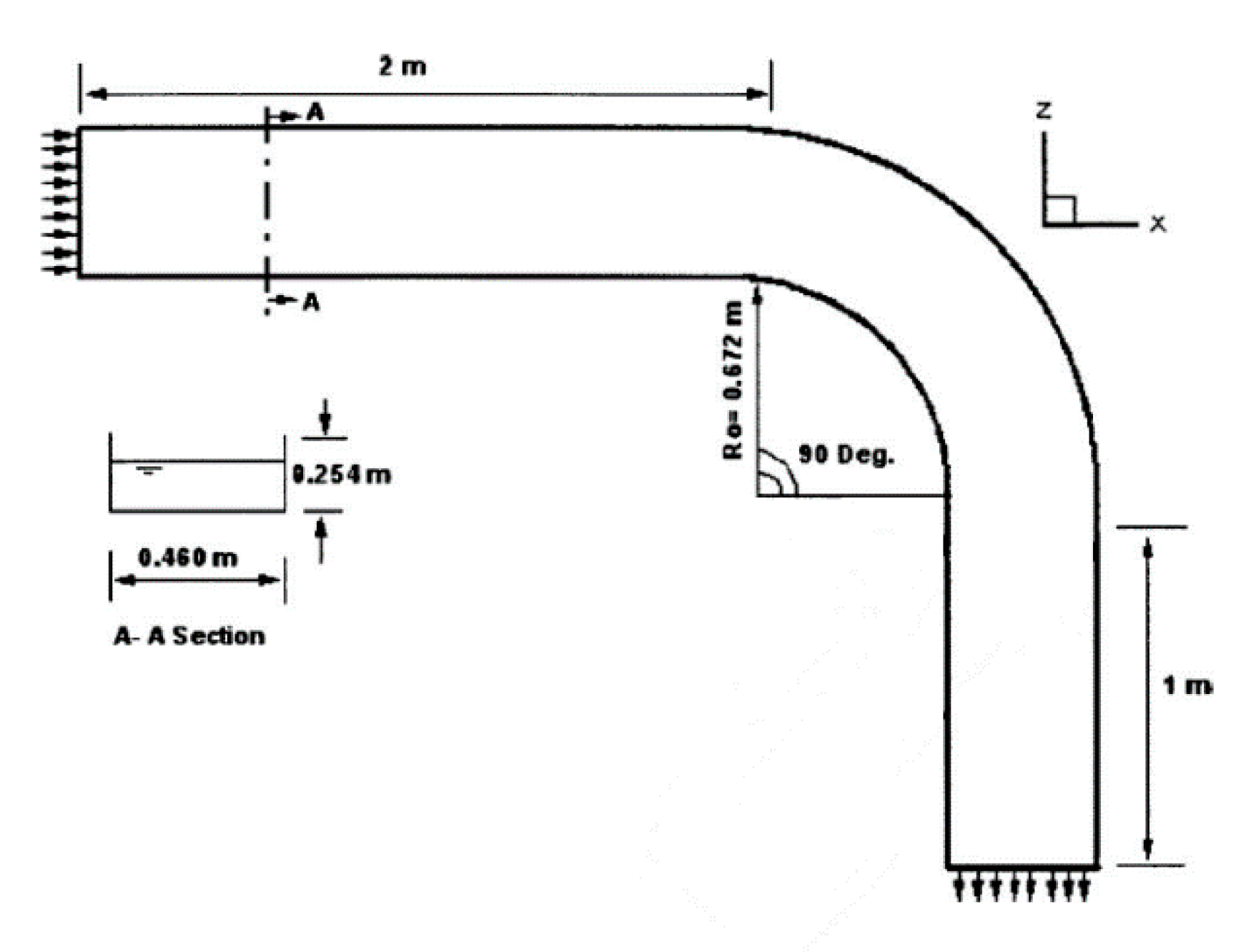
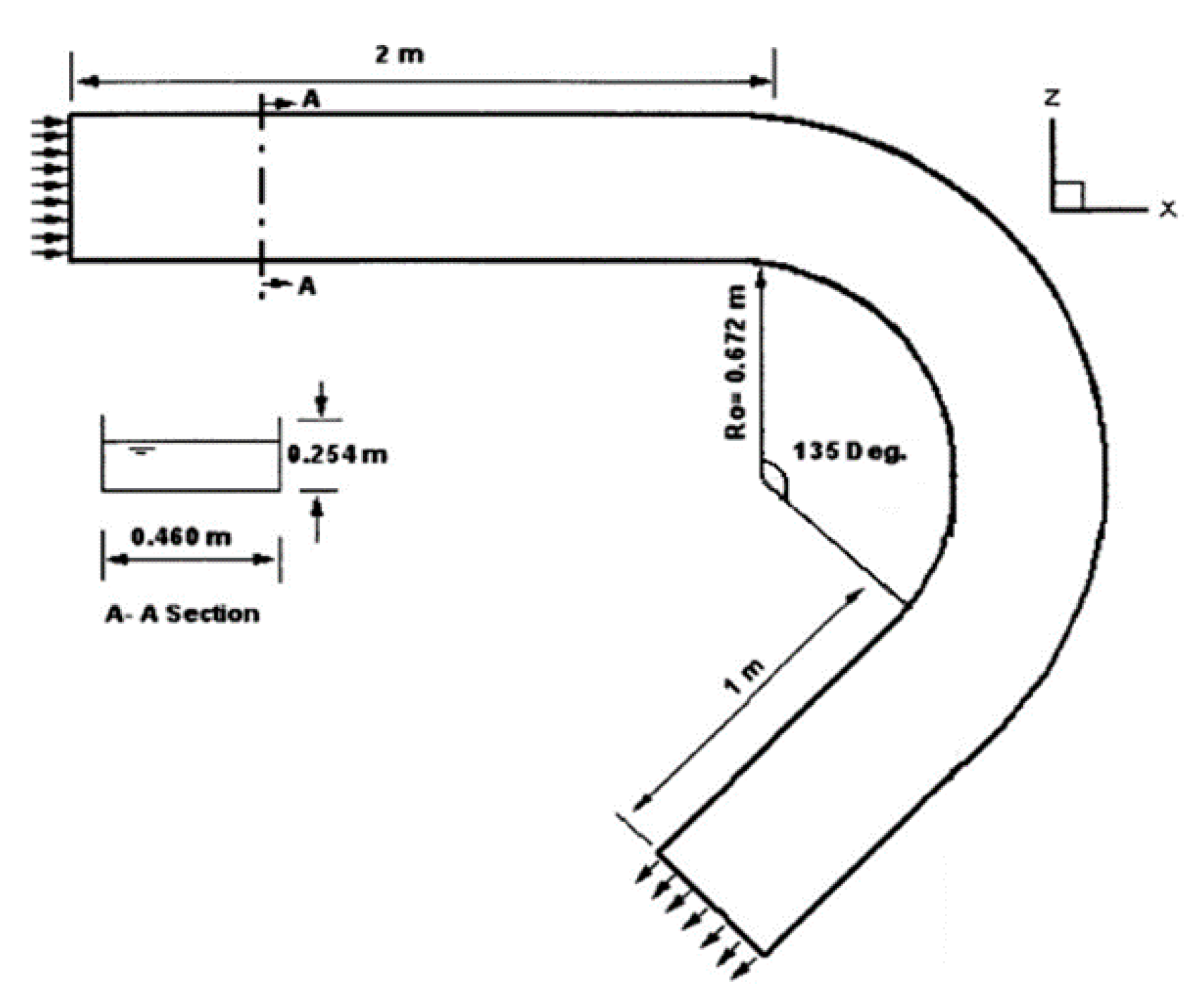

| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| S-shape with two identical 90° reverse bends | Standard k-ε low-Reynolds number k-ω | k-ω model is better than the k-ɛ model in simulating the transverse velocities, which form the secondary flow phenomenon. | (Khosronejad et al., 2007) [20] |
| U-shaped mildly curved channel having a U-shape | Depth-averaged 2D numerical model | Generally, there was an agreement between the simulated and measured surface elevations at the inner, outer bank, and centerline. | (Duan, 2004) [50] |
| U-shaped sharply curved channel in 180° bend | Depth-averaged 2D numerical model | There is good agreement between the simulated and measured results. | (Duan, 2004) [50] |
| A channel in 90° bend | low-Reynolds number k-ω, k-ε (realizable), k-ε (RNG) and LES models | The performance of k-ε (RNG), k-ω and k-ε (realizable) models was good in simulating the flow in the bend, while the LES model has not shown its capability in simulating the flow in channel bends, especially after the curve. | (Ghaneeizad et al., 2010) [51] |
| A channel in 90° bend | k-ε (RNG) | The results of the comparison between the numerical model and the experimental data indicated that there is an acceptable level of agreement. | (Gholami et al., 2014) [52] |
| The flume of two successive 180° bends | RANS including (standard k-ε, standard k-ω), LES | Both RANS simulation and LES model performed well in predicting the primary and an outer bank secondary cell at the peak of the bend. | (Stoesser et al., 2010) [53] |
| The flume of two successive 180° bends | Standard k-ε model, and the non-linear k-ε model | The two models showed the counter-clockwise secondary cell inherited from the first bend, while only the non-linear k-ε model showed the counter-rotating secondary cell of the previous bend, which is coincident with the higher primary velocities. | (Fraga et al., 2012) [54] |
| U-shaped sharply curved channel in 180° bend | Standard k–ε model and the realizable k–ε model | The standard k–ε model performed better than the realizable k-ε model. | (Shaheed et al., 2018) [55] |
| A channel in 135° bend with side slopes | Standard k-ε, (RNG) k-ε, realizable k-ε, k-ω, and (SST) k-ω) | The realizable k-ε model was the best in capturing the outer bank cells among the tested models. | (Yan et al., 2020) [56] |
| A mild 180° bend with a rectangular section and rotating annular flumes | LES and RANS (k-ɛ model) | The outer bank cell was reproduced well by the LES computations, unlike the RANS computations. | (Booij, 2003) [7] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| The flume consists of a single meander of two 90° bends in alternating directions | Depth-averaged 2D numerical model | There is an agreement between the simulated and measured results. | (Duan, 2004) [50] |
| Three different meander situations were used including wide, shallow channels with a smooth bed, and two narrow channels with one having a smooth and the other a rough bed. | Standard k-ɛ turbulence model | The agreement was fairly good in the case of the smooth bed for the vertical profiles of longitudinal velocity, but it was not so good for the case of the rough bed. | (Demuren and Rodi, 1986) [71] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| A channel in 90° bend | Standard k-ε model and the low-Reynolds number k-ω model | The low-Reynolds k-ω turbulence model is better than the standard k-ε model | (Khosronejad et al., 2007) [20] |
| A channel in 135° bend | Standard k-ε model and the low-Reynolds number k-ω model | The low-Reynolds k-ω turbulence model is better than the standard k-ε model | (Khosronejad et al., 2007) [20] |
| A channel in 180° bend | k-ε turbulence model | There is good agreement between the measurements and the predicted results | (Wu et al., 2000) [40] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| A channel in 193° bend | The k-ω Shear Stress Transport (SST) model, or the Spalart–Allmaras (SA) model in low-Reynolds number versions | It could be considered that the accuracy and predictive capacity of the model is satisfactory. | (Zeng et al., 2008) [24] |
| A channel in 193° bend | LES model | There is a good qualitative agreement between the LES model and the experimental findings | (van Balen et al., 2010) [77] |
| Run | Q (l/s) | Vav (m/s) | H (m) | B (m) | Ks (m) | Re |
|---|---|---|---|---|---|---|
| A | 89 | 0.49 | 0.141 | 1.3 | 0.037 | 68,000 |
| B | 89 | 0.49 | 0.141 | 1.3 | 0.006–0.037 | 68,000 |
| C | 89 | 0.49 | 0.141 | 1.3 | 0.006 | 68,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaheed, R.; Mohammadian, A.; Yan, X. A Review of Numerical Simulations of Secondary Flows in River Bends. Water 2021, 13, 884. https://doi.org/10.3390/w13070884
Shaheed R, Mohammadian A, Yan X. A Review of Numerical Simulations of Secondary Flows in River Bends. Water. 2021; 13(7):884. https://doi.org/10.3390/w13070884
Chicago/Turabian StyleShaheed, Rawaa, Abdolmajid Mohammadian, and Xiaohui Yan. 2021. "A Review of Numerical Simulations of Secondary Flows in River Bends" Water 13, no. 7: 884. https://doi.org/10.3390/w13070884






