Numerical Analysis on the Heat Transfer Characteristics of Supercritical Water in Vertically Upward Internally Ribbed Tubes
Abstract
:1. Introduction
2. Numerical Models
2.1. Physical Model
2.2. Transport Equations
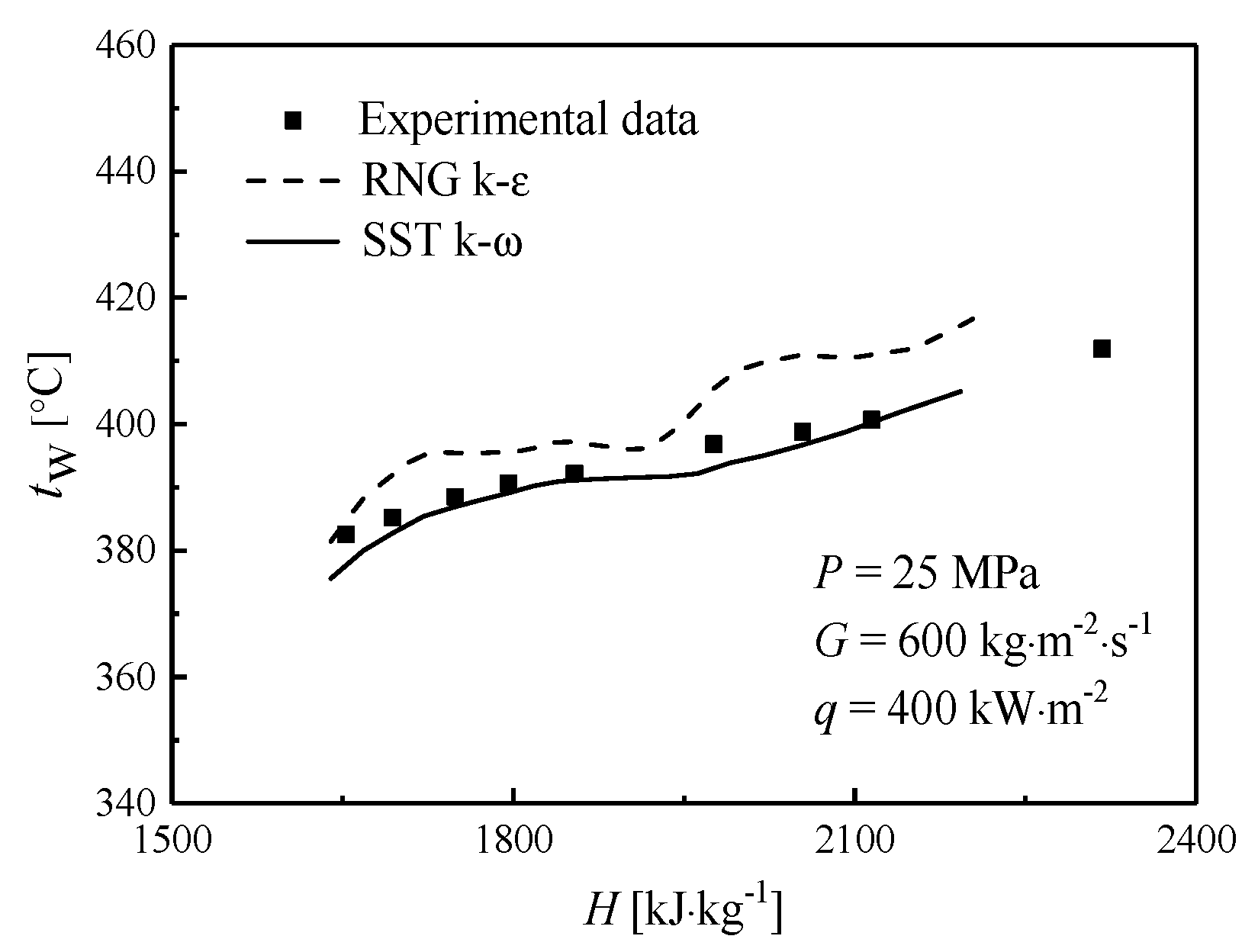
2.3. Numerical Method
2.4. Turbulence Model
3. Results and Discussions
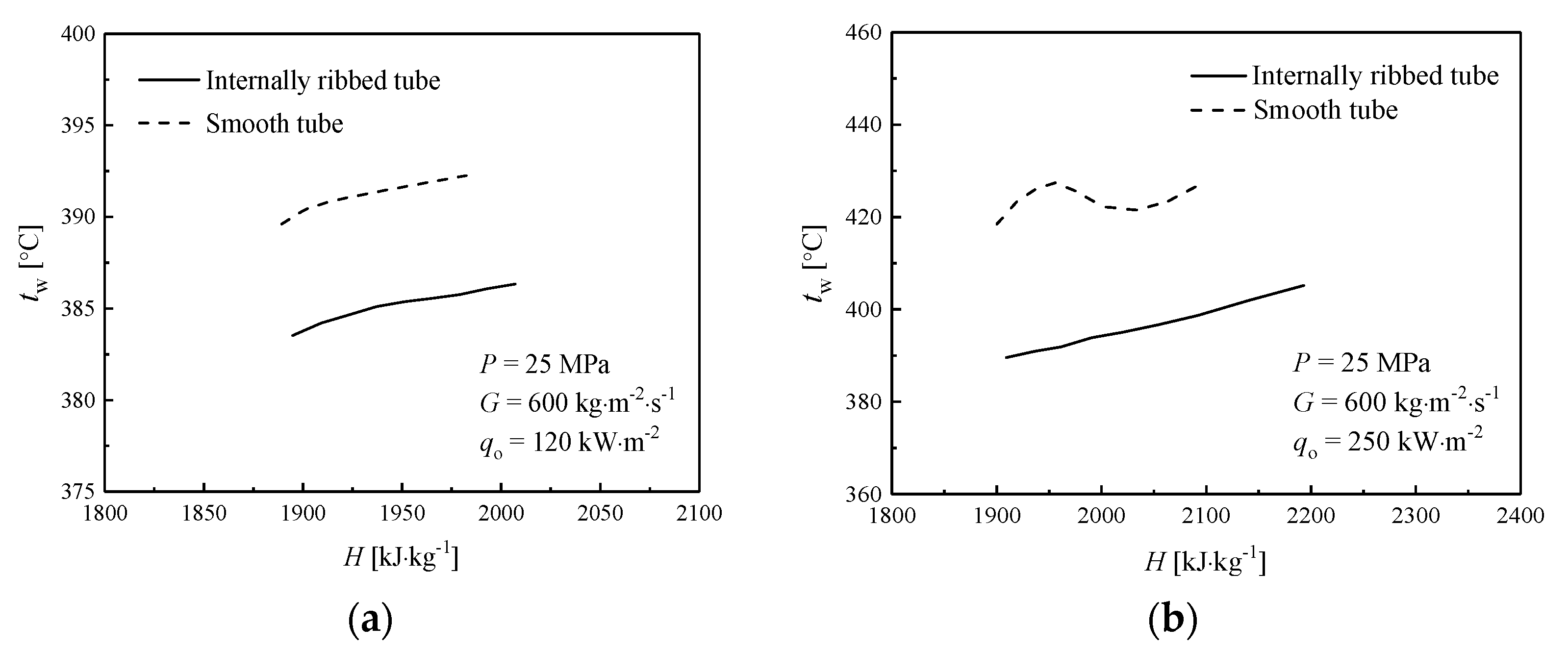
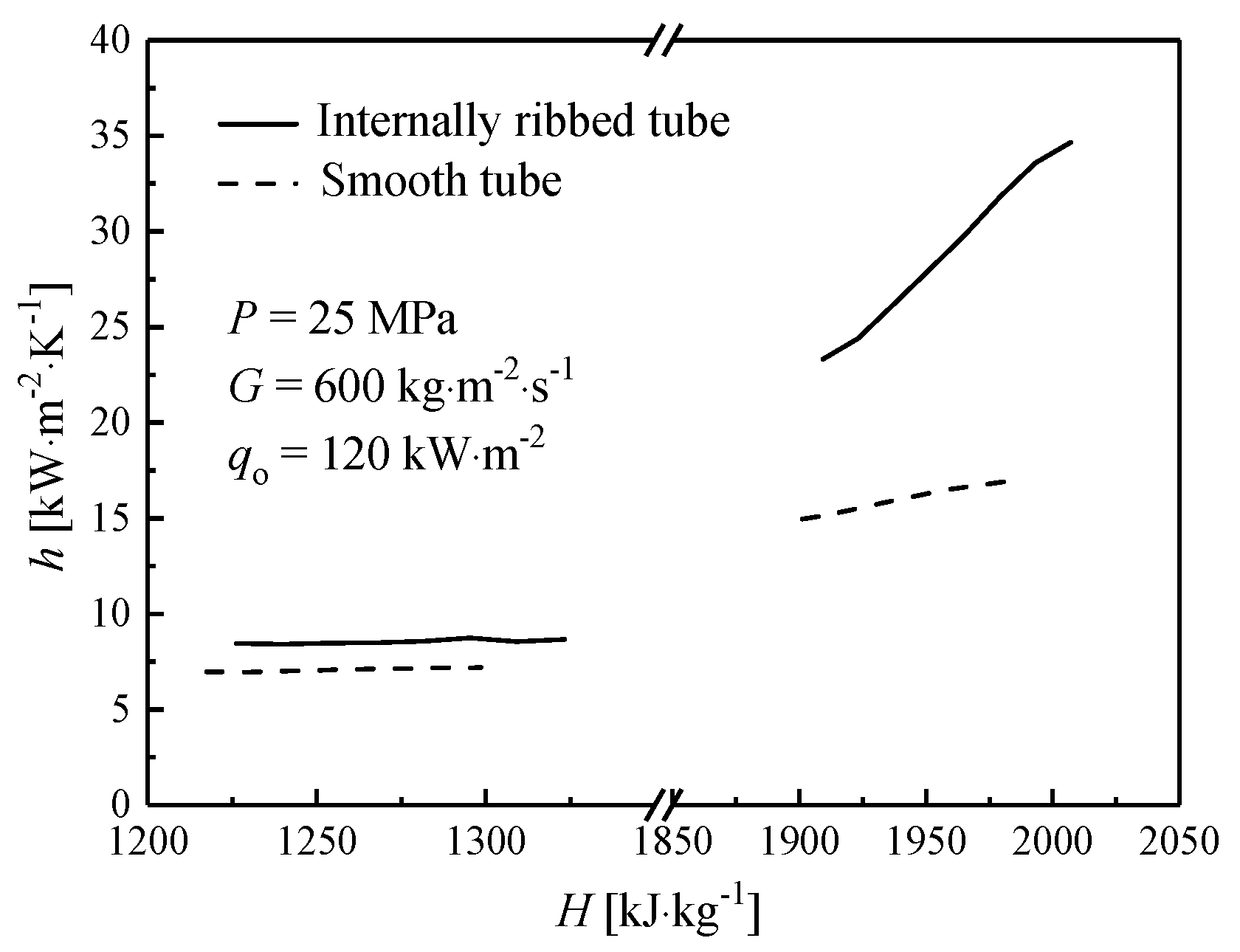
3.1. The Turbulent Heat Transfer of Supercritical Water in IRTs and STs
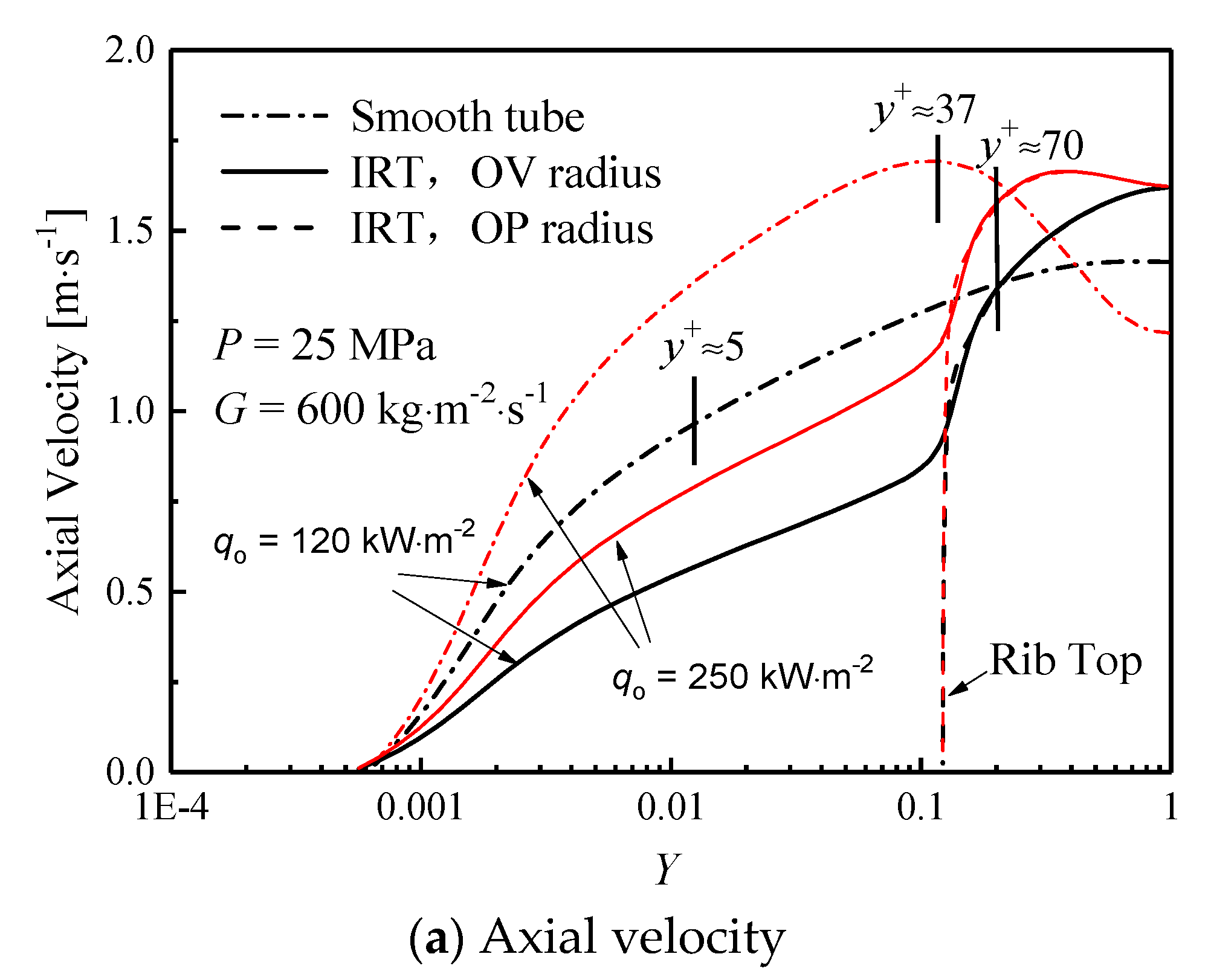
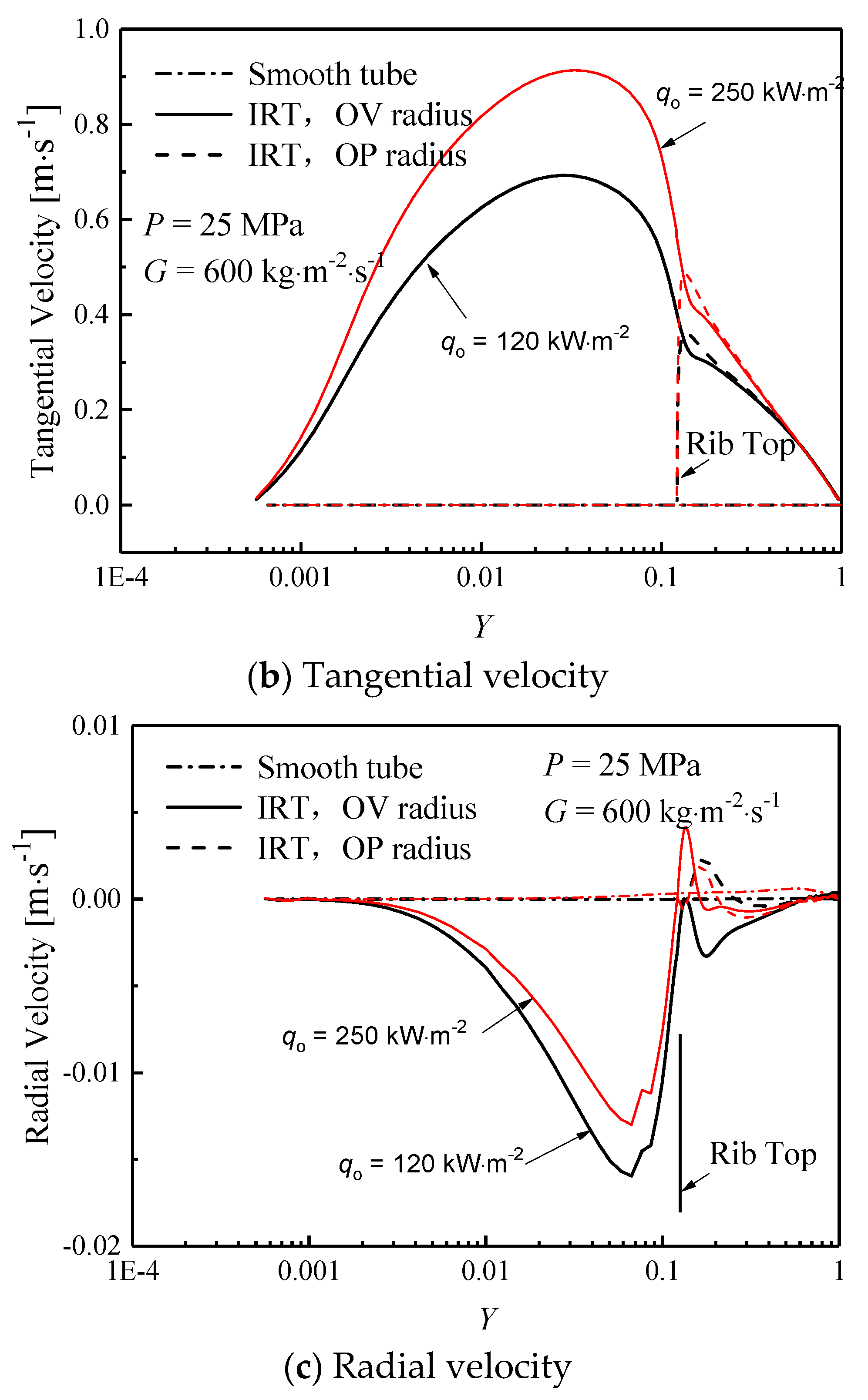
3.2. Distribution of Velocity Components in the Near-Wall Region
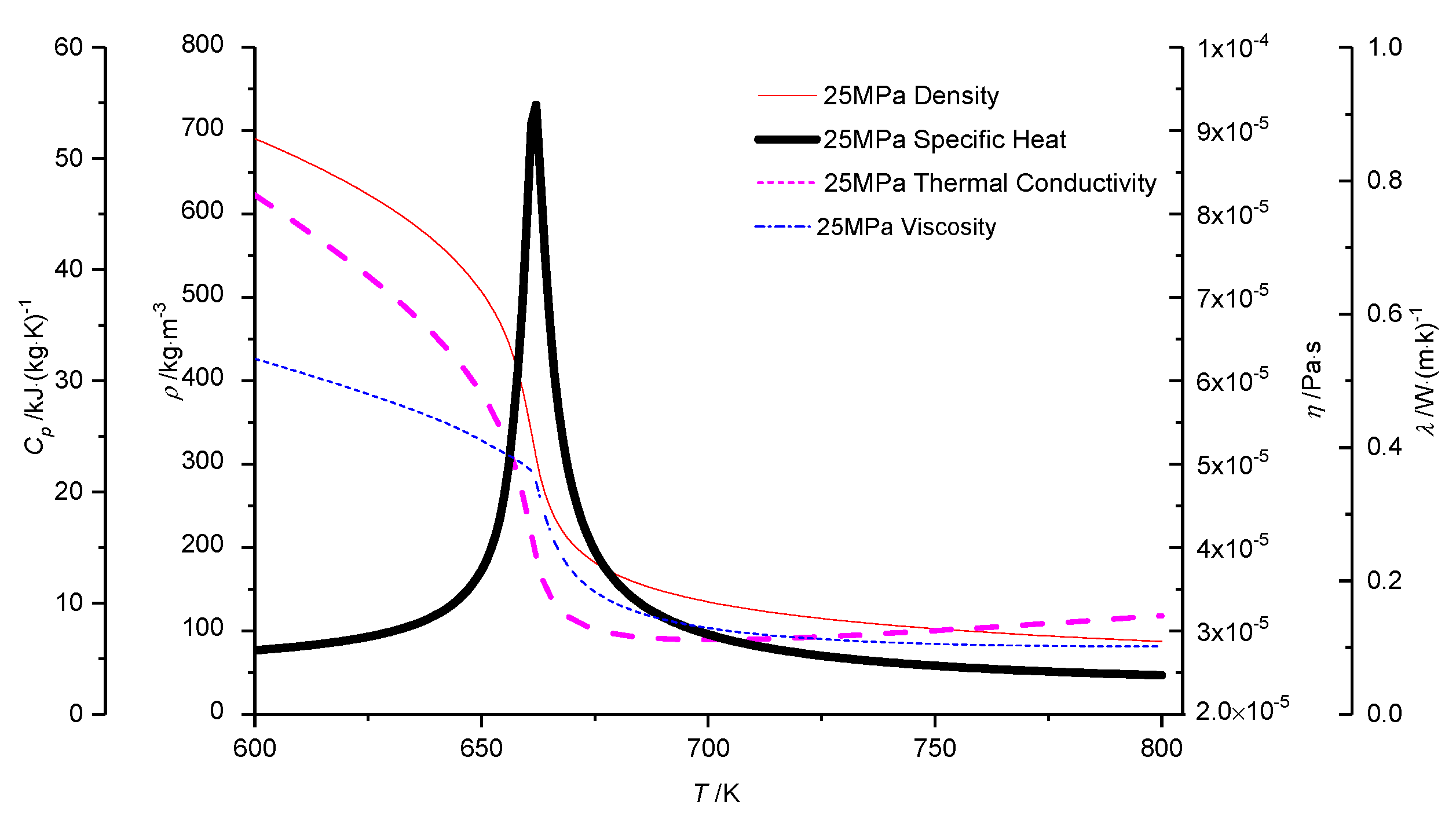
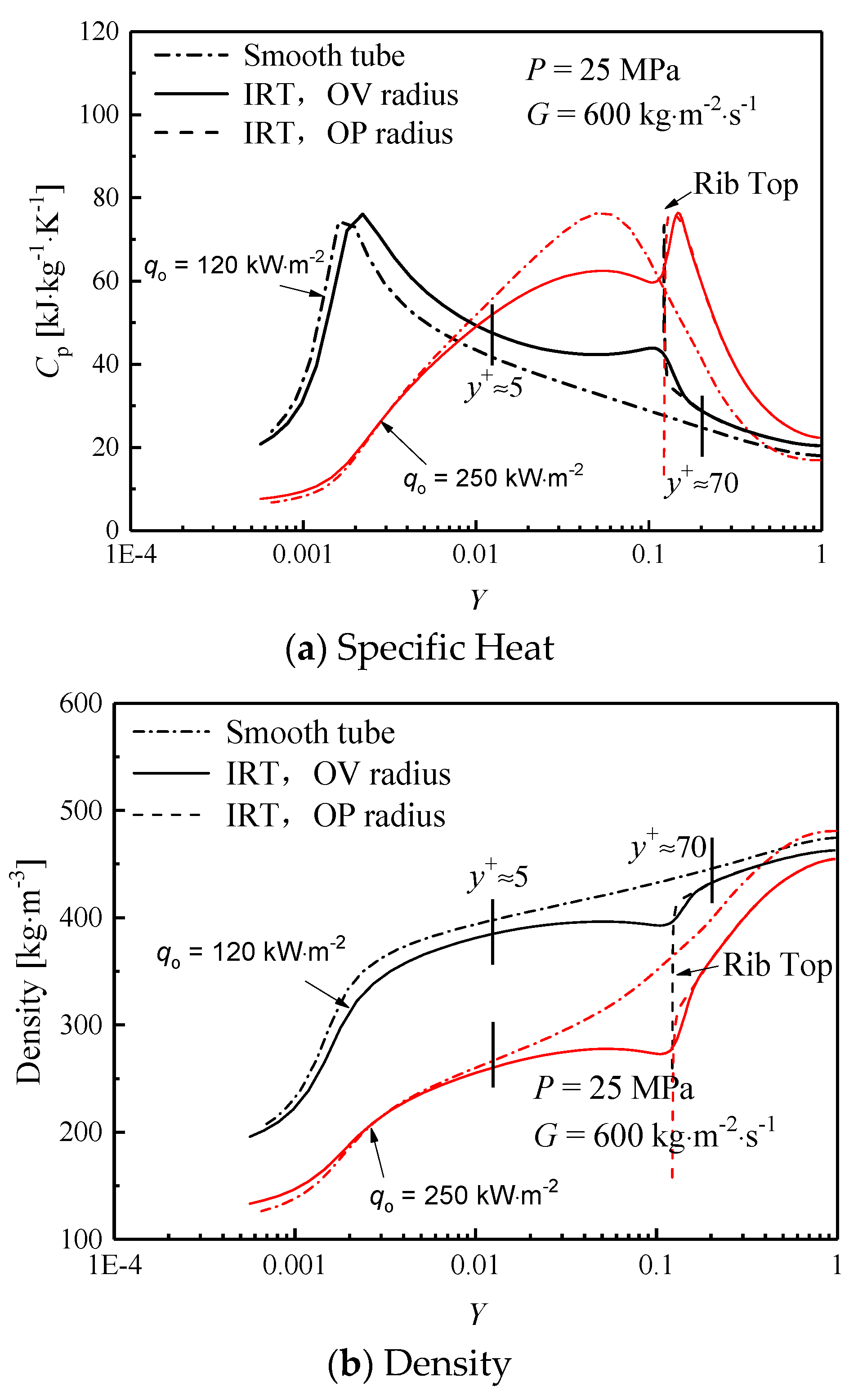
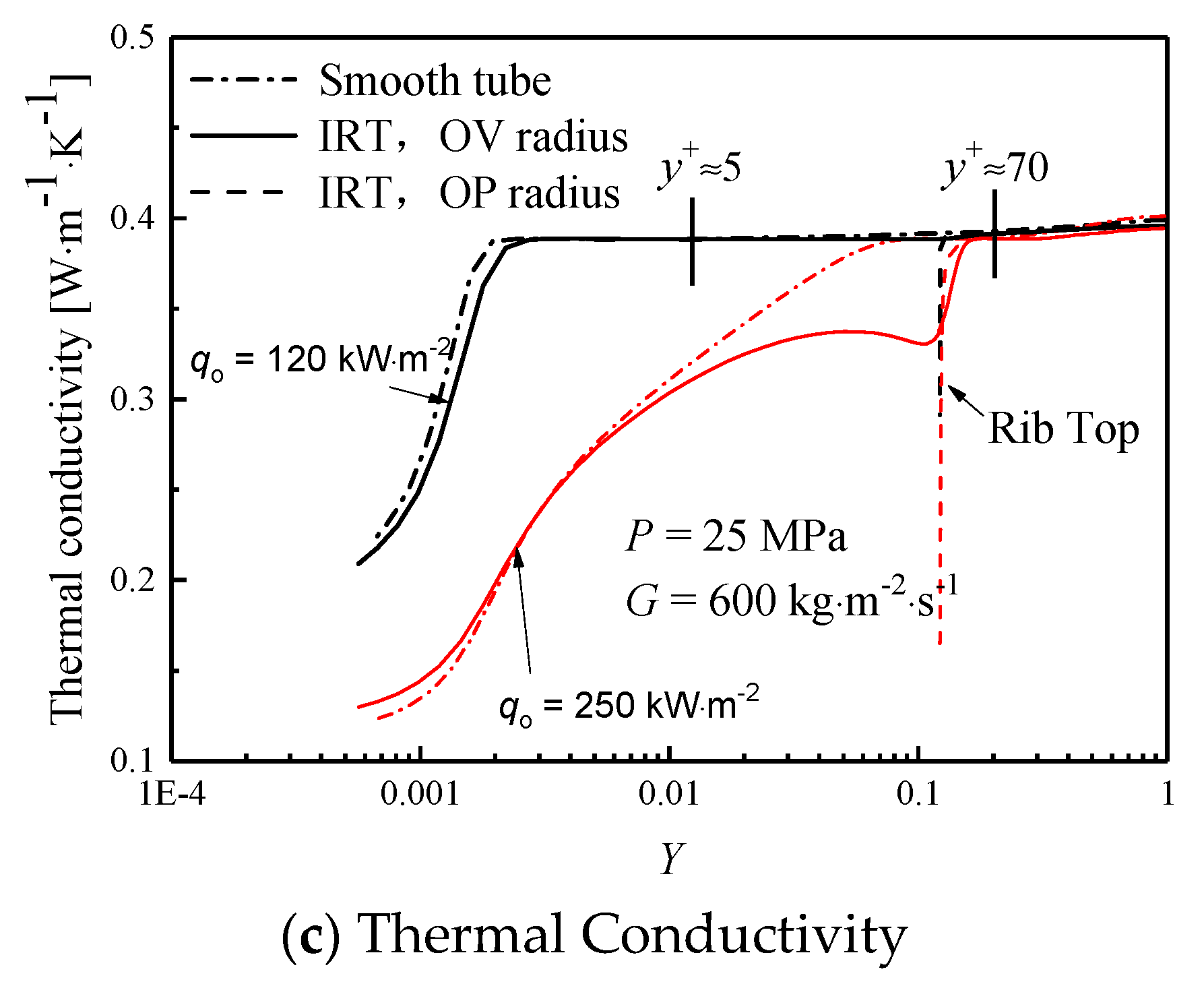
3.3. Distribution of Thermophysical Properties in the Near-Wall Region
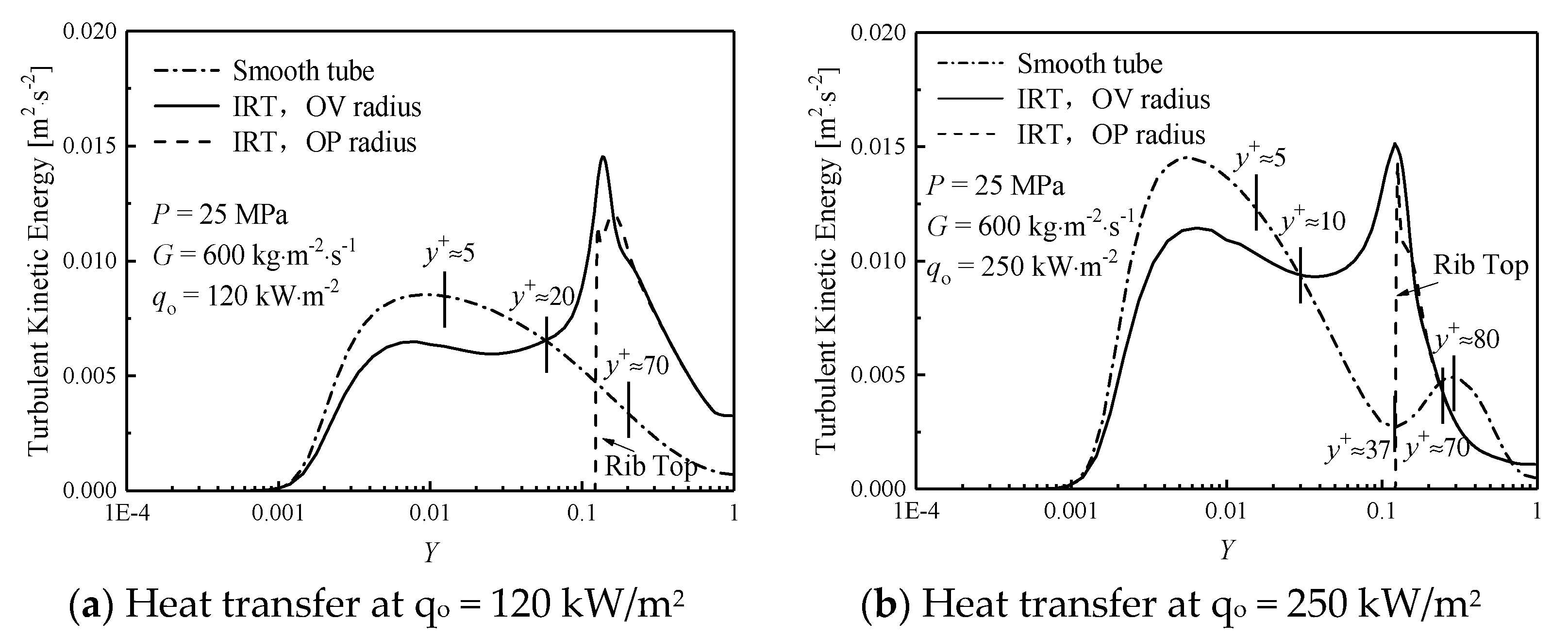
3.4. Distribution of Turbulent Kinetic Energy within Boundary Layer
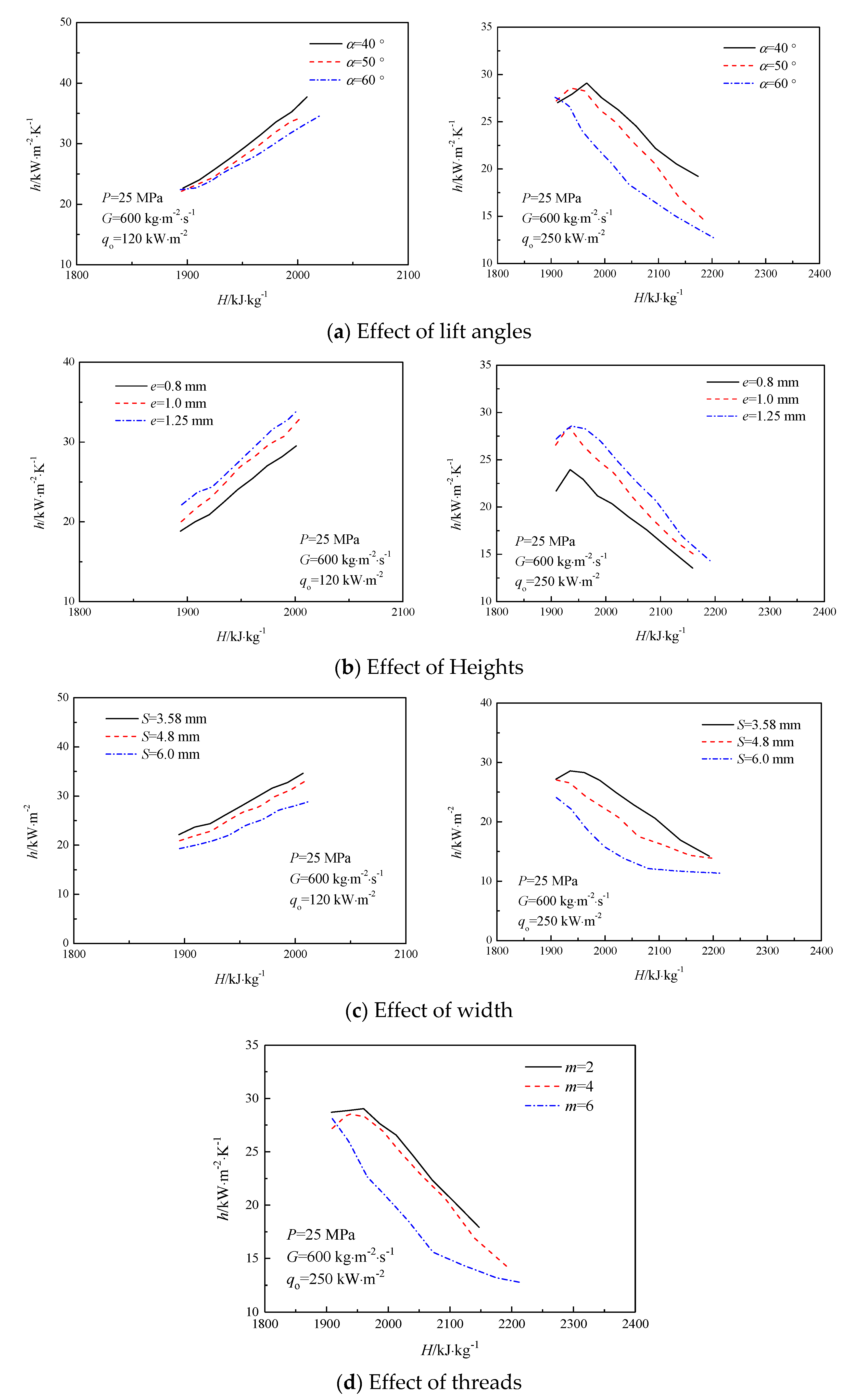
3.5. Effect of Rib Structure on Heat Transfer in IRTs
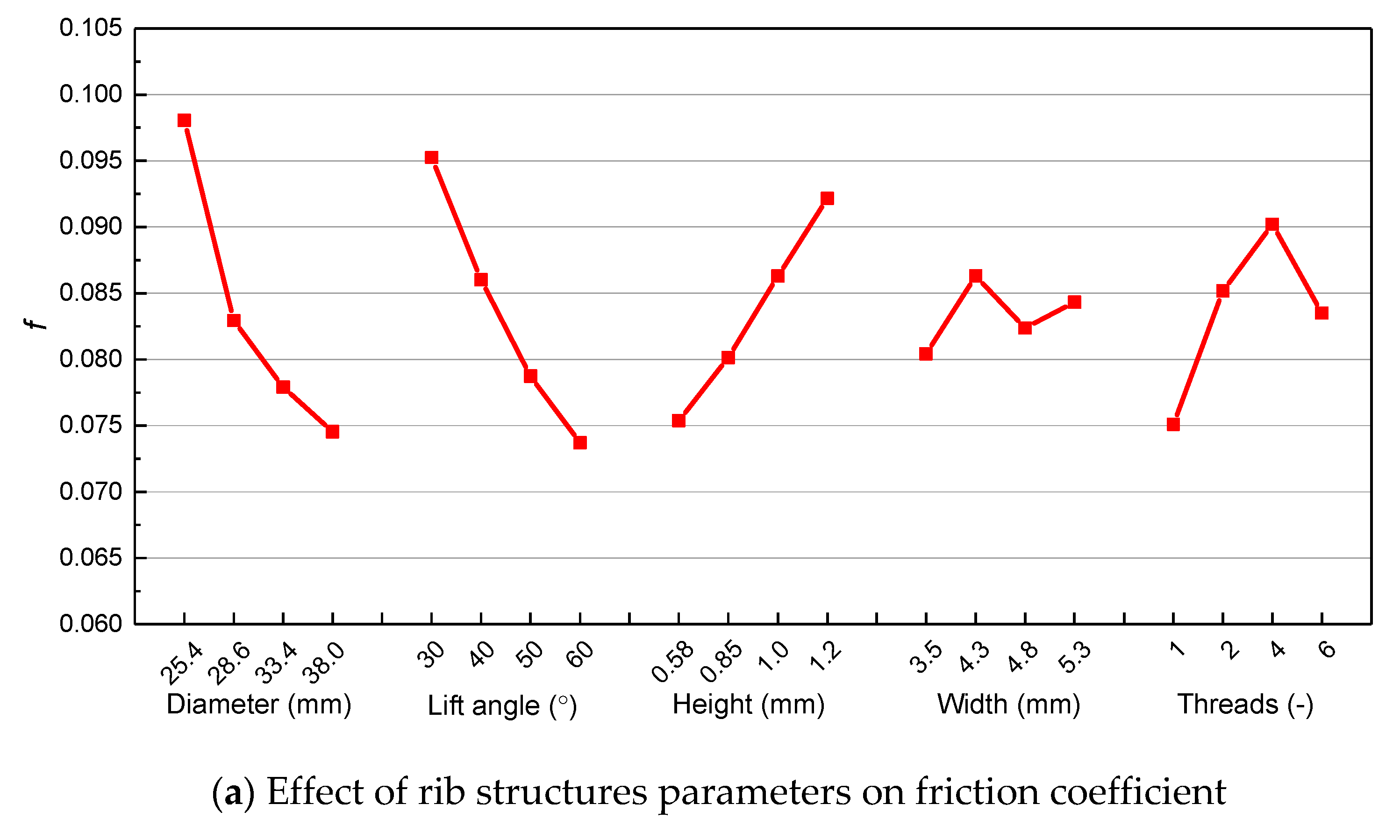
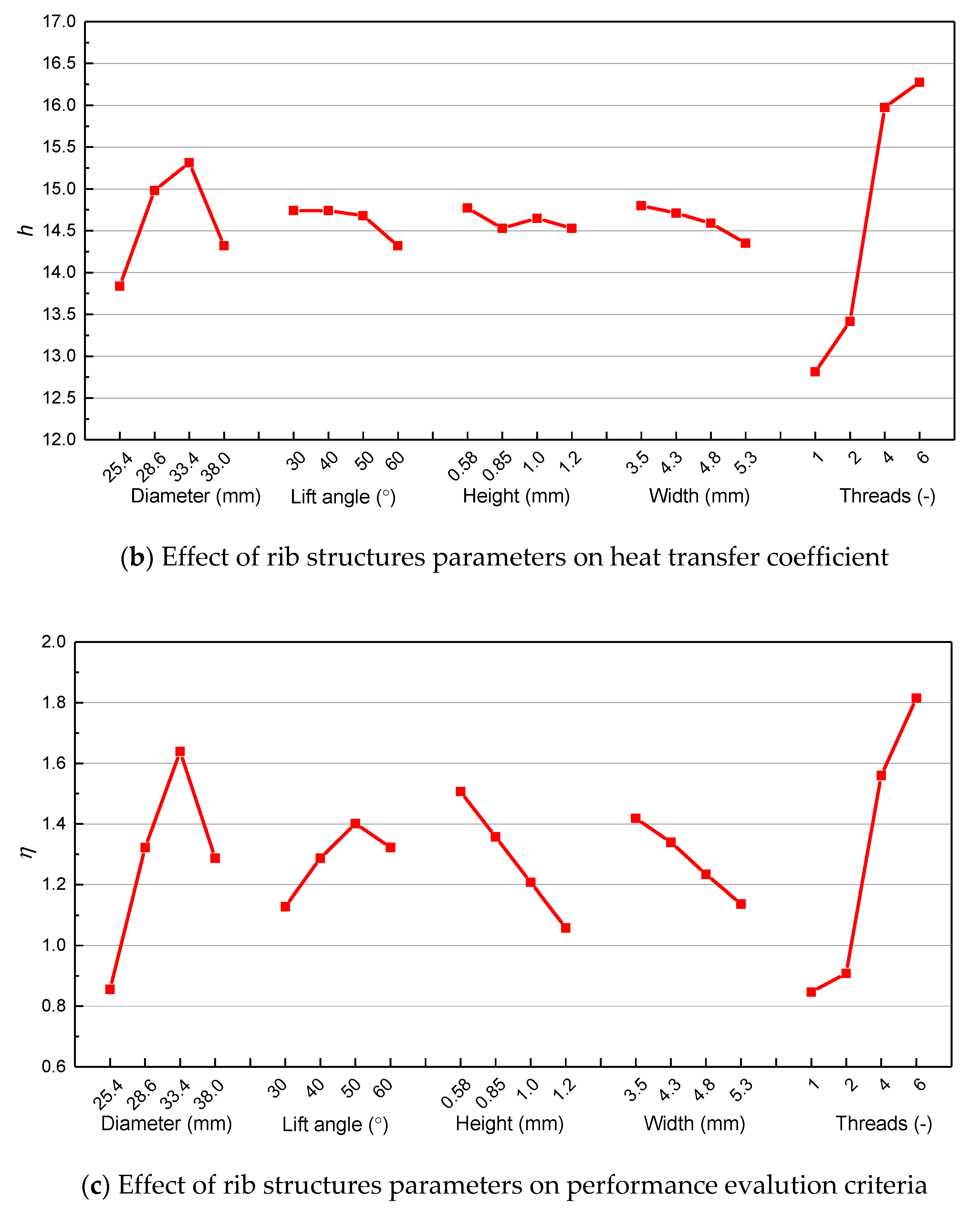
3.6. Optimal Rib Structures in IRTs
4. Conclusions
- IRTs can enhance the heat transfer to supercritical water as a result of the generation of obvious spiral flow, which produces significant circumferential and radial motion in the cross-section. At low heat fluxes, the temperature of IRT is lower than that in ST by 6~7 °C. At high heat fluxes, deteriorated heat transfer occurs in smooth tube, but not happens in IRTs, the maximum temperature difference is 36 °C. The heat transfer enhancement is more pronounced in the pseudocritical region, where the ratio between IRT and ST is about 1.81, but the ratio is only 1.21 in the low enthalpy region.
- In the cross-section, axial velocity suppressed, but tangential and radial velocity increases as a result of disturbance of spiral ribs, the velocity deviation between IRT and ST is about 20–50%. At low heat flux, the specific heat of supercritical water in IRT is about 3% greater than that of ST within the viscous sublayer (y+ < 5), resulting in a better heat transfer capability. However, at high heat flux, the heat transfer deteriorates occurs in ST because the heating wall is covered by a thin layer with high-temperature but low-density, low-thermal conductivity (a 20% reduction) fluids, but for IRTs, heat transfer enhancement occurs, where the ribs make the fluid swirling and promote the heavy fluid migrate to the wall, and simultaneously restrict the light fluid (with low density and poor thermal conductivity) toward the center region.
- In IRTs, a higher turbulent kinetic energy observed in the transition region of the turbulent boundary layer. At high heat flux, the turbulent kinetic energy in ST got a minimum value (=0.0025 m2⋅s−2) in the transition region of the turbulent boundary layer, and the axial velocity at this position reaches the maximum value (=1.7 m⋅s−1), which is a major cause to the occurrence of HTD. Due to the spiral flow induced by the internal rib, IRT can enhance the turbulent kinetic energy in the transition region and avoid the occurrence of the minimum value of the turbulent kinetic energy. IRT avoids (or postpones) the occurrence of HTD in supercritical water at high heat flux.
- With the increase in the lift angle of ribs, the HTC decreases; with the increase in the rib height, the HTC increases. As the circumferential rib width increases, the heat transfer coefficient decreases. When the threads number is relatively small (m ≤ 2), the heat transfer coefficient essentially unchanged, but if the threads number is high (m ≥ 4), the heat transfer coefficient change remarkable.
- An optimal rib structure has been obtained. When the diameter is 33.4 mm, lift angle is 50 degrees, height is 0.58 mm, width is 3.5 mm, threads number is 6, the corresponding overall performance is the best, which can be applied in engineering.
5. Further Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cp | specific heat at constant pressure, J/kg K |
| D | diameter, mm |
| e | height, mm |
| f | frictional coefficient |
| G | mass flux, kg/m2s |
| g | gravitational acceleration, m/s2 |
| H | enthalpy, kJ·kg−1 |
| h | heat transfer coefficient, kW·m−2·K−1 |
| k | turbulent kinetic energy, m2·s−2 |
| L | length, m |
| m | threads |
| Nu | Nusselt number |
| P | Pressure, MPa |
| p | pitch, mm |
| Pr | Prandtl number |
| q | heat flux, kW·m−2 |
| R | radius, mm |
| r | distance, mm |
| t | Time, s |
| Re | Reynolds number |
| S | width, mm |
| Greek Letters | |
| α | lift angel, ° |
| ΔP | pressure drop, kPa |
| β | thermal expansion coefficient, 1/°C |
| δ | thickness, mm |
| ε | turbulent dissipation rate, m2/s3 |
| η | Performance |
| λ | Thermal conductivity, W·m−1·K−1 |
| μ | dynamic viscosity, Pa s |
| μt | turbulent eddy viscosity, Pa s |
| k | turbulent kinetic energy, kg⋅m/s2 |
| ρ | density, kg/m3 |
| ω | Specific dissipation, 1/s |
| Y | Non-Dimensional Distance; (1-r/Ri,max) |
| Subscripts or superscripts | |
| b | bulk |
| i, j, k | i, j, k components |
| pc | pseudocritical |
| t | turbulent |
References
- Swenson, H.S.; Carver, J.R.; Szoeke, G. The effects of nucleate boiling versus film boiling on heat transfer in power boiler tubes. J. Eng. Power 1962, 84, 365–371. [Google Scholar] [CrossRef]
- Ackerman, J.W. Pseudoboiling heat transfer to supercritical pressure water in smooth and ribbed tubes. J. Heat Transf. Trans. ASME 1970, 92, 490–497. [Google Scholar] [CrossRef]
- Watson, G.; Lee, R. Critical heat flux in inclined and vertical smooth and ribbed tubes. In Proceedings of the 5th International Heat Transfer Conference, Tokyo, Japan, 3–7 September 1974; pp. 275–279. [Google Scholar]
- Griem, H. A new procedure for the prediction of forced convection heat transfer at near- and supercritical pressure. Heat Mass Transf. 1996, 31, 301–305. [Google Scholar] [CrossRef]
- Köhler, W.; Kastner, W. Heat transfer and pressure loss in rifled tubes. In Proceedings of the 8th International Heat Transfer Conference, San Francisco, CA, USA, 17–22 August 1986; pp. 2861–2865. [Google Scholar]
- Cheng, L.X.; Chen, T.K. Study of vapor liquid two-phase frictional pressure drop in a vertical heated spirally internally ribbed tube. Chem. Eng. Sci. 2007, 62, 783–792. [Google Scholar] [CrossRef]
- Cheng, L.X.; Chen, T.K. Study of single phase flow heat transfer and friction pressure drop in a spiral internally ribbed tube. Chem. Eng. Technol. 2006, 29, 588–595. [Google Scholar] [CrossRef]
- Cheng, L.X.; Chen, T.K. Enhanced heat transfer characteristics of upward flow boiling of kerosene in a vertical spirally internally ribbed tube. Chem. Eng. Technol. 2006, 29, 1233–1241. [Google Scholar] [CrossRef]
- Cheng, L.X.; Xia, G. Experimental study of CHF in a vertical spirally internally ribbed tube under the condition of high pressures. Int. J. Therm. Sci. 2002, 41, 396–400. [Google Scholar] [CrossRef]
- Cheng, L.X.; Chen, T.K. Flow boiling heat transfer in a vertical spirally internally ribbed tube. Heat Mass Transf. 2001, 37, 229–236. [Google Scholar] [CrossRef]
- Wang, J.G.; Li, H.X.; Guo, B.; Yu, S.Q. Heat transfer of water at supercritical pressures in vertically-upward internally-ribbed tubes. J. Eng. Thermophys. 2009, 30, 423–427. [Google Scholar]
- Wang, J.; Li, H.; Yu, S.; Chen, T. Investigation on the characteristics and mechanisms of unusual heat transfer of supercritical pressure water in vertically-upward tubes. Int. J. Heat Mass Transf. 2011, 54, 1950–1958. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Yu, S.; Chen, T. Comparison of the heat transfer characteristics of supercritical pressure water to that of subcritical pressure water in vertically-upward tubes. Int. J. Multiph. Flow 2011, 37, 769–776. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Guo, B.; Yu, S.; Zhang, Y.; Chen, T. Investigation of forced convection heat transfer of supercritical pressure water in a vertically upward internally ribbed tube. Nucl. Eng. Des. 2009, 239, 1956–1964. [Google Scholar] [CrossRef]
- Pan, J.; Yang, D.; Dong, Z.; Zhu, T.; Bi, Q. Experimental investigation on heat transfer characteristics of low mass flux rifled tube with upward flow. Int. J. Heat Mass Transf. 2011, 54, 2952–2961. [Google Scholar] [CrossRef]
- Yang, D.; Pan, J.; Zhou, C.Q.; Zhu, X.; Bi, Q.; Chen, T. Experimental investigation on heat transfer and frictional characteristics of vertical upward rifled tube in supercritical CFB boiler. Exp. Therm. Fluid Sci. 2011, 35, 291–300. [Google Scholar] [CrossRef]
- Taklifi, A.; Hanafizadeh, P.; Behabadi, M.A.; Aliabadi, A. Experimental investigation on heat transfer and pressure drop of supercritical water flows in an inclined rifled tube. J. Supercrit. Fluids 2016, 107, 209–218. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, D.; Mao, K.; Long, J.; Wang, S. Heat transfer characteristics of water flowing in a vertical upward rifled tube with low mass flux. Exp. Therm. Fluid Sci. 2016, 70, 341–353. [Google Scholar] [CrossRef]
- Zhao, Z.X.; Wang, X.Y.; Che, D.F. Numerical study on heat transfer and resistance characteristics of supercritical water inside internally-ribbed tube. Heat Mass Transf. 2014, 50, 559–572. [Google Scholar] [CrossRef]
- Xu, W.; Wang, W.; Du, X.; Zhu, X. Numerical investigation on the secondary flow of supercritical water in a four-head internally ribbed tube. Appl. Therm. Eng. 2017, 120, 708–718. [Google Scholar] [CrossRef]
- Nishikawa, K.; Fujii, T.; Yoshida, S. Flow boiling crisis in grooved boiler-tubes. In Proceedings of the 5th International Heat Transfer Conference, Tokyo, Japan, 3–7 September 1974; pp. 270–274. [Google Scholar]
- Kim, C.H.; Bang, I.C.; Chang, S.H. Critical heat flux performance for flow boiling of R-134a in vertical uniformly heated smooth tube and rifled tubes. Int. J. Heat Mass Transf. 2005, 48, 2868–2877. [Google Scholar] [CrossRef]
- Hawig, A.A. CFD Study on the Heat Transfer in Vertical Rifled Tube with Different Helical Angles; Tun Hussein Onn University of Malaysia: Johor, Malaysia, 2010. [Google Scholar]
- Koshad, R.A.S. CFD Simulation of Heat Transfer in Vertical Ribbed Tube; Tun Hussein Onn University of Malaysia: Johor, Malaysia, 2011. [Google Scholar]
- Lam, S.P. Analysis of the Flow Characteristic Inside a Heated and Unheated Horizontal Rifled Tube; Tun Hussein Onn University of Malaysia: Johor, Malaysia, 2012. [Google Scholar]
- Li, Z.; Lu, J.; Tang, G.; Liu, Q.; Wu, Y. Effects of rib geometries and property variations on heat transfer to supercritical water in internally ribbed tubes. Appl. Therm. Eng. 2015, 78, 303–314. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Y.; Tang, G.; Zhang, D.; Lu, J. Comparison between heat transfer to supercritical water in a smooth tube and in an internally ribbed tube. Int. J. Heat Mass Transf. 2015, 84, 529–541. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Roelofs, F. CFD Analyses of Heat Transfer to Supercritical Water Flowing Vertically Upward in a Tube; Jahrestagung Kerntechnik: Nuremberg, Germany, 2004. [Google Scholar]
- Liu, L.; Xiao, Z.; Yan, X.; Zeng, X.; Huang, Y. Heat transfer deterioration to supercritical water in circular tube and annular channel. Nucl. Eng. Des. 2013, 255, 97–104. [Google Scholar] [CrossRef]
- Mirkhani, N.; Taklifi, A.; Hanafizadeh, P.; Aliabadi, A. Numerical Study on the Hydraulic and Thermal Performance of Internally Ribbed Tubes in Supercritical Pressure and Subcritical Two-phase Flows. J. Supercrit. Fluids 2018, 136, 21–28. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties—REFPROP; U.S. Department of Commerce Technology Administration: Gaithersburg, MD, USA, 2013.
- Zhang, Q.; Li, H.; Zhang, W.; Li, L.; Lei, X. Experimental study on heat transfer to the supercritical water upward flow in a vertical tube with internal helical ribs. Int. J. Heat Mass Transf. 2015, 89, 1044–1053. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Moya-Rico, J.D.; Molina, A.E.; Almendros-Ibáñez, J.A. Numerical and experimental study of the heat transfer process in a double pipe heat exchanger with inner corrugated tubes. Int. J. Therm. Sci. 2020, 158, 106526. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Lee, K.S.; Li, B. Optimal design of a double pipe heat exchanger based on the outward helically corrugated tube. Int. J. Heat Mass Transf. 2019, 135, 706–716. [Google Scholar] [CrossRef]
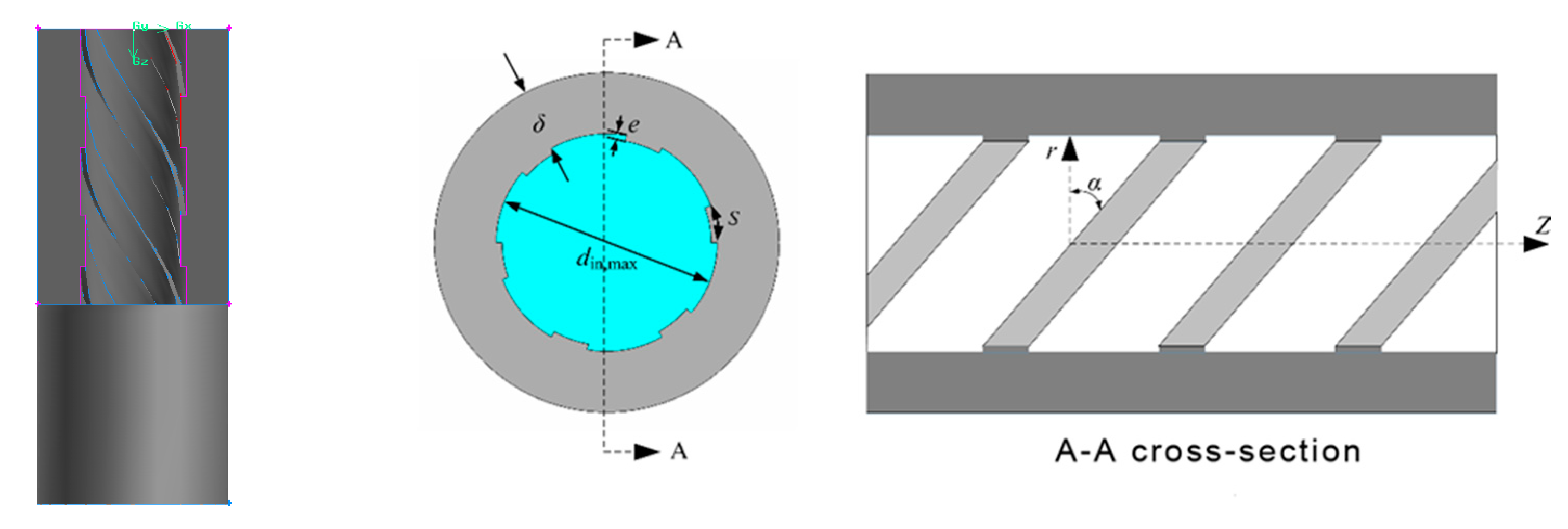
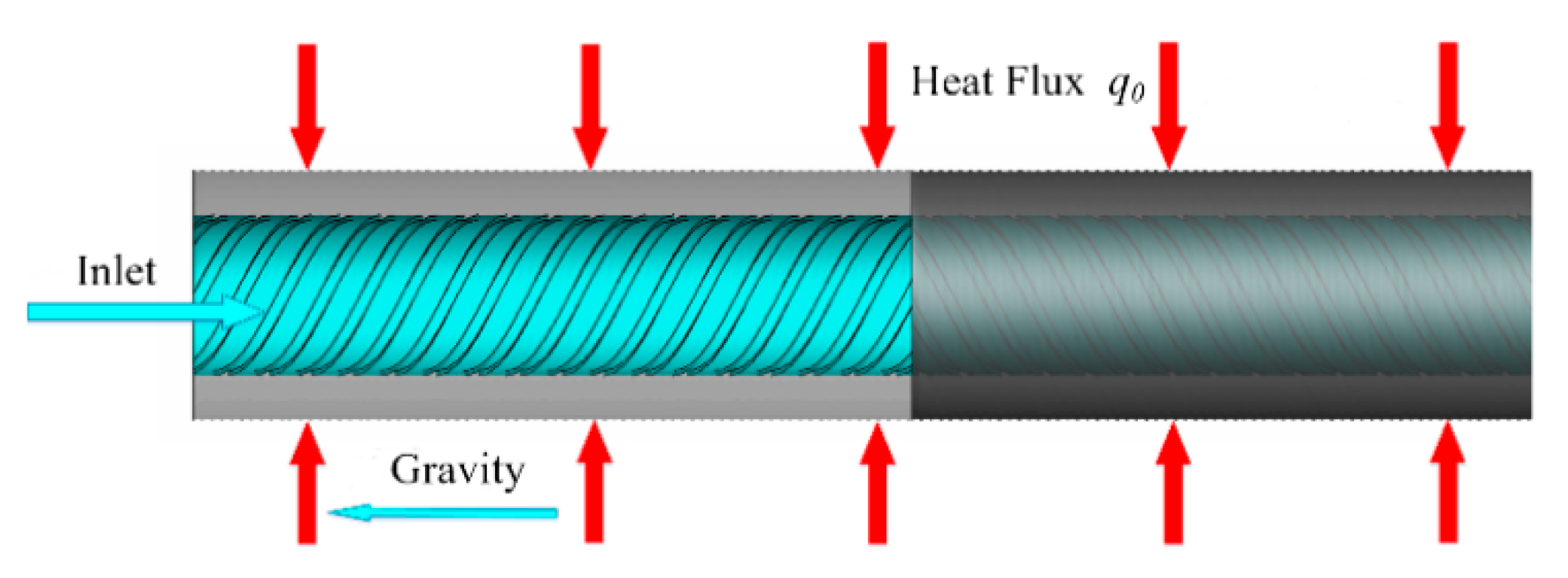

| Author | m | p/mm | e/mm | S/mm | α/° | D/mm |
|---|---|---|---|---|---|---|
| Ackerman [2] | 6 | 21.84 | — | — | — | 18.03 |
| Griem [4] | — | — | — | — | — | 24 |
| Cheng [6,7] | 4 | 10.04 | 0.58 | 4.61 | 49.3 | 11.69 |
| Cheng [8,9,10] | 4 | 21 | 0.81 | 4.8 | 61.15 | 15.24 |
| Wang [11,12,13] | 4 | 21.55 | 0.85 | 4.8 | 60 | 15.24 |
| Wang [14] | 6 | 11.61 | 1.20 | 4.8 | 50 | 17.63 |
| Pan [15] | 4 | 19 | 0.92 | 4.62 | 50.5 | 19.4 |
| Yang [16] | 4 | 22.7 | 0.85 | 5.3 | 54 | 20.3 |
| Taklifi [17] | 6 | 10.8 | 1.2 | 4.77 | 45 | 19 |
| Shen [18] | 4 | 18.1 | 1.24 | 6.2 | 50 | 19.1 |
| Structural Parameters | Fixed Rib Structure | Variable Rib Structures |
|---|---|---|
| Outside diameter (d0) | 33.40 mm | 25.4, 28.6, 33.4, 38 mm |
| Maximum inside diameter (di,max) | 20.62 mm | 20.62 mm |
| Length (L) | 2510 mm | 2510 mm |
| Number of threads (m) | 6 | 1, 2, 4, 6 |
| Rib width (S) | 3.58 mm | 3.5, 4.3, 4.8, 6.0 mm |
| Rib height (e) | 0.8 mm | 0.58, 0.85, 1.0, 1.2 mm |
| Rib lift angle (α) | 30° | 30, 40, 50, 60° |
| Pitch (p) | 12.87 mm | 12.87 mm |
| Lead (m × p) | 77.2 mm | 51.48, 77.22, 102.96 mm |
| Criteria | Diameter (mm) | Lift Angle (°) | Height (mm) | Width (mm) | Threads (-) |
|---|---|---|---|---|---|
| h | 33.4 | 30 | 0.58 | 3.5 | 6 |
| f | 38 | 60 | 0.58 | 3.5 | 1 |
| η | 33.4 | 50 | 0.58 | 3.5 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Guo, Z.; Peng, R.; Li, H. Numerical Analysis on the Heat Transfer Characteristics of Supercritical Water in Vertically Upward Internally Ribbed Tubes. Water 2021, 13, 621. https://doi.org/10.3390/w13050621
Lei X, Guo Z, Peng R, Li H. Numerical Analysis on the Heat Transfer Characteristics of Supercritical Water in Vertically Upward Internally Ribbed Tubes. Water. 2021; 13(5):621. https://doi.org/10.3390/w13050621
Chicago/Turabian StyleLei, Xianliang, Ziman Guo, Ruifeng Peng, and Huixiong Li. 2021. "Numerical Analysis on the Heat Transfer Characteristics of Supercritical Water in Vertically Upward Internally Ribbed Tubes" Water 13, no. 5: 621. https://doi.org/10.3390/w13050621





