Forecasting Summer Rainfall and Streamflow over the Yangtze River Valley Using Western Pacific Subtropical High Feature
Abstract
:1. Introduction
2. Dataset Description
2.1. Rainfall Data and Streamflow
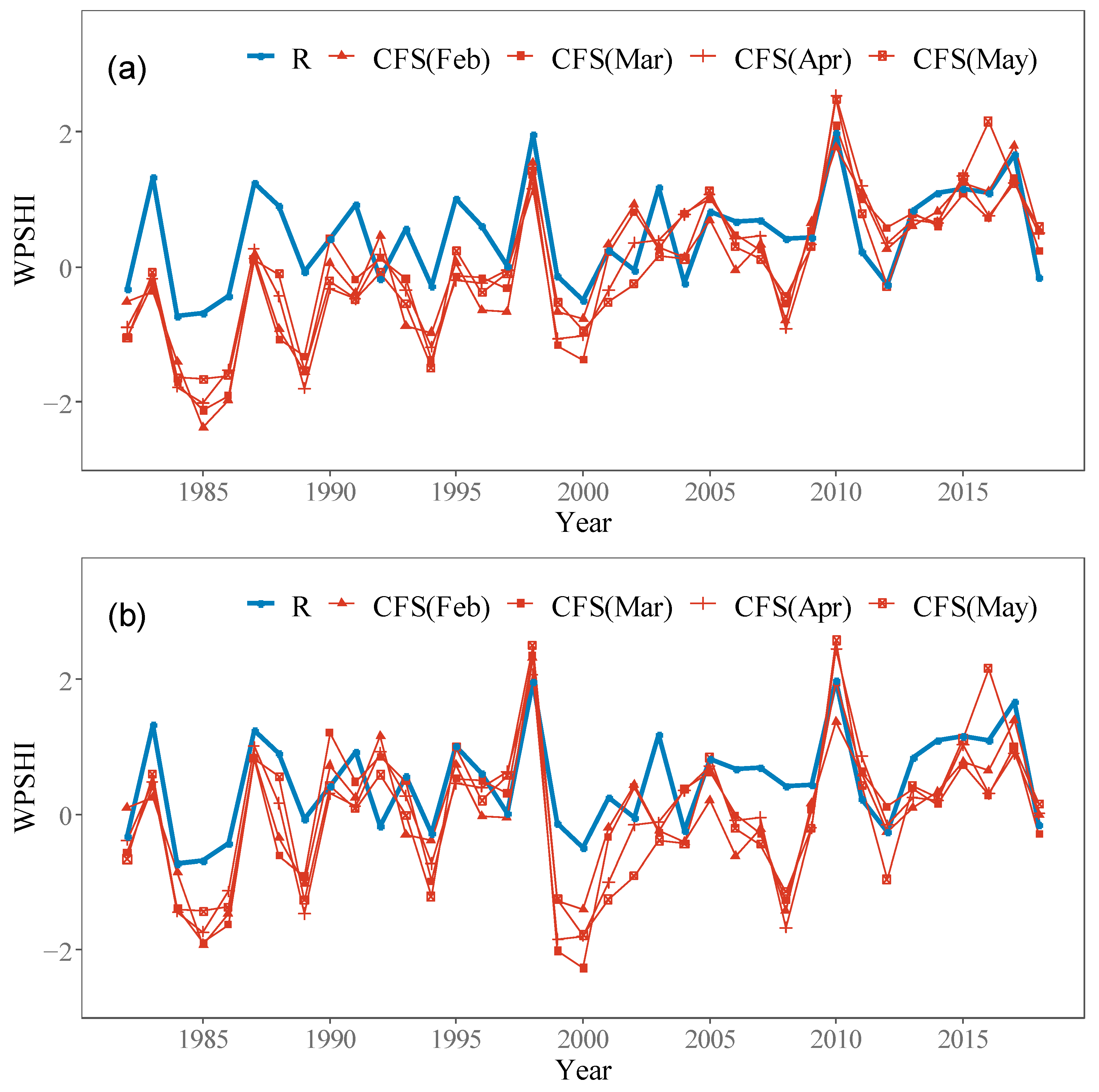
2.2. Reanalysis Dataset and Hindcasts of CFSv2
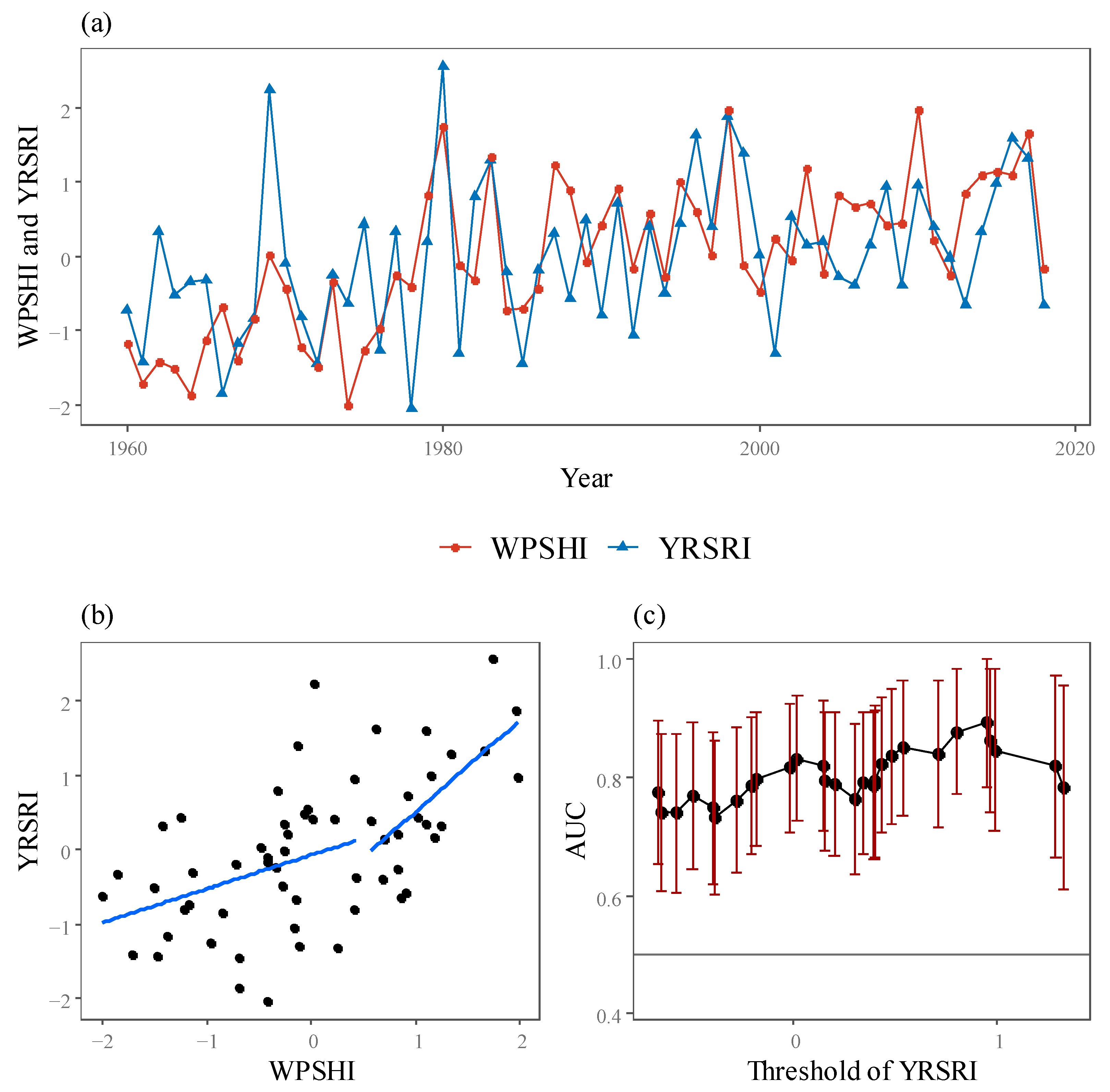
2.3. Definition of WPSHI
3. ROC Analysis
4. Modelling Methodology
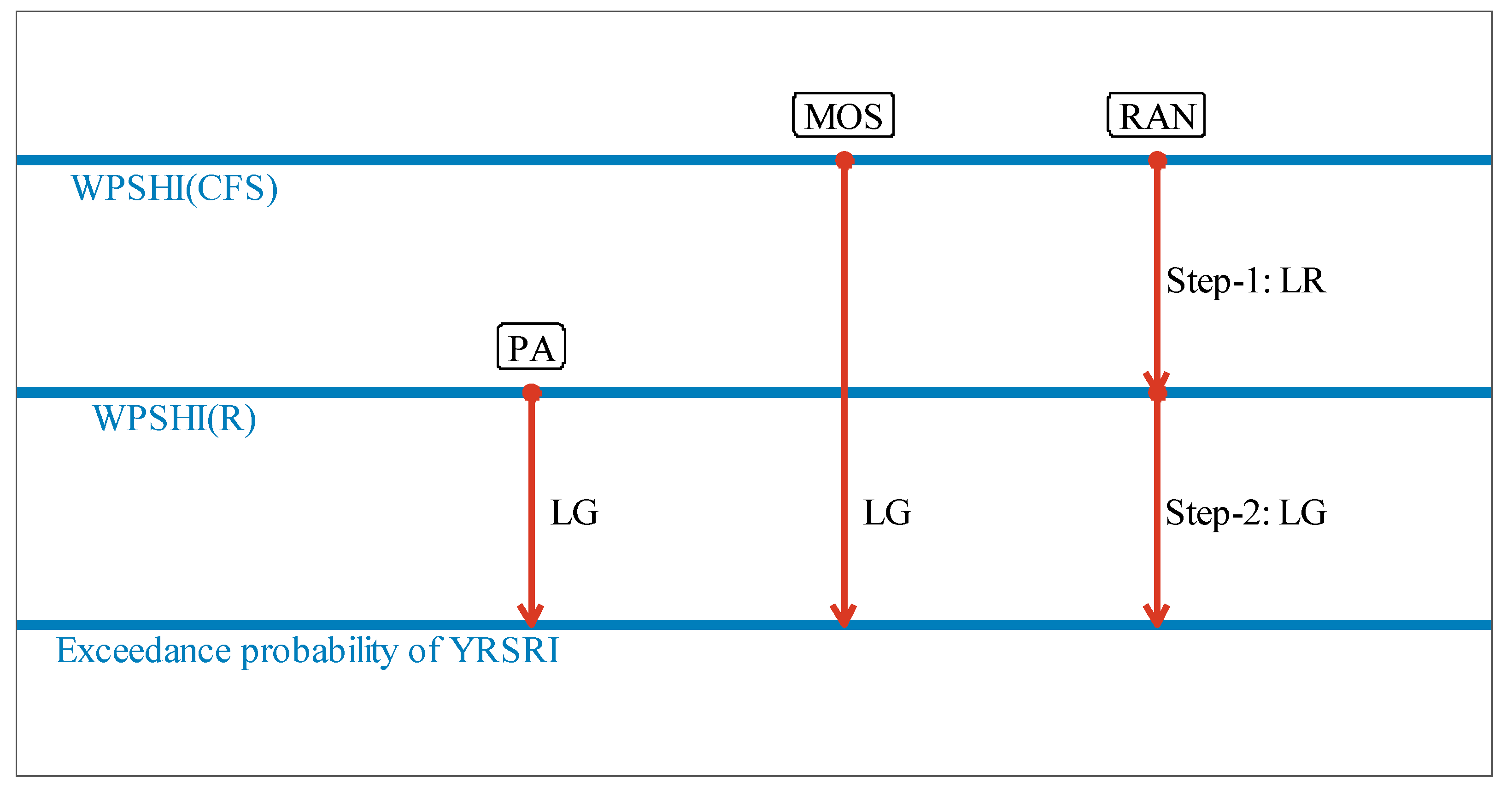
4.1. Three Testing Procedures
4.2. Logistic Regression
4.3. Exceedance Probability Forecast
- The series of thresholds are selected based on the observation of the predictand . First, sort the Y values in the samples in 1982–2018 as the descending order , where n is the number of all samples. Then, the thresholds used here are . This setting will make at least 5 samples for the positive or negative class.
- Choose one threshold in step 1 and one test year in the sample set (1982–2018). All samples can be divided into two classes based on the value of the predictand , i.e., years with (the positive class) and years with (the negative class). Use the training set to fit a logistic regression, and then use the fitted model to forecast for the test year.
- Repeat step 2 for all threshold and all test years.
4.4. Skill Metric along the Threshold
5. Results
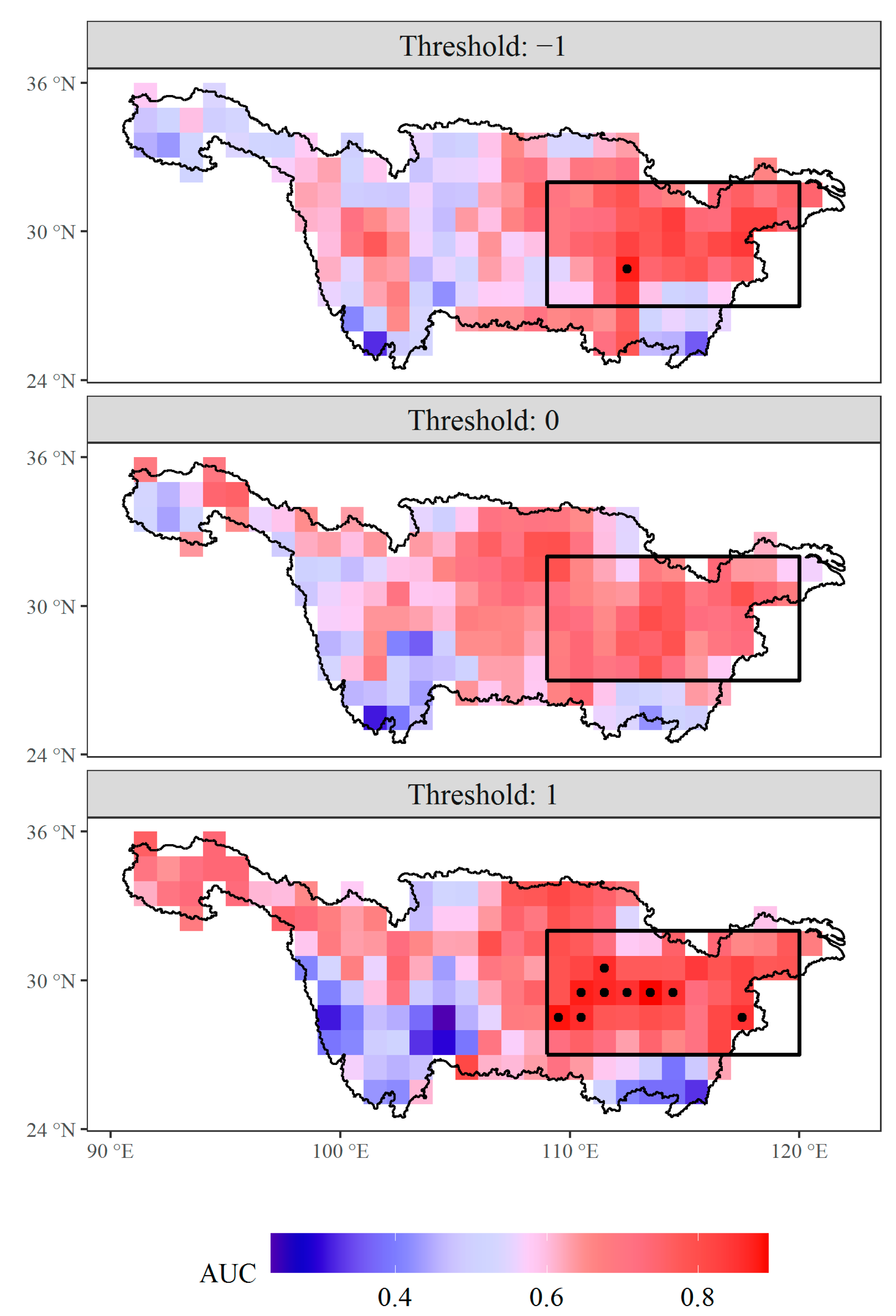
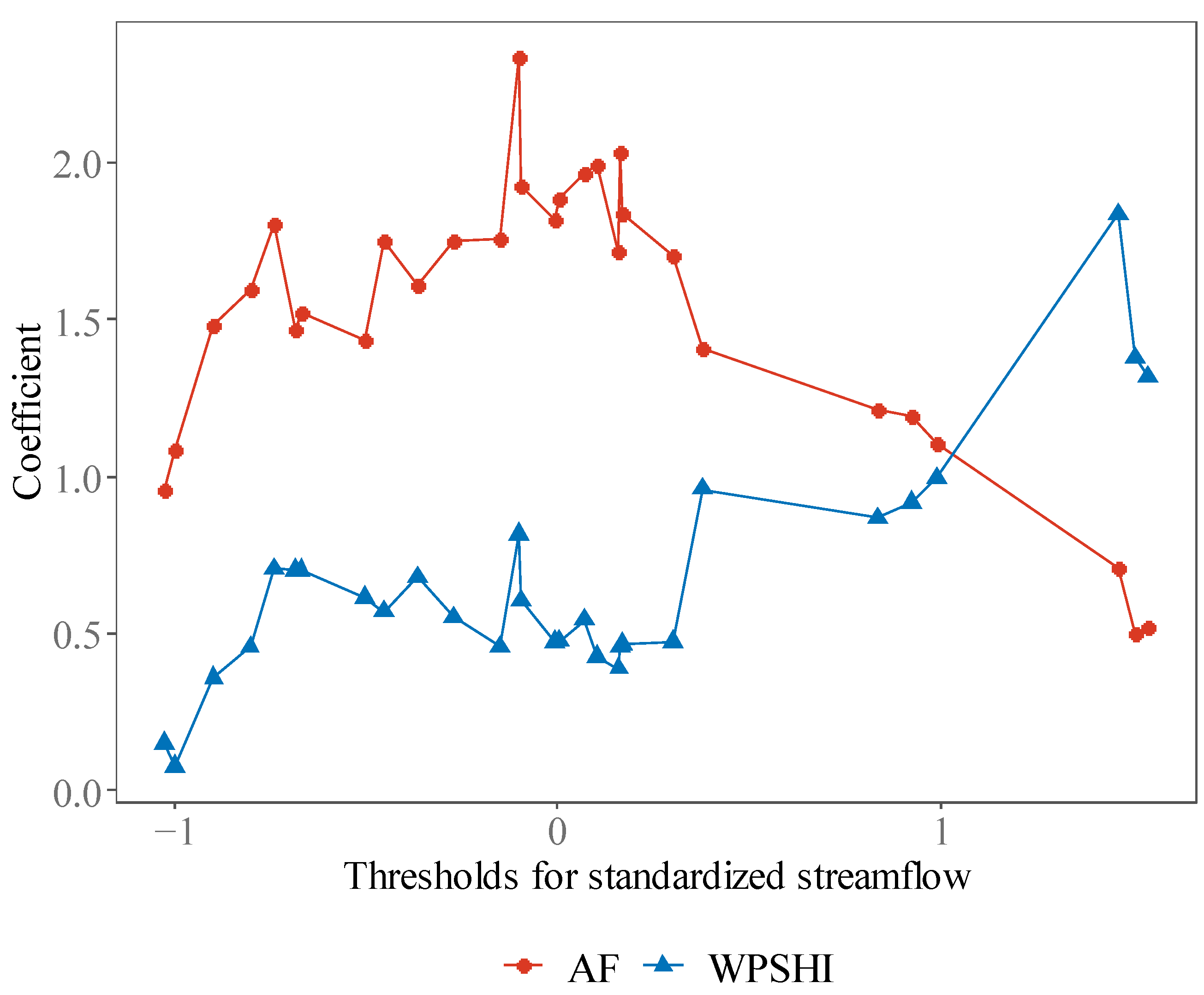
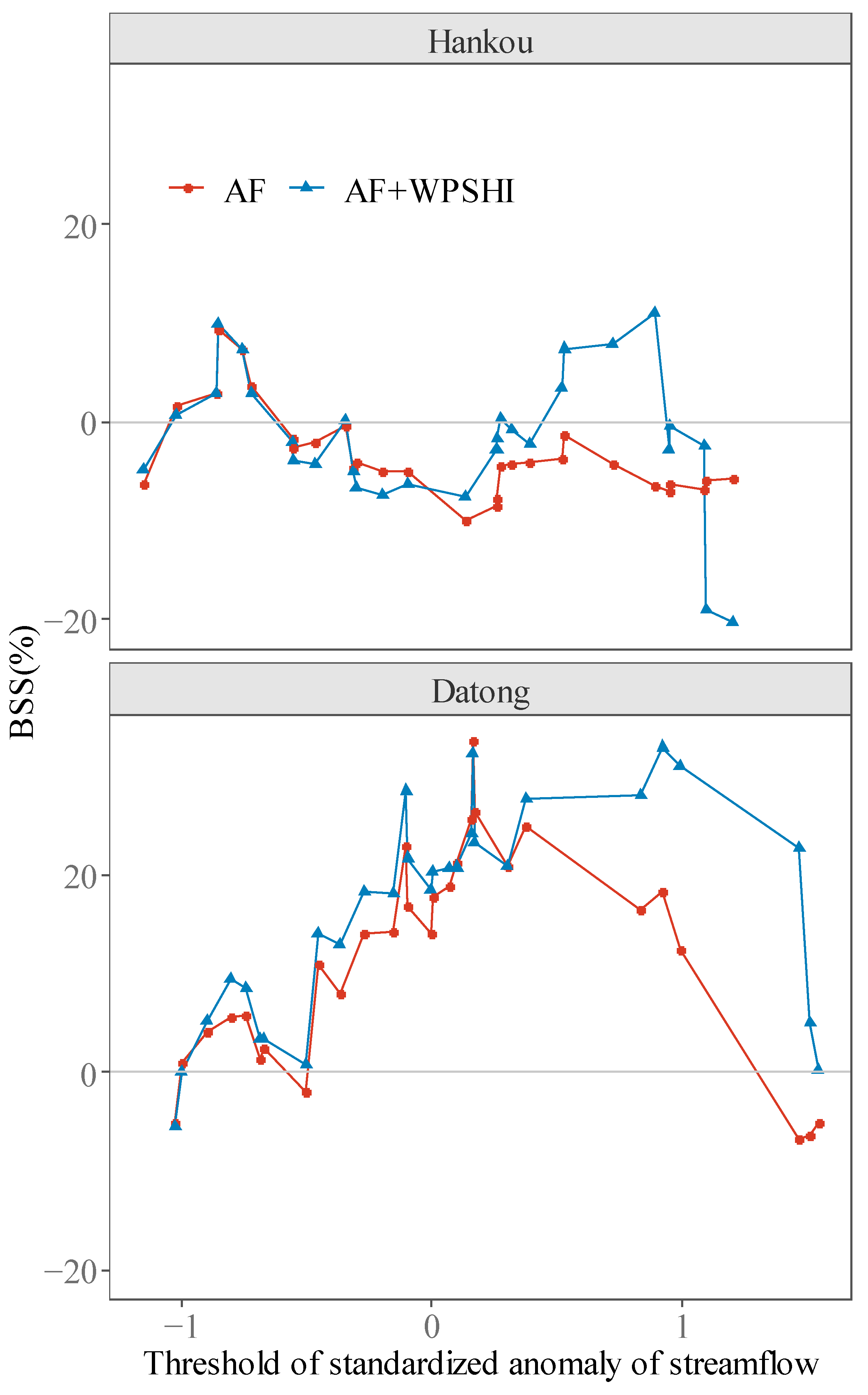
5.1. Results of PA
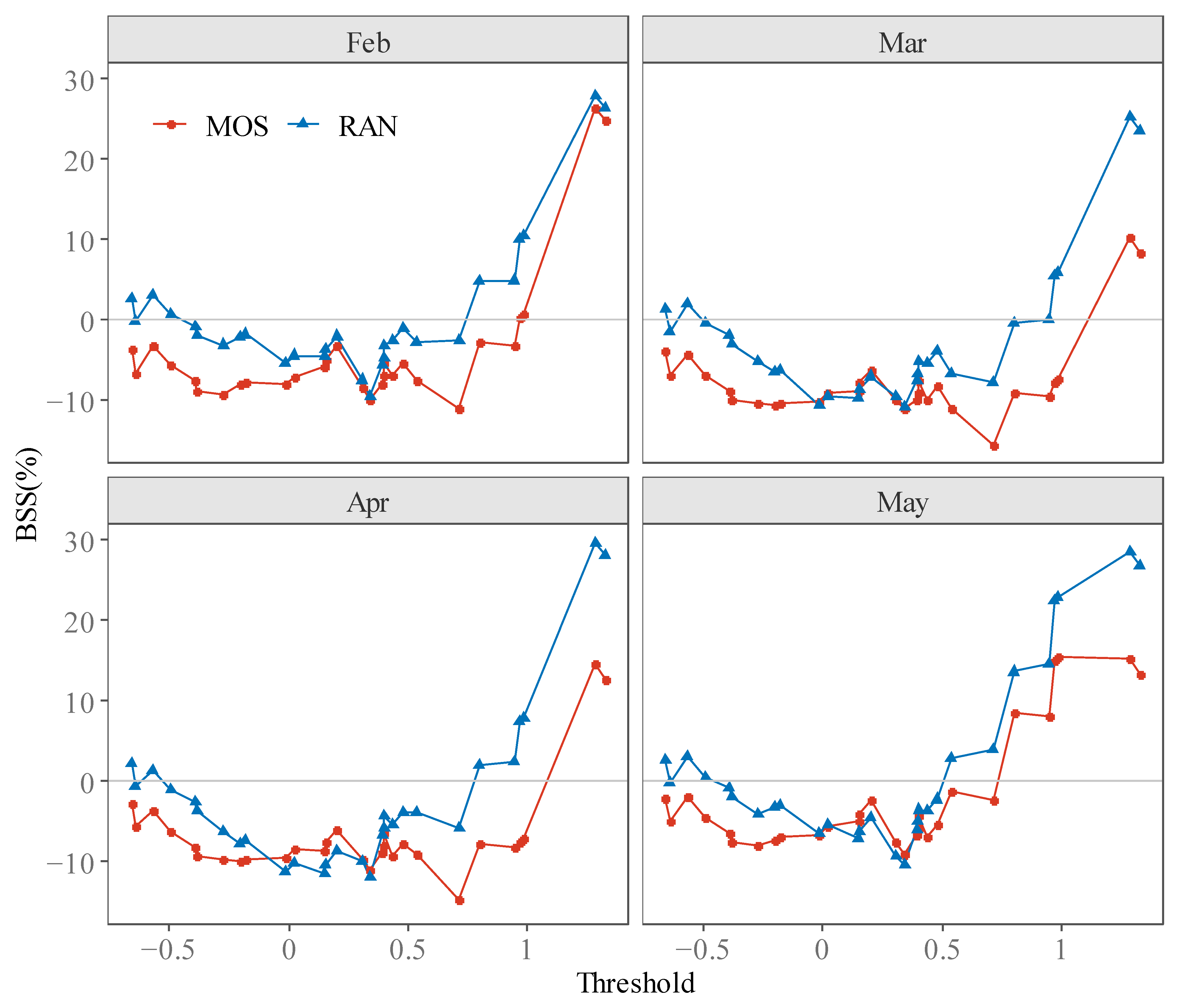
5.2. Results of MOS and RAN
6. Discussion
7. Conclusions
- The rainfall over the Yangtze River Valley is more sensitive to the variability of WPSHI when WPSHI is high, while when WPSHI is less than 0.5, the rainfall shows low sensitivity. Furthermore, the middle and lower reaches of Yangtze River Valley show higher sensitivity to the variability of WPSHI than other regions. This characteristic leads to higher forecasting skill of exceedance probability forecasts corresponding to larger thresholds of rainfall.
- The analysis of predictability of summer streamflow of the Yangtze River Valley shows that WPSHI can only enhance the forecasting skill for binary classification corresponding to larger thresholds of streamflow.
- A comparison between two postprocessing approaches shows that the RAN approach shows a higher skill than model output statistics (MOS), as RAN can utilize more samples than MOS.
- When building a long-term forecasting model for generating exceedance probability forecasts, one should notice the effect of the threshold, and find a proper threshold with a higher skill.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shams, M.S.; Anwar, F.A.H.M.; Lamb, K.W.; Bari, M. Relating ocean-atmospheric climate indices with australian river streamflow. J. Hydrol. 2018, 556, 294–309. [Google Scholar] [CrossRef]
- Araghinejad, S.; Burn, D.; Karamouz, M. Long-lead probabilistic forecasting of streamflow using ocean-atmospheric and hydrological predictors. Water Resour. Res. 2006, 42, W03431. [Google Scholar] [CrossRef] [Green Version]
- Kullmann, H.; Baldauf, S.A.; Bakker, T.C.M.; Frommen, J.G. Seasonal forecast for local precipitation over northern taiwan using statistical downscaling. J. Geophys. Res. Atmos. 2008, 113, D12. [Google Scholar]
- Guo, Y.; Li, J.; Li, Y. Seasonal forecasting of north china summer rainfall using a statistical downscaling model. J. Appl. Meteorol. Climatol. 2014, 53, 1739–1749. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Ha, K.; Wang, B.; Schemm, J. Deficiencies and possibilities for long-lead coupled climate prediction of the western north pacific-east asian summer monsoon. Clim. Dyn. 2011, 36, 1173–1188. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Wang, H. A statistical downscaling model for forecasting summer rainfall in china from demeter hindcast datasets. Weather. Forecast. 2012, 27, 608–628. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, Q.J.; Bennett, J.C.; Schepen, A.; Pappenberger, F.; Pokhrel, P.; Wang, Z. Statistical calibration and bridging of ecmwf system4 outputs for forecasting seasonal precipitation over china. J. Geophys. Res. Atmos. 2014, 119, 7116–7135. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, B.; Lee, J.-Y. Subtropical high predictability establishes a promising way for monsoon and tropical storm predictions. Proc. Natl. Acad. Sci. USA 2013, 110, 2718–2722. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Wood, E.F. Downscaling precipitation or bias-correcting streamflow? Some implications for coupled general circulation model (cgcm)-based ensemble seasonal hydrologic forecast. Water Resour. Res. 2012, 48, 12519. [Google Scholar] [CrossRef]
- Tisseuil, C.; Vrac, M.; Lek, S.; Wade, A.J. Statistical downscaling of river flows. J. Hydrology 2010, 385, 279–291. [Google Scholar] [CrossRef]
- Sachindra, D.; Huang, F.; Barton, A.; Perera, B. Least square support vector and multi-linear regression for statistically downscaling general circulation model outputs to catchment streamflows. Int. J. Climatol. 2013, 33, 1087–1106. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Mujumdar, P.P. Statistical downscaling of gcm simulations to streamflow using relevance vector machine. Adv. Water Resour. 2008, 31, 132–146. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Huang, G. Characteristics and variations of the east asian monsoon system and its impacts on climate disasters in china. Adv. Atmos. Sci. 2007, 24, 993–1023. [Google Scholar] [CrossRef]
- Luo, S.; Jin, Z. Statistical analysis for sea surface temperature over the south china sea, behavior of subtropical high over the west pacific and monthly mean rainfall over the changjiang middle and lower reaches. Chin. J. Atmos. Sci. 1986, 10, 409–418. [Google Scholar]
- Zhang, J.; Chen, X. The operational seasonal forecasting of the summer rainfall in china. Adv. Atmos. Sci. 1987, 4, 349–362. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Wang, L.; Lin, Z. Characteristics, processes, and causes of the spatio-temporal variabilities of the east asian monsoon system. Adv. Atmos. Sci. 2012, 29, 910–942. [Google Scholar] [CrossRef]
- Blschl, G.; Bierkens, M.; Chambel, A.; Cudennec, C.; Zhang, Y. Twenty-three unsolved problems in hydrology (uph)-A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global land precipitation: A 50-yr monthly analysis based on gauge observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The ncep/ncar 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.; Iredell, M. The ncep climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Lang, Y.; Ye, A.; Gong, W.; Miao, C.; Di, Z.; Xu, J.; Liu, Y.; Luo, L.; Duan, Q. Evaluating skill of seasonal precipitation and temperature predictions of ncep cfsv2 forecasts over 17 hydroclimatic regions in china. J. Hydrometeorol. 2014, 15, 1546–1559. [Google Scholar] [CrossRef]
- Silva, G.A.M.; Dutra, L.M.M.; Rocha, R.P.D.; Ambrizzi, T.; Leiva, É. Preliminary analysis on the global features of the ncep cfsv2 seasonal hindcasts. Adv. Meteorol. 2014, 2014, 117–128. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Kousky, V.E.; Higgins, R.W.; Yoo, S.H.; Liang, J.; Fan, Y. Simulations and seasonal prediction of the asian summer monsoon in the ncep climate forecast system. J. Clim. 2008, 21, 3755–3775. [Google Scholar] [CrossRef]
- Sui, C.H.; Chung, P.H.; Li, T. Interannual and interdecadal variability of the summertime western north pacific subtropical high. Geophys. Res. Lett. 2007, 34, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Chen, M.; Zhang, L.; Wang, W.; Xue, Y.; Wen, C.; Marx, L.; Huang, B. An analysis of the nonstationarity in the bias of sea surface temperature forecasts for the ncep climate forecast system (cfs) version 2. Mon. Weather. Rev. 2011, 140, 3003–3016. [Google Scholar] [CrossRef]
- Luca, D.L.D.; Versace, P. Diversity of rainfall thresholds for early warning of hydro-geological disasters. Adv. Geosci. 2017, 44, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, T. An introduction to roc analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Gong, D.Y.; Ho, C.H. Shift in the summer rainfall over the yangtze river valley in the late 1970s. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Marzban, C.; Sandgathe, S.; Kalnay, E. Mos, perfect prog, and reanalysis. Mon. Weather. Rev. 2006, 134, 657–663. [Google Scholar] [CrossRef]
- Salimun, E.; Tangang, F.T.; Juneng, L.; Zwiers, F.W.; Merryfield, W.J. Skill evaluation of the cancm4 and its mos for seasonal rainfall forecast in malaysia during the early and late winter monsoon periods. Int. J. Climatol. 2016, 36, 439–454. [Google Scholar] [CrossRef]
- Prasad, K.; Dash, S.K.; Mohanty, U.C. A logistic regression approach for monthly rainfall forecasts in meteorological subdivisions of india based on demeter retrospective forecasts. Int. J. Climatol. 2010, 30, 1577–1588. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.; Hastie, T.; Friedman, J.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Provost, F. Machine learning from imbalanced data sets 101. In Proceedings of the AAAI’2000 Workshop on Imbalanced Data sets, Austin, TX, USA, 31 July 2000; pp. 1–3. [Google Scholar]
- Pya, N.; Wood, S.N. Shape constrained additive models. Stat. Comput. 2015, 25, 543–559. [Google Scholar] [CrossRef]
- Piechota, T.C.; Chiew, F.H.; Dracup, J.A.; McMahon, T.A. Development of exceedance probability streamflow forecast. J. Hydrol. Eng. 2001, 6, 20–28. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K.; Zhang, Y. A statistical downscaling model for summer rainfall over china stations based on the climate forecast system. Chin. J. Atmos. Sci. 2013, 37, 1287–1296. [Google Scholar]
- Kelman, I.; Glantz, M.H. Early warning systems defined. In Reducing Disaster: Early Warning Systems for Climate Change; Singh, A., Zommers, Z., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 89–108. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; Chen, Y.; Huang, Q.; Wang, W.; Li, G. Forecasting Summer Rainfall and Streamflow over the Yangtze River Valley Using Western Pacific Subtropical High Feature. Water 2021, 13, 2580. https://doi.org/10.3390/w13182580
He R, Chen Y, Huang Q, Wang W, Li G. Forecasting Summer Rainfall and Streamflow over the Yangtze River Valley Using Western Pacific Subtropical High Feature. Water. 2021; 13(18):2580. https://doi.org/10.3390/w13182580
Chicago/Turabian StyleHe, Ranran, Yuanfang Chen, Qin Huang, Wenpeng Wang, and Guofang Li. 2021. "Forecasting Summer Rainfall and Streamflow over the Yangtze River Valley Using Western Pacific Subtropical High Feature" Water 13, no. 18: 2580. https://doi.org/10.3390/w13182580




