Corrections of Precipitation Particle Size Distribution Measured by a Parsivel OTT2 Disdrometer under Windy Conditions in the Antisana Massif, Ecuador
Abstract
:1. Introduction
2. Sites, Data, and Methods
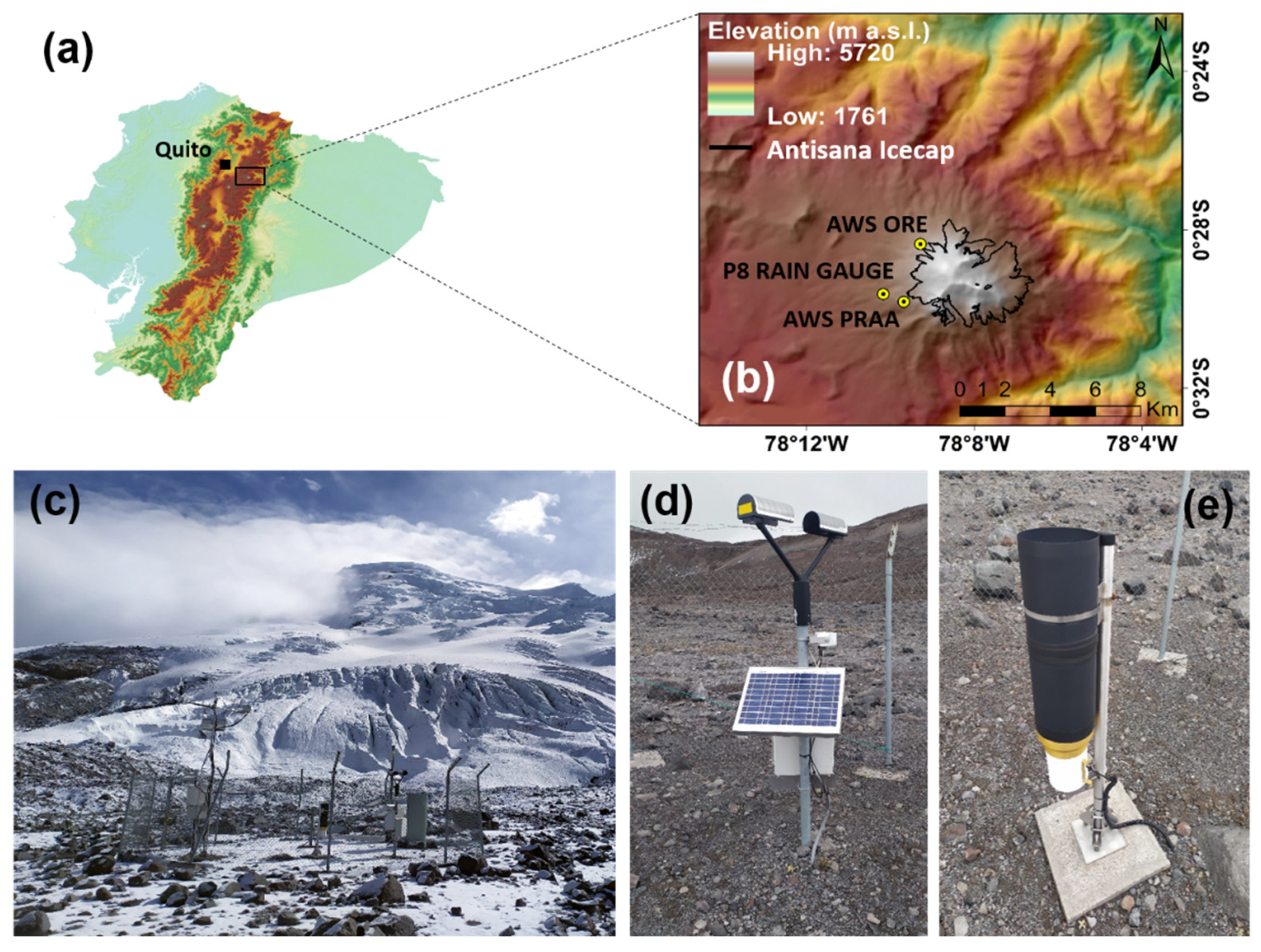
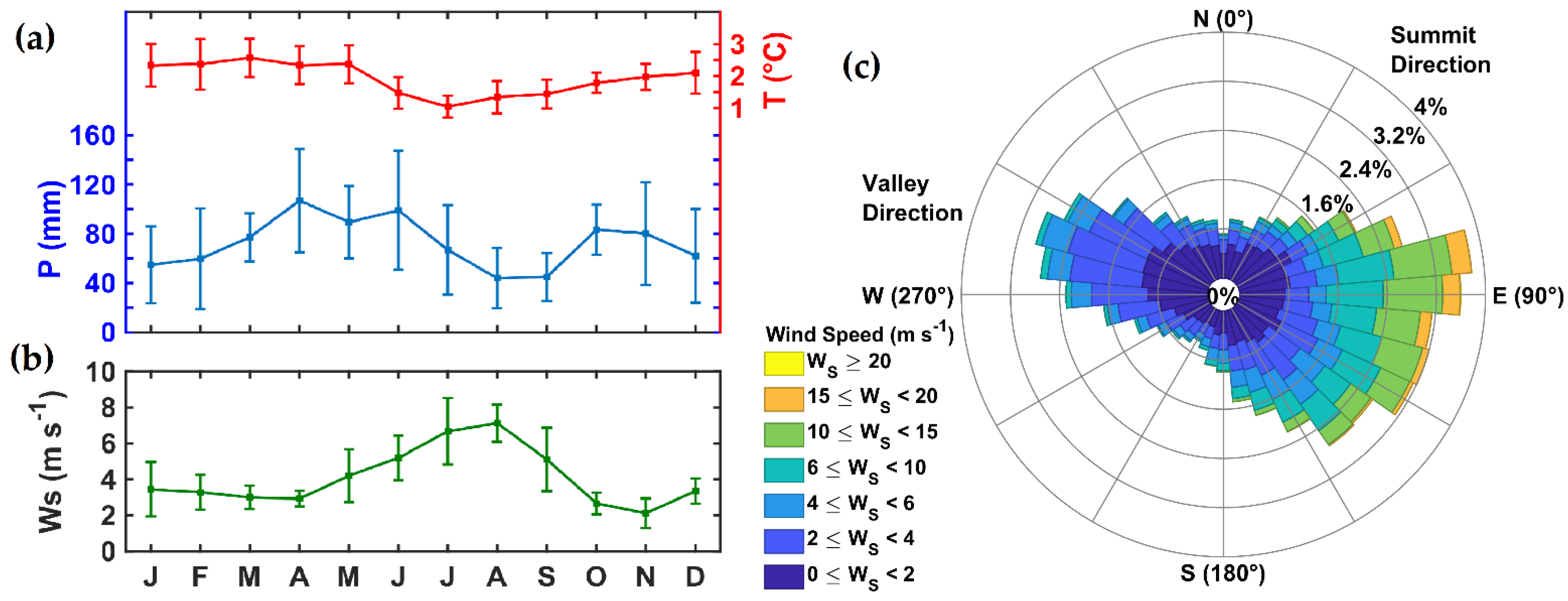
2.1. Site
2.2. Measuring Devices
2.2.1. Rain Gauge
2.2.2. Disdrometer
2.2.3. Additional Measurements
2.3. Study Period and Quality Control
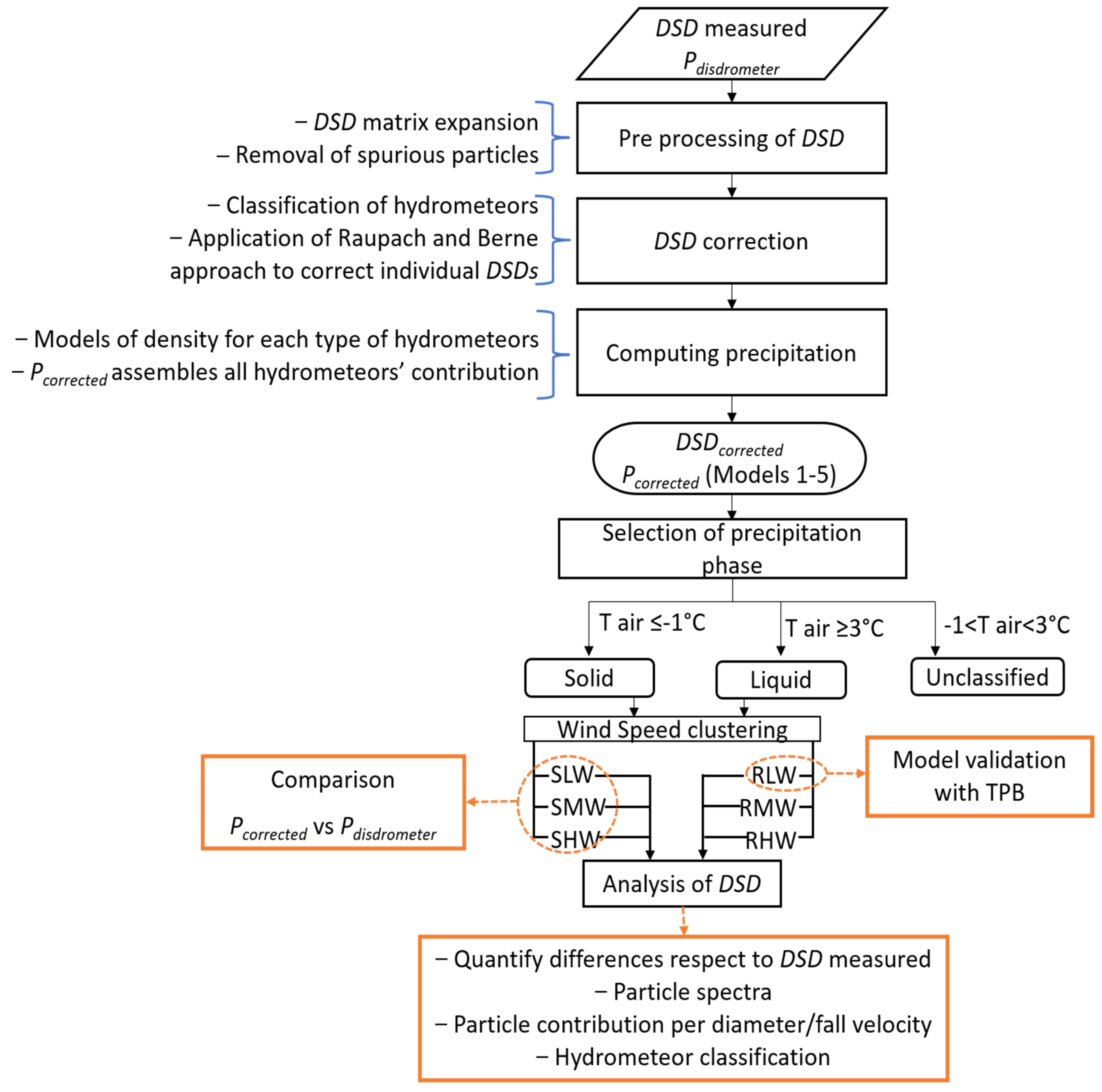
3. Methods
3.1. Pre-Processing of Diameter Size Distributions (DSD)
3.1.1. DSD Matrix Expansion
3.1.2. Diameter Based DSD Filtering
- F1: The particles with diameter D < 0.25 mm were removed because they are outside the sensitivity range of the instrument due to their low signal-to-noise ratio [17].
- F2: Measurements during high wind speeds are prone to particles misclassification causing large particles of DSD to appear with slow fall velocity. Therefore, particles with D > 10 mm and v < 1 ms−1 were removed as suggested by Friedrich et al. [24].
- F3: Particles with diameter D < 2 mm and fall velocities 60% smaller than the fall velocity–diameter relationship of rain were removed to filter hydrometeors related to splashing [24]. These particles would have hit the housing of the disdrometer, breaking apart and rebounding back into the sampling area appearing as slow raindrops in the measured DSD.
- F4: Finally, particles with D > 20 mm were also removed because storms with large hail are more recurrent in mid-latitudes and rarely occur in the tropics [49]; therefore, the last two diameter bins were left empty.
3.2. Correction of DSD
3.2.1. DSD Decomposition
3.2.2. Velocity Class per Diameter Shifting
3.3. Calculation of Precipitation Rate
3.4. Selection of Precipitation Types
3.5. Clustering of Solid and Liquid Precipitation by Wind Speed
4. Results
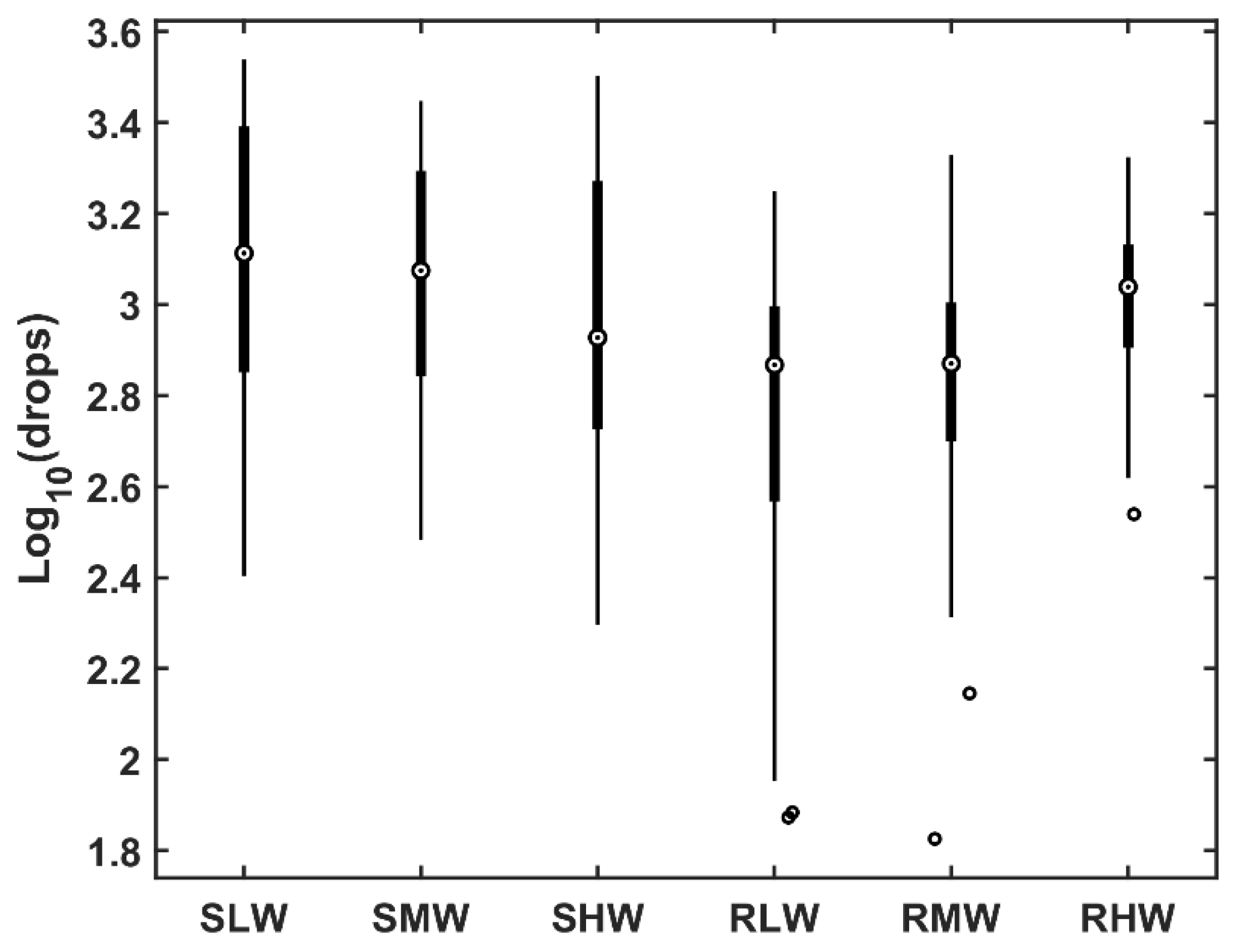
4.1. Solid and Liquid Precipitation
4.2. Clusters of Liquid and Solid Precipitation according to the Wind Speed Regime
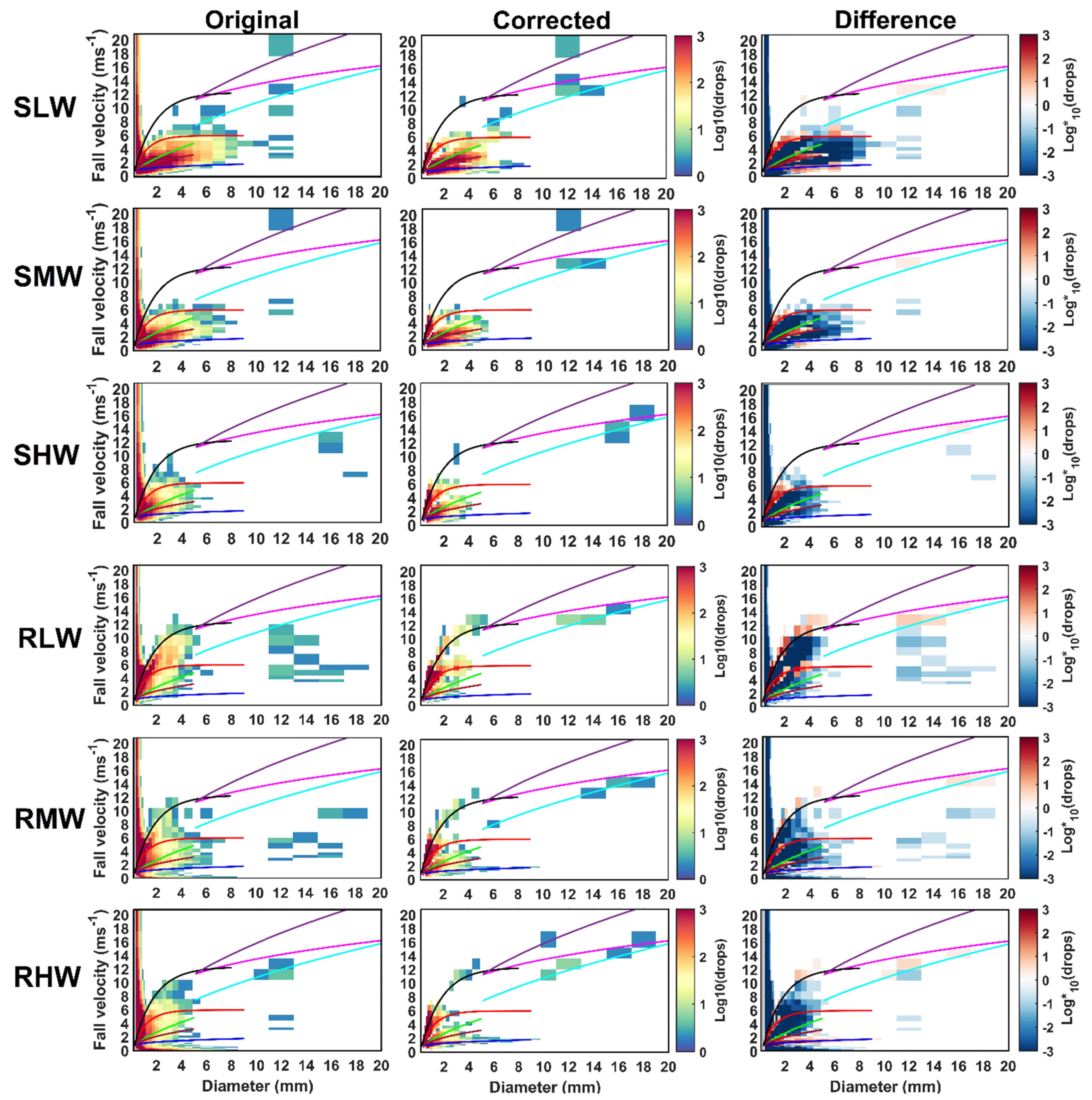
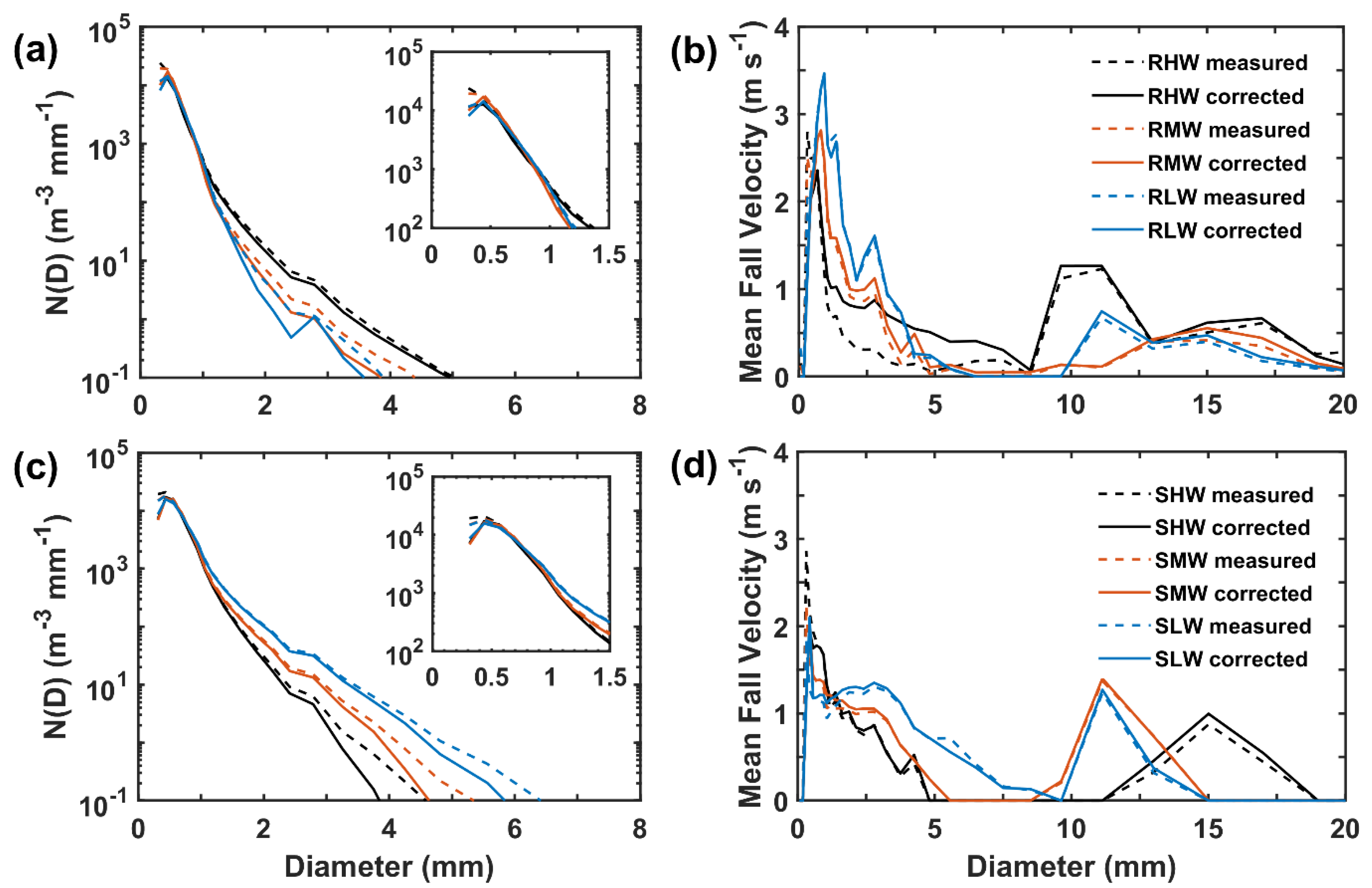
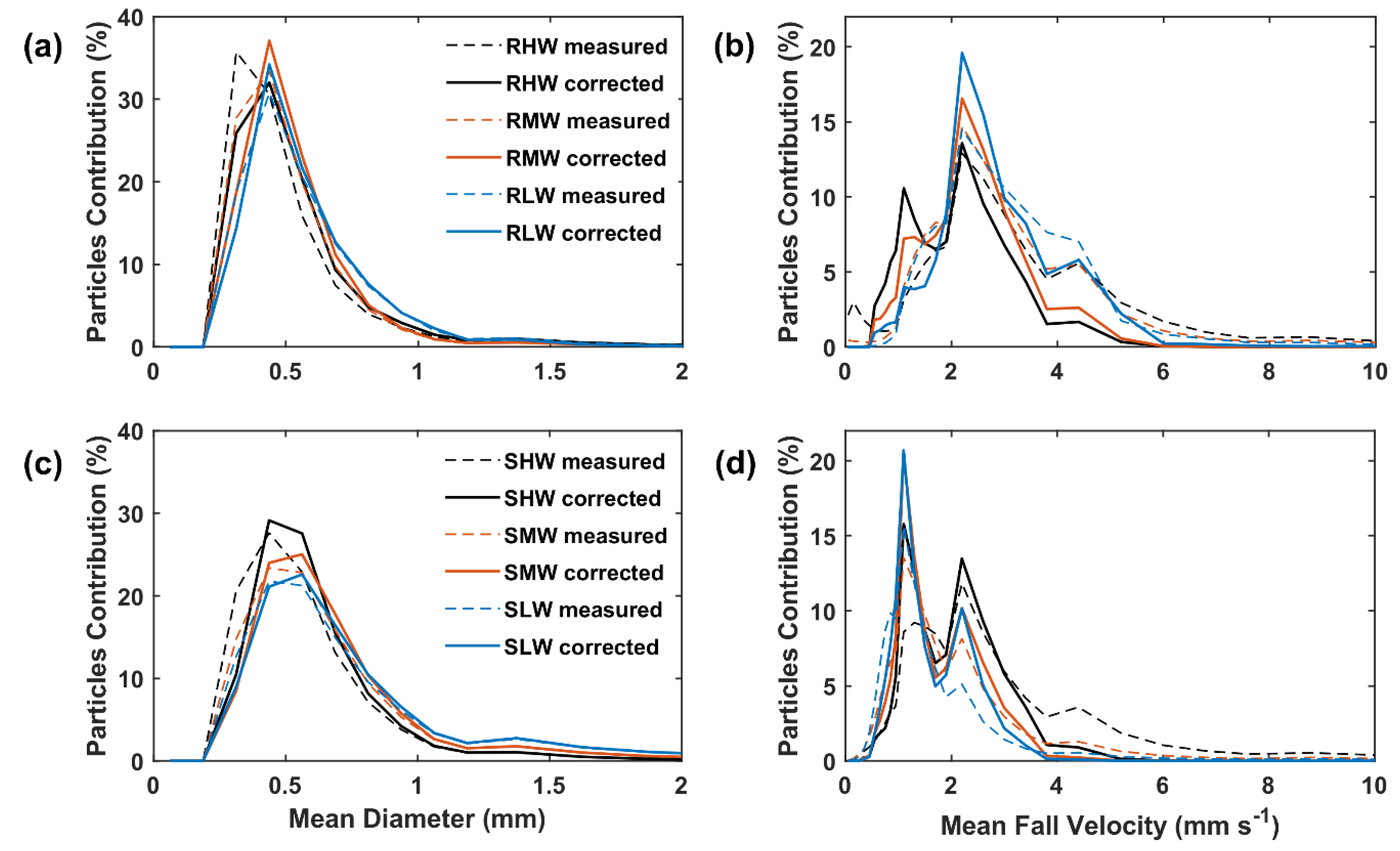
4.3. The Corrected Drop Size Distributions (DSDs)
4.3.1. Characteristics of Corrected DSD
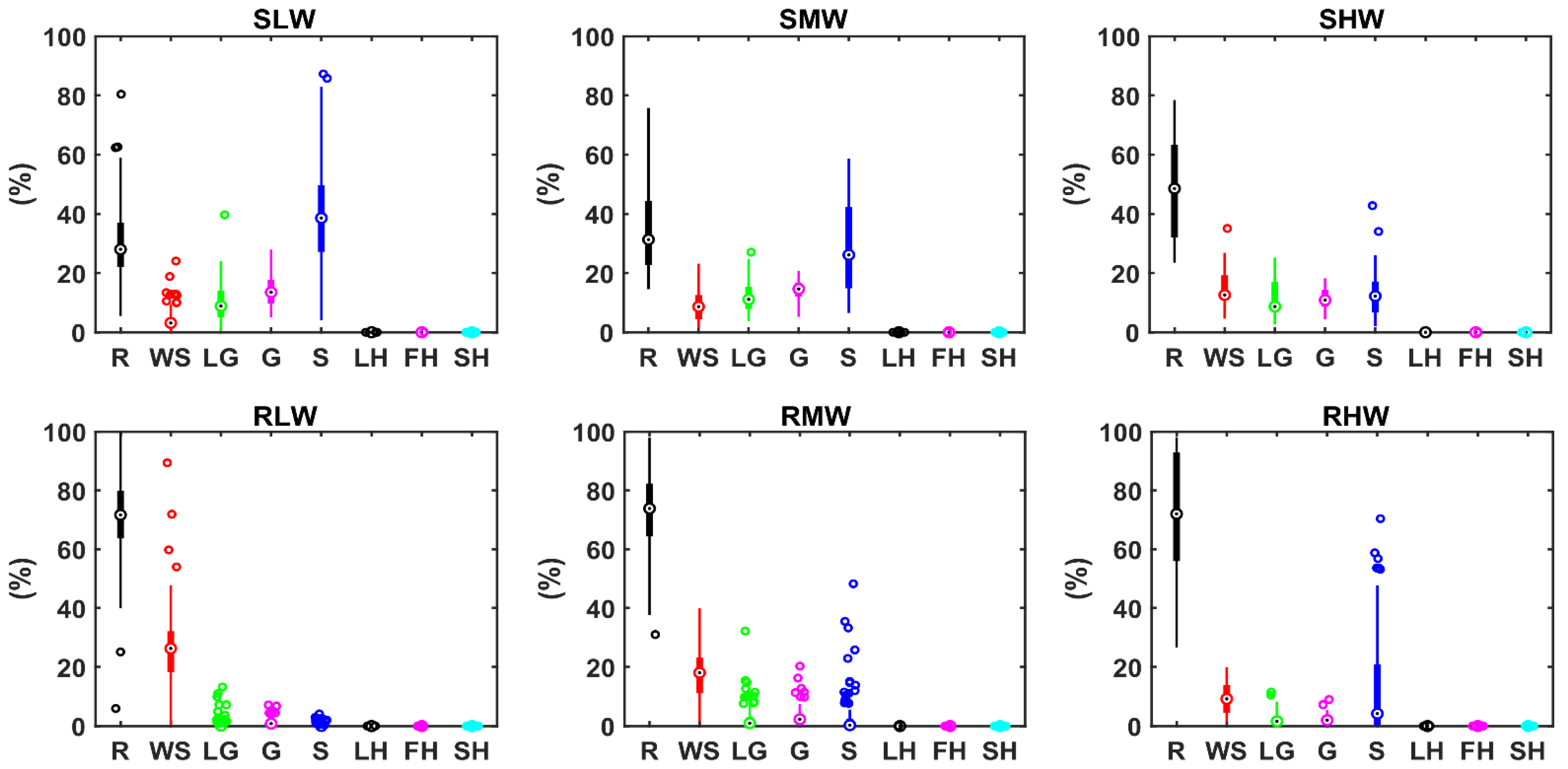
4.3.2. Composition Analysis of Corrected DSD
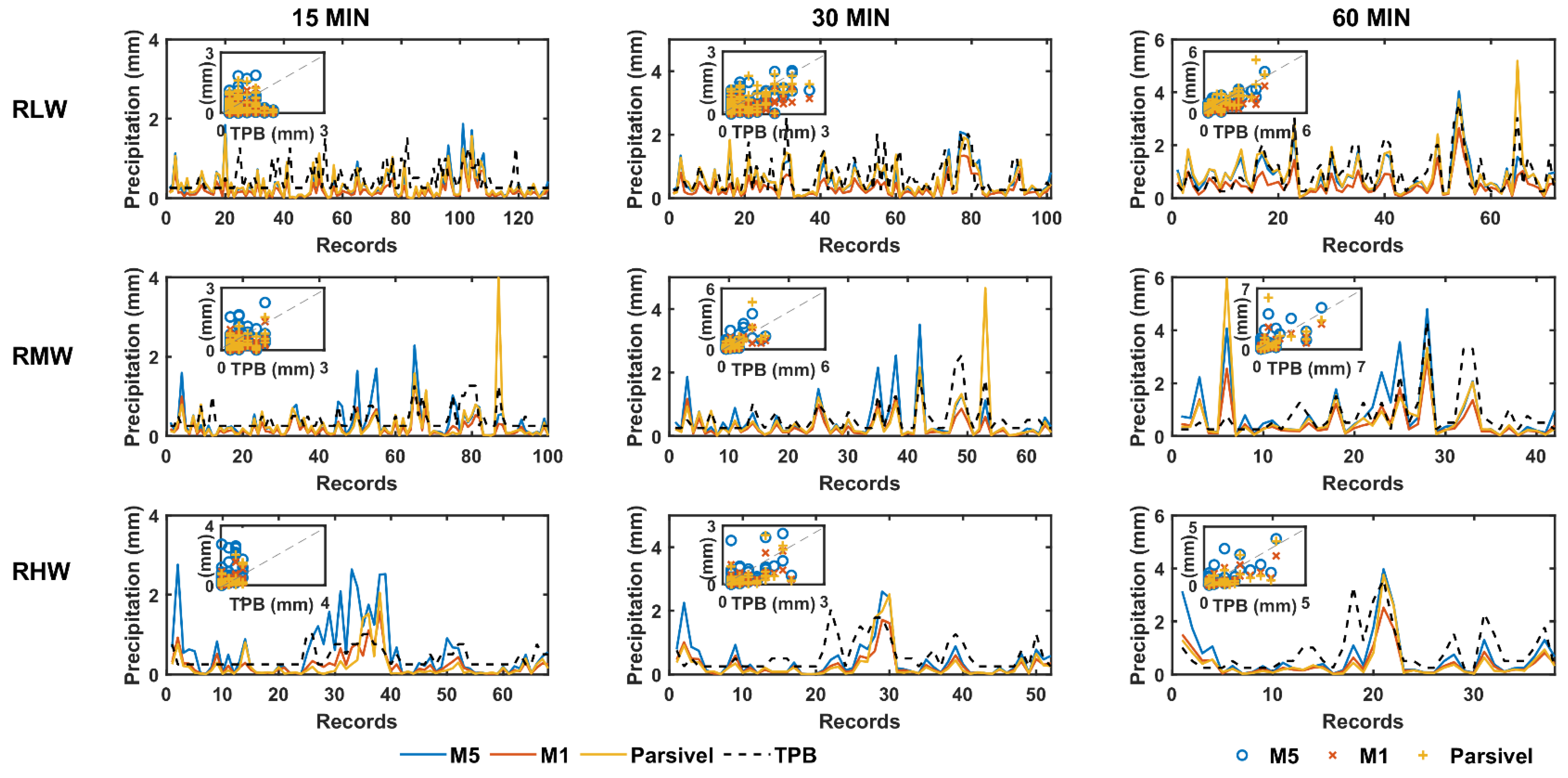
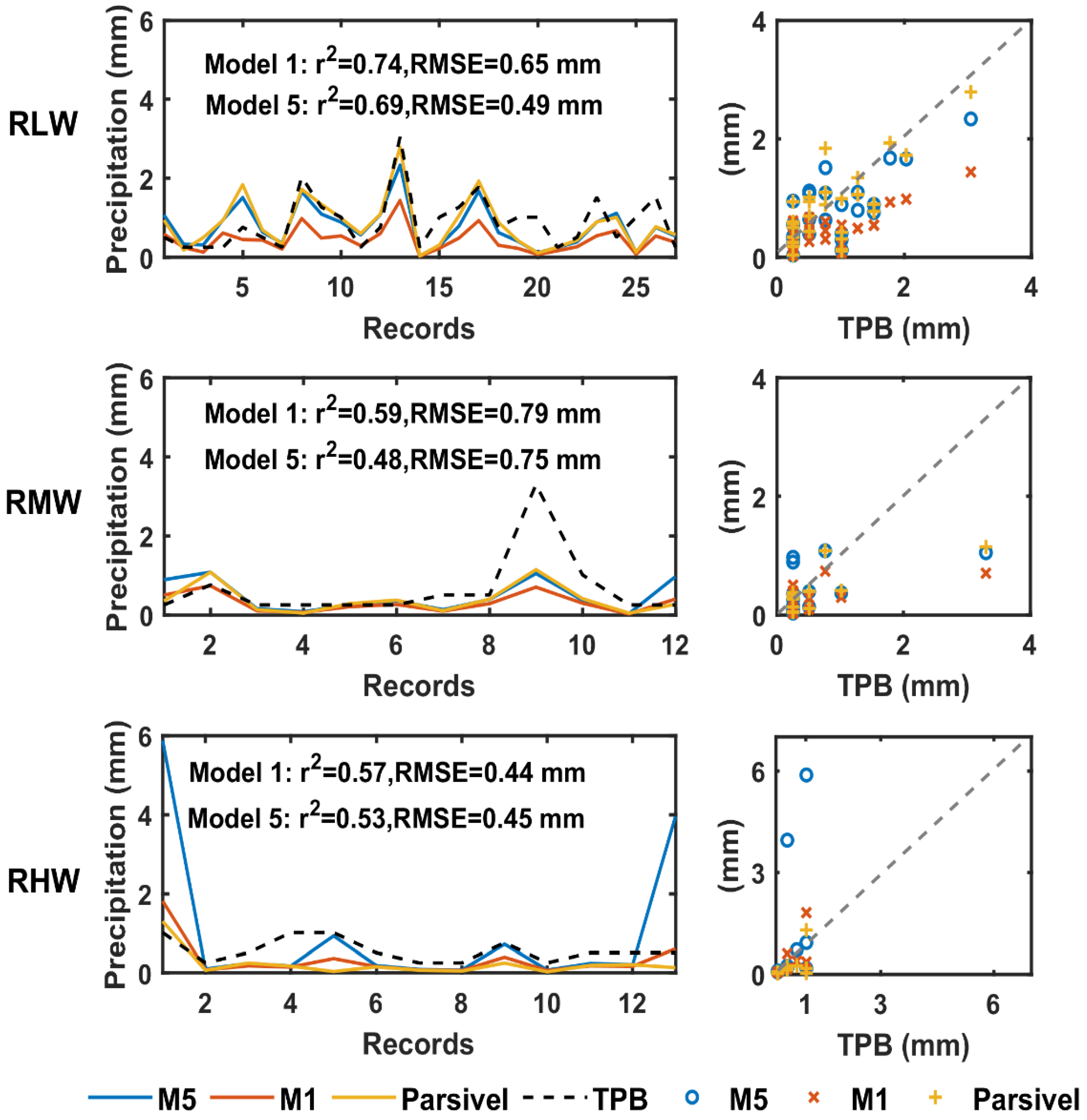
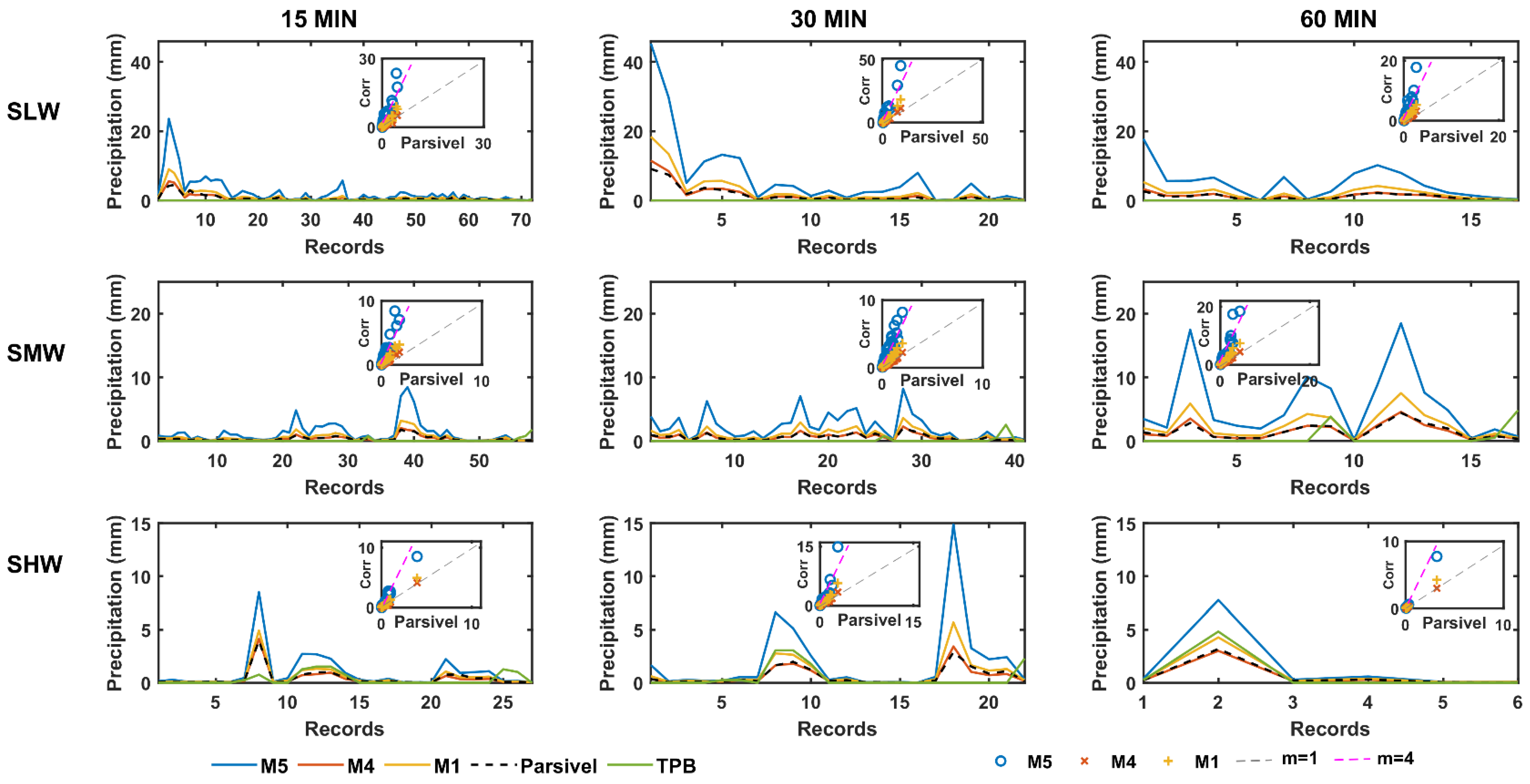
4.4. Corrected Precipitation according to Particle Density Models
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Disdrometer Precipitation | Identified Precipitation (Based in Ta) | N | Ta (°C) | Td (°C) | q (g kg−1) | RH (%) | Ws (m s−1) |
|---|---|---|---|---|---|---|---|
| Rainfall | Liquid | 179 | 3.63 | 2.26 | 7.93 | 90.97 | 4.19 |
| Mix | 46 | 3.68 | 0.71 | 7.11 | 81.23 | 6.58 | |
| Snowfall | 73 | 3.81 | 0.17 | 6.82 | 77.26 | 9.46 | |
| Rainfall | Solid | 3 | −1.67 | −2.38 | 5.72 | 94.9 | 6.71 |
| Mix | 2 | −1.45 | −1.70 | 6.01 | 98.15 | 3.53 | |
| Snowfall | 154 | −1.48 | −1.87 | 5.94 | 97.16 | 3.21 |
References
- Schreiner-McGraw, A.P.; Ajami, H. Impact of Uncertainty in Precipitation Forcing Data Sets on the Hydrologic Budget of an Integrated Hydrologic Model in Mountainous Terrain. Water Resour. Res. 2020, 56, e2020WR027639. [Google Scholar] [CrossRef]
- Praskievicz, S.; Chang, H. A review of hydrological modelling of basin-scale climate change and urban development impacts. Prog. Phys. Geogr. 2009, 33, 650–671. [Google Scholar] [CrossRef]
- Kotamarthi, V.; Mearns, L.; Hayhoe, K.; Castro, C.L.; Wuebbles, D. Use of Climate Information for Decision-Making and Impacts Research: State of Our Understanding. Strateg. Environ. Res. Dev. Progr. 2016, 1–55. [Google Scholar] [CrossRef]
- Buytaert, W.; Moulds, S.; Acosta, L.; De Bièvre, B.; Olmos, C.; Villacis, M.; Tovar, C.; Verbist, K.M.J.J. Glacial melt content of water use in the tropical Andes. Environ. Res. Lett. 2017, 12, 114014. [Google Scholar] [CrossRef]
- Simpson, M.J.; Hirsch, A.; Grempler, K.; Lupo, A. The importance of choosing precipitation datasets. Hydrol. Process. 2017, 31, 4600–4612. [Google Scholar] [CrossRef]
- Sieck, L.C.; Burges, S.J.; Steiner, M. Challenges in obtaining reliable measurements of point rainfall. Water Resour. Res. 2007, 43, 1–23. [Google Scholar] [CrossRef]
- Thériault, J.M.; Rasmussen, R.; Ikeda, K.; Landolt, S. Dependence of Snow Gauge Collection Efficiency on Snowflake Characteristics. J. Appl. Meteorol. Climatol. 2012, 5, 745–762. [Google Scholar] [CrossRef] [Green Version]
- Baghapour, B.; Sullivan, P.E. A CFD study of the influence of turbulence on undercatch of precipitation gauges. Atmos. Res. 2017, 197, 265–276. [Google Scholar] [CrossRef]
- Colli, M.; Pollock, M.; Stagnaro, M.; Lanza, L.G.; Dutton, M.; O’Connell, E. A Computational Fluid-Dynamics Assessment of the Improved Performance of Aerodynamic Rain Gauges. Water Resour. Res. 2018, 54, 779–796. [Google Scholar] [CrossRef]
- Colli, M.; Stagnaro, M.; Lanza, L.G.; Rasmussen, R.; Thériault, J.M. Adjustments for Wind-Induced Undercatch in Snowfall Measurements Based on Precipitation Intensity. J. Hydrometeorol. 2020, 21, 1039–1050. [Google Scholar] [CrossRef] [Green Version]
- Pollock, M.D.; O’Donnell, G.; Quinn, P.; Dutton, M.; Black, A.; Wilkinson, M.E.; Colli, M.; Stagnaro, M.; Lanza, L.G.; Lewis, E.; et al. Quantifying and Mitigating Wind-Induced Undercatch in Rainfall Measurements. Water Resour. Res. 2018, 54, 3863–3875. [Google Scholar] [CrossRef]
- Cauteruccio, A.; Lanza, L.G. Parameterization of the Collection Efficiency of a Cylindrical Catching-Type Rain Gauge Based on Rainfall Intensity. Water 2020, 12, 3431. [Google Scholar] [CrossRef]
- Fassnacht, S.R. Estimating Alter-shielded gauge snowfall undercatch, snowpack sublimation, and blowing snow transport at six sites in the coterminous USA. Hydrol. Process. 2004, 18, 3481–3492. [Google Scholar] [CrossRef]
- Sugiura, K.; Ohata, T.; Yang, D. Catch Characteristics of Precipitation Gauges in High-Latitude Regions with High Winds. J. Hydrometeorol. 2006, 7, 984–994. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Rasmussen, R.; Wolff, M.; Baker, B.; Hall, M.E.; Meyers, T.; Landolt, S.; Jachcik, A.; Isaksen, K.; Brækkan, R.; et al. The quantification and correction of wind-induced precipitation measurement errors. Hydrol. Earth Syst. Sci. 2017, 21, 1973–1989. [Google Scholar] [CrossRef] [Green Version]
- Löffler-Mang, M.; Joss, J. An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Latorre, B.; Fernández-Raga, M. Comparison of precipitation measurements by OTT Parsivel2 and Thies LPM optical disdrometers. Hydrol. Earth Syst. Sci. 2018, 22, 2811–2837. [Google Scholar] [CrossRef] [Green Version]
- Ji, L.; Chen, H.; Li, L.; Chen, B.; Xiao, X.; Chen, M.; Zhang, G. Raindrop Size Distributions and Rain Characteristics Observed by a PARSIVEL Disdrometer in Beijing, Northern China. Remote Sens. 2019, 11, 1479. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; He, B.; Zhao, S.; Hu, S.; Liu, L. Comparative measurement of rainfall with a precipitation micro-physical characteristics sensor, a 2D video disdrometer, an OTT PARSIVEL disdrometer, and a rain gauge. Atmos. Res. 2019, 229, 100–114. [Google Scholar] [CrossRef]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the New Version of the Laser-Optical Disdrometer, OTT Parsivel2. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Bendix, J. Analysis of Rain Types and Their Z-R Relationships at Different Locations in the High Andes of Southern Ecuador. J. Appl. Meteorol. Climatol. 2017, 56, 3065–3080. [Google Scholar] [CrossRef]
- Basantes-Serrano, R. Contribution à L’étude de L’évolution des Glaciers et du Changement Climatique dans les Andes Équatoriennes Depuis les Années 1950. Ph.D. Dissertation, Université Grenoble Alpes, Grenoble, France, 2015. Available online: http://theses.fr/2015GREAU009 (accessed on 9 September 2021).
- Jaffrain, J.; Berne, A. Experimental Quantification of the Sampling Uncertainty Associated with Measurements from PARSIVEL Disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-Size Distributions in Thunderstorms Measured by Optical Disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Correction of raindrop size distributions measured by Parsivel disdrometers, using a two-dimensional video disdrometer as a reference. Atmos. Meas. Tech. 2015, 8, 343–365. [Google Scholar] [CrossRef] [Green Version]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL Snow Observations: A Critical Assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Jia, X.; Liu, Y.; Ding, D.; Ma, X.; Chen, Y.; Bi, K.; Tian, P.; Lu, C.; Quan, J. Combining disdrometer, microscopic photography, and cloud radar to study distributions of hydrometeor types, size and fall velocity. Atmos. Res. 2019, 228, 176–185. [Google Scholar] [CrossRef]
- Brawn, D.; Upton, G. Estimation of an atmospheric gamma drop size distribution using disdrometer data. Atmos. Res. 2008, 87, 66–79. [Google Scholar] [CrossRef]
- Park, S.G.; Kim, H.L.; Ham, Y.W.; Jung, S.H. Comparative Evaluation of the OTT PARSIVEL2 Using a Collocated Two-Dimensional Video Disdrometer. J. Atmos. Ocean. Technol. 2017, 34, 2059–2082. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, L.; Yang, D.; Xiao, Y.; Zhang, L.; Qiao, Y. Analysis of Raindrop Size Distribution Characteristics in Permafrost Regions of the Qinghai-Tibet Plateau Based on New Quality Control Scheme. Water 2019, 11, 2265. [Google Scholar] [CrossRef] [Green Version]
- Nord, G.; Boudevillain, B.; Berne, A.; Branger, F.; Braud, I.; Dramais, G.; Gérard, S.; Le Coz, J.; Legoût, C.; Molinié, G.; et al. A high space-time resolution dataset linking meteorological forcing and hydro-sedimentary response in a mesoscale Mediterranean catchment (Auzon) of the Ardèche region, France. Earth Syst. Sci. Data 2017, 9, 221–249. [Google Scholar] [CrossRef] [Green Version]
- Raupach, T.H.; Berne, A. Invariance of the Double-Moment Normalized Raindrop Size Distribution through 3D Spatial Displacement in Stratiform Rain. J. Appl. Meteorol. Climatol. 2017, 56, 1663–1680. [Google Scholar] [CrossRef]
- Taufour, M.; Vié, B.; Augros, C.; Boudevillain, B.; Delanoë, J.; Delautier, G.; Ducrocq, V.; Lac, C.; Pinty, J.P.; Schwarzenböck, A. Evaluation of the two-moment scheme LIMA based on microphysical observations from the HyMeX campaign. Q. J. R. Meteorol. Soc. 2018, 144, 1398–1414. [Google Scholar] [CrossRef]
- Pouget, J.C.; Proaño, D.; Vera, A.; Villacís, M.; Condom, T.; Escobar, M.; Le Goulven, P.; Calvez, R. Modélisation glacio-hydrologique et gestion des ressources en eau dans les Andes équatoriennes: L’exemple de Quito. Hydrol. Sci. J. 2017, 62, 431–446. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Garreaud, R.; Poveda, G.; Arias, P.A.; Molina-Carpio, J.; Masiokas, M.; Viale, M.; Scaff, L. Hydroclimate of the Andes Part I: Main Climatic Features. Front. Earth Sci. 2020, 8, 64. [Google Scholar] [CrossRef] [Green Version]
- Francou, B.; Vuille, M.; Favier, V.; Cáceres, B. New evidence for an ENSO impact on low-latitude glaciers: Antizana 15, Andes of Ecuador, 0°28′S. J. Geophys. Res. Atmos. 2004, 109, 1–17. [Google Scholar] [CrossRef]
- Favier, V.; Wagnon, P.; Chazarin, J.P.; Maisincho, L.; Coudrain, A. One-year measurements of surface heat budget on the ablation zone of Antizana Glacier 15, Ecuadorian Andes. J. Geophys. Res. Atmos. 2004, 109, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Basantes-Serrano, R.; Rabatel, A.; Francou, B.; Vincent, C.; Maisincho, L.; Cáceres, B.; Galarraga, R.; Alvarez, D. Slight mass loss revealed by reanalyzing glacier mass-balance observations on Glaciar Antisana 15α (inner tropics) during the 1995-2012 period. J. Glaciol. 2016, 62, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Jomelli, V.; Favier, V.; Rabatel, A.; Brunstein, D.; Hoffmann, G.; Francou, B. Fluctuations of glaciers in the tropical Andes over the last millennium and palaeoclimatic implications: A review. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 269–282. [Google Scholar] [CrossRef]
- Sklenár, P.; Kuècerová, A.; Macková, J.; Macek, P. Temporal variation of climate in the high-elevation páramo of Antisana, Ecuador. Suppl. Geogr. Fis. Din. Quat. 2015, 38, 67–78. [Google Scholar] [CrossRef]
- Campbell, S. CS705 Snowfall Adapter Instruction Manual for Rain Gages with 8 in. orifices. Campbell Scientific Inc. 2017. Available online: https://www.campbellsci.com/cs705 (accessed on 29 June 2021).
- Nešpor, V.; Sevruk, B. Estimation of Wind-Induced Error of Rainfall Gauge Measurements Using a Numerical Simulation. J. Atmos. Ocean. Technol. 1999, 16, 450–464. [Google Scholar] [CrossRef]
- Duchon, C.E.; Biddle, C.J. Undercatch of tipping-bucket gauges in high rain rate events. Adv. Geosci. 2010, 25, 11–15. [Google Scholar] [CrossRef] [Green Version]
- OTT. Present Weather Sensor OTT Parsivel2 Operating Instructions. OTT Hydromet GmbH 2016. Available online: https://www.fondriest.com/pdf/ott_parsivel2_manual.pdf (accessed on 29 June 2021).
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation, 2nd ed.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Villalobos-Puma, E.; Martinez-Castro, D.; Flores-Rojas, J.L.; Saavedra-Huanca, M.; Silva-Vidal, Y. Diurnal Cycle of Raindrops Size Distribution in a Valley of the Peruvian Central Andes. Atmosphere 2020, 11, 38. [Google Scholar] [CrossRef] [Green Version]
- Bolton, D. The Computation of Equivalent Potential Temperature. Mon. Weather Rev. 1980, 108, 1046–1053. [Google Scholar] [CrossRef] [Green Version]
- Stafford, R. Random Vectors with Fixed Sum. MATLAB Central File Exchange. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/9700-random-vectors-with-fixed-sum (accessed on 6 November 2020).
- Kumar, S.; Silva, Y. Distribution of hydrometeors in monsoonal clouds over the South American continent during the austral summer monsoon: GPM observations. Int. J. Remote Sens. 2020, 41, 3677–3707. [Google Scholar] [CrossRef]
- Thériault, J.M.; Stewart, R.E.; Henson, W. On the Dependence of Winter Precipitation Types on Temperature, Precipitation Rate, and Associated Features. J. Appl. Meteorol. Climatol. 2010, 49, 1429–1442. [Google Scholar] [CrossRef] [Green Version]
- Harpold, A.A.; Kaplan, M.; Klos, P.Z.; Link, T.; McNamara, J.P.; Rajagopal, S.; Schumer, R.; Steele, C.M. Rain or snow: Hydrologic processes, observations, prediction, and research needs. Hydrol. Earth Syst. Sci. 2016, 21, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Löffler-Mang, M. Observations of Precipitation Size and Fall Speed Characteristics within Coexisting Rain and Wet Snow. J. Appl. Meteorol. Climatol. 2006, 45, 1450–1464. [Google Scholar] [CrossRef] [Green Version]
- Gunn, R.; Kinzer, G.D. The Terminal Velocity of Fall for Water Droplets in Stagnant Air. J. Atmos. Sci. 1949, 6, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Locatelli, J.D.; Hobbs, P.V. Fall speeds and masses of solid precipitation particles. J. Geophys. Res. 1974, 79, 2185–2197. [Google Scholar] [CrossRef]
- Knight, N.C.; Heymsfield, A.J. Measurement and Interpretation of Hailstone Density and Terminal Velocity. J. Atmos. Sci. 1983, 40, 1510–1516. [Google Scholar] [CrossRef] [Green Version]
- Fehlmann, M.; Rohrer, M.; Von Lerber, A.; Stoffel, M. Automated precipitation monitoring with the Thies disdrometer: Biases and ways for improvement. Atmos. Meas. Tech. 2020, 13, 4683–4698. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of Raindrop Sizes and Fall Velocities in a Semiarid Plateau Climate: Convective versus Stratiform Rains. J. Appl. Meteorol. Climatol. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Foote, G.B.; Du Toit, P.S. Terminal Velocity of Raindrops Aloft. J. Appl. Meteorol. Climatol. 1969, 8, 249–253. [Google Scholar] [CrossRef] [Green Version]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Boudala, F.S.; Isaac, G.A.; Rasmussen, R.; Cober, S.G.; Scott, B. Comparisons of Snowfall Measurements in Complex Terrain Made During the 2010 Winter Olympics in Vancouver. Pure Appl. Geophys. 2014, 171, 113–127. [Google Scholar] [CrossRef]
- Brandes, E.A.; Ikeda, K.; Zhang, G.; Schönhuber, M.; Rasmussen, R.M. A Statistical and Physical Description of Hydrometeor Distributions in Colorado Snowstorms Using a Video Disdrometer. J. Appl. Meteorol. Climatol. 2007, 46, 634–650. [Google Scholar] [CrossRef]
- Yu, T.; Chandrasekar, V.; Xiao, H.; Joshil, S.S. Characteristics of Snow Particle Size Distribution in the PyeongChang Region of South Korea. Atmosphere 2020, 11, 1093. [Google Scholar] [CrossRef]
- Zawadzki, I.; Szyrmer, W.; Bell, C.; Fabry, F. Modeling of the Melting Layer. Part III: The Density Effect. J. Atmos. Sci. 2005, 62, 3705–3723. [Google Scholar] [CrossRef]
- Heymsfield, A.; Wright, R. Graupel and Hail Terminal Velocities: Does a “Supercritical” Reynolds Number Apply? J. Atmos. Sci. 2014, 71, 3392–3403. [Google Scholar] [CrossRef]
- Knight, C.; Knight, N.; Brooks, H.E.; Skripnikova, K. Hail and Hailstorms. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- List, R. Kennzeichen Atmosphärischer Eispartikeln. Z. Angew. Math. Phys. 1958, 9, 180–192. [Google Scholar] [CrossRef]
- Harder, P.; Pomeroy, J. Estimating precipitation phase using a psychrometric energy balance method. Hydrol. Process. 2013, 27, 1901–1914. [Google Scholar] [CrossRef]
- Wagnon, P.; Lafaysse, M.; Lejeune, Y.; Maisincho, L.; Rojas, M.; Chazarin, J.P. Understanding and modeling the physical processes that govern the melting of snow cover in a tropical mountain environment in Ecuador. J. Geophys. Res. Atmos. 2009, 114, 1–14. [Google Scholar] [CrossRef]
- MacKay, D.J.C. An Example Inference Task: Clustering. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003; Chapter 20. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Montero-Martínez, G.; García-García, F. On the behaviour of raindrop fall speed due to wind. Q. J. R. Meteorol. Soc. 2016, 142, 2013–2020. [Google Scholar] [CrossRef]
- Testik, F.Y.; Pei, B. Wind Effects on the Shape of Raindrop Size Distribution. J. Hydrometeorol. 2017, 18, 1285–1303. [Google Scholar] [CrossRef]
- Fujiyoshi, Y.; Muramoto, K. The Effect of Breakup of Melting Snowflakes on the Resulting Size Distribution of Raindrops. J. Meteorol. Soc. Japan 1996, 74, 343–353. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.C. Performance of Several Present Weather Sensors as Precipitation Gauges. In Proceedings of the Technical Conference (TECO) on Meteorological and Environmental Methods of Observation, Brussels, Belgium, 16–18 October 2012. [Google Scholar]
- Zhang, L.; Zhao, L.; Xie, C.; Liu, G.; Gao, L.; Xiao, Y.; Shi, J.; Qiao, Y. Intercomparison of Solid Precipitation Derived from the Weighting Rain Gauge and Optical Instruments in the Interior Qinghai-Tibetan Plateau. Adv. Meteorol. 2015. [Google Scholar] [CrossRef] [Green Version]
- Ye, H.; Cohen, J.; Rawlins, M. Discrimination of Solid from Liquid Precipitation over Northern Eurasia Using Surface Atmospheric Conditions. J. Hydrometeorol. 2013, 14, 1345–1355. [Google Scholar] [CrossRef] [Green Version]
- Froidurot, S.; Zin, I.; Hingray, B.; Gautheron, A. Sensitivity of Precipitation Phase over the Swiss Alps to Different Meteorological Variables. J. Hydrometeorol. 2014, 15, 685–696. [Google Scholar] [CrossRef]
- L’Hôte, Y.; Chevallier, P.; Coudrain, A.; Lejeune, Y.; Etchevers, P. Relationship between precipitation phase and air temperature: Comparison between the Bolivian Andes and the Swiss Alps. Hydrol. Sci. J. 2005, 50, 989–997. [Google Scholar] [CrossRef]
- Cha, J.W.; Yum, S.S. Characteristics of Precipitation Particles Measured by PARSIVEL Disdrometer at a Mountain and a Coastal Site in Korea. Asia-Pac. J. Atmos. Sci. 2020, 57, 261–276. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Hu, W.; Pu, J. Characteristics of the raindrop size distribution for freezing precipitation observed in southern China. J. Geophys. Res. Atmos. 2011, 116, 1–10. [Google Scholar] [CrossRef]
- Merenti-Välimäki, H.-L.; Lönnqvist, J.; Laininen, P. Present weather: Comparing human observations and one type of automated sensor. Meteorol. Appl. 2001, 8, 491–496. [Google Scholar] [CrossRef]
- Stewart, R.E.; Thériault, J.M.; Henson, W. On the Characteristics of and Processes Producing Winter Precipitation Types near 0 °C. Bull. Am. Meteorol. Soc. 2015, 96, 623–639. [Google Scholar] [CrossRef] [Green Version]
| T Air (°C) | RH (%) | q (g kg−1) | T Dewpoint (°C) | Wind Speed (m s−1) | Rain Rate (mm h−1) | |
|---|---|---|---|---|---|---|
| P05 | −0.9 | 48 | 4.1 | −6.7 | 0.6 | 0.03 |
| P95 | 5.6 | 99 | 7.9 | 2.2 | 12.2 | 4.08 |
| Mean | 2.1 | 81 | 6.3 | −1.2 | 4.6 | 1 |
| Type of Hydrometeor | Diameter Range (mm) | Fall Velocity (m s−1) |
|---|---|---|
| Rain | 0.25 ≤ D ≤ 8 AM18 | 9.65 − (10.3 e−0.6D) GK49, AT73 |
| Snow | 0.5 ≤ D ≤ 9FH20 | 0.79D0.27 FH20, LH74 |
| Wet Snow | 0.5 ≤ D ≤ 9 FH20 | 4.65 − (5 e−0.95D) FH20 |
| Lump Graupel | 0.5 ≤ D ≤ 5 LH74 | 1.3 D0.66 LH74 |
| Graupel | 1.16 D0.46 LH74 | |
| Soft Hail | 5 ≤ D ≤ 20 FR13 | 8.445(0.1D)0.553 KN83 |
| Fresh Hail | 12.43(0.1D)0.5 FR13 | |
| Lump Hail | 10.58 (0.1D)0.267 KN83 |
| M1 | M2 | M3 | M4 | M5 | |
|---|---|---|---|---|---|
| Rain | 1 | 1 | 1 | 1 | 1 |
| Snow | YU20 | BR07 | YU20 | BR07 | 1 |
| Wet snow | 0.2 | 0.2 | 0.2 | 0.2 | 1 |
| Lump graupel | 0.7 | 0.7 | 0.44 | 0.44 | 1 |
| Graupel | 0.5 | 0.5 | 0.33 | 0.33 | 1 |
| Soft hail | 0.61 | 0.61 | 0.61 | 0.61 | 1 |
| Fresh hail | 0.7 | 0.7 | 0.61 | 0.61 | 1 |
| Lump hail | 0.91 | 0.82 | 0.9 | 0.82 | 1 |
| Integration Time | 15 min | 30 min | 60 min |
|---|---|---|---|
| Total records | 36 496 | 18 248 | 9124 |
| Retrieved measurements | 35 603 | 17 769 | 8857 |
| Error flags | 486 | 118 | 74 |
| Precipitation records | 7776 | 4547 | 2711 |
| Precipitation with R > 0.01 mm h−1 | 7724 | 4455 | 2595 |
| Valid DSD | 5004 | 2934 | 1680 |
| Common high-quality records | 4983 | 2876 | 1611 |
| Identified Solid precipitation (Ta ≤ −1 °C) | 159 (3%) | 86 (3%) | 40 (2%) |
| Identified Liquid precipitation (Ta ≥ 3 °C) | 298 (6%) | 217(7%) | 152 (9%) |
| Unclassified precipitation (−1 °C < Ta < 3 °C) | 4526 (91%) | 2573 (90%) | 1419 (89%) |
| Disdrometer Precipitation Phase (DPP) | |||
|---|---|---|---|
| Identified Precipitation | Snowfall | Mix | Rainfall |
| Liquid | 73 (23.6) | 46 (15.4) | 179 (61) |
| RLW | 6(4.6) | 12(9.2) | 112 (86.2) |
| RMW | 26 (26) | 21(21) | 53 (53) |
| RHW | 41 (60.3) | 13 (19.1) | 14 (20.6) |
| Solid | 154 (96.8) | 2 (1.3) | 3 (1.9) |
| SLW | 72(97.3) | 1 (1.3) | 1 (1.3) |
| SMW | 56(96.6) | 1 (1.7) | 1 (1.7) |
| SHW | 26 (96.3) | 0 (0) | 1 (3.7) |
| Precipitation Phase (Based on Ta) | Cluster | N (%) | Ta (°C) | Td (°C) | q (g kg−1) | RH (%) | Ws (m s−1) |
|---|---|---|---|---|---|---|---|
| Liquid | RLW | 130 (44) | 3.57 | 2.32 | 7.96 | 91.67 | 2.62 |
| RMW | 100 (35) | 3.66 | 1.3 | 7.41 | 84.88 | 5.92 | |
| RHW | 68 (20) | 3.93 | 0.28 | 6.87 | 77.32 | 11.93 | |
| Solid | SLW | 74 (47) | −1.39 | −1.63 | 6.05 | 98.35 | 1.74 |
| SMW | 58 (36) | −1.57 | −2.04 | 5.87 | 96.64 | 3.68 | |
| SHW | 27 (17) | −1.5 | −2.22 | 5.79 | 94.9 | 6.53 |
| Particles Filtered (%) | logNorm (log (Particles)) | Number of Particles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | FT | Measured | Corrected | ||
| Rain | 1.8 × 10−4 | 4.4 × 10−4 | 0.74 | 1.4 × 10−4 | 11.56 | 12.3 | 2.85 | 1.01 × 104 | 9.34 × 103 |
| RLW | 2.9 × 10−4 | 6.2 × 10−4 | 0.24 | 0 | 5.62 | 5.12 | 2.77 | 9.68 × 103 | 8.91 × 103 |
| RMW | 1.1 × 10−4 | 4.6 × 10−4 | 0.83 | 2 × 10−4 | 14.06 | 11.23 | 2.84 | 1.09 × 104 | 1.02 × 104 |
| RHW | 0.7 × 10−4 | 3.2 × 10−4 | 1.55 | 3.2 × 10−4 | 19.25 | 18.36 | 3.01 | 9.29 × 103 | 8.97 × 103 |
| Snow | 0 | 2.1 × 10−4 | 4.25 | 0 | 7.02 | 11.28 | 3.04 | 1.82 × 104 | 1.65 × 104 |
| SLW | 0 | 2.8 × 10−4 | 5.11 | 0 | 4.49 | 9.61 | 3.08 | 1.91 × 104 | 1.71 × 104 |
| SMW | 0 | 0 | 3.92 | 0 | 7.44 | 11.36 | 3.04 | 1.78 × 104 | 1.63 × 104 |
| SHW | 0 | 0 | 2.62 | 0 | 13.07 | 15.69 | 2.96 | 1.66 × 104 | 1.55 × 104 |
| 15 min | 30 min | 60 min | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | RMSE | Diff | Acr | r2 | RMSE | Diff | Acr | r2 | RMSE | Diff | Acr | |
| RLW | ||||||||||||
| M1 | 0.18 | 0.44 | −0.61 | 0.39 | 0.56 | 0.54 | −0.51 | 0.49 | 0.76 | 0.69 | −0.45 | 0.55 |
| M2 | 0.19 | 0.44 | −0.61 | 0.39 | 0.56 | 0.54 | −0.51 | 0.49 | 0.76 | 0.69 | −0.45 | 0.55 |
| M3 | 0.19 | 0.44 | −0.62 | 0.38 | 0.56 | 0.55 | −0.51 | 0.49 | 0.76 | 0.69 | −0.45 | 0.55 |
| M4 | 0.19 | 0.44 | −0.62 | 0.38 | 0.56 | 0.55 | −0.52 | 0.48 | 0.76 | 0.69 | −0.45 | 0.55 |
| M5 | 0.17 | 0.46 | −0.35 | 0.65 | 0.58 | 0.47 | −0.2 | 0.8 | 0.78 | 0.51 | −0.1 | 0.9 |
| RMW | ||||||||||||
| M1 | 0.42 | 0.36 | −0.54 | 0.46 | 0.65 | 0.46 | −0.49 | 0.51 | 0.68 | 0.73 | −0.38 | 0.62 |
| M2 | 0.42 | 0.36 | −0.56 | 0.44 | 0.66 | 0.46 | −0.50 | 0.50 | 0.69 | 0.73 | −0.40 | 0.60 |
| M3 | 0.43 | 0.36 | −0.57 | 0.43 | 0.66 | 0.47 | −0.53 | 0.47 | 0.69 | 0.74 | −0.42 | 0.58 |
| M4 | 0.42 | 0.37 | −0.59 | 0.41 | 0.65 | 0.48 | −0.54 | 0.46 | 0.69 | 0.75 | −0.44 | 0.56 |
| M5 | 0.42 | 0.40 | −0.20 | 0.80 | 0.64 | 0.51 | −0.15 | 0.85 | 0.66 | 0.84 | 0.04 | 1.04 |
| RHW | ||||||||||||
| M1 | 0.58 | 0.30 | −0.43 | 0.57 | 0.59 | 0.51 | −0.54 | 0.46 | 0.70 | 0.77 | −0.52 | 0.48 |
| M2 | 0.54 | 0.32 | −0.52 | 0.48 | 0.58 | 0.52 | −0.57 | 0.43 | 0.70 | 0.80 | −0.55 | 0.45 |
| M3 | 0.59 | 0.30 | −0.45 | 0.55 | 0.60 | 0.51 | −0.56 | 0.44 | 0.72 | 0.78 | −0.55 | 0.45 |
| M4 | 0.55 | 0.32 | −0.54 | 0.46 | 0.59 | 0.53 | −0.60 | 0.40 | 0.72 | 0.81 | −0.59 | 0.41 |
| M5 | 0.53 | 0.64 | 0.37 | 1.37 | 0.55 | 0.53 | −0.27 | 0.73 | 0.67 | 0.74 | −0.23 | 0.77 |
| Liquid Precipitation | ||||||||||||
| M1 | 0.34 | 0.39 | −0.55 | 0.45 | 0.59 | 0.51 | −0.51 | 0.49 | 0.71 | 0.72 | −0.45 | 0.55 |
| M2 | 0.34 | 0.39 | −0.58 | 0.42 | 0.59 | 0.52 | −0.52 | 0.48 | 0.71 | 0.73 | −0.46 | 0.54 |
| M3 | 0.35 | 0.39 | −0.57 | 0.43 | 0.6 | 0.52 | −0.53 | 0.47 | 0.72 | 0.73 | −0.47 | 0.53 |
| M4 | 0.34 | 0.39 | −0.59 | 0.41 | 0.59 | 0.52 | −0.54 | 0.46 | 0.72 | 0.74 | −0.48 | 0.52 |
| M5 | 0.31 | 0.49 | −0.15 | 0.85 | 0.58 | 0.5 | −0.2 | 0.8 | 0.7 | 0.68 | −0.1 | 0.9 |
| 15 min | 30 min | 60 min | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | Diff | Acr | RMSE | Diff | Acr | RMSE | Diff | Acr | |
| SLW | |||||||||
| M1 | 0.84 | 0.71 | 1.71 | 2.49 | 0.88 | 1.88 | 1.15 | 0.88 | 1.88 |
| M2 | 0.68 | 0.44 | 1.44 | 2.08 | 0.64 | 1.64 | 0.67 | 0.44 | 1.44 |
| M3 | 0.35 | 0.29 | 1.29 | 0.97 | 0.37 | 1.37 | 0.65 | 0.52 | 1.52 |
| M4 | 0.23 | 0.02 | 1.02 | 0.58 | 0.14 | 1.14 | 0.20 | 0.08 | 1.08 |
| M5 | 3.49 | 3.08 | 4.08 | 9.80 | 3.60 | 4.60 | 5.37 | 3.82 | 4.82 |
| SMW | |||||||||
| M1 | 0.38 | 0.64 | 1.64 | 0.54 | 0.65 | 1.65 | 1.36 | 0.67 | 1.67 |
| M2 | 0.24 | 0.29 | 1.29 | 0.28 | 0.27 | 1.27 | 0.85 | 0.36 | 1.36 |
| M3 | 0.20 | 0.33 | 1.33 | 0.29 | 0.35 | 1.35 | 0.63 | 0.31 | 1.31 |
| M4 | 0.08 | −0.02 | 0.98 | 0.09 | −0.04 | 0.96 | 0.23 | 0.00 | 1.00 |
| M5 | 1.61 | 2.61 | 3.61 | 2.20 | 2.58 | 3.58 | 5.99 | 2.77 | 3.77 |
| SHW | |||||||||
| M1 | 0.23 | 0.25 | 1.25 | 0.67 | 0.48 | 1.48 | 0.44 | 0.33 | 1.33 |
| M2 | 0.17 | 0.11 | 1.11 | 0.45 | 0.26 | 1.26 | 0.22 | 0.16 | 1.16 |
| M3 | 0.11 | 0.04 | 1.04 | 0.33 | 0.17 | 1.17 | 0.14 | 0.11 | 1.11 |
| M4 | 0.10 | −0.10 | 0.90 | 0.18 | −0.05 | 0.95 | 0.08 | −0.05 | 0.95 |
| M5 | 1.10 | 1.30 | 2.30 | 2.93 | 2.19 | 3.19 | 1.88 | 1.32 | 2.32 |
| Solid Precipitation | |||||||||
| M1 | 0.63 | 0.62 | 1.62 | 1.39 | 0.73 | 1.73 | 1.17 | 0.72 | 1.72 |
| M2 | 0.49 | 0.35 | 1.35 | 1.11 | 0.44 | 1.44 | 0.71 | 0.37 | 1.37 |
| M3 | 0.27 | 0.26 | 1.26 | 0.56 | 0.33 | 1.33 | 0.60 | 0.37 | 1.37 |
| M4 | 0.17 | −0.01 | 0.99 | 0.32 | 0.04 | 1.04 | 0.20 | 0.03 | 1.03 |
| M5 | 2.61 | 2.69 | 3.69 | 5.49 | 2.98 | 3.98 | 5.29 | 3.04 | 4.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gualco, L.F.; Campozano, L.; Maisincho, L.; Robaina, L.; Muñoz, L.; Ruiz-Hernández, J.C.; Villacís, M.; Condom, T. Corrections of Precipitation Particle Size Distribution Measured by a Parsivel OTT2 Disdrometer under Windy Conditions in the Antisana Massif, Ecuador. Water 2021, 13, 2576. https://doi.org/10.3390/w13182576
Gualco LF, Campozano L, Maisincho L, Robaina L, Muñoz L, Ruiz-Hernández JC, Villacís M, Condom T. Corrections of Precipitation Particle Size Distribution Measured by a Parsivel OTT2 Disdrometer under Windy Conditions in the Antisana Massif, Ecuador. Water. 2021; 13(18):2576. https://doi.org/10.3390/w13182576
Chicago/Turabian StyleGualco, Luis Felipe, Lenin Campozano, Luis Maisincho, Leandro Robaina, Luis Muñoz, Jean Carlos Ruiz-Hernández, Marcos Villacís, and Thomas Condom. 2021. "Corrections of Precipitation Particle Size Distribution Measured by a Parsivel OTT2 Disdrometer under Windy Conditions in the Antisana Massif, Ecuador" Water 13, no. 18: 2576. https://doi.org/10.3390/w13182576







