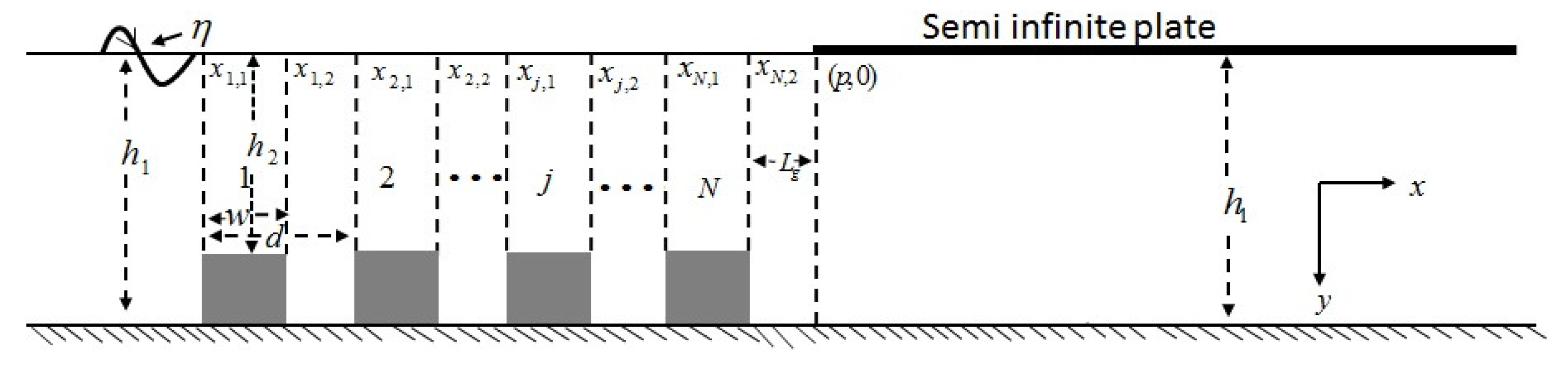
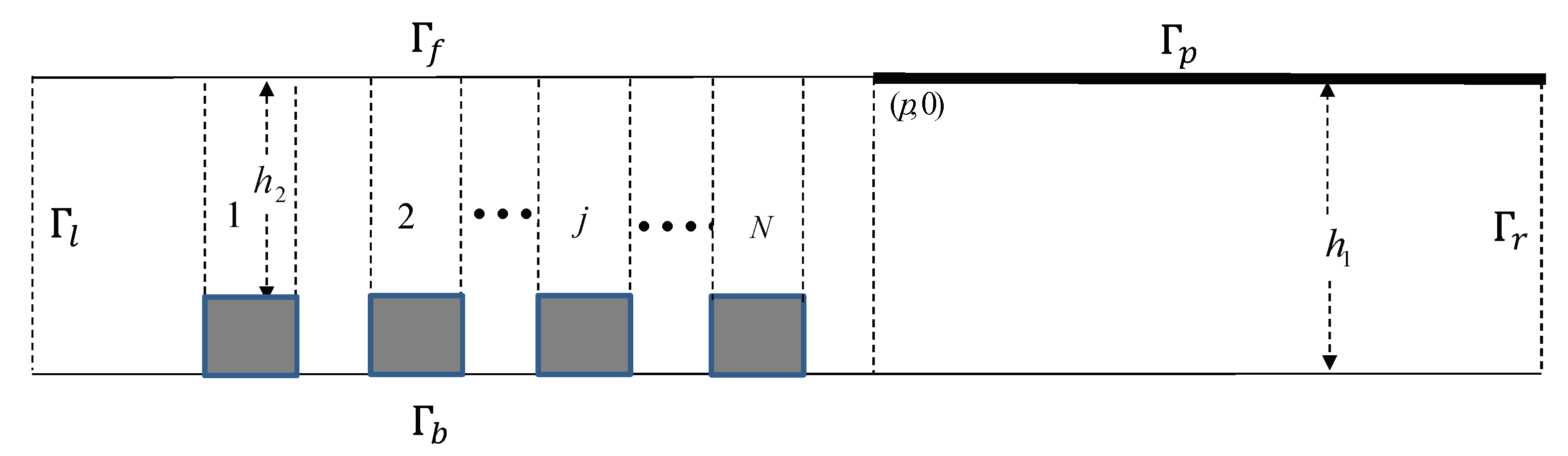
In this section, using MATLAB software, numerical codes are written to analyze the effect of a semi-infinite floating plate on Bragg scattering of surface waves by multiple undulations in the seabed. Various non-dimensional physical parameters, such as width
, gap between the leading edges of two adjacent trenches/breakwaters
of trench/breakwater, gap between right-most trench/breakwater, and plate
, are considered for the analysis of Bragg scattering of gravity waves, as in Kar et al. [
18]. Moreover, the values of different physical parameters, such as water depth
m, incident wavelength
m, and plate rigidity
(same as considered by Kalyanaraman et al. [
12]), and mass density of the plate is
, with density of ice
kg m
, plate thickness
m, density of water
kg m
, and
ms
are kept fixed, unless stated otherwise.
6.1. Semi-Infinite Plate in the Absence of Bottom Undulation
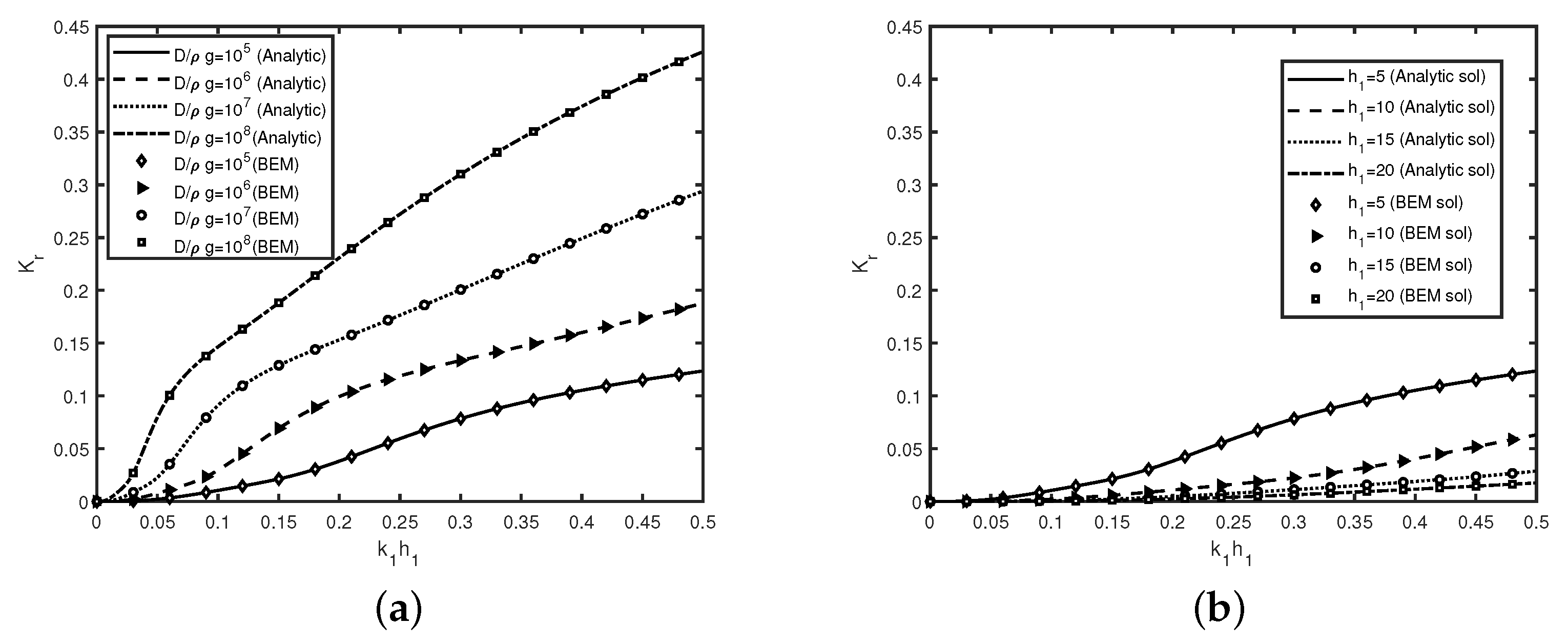
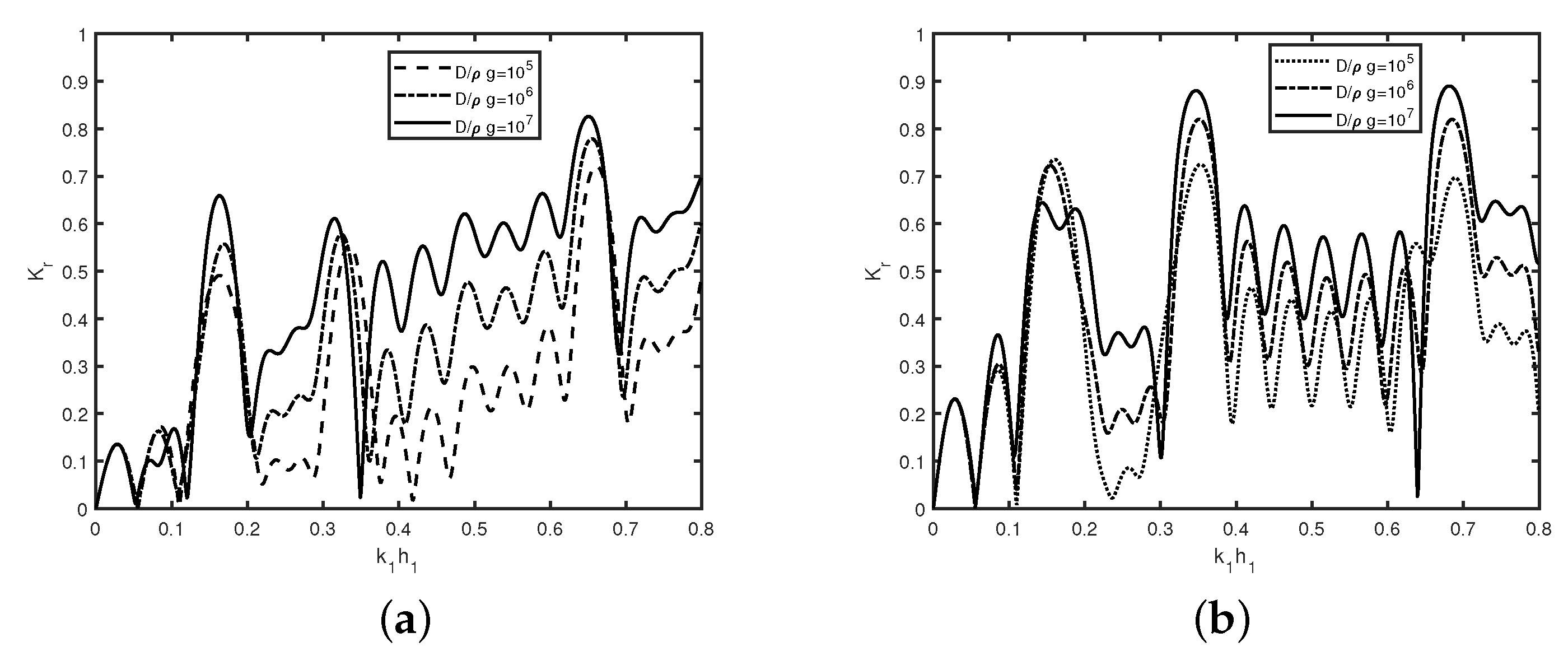
In
Figure 3, the reflection coefficient
is plotted against wavenumber
for different values of (
Figure 3a) rigidity
with
m and (
Figure 3b) water depth
with rigidity
in the absence of bottom bed undulation. In
Table 1, the energy identity as in Equation (
31) for various wave number are computed in case of waves scattering by semi-infinite floating flexible plate in finite water depth. The relative errors corresponding to
Figure 3a is provided in
Table 2. It is to be noted that the relative error is calculated by comparing the BEM-based results with the analytic results.
Table 2 reveals that the maximum relative error is less than 5%, which depends on the wave number
.
Figure 3a shows that, for a higher wave number, reflection increases rapidly compared to the lower wavenumber values.
Figure 3a depicts that, with an increase of rigidity of ice-sheet, wave reflection coefficient
increases, which is similar as observed in Sahoo et al. [
3]. In
Figure 3b, reflection coefficient
decreases as water depth
increases with an increases in wavenumber
which may be due to less resonance in higher water depth
.
Figure 3 reveals that resonance in wave reflection does not occur as the wave number increases for the semi-infinite plate in the absence of seabed undulations. Further,
Figure 3a,b reveal that rigidity of the plate has more effect on wave reflection compared to water depth. Moreover, both the sub-figures reveal that the various computational results obtained via the numerical method agree well with the analytic solution, as discussed in the case of long waves. Thus, in the subsequent study, our analyses will be based on the analytic solution associated with long waves.
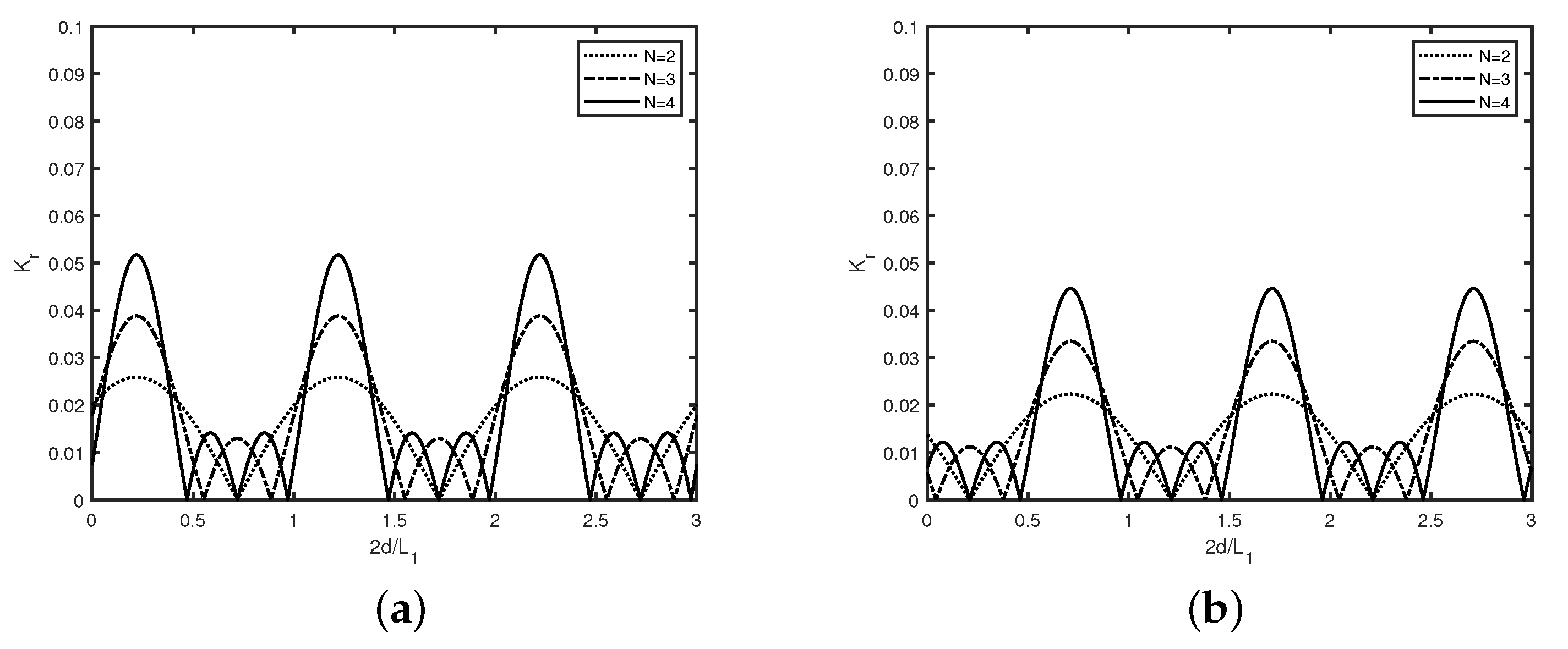
6.2. Trenches/Breakwaters in the Absence of Semi-Infinite Plate
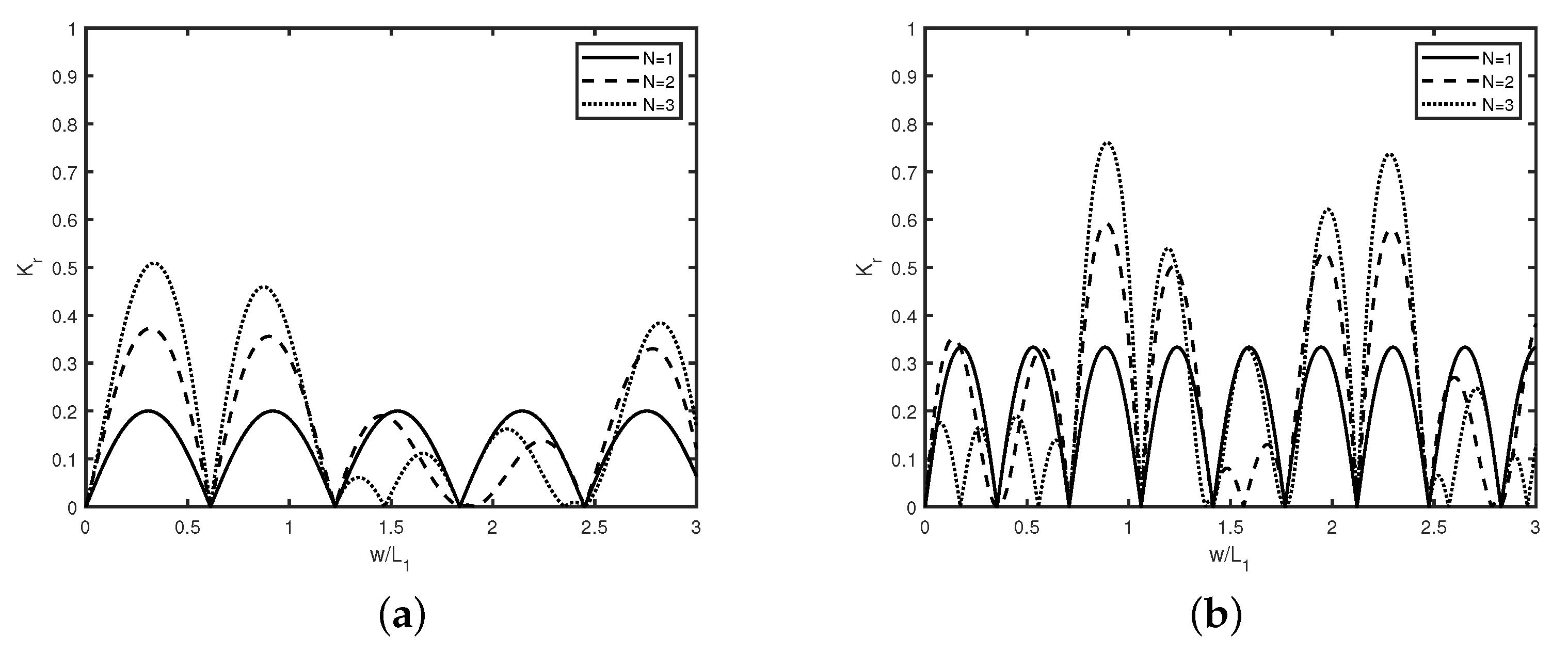
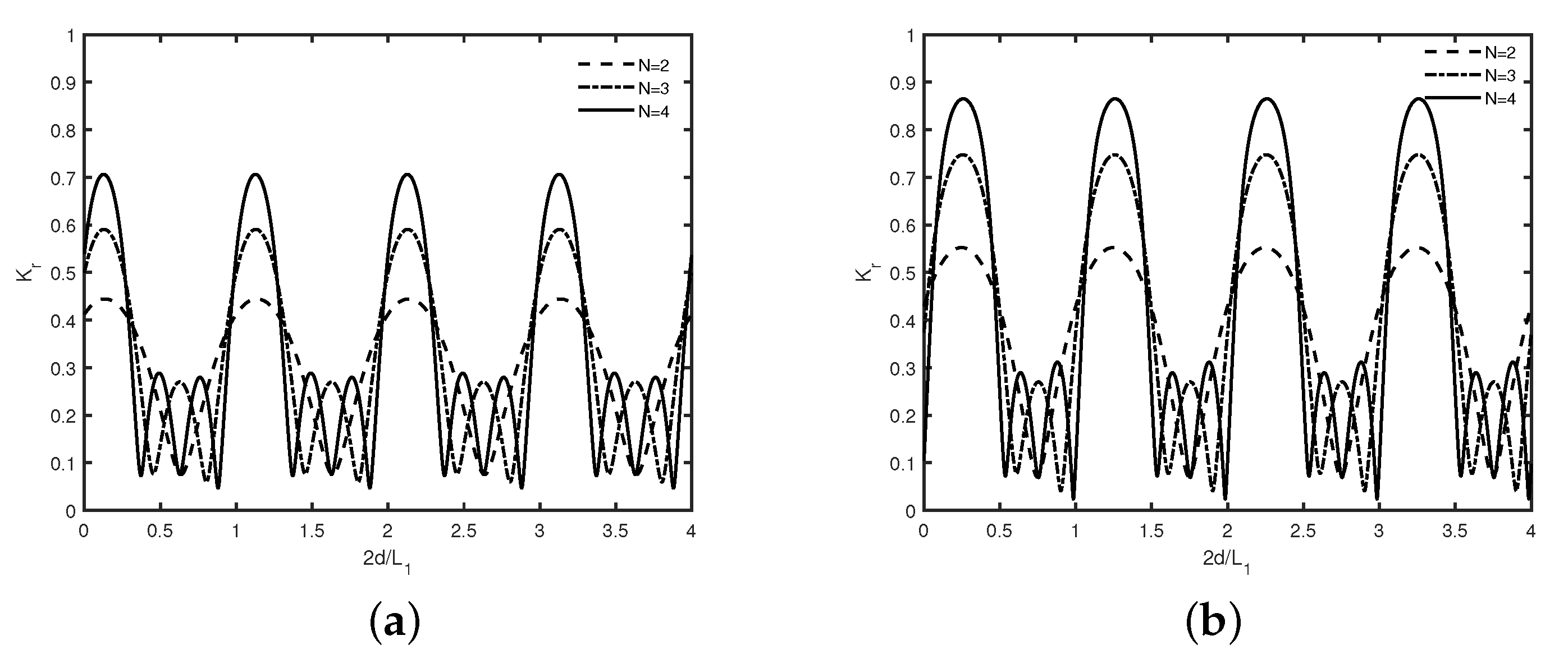
The reflection coefficient
versus trench width
is plotted in
Figure 4 for different number
N of rectangular (a) trenches and (b) breakwaters in the absence of semi-infinite plate with gap
,
m.
Figure 4a depicts the occurrence of common zero minima in wave reflection irrespective of the number of trenches when
is an integer multiple of 0.6 and alternately maxima occur between two consecutive zero minima in wave reflection. On the other hand,
Figure 4b reveals that, in case of breakwaters, zeros in reflection occur when
is an integer multiple of 0.35, whilst maxima in wave reflection occurs between consecutive minima. Further, both the sub-figures depict that the reflection coefficient increases as the number of submerged trenches/breakwaters increases. A comparison of both the sub-figures reveals that optima in wave reflection occur for smaller values of
in case of submerged breakwaters than that of the submerged trenches. Further, for the same number of trenches/breakwaters, it may be noted that the maximum amplitude of wave reflection is smaller in the case of submerged trenches than that of the breakwaters. Further, both the sub-figures depict that Bragg reflection occurs in the presence of multiple submerged trenches and breakwaters. Moreover, occurrence of sub-harmonic peaks are noticed when the number of trenches/breakwaters are more than two, which is similar to the observation made in Kar et al. [
29,
30]. In the subsequent analyses, the values of
in case of submerged trenches and
in case of breakwaters are kept fixed, unless otherwise mentioned.
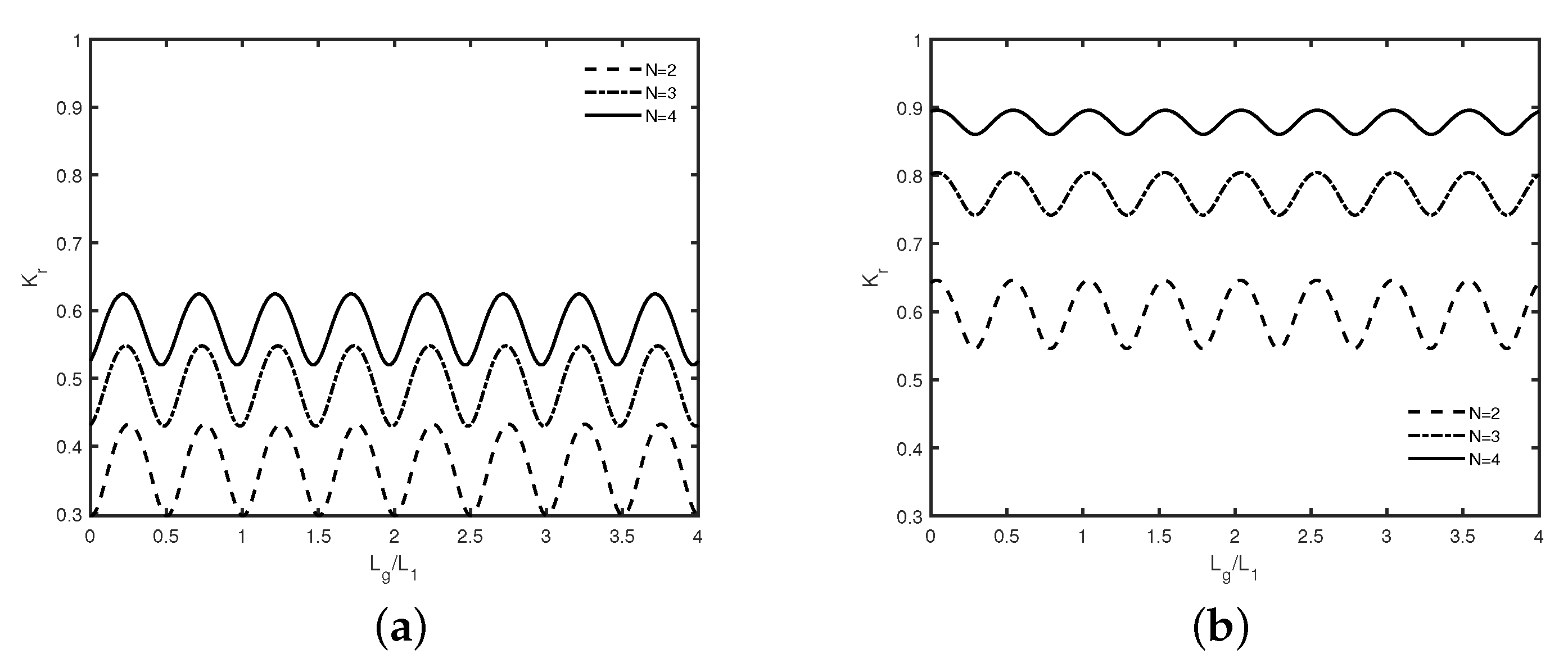
In
Figure 5, reflection coefficient
is plotted against gap
for different number
N of rectangular (
Figure 5a) trenches with width
and (
Figure 5b) breakwaters with width
in the absence of semi-infinite plate with
m.
Figure 5a shows that all the curves attain their minima for
in the case of trenches, whereas, in
Figure 5b, all curves attain their minima for
. Therefore, both the figures reveal that, in the case of an even number of trenches or breakwaters, all the curves match if the gap in between the adjacent sides of trenches or breakwaters is half of the wavelength of the incident wave, i.e.,
. Hence, we keep fix the values of
in case of trenches, whereas
in case of breakwaters for which minima in wave reflection occur in case of even and odd number of trenches or breakwaters. Further, it may be noted that, between two harmonic peaks,
sub-harmonic peaks occur, with
N being the number of submerged trenches/breakwaters with Bragg reflection occurring in the presence of multiple undulations irrespective of submerged trenches or breakwaters. A similar observation has been noticed in
Figure 4.
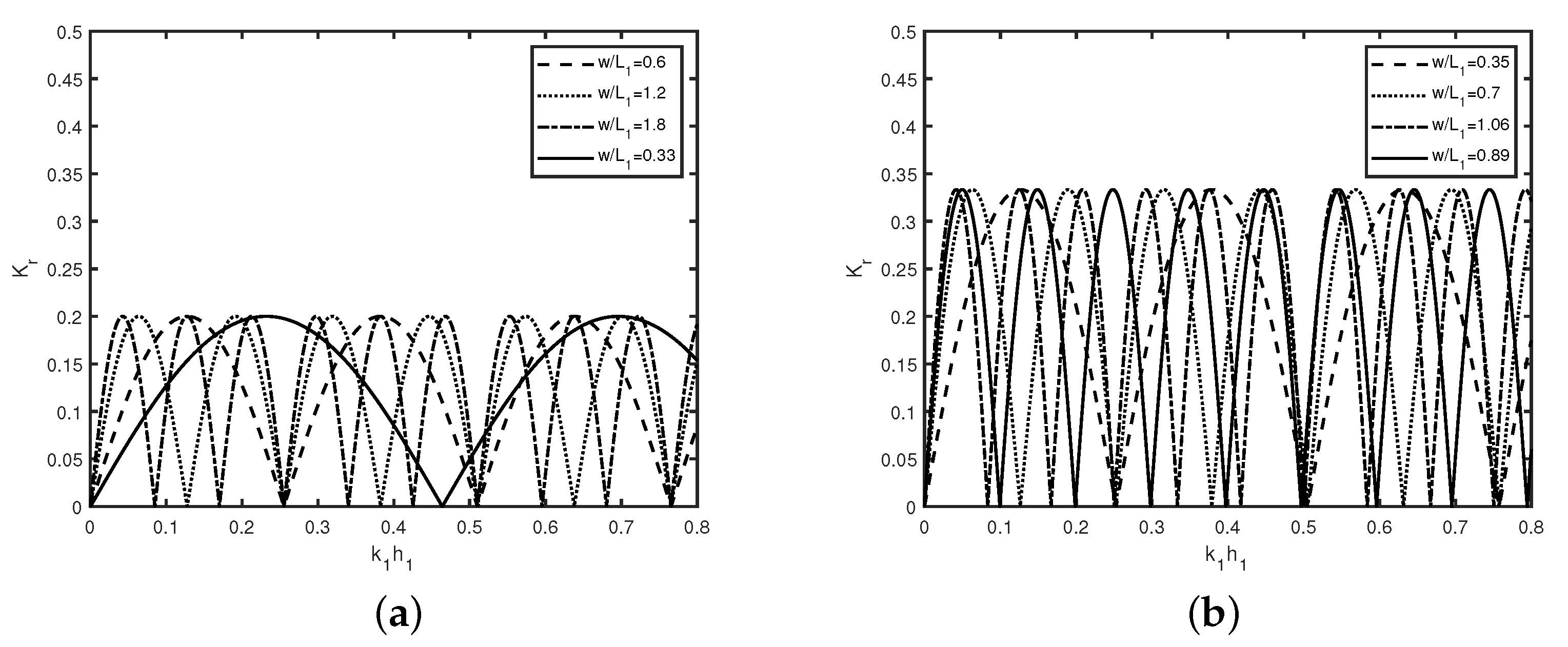
In
Figure 6, the variation of the reflection coefficient
versus wave number
is shown for a single rectangular submerged (
Figure 6a) trench and (
Figure 6b) breakwater in the absence of semi-infinite plate for different widths
, as mentioned in
Table 3. It is observed that a complete cycle occur when wave number
irrespective of single trench or breakwater (see
Table 4). Further, common maxima/minima occur in wave reflection in case of trenches and breakwaters within periodic range of the values of
. Similar results has been observed in
Figure 4 and
Figure 5 with variation of gap, as well as width of trenches/breakwaters, and also in Reference [
18]. Moreover,
Figure 6a,b reveal that the amplitude of the peaks are constant irrespective of the width
for a single trench/breakwater.
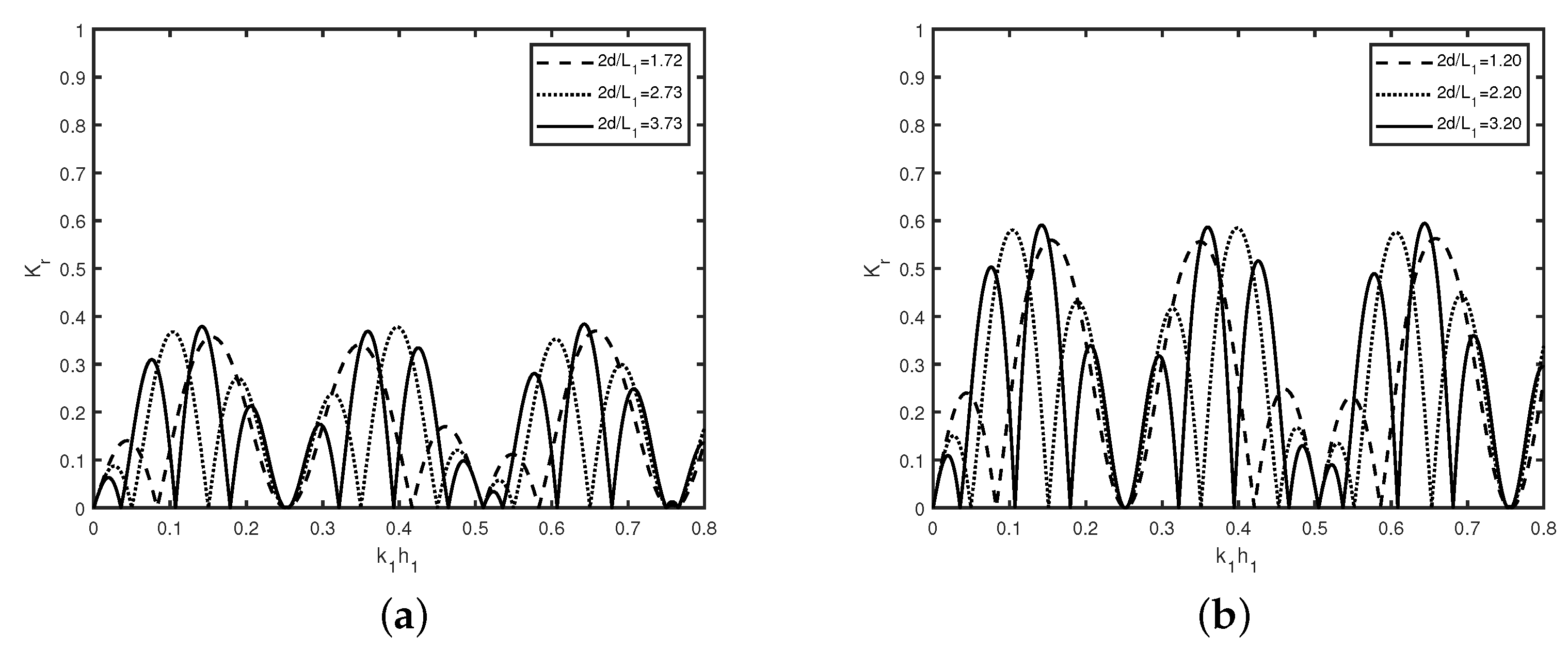
In
Figure 7, the variation of reflection coefficient
versus wave number
is exhibited in case of double rectangular (
Figure 7a) trenches with width
and (
Figure 7b) breakwaters with
for different values of
in the absence of semi-infinite plate.
Figure 7a,b reveal that cycles are completed at the same values of wave number
. Moreover, amplitude of peak in the reflection coefficient
remains constant for different values of
in case of both of trenches and breakwaters. Further,
Figure 7 reveals that, with an increase in gap
, amplitude of harmonic peak in wave reflection increases in each cycle with an increase in wave number
. Further, it may be noted that sub-harmonic peak does not occur as reflection coefficient
is plotted in case of double trenches and breakwaters.
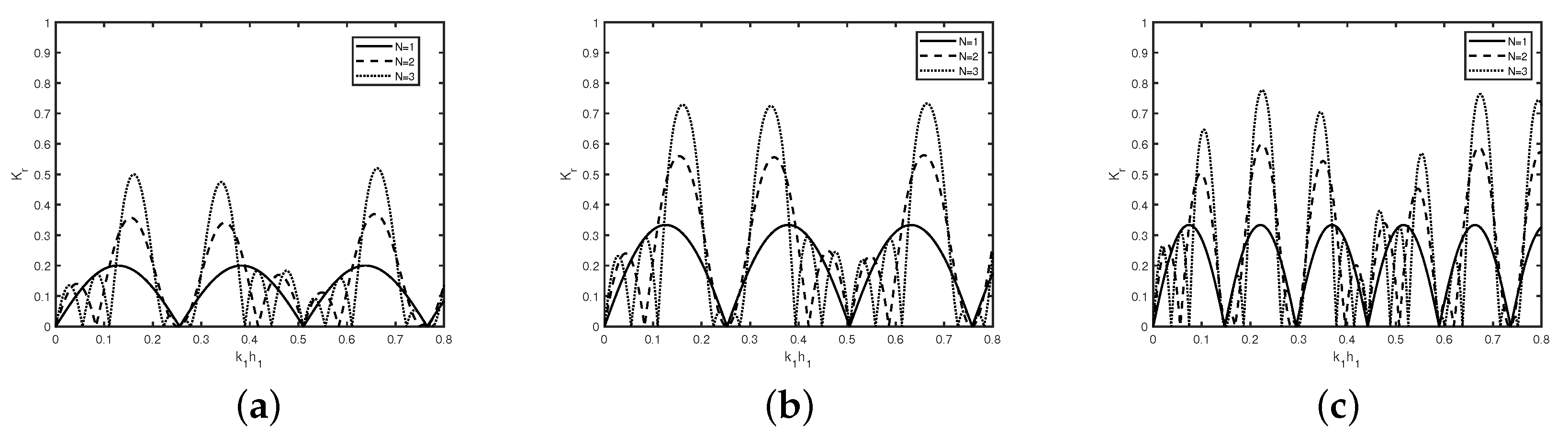
In
Figure 8, the reflection coefficient
is plotted against wavenumber
for different number
N of rectangular (
Figure 8a) trenches with width
,
and (
Figure 8b) breakwaters with
,
in the absence of semi-infinite plate.
Figure 8a reveals that three full cycles are completed in case of trenches at
, whereas, in
Figure 8b, in case of breakwaters, three full cycles are completed for the same wavenumber in the range
with an increase in
N for different values of trenches and breakwaters widths and gap as mentioned in
Table 3.
Figure 8a,c describes the comparison between the trenches and breakwaters. It is observed that the number of full cycles in the case of trenches is two less than that of breakwaters. This happens due to the formation of nodes or anti-nodes along the interface boundaries of the trenches and breakwaters. Moreover, the number of common zero minima in the case of breakwaters is two greater than that of trenches. Further, the amplitude of the harmonic peaks, i.e., peaks in each bandwidth are not equal as the number of trenches or breakwaters increases. As the number of trenches or breakwaters
N increases, the sub-harmonic peaks occur, which is similar to that of the phenomena observed in Kar et al. [
29] in the case of scattering of gravity waves by an array of trenches.
In
Figure 9, the reflection coefficient
is plotted against wave number
for different depths
of (
Figure 9a) submerged trenches with
,
and (
Figure 9b) breakwaters with
,
in the absence of semi-infinite plate with
.
Figure 9a reveals that, with an increase in trench depth, the reflection coefficient increases with a rise in wave number.
Figure 9b reveals that, as breakwater height decreases, wave reflection coefficient
decreases with an increase in wave number
, which occurs as more wave energy is trapped due to higher values of breakwaters height. From
Figure 9a,b, it is observed that, for a smaller wave number, phase-shift of the wave reflection matches, whereas, for a higher wave number, it does not occur.
6.3. Plate-Trench Combination
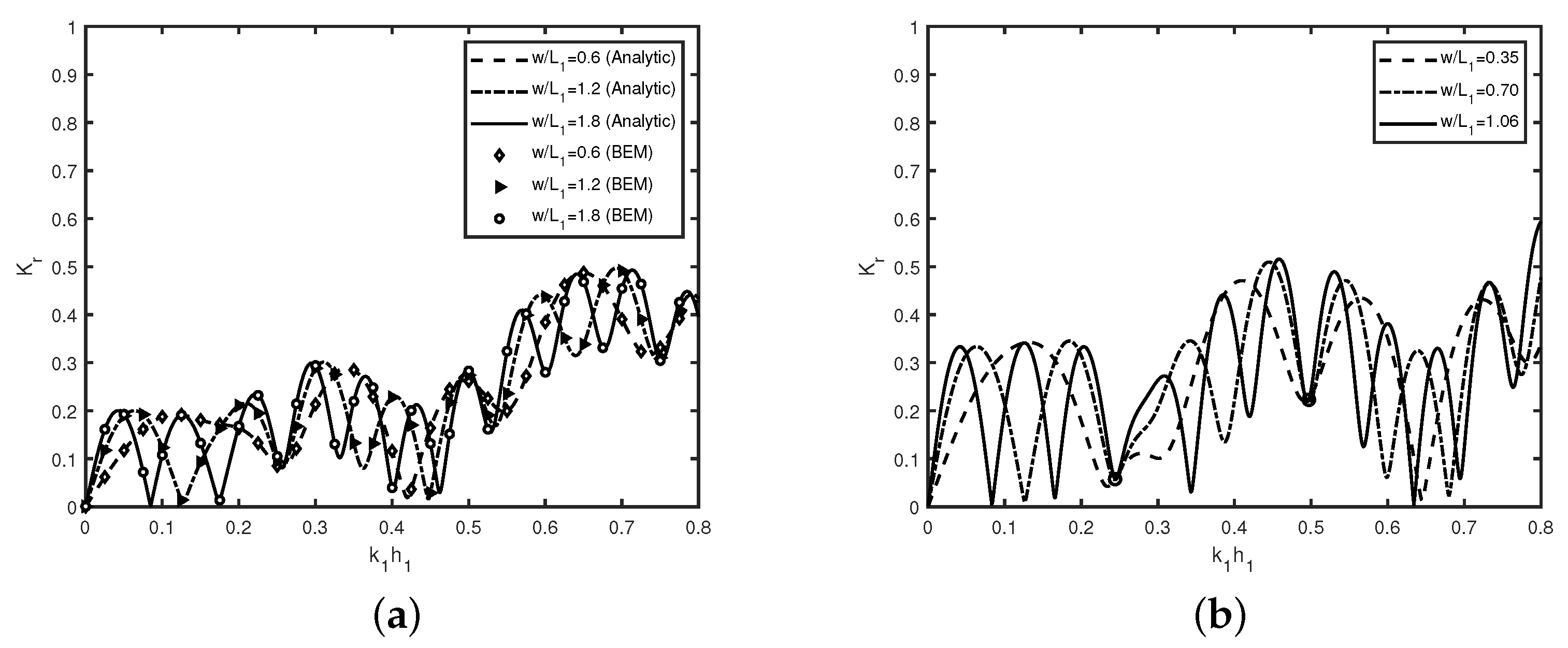
In
Figure 10, the variation of the reflection coefficient
versus wavenumber
is demonstrated for different values of single (
Figure 10a) trench and (
Figure 10b) breakwater width
(as mentioned in
Table 3) with plate rigidity
in the presence of semi-infinite plate.
Figure 10a reveals that results obtained by both analytic and numerical methods agree well in the presence of a single trench and a semi-infinite plate.
Figure 10a depicts that number of complete cycles are fixed, as observed in
Figure 6a. However, because of the presence of floating plate, wave reflection increases, in general, irrespective of the values of the wavenumber
, and zero minima in wave reflection does not occur for higher values of wave number, which is due to the partial reflection of surface waves with an increase in wavenumber, as observed in
Figure 3. The notation ‘∘’ denotes the points where minima in wave reflection occur exactly for the same wave number except for certain non-zero values of the reflection coefficient. Further,
Figure 10b reveals that the number of common minima in wave reflection remains the same as observed in
Figure 6b in the absence of floating plate. Similar phenomena is observed in the case of Bragg reflection of surface gravity waves by an array of rectangular breakwaters in the presence of a floating dock, as in Kar et al. [
30].
Figure 10a,b reveals that the number of bandwidth remain constant irrespective of the increase in the width of the trench/breakwater
. However, the number of oscillations in each cycle/bandwidth increases apart from an increase in the value of minima in wave reflection, which is due to the presence of the floating elastic plate.
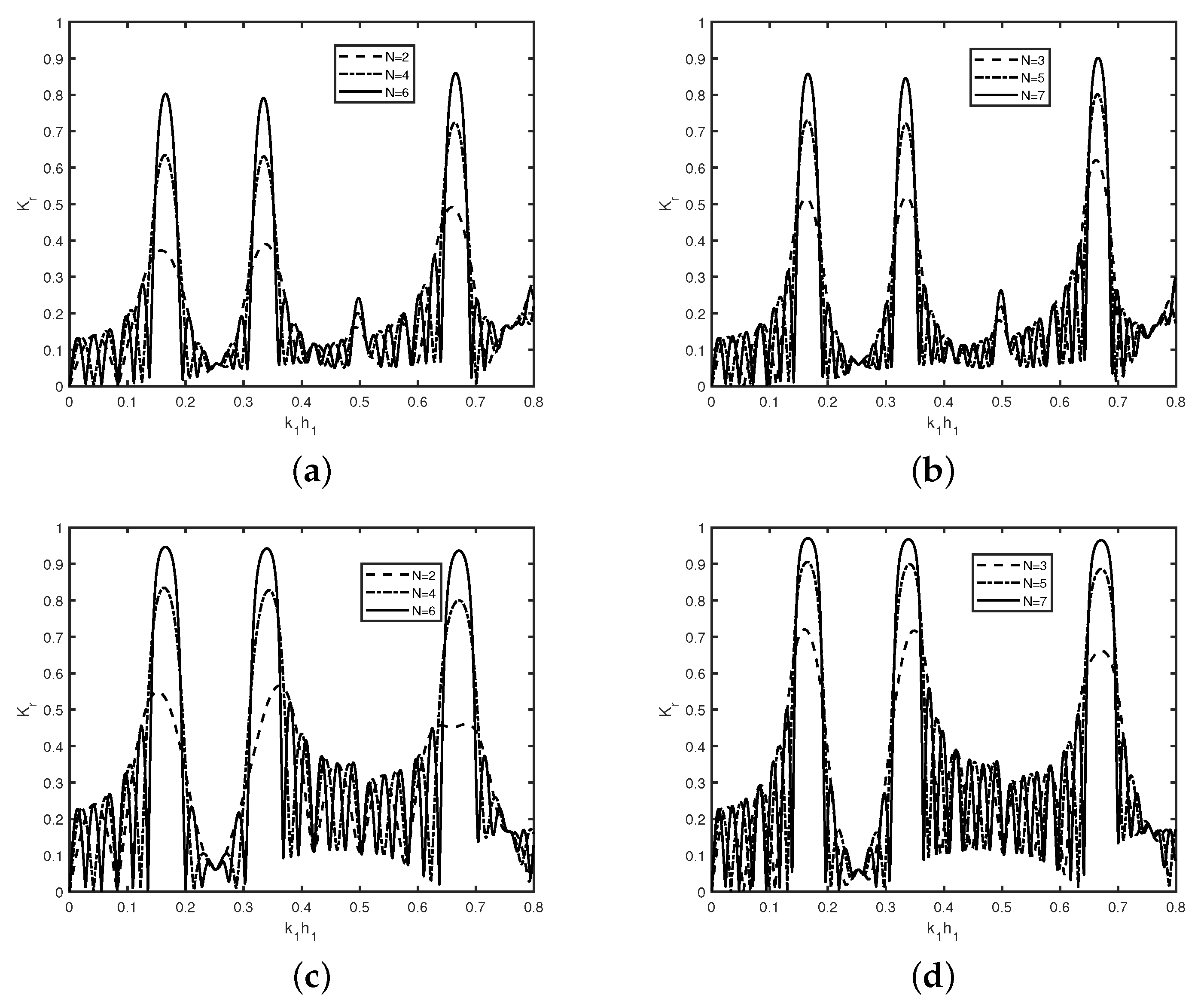
In
Figure 11, the variation of the reflection coefficient
versus wave number
is exhibited for different number
N of trenches in
Figure 11a,b with
and
, and breakwaters in
Figure 11c,d with
and
in the presence of the semi-infinite plate with
and
.
Figure 11 reveals that, with an increase in the number
N of trenches and breakwaters, the amplitude of peak in the band-width increases, whereas the length of the band-width decreases. The decrease in bandwidth is due to an increase in the resonating interaction within the gap between the trenches and breakwater, whilst the increase in the amplitude of the resonating peaks is due to the superposition of the higher number of standing waves generated within the trenches/breakwaters and the gaps between them. Further, it is observed that, irrespective of trenches and breakwaters, for a certain wave-number, common minimum occurs when
N is even, whereas maximum occurs at
out of phase when
N is odd. A similar observation has been found in the absence of the semi-infinite plate in Kar et al. [
18], except the rise in the minima in wave reflection in the presence of the plate. However, Bragg reflection occurs in both the cases of multiple trenches and breakwaters in isolation in the presence of the semi-infinite plate. Moreover, at
, one cycle is completed in the case of breakwaters, whereas, in the case of trenches, one sub-harmonic peak is observed, which is similar to
Figure 10. A comparison among the
Figure 6,
Figure 8,
Figure 10, and
Figure 11 depicts that, in the presence of semi-infinite plate, the position of cycle shifts upward, as observed in the absence of semi-infinite plate.
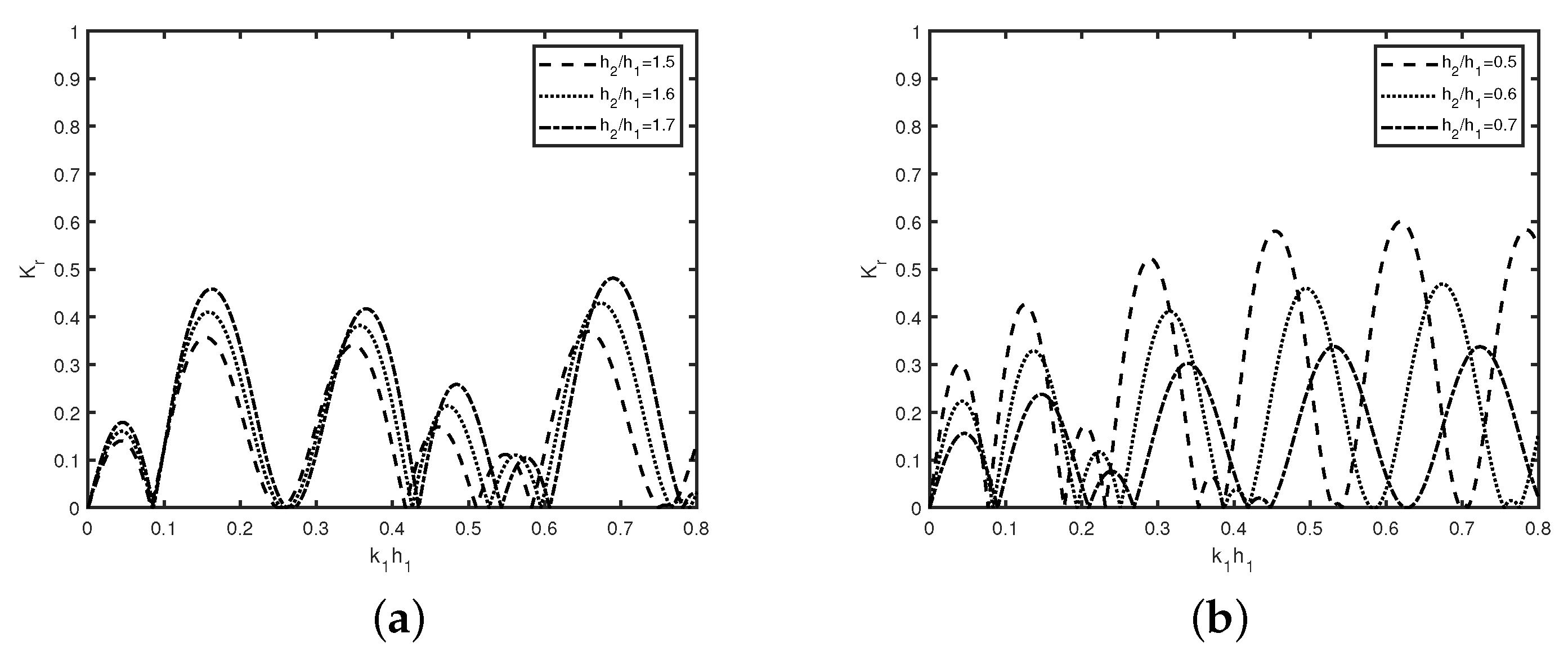
In
Figure 12, the reflection coefficient
is plotted against the wavenumber
for different values of depth ratios
of (
Figure 12a) trenches with
, and (
Figure 12b) breakwaters with
,
in the presence of a semi-infinite plate.
Figure 12 reveals that the reflection coefficient
increases, in general, with an increase in depth ratio
in case of multiple trenches, whilst wave reflection decreases in the case of breakwaters, which is similar as observed in
Figure 9. Further, zero reflection does not occur in the presence of a semi-infinite plate. Further, it is observed that higher wave reflection occur with an increase
, which is due to the combined effect of Bragg reflection due to multiple bottom undulations and the wave reflection by the semi-infinite plate, which is clear from
Figure 3 and
Figure 9. Moreover, optima in wave reflection occur for smaller values of wavenumber with an increase in depth of the trench and the height of the breakwater due to the variation in the wavelength of the standing waves generated over the trench/breakwater.
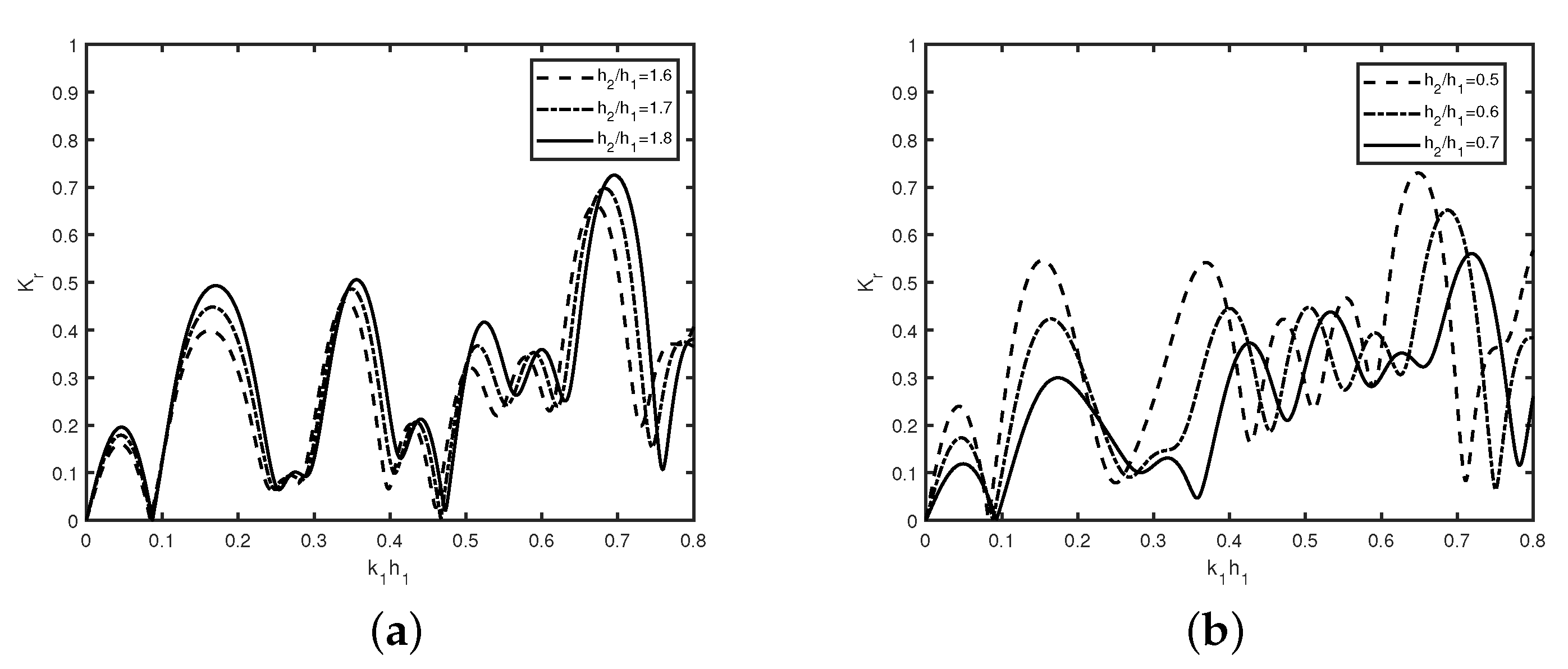
In
Figure 13, the reflection coefficient
is plotted against the wavenumber
for different values of rigidity
in case of (
Figure 13a) trenches with
,
(
Figure 13b) breakwaters with
,
in the presence of semi-infinite plate with
and
. It is observed that the wave reflection increases as in oscillatory for higher values of wave number with an increase in the structural rigidity
, which is due to the reflection of the higher amount of wave energy by the semi-infinite plate, as observed in
Figure 3a. However, the number of oscillation remains the same as the number of submerged trenches/breakwaters remain unchanged. As the rigidity of the plate
increases, the wave reflection increases, which is similar as observed in
Figure 3a. Moreover, the number of oscillations in wave reflection remains unchanged with an increase in rigidity
, which is due to the presence of the same no of trenches/breakwaters.
In
Figure 14, the variation of reflection coefficient
versus gap width
is demonstrated for different number of (
Figure 14a) submerged trenches with
and (
Figure 14b) breakwaters with
in the presence of the semi-infinite plate with
and
.
Figure 14 demonstrates that the reflection coefficient
is periodically oscillatory in nature with an increase in the gap width
, which is similar to that of
Figure 5. However, wave reflection increases, in general, with an increase in the gap width in the presence of the semi-infinite plate. A comparison of
Figure 14a,b reveals that both the sub-figures have the same number of harmonic peaks, whereas the bandwidth of each harmonic peaks shifts forward in the case of breakwaters than that of trenches, which is due to the change of phase of the seabed profiles from trenches to that of breakwaters.
Figure 15 exhibits the variation of the reflection coefficient
versus the gap between the semi-infinite plate and the adjacent submerged trench/breakwater
for different number
N of (
Figure 15a) trenches with
,
, and (
Figure 15b) breakwaters with
,
in the presence of the semi-infinite plate with
.
Figure 15 reveals that irrespective of No. of trenches/breakwaters, periodic oscillatory patterns in the wave reflection is observed. Further, with an increase in number of trenches/breakwaters
N, amplitude of reflection increases. Moreover, the reflection pattern in the case of submerged trenches is 180
out of phase to that of breakwaters, which is similar to that of
Figure 11c,d.