The Effect of a Backward-Facing Step on Flow and Heat Transfer in a Polydispersed Upward Bubbly Duct Flow
Abstract
:1. Introduction
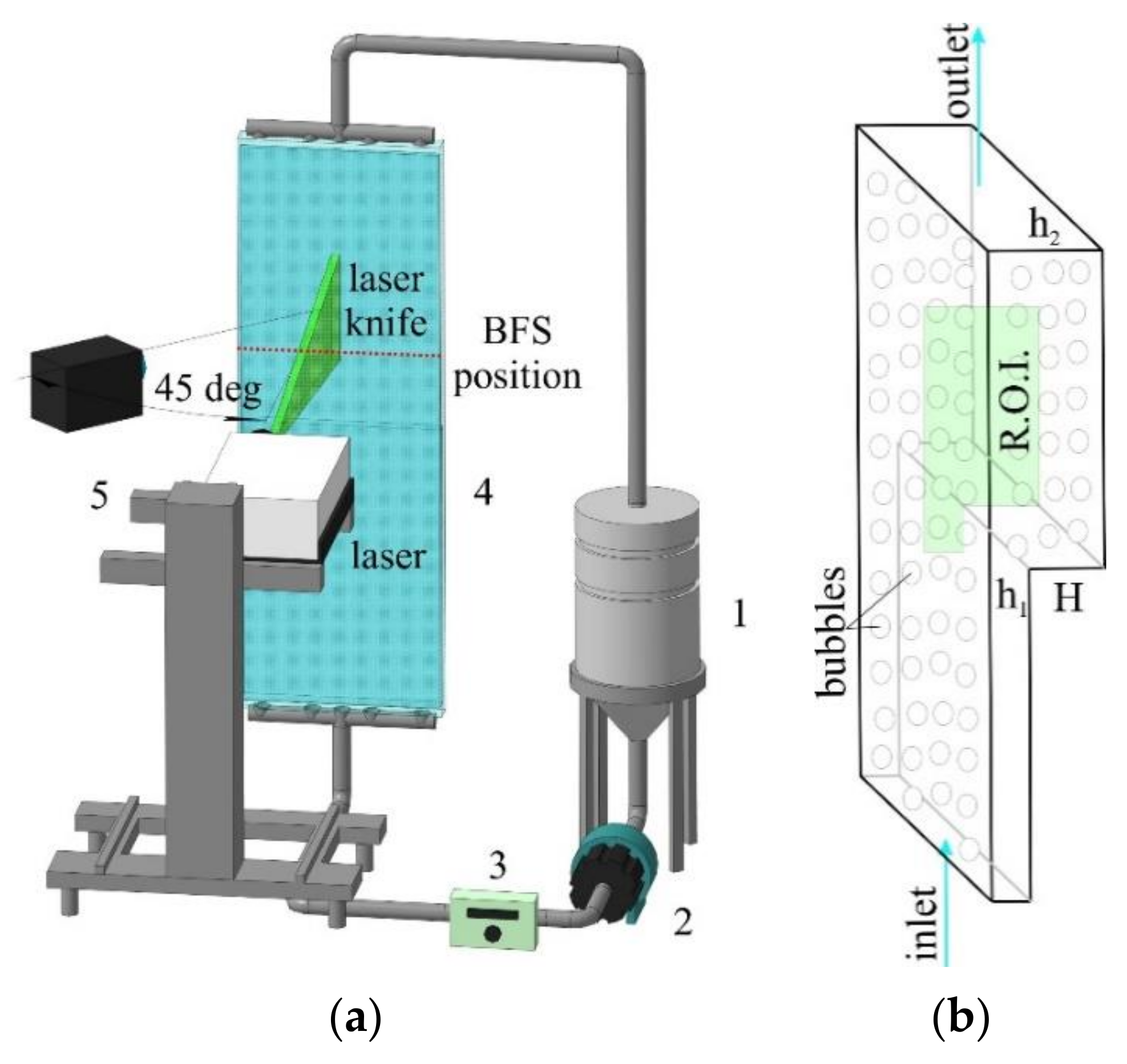
2. Measurement Setup
3. Mathematical Model and Method of Numerical Realization
3.1. D RANS + SMC “In-House” Numerical Code
3.2. D RANS + SST and LES (Ansys CFD Package)
4. Comparison with Experimental and Numerical Results
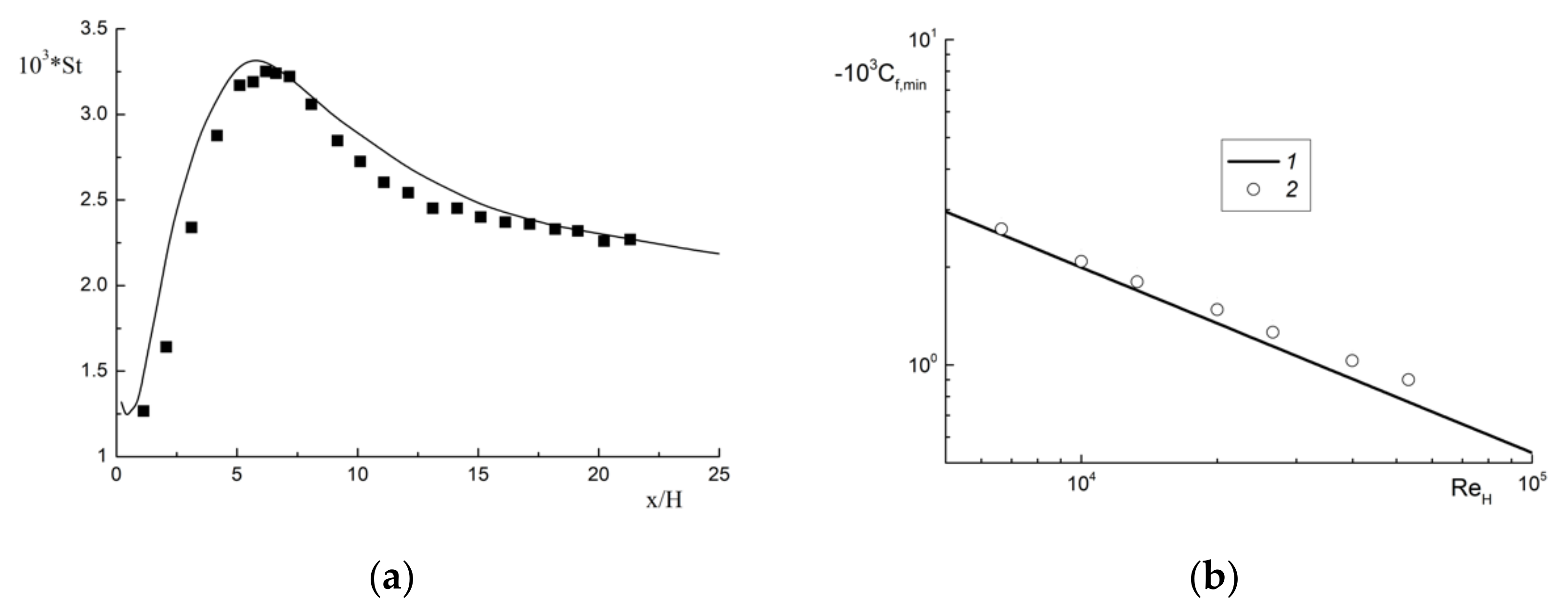
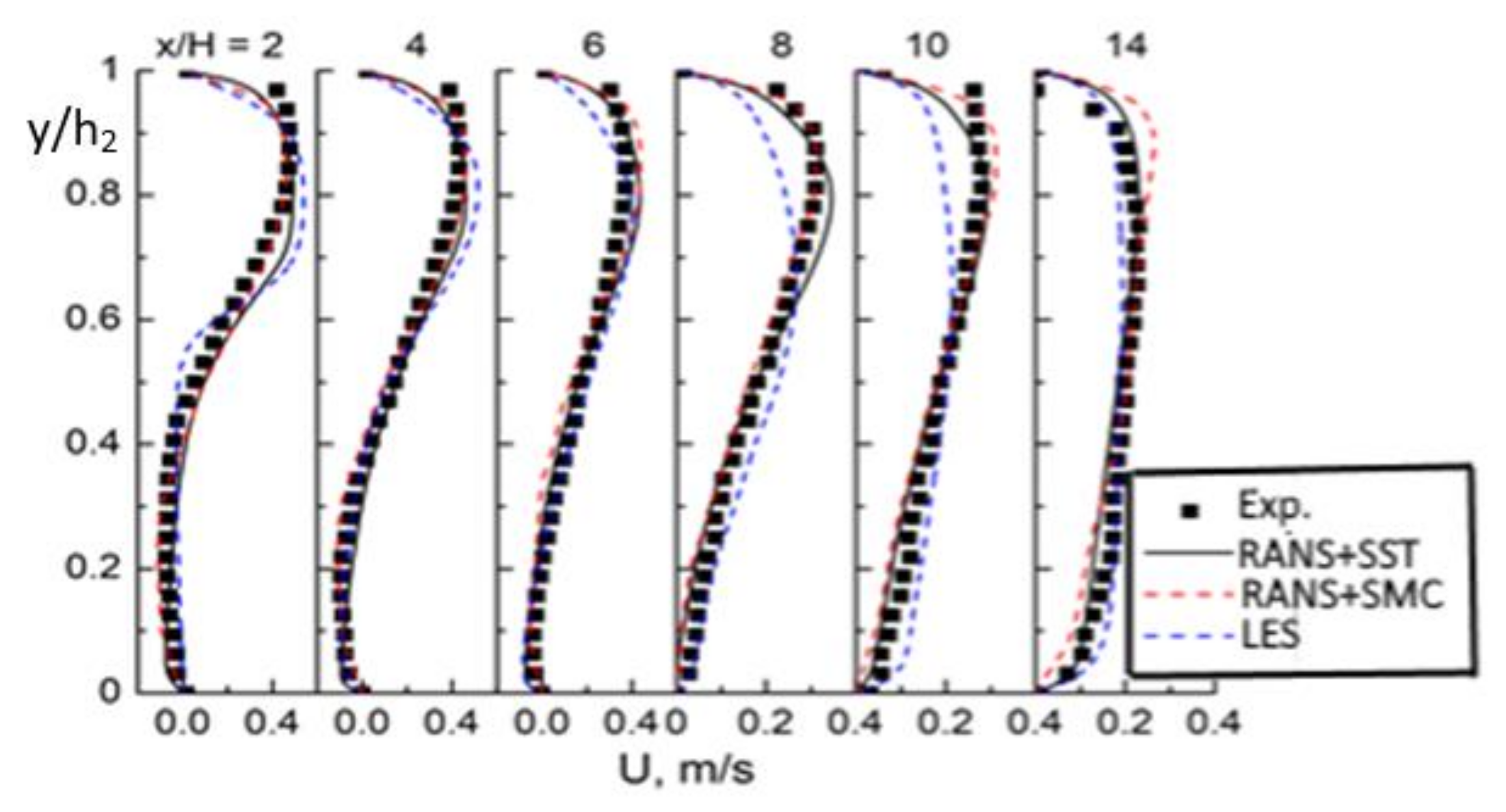
4.1. Single-Phase Flow in the BFS
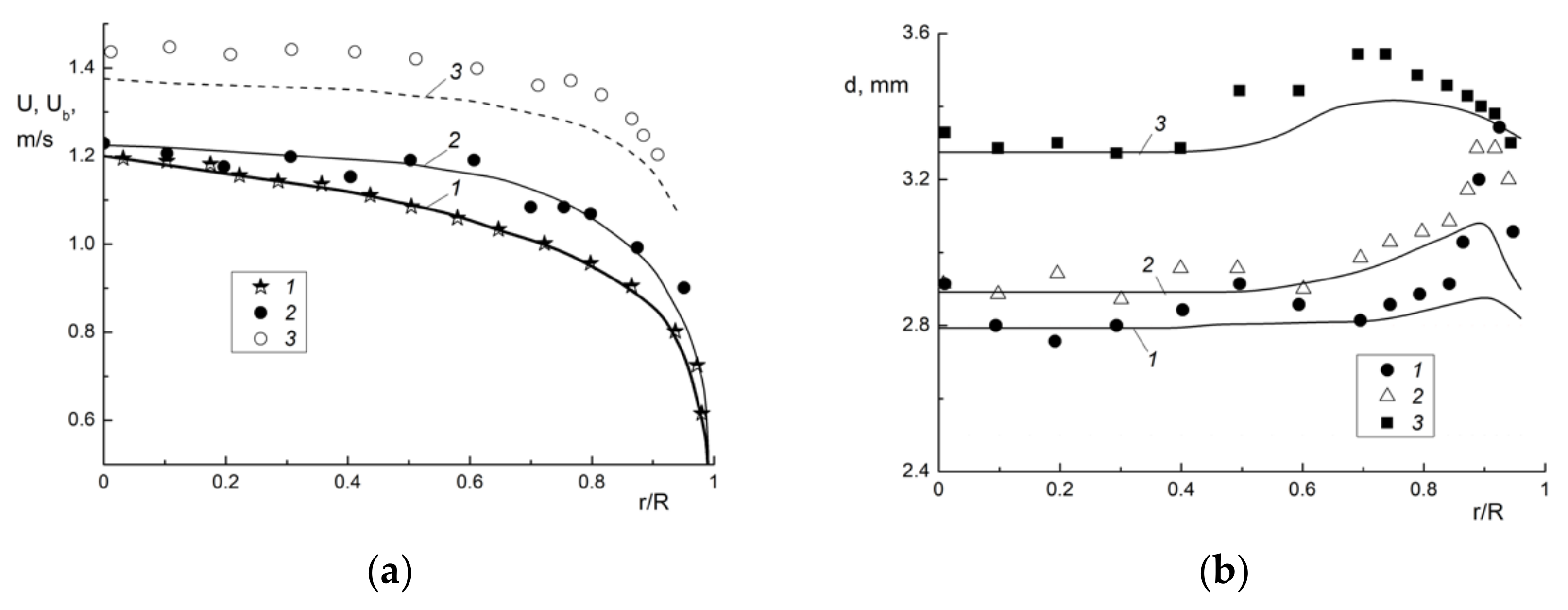
4.2. Two-Phase Bubbly Flow in Round Vertical Pipe
4.3. Two-Phase Bubbly Flow in the BFS
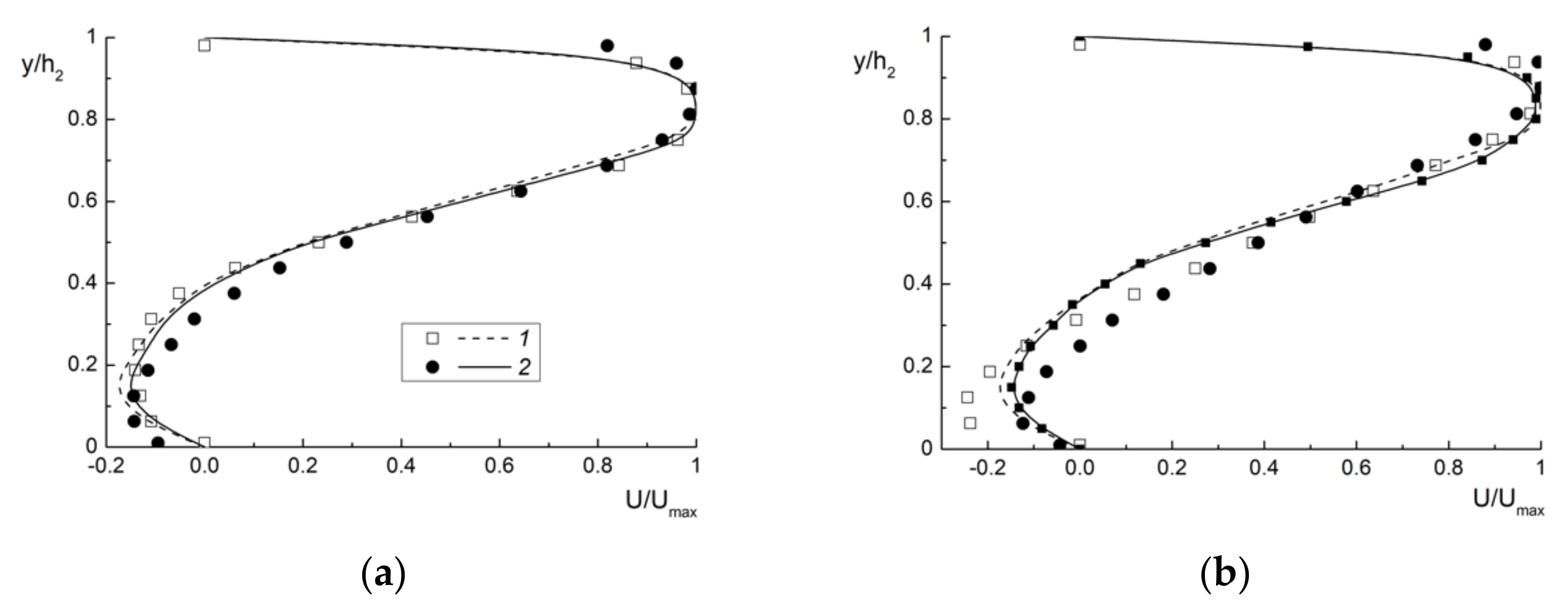
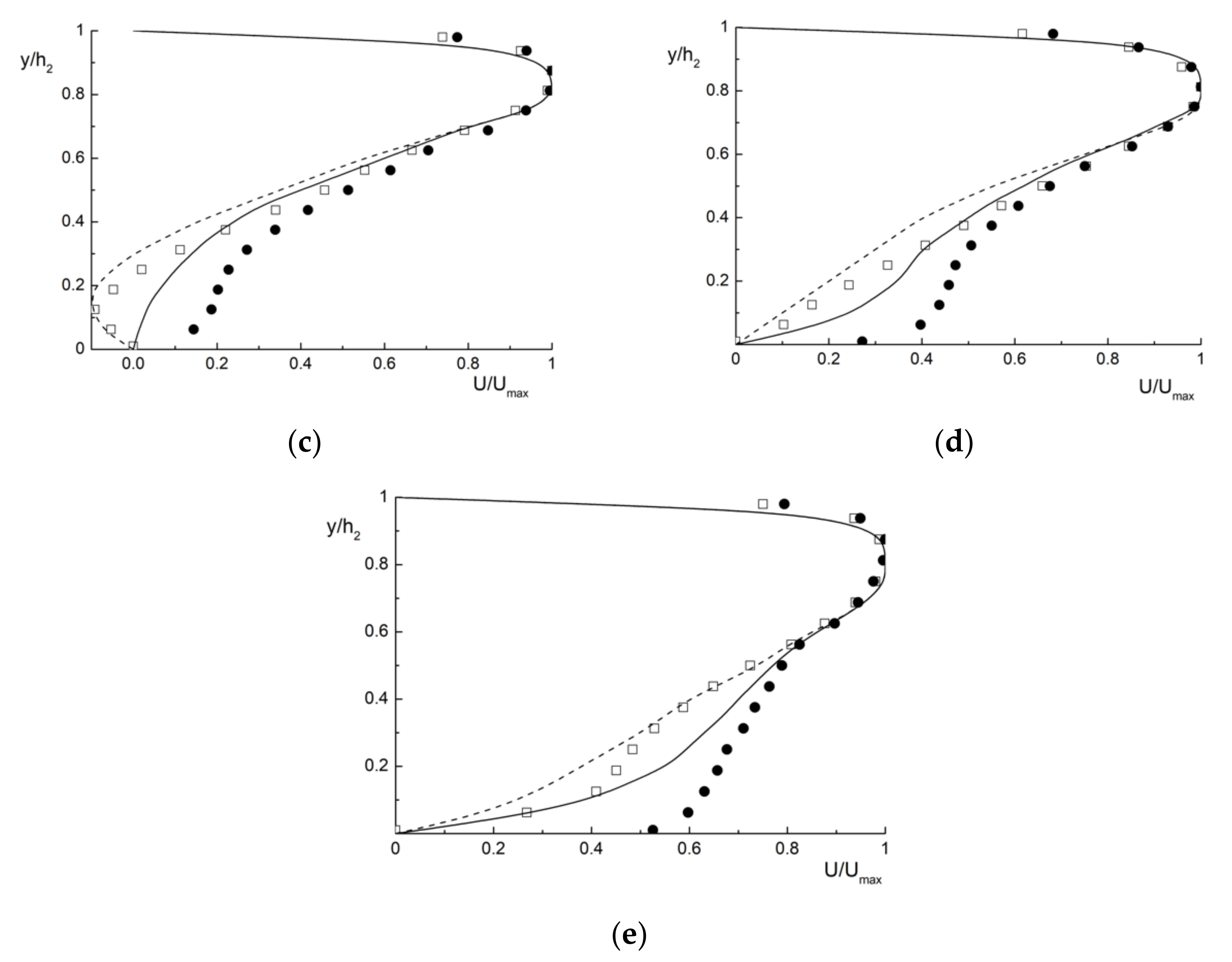
4.4. Two-Phase Bubbly Flow behind a Backward-Facing Step. Our Measurements and Numerical Simulation and Their Discussion
5. Numerical Results and Its Discussion
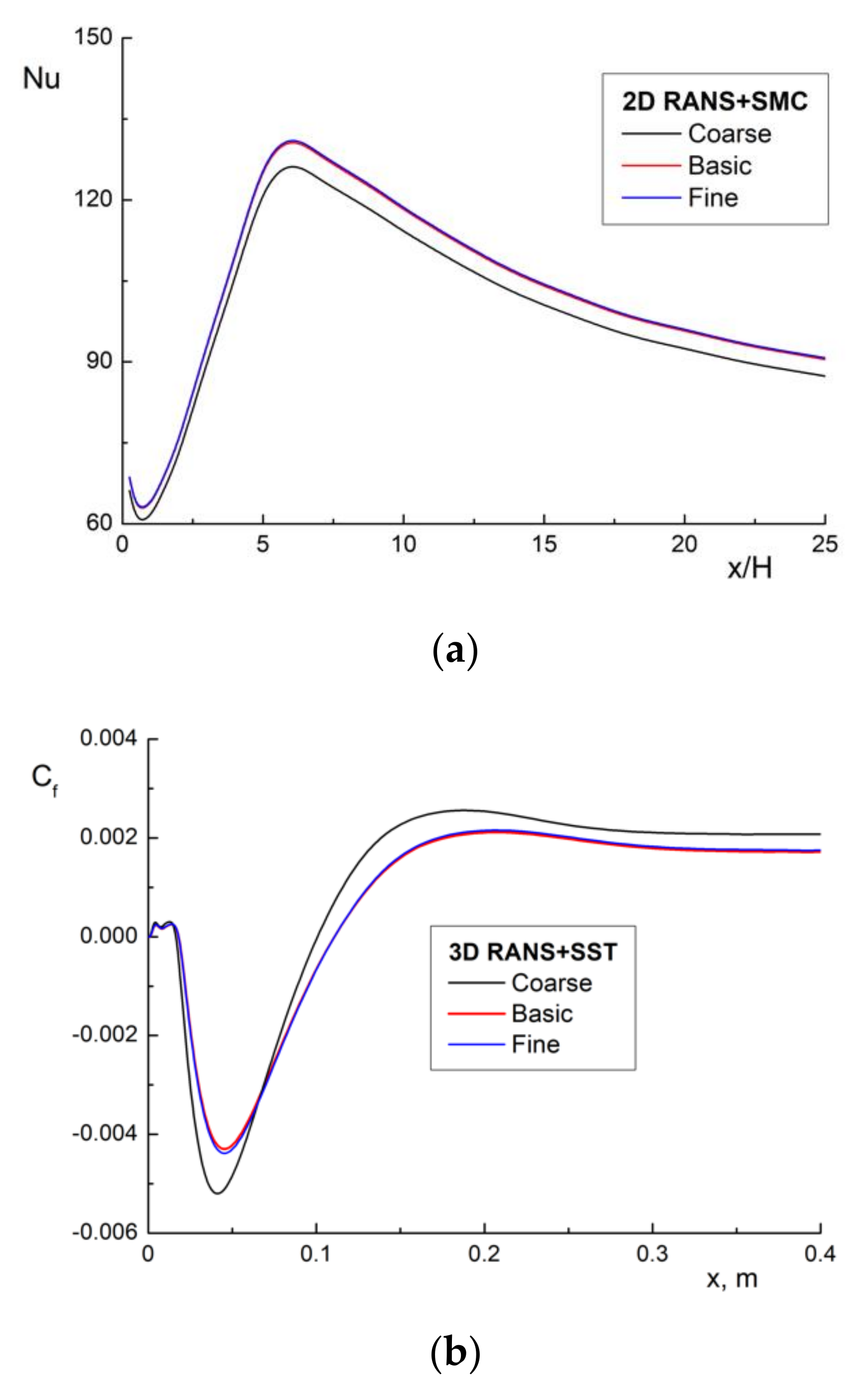
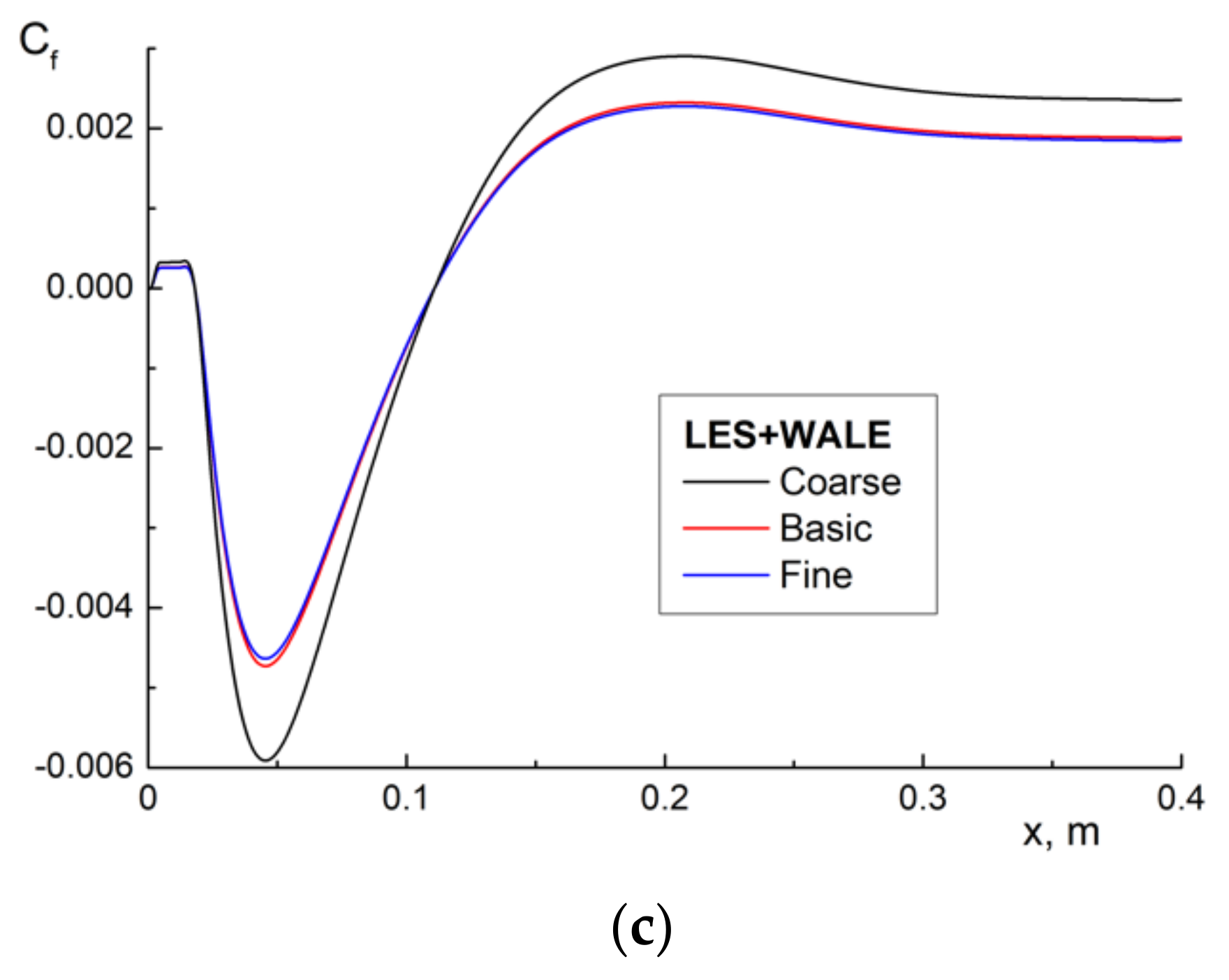
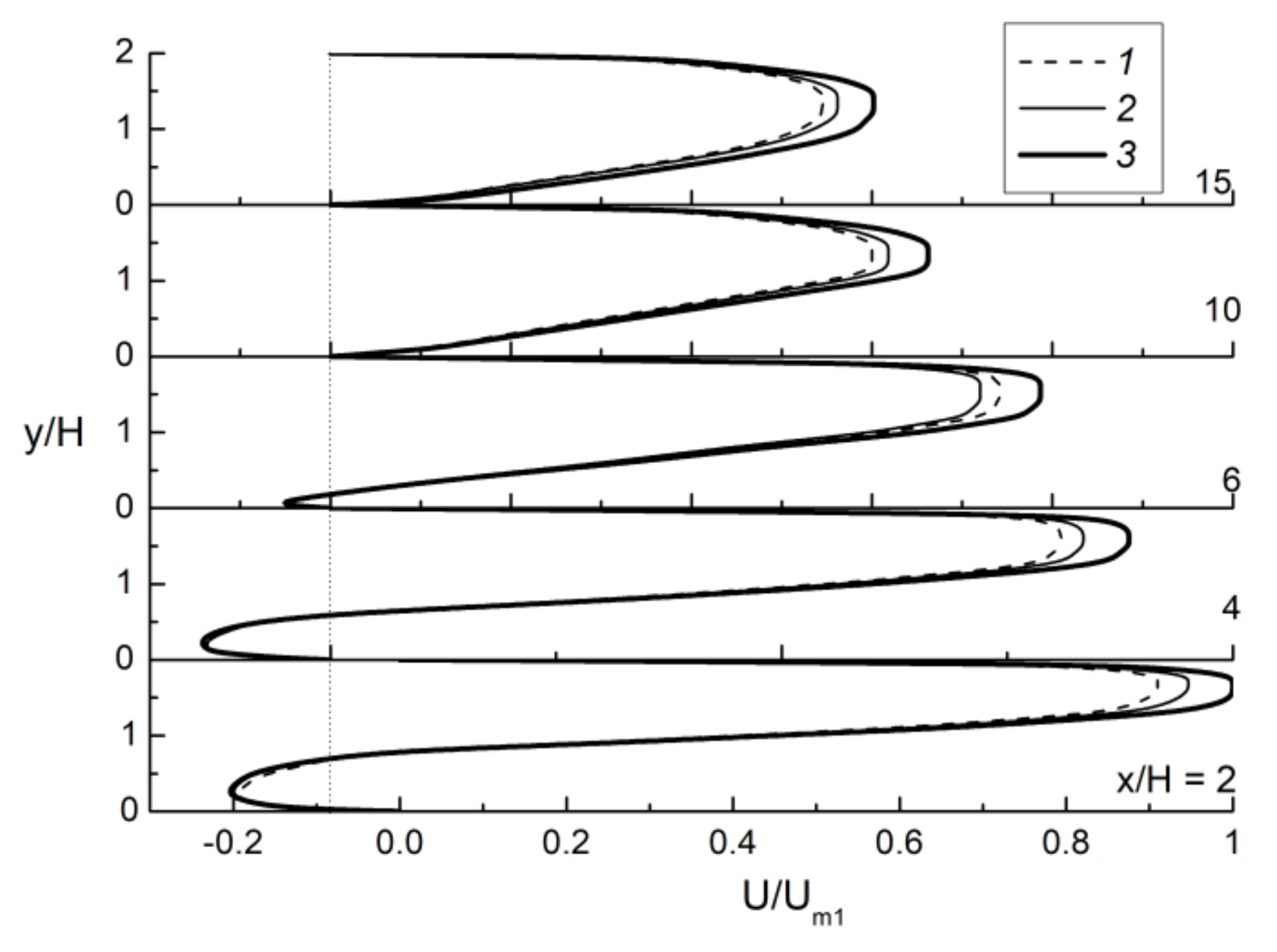
5.1. Single-Phase Fluid Flow in a Backward-Facing Step Flow
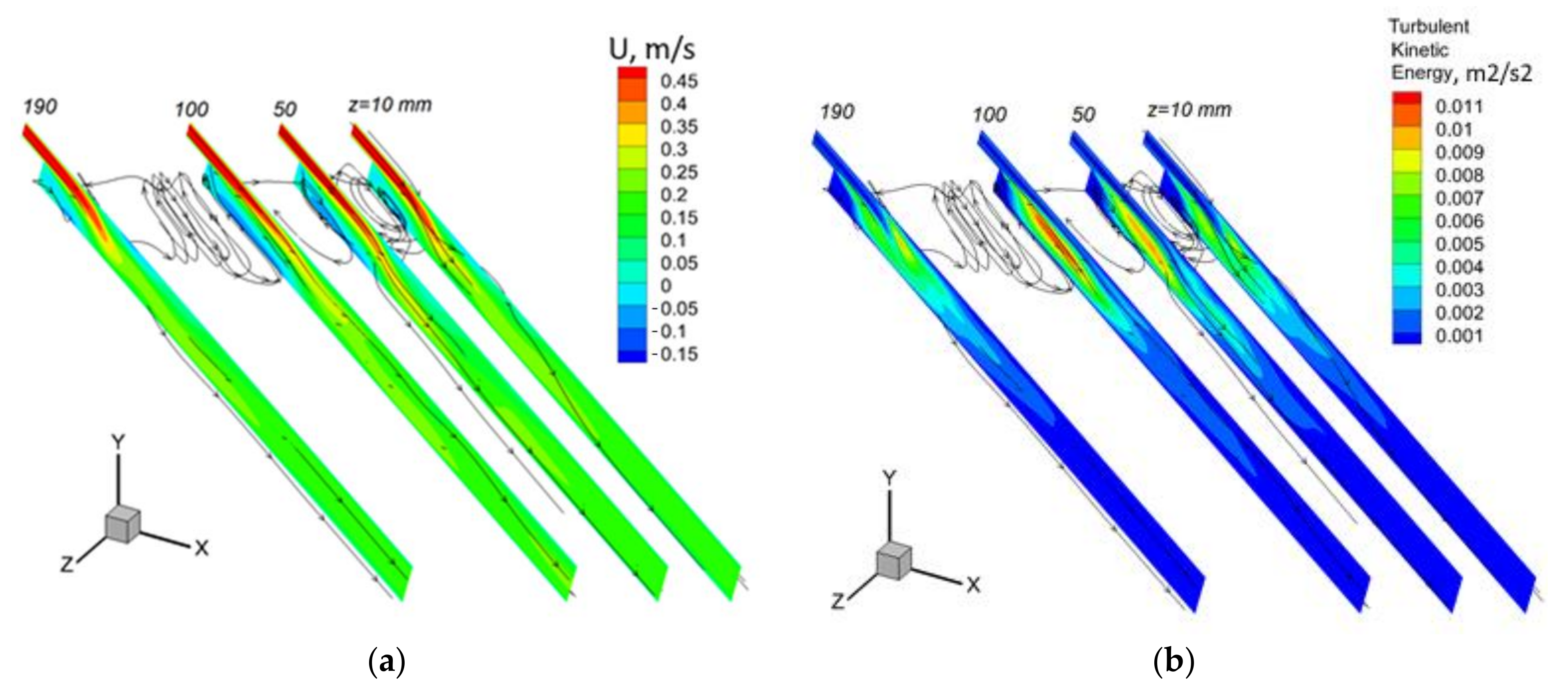
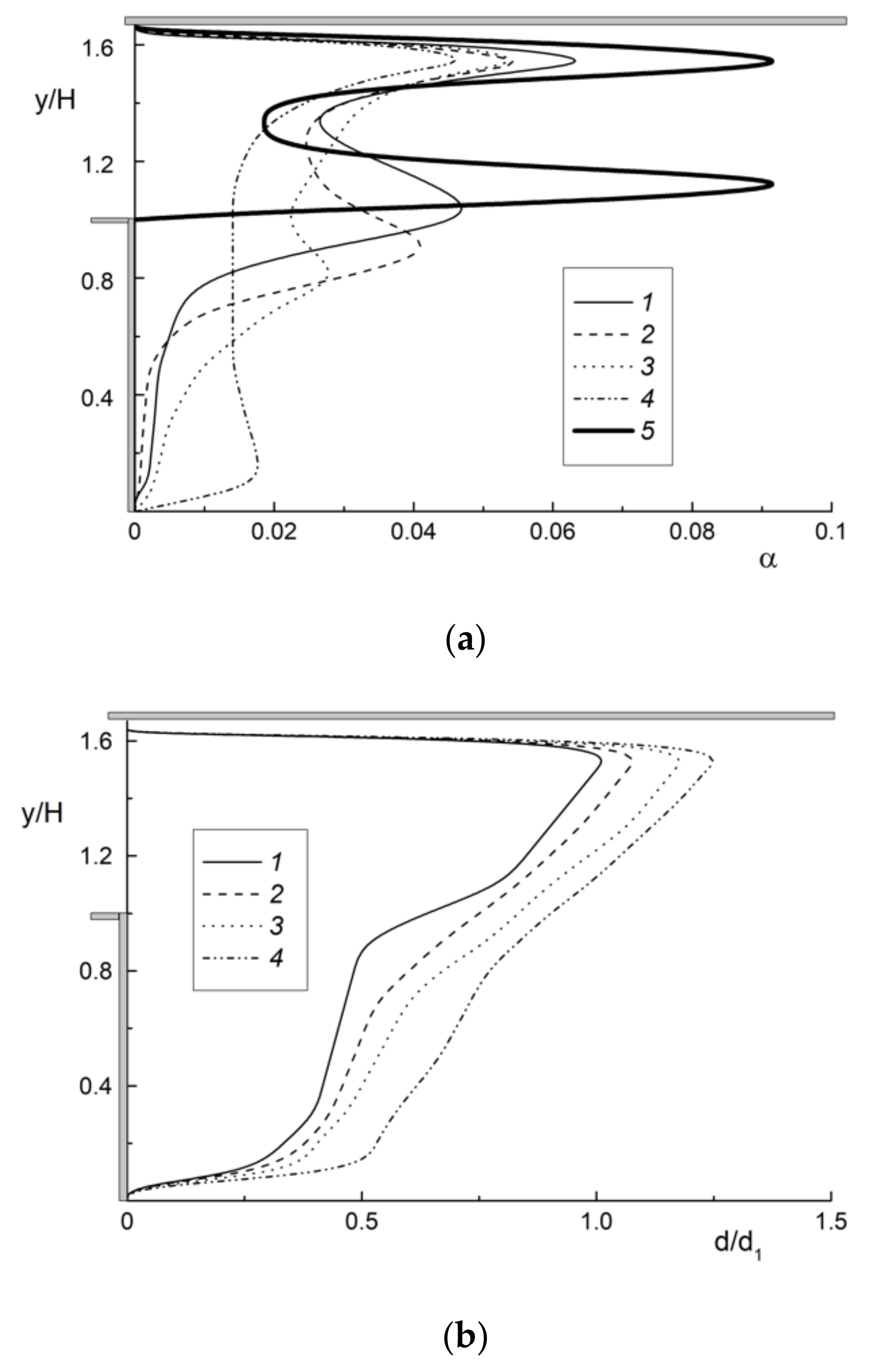
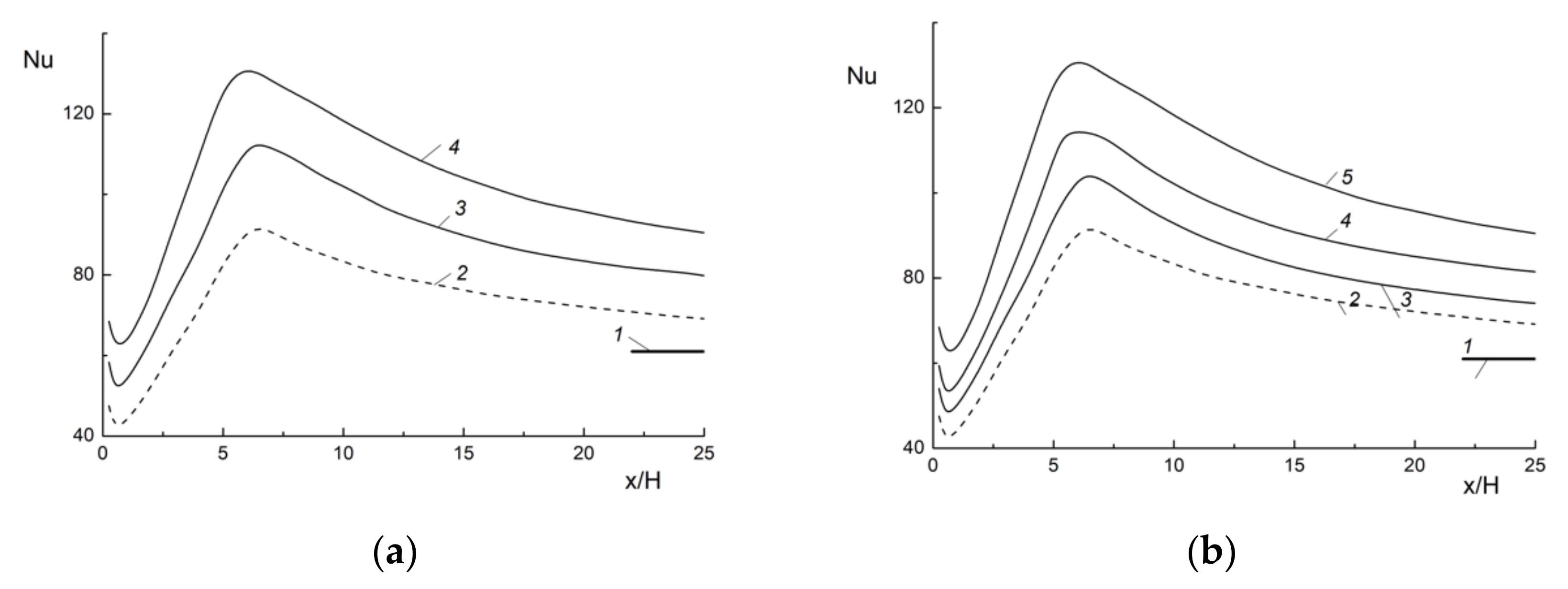
5.2. Upward Bubbly Flow in a Backward-Facing Step Flow
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| wall friction coefficient | |
| CP | heat capacity |
| d | mean bubble Sauter diameter |
| h1 | height of the duct before the sudden expansion |
| h2 | height of the duct after the sudden expansion |
| H | step height |
| J | and Jb superficial velocity of carrier fluid (water) and gas bubbles respectively |
| turbulent kinetic energy | |
| L | duct length |
| Nusslet number | |
| ReH = Um1H/ν | the Reynolds number |
| St = h/(ρCpU m1) | Stanton number |
| T | temperature |
| Um1 | mean-mass flow velocity |
| U* | friction velocity |
| x | streamwise coordinate |
| xR | position of the flow reattachment point |
| xNu_max | position of the peak of heat transfer rate |
| y | distance normal from the wall |
| Subscripts | |
| 0 | single-phase fluid (water) flow |
| 1 | initial condition |
| W | wall |
| b | bubble |
| l | liquid |
| m | mean-mass |
| Greek | |
| Φ | volume fraction |
| α | void fraction |
| β | gas volumetric flow rate ratio |
| ε | dissipation of the turbulent kinetic energy |
| λ | thermal conductivity |
| ρ | density |
| ν | kinematic viscosity |
| τW | wall shear stress |
| Acronym | |
| BFS | backward-facing step |
| CV | control volume |
| DNS | direct numerical simulation |
| ER | expansion ratio |
| LES | large eddy simulation |
| PIV | particle image velocimetry |
| PLIF | planar laser induced fluorescence |
| RANS | Reynolds-averaged Navier-Stokes |
| ROI | region of interests |
| SMC | second moment closure |
| SST | shear stress tensor |
| TKE | turbulent kinetic energy |
References
- Nigmatulin, R.I. Dynamics of Multiphase Media; Hemisphere: New York, NY, USA, 1991; Volume 1. [Google Scholar]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Aloui, F.; Souhar, M. Experimental study of a two-phase bubbly flow in a flat duct symmetric sudden expansion. Part I: Visulization, pressure and void fraction. Int. J. Multiph. Flow 1996, 22, 651–665. [Google Scholar] [CrossRef]
- Schmidt, J.; Friedel, L. Two-phase pressure change across sudden expansions in duct areas. Chem. Eng. Commun. 1996, 141, 175–190. [Google Scholar] [CrossRef]
- Aloui, F.; Doubliez, L.; Legrand, J.; Souhar, M. Bubbly flow in an axisymmetric sudden expansion: Pressure drop, void fraction, wall shear stress, bubble velocities and sizes. Exp. Therm. Fluid Sci. 1999, 19, 118–130. [Google Scholar] [CrossRef]
- Ahmed, W.H.; Ching, C.Y.; Shoukri, M. Development of two-phase flow downstream of a horizontal sudden expansion. Int. J. Heat Fluid Flow 2008, 29, 194–206. [Google Scholar] [CrossRef]
- Balakhrisna, T.; Ghosh, S.; Das, G.; Das, P.K. Oil–water flows through sudden contraction and expansion in a horizontal pipe—phase distribution and pressure drop. Int. J. Multiph. Flow 2010, 36, 13–24. [Google Scholar] [CrossRef]
- Arabi, A.; Salhi, Y.; Si-Ahmed, E.K.; Legrand, J. Influence of a sudden expansion on slug flow characteristics in a horizontal two-phase flow: A pressure drop fluctuations analysis. Meccanica 2018, 53, 3321–3338. [Google Scholar] [CrossRef]
- Zhang, D.W.; Goharzadeh, A. Effect of sudden expansion on two-phase flow in a horizontal pipe fluid dynamics. Fluid Dyn. 2019, 54, 123–136. [Google Scholar] [CrossRef]
- Kim, Y.; Park, H. Upward bubbly flows in a square pipe with a sudden expansion: Bubble dispersion and reattachment length. Int. J. Multiph. Flow 2019, 118, 254–269. [Google Scholar] [CrossRef]
- Krepper, E.; Beyer, M.; Frank, T.; Lucas, D.; Prasser, H.-M. CFD modelling of polydispersed bubbly two-phase flow around an obstacle. Nucl. Eng. Des. 2009, 239, 2372–2381. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Modeling of the flow patterns and heat transfer in a turbulent bubbly polydispersed flow downstream of a sudden pipe expansion. Int. J. Heat Mass Transfer 2016, 101, 1251–1262. [Google Scholar] [CrossRef]
- Bogatko, T.V.; Pakhomov, M.A. Modeling bubble distribution and heat transfer in polydispersed gas-liquid flow in a backward-facing step. IOP J. Phys. Conf. Ser. 2020, 1677, 012052. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Krepper, E.; Lucas, D.; Frank, T.; Prasser, H.-M.; Zwart, P.J. The inhomogeneous MUSIG model for the simulation of polydispersed flows. Nucl. Eng. Des. 2008, 238, 1690–1702. [Google Scholar] [CrossRef]
- Lakehal, D.; Smith, B.L.; Milelli, M. Large-eddy simulation of bubbly turbulent shear flows. J. Turbul. 2002, 3, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Dhotre, M.T.; Niceno, B.; Smith, B.L. Large eddy simulation of a bubble column using dynamic sub-grid scale model. Chem. Eng. J. 2008, 136, 337–348. [Google Scholar] [CrossRef]
- Long, S.; Yang, J.; Huang, X.; Li, G.; Shi, W.; Sommerfeld, M.; Yang, X. Large-eddy simulation of gas-liquid two-phase flow in a bubble column reactor using a modified sub-grid scale model with the consideration of bubble-eddy interaction. Int. J. Heat Mass Transfer 2020, 161, 120240. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Mukin, R.V.; Mukina, L.S.; Strizhov, V.F. Development of a diffusion-inertia model for calculating bubble turbulent flows: Isothermal polydispersed flow in a vertical pipe. High Temp. 2012, 50, 621–630. [Google Scholar] [CrossRef]
- Mukin, R.V. Modeling of bubble coalescence and break-up in turbulent bubbly flow. Int. J. Multiphase Flow 2014, 62, 52–66. [Google Scholar] [CrossRef]
- Lehr, F.; Mewes, D. A transport equation for the interfacial area density applied to bubble columns. Chem. Eng. Sci. 2001, 56, 1159–1166. [Google Scholar] [CrossRef]
- Pour, M.; Nassab, S. Numerical investigation of forced laminar convection flow of nanofluids over a backward facing step under bleeding condition. J. Mech. 2012, 28, N7–N12. [Google Scholar] [CrossRef]
- Lobanov, P.D.; Pakhomov, M.A.; Terekhov, V.I. Experimental and numerical study of the flow and heat transfer in a bubbly turbulent flow in a pipe with sudden expansion. Energies 2019, 12, 2375. [Google Scholar] [CrossRef] [Green Version]
- Poletaev, I.; Tokarev, M.P.; Pervunin, K.S. Bubble patterns recognition using neural networks: Application to the analysis of a two -phase bubbly jet. Int. J. Multiph. Flow 2020, 126, 103194. [Google Scholar] [CrossRef]
- Cerqueira, R.F.L.; Paladino, E.E. Development of a deep learning-based image processing technique for bubble pattern recognition and shape reconstruction in dense bubbly flows. Chem. Eng. Sci. 2021, 230, 116163. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical modeling of two-phase flow. Ann. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M. A statistical model for predicting the fluid displaced/added mass and displaced heat capacity effects on transport and heat transfer of arbitrary density particles in turbulent flows. Int. J. Heat Mass Transfer 2011, 54, 4247–4265. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Modeling of flow structure, bubble distribution, and heat transfer in polydispersed turbulent bubbly flow using the method of delta function approximation. J. Eng. Thermophys. 2019, 28, 453–471. [Google Scholar] [CrossRef]
- Drew, D.A.; Lahey, R.T., Jr. Application of general constitutive principles to the derivation of multidimensional two-phase flow equations. Int. J. Multiph. Flow 1979, 5, 243–264. [Google Scholar] [CrossRef]
- Fadai-Ghotbi, A.; Manceau, R.; Boree, J. Revisiting URANS computations of the backward-facing step flow using second moment closures. Influence of the numerics. Flow Turbul. Combust 2008, 81, 395–410. [Google Scholar] [CrossRef]
- Lopez de Bertodano, M.; Lee, S.J.; Lahey, R.T., Jr.; Drew, D.A. The prediction of two-phase turbulence and phase distribution using a Reynolds stress model. ASME J. Fluids Eng. 1990, 112, 107–113. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Song, C.-H.; Bae, B.U.; Euh, D.J. Modeling of bubble coalescence and break-up considering turbulent suppression phenomena in bubbly two-phase flow. Int. J. Multiph. Flow 2013, 54, 31–42. [Google Scholar] [CrossRef]
- Hanjalic, K.; Jakirlic, S. Contribution towards the second-moment closure modelling of separating turbulent flows. Comput. Fluids 1998, 27, 137–156. [Google Scholar] [CrossRef]
- Available online: www.ansys.com.
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Vogel, J.C.; Eaton, J.K. Combined heat transfer and fluid dynamics measurements downstream of a backward facing step. ASME J. Heat Transfer 1985, 107, 922–929. [Google Scholar] [CrossRef]
- Tihon, J.; Legrand, J.; Legentilhomme, P. Near-wall investigation of backward-facing step flows. Exp. Fluids 2001, 31, 484–493. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M.; Xiao, Z. Axial interfacial area transport of vertical bubbly flows. Int. J. Heat Mass Transfer 2001, 44, 1869–1888. [Google Scholar] [CrossRef]
- Bel Fdhila, R. Analyse Experimental et Modelisation d’un Ecoulement Vertical a Bulles dans un Elargissement Brusque. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 1991. [Google Scholar]
- Papoulias, D.; Splawski, A.; Vikhanski, A.; Lo, S. Eulerian multiphase predictions of turbulent bubbly flow in a step-channel expansion. In Proceedings of the Nineth International Conference on Multiphase Flow ICMF-2016, Firenze, Italy, 22–27 May 2016. [Google Scholar]
- Eaton, J.K.; Johnston, J.P. Review of research on subsonic turbulent flow reattachment. AIAA J. 1981, 19, 1093–1100. [Google Scholar] [CrossRef]
- Chen, L.; Asai, K.; Nonomura, T.; Xi, G.N.; Liu, T.S. A review of backward-facing step (BFS) flow mechanisms, heat transfer and control. Thermal Sci. Eng. Progr. 2018, 6, 194–216. [Google Scholar] [CrossRef]
- Wang, H.G.; Zhang, C.G.; Xiong, H.B. Growth and collapse dynamics of a vapor bubble near or at a wall. Water 2021, 13, 12. [Google Scholar] [CrossRef]
- Kashinsky, O.N.; Chinak, A.V.; Kaipova, E.V. Bubbly gas-liquid flow in an inclined rectangular channel. Thermophys. Aeromech. 2003, 10, 69–75. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogatko, T.V.; Chinak, A.V.; Evdokimenko, I.A.; Kulikov, D.V.; Lobanov, P.D.; Pakhomov, M.A. The Effect of a Backward-Facing Step on Flow and Heat Transfer in a Polydispersed Upward Bubbly Duct Flow. Water 2021, 13, 2318. https://doi.org/10.3390/w13172318
Bogatko TV, Chinak AV, Evdokimenko IA, Kulikov DV, Lobanov PD, Pakhomov MA. The Effect of a Backward-Facing Step on Flow and Heat Transfer in a Polydispersed Upward Bubbly Duct Flow. Water. 2021; 13(17):2318. https://doi.org/10.3390/w13172318
Chicago/Turabian StyleBogatko, Tatiana V., Aleksandr V. Chinak, Ilia A. Evdokimenko, Dmitriy V. Kulikov, Pavel D. Lobanov, and Maksim A. Pakhomov. 2021. "The Effect of a Backward-Facing Step on Flow and Heat Transfer in a Polydispersed Upward Bubbly Duct Flow" Water 13, no. 17: 2318. https://doi.org/10.3390/w13172318





