Solitary Wave Generation and Propagation under Hypergravity Fields
Abstract
:1. Introduction
2. General Scaling Laws
3. Wave Generation
4. Governing Equations and Boundary Conditions
4.1. Governing Equations
4.2. Initial and Boundary Conditions
4.3. Numerical Method
5. Results and Discussion
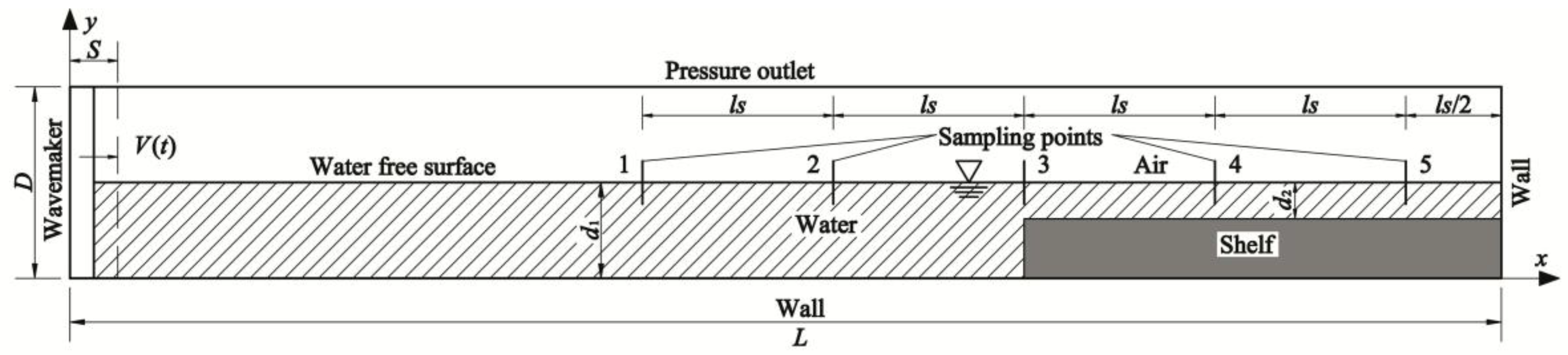
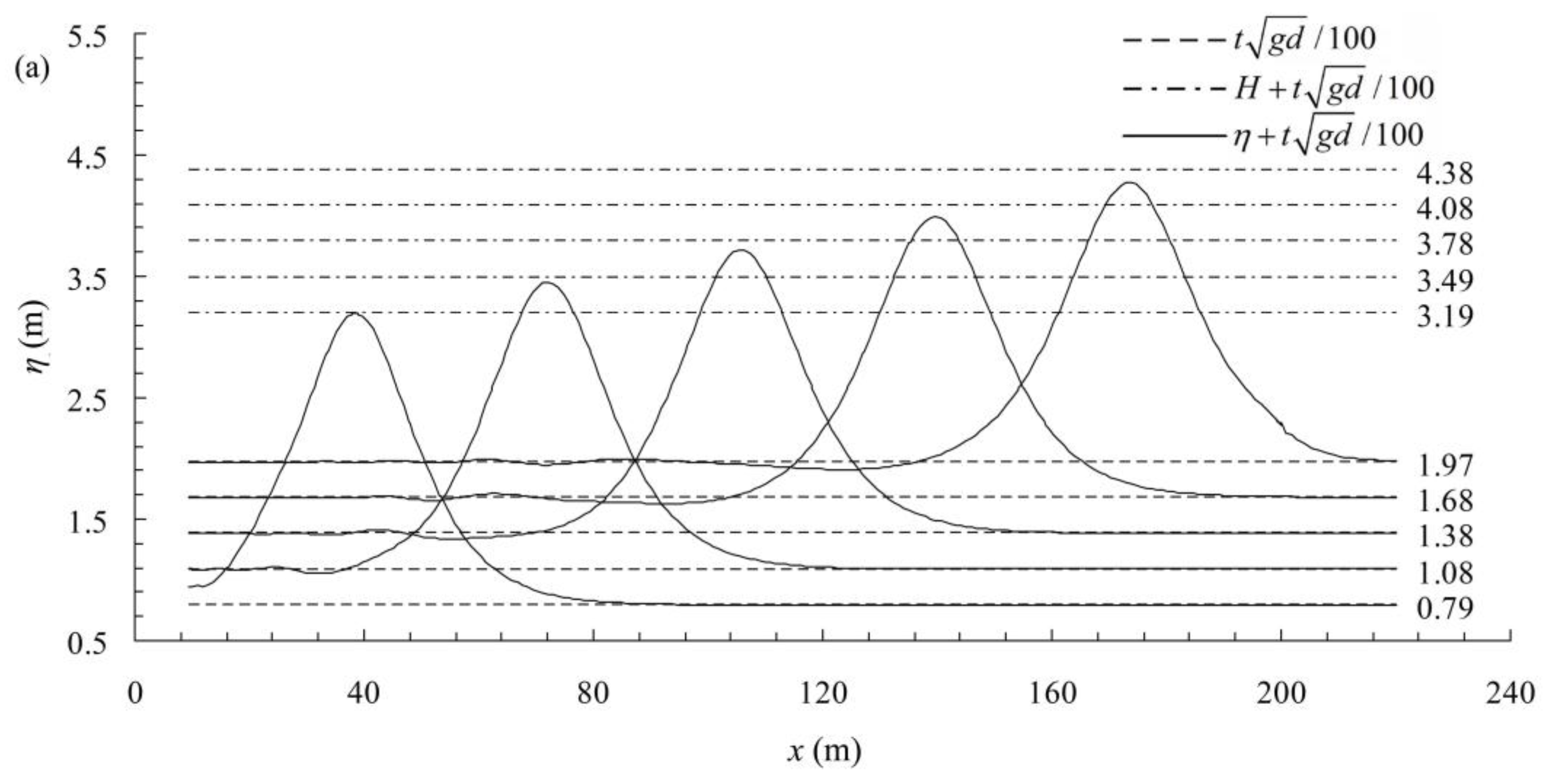
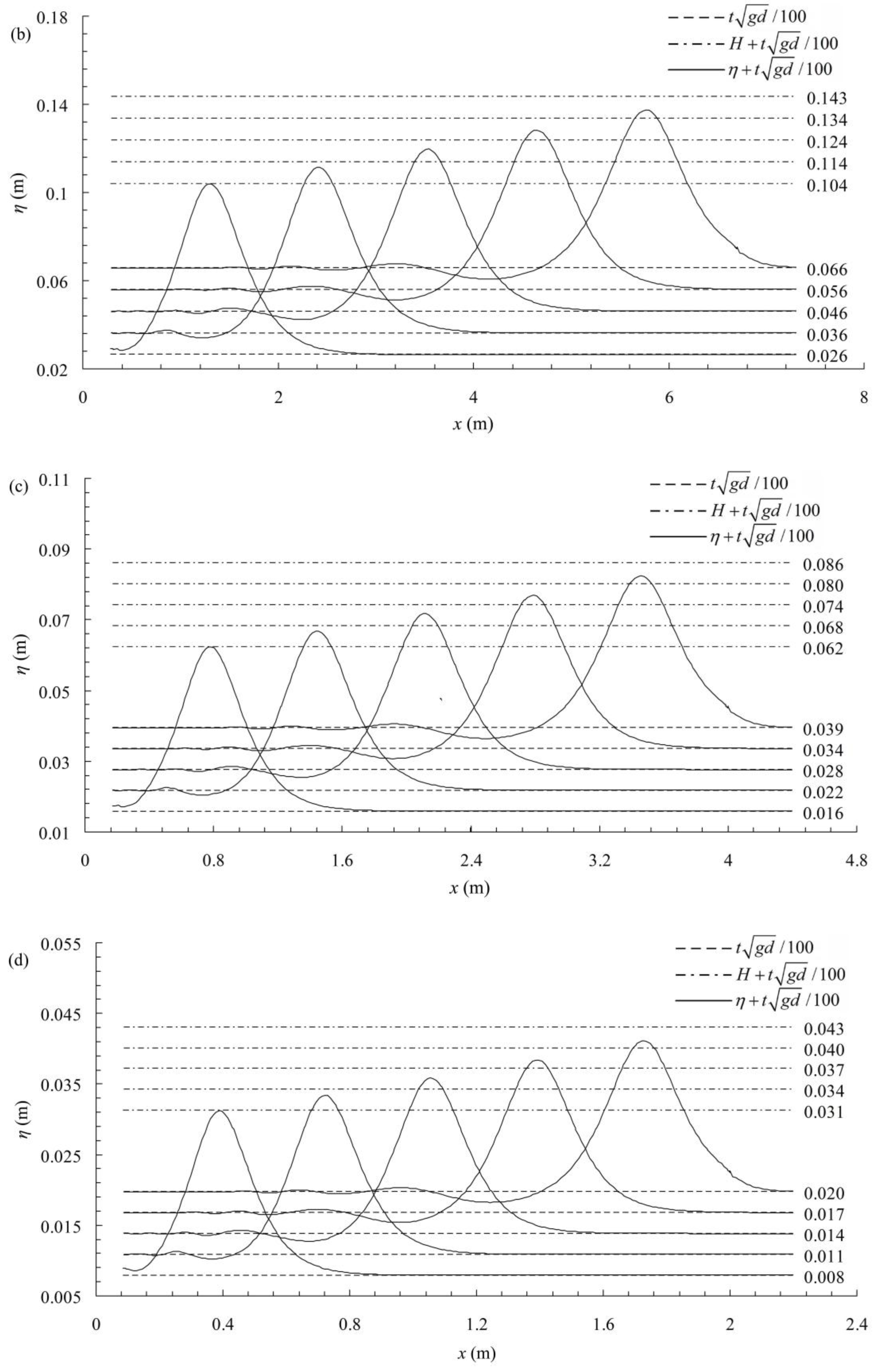
5.1. Solitary Wave Generation and Propagation in a Constant Water Depth
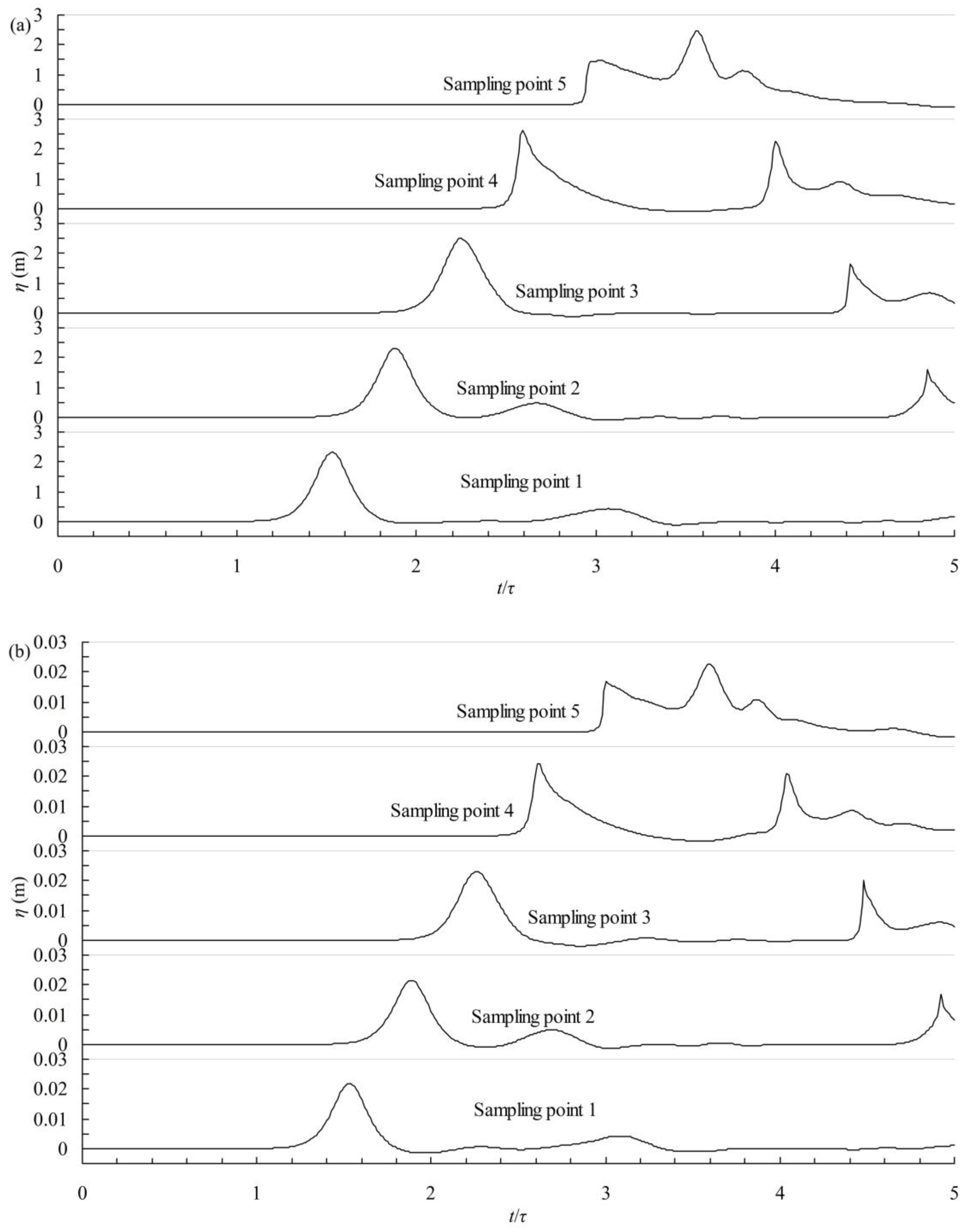
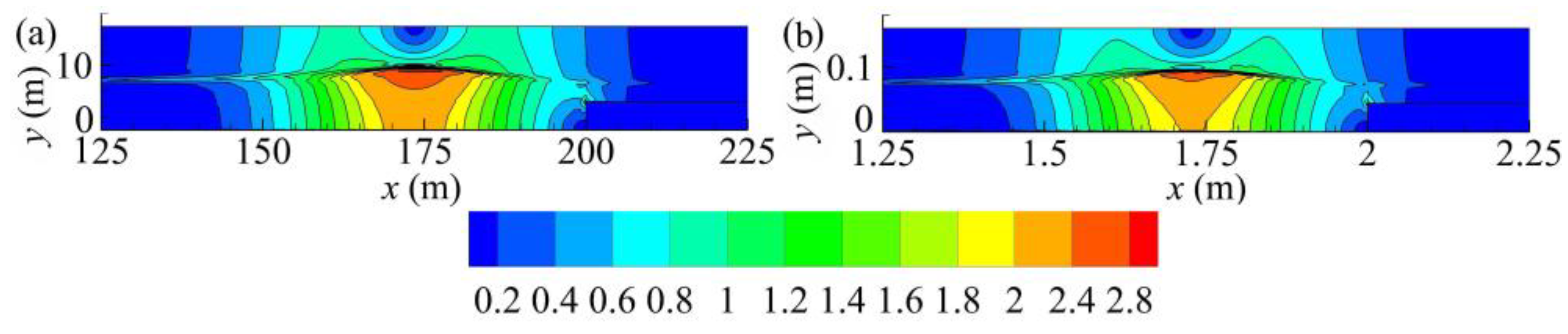
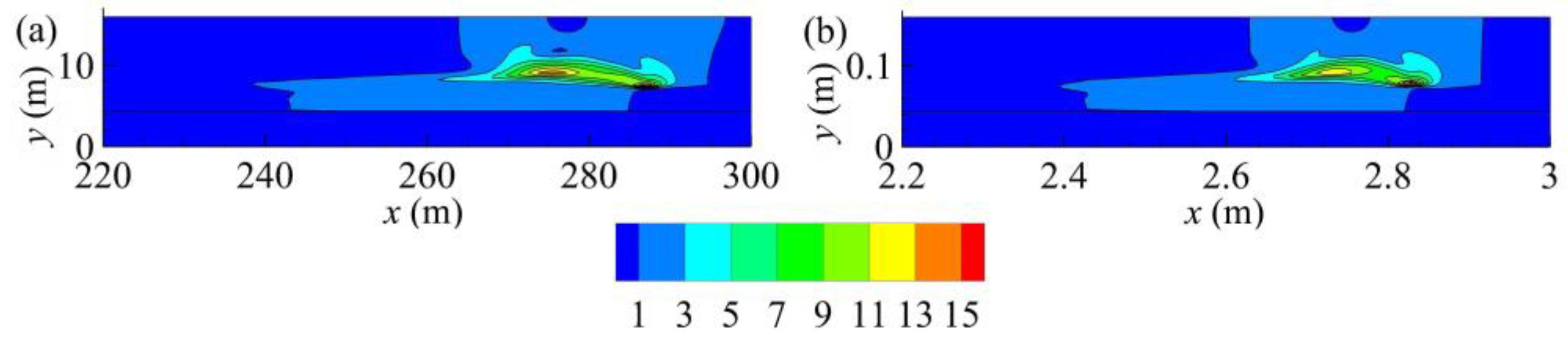
5.2. Solitary Wave Interacting with Shelf
5.3. Comparison of the Simulated Velocity Fields and Dynamic Pressures under Different Gravity Fields
6. Conclusions
- (1)
- The waveform obtained from the simulations performed under different gravity fields exhibit good agreement at the macroscale, indicating that solitary waves can be steadily generated and propagated within hypergravity fields. Consequently, wave breaking, impingement, run-up, and the other phenomena that have been observed during wave-coasting interactions, which have drawn considerable attention, can be studied using a downscaled model.
- (2)
- Although the waveform and static pressure field agree well at the macroscale, some discrepancies are detected within the details. Due to the ignored viscosity and surface tension similarity, some of the features of solitary waves are affected by the scale effect, including wave attenuation and time lag. Wave attenuation may be more serious in a small-scale model experiment performed within a hypergravity field, and can cause the time lag to become more serious. However, wave attenuation and time lag can be offset by a well-considered incident wave condition.
- (3)
- Since both the velocity and dynamic pressure are sensitive to the wave attenuation, time lag and fluid viscosity, some discrepancies can be found in the velocity field and dynamic pressure profiles. However, a well-designed initial incident wave can weaken the discrepancies in the velocity field and dynamic pressure.
Author Contributions
Funding
Conflicts of Interest
References
- Kendon, E.J.; Roberts, N.M.; Fowler, H.J.; Roberts, M.J.; Chan, S.C.; Senior, C.A. Heavier summer downpours with climate change revealed by weather forecast resolution model. Nat. Clim. Chang. 2014, 4, 570–576. [Google Scholar] [CrossRef]
- Liang, Q.H.; Chen, K.C.; Hou, J.M.; Xiong, Y.; Wang, G.; Qiang, J. Hydrodynamic modelling of flow impact on structures under extreme flow conditions. J. Hydrodyn. Ser. B 2016, 28, 267–274. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Wang, B.L.; Fan, T.T.; Liu, H. Numerical analysis of impacts of 2011 Japan Tohoku tsunami on China Coast. J. Hydrodyn. Ser. B 2013, 25, 580–590. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Zhao, X.; Wang, B.L.; Dias, F.; Liu, H. Characteristics of wave amplitude and currents in South China Sea induced by a virtual extreme tsunami. J. Hydrodyn. Ser. B 2017, 29, 377–392. [Google Scholar] [CrossRef]
- Chen, J.; Guan, Z.; Jiang, C.B. Study of sediment transport by tsunami waves: V: Influence of mangrove. Adv. Water Sci. 2016, 27, 206–213. [Google Scholar]
- Tripepi, G.; Aristodemo, F.; Veltri, P. On-bottom stability analysis of cylinders under tsunami-like solitary waves. Water 2018, 10, 487. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunamis-the Propagation of Long Waves onto a Shelf; California Institute of Technology: Pasadena, CA, USA, 1979. [Google Scholar]
- Stansby, P.K. Solitary wave run up and overtopping by a semi-implicit finite-volume shallow-water Boussinesq model. J. Hydraul. Res. 2003, 41, 639–647. [Google Scholar] [CrossRef]
- Dong, G.H.; Ma, X.Z.; Perlin, M.; Ma, Y.X.; Yu, B.; Wang, G. Experimental study of long wave generation on sloping bottoms. Coast. Eng. 2009, 56, 82–89. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Wu, N.J.; Tsay, T.K.; Chen, Y.Y. Generation of stable solitary waves by a piston-type wave maker. Wave Motion 2014, 51, 240–255. [Google Scholar] [CrossRef]
- Dong, J.; Wang, B.L.; Liu, H. Run-up of non-breaking double solitary waves with equal wave heights on a plane beach. J. Hydrodyn. Ser. B 2014, 26, 939–950. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, B.; Liu, H. Characteristics of tsunami motion and energy budget during runup and rundown processes over a plane beach. Phys. Fluids 2012, 24, 62–107. [Google Scholar] [CrossRef]
- Kelman, I.; Spence, R. An overview of flood actions on buildings. Eng. Geol. 2004, 73, 297–309. [Google Scholar] [CrossRef]
- Masselink, G.; Ruju, A.; Conley, D.; Turner, L.; Ruessink, G.; Matias, A.; Thompson, C.; Castelle, B.; Puleo, J.; Citerone, V.; et al. Large-scale barrier dynamics experiment II (BARDEX II): Experimental design, instrumentation, test program, and data set. Coast. Eng. 2016, 113, 3–18. [Google Scholar] [CrossRef]
- Blenkinsopp, C.E.; Matias, A.; Howe, D.; Castelle, B.; Marieu, V.; Turner, I.L. Wave runup and overwash on a prototype-scale sand barrier. Coast. Eng. 2016, 113, 88–103. [Google Scholar] [CrossRef]
- Matias, A.; Masselink, G.; Castelle, B.; Blenkinsoop, C.E.; Kroon, A. Measurements of morphodynamic and hydrodynamic overwash processes in a large-scale wave flume. Coast. Eng. 2016, 113, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.N. Geotechnical Engineering Technology; Blackie Academic & professional: London, UK, 1995. [Google Scholar]
- Brennan, A.J.; Ghahremani, M.; Brown, M.J. Strength reduction for upheaval buckling of buried pipes in blocky clay backfill. Ocean Eng. 2017, 130, 210–217. [Google Scholar] [CrossRef] [Green Version]
- Baziar, M.H.; Nabizadeh, A.; Mehrabi, R.; Lee, C.J.; Hung, W.Y. Evaluation of underground tunnel response to reverse fault rupture using numerical approach. Soil Dyn. Earthq. Eng. 2016, 83, 1–17. [Google Scholar] [CrossRef]
- Candia, G.; Mikola, R.G.; Sitar, N. Seismic response of retaining walls with cohesive backfill: Centrifuge model studies. Soil Dyn. Earthq. Eng. 2016, 90, 411–419. [Google Scholar] [CrossRef] [Green Version]
- Coulter, S.E.; Phillips, R. Simulating submarine slope instability initiation using centrifuge model testing. In 1st International Symposium on Submarine Mass Movements and Their Consequences; Springer: Dordrecht, The Netherlands, 2003; pp. 29–36. [Google Scholar]
- Coulter, S.E. Seismic Initiation of Submarine Slope Failures Using Physical Modeling in a Geotechnical Centrifuge; Memorial University of Newfoundland: St. John’s, NL, Canada, 2008. [Google Scholar]
- Gue, C.S. Submarine Landslide Flows Simulation through Centrifuge Modelling; University of Cambridge: Cambridge, UK, 2012. [Google Scholar]
- Sekiguchi, H.; Kita, K.; Sassa, S.; Shimamura, T. Generation of progressive fluid waves in a geo-centrifuge. Geotech. Test. J. 1998, 21, 95–101. [Google Scholar]
- Sassa, S.; Sekiguchi, H. Wave-induced liquefaction of beds of sand in a centrifuge. Géotechnique 1999, 49, 621–638. [Google Scholar] [CrossRef]
- Sassa, S.; Sekiguchi, H.; Miyamoto, J. Analysis of progressive liquefaction as a moving-boundary problem. Géotechnique 2001, 51, 847–857. [Google Scholar] [CrossRef]
- Nallayarasu, S.; Fatt, C.H.; Shankar, N.J. Estimation of incident and reflection waves in regular wave experiments. Ocean Eng. 1995, 22, 77–86. [Google Scholar] [CrossRef]
- Ursell, F.; Dean, R.G.; Yu, Y.S. Forced small-amplitude water: A comparison of theory and experiment. J. Fluid Mech. 1960, 7, 33–52. [Google Scholar] [CrossRef]
- Schäffer, H.A. Second-order wavemaker theory for irregular waves. Ocean Eng. 1996, 23, 47–88. [Google Scholar] [CrossRef]
- Spinneken, J.; Swan, C. Second-order wave maker theory using force-feedback control. Part I: A new theory for regular wave generation. Ocean Eng. 2009, 36, 539–548. [Google Scholar] [CrossRef] [Green Version]
- Doorslaer, K.V.; Romano, A.; Rouck, J.D.; Kortenhaus, A. Impacts on a storm wall caused by non-breaking waves overtopping a smooth dike slope. Coast. Eng. 2017, 120, 93–111. [Google Scholar] [CrossRef]
- Whittaker, C.N.; Fitzgerald, C.J.; Raby, A.C.; Taylor, P.H.; Orszaghova, J.; Borthwick, A.G.L. Optimisation of focused wave group runup on a plane beach. Coast. Eng. 2017, 121, 44–55. [Google Scholar] [CrossRef] [Green Version]
- Anbarsooz, M.; Passandieh-Fard, M.; Moghiman, M. Fully nonlinear viscous wave generation in numerical wave tanks. Ocean Eng. 2013, 59, 73–85. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transfer 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemishpere Publishing Corporation: New York, NY, USA, 1980. [Google Scholar]
- Barnes, F.J.; Bromly, J.H.; Edwards, T.J.; Madngezewsky, R. NOx emissions from radiant gas burners. J. Inst. Energy 1988, 155, 84–188. [Google Scholar]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. Numer. Methods Fluid Dyn. 1982, 24, 273–285. [Google Scholar]
- Chen, Z.C. Centrifugal Modeling Test on Wave-Induced dynamic Response of Seabed; Dalian University of Technology: Dalian, China, 2013. [Google Scholar]





| Parameter | Dimension | Model Scaling (General) | Model Scaling (This Study) |
|---|---|---|---|
| Acceleration due to gravity | LT−2 | N | N |
| Wave length | L | n | 1/N |
| Wave height | L | n | 1/N |
| Water depth | L | n | 1/N |
| Piston stroke | L | n | 1/N |
| Time | T | N−1/2n1/2 | 1/N |
| Wave celerity | LT−1 | N1/2n1/2 | 1 |
| Density | ML−3 | 1 | 1 |
| Static pressure | ML−1T−2 | Nn | 1 |
| Kinematic viscosity coefficient | L2T−1 | N1/2n3/2 | 1 |
| Case Number | H (m) | d1 (m) | d2 (m) | H/d1 | d1/d2 | S (m) | τ (s) | L (m) | D (m) |
|---|---|---|---|---|---|---|---|---|---|
| Under the normal gravity (1 g) field | |||||||||
| 011 | 1.2 | 6 | 2.27 | 0.2 | 2.64 | 6.20 | 14.75 | 300 | 10 |
| 012 | 1.8 | 6 | 2.27 | 0.3 | 2.64 | 7.59 | 11.86 | ||
| 013 | 2.4 | 7 | 2.65 | 0.34 | 2.64 | 9.47 | 11.91 | 16 | |
| Under 30 times the normal gravity (30 g) field | |||||||||
| 301 | 0.04 | 0.2 | 0.076 | 0.2 | 2.64 | 0.21 | 0.49 | 10 | 0.33 |
| 302 | 0.06 | 0.2 | 0.076 | 0.3 | 2.64 | 0.25 | 0.40 | ||
| 303 | 0.08 | 0.23 | 0.088 | 0.34 | 2.64 | 0.32 | 0.40 | 0.53 | |
| Under 50 times the normal gravity (50 g) field | |||||||||
| 501 | 0.024 | 0.12 | 0.045 | 0.2 | 2.64 | 0.12 | 0.29 | 6 | 0.2 |
| 502 | 0.036 | 0.12 | 0.045 | 0.3 | 2.64 | 0.15 | 0.24 | ||
| 503 | 0.048 | 0.14 | 0.053 | 0.34 | 2.64 | 0.19 | 0.24 | 0.32 | |
| Under 100 times the normal gravity (100 g) field | |||||||||
| 101 | 0.012 | 0.06 | 0.023 | 0.2 | 2.64 | 0.06 | 0.15 | 3 | 0.1 |
| 102 | 0.018 | 0.06 | 0.023 | 0.3 | 2.64 | 0.08 | 0.12 | ||
| 103 | 0.024 | 0.07 | 0.027 | 0.34 | 2.64 | 0.09 | 0.12 | 0.16 | |
| No. | 0.8 τ | 1.1 τ | 1.4 τ | 1.7 τ | 2.0 τ | εa (%) | No. | 0.8 τ | 1.1 τ | 1.4 τ | 1.7 τ | 2.0 τ | εa (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 011 | 121 | 120 | 119 | 118 | − | 0.19 | 501 | 2.39 | 2.34 | 2.31 | 2.28 | − | 0.40 |
| 012 | 181 | 179 | 177 | 175 | 174 | 0.30 | 502 | 3.53 | 3.43 | 3.37 | 3.32 | 3.28 | 0.62 |
| 013 | 240 | 237 | 234 | 231 | 230 | 0.34 | 503 | 4.66 | 4.51 | 4.41 | 4.34 | 4.30 | 0.71 |
| 301 | 3.98 | 3.91 | 3.85 | 3.81 | − | 0.36 | 101 | 1.19 | 1.17 | 1.15 | 1.14 | − | 0.36 |
| 302 | 5.89 | 5.72 | 5.61 | 5.53 | 5.47 | 0.64 | 102 | 1.77 | 1.72 | 1.68 | 1.66 | 1.64 | 0.65 |
| 303 | 7.76 | 7.52 | 7.36 | 7.24 | 7.16 | 0.69 | 103 | 2.33 | 2.26 | 2.21 | 2.17 | 2.14 | 0.69 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.-S.; Li, M.-H.; Li, D.-W. Solitary Wave Generation and Propagation under Hypergravity Fields. Water 2018, 10, 1381. https://doi.org/10.3390/w10101381
Wang Q-S, Li M-H, Li D-W. Solitary Wave Generation and Propagation under Hypergravity Fields. Water. 2018; 10(10):1381. https://doi.org/10.3390/w10101381
Chicago/Turabian StyleWang, Qiao-Sha, Ming-Hai Li, and Dai-Wei Li. 2018. "Solitary Wave Generation and Propagation under Hypergravity Fields" Water 10, no. 10: 1381. https://doi.org/10.3390/w10101381




