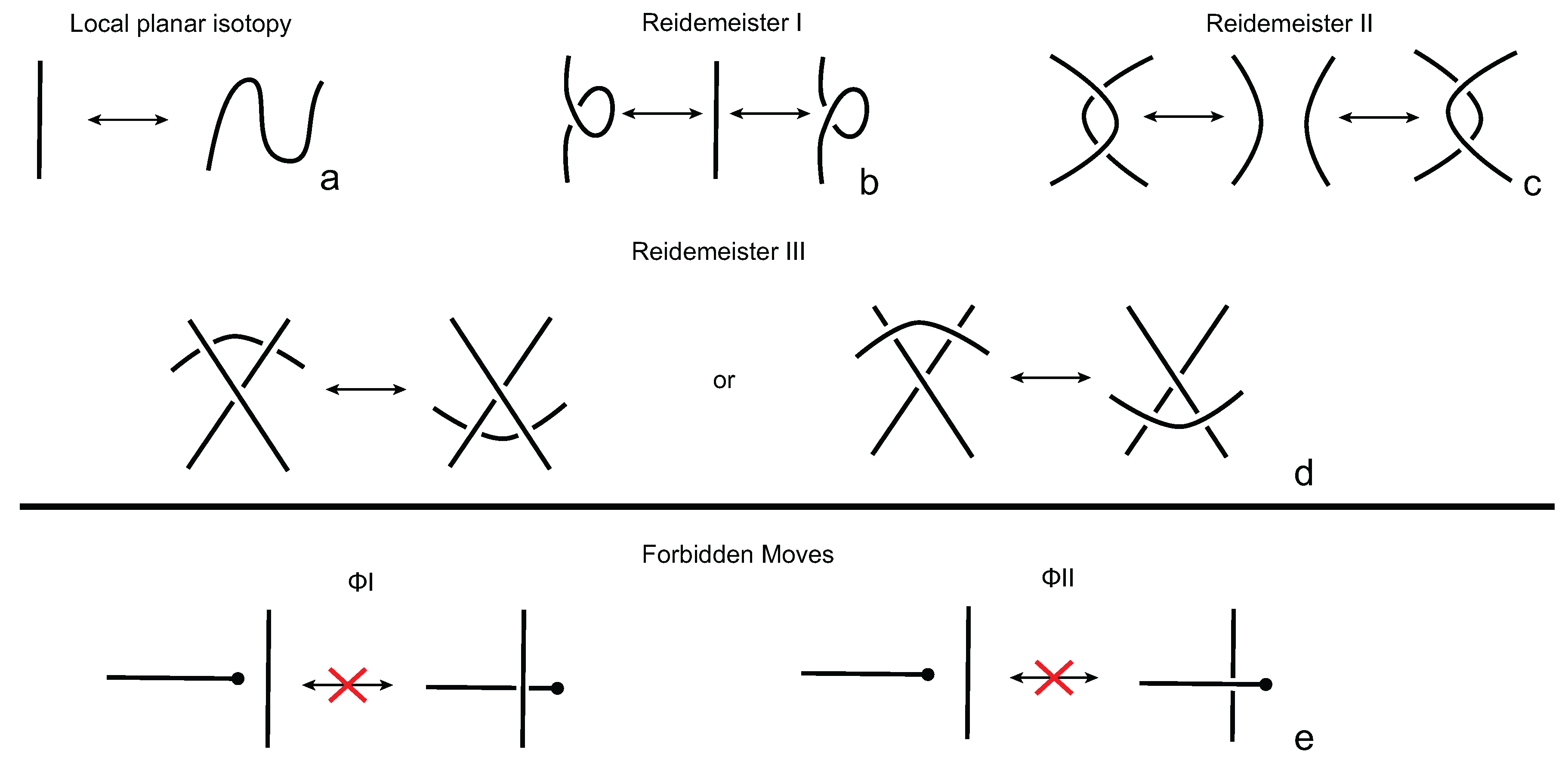3.1. Analyzing Open Protein Chains Using Knotoids
Proteins appear in various, quite often very complicated conformations and, as such, the study of their topology has proven to be a challenge. In order to determine the entanglement type of a protein, one usually considers its backbone as an open polygonal curve and then simplifies it by applying an algorithm that preserves the underlying topology. Probably the most well-known technique in the literature is the triangle elimination or KMT (Koniaris-Muthukumar-Taylor) algorithm [
18,
19,
20]. Many suggestions have been made on how to close an open 3D curve and they fall into two large categories [
1,
3,
19,
21,
22,
23,
24,
25]. First are the single closure techniques, such as the direct closure [
19] and the out of the center of mass closure [
3] techniques, where the chain is closed by a single arc that connects the endpoints. These methods are computationally fast but depending on the particular closure recipe the same protein may end up forming different knots. The second category comprises probabilistic methods such as the uniform closure technique [
22,
24,
25], where the chain is first placed inside a large enough sphere (usually a radius of twice the length of the chain will be enough) and a simplification algorithm is applied. Each point of the sphere is now a possible closure point of the open chain. The closure is achieved by picking a point and then extending two rays, one from each endpoint of the chain, towards the chosen point and connecting them. The knot type, as in the case of knotoids that was discussed above, is a probability distribution. Such methods are less biased but they are more computationally intensive as the knot type of each closure has to be computed. Both categories have the disadvantage of altering the geometry of the studied object.
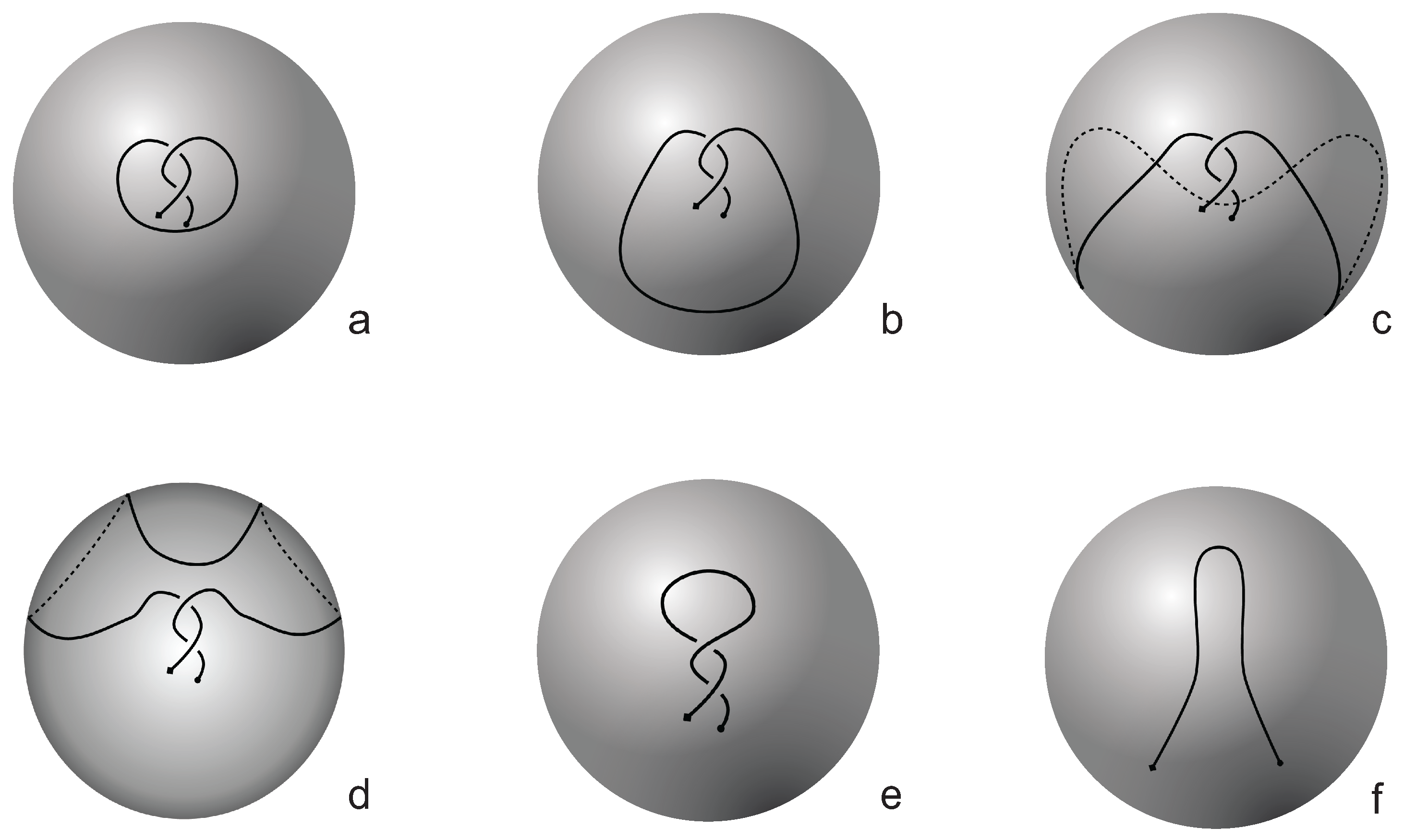
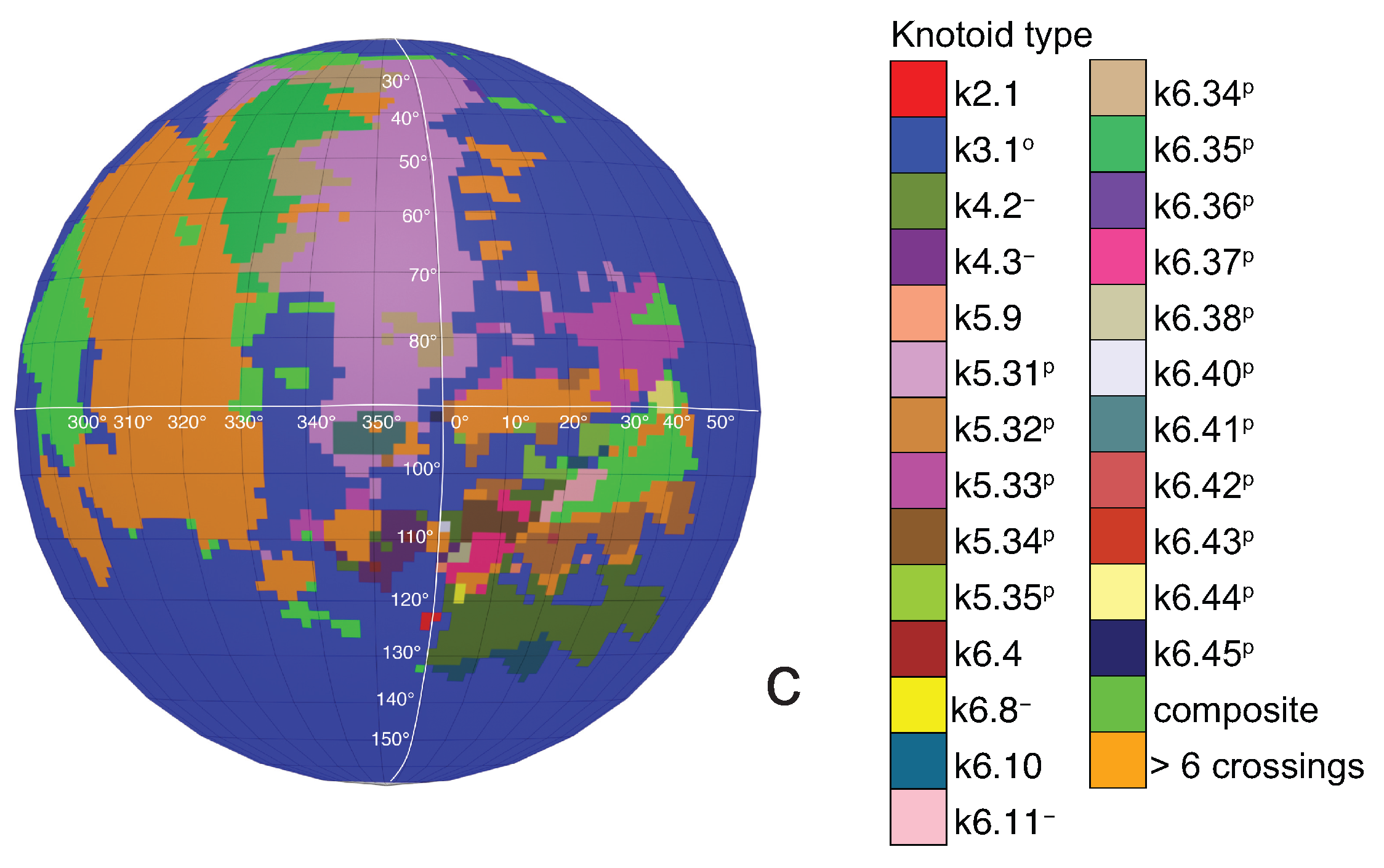
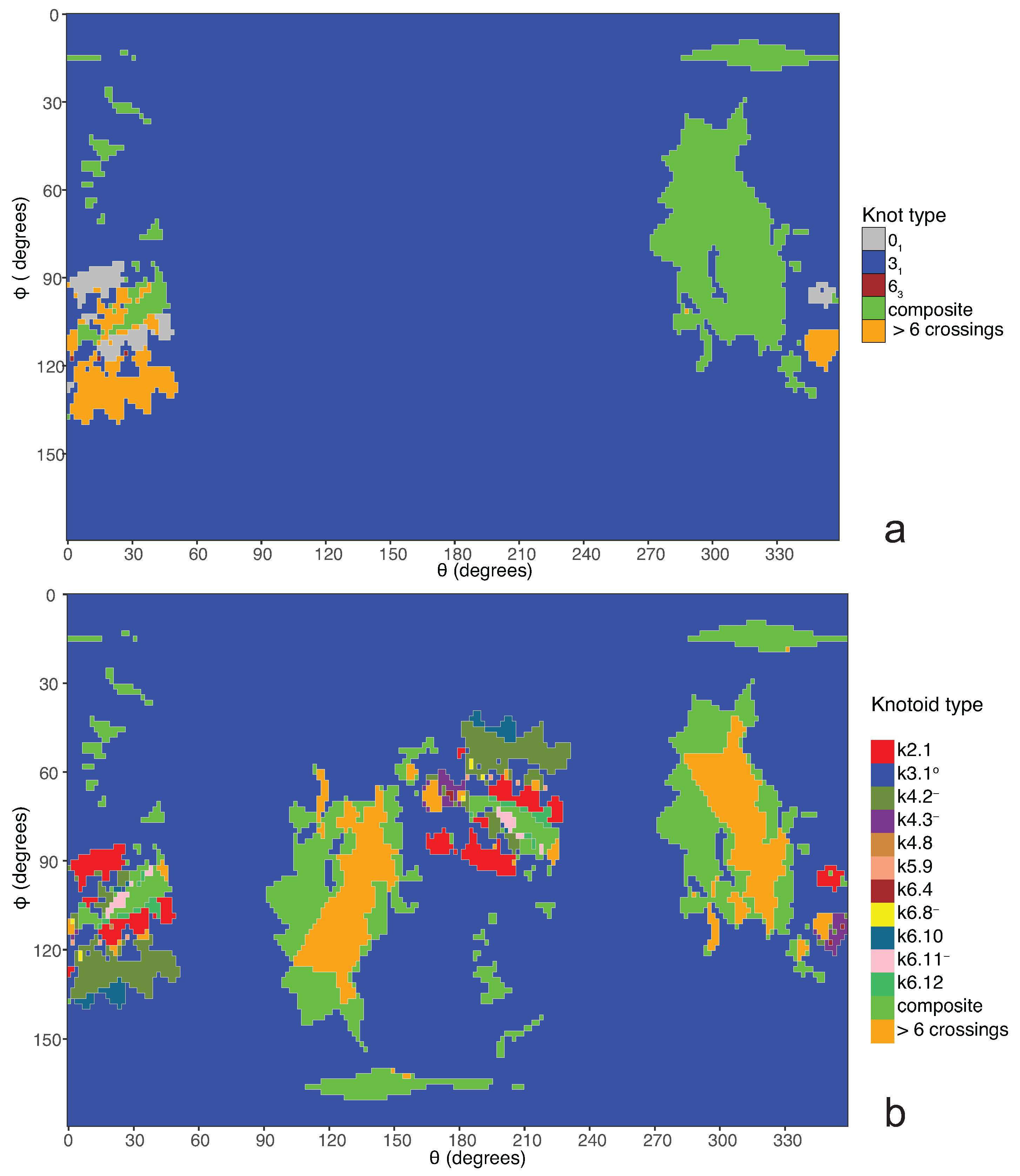
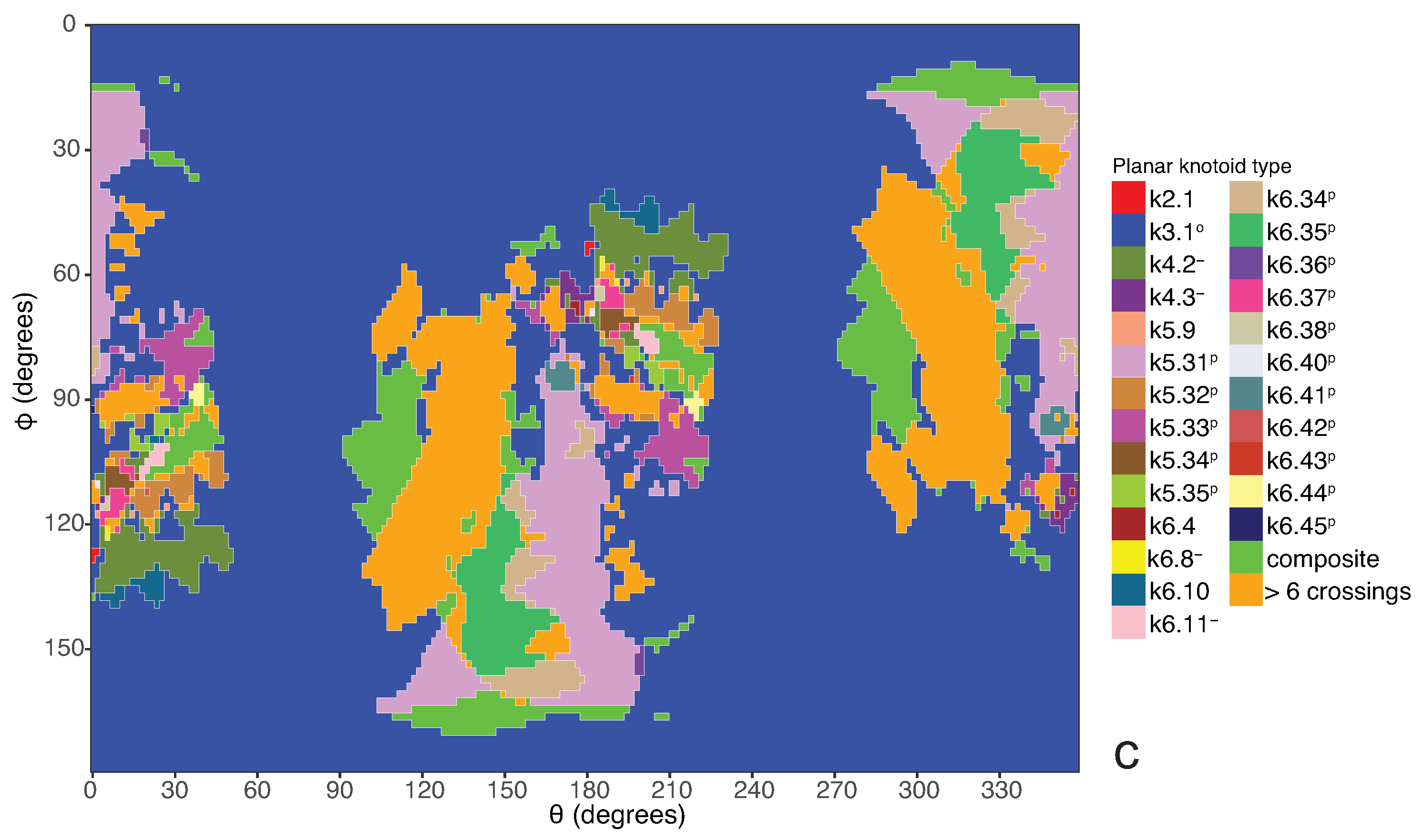
If one now chooses to study the entanglement of the protein backbone using the concept of knotoids, then the procedure is similar to the case of the uniform closure. Once again, the protein chain lies into a large enough sphere, but in this case each point of the sphere corresponds to a projection direction on a surface that lies outside the sphere. When the projection direction is determined, the two infinite lines are introduced and a simplification algorithm is applied on the chain in a way that the infinite lines are never crossed. The results then can be summarized on a map that identifies regions on a sphere and each distinct region corresponds to the projection directions in spherical coordinates that produce the same knotoid type. Moreover, each distinct region is color coded according to the knotoid type it carries. We shall call such a map the projection globe of a protein.
Coming back to the discussion in
Section 2 and considering the differences between planar and spherical knotoids, one can further refine the projection map of an open protein chain by refraining from pushing arcs around the surface of the sphere and considering projections of the chain on a plane instead. This will allow projections that were previously detected as unknotted to emerge as non-trivial planar knotoids. In this paper, we apply this approach to the protein with Protein Database (PDB) entry 3KZN (
N-acetyl-
l-ornithine) [
26]. This protein is known to form a trefoil knot or a
knot-type knotoid. Recall that knot-type knotoids have both endpoints in the same region of the diagram and if one decides to close the diagram with an arc, the newly introduced arc may not create any additional crossings to the diagram. In our notation, a knotoid is represented by
, where
X is the number of crossings of the knotoid diagram in question and
Y corresponds to the position of the knotoid in our table among knotoids with the same number of crossings. Moreover, an exponent
indicates a knot-type knotoid, an exponent
a planar knotoid, and an exponent
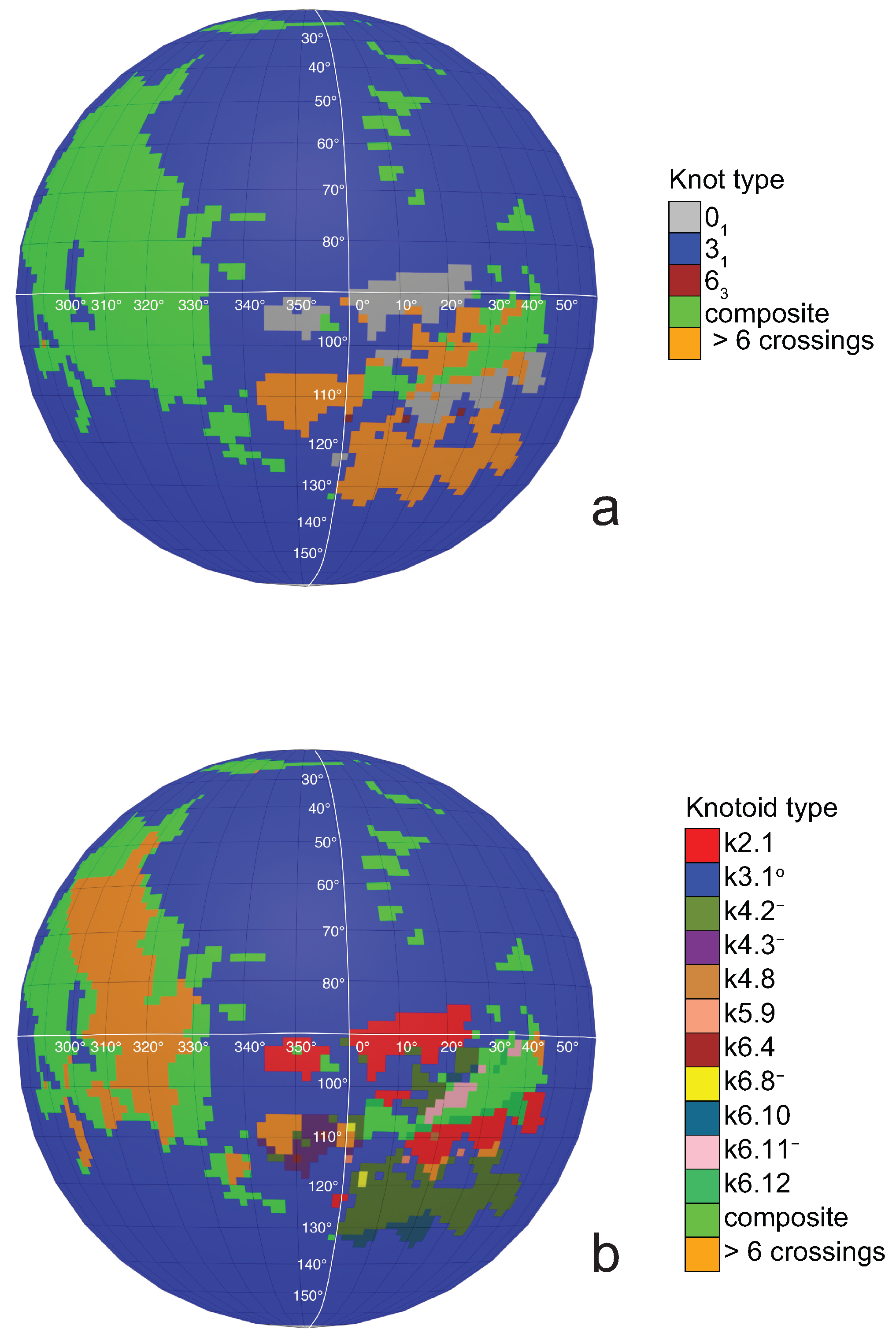
a knotoid with its crossings inverted. Comparing now the projection globe obtained from the planar knotoids approach to the one derived from the spherical knotoids approach, as well as to the one that is derived from the uniform closure technique, we can see that new regions are gradually emerging as we move from knots to spherical knotoids and then to planar knotoids (see
Figure 4). The reason behind this is that the number of classes of planar knotoids is larger than the number of classes of spherical knotoids, as discussed in
Section 2 and shown in
Figure 3. The diagrams in
Figure 3 show a configuration that will simplify if the arc surrounding the endpoints could be swung all the way around a two- dimensional sphere. This cannot be done in the plane, and thus the diagram represents a knotoid that is not trivial in the plane but is trivial on the sphere.
Figure 5 shows equirectangular projections of each projection globe shown in
Figure 4. From the above we can conclude that analyzing open protein chains as planar knotoids reveals more details of their topology.
3.2. A Topological Model for Bonded Open Protein Chains
Motivated by the ideas in [
13,
14], in this section we introduce a purely topological model for analyzing the topology of bonded open protein chains in terms of planar (multi-) knotoids.
A bonding site of a protein chain consists of two local strands of the chain and a bonding arc with its ends based on these strands, as illustrated in
Figure 6. We adopt the projection of a space curve into planes resulting in knotoid diagrams, to a projection for a bonded protein chain. More precisely, we choose a projection direction determined by two parallel (infinite) lines passing through the termini of the chain and we project the protein chain into the plane that is orthogonal to these lines. We only consider projection directions that give a generic diagram, in the sense that we have only finitely many self-crossing points and that a bonding site is represented in the projection in a parallel or in anti-parallel fashion. The information of each bond is represented with dotted segments connecting the two ends involved. Endowing each self-intersection point with the weaving information of the chain in the space, we obtain an open-ended knotted diagram in the projection plane with the extra information of bonds. We call such a diagram a
bonded knotoid diagram.
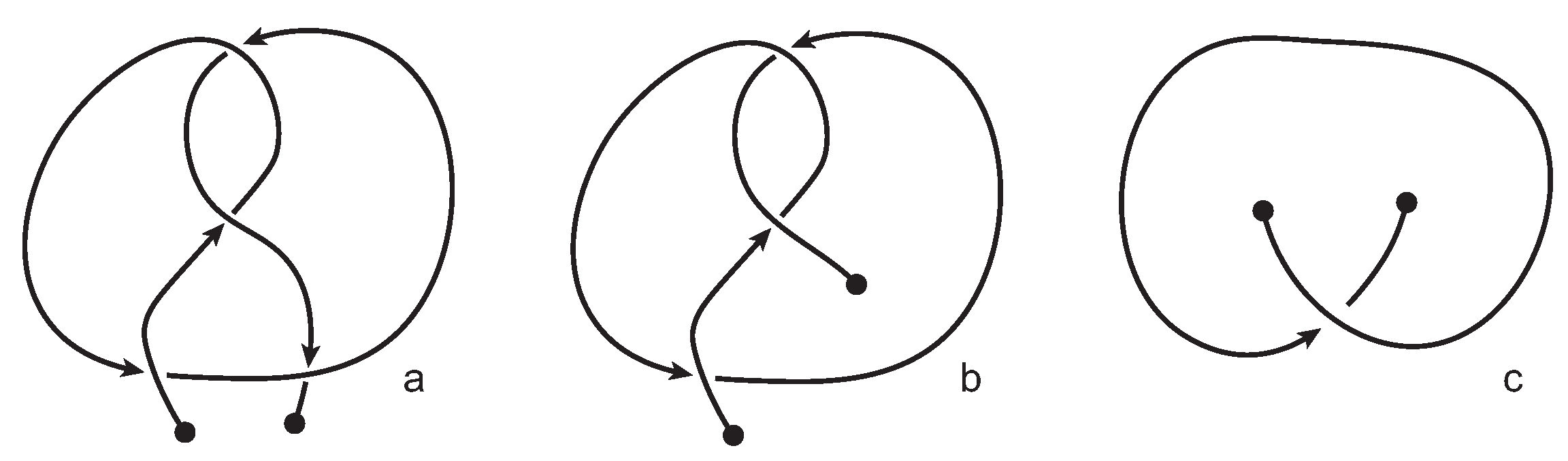
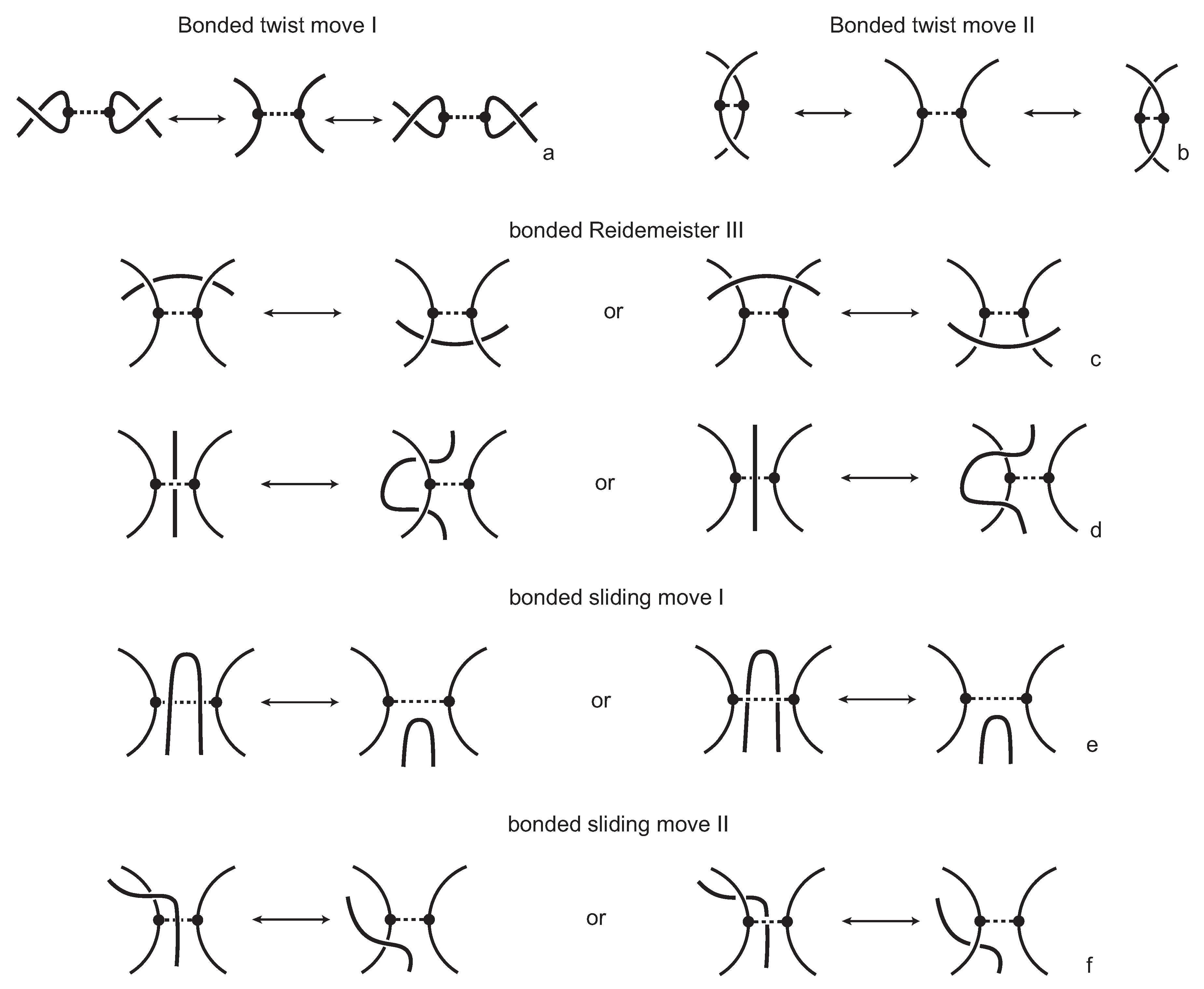
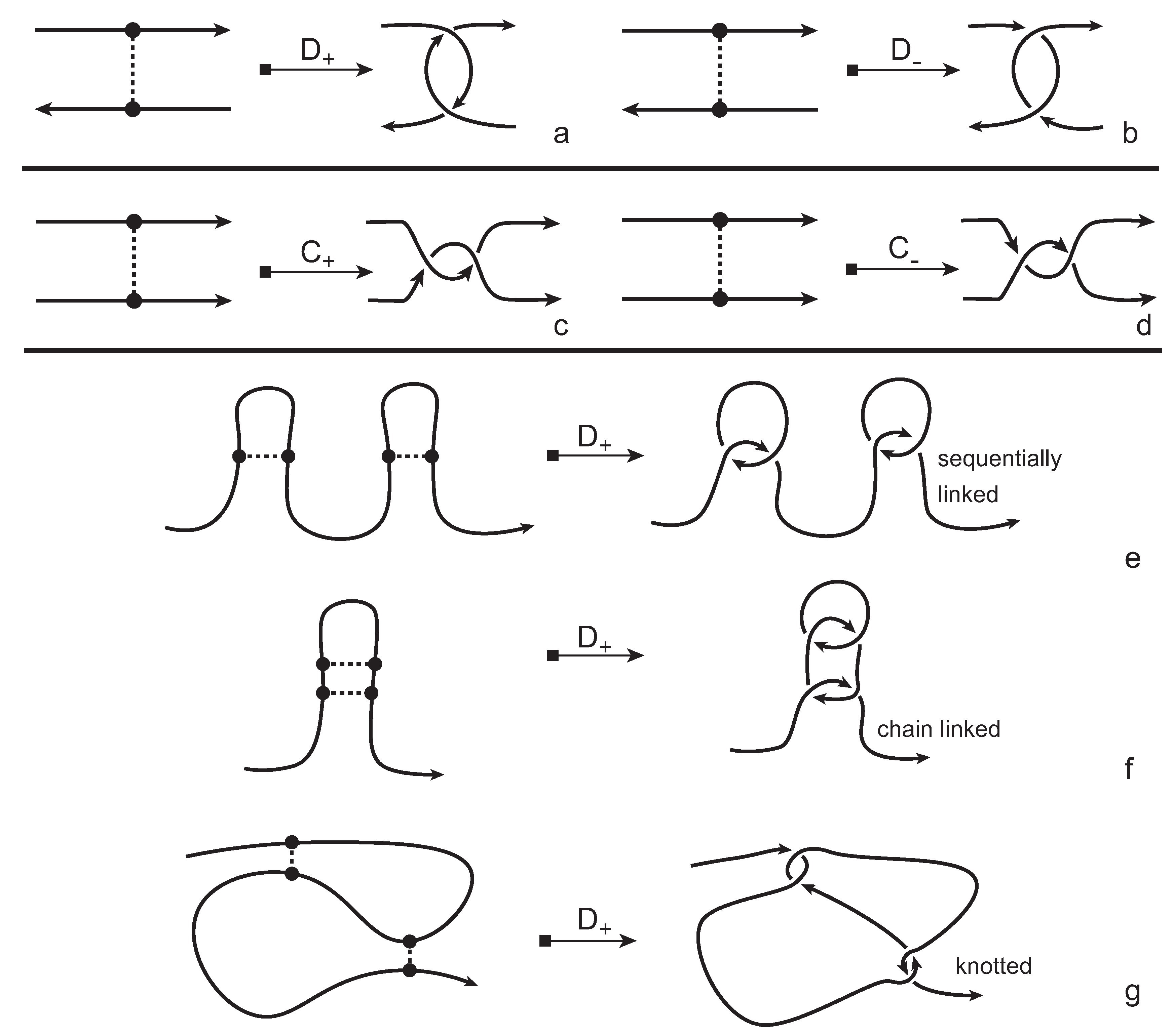
We consider each bonding site in a bonded knotoid diagram locally as a rigid planar formation. As such, a bonding arc in a diagram is not subjected to any topological deformations in the plane such as bending, shrinking or enlarging, and any twisting of the bonding arc is avoided. On the other hand, local strands of bonding sites are topologically flexible. More precisely, we allow on bonded knotoid diagrams the usual Reidemeister moves for knotoids away from the bonds and away from any of the endpoints, and also we allow the bonded moves illustrated in
Figure 6, each of which is realized in bonding sites. As seen in
Figure 6a–d, the first two moves, namely bonded twist moves 1 and 2, introduce a twisting in the strands neighboring the bonds. These moves result from a 180-degree turn of the bond, about the vertical and the horizontal axes, respectively. The bonded Reidemeister III move allows an edge of the diagram to slide over or under a bond as a whole without any other change in the bonded knotoid diagram. An edge may be located over or under a bonding arc. The bonded slide moves illustrated in
Figure 6e,f allow the movement of such an edge located in between the local strands of the bonding site, so that the bonding site is free from any edges other than the bonding arc. The above moves generate an isotopy relation for bonded knotoid diagrams and an isotopy class of bonded knotoid diagrams is a
bonded knotoid. The isotopy moves of bonded knotoid diagrams are analogous to what is known in graph theory as rigid vertex isotopy moves [
27], if one replaces a bonding site with a rigid vertex.
In order to obtain a (multi-) knotoid diagram from a bonded knotoid diagram, we substitute each bonding site by a chosen full twist (a 360-degree twist) using the following convention. If the local strands are directed anti-parallel then we substitute the bonding site by a full twist of the strands along the bonding arc, as illustrated in
Figure 7a,b, and the substitution is known as being of type
D. If the local strands are directed parallel then we substitute the site by a full twist of the strands, as shown in
Figure 7c,d and the substitution is known to be of type
C. Note that insertions of type
D make disconnections in the diagram, while those of type
C retain connectivity. Either type of full twists can be positive (right-handed) or negative (left-handed). In this paper, all full-twist substitutions are of a positive type. After replacing all bonding sites we end up with a planar (multi-) knotoid diagram. Besides, the isotopy moves defined on bonded knotoid diagrams are consistent with the isotopy moves defined on knotoid diagrams after making the twist substitutions. It follows that if two bonded knotoid diagrams are isotopic then the corresponding (multi-) knotoid diagrams obtained by full-twist substitutions are isotopic. This means that any topological invariant of knotoids can be used for analyzing the topological type of a knotted bonded open protein chain modeled by a bonded knotoid. There are mainly three types of protein bonds: sequential, nested, and pseudoknot-like type bonds, as illustrated in
Figure 7e–g. As we see in the figure, all these types of bonds are detected by type
D substitutions as compared to the same formations with the bonds ignored. This fact can be proved by applying knotoid invariants such as the Turaev loop bracket polynomial and the arrow polynomial.
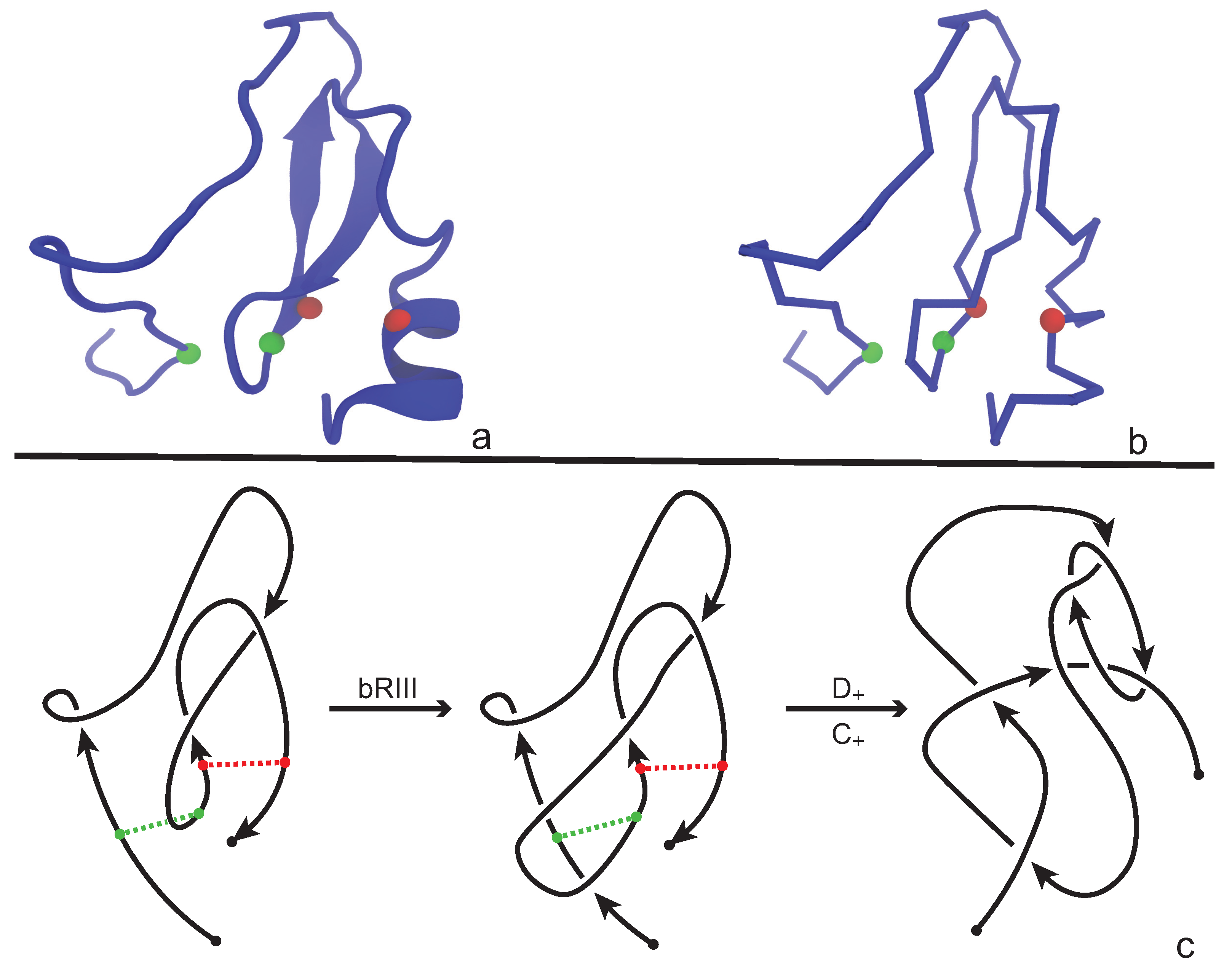
An application of our model is illustrated in
Figure 8 where we consider the protein with PDB entry 2LFK (NMR solution structure of native TdPI-short) [
28]. This protein contains two cysteine bridges that appear between residues 24 and 51 (shown as green beads), and between 52 and 69 (shown as red beads) in
Figure 8a,b. For demonstrative reasons we will discuss the application of our model on a single fixed projection, however one has to have in mind that, following
Section 3.1, several projections of the backbone have to be analyzed in order to obtain an accurate overview of the topology of the chain. We proceed now and consider the projection of the protein chain that is shown in
Figure 8c, which is a bonded knotoid diagram with two bonding sites. Notice that in the green bonding site an arc of the diagram crosses over the bonding arc and so an immediate application of a full-twist is not possible at this state. However, an application of a bonded Reidemeister III move pushes the arc to the left, allowing now the application of a type
full-twist since the green bonding site is in a parallel fashion. The situation for the red bonding site is straightforward. Here, we observe that the bonding site is in anti-parallel fashion and so a type
full-twist substitution is immediately applied giving rise to a multi-knotoid diagram with two components that can be evaluated with any invariant for knotoids such as the Turaev loop bracket polynomial or the arrow polynomial. Of course, if one drops the bonding information, the structure becomes unknotted. We note here that the same protein has been analyzed in [
11,
12] for the existence of links where the cysteine bridges are closed with a direct line instead of a full-twist substitution. This explains the difference in the detected link type.
An Application to Complex Lassos
A lasso is formed when a disulphide bond between two amino acids of the protein backbone creates a closed loop that is called a
cysteine or
covalent loop (see
Figure 9). The parts of the chain that are not involved in the spanning of the loop are the
tails of the lasso and if they are short enough, the resulting structure is unknotted. However, in general cases at least one of the tails is long enough to pass through the loop. There is great interest in understanding the impact of the existence of lassos on the function and stability of proteins, as well as the way these structures fold and so it is important to be able to distinguish between different types of lassos. In other words, we would like to know if and how many times a tail is threaded through the loop. Until now, such an analysis was achieved using a technique called minimal surface analysis. This technique is geometrical and it determines how many times a tail pierces the minimal surface that can be spanned by the covalent loop. In what follows, we propose an approach that utilizes bonded knotoid diagrams and we apply it on all motifs that are presented in [
9].
The protein chain together with the bonding information, that is the indices of the residues that form the covalent bond, is placed inside a large enough sphere and then is projected on a number of different planes. In this way, a bonded knotoids diagram is obtained from each projection and so we proceed with applying the method that was discussed in
Section 3.2. Since the bonding site of every lasso is in an antiparallel fashion, we apply a single positive or negative type
D full-twist and then we evaluate the resulting diagram. The sign of the full-twist substitution is determined by the sign of the crossing of the diagram that determines the first piercing of the loop.
The simplest lassos are
and
in which the tail either does not pierce the loop at all, or does so only once. They are distinguished immediately by our method, since the twist insertion at the site of the cysteine bond produces the non-equivalent multi-knotoids
and
, respectively (see
Figure 9a,b). The cases of lassos
, where
is the number of times that the tail is threaded through the loop, require more attention. The amount of times that a tail pierces the loop creates slipknot-like forms in the conformation that remain undetected by regular topological tools (knot invariants). Indeed, twist insertion will produce a multi-knotoid diagram that is topologically equivalent to either
or
, depending on whether
i is even or odd. Therefore, in order to distinguish lassos of this type, we have to go back to the 3D chain and study all possible substructures of it that include the bonding site. Through progressive trimming of the C terminus of the chain, by projecting, by twist insertions, and by evaluations of the resulting diagrams we can see that for the case of
(see
Figure 9c), the trimming process causes the resulting multi-knotoids to shift between types
,
, and
. During this process, the multi-knotoid of type
, which corresponds to the subchain which has one endpoint inside the loop, is achieved twice which confirms the fact that one tail of the lasso is weaved through the loop twice. The cases of
with larger number of piercings are totally analogous with the multi-knotoid
appearing
i times. Finally, the cases of lassos
(
Figure 9d) and
(
Figure 9e) are even more complicated, since the twist insertion produces the same diagram for both. However, the trimming the C terminus of the 3D chain of
soon comes to an end. Otherwise, the bonding site will be destroyed, while for the case of
there is no such issue and thus the chain includes a wider spectrum of non-trivial substructures.
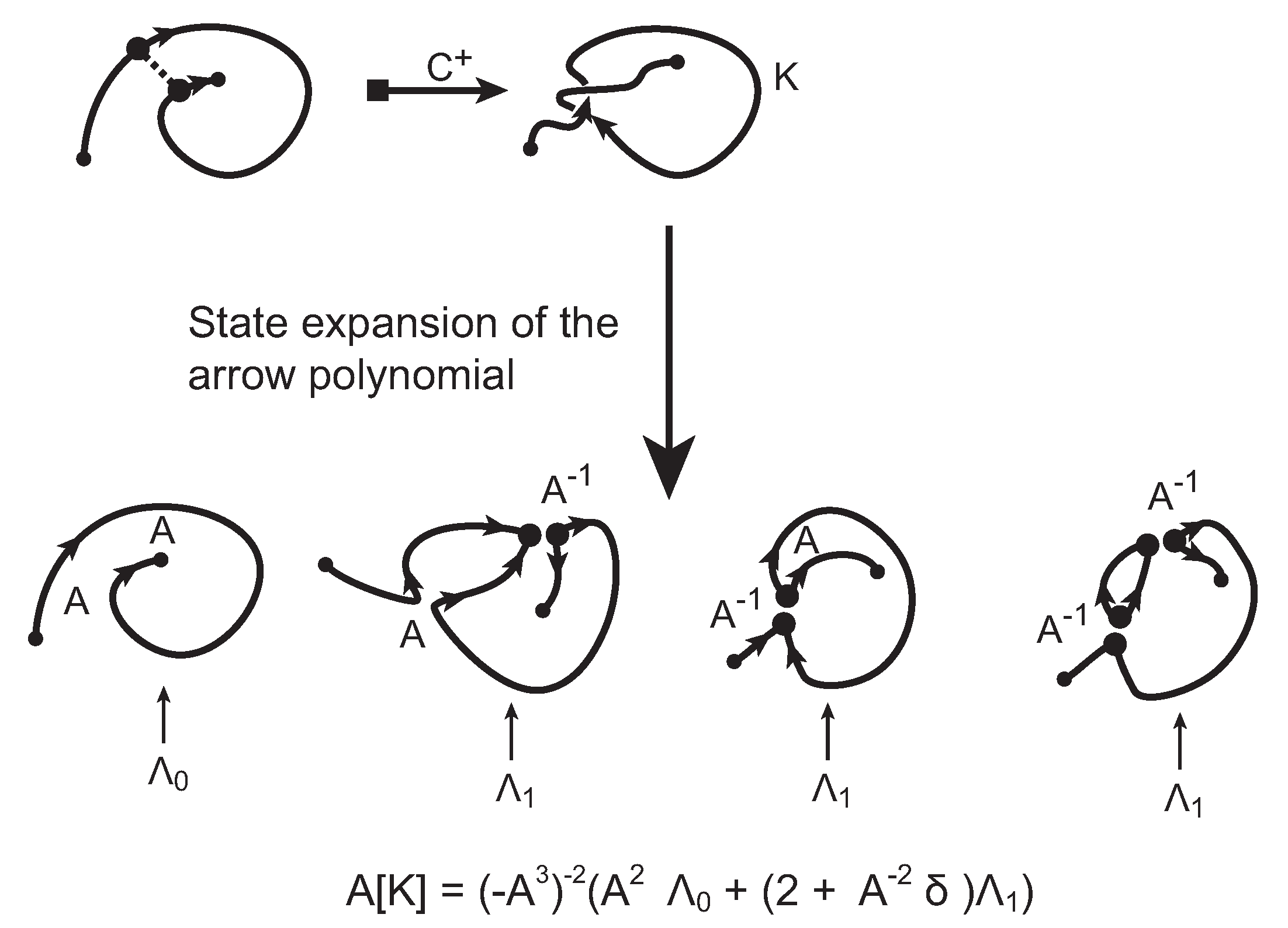
The evaluation of the topological type of such multi-knotoid diagrams can be achieved by the Turaev loop bracket polynomial. Alternatively, one may use the arrow polynomial in order to track the placement of the endpoints of the backbone after each trimming. More precisely, the arrow polynomial gives an estimation for the distance between the endpoints of a diagram, that is the least number of arcs that one has to cross in order to connect the two endpoints. This distance is defined as the
height of the knotoid [
16,
17].