A Dynamic Model of Drag Force for Catalytic Micromotors Based on Navier–Stokes Equations
Abstract
:1. Introduction
2. Theory and Method
3. Results and Discussions
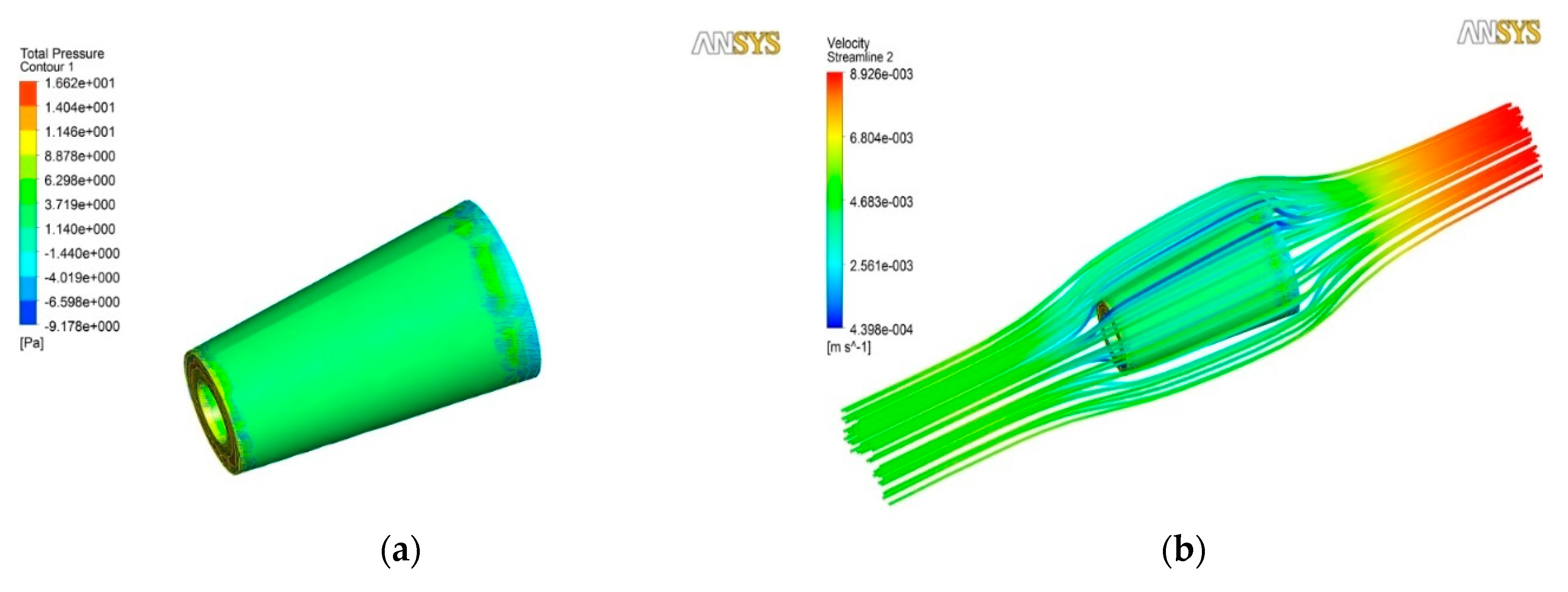
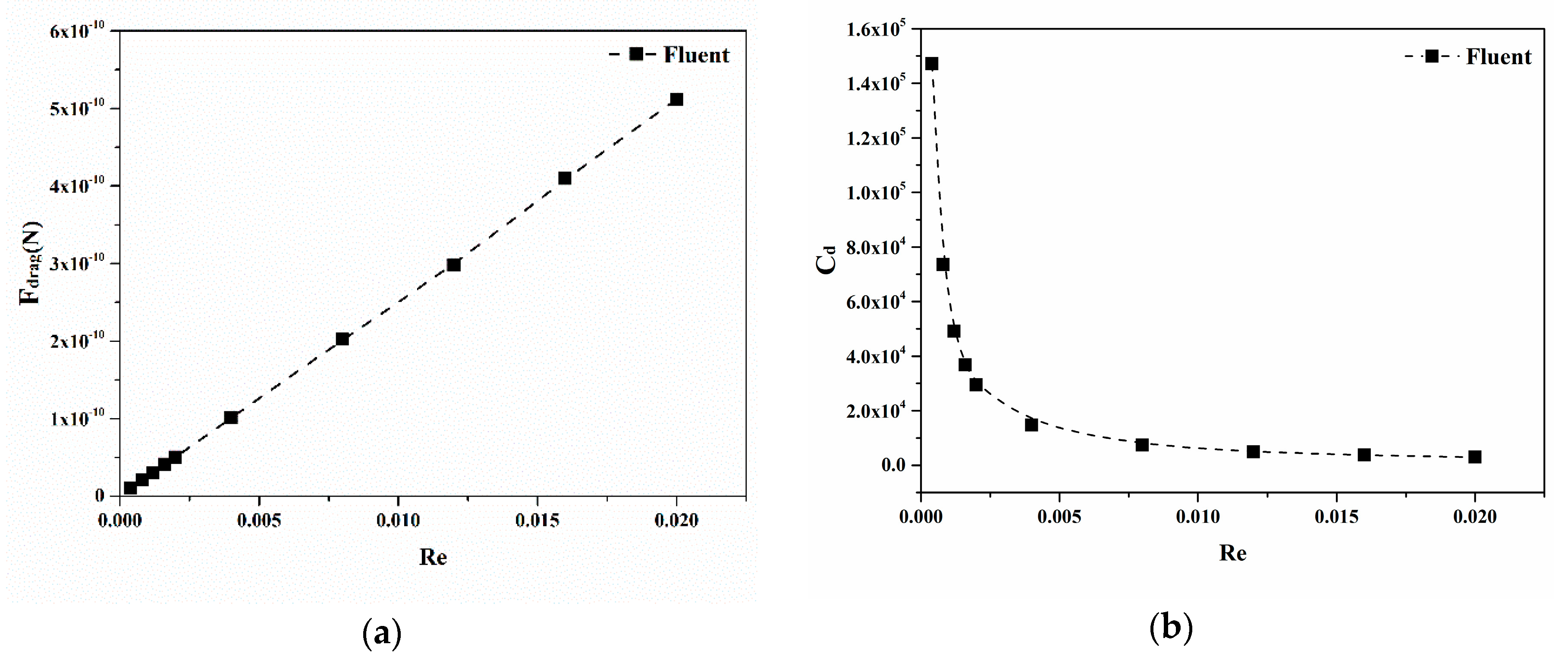
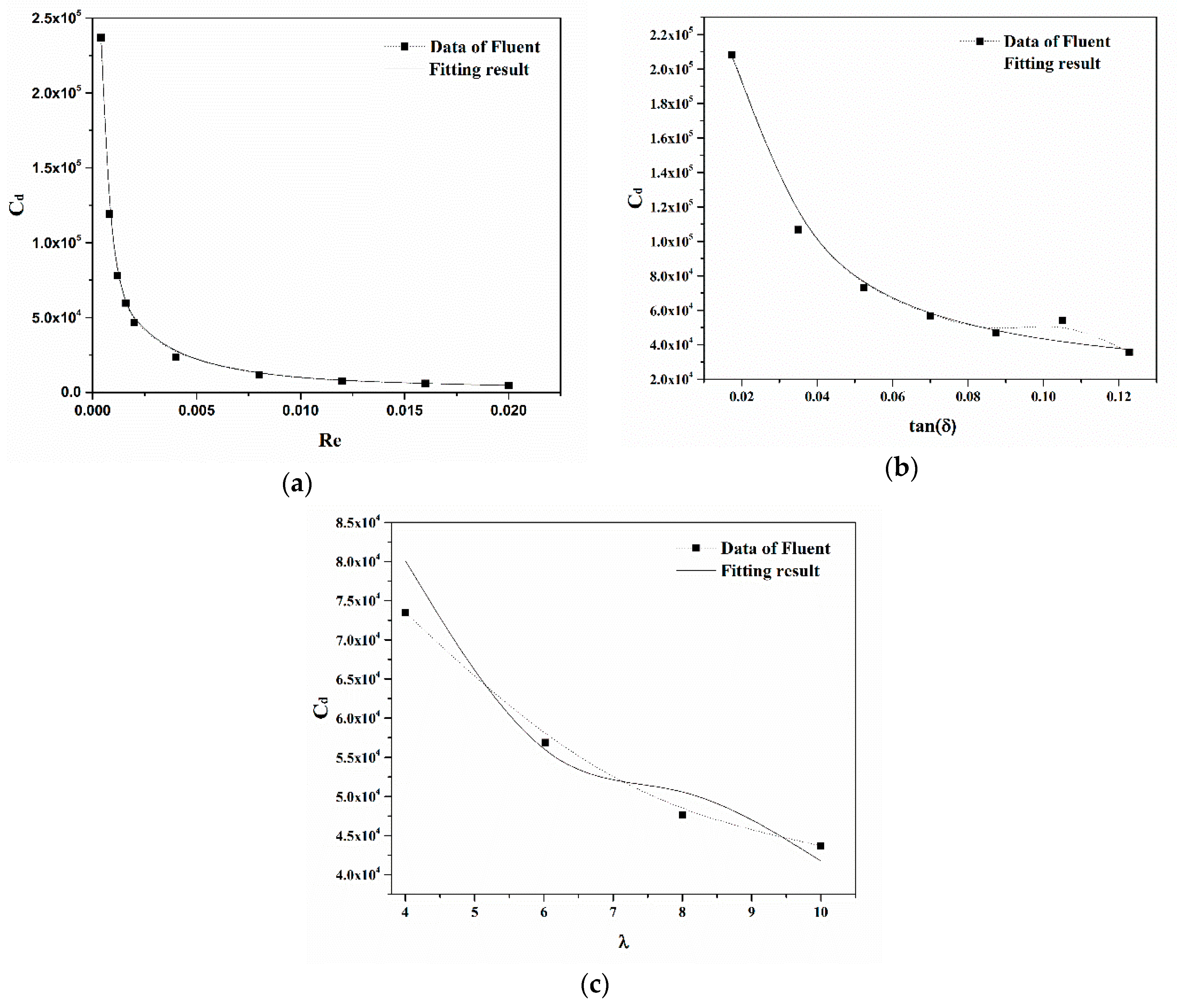
3.1. Calculation Results for Different Numerical Models
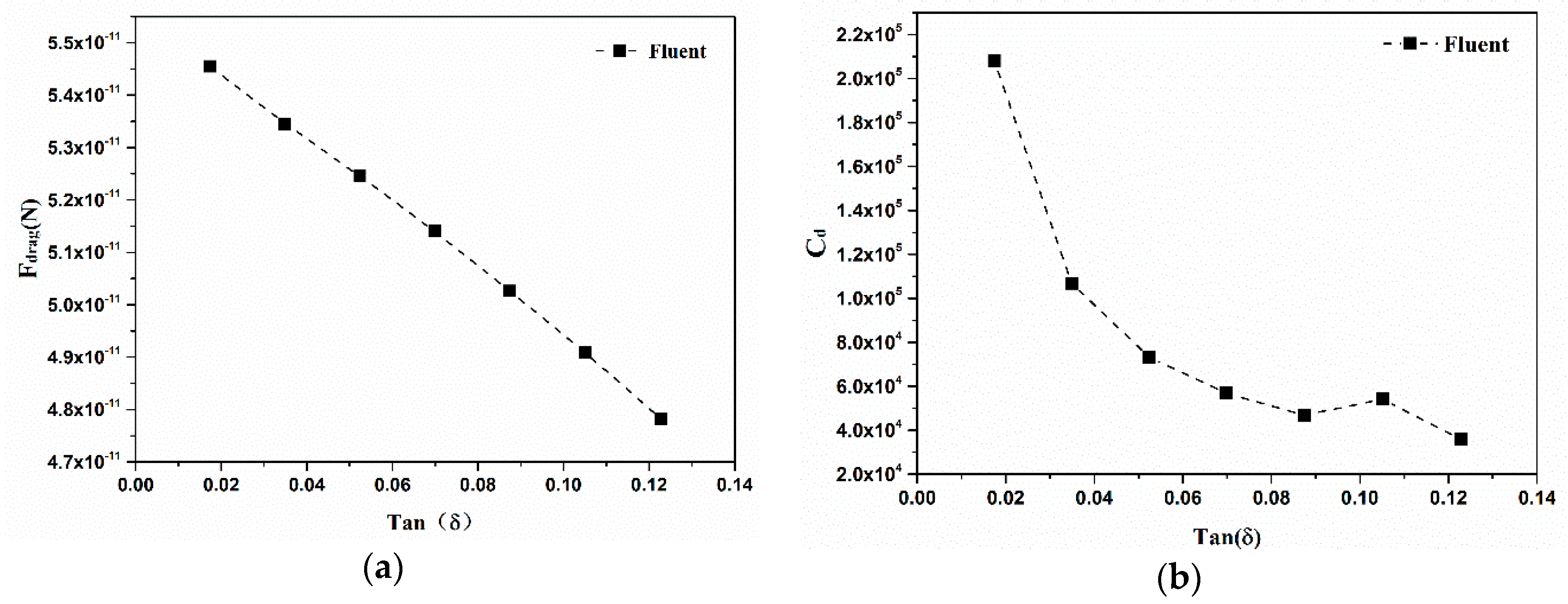
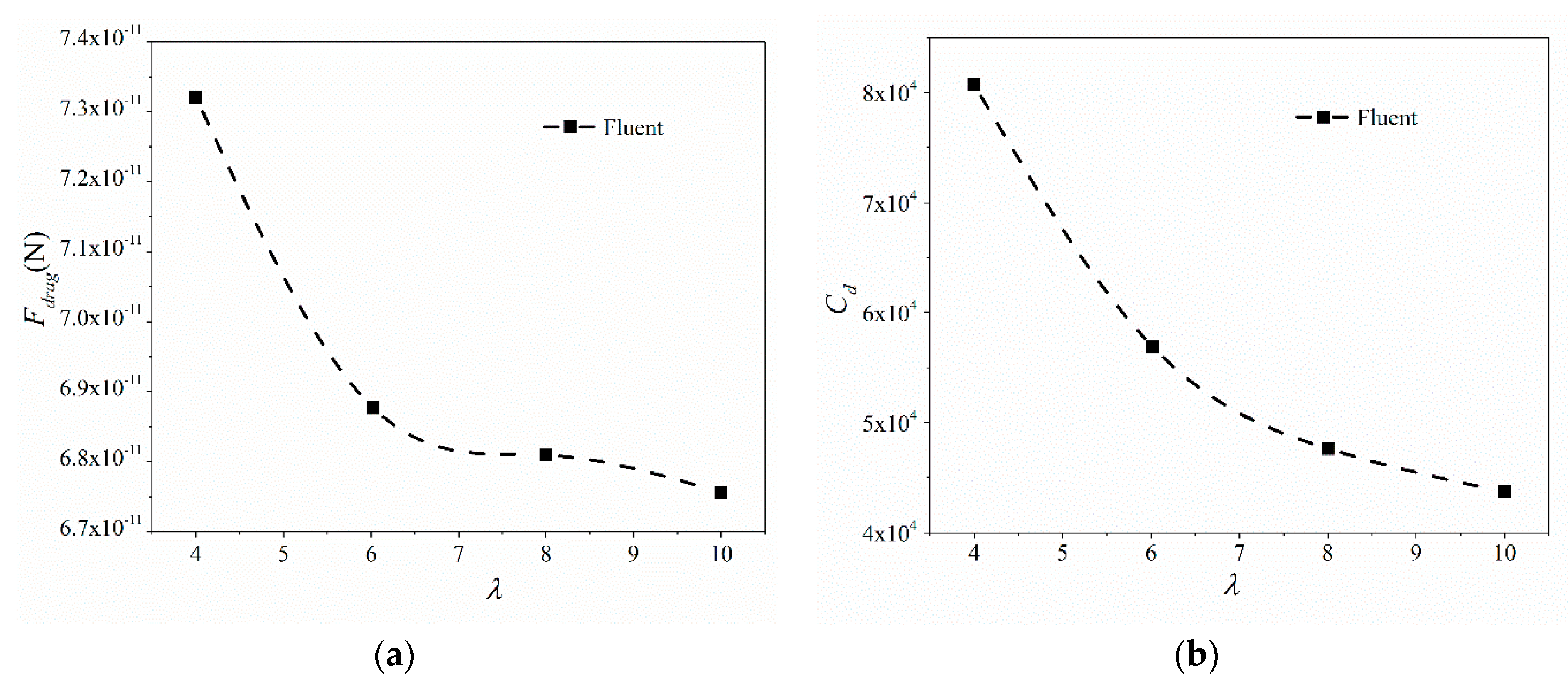
3.2. Numerical Relationship
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, X.; Hahn, K.; Sanchez, S. Catalytic mesoporous janus nanomotors for active cargo delivery. J. Am. Chem. Soc. 2015, 137, 4976–4979. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.; Kagan, D.; Jack Hu, C.; Campuzano, S.; Lobo-Castañon, M.J.; Lim, N.; Kang, D.Y.; Zimmerman, M.; Zhang, L.; Wang, J. Micromachine-enabled capture and isolation of cancer cells in complex media. Angew. Chem. Int. Ed. 2011, 50, 4161–4164. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Li, L.; Song, W.; Wang, L.; Shao, G.; Zhang, G. Self-propelled multilayered microrockets for pollutants purification. ECS J. Solid State Sci. Technol. 2015, 4, S3016–S3019. [Google Scholar] [CrossRef]
- Soler, L.; Magdanz, V.; Fomin, V.M.; Sanchez, S.; Schmidt, O.G. Self-propelled micromotors for cleaning polluted water. ACS Nano 2013, 7, 9611–9620. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Kagan, D.; Pak, O.S.; Clawson, C.; Campuzano, S.; Chuluun-Erdene, E.; Shipton, E.; Fullerton, E.E.; Zhang, L.; Lauga, E. Cargo-towing fuel-free magnetic nanoswimmers for targeted drug delivery. Small 2012, 8, 460–467. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Wang, J. Synthetic micro/nanomotors in drug delivery. Nanoscale 2014, 6, 10486–10494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xing, M.; Yun, Z.; Kee Woei, N.; Yanli, Z. Integrated hollow mesoporous silica nanoparticles for target drug/siRNA co-delivery. Chem. A Eur. J. 2013, 19, 15593–15603. [Google Scholar]
- Xi, W.; Solovev, A.A.; Ananth, A.N.; Gracias, D.H.; Sanchez, S.; Schmidt, O.G. Rolled-up magnetic microdrillers: Towards remotely controlled minimally invasive surgery. Nanoscale 2013, 5, 1294. [Google Scholar] [CrossRef] [PubMed]
- Flynn, A.M.; Udayakumar, K.R.; Barrett, D.S. Tomorrow’s Surgery: Micromotors and Microrobots. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/41509/AI_WP_337.pdf?sequence=4 (accessed on 11 September 2018).
- Kagan, D.; Campuzano, S.; Balasubramanian, S.; Kuralay, F.; Flechsig, G.U.; Wang, J. Functionalized micromachines for selective and rapid isolation of nucleic acid targets from complex samples. Nano Lett. 2011, 11, 2083–2087. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Soto, F.; Gao, W.; Dong, R.; Garcia-Gradilla, V.; Magaña, E.; Zhang, X.; Wang, J. Reversible swarming and separation of self-propelled chemically powered nanomotors under acoustic fields. J. Am. Chem. Soc. 2015, 137, 2163–2166. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Li, T.; Li, L.; Wang, J.; Song, W.; Zhang, G. Microrocket based viscometer. ECS J. Solid State Sci. Technol. 2015, 4, S3020–S3023. [Google Scholar] [CrossRef]
- Wei, G.; Sirilak, S.; Jahir, O.; Joseph, W. Highly efficient catalytic microengines: Template electrosynthesis of polyaniline/platinum microtubes. J. Am. Chem. Soc. 2011, 133, 11862–11864. [Google Scholar]
- Gao, W.; Sattayasamitsathit, S.; Wang, J. Catalytically propelled micro-/nanomotors: How fast can they move? Chem. Rec. 2012, 12, 224–231. [Google Scholar] [CrossRef] [PubMed]
- Li, L.Q.; Wang, J.Y.; Li, T.L.; Song, W.P.; Zhang, G.Y. A unified model of drag force for bubble-propelled catalytic micro/nano-motors with different geometries in low Reynolds number flows. J. Appl. Phys. 2015, 117, 104301–104308. [Google Scholar] [CrossRef]
- Wei, G.; Pei, A.; Feng, X.; Hennessy, C.; Wang, J. Organized self-assembly of Janus micromotors with hydrophobic hemispheres. J. Am. Chem. Soc. 2013, 135, 998–1001. [Google Scholar]
- Araki, T.; Fukai, S. Controlled motion of Janus particles in periodically phase-separating binary fluids. Soft Matter 2015, 11, 3470–3479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Q.; Dong, R.; Chang, X.; Ren, B.; Tong, Z. Spiropyran-decorated SiO2-Pt Janus micromotor: Preparation and light-induced dynamic self-assembly and disassembly. ACS Appl. Mater. Interfaces 2015, 7, 24585–24591. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, X.; Cui, H.; Silber-Li, Z. The self-propulsion of the spherical Pt-SiO2 janus micro-motor. Micromachines 2017, 8, 123. [Google Scholar] [CrossRef]
- Wei, W.; Li, S.; Lamar, M.; Suzanne, A.; Huang, T.J.; Mallouk, T.E. Acoustic propulsion of nanorod motors inside living cells. Angew. Chem. 2014, 53, 3201–3204. [Google Scholar]
- Zacharia, N.S.; Sadeq, Z.S.; Ozin, G.A. Enhanced speed of bimetallic nanorod motors by surface roughening. Chem. Commun. 2009, 39, 5856–5858. [Google Scholar] [CrossRef] [PubMed]
- Paxton, W.F.; Kistler, K.C.; Olmeda, C.C.; Sen, A.; Angelo, S.K.S.; Cao, Y.; Mallouk, T.E.; Lammert, P.E.; Crespi, V.H. Catalytic nanomotors: Autonomous movement of striped nanorods. J. Am. Chem. Soc. 2004, 126, 13424–13431. [Google Scholar] [CrossRef] [PubMed]
- Kovtyukhova, N.I. Toward understanding of the propulsion mechanism of rod-shaped nanoparticles that catalyze gas-generating reactions. J. Phys. Chem. C 2008, 112, 6049–6056. [Google Scholar] [CrossRef]
- Fournier-Bidoz, S.; Arsenault, A.C.; Manners, I.; Ozin, G.A. Synthetic self-propelled nanorotors. Chem. Commun. 2005, 4, 441–443. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Manjare, M.; Zhao, Y. Catalytic nanoshell micromotors. J. Phys. Chem. C 2013, 117, 21590–21596. [Google Scholar] [CrossRef]
- Zhao, G.; Pumera, M. Geometric asymmetry driven Janus micromotors. Nanoscale 2014, 6, 11177–11180. [Google Scholar] [CrossRef] [PubMed]
- Ning, H.; Zhang, Y.; Zhu, H.; Ingham, A.; Huang, G.; Mei, Y.; Solovev, A.A. Geometry design, principles and assembly of micromotors. Micromachines 2018, 9, 75. [Google Scholar] [CrossRef]
- Gao, W.; Sirilak, S.; Aysegul, U.; Allen, P.; Adam, P.; Joseph, W. Polymer-based tubular microbots: Role of composition and preparation. Nanoscale 2012, 4, 2447–2453. [Google Scholar] [CrossRef] [PubMed]
- Fomin, V.M.; Hippler, M.; Magdanz, V.; Soler, L.; Sanchez, S.; Schmidt, O.G. Propulsion mechanism of catalytic microjet engines. IEEE Trans. Robot. 2014, 30, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Mei, Y.; Solovev, A.A.; Samuel, S.; Schmidt, O.G. Rolled-up nanotech on polymers: From basic perception to self-propelled catalytic microengines. Chem. Soc. Rev. 2011, 40, 2109–2119. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chi, Q.; Liu, L.; Liu, Q.; Bai, T.; Wang, Q. A viscosity-based model for bubble-propelled catalytic micromotors. Micromachines 2017, 8, 198. [Google Scholar] [CrossRef]
- Manjare, M.; Yang, B.; Zhao, Y.P. Bubble driven quasioscillatory translational motion of catalytic micromotors. Phys. Rev. Lett. 2012, 109, 128305. [Google Scholar] [CrossRef] [PubMed]
- Manjare, M.; Yang, B.; Zhao, Y.P. Bubble-propelled microjets: Model and experiment. J. Phys. Chem. C 2013, 117, 4657–4665. [Google Scholar] [CrossRef]
- Wang, H.; Moo, J.G.; Pumera, M. Tissue cell assisted fabrication of tubular catalytic platinum microengines. Nanoscale 2014, 6, 11359–11363. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.; Moo, J.G.S.; Pumera, M. From nanomotors to micromotors: The Influence of the size of an autonomous bubble-propelled device upon its motion. ACS Nano 2016, 10, 5041–5050. [Google Scholar]
- Cox, R.G. The motion of long slender bodies in a viscous fluid part 1. General theory. J. Fluid Mech. 1970, 44, 791–810. [Google Scholar] [CrossRef]
- Li, J.X.; Huang, G.S.; Ye, M.M.; Li, M.L.; Liu, R.; Mei, Y.F. Dynamics of catalytic tubular microjet engines: Dependence on geometry and chemical environment. Nanoscale 2011, 3, 5083–5089. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, J.; Li, T.; Song, W.; Zhang, G. Hydrodynamics and propulsion mechanism of self-propelled catalytic micromotors: Model and experiment. Soft Matter 2014, 10, 7511–7518. [Google Scholar] [CrossRef] [PubMed]
- Sarkis, B.; Folio, D.; Ferreira, A.E.F. Catalytic tubular microjet propulsion model for endovascular navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 3537–3542. [Google Scholar]
- ANSYS FLUENT 12.0 Theory Guide 2009. Available online: http://www.afs.enea.it/project/neptunius/docs/fluent/html/th/main_pre.htm (accessed on 11 September 2018).
- Launder, B.E.; Spalding, D.B. PAPER 8—The numerical computation of turbulent flows. In Numerical Prediction of Flow Heat Transfer Turbulence and Combustion; Elsevier: New York, NY, USA, 1983; pp. 96–116. [Google Scholar]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics; Sprigner: Berlin, Germany, 1999. [Google Scholar]
- Clancy, L.J. Aerodynamics; Halsted Press: New York, NJ, USA, 1975. [Google Scholar]
- Mishra, A.A.; Iaccarino, G.; Duraisamy, K. Sensitivity of flow evolution on turbulence structure. Phys. Rev. Fluids 2016, 1, 052402. [Google Scholar] [CrossRef]
- Iaccarino, G.; Mishra, A.A.; Ghili, S. Eigenspace perturbations for uncertainty estimation of single-point turbulence closures. Phys. Rev. Fluids 2017, 2, 024605. [Google Scholar] [CrossRef]


| Model Parameters | Values |
|---|---|
| α | 34,543.88 |
| β | −0.08 |
| γ | −175,790.03 |
| ξ | 307,718.72 |
| ζ | 350.84 |
| Influence Factor | Individual Fitting Error |
|---|---|
| Re | 0.0165 |
| tanδ | 0.0901 |
| λ | 0.0909 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Chi, Q.; Bai, T.; Wang, Q.; Liu, L. A Dynamic Model of Drag Force for Catalytic Micromotors Based on Navier–Stokes Equations. Micromachines 2018, 9, 459. https://doi.org/10.3390/mi9090459
Wang Z, Chi Q, Bai T, Wang Q, Liu L. A Dynamic Model of Drag Force for Catalytic Micromotors Based on Navier–Stokes Equations. Micromachines. 2018; 9(9):459. https://doi.org/10.3390/mi9090459
Chicago/Turabian StyleWang, Zhen, Qingjia Chi, Tao Bai, Qiang Wang, and Lisheng Liu. 2018. "A Dynamic Model of Drag Force for Catalytic Micromotors Based on Navier–Stokes Equations" Micromachines 9, no. 9: 459. https://doi.org/10.3390/mi9090459





