Thermally Developing Flow and Heat Transfer in Elliptical Minichannels with Constant Wall Temperature
Abstract
:1. Introduction
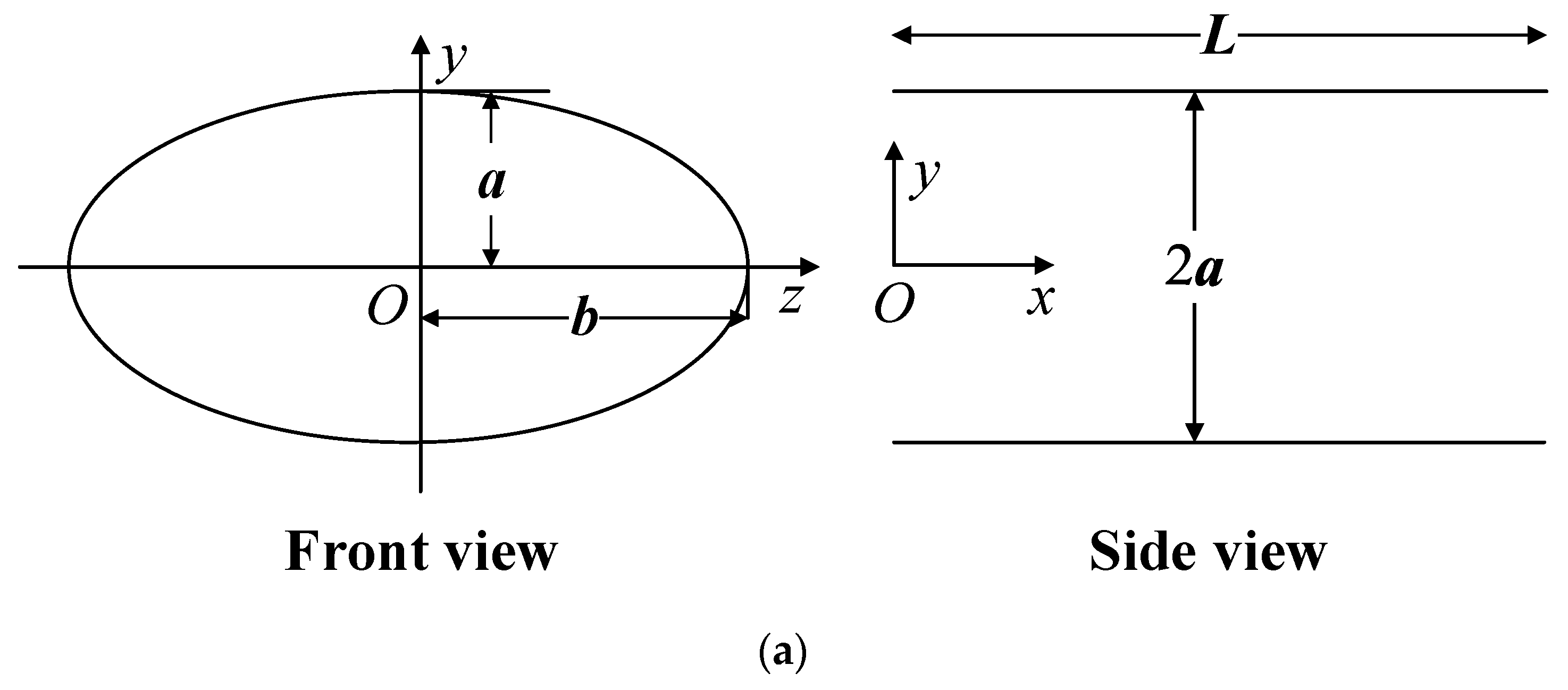
2. Mathematical Formulations
2.1. Solution Method
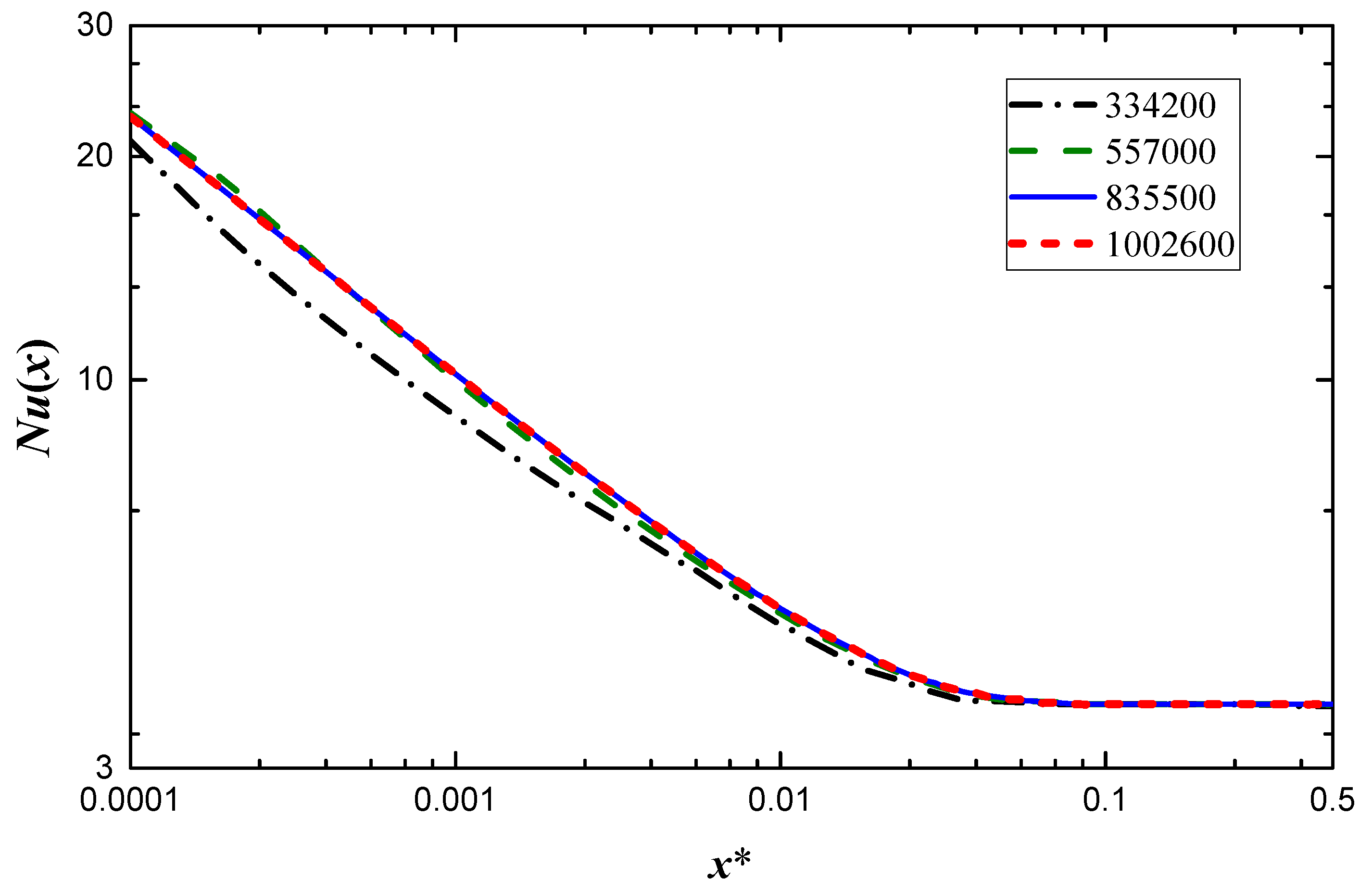
2.2. Grid Independence
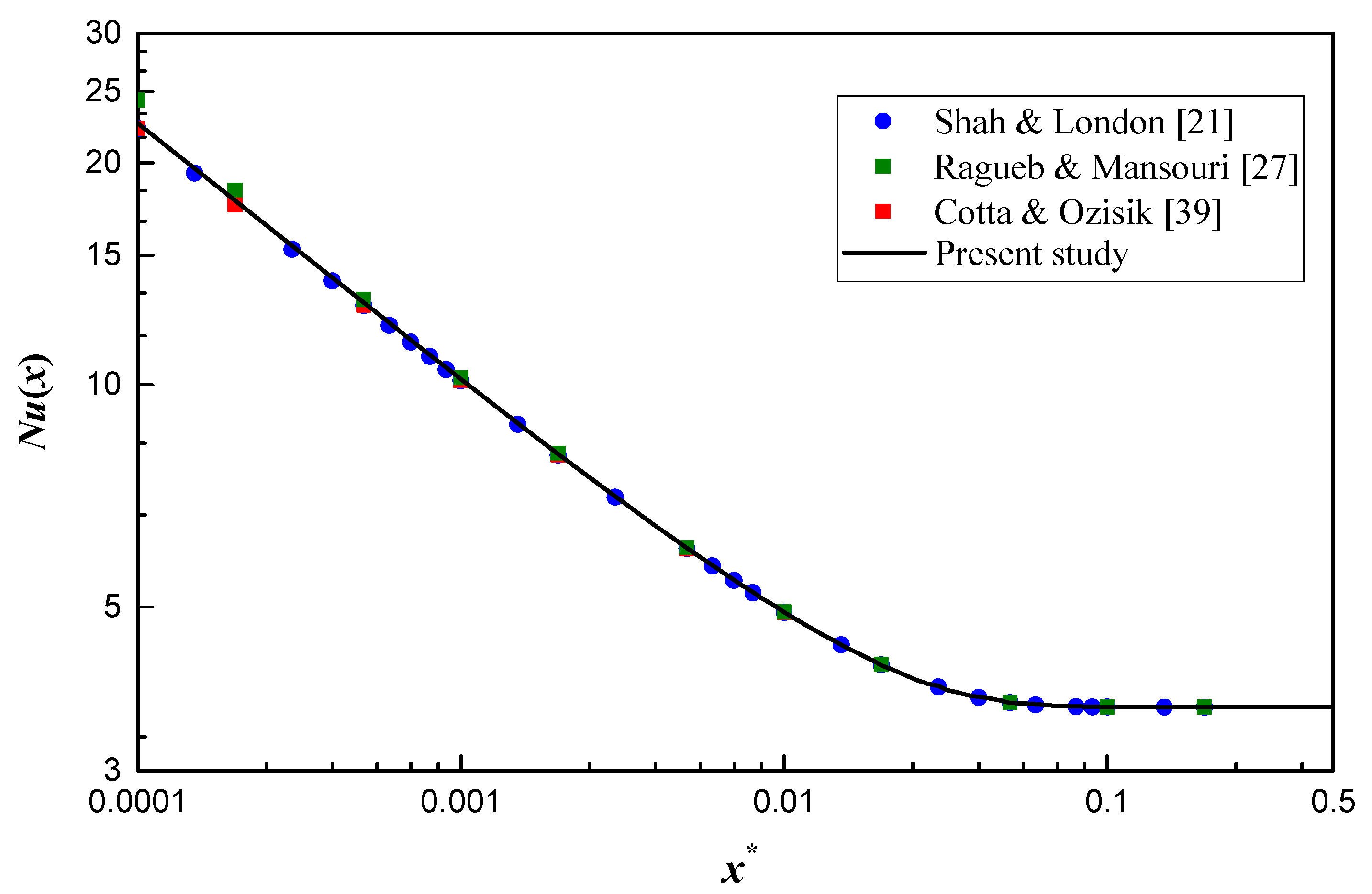
2.3. Model Validation
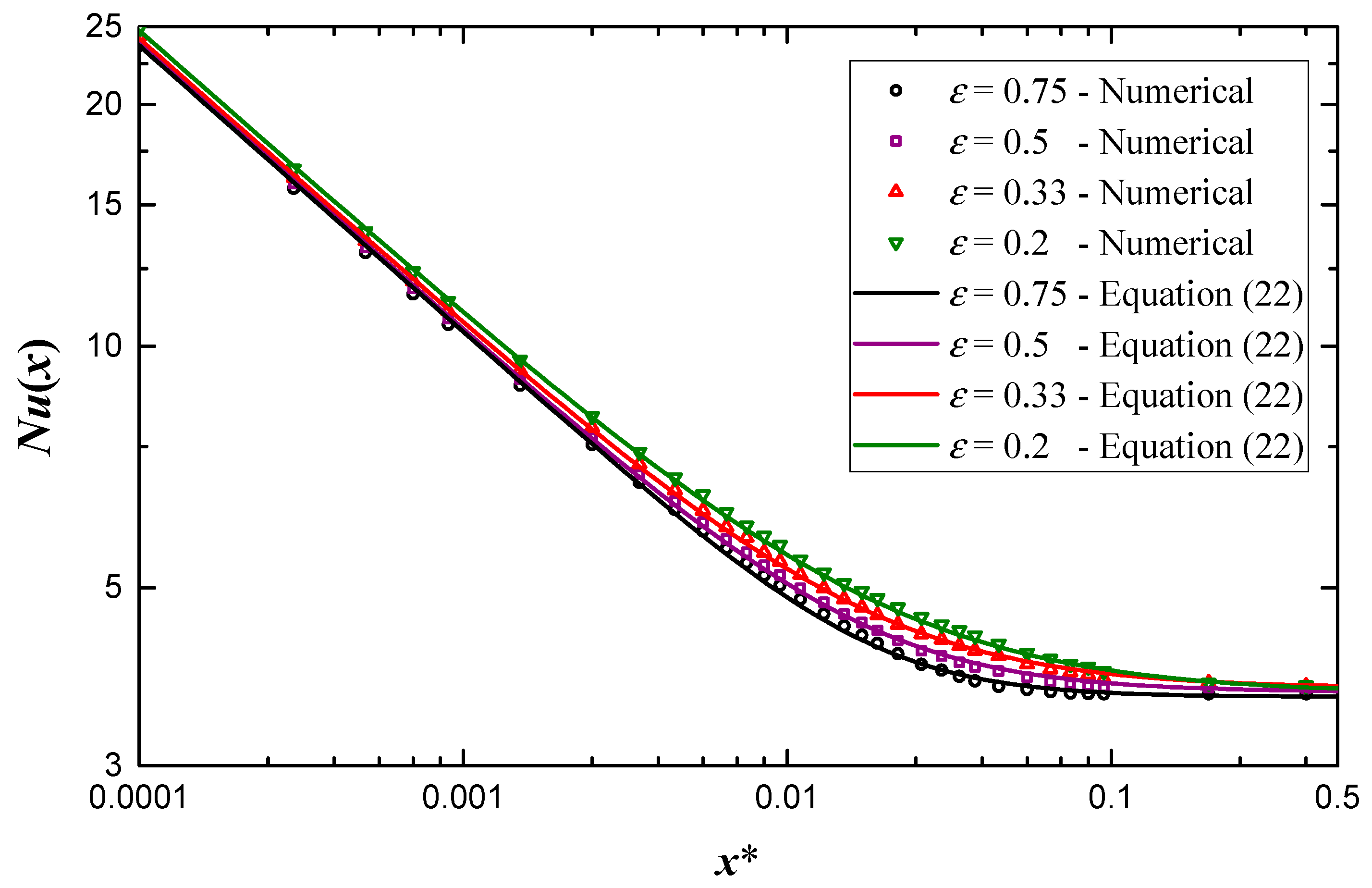
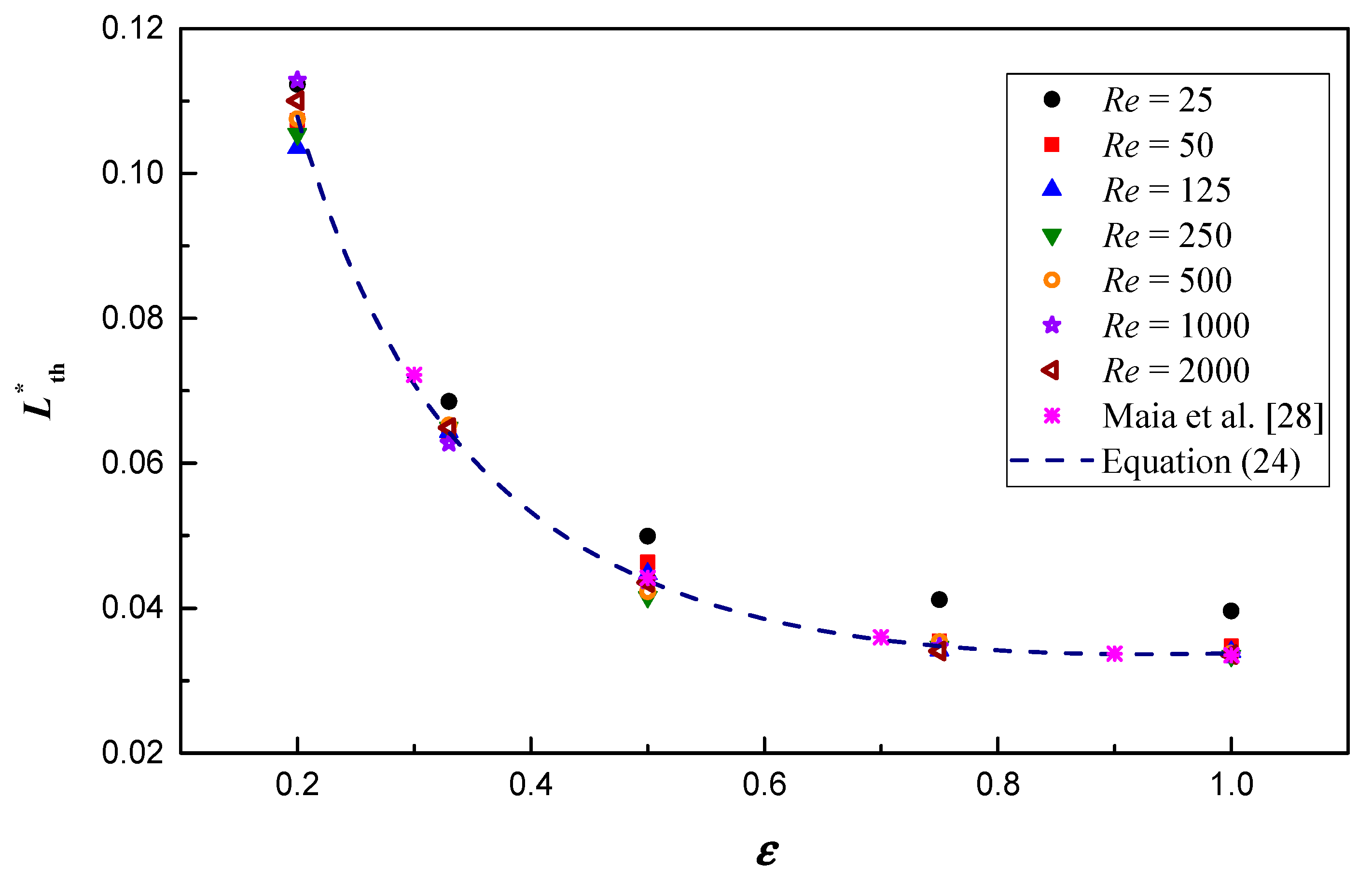
3. Results and Discussion
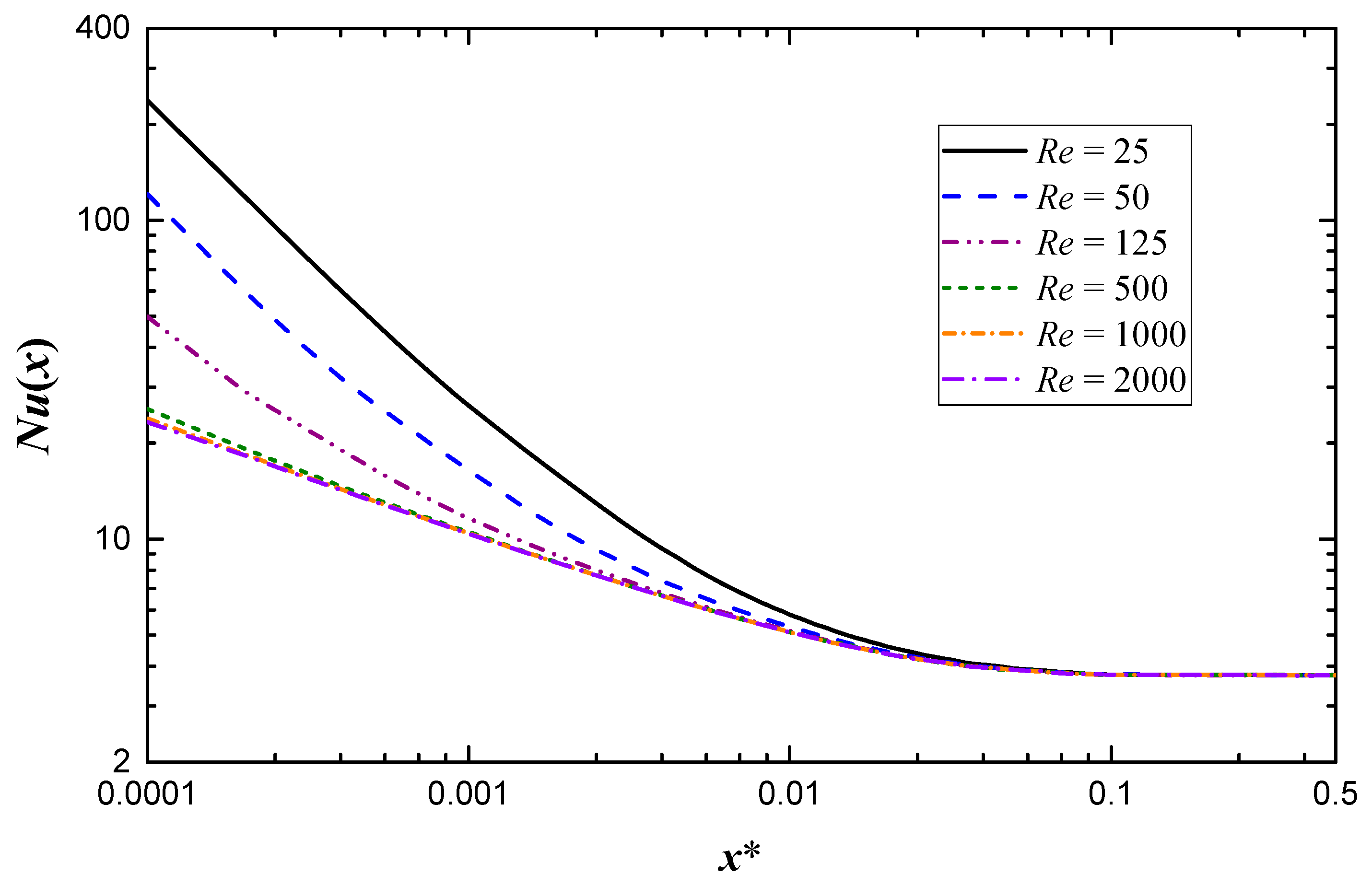
3.1. Local Nusselt Number
3.2. Thermal Entrance Length
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | flow area, m2 |
| a | minor semi-axis of ellipse, m |
| b | major semi-axis of ellipse, m |
| cp | specific heat, J/(kg K) |
| Dh | hydraulic diameter, m |
| e | eccentricity of the ellipse |
| h | convective heat transfer coefficient, W/(m2 K) |
| Kn | Knudsen number |
| L | channel length, m |
| Nu | Nusselt number, = hDh/λ |
| P | wetted perimeter, m |
| p | pressure, |
| Pr | Prandtl number = μcp/λ |
| q’’ | wall heat flux, W/m2 |
| Re | Reynolds number, = |
| T | temperature, K |
| U | non-dimensional velocity |
| u | velocity, m/s |
| X, Y, Z | non-dimensional Cartesian coordinates |
| x, y, z | Cartesian coordinates, m |
| x* | dimensionless axial distance, = x/(DhRePr) |
| Greek symbols | |
| α | non-dimensional minor semi-axis of ellipse |
| β | non-dimensional major semi-axis of ellipse |
| ε | aspect ratio, = a/b |
| θ | dimensionless temperature |
| λ | fluid thermal conductivity, W/(m K) |
| μ | dynamic viscosity, |
| ρ | fluid density, kg/m3 |
| Г | cross section contour |
| Ω | cross-section domain |
| Subscripts | |
| m | mean |
| th | thermal |
| w | wall |
References
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Sun, W.; Kakac, S.; Yazicioglu, A.G. A numerical study of single-phase convective heat transfer in microtubes for slip flow. Int. J. Therm. Sci. 2007, 46, 1084–1094. [Google Scholar] [CrossRef]
- Khan, A.L.; Dutta, P. Analytical solution of time-periodic electroosmotic flow through cylindrical microchannel with non-uniform surface potential. Micromachines 2019, 10, 498. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.T.; Peng, X.F.; Wang, B.X. Variable-property effect on liquid flow and heat transfer in microchannels. Chem. Eng. J. 2008, 141, 346–353. [Google Scholar] [CrossRef]
- Maqableh, A.M.; Khadrawi, A.F.; Al-Nimr, M.A.; Ammourah, S.A.; Benim, A.C. Heat transfer characteristics of parallel and counter flow micro-channel heat exchangers with varying wall resistance. Prog. Comput. Fluid Dyn. 2011, 11, 318–328. [Google Scholar] [CrossRef]
- Meskos, S.; Stefanov, S.; Valougeorgis, D. Gas mixing and final mixture composition control in simple geometry micro-mixers via DSMC analysis. Micromachines 2019, 10, 178. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y.S. Slip flow heat transfer in annular microchannels with constant heat flux. J. Heat Transf. 2008, 130, 92401. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Campo, A.; Saidur, R. Experimental study of forced and free convective heat transfer in the thermal entry region of horizontal concentric annuli. Int. Commun. Heat Mass Transf. 2010, 37, 739–747. [Google Scholar] [CrossRef]
- Hong, C.; Asako, Y.; Suzuki, K. Convection heat transfer in concentric micro annular tubes with constant wall temperature. Int. J. Heat Mass Transf. 2011, 54, 5242–5252. [Google Scholar] [CrossRef]
- Lee, S.Y.; Wereley, S.T.; Gui, L.; Qu, W.; Mudawar, I. Microchannel flow measurement using micro particle image velocimetry. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, New Orleans, LA, USA, 17 November 2002. [Google Scholar]
- Lee, S.Y.; Jang, J.; Wereley, S.T. Effects of planar inlet plenums on the hydrodynamically developing flows in rectangular microchannels of complementary aspect ratios. Microfluid. Nanofluidics 2008, 5, 1–12. [Google Scholar] [CrossRef]
- Ma, N.; Duan, Z.; Ma, H.; Su, L.; Liang, P.; Ning, X.; He, B.; Zhang, X. Lattice Boltzmann simulation of the hydrodynamic entrance region of rectangular microchannels in the slip regime. Micromachines 2018, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Ma, H.; He, B.; Su, L.; Zhang, X. Pressure drop of microchannel plate fin heat sinks. Micromachines 2019, 10, 80. [Google Scholar] [CrossRef] [PubMed]
- Siyabi, I.A.; Khanna, S.; Sundaram, S.; Mallick, T. Experimental and numerical thermal analysis of multi-layered microchannel heat sink for concentrating photovoltaic application. Energies 2019, 12, 122. [Google Scholar] [CrossRef]
- Ma, H.; Duan, Z.; Su, L.; Ning, X.; Bai, J.; Lv, X. Fluid flow and entropy generation analysis of Al2O3–water nanofluid in microchannel plate fin heat sinks. Entropy 2019, 21, 739. [Google Scholar] [CrossRef]
- Renksizbulut, M.; Niazmand, H. Laminar flow and heat transfer in the entrance region of trapezoidal channels with constant wall temperature. J. Heat Transf. 2006, 128, 63–74. [Google Scholar] [CrossRef]
- Pitakarnnop, J.; Geoffroy, S.; Colin, S.; Baldas, L. Slip flow in triangular and trapezoidal microchannels. Int. J. Heat Technol. 2008, 26, 167–174. [Google Scholar]
- Kewalramani, G.V.; Hedau, G.; Saha, S.K.; Agrawal, A. Empirical correlation of laminar forced convective flow in trapezoidal microchannel based on experimental and 3D numerical study. Int. J. Therm. Sci. 2019, 142, 422–433. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. The influence of hybrid nanofluids on the performances of elliptical tube: Recent research and numerical study. Int. J. Heat Mass Transf. 2019, 129, 132–143. [Google Scholar] [CrossRef]
- Ragueb, H.; Mansouri, K. An analytical study of the periodic laminar forced convection of non-Newtonian nanofluid flow inside an elliptical duct. Int. J. Heat Mass Transf. 2018, 127, 469–483. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Abdel-Wahed, R.M.; Attia, A.E.; Hifni, M.A. Experiments on laminar flow and heat transfer in an elliptical duct. Int. J. Heat Mass Transf. 1984, 27, 2397–2413. [Google Scholar] [CrossRef]
- Velusamy, K.; Garg, V.K. Entrance flow in elliptical ducts. Int. J. Numer. Methods Fluids 1993, 17, 1079–1096. [Google Scholar] [CrossRef]
- Sakalis, V.D.; Hatzikonstantinou, P.M.; Kafousias, N. Thermally developing flow in elliptic ducts with axially variable wall temperature distribution. Int. J. Heat Mass Transf. 2001, 45, 25–35. [Google Scholar] [CrossRef]
- Papadopoulos, P.K.; Hatzikonstantinou, P.M. Numerical study of laminar fluid flow in a curved elliptic duct with internal fins. Int. J. Heat Fluid Flow 2008, 29, 540–544. [Google Scholar] [CrossRef]
- Shariat, M.; Akbarinia, A.; Nezhad, A.H.; Behzadmehr, A.; Laur, R. Numerical study of two phase laminar mixed convection nanofluid in elliptic ducts. Appl. Therm. Eng. 2011, 31, 2348–2359. [Google Scholar] [CrossRef] [Green Version]
- Ragueb, H.; Mansouri, K. A numerical study of viscous dissipation effect on non-Newtonian fluid flow inside elliptical duct. Energy Convers. Manag. 2013, 68, 124–132. [Google Scholar] [CrossRef]
- Maia, C.R.M.; Aparecido, J.B.; Milanez, L.F. Heat transfer in laminar flow of non-Newtonian fluids in ducts of elliptical section. Int. J. Therm. Sci. 2006, 45, 1066–1072. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y.S. Slip flow in elliptic microchannels. Int. J. Therm. Sci. 2007, 46, 1104–1111. [Google Scholar] [CrossRef]
- Vocale, P.; Morini, G.L.; Spiga, M. Dilute gas flows through elliptic microchannels under H2 boundary conditions. Int. J. Heat Mass Transf. 2014, 71, 376–385. [Google Scholar] [CrossRef]
- Vocale, P.; Morini, G.L.; Spiga, M. Convective heat transfer in elliptical microchannels under slip flow regime and H1 boundary conditions. J. Heat Transf. 2016, 138, 1–7. [Google Scholar] [CrossRef]
- Wang, C.Y. Ritz method for slip flow in curved micro-ducts and application to the elliptic duct. Meccanica 2016, 51, 1069–1076. [Google Scholar] [CrossRef]
- Su, L.; Duan, Z.; He, B.; Ma, H.; Ding, G. Laminar flow and heat transfer in the entrance region of elliptical minichannels. Int. J. Heat Mass Transf. 2019, 145, 118717. [Google Scholar] [CrossRef]
- Hamadneh, N.N.; Khan, W.A.; Khan, I.; Alsagri, A.S. Modeling and optimization of gaseous thermal slip flow in rectangular microducts using a particle swarm optimization algorithm. Symmetry 2019, 11, 488. [Google Scholar] [CrossRef]
- Colin, S. Gas microflows in the slip flow regime: A critical review on convective heat transfer. Trans. ASME J. Heat Transf. 2012, 134, 020908. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.; Wu, K.; Zhang, T.; Feng, D.; Huang, L.; Shi, Y.; Ramachandran, H.; Li, X. An analytical model for gas transport through elliptical nanopores. Chem. Eng. Sci. 2019, 199, 199–209. [Google Scholar] [CrossRef]
- Mchale, J.P.; Garimella, S.V. Heat transfer in trapezoidal microchannels of various aspect ratios. Int. J. Heat Mass Transf. 2010, 53, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Fluent, Inc. FLUENT 6.3 User’s Guide; Fluent, Inc.: Lebanon, NH, USA, 2006. [Google Scholar]
- Cotta, R.M.; Özisik, M.N. Laminar forced convection of power law non-Newtonian fluids inside ducts. Wärme-und Stoffübertragung 1986, 20, 211–218. [Google Scholar] [CrossRef]
- Churchill, S.W.; Usagi, R. A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 1972, 18, 1121–1128. [Google Scholar] [CrossRef]
- Hong, F.; Cheng, P. Three dimensional numerical analyses and optimization of offset strip-fin microchannel heat sinks. Int. Commun. Heat Mass Transf. 2009, 36, 651–656. [Google Scholar] [CrossRef]
- Lee, Y.J.; Singh, P.K.; Lee, P.S. Fluid flow and heat transfer investigations on enhanced microchannel heat sink using oblique fins with parametric study. Int. J. Heat Mass Transf. 2015, 81, 325–336. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.; Xie, G.; Sunden, B. Numerical analysis of constructal water-cooled microchannel heat sinks with multiple bifurcations in the entrance region. Numer. Heat Transf. Part A Appl. 2015, 67, 632–650. [Google Scholar] [CrossRef]
- Hettiarachchi, H.D.M.; Golubovic, M.; Worek, W.M.; Minkowycz, W.J. Three-dimensional laminar slip-flow and heat transfer in a rectangular microchannel with constant wall temperature. Int. J. Heat Mass Transf. 2008, 51, 5088–5096. [Google Scholar] [CrossRef]

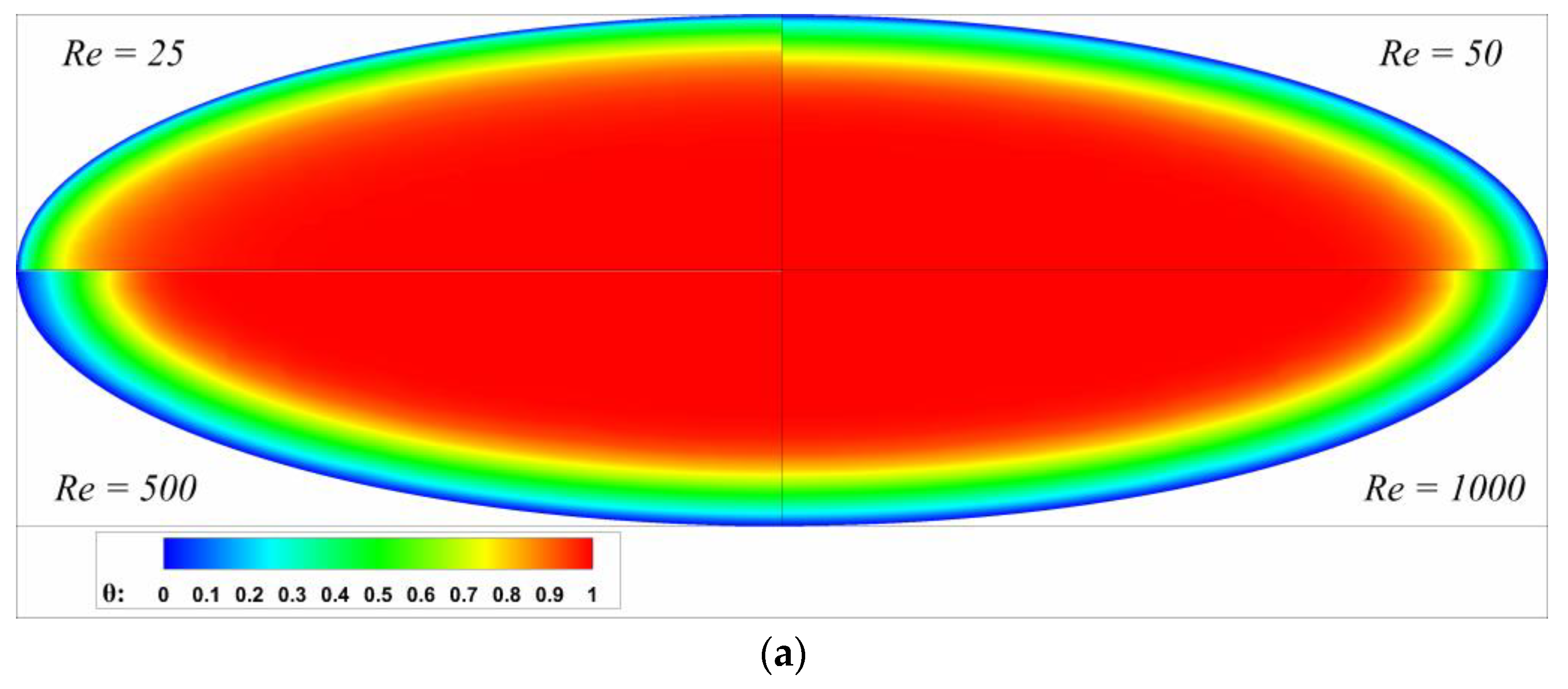
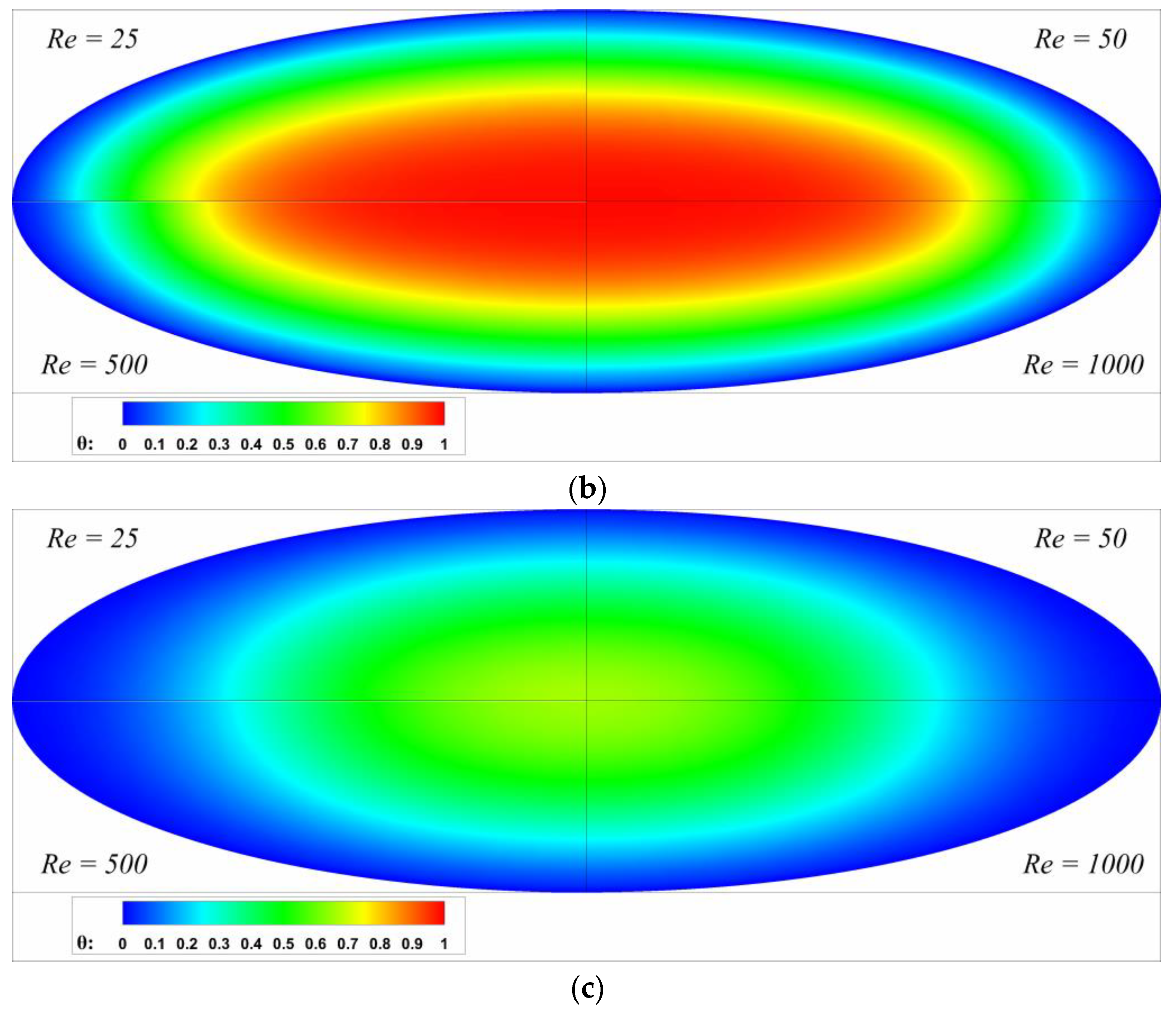
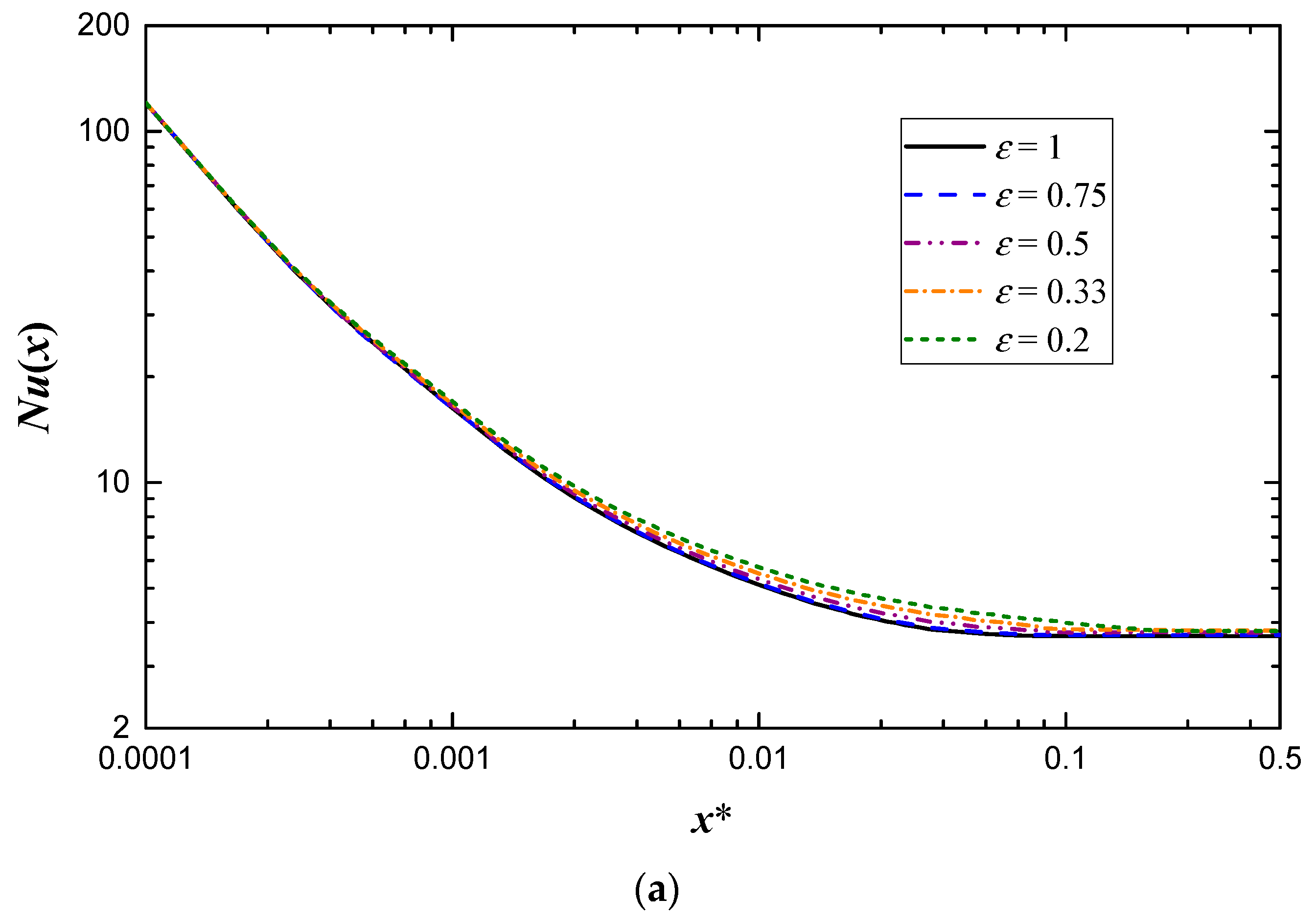
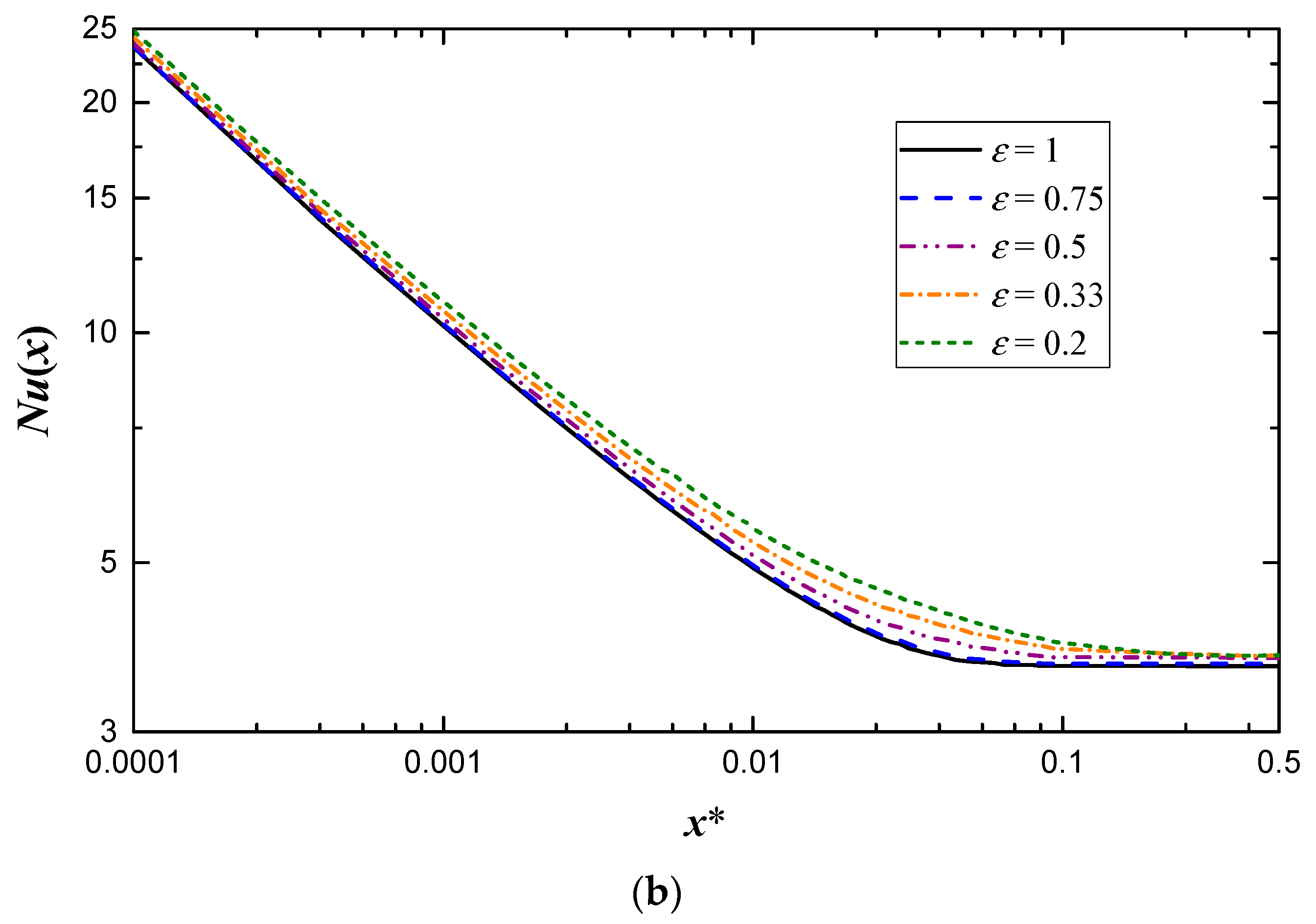
| Aspect Ratio | Re = 500 | Re = 1000 | Re = 2000 | |||
|---|---|---|---|---|---|---|
| C | N | C | N | C | N | |
| ε = 0.2 | 0.794 | 2.60 | 0.920 | 2.80 | 0.955 | 2.80 |
| ε = 0.33 | 0.785 | 3.00 | 0.900 | 3.24 | 0.944 | 3.24 |
| ε = 0.5 | 0.776 | 3.40 | 0.887 | 3.80 | 0.927 | 3.80 |
| ε = 0.75 | 0.759 | 3.80 | 0.883 | 4.78 | 0.916 | 4.78 |
| ε = 1 | 0.753 | 3.80 | 0.879 | 4.78 | 0.902 | 4.78 |
| n | −0.379 | −0.357 | −0.350 | |||
| Re | x* | ε = 0.2 | ε = 0.33 | ε = 0.5 | ε = 0.75 | ε = 1 |
|---|---|---|---|---|---|---|
| 25 | 0.0001 | 237.7 | 237.5 | 237.4 | 237.2 | 237.2 |
| 0.0002 | 119.5 | 119.4 | 119.4 | 119.2 | 119.1 | |
| 0.0005 | 49.12 | 49.01 | 48.85 | 48.68 | 48.66 | |
| 0.001 | 26.77 | 26.57 | 26.24 | 26.19 | 26.05 | |
| 0.005 | 8.622 | 8.385 | 8.146 | 7.988 | 7.940 | |
| 0.01 | 6.256 | 6.017 | 5.803 | 5.645 | 5.604 | |
| 50 | 0.0001 | 120.7 | 120.6 | 120.6 | 120.5 | 120.2 |
| 0.0002 | 60.29 | 60.25 | 60.24 | 60.06 | 59.82 | |
| 0.0005 | 27.56 | 27.36 | 26.97 | 26.73 | 26.93 | |
| 0.001 | 17.02 | 16.73 | 16.46 | 16.30 | 16.29 | |
| 0.005 | 7.215 | 6.966 | 6.755 | 6.599 | 6.558 | |
| 0.01 | 5.742 | 5.512 | 5.306 | 5.152 | 5.114 | |
| 125 | 0.0001 | 50.13 | 50.03 | 49.86 | 49.69 | 49.53 |
| 0.0002 | 29.92 | 29.67 | 29.16 | 28.89 | 29.16 | |
| 0.0005 | 17.33 | 16.99 | 16.72 | 16.51 | 16.49 | |
| 0.001 | 12.18 | 11.87 | 11.63 | 11.43 | 11.40 | |
| 0.005 | 6.696 | 6.526 | 6.308 | 6.139 | 6.116 | |
| 0.01 | 5.578 | 5.353 | 5.148 | 4.985 | 4.958 | |
| 250 | 0.0001 | 33.19 | 32.90 | 32.45 | 32.31 | 32.30 |
| 0.0002 | 22.43 | 22.06 | 21.66 | 21.47 | 21.46 | |
| 0.0005 | 14.81 | 14.45 | 14.20 | 14.00 | 13.93 | |
| 0.001 | 11.22 | 11.00 | 10.76 | 10.58 | 10.53 | |
| 0.005 | 6.677 | 6.441 | 6.234 | 6.079 | 6.041 | |
| 0.01 | 5.550 | 5.325 | 5.121 | 4.968 | 4.931 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Duan, Z.; He, B.; Ma, H.; Xu, Z. Thermally Developing Flow and Heat Transfer in Elliptical Minichannels with Constant Wall Temperature. Micromachines 2019, 10, 713. https://doi.org/10.3390/mi10100713
Su L, Duan Z, He B, Ma H, Xu Z. Thermally Developing Flow and Heat Transfer in Elliptical Minichannels with Constant Wall Temperature. Micromachines. 2019; 10(10):713. https://doi.org/10.3390/mi10100713
Chicago/Turabian StyleSu, Liangbin, Zhipeng Duan, Boshu He, Hao Ma, and Zairan Xu. 2019. "Thermally Developing Flow and Heat Transfer in Elliptical Minichannels with Constant Wall Temperature" Micromachines 10, no. 10: 713. https://doi.org/10.3390/mi10100713





