A Robust Algorithm of Multiquadric Method Based on an Improved Huber Loss Function for Interpolating Remote-Sensing-Derived Elevation Data Sets
Abstract
:1. Introduction
2. Related Works
3. Proposed Robust Algorithm
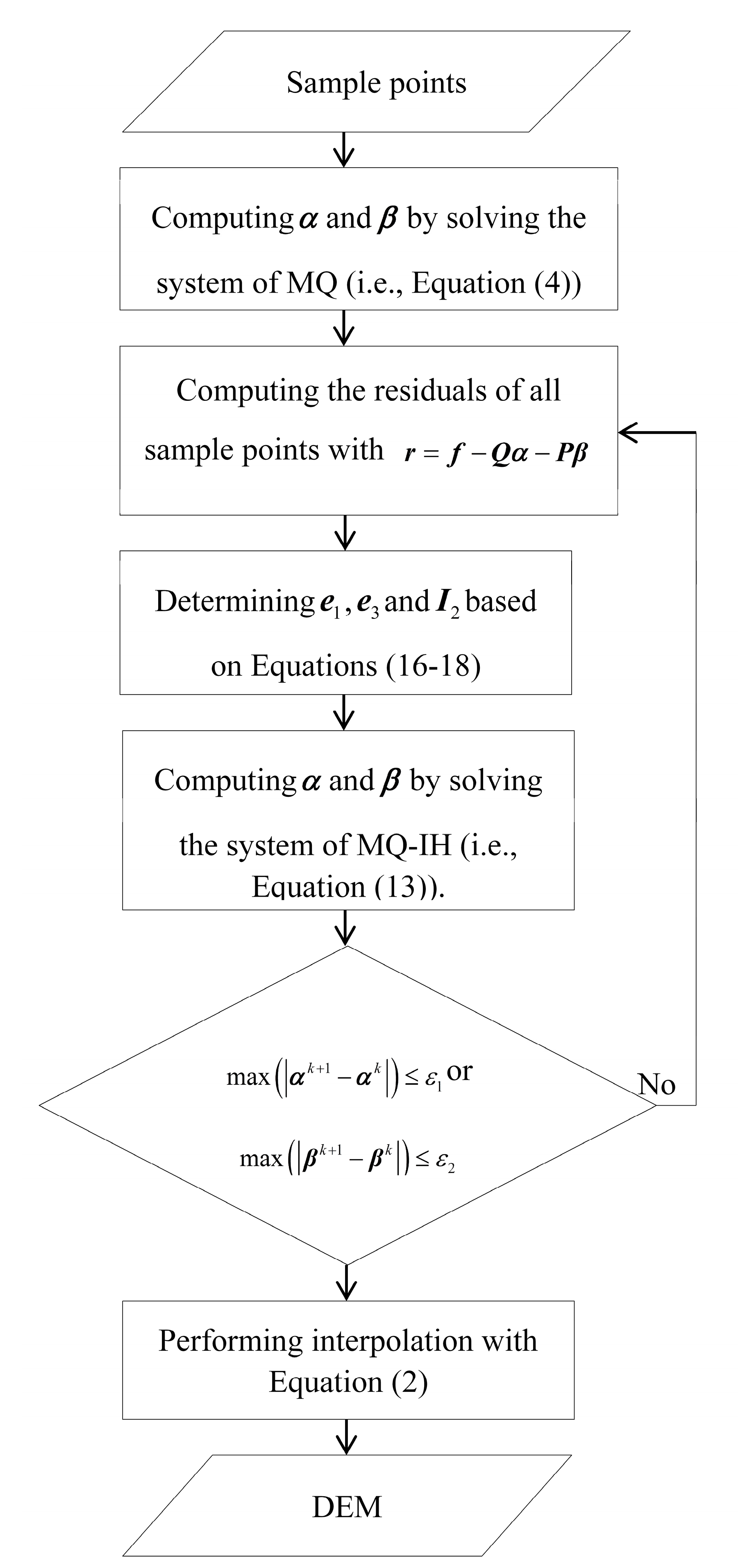
- (1)
- Solving the linear systems of the classical MQ method (i.e., Equation (4)) to obtain α and β. The parameter λ is pre-determined by the k-fold cross-validation (e.g., k = 10) technique [51].
- (2)
- Computing the residuals of all sample points with r = f − Qα − Pβ.
- (3)
- Determining e1, e3 and I2 based on Equations (16–18).
- (4)
- Computing α and β based on Equation (13).
- (5)
- Repeating 2–4 until either max(|αk+1 − αk|) or max(|βk+1 − βk|) is smaller than a pre-set tolerance. In this paper, the pre-set tolerance is set as 0.01.
- (6)
- Carrying out interpolations with Equation (2).
4. Experimental Verification
4.1. Numerical Test

| Case | Error Distribution | Method | RMSE | MaxE | MinE |
|---|---|---|---|---|---|
| Case 1 | N (0, 1) | MQ-IH | 0.2162 | 0.7026 | −0.6802 |
| MQ-CH | 0.2116 | 0.6751 | −0.6981 | ||
| Classical MQ | 0.2111 | 0.6806 | −0.6754 | ||
| MQ-L | 0.3992 | 2.1558 | −1.3729 | ||
| Case 2 | (1 − θ) × N (0, 1) + θ × N (0, 52); θ = 0.1 | MQ-IH | 0.2227 | 1.0110 | −1.0066 |
| MQ-CH | 0.2579 | 1.0610 | −0.9575 | ||
| Classical MQ | 0.4610 | 1.9612 | −1.3051 | ||
| MQ-L | 0.4494 | 2.6757 | −2.4062 | ||
| (1 − θ) × N (0, 1) + θ × N (0, 52); θ = 0.2 | MQ-IH | 0.2541 | 0.7643 | −0.9459 | |
| MQ-CH | 0.3828 | 1.8248 | −1.0014 | ||
| Classical MQ | 0.7009 | 2.5330 | −1.7434 | ||
| MQ-L | 0.5690 | 2.4362 | −3.5633 | ||
| (1 − θ) × N(0, 1) + θ × N (0, 52); θ = 0.3 | MQ-IH | 0.3543 | 1.1015 | −1.3773 | |
| MQ-CH | 0.6180 | 2.0798 | −2.5702 | ||
| Classical MQ | 1.0788 | 3.3844 | −6.1778 | ||
| MQ-L | 0.6858 | 3.0878 | −4.7632 | ||
| Case 3 | C (0, 1) | MQ-IH | 0.3698 | 0.8894 | −1.0187 |
| MQ-CH | 0.3916 | 1.0638 | −1.4952 | ||
| Classical MQ | 1.4591 | 5.0341 | −4.7246 | ||
| MQ-L | 0.6099 | 3.1236 | −3.5425 |
4.2. A Real-World Example
4.2.1. Study Site and Data Capture

4.2.2. Interpolation Methods
4.2.3. Results
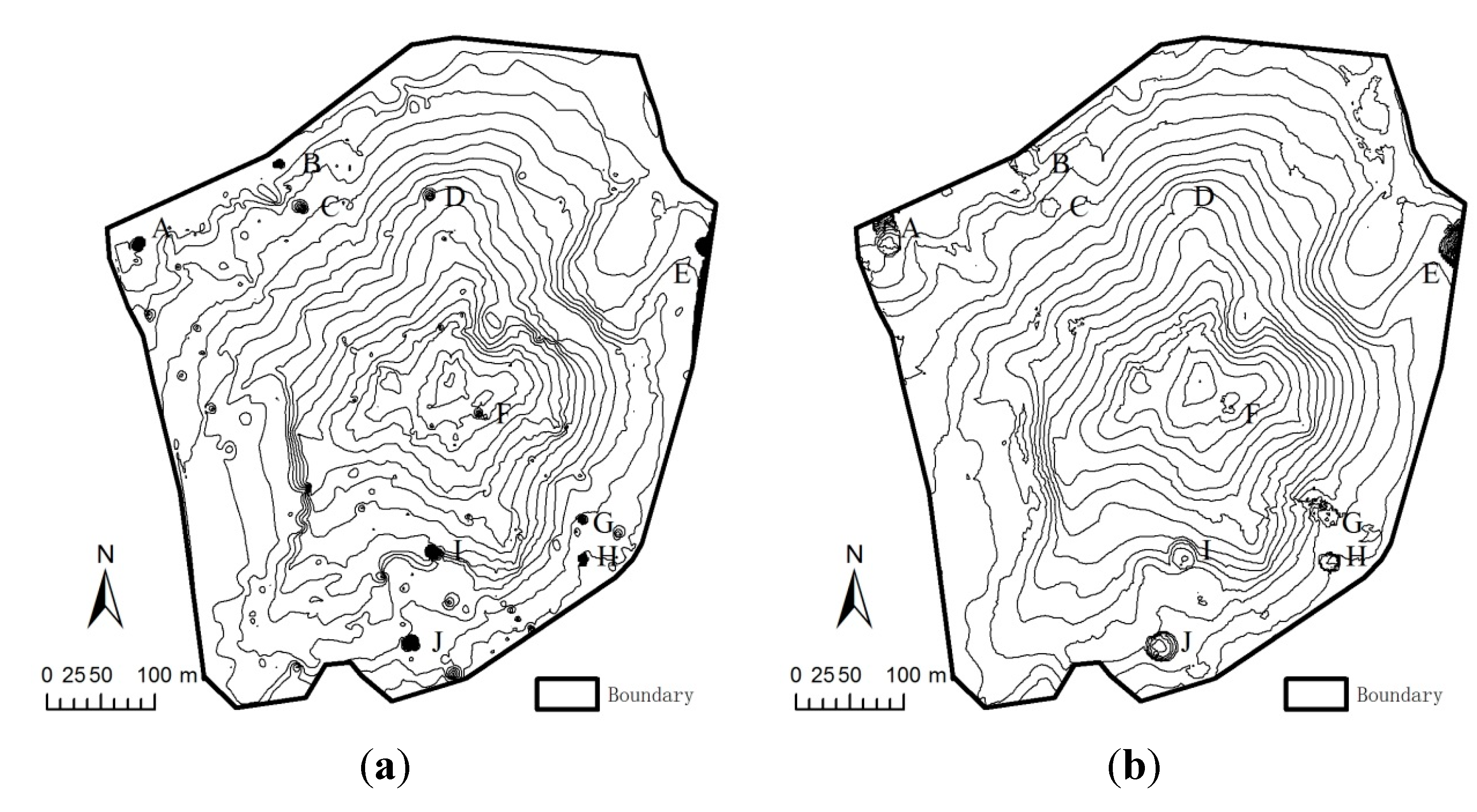
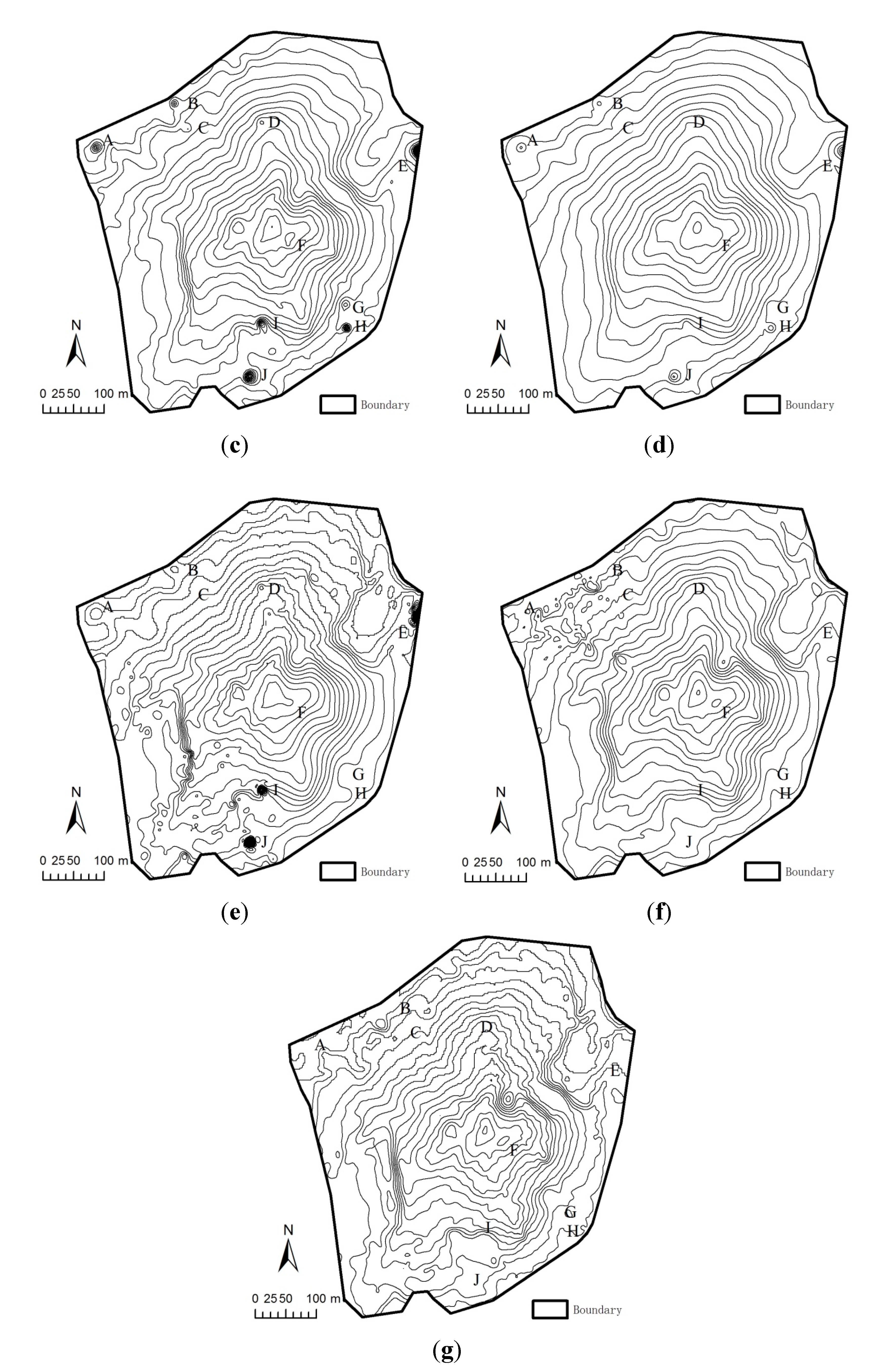

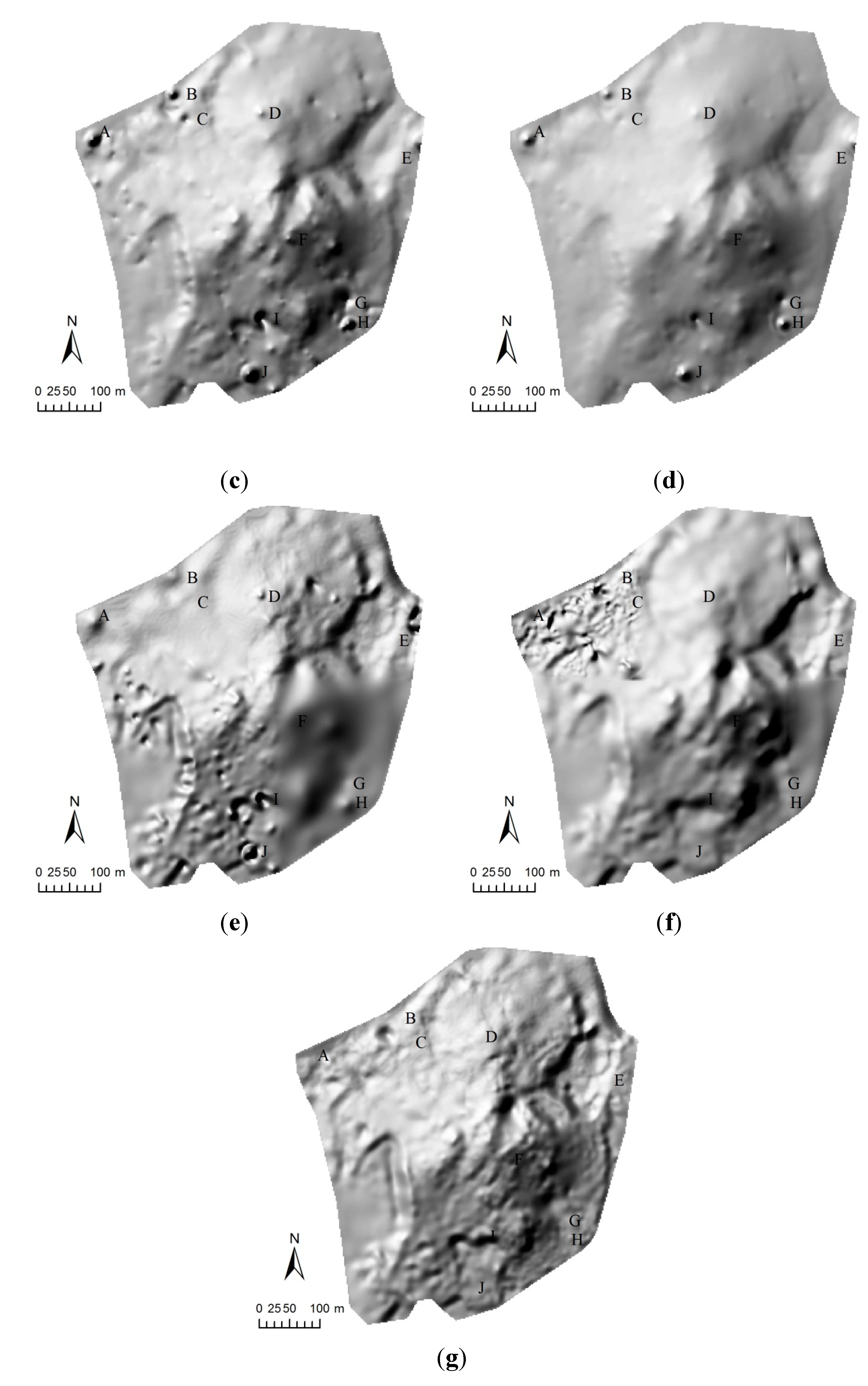
| Number of Sample Points | 6797 | 3822 | 1699 |
|---|---|---|---|
| Point space (m) | 0.15 | 0.2 | 0.3 |
| PS | Accuracy Measures | Methods | ||||||
|---|---|---|---|---|---|---|---|---|
| NN | OK | ANUDEM5 | ANUDEM6 | MQ | MQ-CH | MQ-IH | ||
| 0.15 | RMSE | 1.91 | 1.38 | 2.38 | 2.36 | 2.80 | 1.17 | 0.97 |
| MaxE | 1.36 | 1.60 | 2.02 | 1.66 | 5.02 | 4.36 | 3.80 | |
| MinE | −25.74 | −18.00 | −33.14 | −32.76 | −35.17 | −5.58 | −5.55 | |
| 0.2 | RMSE | 2.35 | 1.58 | 2.59 | 2.47 | 2.94 | 1.24 | 1.05 |
| MaxE | 1.98 | 1.95 | 2.32 | 1.88 | 5.42 | 4.57 | 4.02 | |
| MinE | −25.88 | −18.72 | −33.97 | −33.14 | −35.84 | −5.94 | −5.91 | |
| 0.3 | RMSE | 2.89 | 1.91 | 2.87 | 2.72 | 3.11 | 1.45 | 1.22 |
| MaxE | 2.04 | 2.03 | 2.68 | 2.03 | 5.88 | 5.01 | 4.88 | |
| MinE | −30.12 | −19.11 | −34.45 | −34.00 | −36.17 | −6.06 | −6.03 | |
| Methods | Time (s) |
|---|---|
| NN | 6.28 |
| OK | - |
| ANUDEM5 | 20.34 |
| ANUDEM6 | 20.34 |
| Classical MQ | 63.25 |
| MQ-CH | 150.17 |
| MQ-IH | 150.17 |
5. Discussion
6. Conclusions
Acknowledgments
Appendix A: the Classical MQ Formulation
Appendix B: MQ-IH Formulation
Author Contributions
Conflicts of Interest
References
- Wilson, J.P. Digital terrain modeling. Geomorphology 2012, 137, 107–121. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Gamba, P.; DELL’ACQUA, F.; Houshmand, B. Comparison and fusion of LiDAR and InSAR digital elevation models over urban areas. Int. J. Remote Sens. 2003, 24, 4289–4300. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C.; O’Kelly, M.E. Detecting outliers in irregularly distributed spatial data sets by locally adaptive and robust statistical analysis and GIS. Int. J. Geogr. Inf. Sci. 2001, 15, 721–741. [Google Scholar] [CrossRef]
- Sun, X.; Rosin, P.L.; Martin, R.R.; Langbein, F.C. Noise in 3D laser range scanner data. In Proceedings of the IEEE International Conference on Shape Modeling and Applications, Stony Brook, NY, USA, 4–6 June 2008; pp. 37–45.
- Nurunnabi, A.; Belton, D.; West, G. Robust statistical approaches for local planar surface fitting in 3D laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 96, 106–122. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Hubert, M. Robust statistics for outlier detection. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 73–79. [Google Scholar] [CrossRef]
- Barnett, V.; Lewis, T. Outliers in Statistical Data; Wiley: New York, NY, USA, 1994; Volume 3. [Google Scholar]
- Höhle, J. Assessing the positional accuracy of airborne laser scanning in urban areas. Photogramm. Record 2013, 28, 196–210. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P. Accuracy assessment of lidar-derived digital elevation models. Photogramm. Record 2008, 23, 148–169. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Sun, X.; Rosin, P.L.; Martin, R.R.; Langbein, F.C. Noise analysis and synthesis for 3D laser depth scanners. Graph. Models 2009, 71, 34–48. [Google Scholar] [CrossRef]
- Rousseeuw, P.; Leroy, A. Robust Regression and Outlier Detection; Wiley-IEEE: New York, NY, USA, 2003. [Google Scholar]
- Chen, C.F.; Yue, T.X.; Dai, H.L.; Tian, M.Y. The smoothness of HASM. Int. J. Geogr. Inf. Sci. 2013, 27, 1651–1667. [Google Scholar] [CrossRef]
- Alfons, A.; Croux, C.; Gelper, S. Sparse least trimmed squares regression for analyzing high-dimensional large data sets. Ann. Appl. Stat. 2013, 7, 226–248. [Google Scholar] [CrossRef]
- Chen, C.F.; Fan, Z.M.; Yue, T.X.; Dai, H.L. A robust estimator for the accuracy assessment of remote-sensing-derived DEMs. Int. J. Remote Sens. 2012, 33, 2482–2497. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Lloyd, C.; Atkinson, P. Deriving DSMs from LiDAR data with kriging. Int. J. Remote Sens. 2002, 23, 2519–2524. [Google Scholar] [CrossRef]
- Lloyd, C.D.; Atkinson, P.M. Deriving ground surface digital elevation models from LiDAR data with geostatics. Int. J. Geogr. Inf. Sci. 2006, 20, 535–563. [Google Scholar] [CrossRef]
- Franke, R. Scattered data interpolation: Tests of some method. Math. Comput. 1982, 38, 181–200. [Google Scholar]
- Aguilar, F.J.; Aguera, F.; Aguilar, M.A.; Carvajal, F. Effects of terrain morphology, sampling density, and interpolation methods on grid DEM accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; Wiley-Interscience: New York, NY, USA, 2004. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Available online: http://www.dbs.ifi.lmu.de/Publikationen/Papers/KDD-96.final.frame.pdf (accessed on 12 January 2015).
- Su, X.; Tsai, C.L. Outlier detection. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 261–268. [Google Scholar] [CrossRef]
- Ruts, I.; Rousseeuw, P.J. Computing depth contours of bivariate point clouds. Comput. Stat. Data Anal. 1996, 23, 153–168. [Google Scholar] [CrossRef]
- Lu, C.T.; Santos, R.F.D.O.S.; Liu, X.; Kou, Y. A graph-based approach to detect abnormal spatial points and regions. Int. J. Artif. Intell. Tools 2011, 20, 721–751. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. ACM SIGMOD Record 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Knorr, E.M.; Ng, R.T.; Tucakov, V. Distance-based outliers: Algorithms and applications. VLDB J. 2000, 8, 237–253. [Google Scholar] [CrossRef]
- Chawla, S.; Sun, P. SLOM: A new measure for local spatial outliers. Knowl. Inf. Syst. 2006, 9, 412–429. [Google Scholar] [CrossRef]
- Chen, D.; Lu, C.T.; Kou, Y.; Chen, F. On detecting spatial outliers. GeoInformatica 2008, 12, 455–475. [Google Scholar] [CrossRef]
- MacEachren, A.M.; Robinson, A.; Hopper, S.; Gardner, S.; Murray, R.; Gahegan, M.; Hetzler, E. Visualizing geospatial information uncertainty: What we know and what we need to know. Cartogr. Geogr. Inf. Sci. 2005, 32, 139–160. [Google Scholar] [CrossRef]
- Podobnikar, T. Methods for visual quality assessment of a digital terrain model. SAPI. EN. S. Surv. Perspect. Integr. Environ. Soc. 2009, 2, 15–24. [Google Scholar]
- Haining, R. Spatial Data Analysis in the Social and Environmental Sciences; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Anselin, L. The Moran scatterplot as an ESDA tool to assess local instability in spatial association. Spat. Anal. Perspect. GIS 1996, 111, 111–125. [Google Scholar]
- Giménez, E.; Crespi, M.; Garrido, M.S.; Gil, A.J. Multivariate outlier detection based on robust computation of Mahalanobis distances. Application to positioning assisted by RTK GNSS Networks. Int. J. Appl. Earth Obs. Geoinf. 2012, 16, 94–100. [Google Scholar] [CrossRef]
- Nurunnabi, A.; West, G.; Belton, D. Outlier detection and robust normal-curvature estimation in mobile laser scanning 3D point cloud data. Pattern Recog. 2015, 48, 1400–1415. [Google Scholar]
- Fleishman, S.; Cohen-Or, D.; Silva, C.T. Robust moving least-squares fitting with sharp features. ACM Trans. Graph. 2005, 24, 544–552. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Masuda, H.; Tanaka, I.; Enomoto, M. Reliable surface extraction from point-clouds using scanner-dependent parameters. Comput. Aid. Design Appl. 2013, 10, 265–277. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vision Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Debese, N.; Moitié, R.; Seube, N. Multibeam echosounder data cleaning through a hierarchic adaptive and robust local surfacing. Comput. Geosci. 2012, 46, 330–339. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Driessen, K.V. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999, 41, 212–223. [Google Scholar] [CrossRef]
- Hubert, M.; Rousseeuw, P.J.; Vanden Branden, K. ROBPCA: A new approach to robust principal component analysis. Technometrics 2005, 47, 64–79. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Hardy, R. Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Chen, C.F.; Yan, C.Q.; Cao, X.W.; Guo, J.Y.; Dai, H.L. A greedy-based multiquadric method for LiDAR-derived ground data reduction. ISPRS J. Photogramm. Remote Sens. 2015, 102, 110–121. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Croux, C. Alternatives to the median absolute deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- An, S.; Liu, W.; Venkatesh, S. Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression. Pattern Recog. 2007, 40, 2154–2162. [Google Scholar] [CrossRef]
- Bailly, J.S.; Le Coarer, Y.; Languille, P.; Stigermark, C.J.; Allouis, T. Geostatistical estimations of bathymetric LiDAR errors on rivers. Earth Surf. Process. Landf. 2010, 35, 1199–1210. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Steiner, S.S. SRTM resample with short distance-low nugget kriging. Int. J. Geogr. Inf. Sci. 2008, 22, 895–906. [Google Scholar] [CrossRef]
- Hutchinson, M.F. A new procedure for gridding elevation and stream line data with automatic removal of spurious pits. J. Hydrol. 1989, 106, 211–232. [Google Scholar] [CrossRef]
- Hutchinson, M.F.; Xu, T.; Stein, J.A. Recent Progress in the ANUDEM Elevation Gridding Procedure. Available online: http://geomorphometry.org/system/files/HutchinsonXu2011geomorphometry.pdf (accessed on 12 January 2015).
- Robertson, G.P. Geostatistics for Environmental Sciences, GS+ Users Guide, Version 5; Gamma Design Software: Plainwell, MI, USA, 2008. [Google Scholar]
- Hutchinson, M.F. A locally adaptive approach to the interpolation of digital elevation models. In Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling NCGIA, University of California, Oakland, CA, USA, 21–25 January 1996; pp. 21–26.
- Chen, C.F.; Li, Y.Y. A robust multiquadric method for digital elevation model construction. Math. Geosci. 2013, 45, 297–319. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; van Driessen, K. Computing LTS regression for large data sets. Data Min. Knowl. Discov. 2006, 12, 29–45. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Li, Y.; Yan, C.; Dai, H.; Liu, G. A Robust Algorithm of Multiquadric Method Based on an Improved Huber Loss Function for Interpolating Remote-Sensing-Derived Elevation Data Sets. Remote Sens. 2015, 7, 3347-3371. https://doi.org/10.3390/rs70303347
Chen C, Li Y, Yan C, Dai H, Liu G. A Robust Algorithm of Multiquadric Method Based on an Improved Huber Loss Function for Interpolating Remote-Sensing-Derived Elevation Data Sets. Remote Sensing. 2015; 7(3):3347-3371. https://doi.org/10.3390/rs70303347
Chicago/Turabian StyleChen, Chuanfa, Yanyan Li, Changqing Yan, Honglei Dai, and Guolin Liu. 2015. "A Robust Algorithm of Multiquadric Method Based on an Improved Huber Loss Function for Interpolating Remote-Sensing-Derived Elevation Data Sets" Remote Sensing 7, no. 3: 3347-3371. https://doi.org/10.3390/rs70303347







