Monitoring and Assessment of Slope Hazards Susceptibility Around Sarez Lake in the Pamir by Integrating Small Baseline Subset InSAR with an Improved SVM Algorithm
Abstract
1. Introduction
2. Study Area and Methodology
2.1. Study Area
2.2. Methodology
2.2.1. Deformation Field Acquisition by the SBAS InSAR Method
2.2.2. Geological Hazard Susceptibility Assessment by the IV-SVM
3. Experiment and Results Analysis
3.1. Experimental Dataset
3.1.1. SAR Dataset
3.1.2. Interferometric Pair Combinations
3.1.3. DEM Data
3.2. Slope Deformation Monitoring
- March 2017–March 2018: Initial deformation on the slope peaked at −280 mm/yr, marking the lowest intensity of deformation.
- March 2018–March 2019: Deformation intensified, reaching a peak of −375 mm/yr, with spatial expansion from north to south.
- March 2019–March 2020: Sustained high deformation persisted, peaking at −420 mm/yr, with increased uplift in the north at +250 mm/yr.
- March 2020–March 2021: A temporary slowdown occurred, peaking at −310 mm/yr, with a reduction in the extent of the deformation.
- March 2021–March 2022: Relative stability was observed, with a peak deformation rate of −340 mm/yr, indicating a brief ‘plateau phase.’
- March 2022–March 2023: Renewed acceleration was noted, peaking at −420 mm/yr, leading to the formation of linear deformation belts along the shoreline.
- March 2023–August 2024: The maximum observed deformation reached −480 mm/yr, while uplift peaked at +300 mm/yr, signaling the onset of a new active phase.
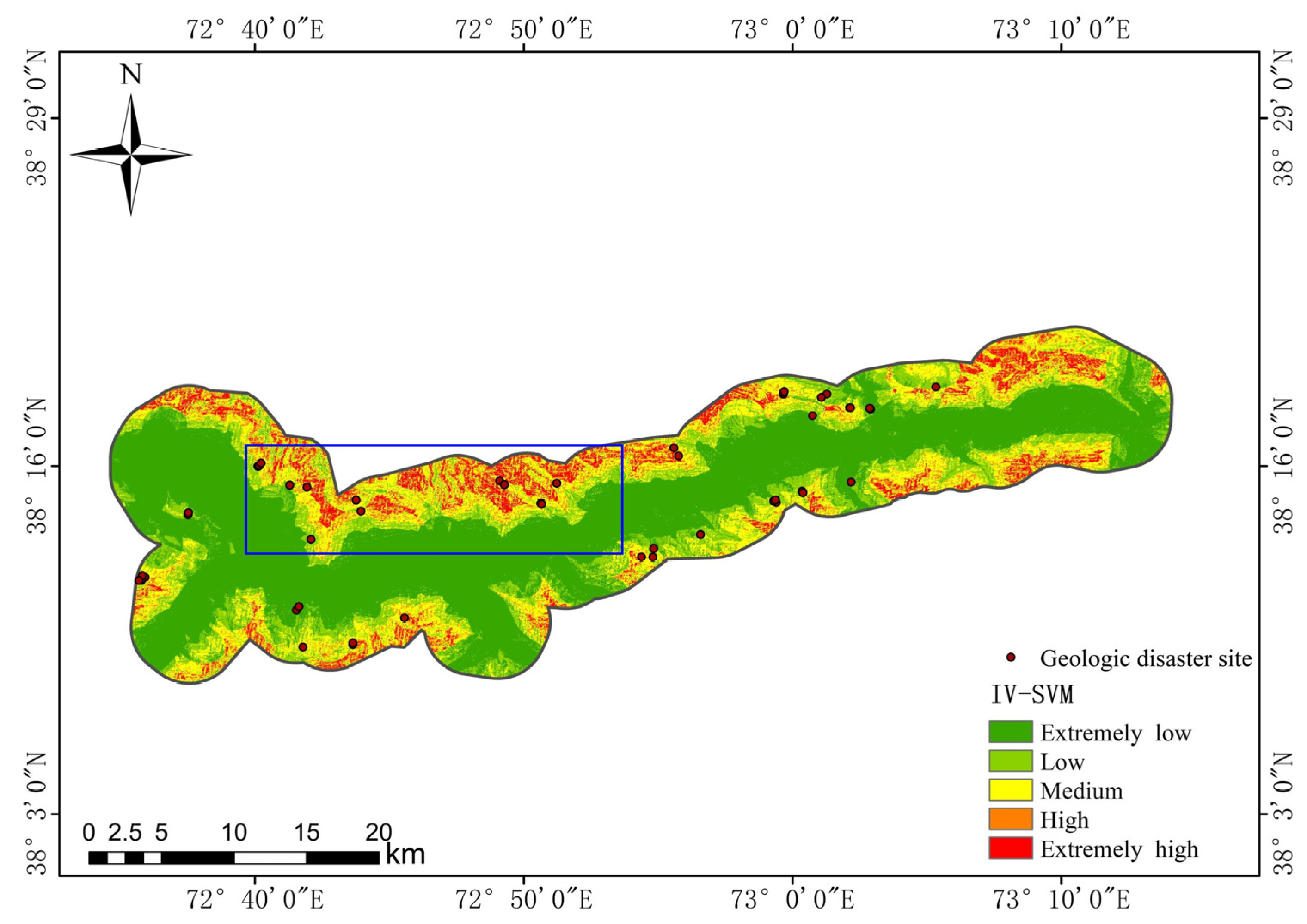
3.3. Geological Hazards Susceptibility Assessments
4. Discussion
5. Conclusions
- (1)
- From March 2017 to August 2024, slope displacement around Sarez Lake shows a persistent west-greater-than-east pattern; some areas exceed 200 mm/yr of deformation, and their peak rates rise stepwise with time.
- (2)
- Susceptibility zoning reveals a “high-flank/low-center” pattern: 15.3% of the area is classified as extremely high risk, whereas extremely low-risk zones occupy 29.1%; recorded hazard density drops correspondingly from 0.180 to 0.005 events km−2.
- (3)
- The accelerating deformation of the slope indicates that the landslide mass may be approaching a new acceleration phase, threatening the dam shoulder stability. Therefore, continuous high-precision GNSS and multi-source SAR/optical monitoring at critical points are urgently required.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, F.C.; Lee, C.F.; Deng, J.H.; Tham, L.G. The 1786 earthquake-triggered landslide dam and subsequent dam-break flood on the Dadu River, southwestern China. Geomorphology 2005, 65, 205–221. [Google Scholar] [CrossRef]
- Mantovani, F.; Vita-Finzi, C. Neotectonics of the Vajont dam site. Geomorphology 2003, 54, 33–37. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, X.; Fang, H.; Wang, W. Dammed Lake Water Volume estimation by satellite imagery and digital elevation model Under Unknown Underwater Terrain Scenario. Nat. Remote Sens. Bull. 2022, 26, 148–154. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Chen, Y.; Zhu, C.; Wei, W. The Lowest-Cost Route and feasibility Analysis for Eastward Water Diversion from Lake Sare. J. Nat. Disaster 2021, 30, 159–167. [Google Scholar]
- Tsou, C.-Y.; Feng, Z.-Y.; Chigira, M. Catastrophic landslide induced by Typhoon Morakot, Shiaolin, Taiwan. Geomorphology 2011, 127, 166–178. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Q.; Li, X.; Chen, C.; Zhou, C.; Wang, C. A review of the research on the failure potential of landslide dams caused by overtopping and seepage. Nat. Hazards 2023, 116, 1375–1408. [Google Scholar] [CrossRef]
- Fan, X.; Dufresne, A.; Subramanian, S.S.; Strom, A.; Hermanns, R.L.; Stefanelli, C.T.; Hewitt, K.; Yunus, A.T.; Dunning, S.; Capra, L. The formation and impact of landslide dams—State of the art. Earth-Sci. Rev. 2020, 203, 103–116. [Google Scholar] [CrossRef]
- Shi, Z.; Guan, S.; Peng, M.; Zhang, L.; Zhu, Y.; Cai, Q. Cascading breaching of the Tangjiashan landslide dam and two smaller downstream landslide dams. Eng. Geol. 2015, 193, 445–458. [Google Scholar] [CrossRef]
- Guo, C.; Montgomery, D.R.; Zhang, Y.; Zhong, N.; Fan, C.; Wu, R.; Yang, Z.; Ding, Y.; Jin, J.; Yan, Y. Evidence for repeated failure of the giant Yigong landslide on the edge of the Tibetan Plateau. Sci. Rep. 2020, 10, 14371. [Google Scholar] [CrossRef]
- Veh, G.; Korup, O.; Walz, A. Hazard from Himalayan glacier lake outburst floods. Proc. Natl. Acad. Sci. USA 2020, 117, 907–912. [Google Scholar] [CrossRef]
- Schuster, R.L.; Alford, D. Usoi landslide dam and Lake Sarez, Pamir Mountains, Tajikistan. Environ. Eng. Geosci. 2004, 10, 151–168. [Google Scholar] [CrossRef]
- Risley, J.C.; Walder, J.S.; Denlinger, R.P. Usoi Dam wave overtopping and flood routing in the Bartang and Panj Rivers, Tajikistan. Nat. Hazards 2006, 38, 375–390. [Google Scholar] [CrossRef]
- Deng, X.; Li, Y.; Zhang, J.; Kong, L.; Abuduwaili, J.; Gulayozov, M.; Kodirov, A.; Ma, L. The Role of Atmospheric Circulation Patterns in Water Storage of the World’s Largest High-Altitude Landslide-Dammed Lake. Atmosphere 2025, 16, 209. [Google Scholar] [CrossRef]
- Alford, D.; Cunha, S.F.; Ives, J.D. Lake Sarez, Pamir Mountains, Tajikistan: Mountain Hazards and Development Assistance. Mt. Res. Dev. 2000, 20, 20–23. [Google Scholar] [CrossRef]
- Ishuk, N.R.; Ishuk, A.R. Once Again on the Problems of Lake Sarez. In Proceedings of the International Conference “Experience in Studying Landslides and Rockfalls in the Territory of Tajikistan and Methods of Engineering Protection”, Dushanbe, Tajikistan, 26–27 September 2002. [Google Scholar]
- Ischuk, A.R. Natural and Artificial Rockslide Dams; Springer: Berlin/Heidelberg, Germany, 2011; pp. 423–440. [Google Scholar]
- Nardini, O.; Confuorto, P.; Intrieri, E.; Montalti, R.; Montanaro, T.; Garcia Robles, J.; Poggi, F.; Raspini, F. Integration of satellite SAR and optical acquisitions for the characterization of the Lake Sarez landslides in Tajikistan. Landslides 2024, 21, 1385–1401. [Google Scholar] [CrossRef]
- World Bank. Project Appraisal Document on a Proposed Grant to the Republic of Tajikistan for a Lake Sarez Risk Mitigation Project; The World Bank: Washington, DC, USA, 2004. [Google Scholar]
- United Nations International Strategy for Disaster Reduction. Sarez Lake: The Latest Achievements and Unsolved Problems; UNISDR Central Asia Office: Dushanbe, Tajikistan, 2009; Available online: https://www.undrr.org/publication/sarez-lake-latest-achievements-and-unresolved-problems (accessed on 18 May 2025).
- Han, J.; Tu, R.; Lu, X.; Fan, L.; Zhuang, W.; Wang, W.; Zhao, F.; Dalai, B.; Shonazarovich, G.M.; Safarov, M. Analysis of BDS/GPS Deformation Monitoring for the Lake Sarez Dam. Remote Sens. 2023, 15, 4773. [Google Scholar] [CrossRef]
- Grebby, S.; Sowter, A.; Gee, D.; Athab, A.; Barreda-Bautista, B.D.; Girindran, R.; Marsh, S. Remote monitoring of groundmoti-on hazards in high-mountain terrain using optical sub-pixel correlation: A case study of Lake Sarez, Tajikistan. Appl. Sci. 2021, 11, 8738. [Google Scholar] [CrossRef]
- Bekaert, D.P.; Handwerger, A.L.; Agram, P.; Kirschbaum, D.B. InSAR-based detection method for mapping and monitoring slow-moving landslides in remote regions with steep and mountainous terrain: An application to Nepal. Remote Sens. Environ. 2020, 249, 111983. [Google Scholar] [CrossRef]
- Cook, M.E.; Brook, M.S.; Hamling, I.J.; Cave, M.; Tunnicliffe, J.F. Investigating slow-moving shallow soil landslides using Sentinel-1 InSAR data in Gisborne, New Zealand. Landslides 2023, 20, 427–446. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhao, C.Y.; Zhang, Q.; Lu, Z.; Li, Z.H.; Yang, C.S.; Zhu, W.; Zeng, J.L.; Chen, L.Q.; Liu, C.J. Integration of Sentinel-1 and Alos/Palsar-2 Sar Datasets for Mapping Active Landslides Along the Jinsha River Corridor, China. Eng. Geol. 2021, 284, 106033. [Google Scholar] [CrossRef]
- Liu, X.K.; Shao, S.; Shao, S. Landslide susceptibility zonation using the Analytical Hierarchy Process (AHP) in the Great Xi’an Region, China. Sci. Rep. 2024, 14, 2941. [Google Scholar] [CrossRef]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslides using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Wubalem, A.; Meten, M. Landslide susceptibility mapping using information value and logistic regression models in Goncha Siso Eneses area, northwestern Ethiopia. SN Appl. Sci. 2020, 2, 807. [Google Scholar] [CrossRef]
- Yao, X.; Tham, L.; Dai, F. Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Shirvani, Z. A holistic analysis for landslide susceptibility mapping applying geographic object-based Random Forest. Remote Sens. 2020, 12, 434. [Google Scholar] [CrossRef]
- El Jazouli, A.; Barakat, A.; Khellouk, R. GIS-multicriteria evaluation using the AHP for landslide susceptibility mapping in Oum Er Rbia high basin (Morocco). Geoenviron. Disasters 2019, 6, 3. [Google Scholar] [CrossRef]
- Lee, S. Cross-verification of spatial logistic regression for landslide susceptibility analysis: A case study of Korea. In Proceedings of the 31st International Symposium on Remote Sensing of Environment, ISRSE 2005: Global Monitoring for Sustainability and Security, St. Petersburg, Russia, 20–24 June 2005. [Google Scholar]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Kulsoom, I.; Hua, W.; Hussain, S.; Chen, Q.; Khan, G.; Shihao, D. SBAS-InSAR based validated landslide susceptibility mapping along the Karakoram Highway: A case study of Gilgit-Baltistan, Pakistan. Sci. Rep. 2023, 13, 3344. [Google Scholar] [CrossRef]
- Achu, A.L.; Aju, C.D.; Di Napoli, M.; Prakash, P.; Gopinath, G.; Shaji, E.; Chandra, V. Machine-learning based landslide susceptibility modelling with emphasis on uncertainty analysis. Geosci. Front. 2023, 14, 101657. [Google Scholar] [CrossRef]
- Tzampoglou, P.; Loukidis, D.; Anastasiades, A.; Tsangaratos, P. Advanced machine learning techniques for enhanced landslide susceptibility mapping: Integrating geotechnical parameters in the case of Southwestern Cyprus. Earth Sci. Inform. 2025, 18, 357. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y. Spatial data analysis and application of evidential belief functions to shallow landslide susceptibility mapping at Mt. Umyeon, Seoul, Korea. Bull. Eng. Geol. Environ. 2017, 76, 1263–1279. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Zhang, W.; He, Y.; Pijush, S. A comprehensive review of machine learning-based methods in landslide susceptibility mapping. Geol. J. 2023, 58, 2283–2301. [Google Scholar] [CrossRef]
- Youssef, K.; Shao, K.; Moon, S.; Bouchard, L.S. Landslide susceptibility modeling by interpretable neural network. Commun. Earth Environ. 2023, 4, 162. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The Staffora River Basin case study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.; Huang, J.; Liu, H.; Fang, Y.; Yu, Y. A comparative study of intelligent prediction models for landslide susceptibility: Random forest and support vector machine. Front. Earth Sci. 2024, 12, 1519771. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]



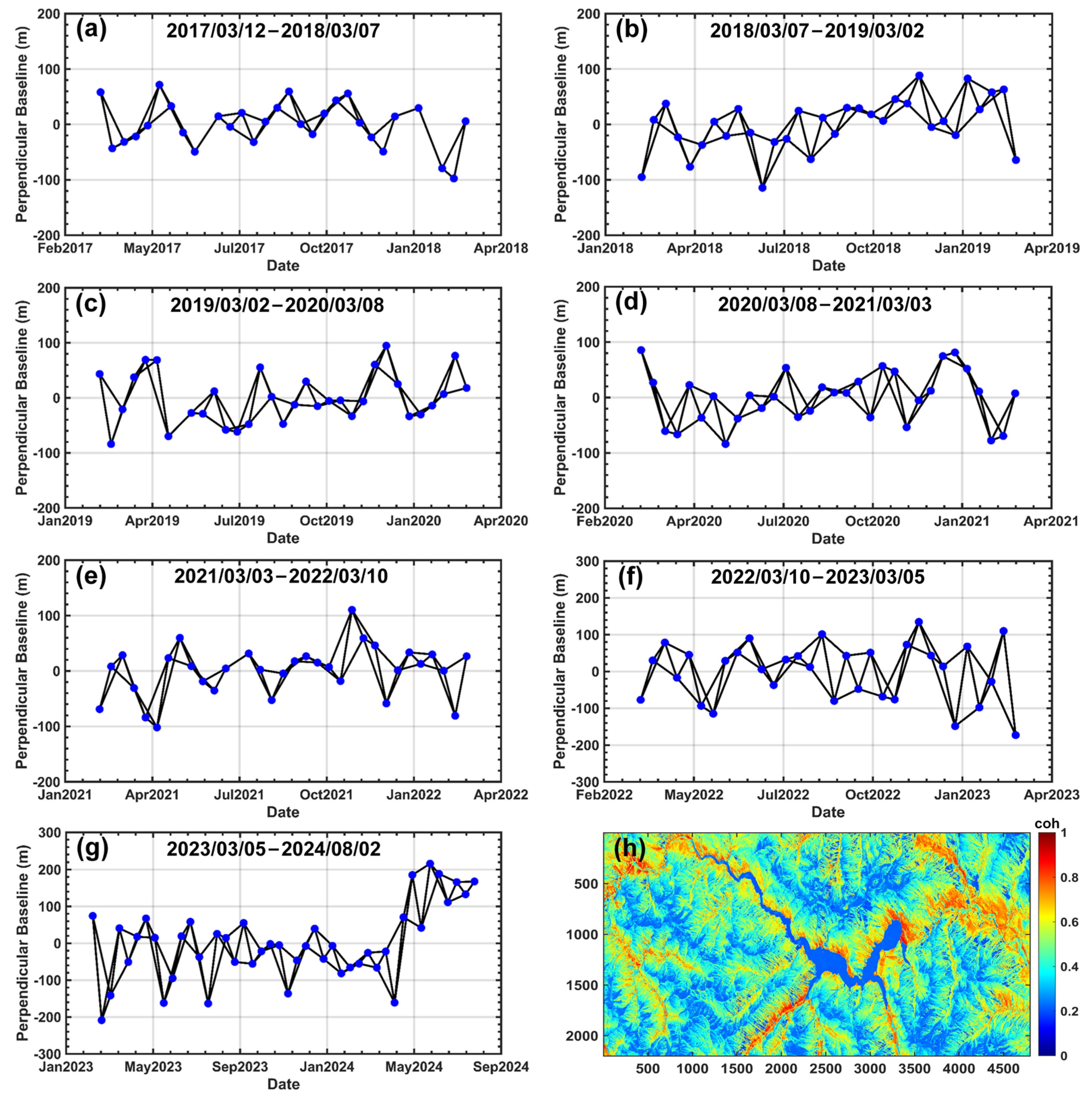








| Image Number | Date | Polarization | Incidence/° | Heading Angle/° | Spatial Baseline/m | Temporal Baseline/Day |
|---|---|---|---|---|---|---|
| 1 | 12 March 2017 | VV | 36.53 | 193.34 | 0 | 0 |
| 2 | 24 March 2017 | VV | 36.53 | 193.34 | −104.044 | 12 |
| 3 | 5 April 2017 | VV | 36.53 | 193.34 | −91.6109 | 24 |
| 4 | 17 April 2017 | VV | 36.53 | 193.34 | −83.0833 | 36 |
| 5 | 29 April 2017 | VV | 36.53 | 193.34 | −61.8433 | 48 |
| 6 | 11 May 2017 | VV | 36.53 | 193.34 | 13.2778 | 60 |
| …… | …… | …… | …… | …… | …… | …… |
| 220 | 2 August 2024 | VV | 36.53 | 193.34 | 155.0932 | 2700 |
| The Susceptibility Partition | Area/km2 | Disaster Points/Each | Density of Disaster Points/(Each/km2) |
|---|---|---|---|
| Extremely low | 201.1689 | 1 | 0.0050 |
| low | 172.4103 | 8 | 0.0464 |
| medium | 107.2800 | 15 | 0.1398 |
| high | 105.9246 | 17 | 0.1605 |
| Extremely high | 105.6528 | 19 | 0.1798 |
| The Susceptibility Partition | IV-SVM | |
|---|---|---|
| Proportion of Disaster Points | Proportion of Area | |
| Extremely low | 1.67% | 29.05% |
| low | 13.33% | 24.90% |
| medium | 25.00% | 15.49% |
| high | 28.33% | 15.30% |
| Extremely high | 31.67% | 15.26% |
| The Susceptibility Partition | Area/km2 | Disaster Points/Each | Density of Disaster Points/(Each/km2) |
|---|---|---|---|
| Extremely low | 343.6722 | 5 | 0.0145 |
| low | 163.6893 | 9 | 0.0550 |
| medium | 90.8685 | 14 | 0.1541 |
| high | 57.4047 | 14 | 0.2439 |
| Extremely high | 36.8019 | 18 | 0.4891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhu, C.; Gulayozov, M.; Li, J.; Chen, B.; Shen, Q.; Zhou, H.; Xiao, W.; Niyazov, J.; Gulakhmadov, A. Monitoring and Assessment of Slope Hazards Susceptibility Around Sarez Lake in the Pamir by Integrating Small Baseline Subset InSAR with an Improved SVM Algorithm. Remote Sens. 2025, 17, 2300. https://doi.org/10.3390/rs17132300
Yu Y, Zhu C, Gulayozov M, Li J, Chen B, Shen Q, Zhou H, Xiao W, Niyazov J, Gulakhmadov A. Monitoring and Assessment of Slope Hazards Susceptibility Around Sarez Lake in the Pamir by Integrating Small Baseline Subset InSAR with an Improved SVM Algorithm. Remote Sensing. 2025; 17(13):2300. https://doi.org/10.3390/rs17132300
Chicago/Turabian StyleYu, Yang, Changming Zhu, Majid Gulayozov, Junli Li, Bingqian Chen, Qian Shen, Hao Zhou, Wen Xiao, Jafar Niyazov, and Aminjon Gulakhmadov. 2025. "Monitoring and Assessment of Slope Hazards Susceptibility Around Sarez Lake in the Pamir by Integrating Small Baseline Subset InSAR with an Improved SVM Algorithm" Remote Sensing 17, no. 13: 2300. https://doi.org/10.3390/rs17132300
APA StyleYu, Y., Zhu, C., Gulayozov, M., Li, J., Chen, B., Shen, Q., Zhou, H., Xiao, W., Niyazov, J., & Gulakhmadov, A. (2025). Monitoring and Assessment of Slope Hazards Susceptibility Around Sarez Lake in the Pamir by Integrating Small Baseline Subset InSAR with an Improved SVM Algorithm. Remote Sensing, 17(13), 2300. https://doi.org/10.3390/rs17132300









