Hyperspectral Image Restoration under Complex Multi-Band Noises
Abstract
:1. Introduction
- The noise in each HSI band is modelled by a Dirichlet process Gaussian mixture model (DP-GMM), in which the Gaussian components of MoG in each band are adaptively determined based on the specific noise complexity of this band. The distinctness of noise structures in different bands is thus able to be faithfully reflected by the model.
- By using the hierarchical Dirichlet process (HDP) technique, we correlate the noise of different bands through a sharing strategy, in which the noise parameters of each band share a high-level noise configuration of the entire HSI.
- A variational Bayes algorithm is readily designed to solve the model, and each of the involved parameters can be effectively updated in closed-form.
2. Preliminaries
2.1. Dirichlet Process
2.2. Hierarchical Dirichlet Process
3. HSIs Restoration Model Based on DP-GMM
3.1. Notation Explanation
3.2. Model Formulation
3.2.1. The DP-GMM Model
3.2.2. LRMF Model
3.2.3. The Entire Graphical Model
4. Variational Inference
5. Experimental Results
5.1. Simulated Data Experiments
- Case 1: For different bands, the noise intensity was equal in this case. Furthermore, the same zero-mean Gaussian noise with was added to all the bands
- Case 2: Entries in all bands were corrupted by zero-mean Gaussian noise but with different intensity. Furthermore, the standard deviation of Gaussian noise that was added to each band of HSIs was uniformly selected from 0.01 to 0.1.
- Case 3: All the bands were corrupted by Gaussian noise as Case 2. Besides, 40 bands of the DC Mall dataset (20 bands of the RemoteImage dataset) were randomly chosen to add deadlines, and the number of deadlines in each band is from 5 to 15 with width 1 or 2.
- Case 4: All the bands were contaminated by Gaussian noise as Case 2. Besides, 40 bands of the DC Mall dataset (20 bands of the RemoteImage) were randomly selected to add stripes, and the number of stripes is from 15 to 40 with width 1 or 2.
- Case 5: All the bands were corrupted by Gaussian noise as Case 2. In addition, different percentages of impulse noises which were uniformly selected from 0 to 0.15 were added to each band.
- Case 6: Each band was contaminated by Gaussian and impulse noise as Case 5. Besides, 20 bands of the DC Mall dataset (10 bands of the RemoteImage dataset) were randomly selected to add deadlines as Case 3, and another 20 bands of the DC Mall dataset (10 bands of the RemoteImage dataset) were randomly selected to add stripes as Case 4.
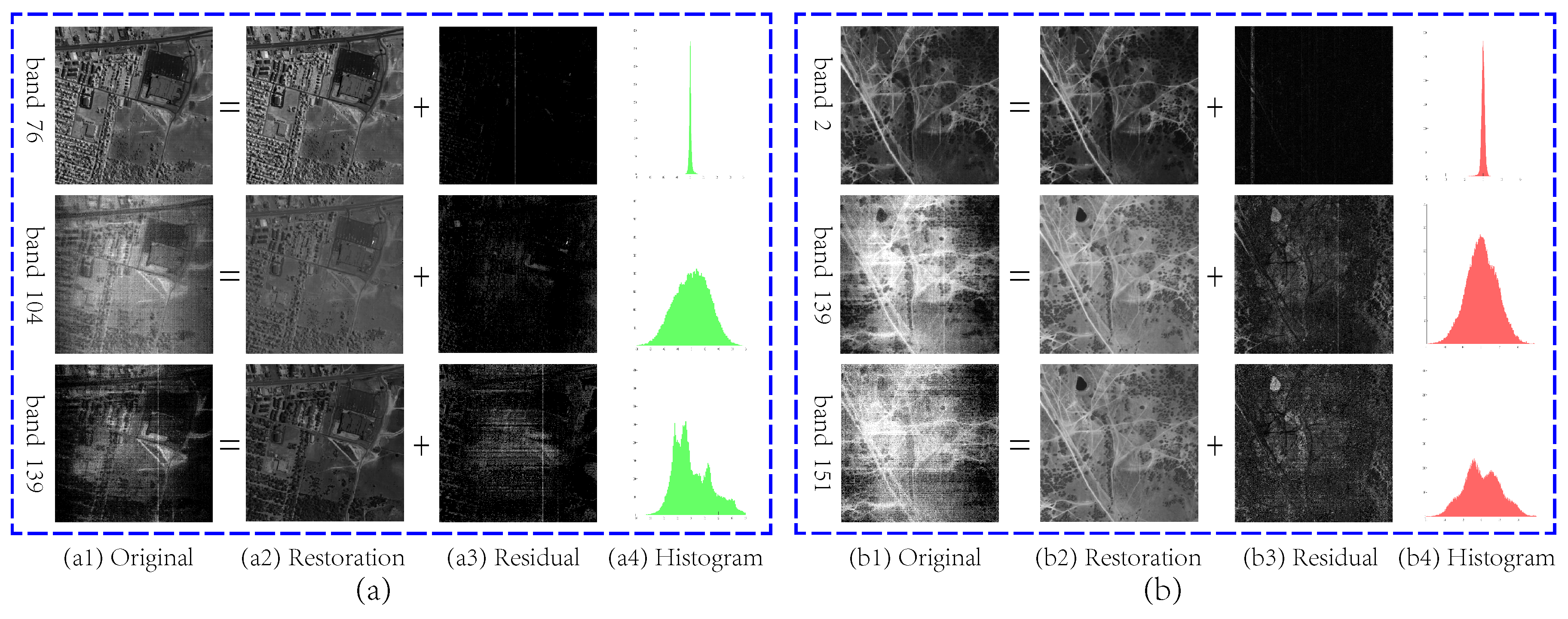
5.2. Real Data Experiments
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Willett, R.M.; Duarte, M.F.; Davenport, M.A.; Baraniuk, R.G. Sparsity and structure in hyperspectral imaging: Sensing, reconstruction, and target detection. IEEE Signal Process. Mag. 2014, 31, 116–126. [Google Scholar] [CrossRef]
- Liu, X.; Bourennane, S.; Fossati, C. Nonwhite noise reduction in hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 368–372. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef] [Green Version]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar]
- Liu, L.; Chen, L.; Chen, C.P.; Tang, Y.Y.; Pun, C.M. Weighted joint sparse representation for removing mixed noise in image. IEEE Trans. Cybern. 2017, 47, 600–611. [Google Scholar] [CrossRef] [PubMed]
- Lerga, J.; Sucic, V.; Vrankić, M. Separable image denoising based on the relative intersection of confidence intervals rule. Informatica 2011, 22, 383–394. [Google Scholar]
- Lerga, J.; Sucic, V.; Sersic, D. Performance analysis of the LPA-RICI denoising method. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 28–33. [Google Scholar]
- Mandic, I.; Peic, H.; Lerga, J.; Stajduhar, I. Denoising of X-ray images using the adaptive algorithm based on the LPA-RICI algorithm. J. Imaging 2018, 4, 34. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.E. Simultaneous dimensionality reduction and denoising of hyperspectral imagery using bivariate wavelet shrinking and principal component analysis. Can. J. Remote Sens. 2008, 34, 447–454. [Google Scholar] [CrossRef]
- Chen, S.L.; Hu, X.Y.; Peng, S.L. Hyperspectral imagery denoising using a spatial-spectral domain mixing prior. J. Comput. Sci. Technol. 2012, 27, 851–861. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 499–515. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, R.; Yu, X. Anisotropic diffusion for hyperspectral imagery enhancement. IEEE Sens. J. 2010, 10, 469–477. [Google Scholar] [CrossRef]
- Zhong, P.; Wang, R. Multiple-spectral-band CRFs for denoising junk bands of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2260–2275. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 11. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Wu, Z.; Shen, Y. Total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. J. Electron. Imaging 2016, 25, 013037. [Google Scholar] [CrossRef]
- Xie, Y.; Qu, Y.; Tao, D.; Wu, W.; Yuan, Q.; Zhang, W. Hyperspectral Image Restoration via Iteratively Regularized Weighted Schatten p-Norm Minimization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4642–4659. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Peng, Y.; Suo, J.; Dai, Q.; Xu, W. Reweighted low-rank matrix recovery and its application in image restoration. IEEE Trans. Cybern. 2014, 44, 2418–2430. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yu, J.; Xue, J.H.; Sun, W. Denoising of hyperspectral images using group low-rank representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4420–4427. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, Q.; Meng, D.; Xu, Z.; Gu, S.; Zuo, W.; Zhang, L. Multispectral images denoising by intrinsic tensor sparsity regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1692–1700. [Google Scholar]
- Karami, A.; Yazdi, M.; Asli, A.Z. Noise reduction of hyperspectral images using kernel non-negative tucker decomposition. IEEE J. Sel. Top. Signal Process. 2011, 5, 487–493. [Google Scholar] [CrossRef]
- Liu, X.; Bourennane, S.; Fossati, C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3717–3724. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1227–1243. [Google Scholar] [CrossRef]
- Letexier, D.; Bourennane, S. Noise removal from hyperspectral images by multidimensional filtering. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2061–2069. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, W.P. Signal denoising using neighbouring dual-tree complex wavelet coefficients. IET Signal Process. 2012, 6, 143–147. [Google Scholar] [CrossRef]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Chen, X.; Han, Z.; Wang, Y.; Zhao, Q.; Meng, D.; Lin, L.; Tang, Y. A general model for robust tensor factorization with unknown noise. arXiv, 2017; arXiv:1705.06755. [Google Scholar]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Cao, X.; Zhao, Q.; Meng, D.; Chen, Y.; Xu, Z. Robust low-rank matrix factorization under general mixture noise distributions. IEEE Trans. Image Process. 2016, 25, 4677–4690. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Denoising hyperspectral image with non-iid noise structure. IEEE Trans. Cybern. 2018, 48, 1054–1066. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, T.S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 209–230. [CrossRef]
- Sethuraman, J. A constructive definition of Dirichlet priors. Stat. Sin. 639–650.
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Sharing clusters among related groups: Hierarchical Dirichlet processes. In Advances in Neural Information Processing Systems 17; MIT Press: Cambridge, MA, USA; Lodon, UK, 2005; pp. 1385–1392. [Google Scholar]
- Rasmussen, C.E. The infinite Gaussian mixture model. In Advances in Neural Information Processing Systems 12; MIT Press: Cambridge, MA, USA; Lodon, UK, 2000; pp. 554–560. [Google Scholar]
- Chen, P.; Wang, N.; Zhang, N.L.; Yeung, D.Y. Bayesian adaptive matrix factorization with automatic model selection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1284–1292. [Google Scholar]
- Meng, D.; De La Torre, F. Robust matrix factorization with unknown noise. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1337–1344. [Google Scholar]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical Dirichlet Processes. Publ. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef] [Green Version]
- Blei, D.M.; Jordan, M.I. Variational inference for Dirichlet process mixtures. Bayesian Anal. 2006, 1, 121–143. [Google Scholar] [CrossRef]
- MacEachern, S.N.; Müller, P. Estimating mixture of Dirichlet process models. J. Comput. Graph. Stat. 1998, 7, 223–238. [Google Scholar]
- Neal, R.M. Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph. Stat. 2000, 9, 249–265. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; pp. 140–155. [Google Scholar]
- Haardt, M.; Strobach, P. Method for High-Resolution Spectral Analysis in Multi Channel Observations Using a Singular Valve Decomposition (SVD) Matrix Technique. US Patent 5,560,367, 1996. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images Of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]










| Noise Case | Evaluation Index | Noise | SVD | BM4D | TDL | WNNM | WSNM | LRMR | LRTV | NMoG | DP-GMM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | MPSNR (dB) | 26.02 | 38.96 | 36.66 | 40.23 | 36.98 | 36.98 | 38.79 | 38.45 | 39.05 | 39.60 |
| MSSIM | 0.7627 | 0.9833 | 0.9728 | 0.9888 | 0.9806 | 0.9801 | 0.9848 | 0.9836 | 0.9865 | 0.9875 | |
| ERGAS | 187.97 | 41.37 | 53.24 | 35.34 | 52.74 | 52.74 | 41.98 | 43.27 | 42.19 | 38.22 | |
| Case 2 | MPSNR (dB) | 23.37 | 35.79 | 34.25 | 26.99 | 36.38 | 36.28 | 36.38 | 36.88 | 37.70 | 38.59 |
| MSSIM | 0.6527 | 0.9600 | 0.9535 | 0.7904 | 0.9750 | 0.9732 | 0.9733 | 0.9739 | 0.9818 | 0.9842 | |
| ERGAS | 280.83 | 67.75 | 70.75 | 191.56 | 55.74 | 56.23 | 55.93 | 59.94 | 49.99 | 43.01 | |
| Case 3 | MPSNR (dB) | 22.51 | 33.90 | 31.67 | 25.12 | 35.99 | 35.34 | 34.45 | 35.96 | 36.99 | 37.99 |
| MSSIM | 0.6317 | 0.9486 | 0.9275 | 0.7465 | 0.9730 | 0.9632 | 0.9619 | 0.9695 | 0.9767 | 0.9827 | |
| ERGAS | 308.89 | 102.41 | 128.78 | 240.34 | 59.22 | 81.04 | 84.31 | 76.22 | 65.47 | 47.72 | |
| Case 4 | MPSNR (dB) | 22.50 | 33.80 | 31.56 | 24.66 | 34.95 | 35.26 | 34.64 | 35.77 | 37.09 | 37.55 |
| MSSIM | 0.6211 | 0.9280 | 0.9010 | 0.7035 | 0.9547 | 0.9690 | 0.9540 | 0.9642 | 0.9753 | 0.9790 | |
| ERGAS | 341.01 | 133.14 | 163.27 | 288.97 | 122.49 | 67.43 | 86.43 | 85.27 | 61.36 | 56.19 | |
| Case 5 | MPSNR (dB) | 16.47 | 27.17 | 25.12 | 21.80 | 34.33 | 34.45 | 35.07 | 36.28 | 36.15 | 37.61 |
| MSSIM | 0.4122 | 0.8299 | 0.7339 | 0.5907 | 0.9263 | 0.9716 | 0.9644 | 0.9686 | 0.9688 | 0.9795 | |
| ERGAS | 601.66 | 206.72 | 225.50 | 319.36 | 183.85 | 72.97 | 64.44 | 78.02 | 126.97 | 48.80 | |
| Case 6 | MPSNR (dB) | 16.07 | 26.86 | 24.54 | 20.59 | 33.04 | 33.79 | 33.76 | 34.60 | 35.88 | 36.98 |
| MSSIM | 0.3946 | 0.8202 | 0.7154 | 0.5412 | 0.8975 | 0.9616 | 0.9544 | 0.9599 | 0.9675 | 0.9782 | |
| ERGAS | 625.80 | 209.85 | 240.57 | 368.62 | 240.41 | 104.08 | 83.47 | 112.62 | 469.93 | 54.68 |
| Noise Case | Evaluation Index | Noise | SVD | BM4D | TDL | WNNM | WSNM | LRMR | LRTV | NMoG | DP-GMM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | MPSNR (dB) | 26.02 | 37.02 | 34.50 | 37.97 | 34.61 | 35.58 | 37.04 | 36.22 | 36.83 | 37.37 |
| MSSIM | 0.6954 | 0.9655 | 0.9267 | 0.9705 | 0.9570 | 0.9575 | 0.9679 | 0.9588 | 0.9700 | 0.9700 | |
| ERGAS | 124.05 | 37.17 | 50.33 | 33.01 | 50.06 | 43.66 | 36.44 | 40.02 | 38.40 | 35.76 | |
| Case 2 | MPSNR (dB) | 23.25 | 33.85 | 32.12 | 27.65 | 34.18 | 33.02 | 34.67 | 34.72 | 35.56 | 35.79 |
| MSSIM | 0.5554 | 0.9272 | 0.8785 | 0.7636 | 0.9399 | 0.8956 | 0.9464 | 0.9406 | 0.9610 | 0.9605 | |
| ERGAS | 186.22 | 54.26 | 64.95 | 112.77 | 50.80 | 82.17 | 47.62 | 47.44 | 44.30 | 42.69 | |
| Case 3 | MPSNR (dB) | 21.86 | 30.67 | 28.78 | 24.63 | 33.56 | 30.52 | 32.46 | 33.86 | 34.40 | 35.93 |
| MSSIM | 0.5233 | 0.8764 | 0.8102 | 0.6693 | 0.9280 | 0.8246 | 0.9220 | 0.9314 | 0.9505 | 0.9600 | |
| ERGAS | 238.56 | 108.86 | 158.23 | 195.47 | 71.79 | 160.74 | 78.50 | 67.54 | 59.01 | 41.9869 | |
| Case 4 | MPSNR (dB) | 22.40 | 33.28 | 30.03 | 25.44 | 33.54 | 32.77 | 33.47 | 33.72 | 34.54 | 35.11 |
| MSSIM | 0.5278 | 0.9056 | 0.8239 | 0.6750 | 0.9326 | 0.9152 | 0.9363 | 0.9310 | 0.9534 | 0.9575 | |
| ERGAS | 213.52 | 81.86 | 106.85 | 162.25 | 61.23 | 85.16 | 59.78 | 66.09 | 55.48 | 47.51 | |
| Case 5 | MPSNR (dB) | 17.15 | 27.98 | 27.65 | 23.99 | 29.82 | 30.75 | 33.77 | 33.52 | 33.61 | 35.63 |
| MSSIM | 0.3155 | 0.7833 | 0.7090 | 0.5614 | 0.7858 | 0.8423 | 0.9351 | 0.9253 | 0.9490 | 0.9562 | |
| ERGAS | 394.87 | 124.32 | 108.07 | 169.46 | 229.53 | 182.01 | 52.78 | 75.27 | 60.58 | 43.26 | |
| Case 6 | MPSNR (dB) | 16.76 | 27.49 | 26.37 | 22.14 | 28.24 | 29.80 | 32.74 | 32.41 | 33.85 | 35.25 |
| MSSIM | 0.3031 | 0.7781 | 0.6717 | 0.4797 | 0.7437 | 0.8153 | 0.9268 | 0.9151 | 0.9497 | 0.9550 | |
| ERGAS | 416.01 | 141.00 | 142.33 | 223.21 | 268.10 | 215.28 | 64.88 | 104.31 | 62.96 | 46.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Z.; Meng, D.; Sun, Y.; Zhao, Q. Hyperspectral Image Restoration under Complex Multi-Band Noises. Remote Sens. 2018, 10, 1631. https://doi.org/10.3390/rs10101631
Yue Z, Meng D, Sun Y, Zhao Q. Hyperspectral Image Restoration under Complex Multi-Band Noises. Remote Sensing. 2018; 10(10):1631. https://doi.org/10.3390/rs10101631
Chicago/Turabian StyleYue, Zongsheng, Deyu Meng, Yongqing Sun, and Qian Zhao. 2018. "Hyperspectral Image Restoration under Complex Multi-Band Noises" Remote Sensing 10, no. 10: 1631. https://doi.org/10.3390/rs10101631





