Augmentation of Traditional Forest Inventory and Airborne Laser Scanning with Unmanned Aerial Systems and Photogrammetry for Forest Monitoring
Abstract
:1. Introduction
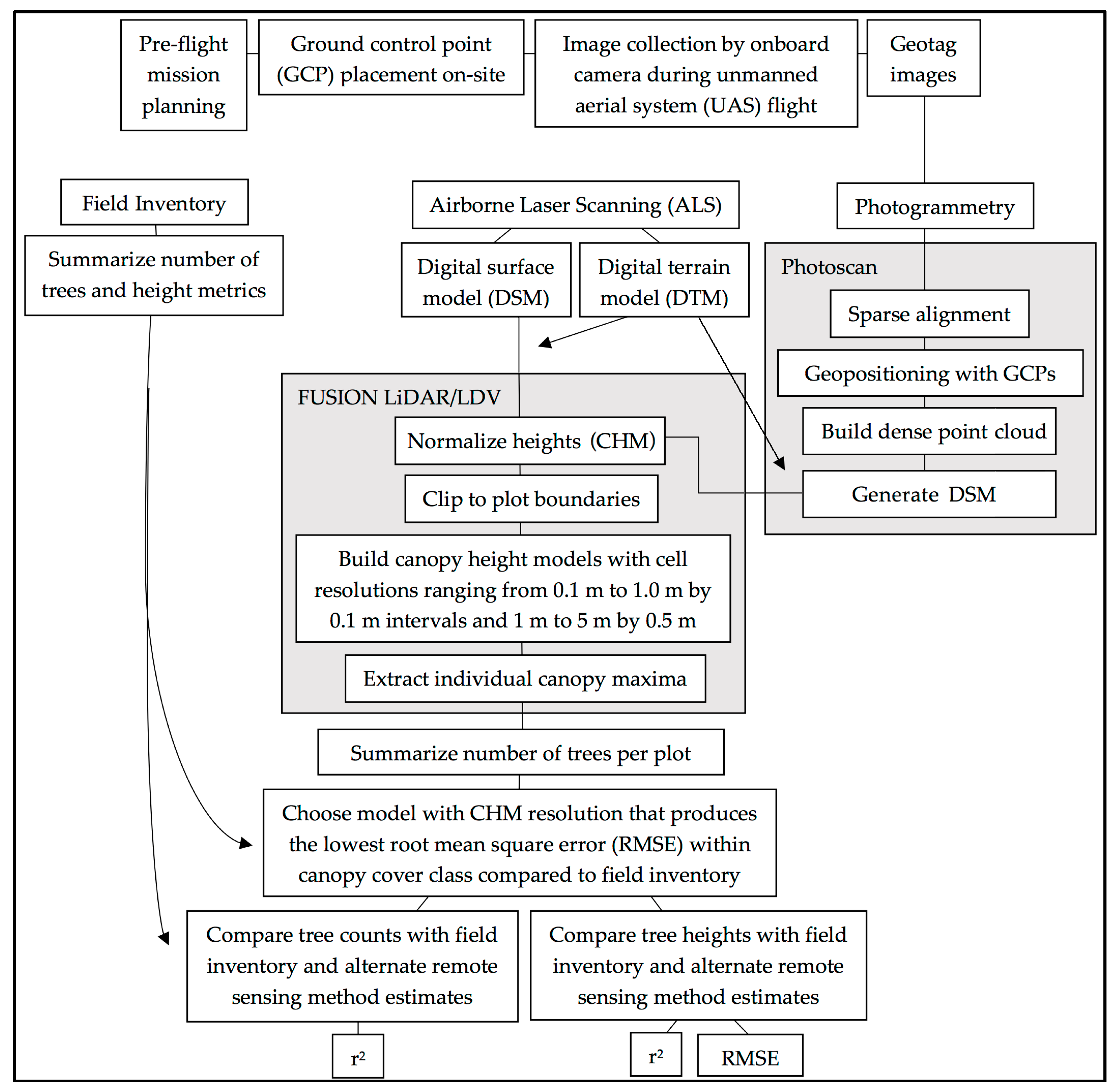
2. Materials and Methods
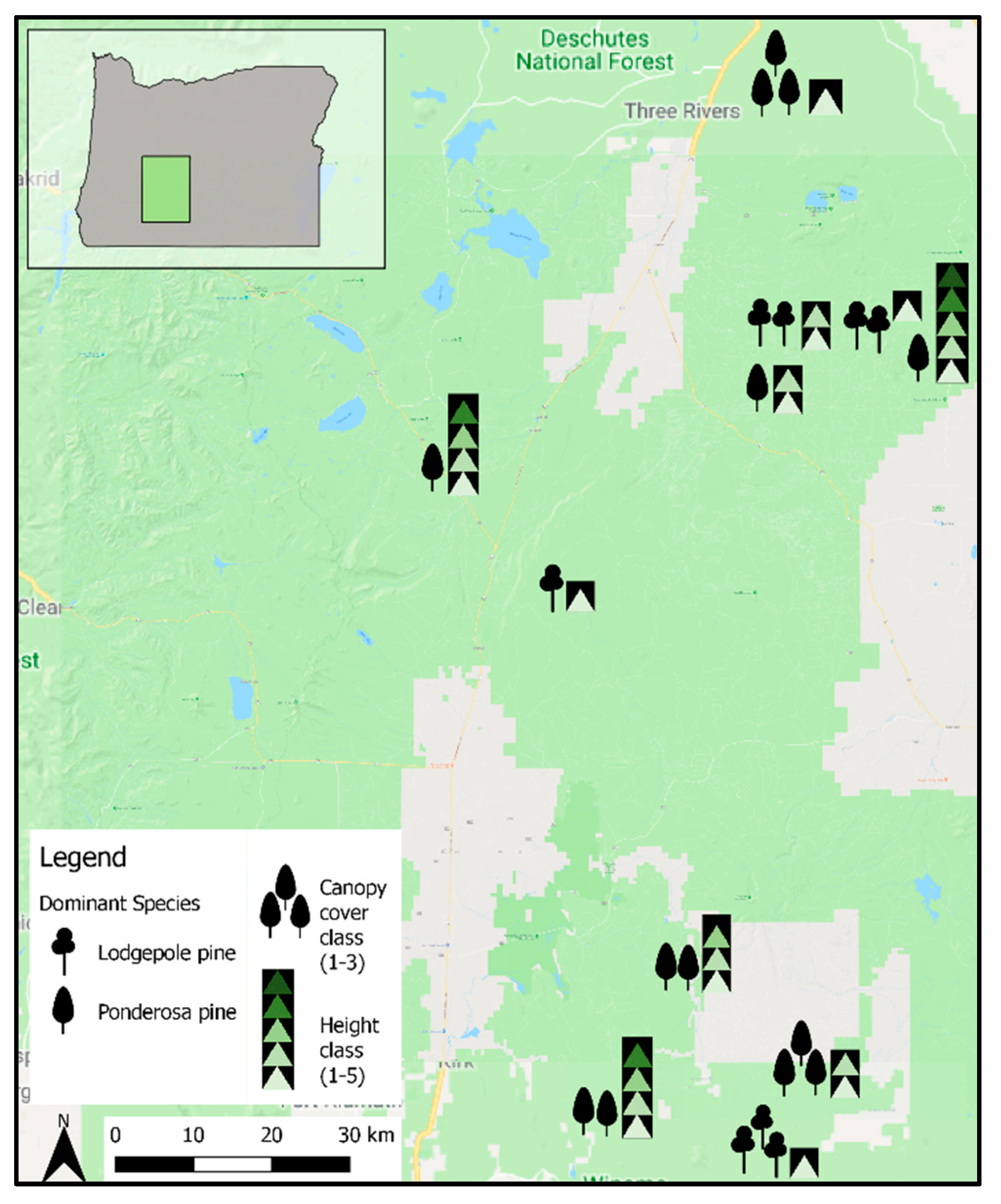
2.1. Forest Inventory and ALS Data
2.2. UAS-Based Photogrammetry Data
2.3. Point Cloud Postprocessing
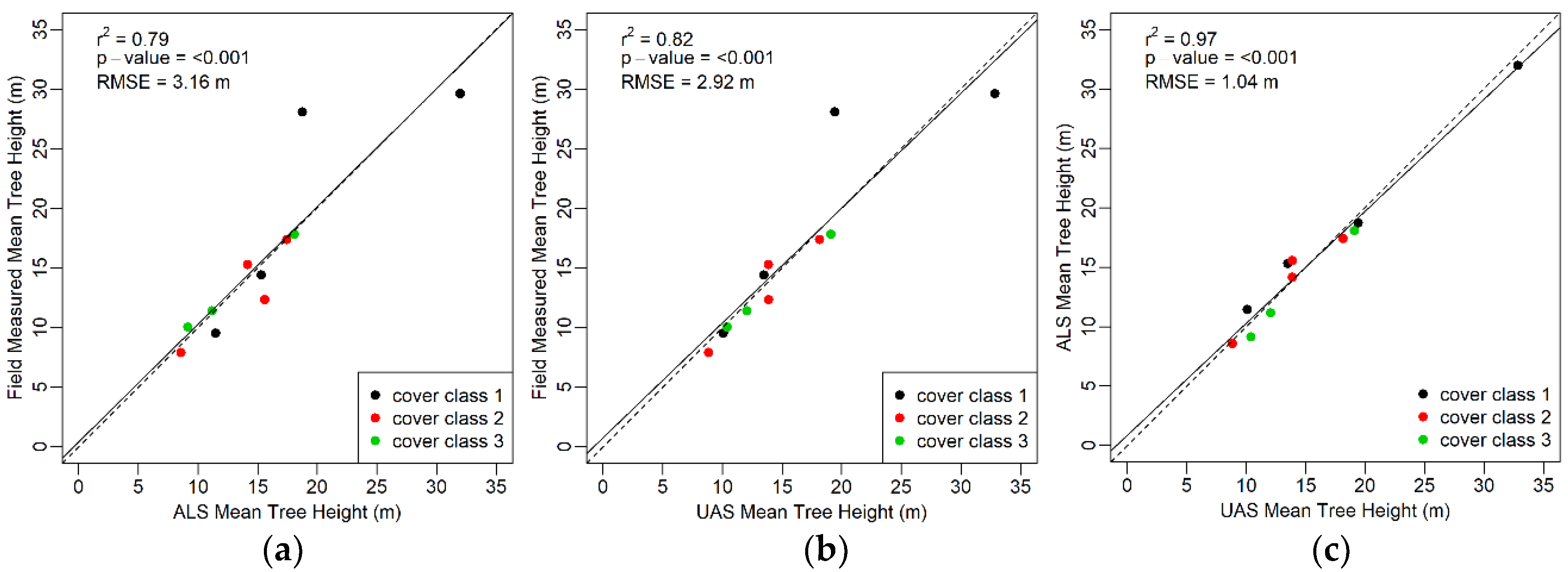
3. Results
3.1. Reconstructions
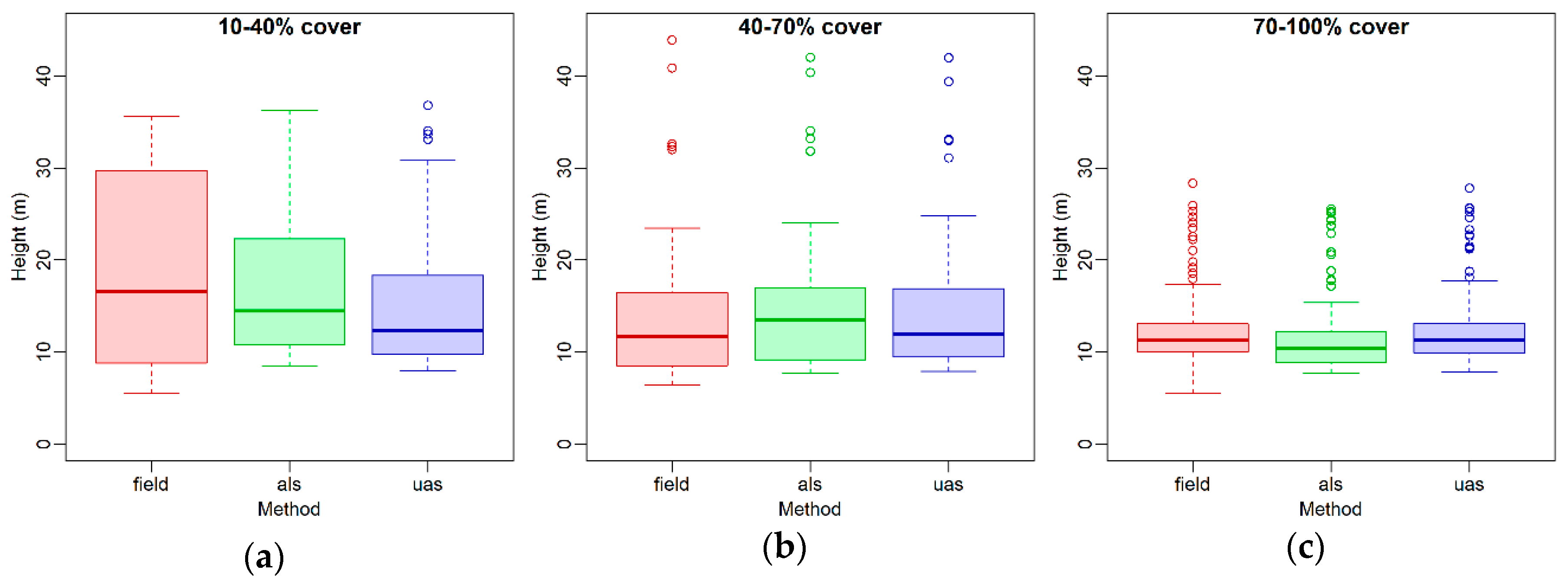
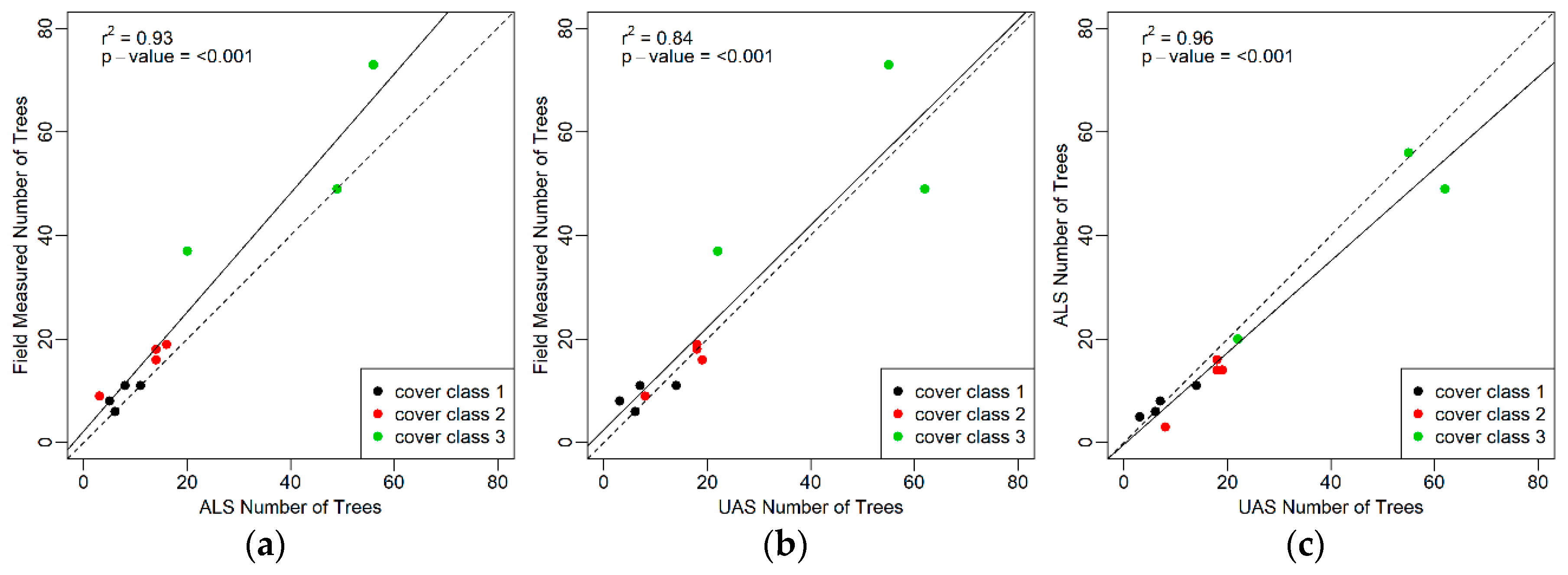
3.2. Tree Metrics
3.3. Growth Observations
4. Discussion
4.1. Reconstructions
4.2. Tree Metrics
4.3. Growth Observations
4.4. Future Applications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UN Food and Agriculture Organization. FRA 2015 Pprocess Document; United Nations: New York, NY, USA, 2016. [Google Scholar]
- USDA Forest Service. Forest Inventory and Analysis National Core Field Guide, Volume 1: Field Data Collection Procedures for Phase 2 Plots; version 7.2; USDA Forest Service: Washington, DC, USA, 2017.
- Mlambo, R.; Woodhouse, I.H.; Gerard, F.; Anderson, K. Structure from motion (SfM) photogrammetry with drone data: A low cost method for monitoring greenhouse gas emissions from forests in developing countries. Forests 2017, 8. [Google Scholar] [CrossRef]
- United Nations. UN-REDD Programme Strategy 20112015; United Nations: New York, NY, USA, 2011. [Google Scholar]
- Goodbody, T.R.H.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef] [Green Version]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Hummel, S.; Hudak, A.T.; Uebler, E.H.; Falkowski, M.J.; Megown, K.A. A comparison of accuracy and cost of LiDAR versus stand exam data for landscape management on the Malheur National Forest. J. For. 2011, 267–273. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Probst, A.; Gatziolis, D.; Liénard, J.F.; Strigul, N. Intercomparison of photogrammetry software for three-dimensional vegetation modelling. R. Soc. Open Sci. 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of forest structure using two UAV techniques: A comparison of airborne laser scanning and structure from motion (SfM) point clouds. Forests 2016, 7. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating tree detection and segmentation routines on very high resolution UAV LiDAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Oborne, M. Mission Planner v.1.3.45. Available online: www.ardupilot.org/planner (accessed on 6 August 2018).
- DroidPlanner Labs. Tower v.1.4.0.1 Beta 1. Available online: www.play.google.com (accessed on 6 August 2018).
- Agisoft, L.L.C. Photoscan Professional Edition v.1.4.2. Available online: www.agisoft.com (accessed on 6 August 2018).
- McGaughey, R.J. FUSION/LIDAR Data Viewer and LIDAR Toolkit v.3.6. Available online: www.forsys.cfr.washington.edu/fusion/fusion_overview.html (accessed on 6 August 2018).
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Messinger, M.; Asner, G.P.; Silman, M. Rapid assessments of Amazon forest structure and biomass using small unmanned aerial systems. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Gatziolis, D.; Liénard, J.F.; Vogs, A.; Strigul, N.S. 3D tree dimensionality assessment using photogrammetry and small unmanned aerial vehicles. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of small forest areas using an unmanned aerial system. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef] [Green Version]
- Gougeon, F.A. A Crown-Following Approach to the Automatic Delineation of Individual Tree Crowns in High Spatial Resolution Aerial Images. Can. J. Remote Sens. 1995, 21, 274–284. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Alonzo, M.; Andersen, H.-E.; Morton, D.C.; Cook, B.D. Quantifying Boreal Forest Structure and Composition Using UAV Structure from Motion. Forests 2018, 9. [Google Scholar] [CrossRef]
- Dalponte, M.; Frizzera, L.; Ørka, H.O.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting stem diameters and aboveground biomass of individual trees using remote sensing data. Ecol. Indic. 2018, 85, 367–376. [Google Scholar] [CrossRef]
- Jeronimo, S.M.A.; Kane, V.R.; Churchill, D.J.; McGaughey, R.J.; Franklin, J.F. Applying LiDAR Individual Tree Detection to Management of Structurally Diverse Forest Landscapes. J. For. 2018, 116, 336–346. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C.; Murray, S.C.; Putman, E.; Pugh, N.A.; Horne, D.W.; Richardson, G.; Sheridan, R.; Rooney, W.L.; Avant, R.; et al. Multitemporal field-based plant height estimation using 3D point clouds generated from small unmanned aerial systems high-resolution imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 31–42. [Google Scholar] [CrossRef]
- Dempewolf, J.; Nagol, J.; Hein, S.; Thiel, C.; Zimmermann, R. Measurement of within-season tree height growth in a mixed forest stand using UAV imagery. Forests 2017, 8. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Keuler, N.S.; Lesak, A.A.; Gobakken, T.; Contrucci, K.; Radeloff, V.C. Improved estimates of forest vegetation structure and biomass with a LiDAR-optimized sampling design. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Woodall, C.; Williams, M.S. Sampling Protocol, Estimation, and Analysis Procedures for the down Woody Materials Indicator of the FIA Program; Gen. Tech. Rep. NC-256; USDA Forest Service, North Central Research Station: St. Paul, MN, USA, 2005. [Google Scholar]
- McGaughey, R.J.; Ahmed, K.; Andersen, H.-E.; Reutebuch, S.E. Effect of Occupation Time on the Horizontal Accuracy of a Mapping-Grade GNSS Receiver under Dense Forest Canopy. Photogramm. Eng. Remote Sens. 2017, 83, 861–868. [Google Scholar] [CrossRef]
- Fritz, A.; Kattenborn, T.; Koch, B. UAV-based photogrammetric point clouds: Tree stem mapping in open stands in comparison to terrestrial laser scanner point clouds. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Rostock, Germany, 21–24 May 2013; Volume XL-1/W2, pp. 141–146. [Google Scholar]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef] [Green Version]
- Whitehead, K.; Hugenholtz, C.H. Remote sensing of the environment with small unmanned aircraft systems (UASs), part 1: A review of progress and challenges. J. Unmanned Veh. Syst. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment a Modern Synthesis. In Vision Algorithms: Theory and Practice; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1883, pp. 298–372. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2016; Available online: http://forsys.cfr.washington.edu/FUSION/fusion_overview.html (accessed on 22 September 2018).
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint Lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Monnet, J.-M.; Mermin, E.; Chanussot, J.; Berger, F. Tree top detection using local maxima filtering: A parameter sensitivity analysis. In Proceedings of the 10th International Conference on LiDAR Applications for Assessing Forest Ecosystems Silvilaser, Freiburg, Germany, 14–17 September 2010. [Google Scholar]
- Keyser, C. Westside Cascades (WC) Variant Overview Forest Vegetation Simulator; U.S. Department of Agriculture, Forest Service, Forest Management Service Center: Fort Collins, CO, USA, 2008.
- Besl, P.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- CloudCompare, Version 2.6.1. GPL Software. 2015. Available online: http://www.cloudcompare.org (accessed on 22 September 2018).
- St-Onge, B.A.; Achaichia, N. Measuring forest canopy height using a combination of lidar and aerial photography data. In Proceedings of the International Archives of Photogrammetry and Remote Sensing, Annapolis, MD, USA, 22–24 October 2001; Volume XXXIV-3/W4, pp. 131–137. [Google Scholar]
- Baltsavias, E.; Gruen, A.; Eisenbeiss, H.; Zhang, L.; Waser, L.T. High-quality image matching and automated generation of 3D tree models. Int. J. Remote Sens. 2008, 29, 1243–1259. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-Landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, X.; Yuan, W.; Cai, Y. Poor textural image matching based on graph theory. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; Volume XLI-B3, pp. 741–747. [Google Scholar]
- Seely, H.E. Computing tree heights from shadows in aerial photographs. For. Chron. 1929, 5, 24–27. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in Geosciences. Wiley-Blackwell: Oxford, UK, 2016; p. 208. [Google Scholar]
- Verma, N.K.; Lamb, D.W. The use of shadows in high spatial resolution, remotely sensed, imagery to estimate the height of individual Eucalyptus trees on undulating land. Rangel. J. 2015, 37, 467–476. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution unmanned aerial vehicle (UAV) imagery, based on structure from motion (SfM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Comparison of UAV photograph-based and airborne lidar-based point clouds over forest from a forestry application perspective. Int. J. Remote Sens. 2016, 38, 1–16. [Google Scholar] [CrossRef]
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to estimating tree height via LiDAR in closed-canopy forest: A parable from western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Seidel, K.W. A Ponderosa Pine-Lodgepole Pine Spacing Study in Central Oregon: Results after 20 Years; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1989. [Google Scholar]
- Lowery, D.P. Ponderosa Pine; An American Wood; USDA Forest Service: Washington, DC, USA, 1984. [Google Scholar]
- USDA NRCS Plant Materials Program. Plant Fact Sheet: Ponderosa Pine; USDA Natural Resources Conservation Science: Washington, DC, USA, 2002.
- Zhang, J.; Hu, J.; Lian, J.; Fan, Z.; Ouyang, X.; Ye, W. Seeing the forest from drones: Testing the potential of lightweight drones as a tool for long-term forest monitoring. Biol. Conserv. 2016, 198, 60–69. [Google Scholar] [CrossRef]
- DOGAMI (Oregon Department of Geology and Mineral Industries). Collecting LiDAR. Available online: http://www.oregongeology.org/lidar/collectinglidar.htm (accessed on 17 June 2018).
- U.S. Geological Survey the National Map: 3D Elevation Program (3DEP). Available online: https://nationalmap.gov/3DEP/ (accessed on 5 August 2018).

| Parameter | Value |
|---|---|
| Scanner | Reigl 680i |
| Mirror | Rotating |
| Field of view | ±30 degrees |
| Flying height | 730 m (2400 ft) aboveground level |
| Pulse rate | 330,000 Hz |
| Scan rate | 200 Hz |
| Beam divergence | ≤0.5 mrad |
| Pulse wavelength | Near infrared, 1064 nm |
| Intensity | 16-bit |
| Processing | Digitized waveform, up to 7 returns per pulse in the study area |
| Canopy Cover Class (Percent) | Number of Plots | Number of Trees on Plot with DBH >= 12.7 cm | Maximum Tree Height (m) | Dominant Species (Number of Plots) |
|---|---|---|---|---|
| I (10–40%) | 4 | 6–12 | 15.5–35.7 | Ponderosa pine (3); Lodgepole pine (1) |
| II (40–70%) | 4 | 9–19 | 9.4–43.9 | Ponderosa pine (2); Lodgepole pine (2) |
| III (70–100%) | 3 | 37–73 | 16.8– 28.3 | Ponderosa pine (2); Lodgepole pine (1) |
| Field | ALS | UAS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CC1 | CC2 | CC3 | CC1 | CC2 | CC3 | CC1 | CC2 | CC3 | |
| CHM cell resolution | -- | -- | -- | 3.0 | 0.3 | 0.2 | 2.5 | 0.4 | 0.3 |
| Tree counts | 36.0 | 62.0 | 159.0 | 30.0 | 47.0 | 125.0 | 30.0 | 63.0 | 139.0 |
| Median tree height (m) | 16.6 | 11.7 | 11.3 | 14.5 | 13.5 | 10.4 | 12.4 | 12.0 | 11.3 |
| Mean tree height (m) | 18.6 | 14.0 | 12.5 | 17.8 | 15.3 | 11.5 | 15.8 | 14.4 | 12.4 |
| SD tree height | 10.3 | 7.9 | 4.3 | 9.2 | 8.3 | 4.1 | 8.9 | 7.6 | 4.1 |
| Min tree height (m) | 5.5 | 6.4 | 5.5 | 8.5 | 7.7 | 7.7 | 8.0 | 7.9 | 7.9 |
| Max tree height (m) | 35.7 | 43.9 | 28.4 | 36.3 | 42.0 | 25.6 | 36.8 | 41.9 | 27.8 |
| ALS vs. Field Measured | UAS vs. Field Measured | |||||
|---|---|---|---|---|---|---|
| CC1 | CC2 | CC3 | CC1 | CC2 | CC3 | |
| CHM cell resolution | 2.50 | 0.40 | 0.30 | 3.00 | 0.30 | 0.20 |
| Mean difference in tree counts (n) | −1.50 | −3.75 | −11.33 | −1.50 | 0.25 | −6.67 |
| Mean difference in min tree height (m) | 4.09 | 0.62 | 1.77 | 4.23 | 0.99 | 1.72 |
| Mean difference in mean tree height (m) | −1.04 | 0.70 | −0.30 | −1.47 | 0.44 | 0.73 |
| Mean difference in max tree height (m) | 0.22 | −0.76 | −1.71 | 0.17 | -0.68 | −1.01 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fankhauser, K.E.; Strigul, N.S.; Gatziolis, D. Augmentation of Traditional Forest Inventory and Airborne Laser Scanning with Unmanned Aerial Systems and Photogrammetry for Forest Monitoring. Remote Sens. 2018, 10, 1562. https://doi.org/10.3390/rs10101562
Fankhauser KE, Strigul NS, Gatziolis D. Augmentation of Traditional Forest Inventory and Airborne Laser Scanning with Unmanned Aerial Systems and Photogrammetry for Forest Monitoring. Remote Sensing. 2018; 10(10):1562. https://doi.org/10.3390/rs10101562
Chicago/Turabian StyleFankhauser, Kathryn E., Nikolay S. Strigul, and Demetrios Gatziolis. 2018. "Augmentation of Traditional Forest Inventory and Airborne Laser Scanning with Unmanned Aerial Systems and Photogrammetry for Forest Monitoring" Remote Sensing 10, no. 10: 1562. https://doi.org/10.3390/rs10101562






