Factors Affecting Spatial Variation in Vegetation Carbon Density in Pinus massoniana Lamb. Forest in Subtropical China
Abstract
:1. Introduction
2. Materials and Methods
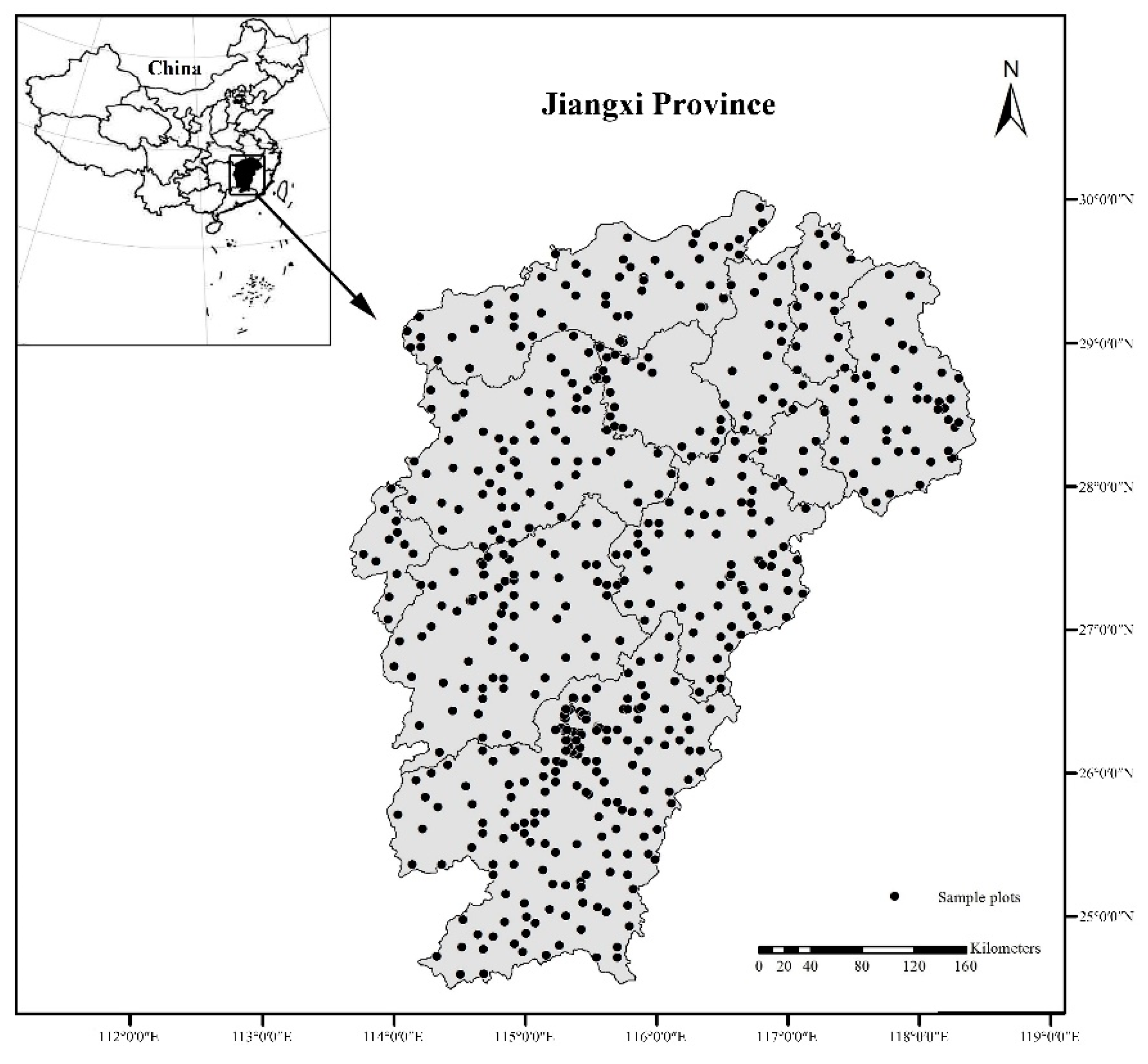
2.1. Study Area
2.2. Data Collection
2.3. Carbon Density Calculations
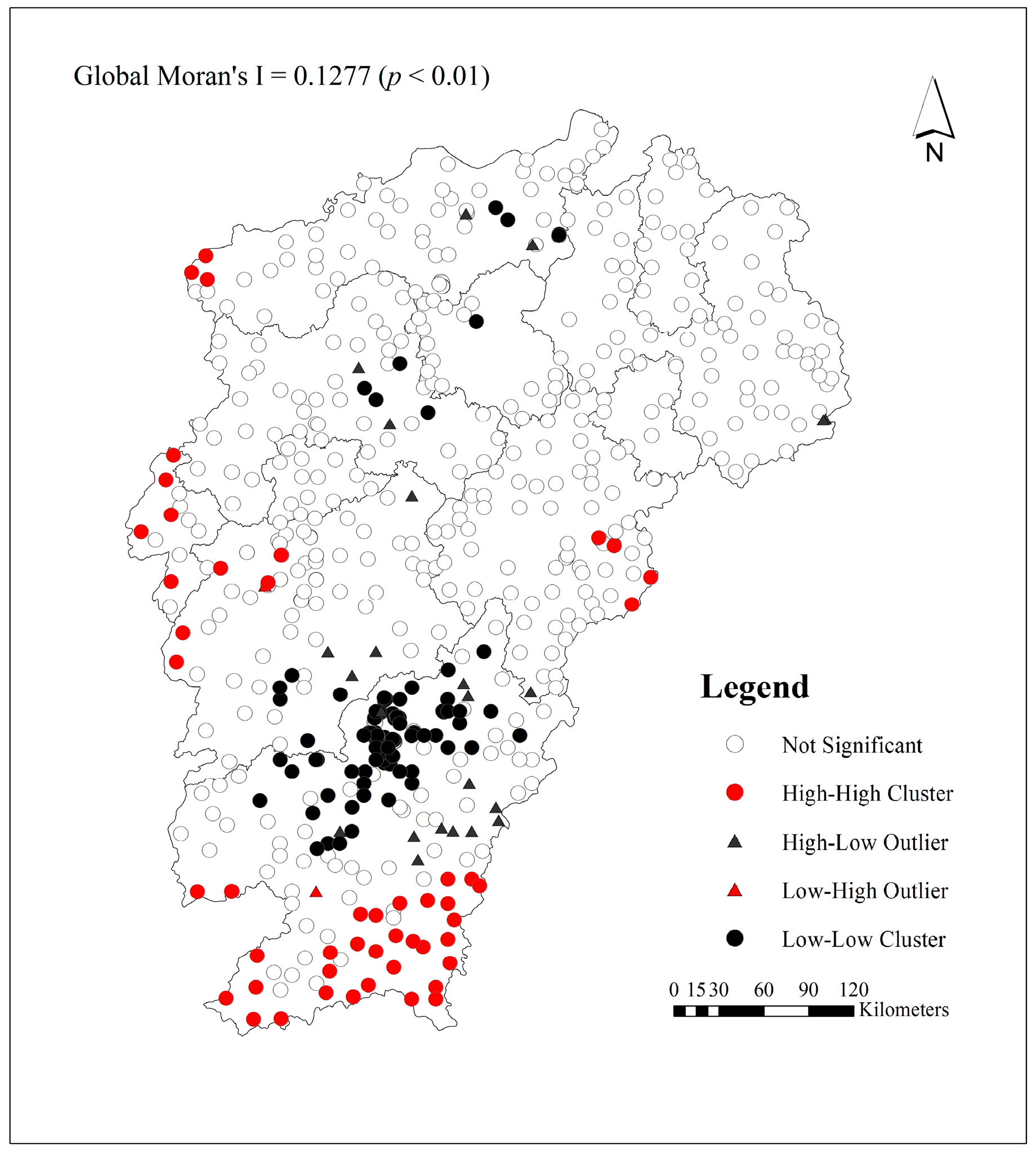
2.4. Spatial Autocorrelation Analyses
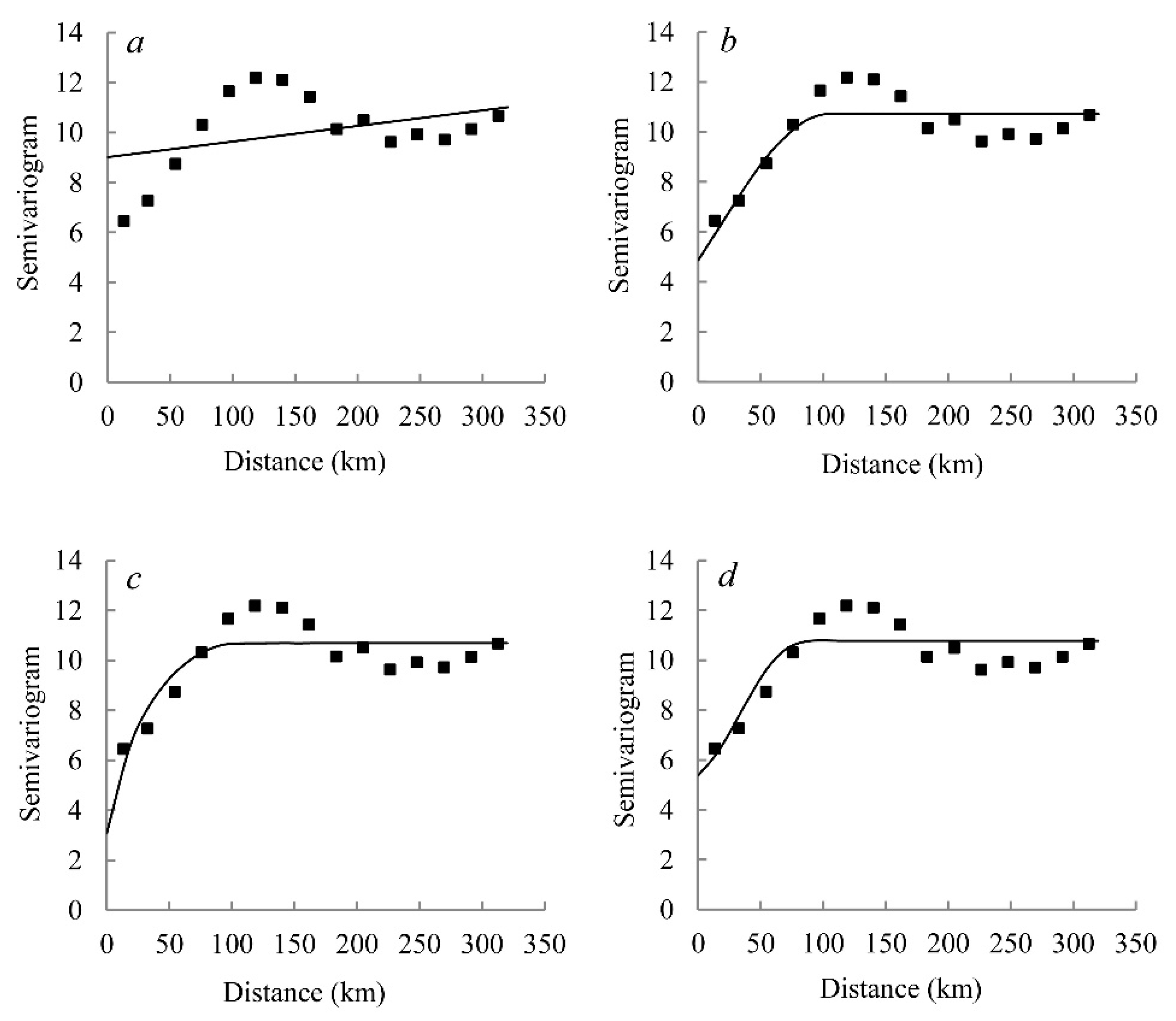
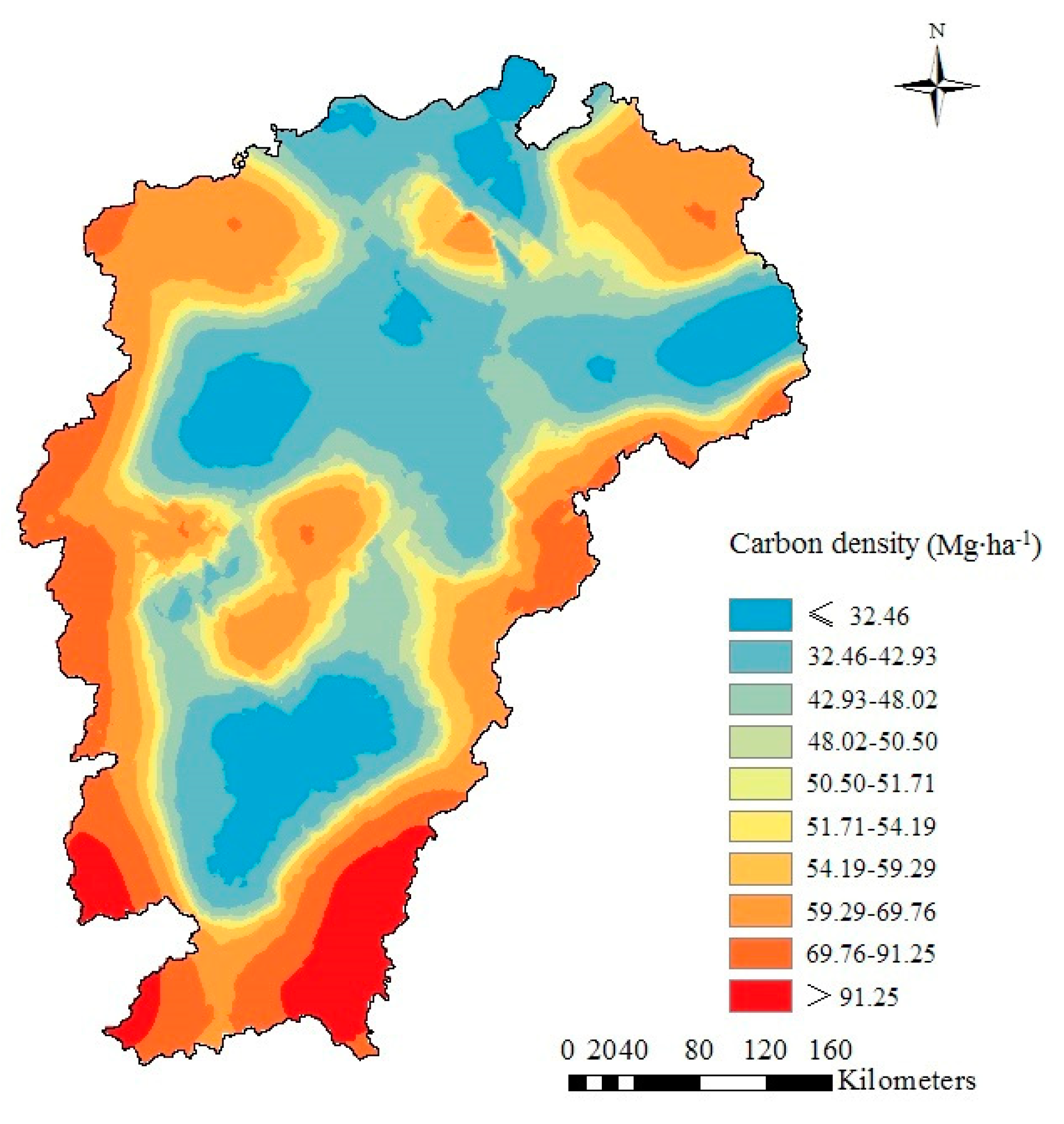
2.5. Geostatistical Analysis
2.6. Statistical Analysis
3. Results and Discussion
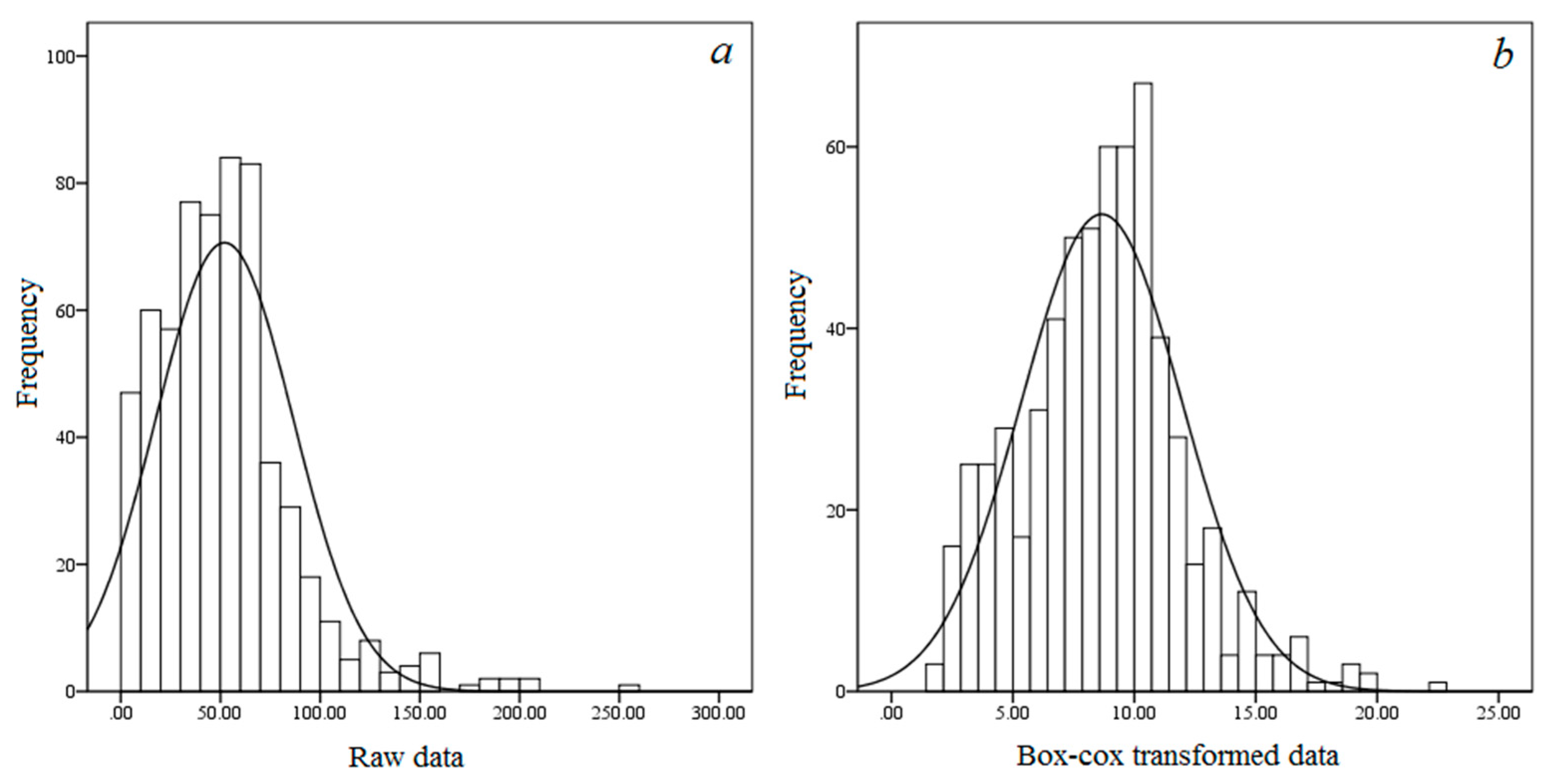
3.1. Descriptive Statistics
3.2. Analysis of Influencing Factors
3.2.1. Environmental Factors Related to Carbon Density
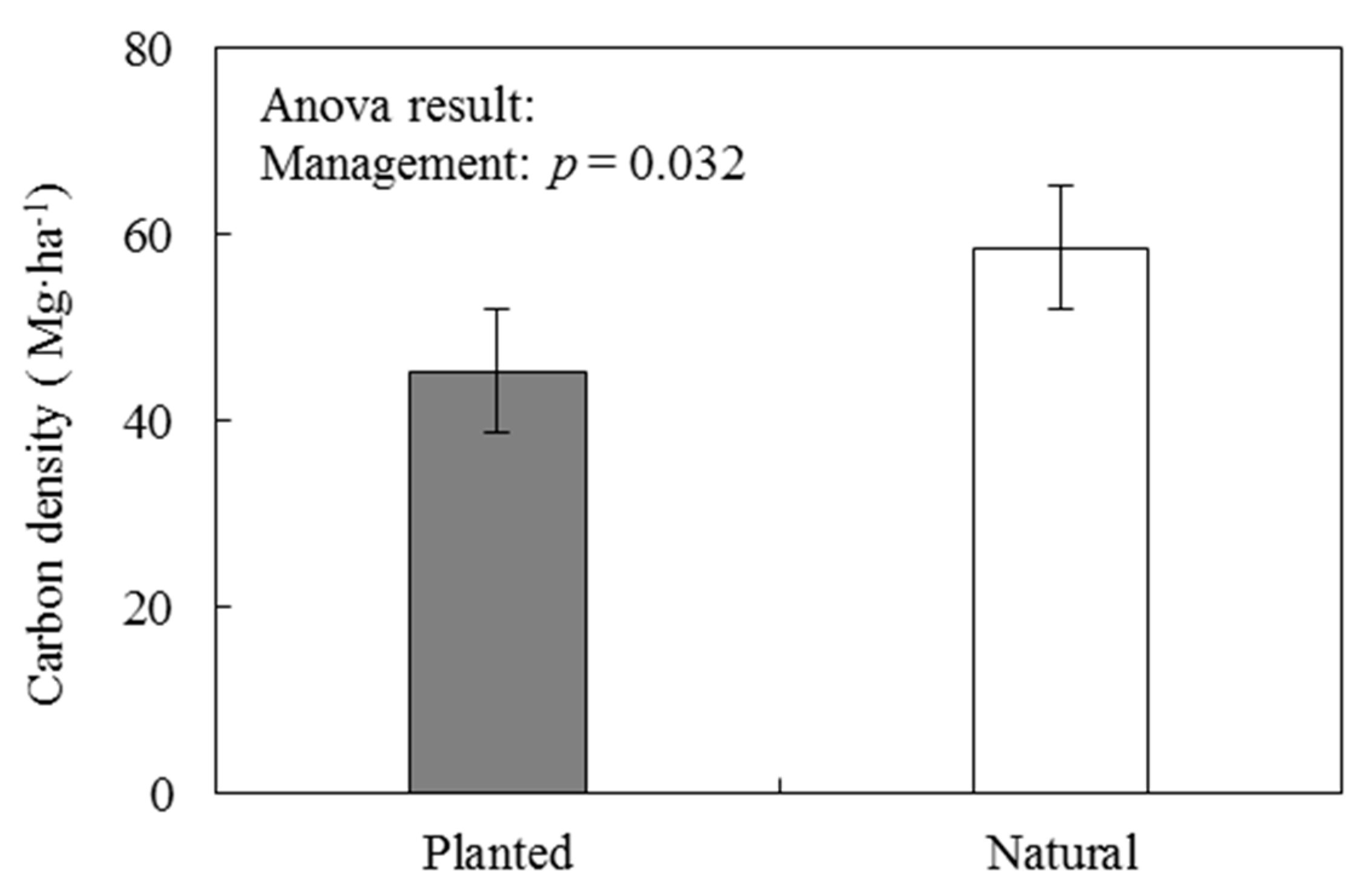
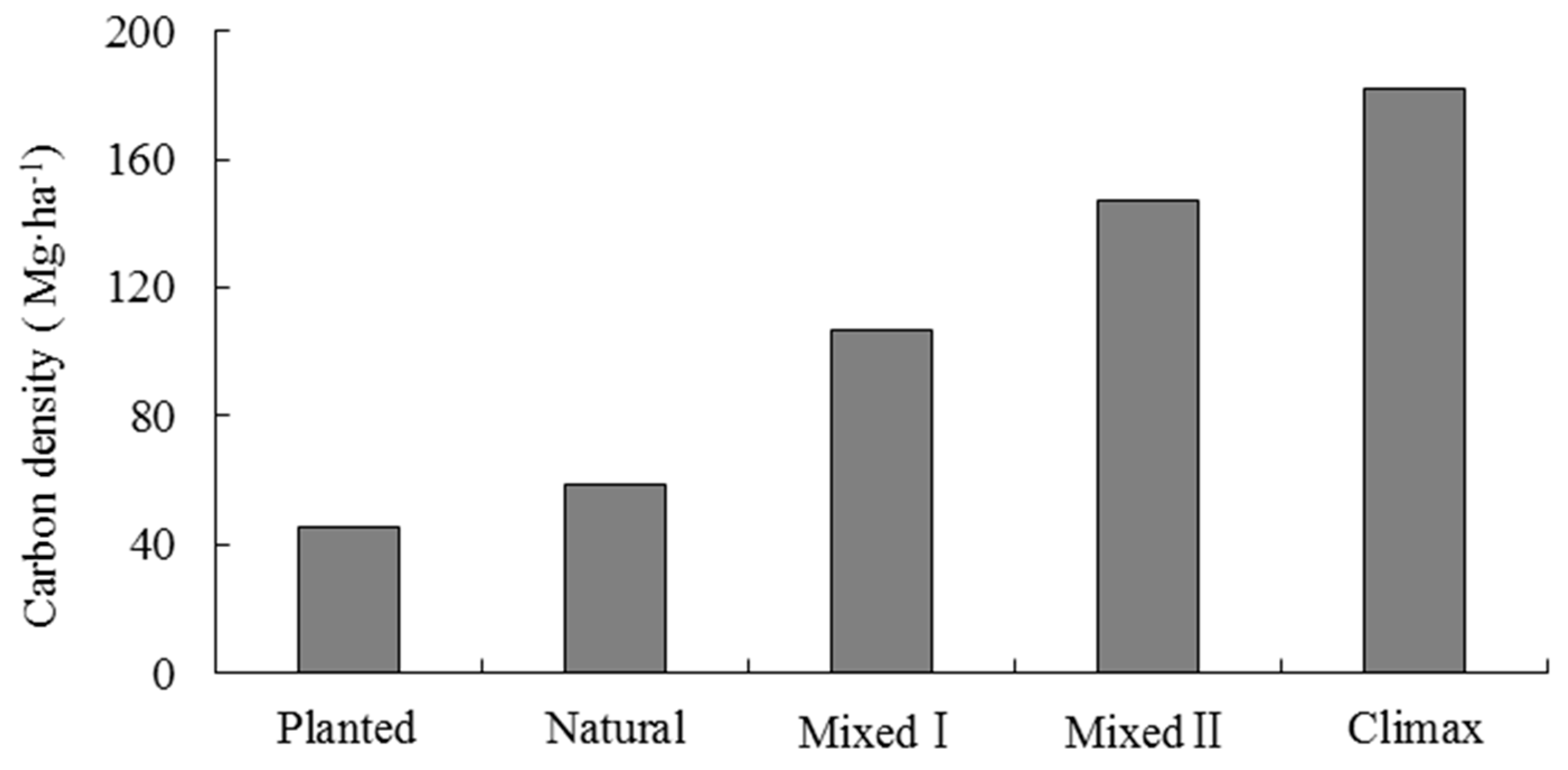
3.2.2. Forest Management Related to Carbon Density
3.3. Spatial Cluster and Spatial Outlier Analysis
3.4. Semivariance Analysis and Spatial Distribution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Vitousek, P.M. Beyond global warming: Ecology and global change. Ecology 1994, 75, 1861–1876. [Google Scholar] [CrossRef]
- Jones, C.; Lowe, J.; Liddicoat, S.; Betts, R. Committed terrestrial ecosystem changes due to climate change. Nat. Geosci. 2009, 2, 484–487. [Google Scholar] [CrossRef]
- Alam, A.; Kilpeläinen, A.; Kellomäki, S. Impacts of initial stand density and thinning regimes on energy wood production and management-related CO2 emissions in boreal ecosystems. Eur. J. For. Res. 2012, 131, 655–667. [Google Scholar] [CrossRef]
- Litton, C.; Raich, J.; Ryan, M. Carbon allocation in forest ecosystems. Glob. Chang. Biol. 2007, 13, 2089–2109. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Chen, H.; Li, L.; Li, P.; Hou, C.; Wan, H.; Zhang, Q.; Zhang, P. Spatial and temporal patterns of carbon storage from 1992 to 2002 in forest ecosystems in Guangdong, Southern China. Plant Soil 2013, 363, 123–138. [Google Scholar] [CrossRef]
- Houghton, R.A. Balancing the global carbon budget. Annu. Rev. Earth Planet. Sci. 2007, 35, 313–347. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Bravo-Oviedo, A.; Lopez-Senespleda, E.; Montero, G.; Rio, M. Do thinnings influence biomass and soil carbon stocks in Mediterranean maritime pine woods. Eur. J. For. Res. 2013, 132, 253–262. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- He, N.; Wen, D.; Zhu, J.; Tang, X.; Yu, G. Vegetation carbon sequestration in Chinese forests from 2010 to 2050. Glob. Chang. Biol. 2016, 23, 1575–1584. [Google Scholar] [CrossRef]
- Dixon, R.K.; Brown, S.; Houghton, R.A.; Trexier, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Wang, C.K. Carbon density and distribution of six Chinese temperate forests. Sci. China Life Sci. 2010, 53, 831–840. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thurner, M.; Beer, C.; Santoro, M.; Carvalhais, N. Carbon stock and density of northern boreal and temperate forests. Glob. Ecol. Biogeogr. 2014, 23, 297–310. [Google Scholar] [CrossRef]
- Pan, P.; Sun, Y.J.; Ouyang, X.Z.; Rao, J.F.; Feng, R.Q.; Yang, Z.Y. Spatial variation of carbon density in Pinus massoniana forest in Jiangxi Province, China. Chin. J. Appl. Ecol. 2019, 30, 1885–1892. [Google Scholar]
- Wang, T.; Wang, G.; Innes, J.L.; Seely, B.; Chen, B. ClimateAP: An application for dynamic local downscaling of historical and future climate data in Asia Pacific. Front. Agric. Sci. Eng. 2017, 4, 448–458. [Google Scholar] [CrossRef]
- Somogyi, Z.; Cienciala, E.; Mäkipää, R.; Muukkonen, P.; Lehtonen, A.; Weiss, P. Indirect methods of large scale forest biomass estimation. Eur. J. For. Res. 2007, 126, 197–207. [Google Scholar] [CrossRef]
- Fang, J.Y.; Chen, A.P.; Peng, C.H.; Zhao, S.Q.; Ci, L.J. Changes in forest biomass carbon storage in China between 1949 and 1988. Science 2001, 291, 2320–2322. [Google Scholar] [CrossRef]
- Jones, D.A.; O’hara, K.L. Carbon density in managed coast redwood stands: Implications for forest carbon estimation. Forestry 2012, 85, 99–110. [Google Scholar] [CrossRef]
- State Forestry Administration. The Ministerial Standard of the People’s Republic of China (LY/T 2263-2014): Tree Biomass Models and Related Parameters to Carbon Accounting for Pinus massoniana; Standards Press of China: Beijing, China, 2014; pp. 2–5. [Google Scholar]
- State Forestry Administration. The Ministerial Standard of the People’s Republic of China (LY/T 2264-2014): Tree Biomass Models and Related Parameters to Carbon Accounting for Cunninghamia Lanceolata; Standards Press of China: Beijing, China, 2014; pp. 2–5. [Google Scholar]
- State Forestry Administration. The Ministerial Standard of the People’s Republic of China (LY/T 2660-2016): Tree Biomass Models and Related Parameters to Carbon Accounting for Schima Superba; Standards Press of China: Beijing, China, 2016; pp. 2–3. [Google Scholar]
- State Forestry Administration. The Ministerial Standard of the People’s Republic of China (LY/T 2658-2016): Tree Biomass Models and Related Parameters to Carbon Accounting for Quercus; Standards Press of China: Beijing, China, 2016; pp. 2–7. [Google Scholar]
- Lu, R.K. Methods of Soil and Agro-Chemical Analysis; China Agricultural Science and Technology Press: Beijing, China, 2000. [Google Scholar]
- Zhang, C.S.; Tang, Y.; Luo, L.; Xu, W.L. Outlier identification and visualization for Pb concentrations in urban soils and its implications for identification of potential contaminated land. Environ. Pollut. 2009, 157, 3083–3090. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Guan, F.; Xia, M.; Tang, X.; Fan, S. Spatial variability of soil nitrogen, phosphorus and potassium contents in Moso bamboo forests in Yong’an City, China. Catena 2017, 150, 161–172. [Google Scholar] [CrossRef]
- Fang, X.; Xue, Z.; Li, B.; An, S. Soil organic carbon distribution in relation to land use and its storage in a small watershed of the Loess Plateau, China. Catena 2012, 88, 6–13. [Google Scholar] [CrossRef]
- Zhou, Y.R.; Yu, Z.L.; Zhao, S.D. Carbon storage and budget of major Chinese forest types. Acta Phytoecologica Sinica 2000, 24, 518–522. [Google Scholar]
- Lan, X.; Du, H.; Song, T.Q.; Zeng, F.P.; Peng, W.X.; Liu, Y.X.; Fan, Z.L.; Zhang, J.Y. Vegetation carbon storage in the main forest types in Guangxi and the related influencing factors. Acta. Ecol. Sin. 2019, 39, 2043–2053. [Google Scholar]
- Zhao, M.; Zhou, G.S. Carbon storage of forest vegetation and its relationship with climatic factors. Sci. Geogr. Sin. 2004, 24, 50–54. [Google Scholar] [CrossRef]
- Fu, W.J.; Jiang, P.K.; Zhou, G.M.; Zhao, K.L. Using Moran’s I and GIS to study the spatial pattern of forest litter carbon density in a subtropical region of southeastern China. Biogeosciences 2014, 11, 2401–2409. [Google Scholar] [CrossRef]
- Xiao, X.; Wei, X.H.; Liu, Y.Q.; Ouyang, X.Z.; Li, Q.L.; Ning, J.K. Aerial seeding: An effective forest restoration method in highly degraded forest landscapes of sub-tropic regions. Forests 2015, 6, 1748–1762. [Google Scholar] [CrossRef]
- Zhan, X. Changes in soil fertility after interplanting pure Pinus massioniana plantations with broadleaved forest under the canopy during 20 years. J. Beijing For. Univ. 2018, 40, 55–62. [Google Scholar]
- Fan, H.B.; Li, Y.Y.; Su, B.Q.; Lin, D.X.; Liu, C.H.; Jiang, Z.K. Allocation pattern of biomass and productivity in the mixed uneven-aged stands of Masson’s pine and hardwood species. Acta Ecol. Sin. 2006, 26, 2463–2473. [Google Scholar]
- Lai, G.Z.; Cao, M.; Pan, P.; Ouyang, X.Z.; Guo, R.; Xiang, Y.X.; Wu, Z.R. Carbon density of vegetation of mixed plantation of Pinus massoniana and Schima superba in different proportions. J. Cent. South Univ. For. Tech. 2018, 38, 108–113. [Google Scholar]
- Fang, Y.T.; Mo, J.M.; Peng, S.L.; Li, D.J. Role of forest succession on carbon sequestration of forest ecosystems in lower subtropical China. Acta Ecol. Sin. 2003, 23, 1685–1694. [Google Scholar]
- Gong, C.; Wang, S.L.; Zeng, Z.Q.; Deng, S.J.; Chen, J.P.; Long, K.S. Carbon storage and its distribution pattern of evergreen broad-leaved forests at different succession stages in mid-subtropical China. Chin. J. Ecol. 2011, 30, 1935–1941. [Google Scholar]
- Fu, W.J.; Fu, Z.J.; Ge, H.L.; Ji, B.Y.; Jiang, P.K.; Li, Y.F.; Wu, J.S.; Zhao, K.L. Spatial variation of biomass carbon density in a subtropical region of southeastern China. Forests 2015, 6, 1966–1981. [Google Scholar] [CrossRef]
- Pan, P.; Zhao, F.; Ning, J.K.; Zhang, L.; Ouyang, X.Z.; Zang, H. Impact of understory vegetation on soil carbon and nitrogen dynamic in aerially seeded Pinus massoniana plantations. PLoS ONE 2018, 13, e0191952. [Google Scholar] [CrossRef] [PubMed]
- Dai, W.; Fu, W.J.; Jiang, P.K.; Zhao, K.L.; Li, Y.H.; Tao, J.X. Spatial pattern of carbon stocks in forest ecosystems of a typical subtropical region of southeastern China. Forest Ecol. Manag. 2018, 409, 288–297. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Sui, Y.Y.; Zhang, X.D.; Meng, K.; Herbert, S.J. Spatial variability of nutrient properties in black soil of northeast China. Pedosphere 2007, 17, 19–29. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.M.; Jin, B.; Qu, M. Carbon storage and density of forest vegetation and its spatial distribution pattern in Shanxi province. J. Arid Land Resour. Environ. 2014, 28, 69–73. [Google Scholar]
- Zhang, F.; Du, Q.; Ge, H.L.; Liu, A.X.; Fu, W.J.; Ji, B.Y. Spatial distribution of forest carbon in Zhejiang Province with geostatistics based on CFI sample plots. Acta Ecol. Sin. 2012, 32, 5275–5286. [Google Scholar] [CrossRef]
- Rahman, M.M.; Khan, M.N.I.; Hoque, A.F.; Ahmed, I. Carbon stock in the Sundarbans mangrove forest: Spatial variations in vegetation types and salinity zones. Wetl. Ecol. Manag. 2015, 23, 269–283. [Google Scholar] [CrossRef]
- Swetnam, T.L.; Brooks, P.D.; Barnard, H.R.; Harpold, A.A.; Gallo, E.L. Topographically driven differences in energy and water constrain climatic control on forest carbon sequestration. Ecosphere 2017, 8, e01797. [Google Scholar] [CrossRef]
- Wen, D.; He, N. Forest carbon storage along the north-south transect of eastern China: Spatial patterns, allocation, and influencing factors. Ecol. Indic. 2016, 61, 960–967. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, X.; Chuai, X.; Yang, H.; Lai, L.; Tan, J. Impact of land use type conversion on carbon storage in terrestrial ecosystems of China: A spatial-temporal perspective. Sci. Rep. 2015, 5, 10233. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Yang, R.; Dong, Y.X.; Liu, Y.X.; Qiu, L.R. The influence of rapid urbanization and land use changes on terrestrial carbon sources/sinks in Guangzhou, China. Ecol. Indic. 2016, 70, 304–316. [Google Scholar] [CrossRef]
- Ford, S.E.; Keeton, W.S. Enhanced carbon storage through management for old-growth characteristic in northern hardwood-conifer forests. Ecosphere 2017, 8, e01721. [Google Scholar] [CrossRef]
- Chen, L.C.; Guan, X.; Li, H.M.; Wang, Q.K.; Zhang, W.D.; Yang, Q.P.; Wang, S.L. Spatiotemporal patterns of carbon storage in forest ecosystems in Hunan Province, China. For. Ecol. Manag. 2019, 432, 656–666. [Google Scholar] [CrossRef]
- Lal, R. Carbon sequestration. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 815–830. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.M.; Zhang, G.L.; Yang, F.; Zhi, J.J.; Yang, F.; Liu, F.; Zhao, Y.G.; Li, D.C. Precise estimation of soil organic carbon stocks in the northeast Tibetan plateau. Sci. Rep. 2016, 6, 21842. [Google Scholar] [CrossRef] [PubMed]
| Factors | Mean | Standard Deviation |
|---|---|---|
| Elevation (m) | 209 | 186.56 |
| Slope (°) | 20 | 10.53 |
| Soil depth (cm) | 76 | 27.62 |
| Stand age (a) | 24 | 10.60 |
| Stand density (N·ha−1) | 1567 | 905.14 |
| Understory vegetation coverage (%) | 68 | 10.02 |
| Mean annual temperature (°C) | 18.5 | 1.09 |
| Mean annual precipitation (mm) | 1645 | 174.66 |
| Variables | Mean | Standard Deviation | |
|---|---|---|---|
| Tree layer | Stem | 24.37 | 16.78 |
| Branch | 8.94 | 4.06 | |
| Foliage | 5.76 | 3.47 | |
| Root | 6.61 | 4.73 | |
| Total | 45.68 | 31.98 | |
| Understory vegetation layer | 4.53 | 2.44 | |
| Litter layer | 1.81 | 0.92 | |
| Item | Mean | SD | CV (%) | Skew | Kurt | K–Sp |
|---|---|---|---|---|---|---|
| Carbon density | 52.02 | 34.51 | 66.34 | 1.53 (0.39) | 4.34 (0.69) | 0.000 (0.054) |
| Factors | Elevation | Slope | Slope Position | Soil Aspect | Stand Age | Stand Density | Understory Vegetation Coverage | Mean Annual Temperature | Mean Annual Precipitation |
|---|---|---|---|---|---|---|---|---|---|
| Carbon density | 0.261 ** | −0.115 ** | 0.095 * | 0.086 * | 0.302 ** | 0.145 ** | 0.140 ** | −0.106 ** | 0.270 ** |
| Elevation | −0.358 ** | 0.207 ** | 0.166 ** | 0.067 | 0.007 | 0.090 * | 0.199 ** | 0.119 ** | |
| Slope | −0.113 ** | −0.058 | −0.031 | −0.008 | −0.128 ** | −0.032 | −0.079 * | ||
| Slope position | 0.029 | 0.049 | 0.093 * | 0.042 | −0.014 | 0.028 | |||
| Soil aspect | −0.008 | 0.085 * | 0.017 | −0.065 | 0.052 | ||||
| Stand age | −0.039 | 0.063 | 0.008 | 0.084 * | |||||
| Stand density | 0.038 | −0.040 | 0.051 | ||||||
| Understory Vegetation Coverage | −0.123 ** | 0.183 ** | |||||||
| Mean annual Temperature | −0.404 ** |
| Model Type | Nugget | Sill | Range/(km) | Nugget/Sill | RSS | R2 |
|---|---|---|---|---|---|---|
| Linear model | 9.02 | 11.01 | 313.05 | 0.82 | 31.4 | 0.143 |
| Spherical model | 4.87 | 10.72 | 103.60 | 0.45 | 9.5 | 0.742 |
| Exponential model | 3.08 | 10.69 | 29.80 | 0.29 | 12.0 | 0.672 |
| Gaussian model | 5.38 | 10.77 | 49.50 | 0.50 | 9.9 | 0.736 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, P.; Sun, Y.; Ouyang, X.; Zang, H.; Rao, J.; Ning, J. Factors Affecting Spatial Variation in Vegetation Carbon Density in Pinus massoniana Lamb. Forest in Subtropical China. Forests 2019, 10, 880. https://doi.org/10.3390/f10100880
Pan P, Sun Y, Ouyang X, Zang H, Rao J, Ning J. Factors Affecting Spatial Variation in Vegetation Carbon Density in Pinus massoniana Lamb. Forest in Subtropical China. Forests. 2019; 10(10):880. https://doi.org/10.3390/f10100880
Chicago/Turabian StylePan, Ping, Yujun Sun, Xunzhi Ouyang, Hao Zang, Jinfeng Rao, and Jinkui Ning. 2019. "Factors Affecting Spatial Variation in Vegetation Carbon Density in Pinus massoniana Lamb. Forest in Subtropical China" Forests 10, no. 10: 880. https://doi.org/10.3390/f10100880





