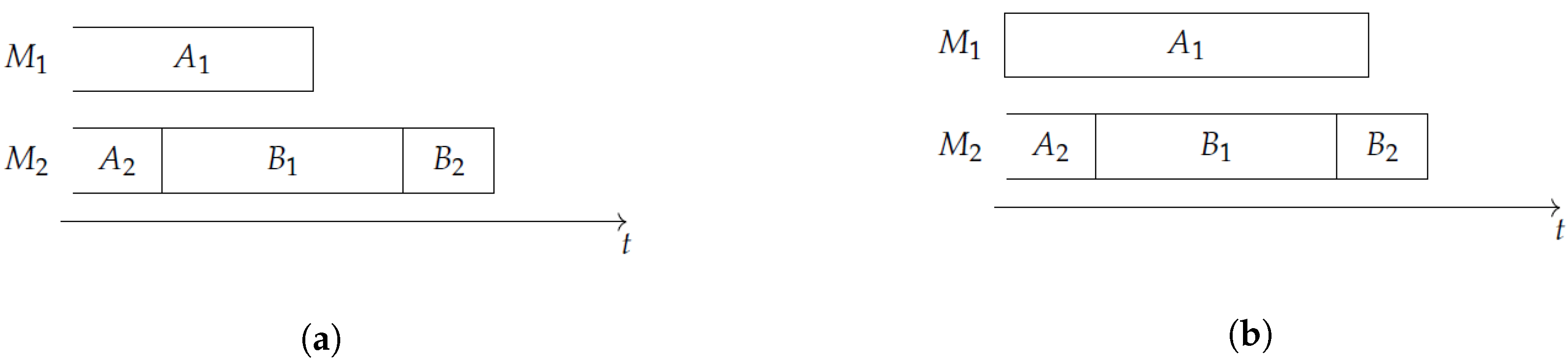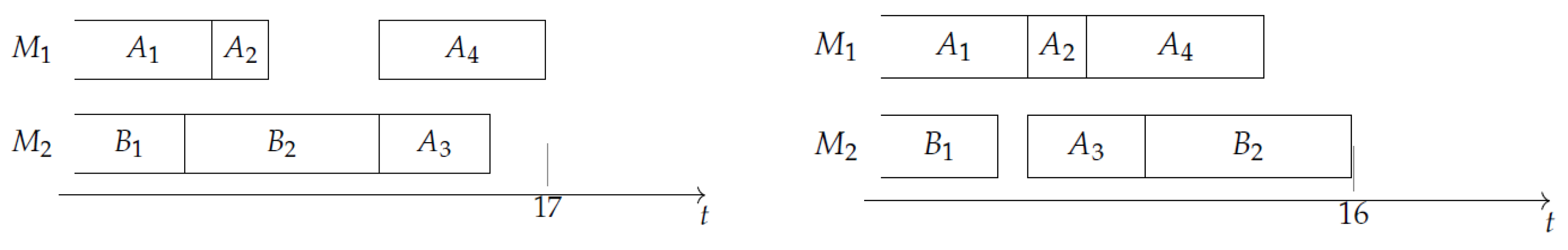1. Introduction
This paper addresses a variant of classical shop scheduling models. While, in classical job shop or flow shop (as well as in the large majority of scheduling problems with precedence constraints), the task of a job cannot start before the previous task of the same job has
finished, we address a situation in which each task of a job cannot start before the previous task of the same job has
started. These types of constraints are known in the literature as
s-precedence constraints. Scheduling problems with s-precedence constraints have been introduced by Kim and Posner [
1] in the case of parallel machines. They showed that makespan minimization is NP-hard, and developed a heuristic procedure deriving tight worst-case bounds on the relative error. Kim, Sung, and Lee [
2] performed a similar analysis when the objective was the minimization of total completion time of the tasks, while Kim [
3] extended the analysis to uniform machines. Tamir [
4] analyzed a parallel-machine problem in which traditional finish–start precedence constraints coexisted with s-precedence constraints (that she renamed
selfish precedence constraints, giving an enjoyable dramatized motivation of the model), and established various worst-case bounds for classical dispatching rules which refer to specific structures of precedence constraints. Indeed, s-precedence constraints also arise in project management, called
start–start precedence constraints (Demeulemeester and Herroelen [
5]), as a result of the elaboration of a work breakdown structure (WBS) and of the coordination among different operational units. To our knowledge, none has addressed job shop and flow shop problems with s-precedence constraints so far.
The problem can be formally introduced as follows. We are given a set of n h, to be processed on a shop with m machines denoted as . Each job consists of a totally ordered set of tasks, , . Task requires processing time on a given machine , . Tasks cannot be preempted. Task can only start after task is started; i.e., there is an s-precedence constraint between tasks and , for all , . A schedule is an assignment of starting times to all tasks so that at any time each machine processes at most one task and all s-precedence constraints are satisfied. The problem is to find a feasible schedule that minimizes makespan.
We characterize the complexity of special cases of the problem, considering a fixed number of jobs and machines. Shop problems with few jobs occur when modeling synchronization and conflicts among processes share common resources. Examples of this situation include scheduling robot moves in flexible robotic cells (Agnetis et al. [
6]), aircraft scheduling during taxiing at an airport so that no aircraft collides (Avella et al. [
7]), or, in container terminals, the synchronization of crane gantry movements once transportation tasks have been assigned (Briskorn and Angeloudis [
8]).
The structure of the paper is as follows. In
Section 2 we consider the job shop scenario, and give a polynomial time algorithm for the problem in which
,
, and each job can visit the machines several times (that is,
recirculation [
9] is allowed). In
Section 3 we focus on the flow shop scenario. We show that the two-machine flow shop can be solved in linear time and we give a polynomial time algorithm for the
m-machine problem with two jobs. In
Section 4 we briefly discuss cases with
and point out open problems.
2. The Job Shop with Two Jobs and Two Machines
In this section we describe a polynomial algorithm for the job shop problem with two jobs and two machines; i.e., . For notation simplicity, in this section we denote the two jobs as A and B, consisting of the sequence of tasks, and , respectively. Task () requires processing time () on machine ().
Obviously, if two consecutive tasks of the same job, say, and , require the same machine, then has to wait for the completion of , but if the machines required by the two operations are different, i.e., , then can start even if has not completed yet. So, unlike the classical job shop setting in which precedence relations are finish-start, in our model it may actually happen that even completes before (the same of course applies to job B).
Given a partial schedule, the first unscheduled tasks of the two jobs will be referred to as the available tasks. Suppose now that one of the two machines, say , has just completed a task, while the other machine, say , is still busy. If both the available tasks require , we say that machine is blocked and this certainly results in idle time on .
We let and denote the first i tasks of A and the first h tasks of B; i.e., and .
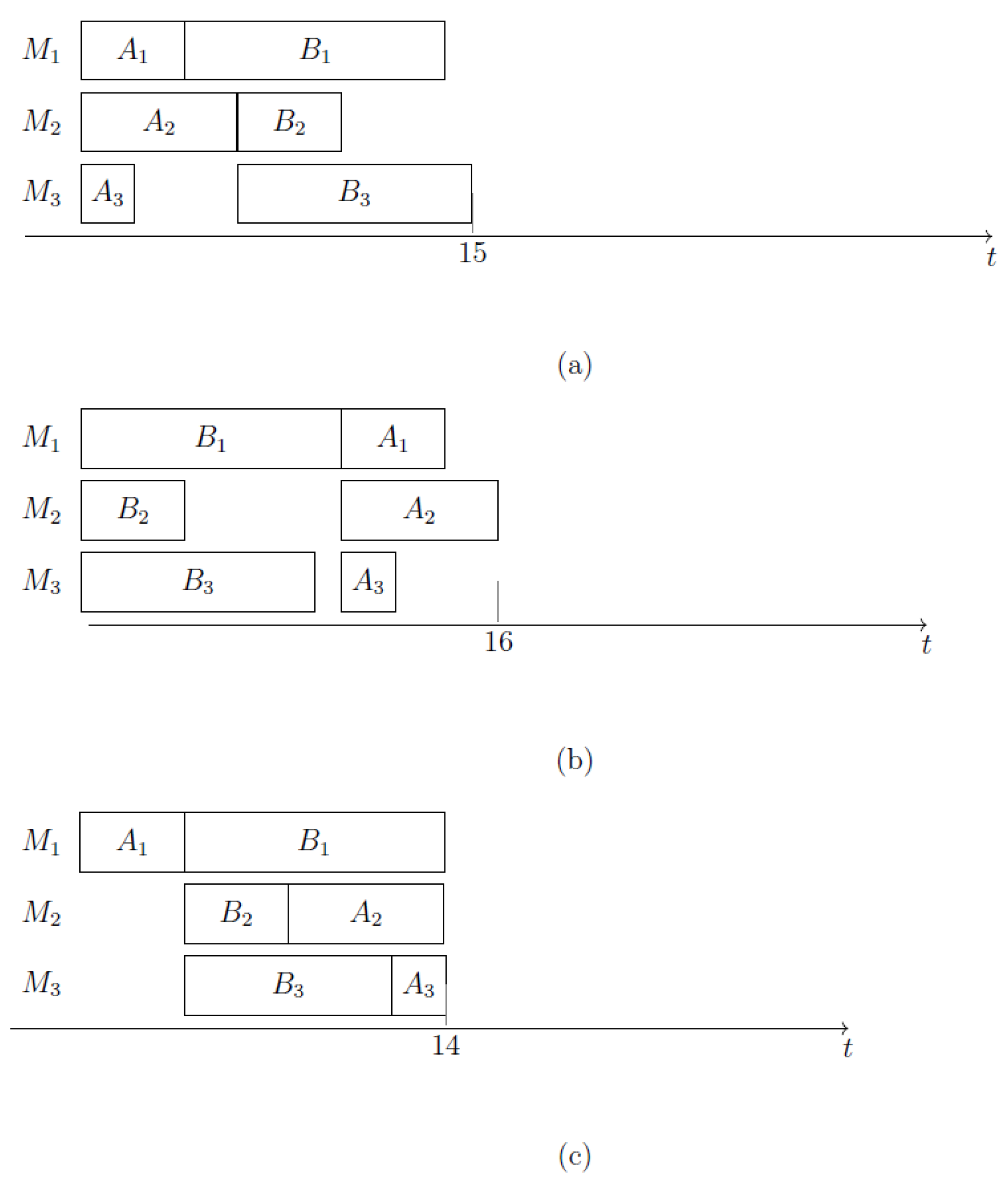
Given A and B, consider any two task subsequences and . We want to characterize the schedules of such that each task starts right after the previous task on the same machine has completed. More formally, a schedule of is a no-idle subschedule (NIS) if, across the span of such a subschedule, the only machine idle time occurs, on one machine, after all the tasks of have started. When and , for some and , then we say that the NIS is an initial no-idle subschedule (INIS).
Consider
Figure 1 and the task set
. The subschedule in
Figure 1a is
not an INIS for
, since on
there is idle time before
starts. On the contrary, in the case depicted in
Figure 1b, the subschedule of
is an INIS. Note that if we restrict our attention to the task set
, then the subschedule in
Figure 1a is an INIS.
2.1. Generating Initial No-Idle Subschedules
We denote by
and
, the subset of tasks of
and
respectively, requiring machine
,
; i.e.,
We also let
and
indicate the total processing time of tasks in
and
; i.e.,
If an INIS of tasks
exists, its makespan is given by
Proposition 1. In any optimal schedule, there are indices i and h such that the subschedule involving tasks is an INIS.
In fact, given an optimal schedule, consider the subschedule of the tasks scheduled on the two machines from time 0 to the end of the first idle interval of the schedule, assuming, e.g., that such an idle interval occurs on . If the subschedule is not an INIS, we can iteratively remove the last task scheduled on in the subschedule, until the definition of INIS is met.
In view of Proposition 1, we are only interested in schedules in which the initial part is an INIS. However, not all initial no-idle subschedules are candidates to be the initial part of an optimal schedule.
We first address the following question. Can we determine all operation pairs such that an INIS of exists? We show next that this question can be answered in polynomial time.
The idea is to build the no-idle partial schedules from the beginning of the schedule onward. To this aim, let us define an unweighted graph G, which we call initial no-idle graph. Nodes of G are denoted as , representing a NIS of (for shortness, we use also to denote the corresponding INIS). If the schedule obtained appending to schedule is still an INIS, we insert node and an arc from to in G. Symmetrically, if the schedule obtained appending to is an INIS, we insert and an arc from to in G.
As illustrated later on (cases below), while building the graph G, we can also determine whether or not a certain INIS can be the initial part of an optimal schedule. If it can, we call it a target node.
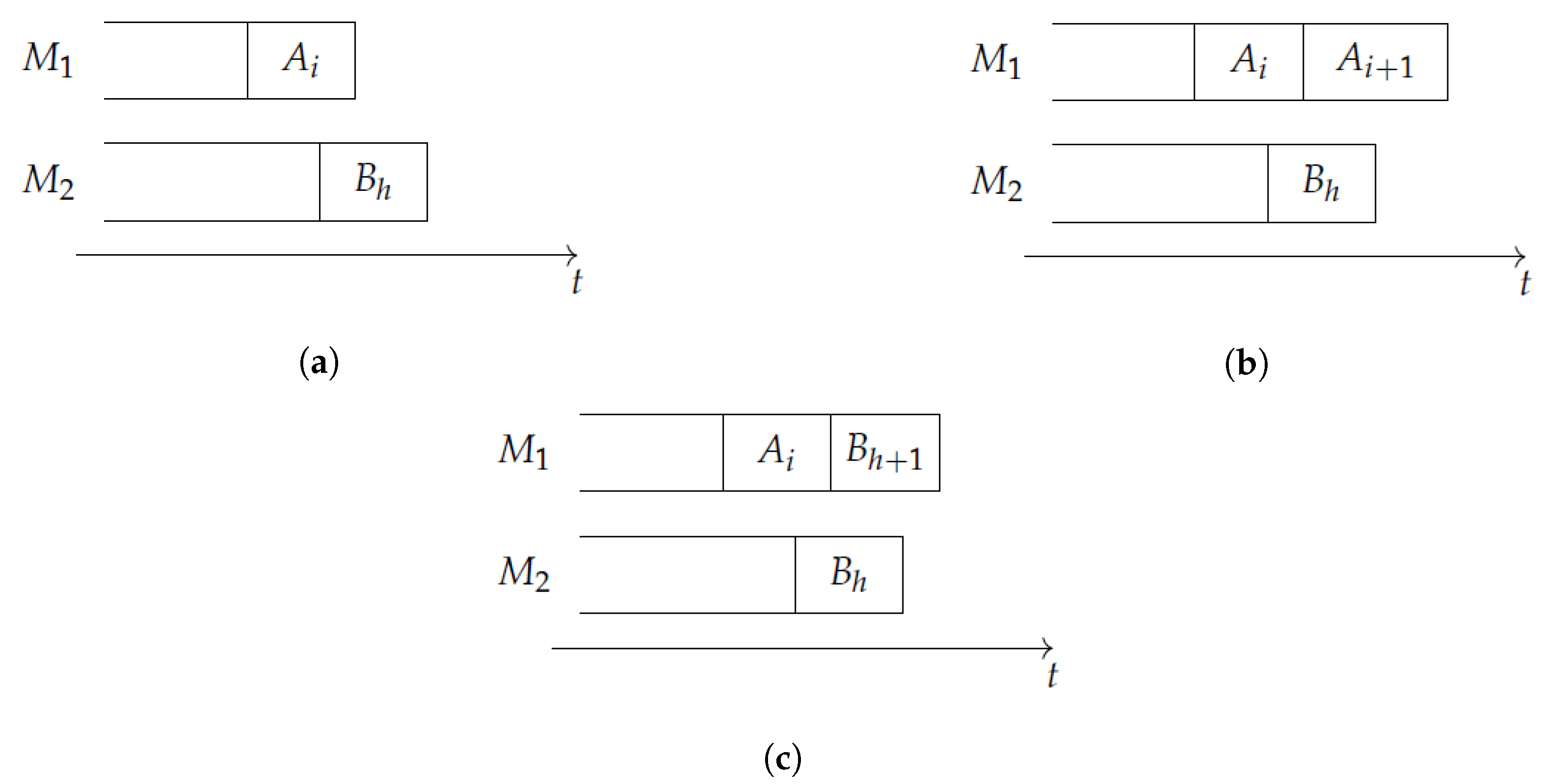
Consider any node in G, and the machine completing soonest in the INIS. Ties can be broken arbitrarily, but to fix ideas, suppose that is still busy when completes. (Note that, since there is no idle time, completes at time .) If and , the two available tasks are and , and four cases can occur.
. In this case,
is necessarily idle until
completes (
Figure 2a). Hence, there is no way to continue an INIS, and therefore node
has no outgoing arcs. In this case,
is a target node.
and
. In this case, when
completes, the only way to continue an INIS is to start task
on
(
Figure 2b). Thus we generate node
and the arc from
to
, which is the only outgoing arc of
. In this case as well,
is a target node.
and
. A symmetrical discussion to the previous case holds; i.e., the only way to continue an INIS is to start task
on
(
Figure 2c), so we generate node
and the arc from
to
, which is the only outgoing arc of
. In this case also,
is a target node.
. In this case, the INIS can be continued in two possible ways; i.e., scheduling either
or
on
(
Figure 2b,c respectively). Therefore,
has two outgoing arcs, pointing towards nodes
and
, respectively. However, in this case
is
not a target node, since there is no point in keeping
idle until the completion of
.
Clearly, if completes before , in the four above cases the roles of and are exchanged. If either or , the above cases simplify as follows, where we assume that ; i.e., job B is finished. (A symmetric discussion holds in .)
. In this case, we can continue an INIS starting task on . Thus we generate node and the arc from to , which is the only outgoing arc of . Node is a target node.
. In this case, is necessarily idle until completes. Hence, there is no way to continue an INIS, and therefore node has no outgoing arcs. In this case, is a target node.
Again, the roles of the two machines are exchanged if frees up before in the partial schedule.
In conclusion, the question of whether a NIS exists for the task set is equivalent to asking whether node can be reached from the dummy initial node on G.
A few words on complexity. Clearly, G has nodes, and each node has at most two outgoing arcs. The graph G can be built very efficiently. In fact, for each node , it can be checked in constant time, which condition holds among – (or – when one of the jobs is over), and hence whether or not it is a target node.
2.2. Minimizing the Makespan
Now we can address the main question. How to schedule the tasks on the two machines so that the overall makespan is minimized. The key idea here is that any active schedule can be seen as the juxtaposition of no-idle subschedules. In fact, suppose that after processing a certain task , one machine stays idle until the other machine completes task . It is important to observe that this may happen for one of two reasons:
When a machine completes, it is blocked because both available tasks require the other machine;
When a machine completes, there is one task the machine can process, but it might be profitable to wait for the other machine to free up another task.
Note that in both of these two cases is a target node of G. On the contrary, if a machine completes a task while the other machine is still busy, and both available tasks require that machine (i.e., is not a target node of G), with no loss of generality we can assume that the machine will immediately start one of them, since otherwise the schedule might turn out non-active (there is no point in waiting for the other machine to complete its task).
If t denotes the makespan of an INIS, the schedule after t is completely independent from the schedule before t. In other words, the optimal solution from t onward is the optimal solution of a problem in which t is indeed time 0, and the two jobs are and . Hence, to address the overall problem, the idea is to build another, higher-level graph in which the arcs specify portions of the overall schedule.
Suppose that is a target node of graph G, and consider the task sets and . We can build a new no-idle graph on these sets, and call it . (Correspondingly, the graph previously denoted as G can be renamed .) Suppose that is a target node in graph . This means that the tasks of the set form a NIS, that we denote by . It is convenient to extend the previous notation, letting denote the set of tasks of that require machine , and analogously we let be the set of tasks of that require . Their total processing times are denoted as and . (The set previously denoted as should now be written .)
We next introduce the (weighted) graph
as follows. As in
G, nodes denote task pairs
. There is an arc
if
is a target node in the graph
; i.e., if the NIS
exists. Such an arc
is weighted by the length of the corresponding NIS; i.e.,
Moreover, contains a (dummy) initial node while the final node is . At this point the reader should have no difficulty in figuring out that the following theorem holds.
Theorem 1. Given an instance of , the optimal schedule corresponds to the shortest path from to on , and its weight gives the minimum makespan.
Now, let us discuss complexity issues. The graph can indeed be generated starting from , and moving schedules forward. From each node of , we can generate the corresponding no-idle graph , and add to all target nodes of . We then connect node in to each of these nodes, weighing the arc with the corresponding length of the NIS. If a target node was already present in , we only add the corresponding new arc. Complexity analysis is, therefore, quite simple. There are nodes in . Each of these nodes has a number of outgoing arcs, whose weight can be computed in . Clearly, finding the shortest path on is not the bottleneck step, and therefore, the following result holds.
Theorem 2. can be solved in .
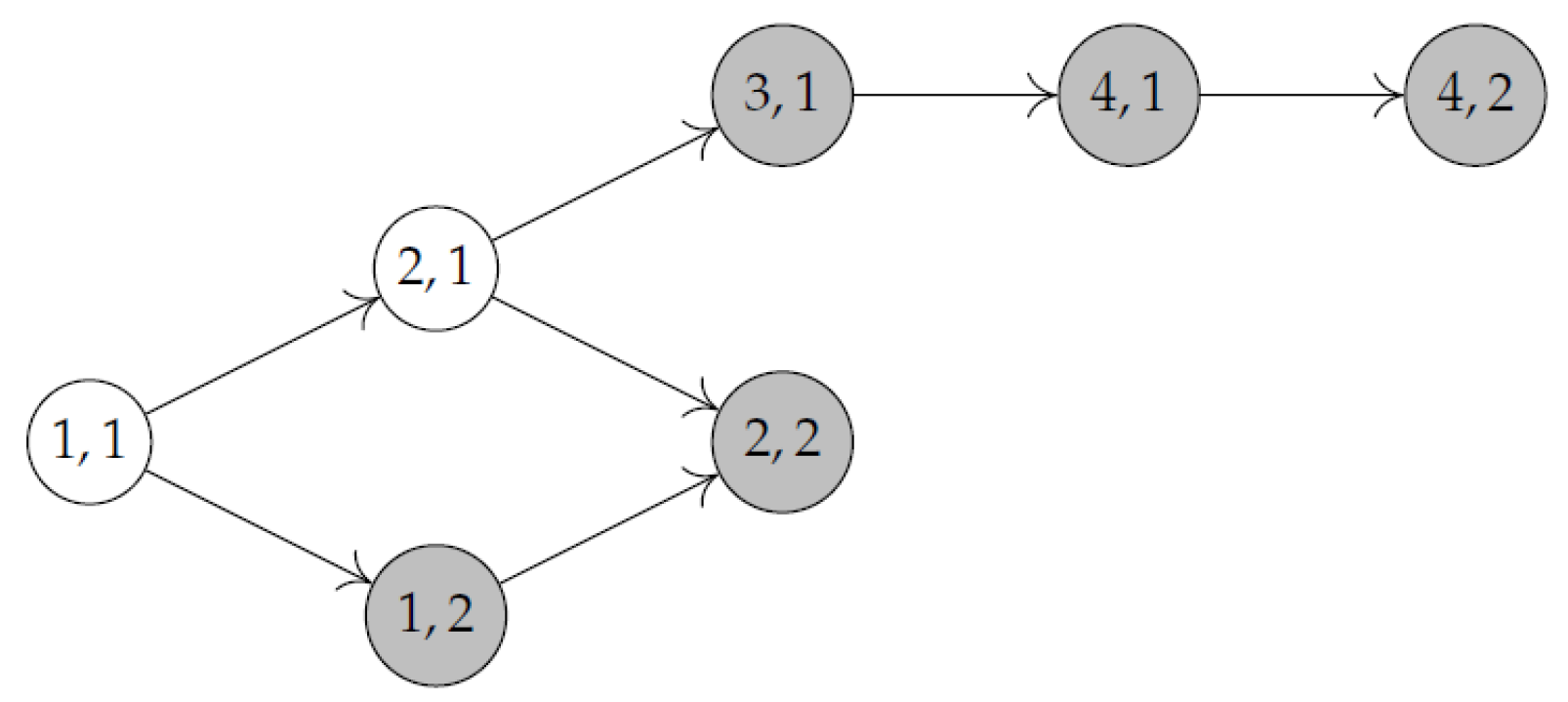
Example 1. Consider the following instance, in which job A has four tasks and job B two tasks. Figure 3a depicts the graph , in which all nodes are target nodes. Figure 3b shows the INIS . At the end of this INIS, machine is blocked, since the next task of A requires and job B is already finished. Notice that is the longest INIS which can be built, but the optimal solution does not contain it. Figure 4a shows the best schedule which can be attained when the INIS , having makespan 17. Figure 4b shows the optimal schedule, having makespan 16. The optimal schedule consists of two no-idle subschedules; namely, the INIS (containing tasks and and corresponding to arc on ), and the NIS (containing tasks and and corresponding to arc on ). For illustrative purposes, Figure 5 shows the graph . Notice that in such a graph, (2,1) is not
a target node. 3. Flow Shop
In this section we consider the flow shop problem, i.e., , in which the job set J contains n jobs, and job requires processing time on machine (here we use index j for both tasks and machines, as there is exactly one task per machine). While in the classical problem a job cannot start on machine before it is completed on , in , a job can start on machine as soon as it is started on .
3.1. Two-Machine Flow Shop ()
We next consider the two-machine flow shop problem, so and denote the processing times of job on and respectively, . Note that, as in the classical , with no loss of generality we can assume that in any feasible schedule the machine processes all the jobs consecutively with no idle time between them. We next show that problem can be solved in linear time.
Proposition 2. Given an instance of , there always exists a schedule having makespan , which is therefore optimal.
Proof. Given an instance of , partition the jobs into two sets, and , such that and . Then, build by scheduling, on both machines, first all jobs of in arbitrary order, and then all jobs of , also in arbitrary order. If we let and denote the completion time of the last job of on and respectively, one has . From the definition of , one gets that up to , no idle time occurs on . From then on, all jobs of are scheduled, and two cases may occur. No idle time ever occurs on , in which case the makespan equals . Some idle time occurs on . Consider the first time that is idle and is still processing a job . Upon completion of , the two machines will simultaneously start the next job, say, , but since , will still be processing it while returns idle. Since all remaining jobs belong to , this will happen for each job until the end of the schedule. In particular, when the last job is scheduled, again, completes first, so in conclusion, the makespan of is . ☐
The above proof contains the solution algorithm. For each job , put it into if and in otherwise. Then, schedule all jobs of followed by all jobs of (in any order). Since establishing whether a job belongs to or can be done in constant time, and since jobs can be sequenced in arbitrary order within each set, we can conclude with the following result.
Theorem 3. can be solved in .
While appears even simpler than the classical , one may wonder whether other simplifications occur for . While the complexity status of is open, we point out a difference between and , which may suggest that the problem with s-precedence constraints is not necessarily easier than the classical counterpart.
It is well known [
10] that in
there always exists an optimal schedule in which the job sequences on
and
are identical, and the same holds for machines
and
. (As a consequence, for
the optimal schedule is a permutation schedule.) This is no more true in
, even with only two jobs.
Example 2. Consider an instance with three machines and two jobs, A and B: Scheduling the jobs in the order AB on all three machines, one gets , and the makespan is attained on machine (see Figure 6a). If they are scheduled in the order BA on all three machines, , and in this case the value of the makespan is attained on (Figure 6b). If jobs are scheduled in the order AB on and BA on and , then (all three machines complete at the same time, Figure 6c), and this is the optimal schedule. 3.2. Flow Shop with Two Jobs and m Machines ()
In what follows we give an Algorithm 1 that solves . Again we denote the two jobs with A and B, and by and the processing time of jobs A and B on machine , , respectively. Notice that a schedule is fully specified by the order of the two jobs on each machine, either AB or BA. In what follows, for a given schedule and a given machine, we call leader the job scheduled first and follower the other job. So if, on a given machine, the jobs are sequenced in the order AB, then, on that machine, A is the leader and B is the follower.
| Algorithm 1 For finding a schedule with if it exists. |
- 1:
Initialize ; - 2:
fordo - 3:
for do - 4:
Compute , , and via ( 1), ( 2), ( 3) and ( 4) respectively; - 5:
end for - 6:
end for - 7:
fordo - 8:
Compute and via ( 5) and ( 6); - 9:
end for - 10:
if or then - 11:
; - 12:
else - 13:
. - 14:
end if
|
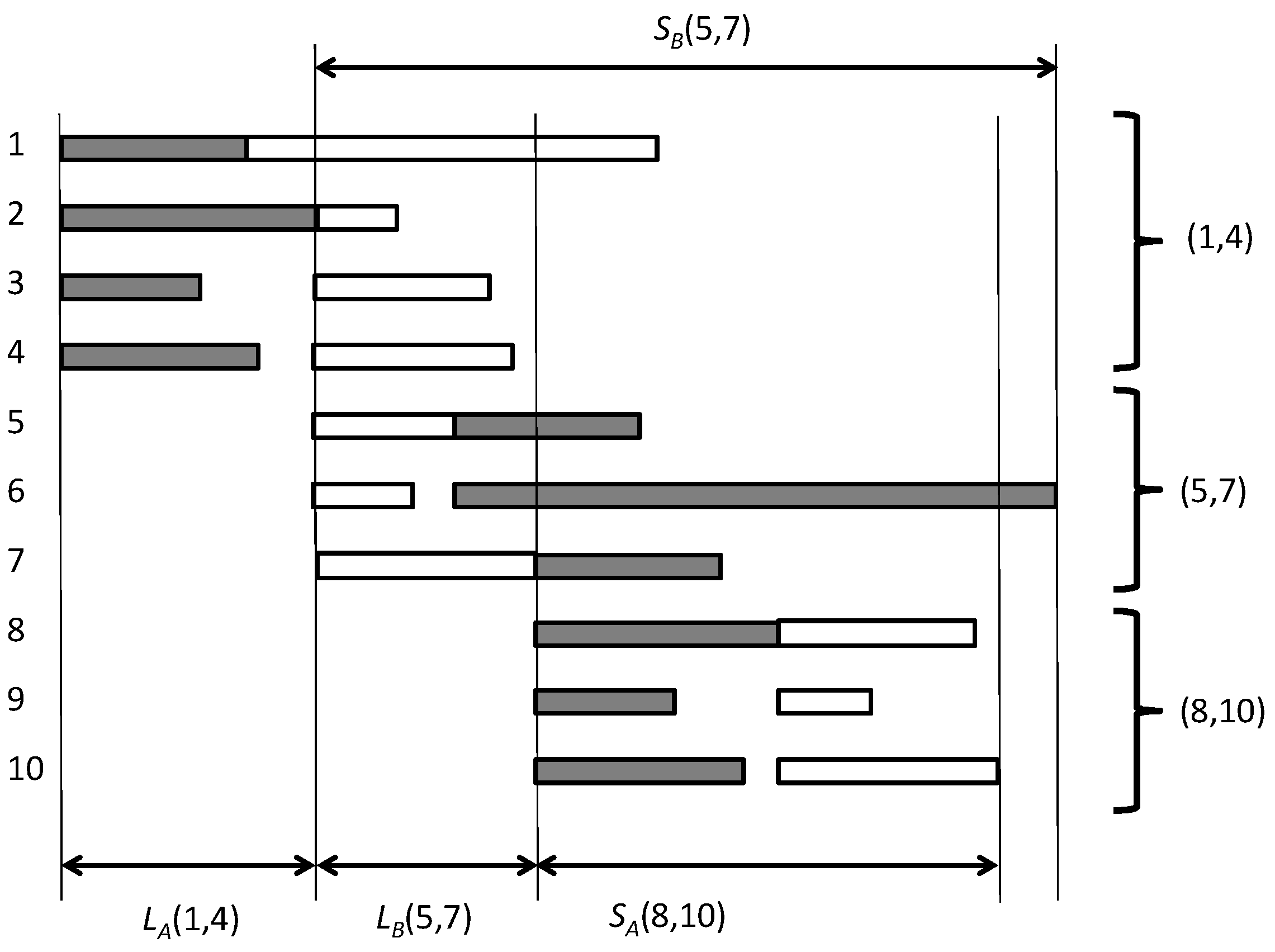
Given any feasible schedule, we can associate with it a decomposition of the
m machines into
blocks, each consisting of a maximal set of consecutive machines in which the two jobs are scheduled in the same order. We denote the block consisting of machines
as
(see
Figure 7). In a block, due to the s-precedence constraints, all the tasks of the leader job start at the same time. Given a block
, we can compute a number of quantities. (Assume for the moment that
.) If, in
, A is the leader, then we call
leader span the length of the longest
A-task in the block, and denote it with
:
and similarly, if B is the leader, the leader span is given by:
Notice that, due to the definition of block, in the block that follows , the roles of leader and follower are exchanged. Hence, the time at which the leader completes its longest task in is also the start time of the other job’s tasks in the next block.
Given a block
, suppose again that A is the leader. We let
indicate the
span of block
; i.e., the difference between the maximum completion time of a B-task and the start time of all A-tasks in
. This is given by:
and exchanging the roles of leader and follower in
, we get
Notice that trivial lower and upper bounds for the minimum makespan are given by
and
respectively. In what follows we address the problem of determining a schedule having a makespan not larger than
K, or prove that it does not exist. Assuming that all processing time values are integers, a binary search over the interval
allows one to establish the value of the minimum makespan.
As we already observed, a relevant difference between and is that, in a feasible schedule for , the value of may not be attained on the last machine, but rather on any machine. This fact requires carefully handling by the algorithm.
Let be the minimum sum of leader spans of all blocks from to , when A is the leader of the last block (i.e., the block including ). Similarly, is the same when B is the leader of the last block. In order to write a functional equation for and , we introduce the notation if and if .
Hence, we write
The first terms accounts for the fact that in the previous block the leader is B, while the rightmost term (
) rules out solutions in which the sum of the start time of the last block and the span of the block itself exceeds
K. Symmetrically, one has:
Expressions (
5) and (
6) are computed for
. If at least one of the values
and
has a finite value, a schedule of makespan not exceeding
K exists. The values of machine index for which each minimum in (
5) and (
6) is attained define the blocks of the schedule, which can, therefore, be easily backtracked.
Equations (
5) and (
6) must be initialized, simply letting
.
Notice that in general one cannot infer the value of the minimum makespan schedule directly from this procedure. If the minimum in the computation of
has been attained for, say, machine
, it does not imply that
is indeed the minimum makespan. This is because the overall makespan may be due to a previous machine, and the algorithm has no control on this aspect. For instance, in the sample schedule of
Figure 7 the makespan is attained on machine
. However, its actual value has no relevance, so long as it does not exceed
K, since it does not affect the values
and
subsequently computed.
Concerning complexity, each computation of (
5) and (
6) requires
comparisons. Since the whole procedure is repeated at each step of a binary search over
, the following result holds.
Theorem 4. Problem can be solved in .