Parametric Study on Effective Thermal Conductivity of Dispersed Disks with Internal Heat Sources
Abstract
1. Introduction
2. Modeling
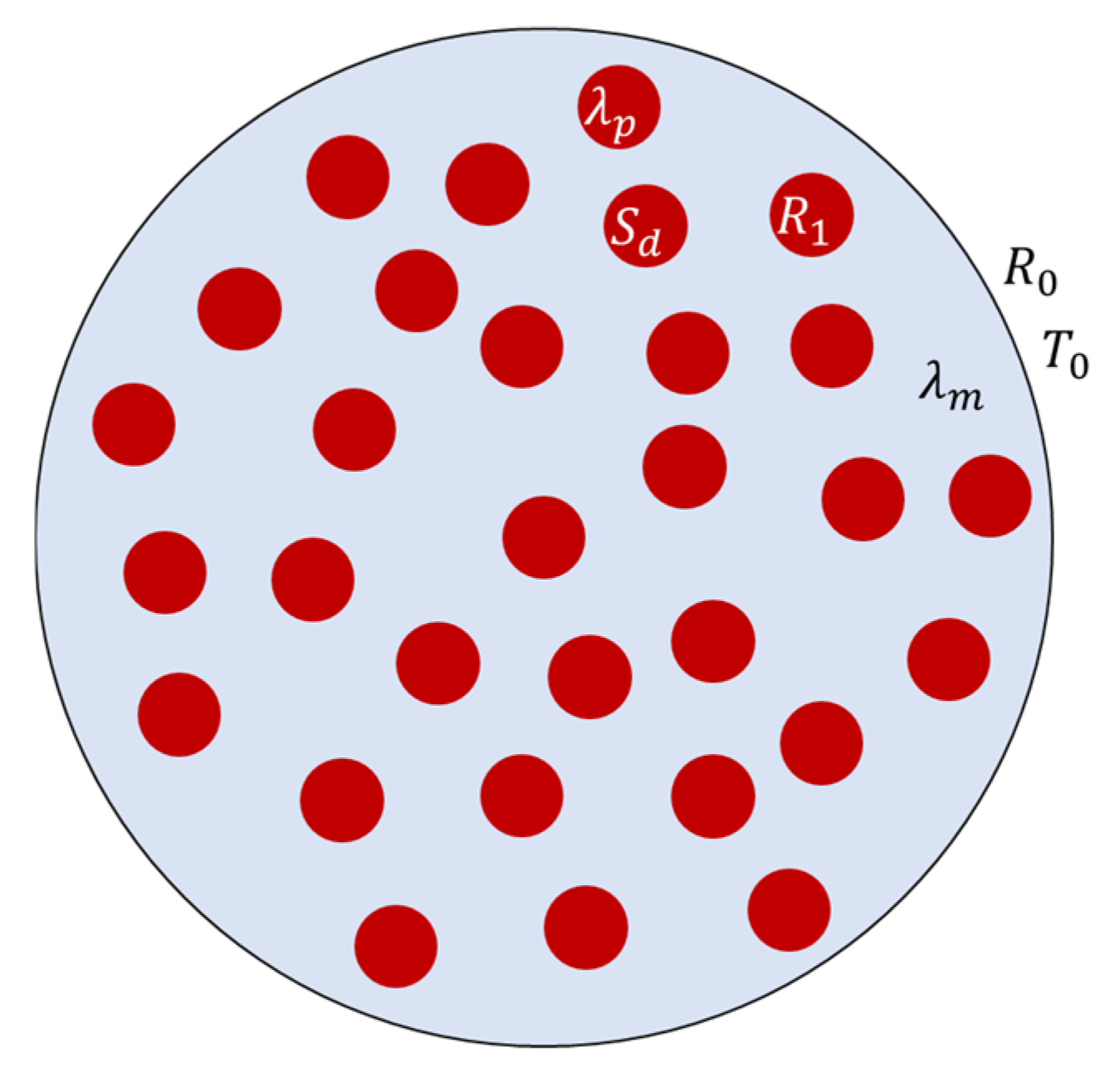
2.1. Numerical Model
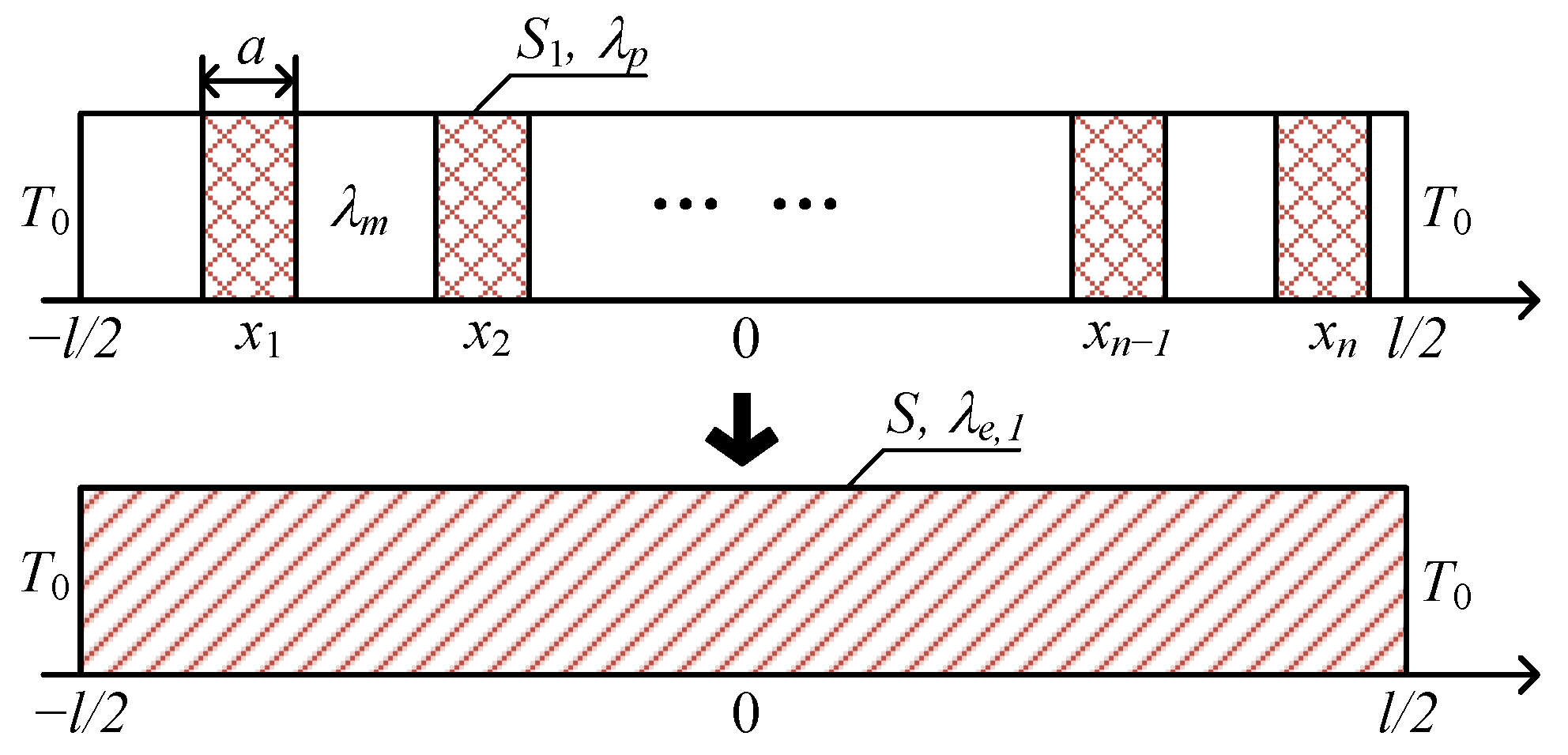
2.1.1. Procedure
- (1)
- The centers of the heat-generating small disks were randomly generated within the large disk, following a uniform distribution, meaning that each position inside the large disk had the same probability. During the generation process, the relative positions of all small disks were checked to ensure that no small disk touched the boundary of the large disk or overlapped with another small disk.
- (2)
- Based on the radius of the large disk, the radius of the small disks, and their coordinates, the geometry and mesh are constructed in COMSOL Multiphysics, followed by a steady-state simulation [29].
- (3)
- The average temperature of the dispersed disk domain is obtained through post-processing, and the corresponding ETC is calculated.
- (4)
- Steps (1)–(3) are repeated 1000 times under the same set of macroscopic parameters, generating 1000 random configurations of disk positions.
- (5)
- The mean value of the 1000 ETC results is taken as the nominal ETC under the given conditions, which helps reduce deviations caused by randomness in individual simulations.
2.1.2. Mesh Independence
2.1.3. Heat Source and Boundary Temperature Independence
2.2. Maxwell–Eucken Model
3. Results and Analysis
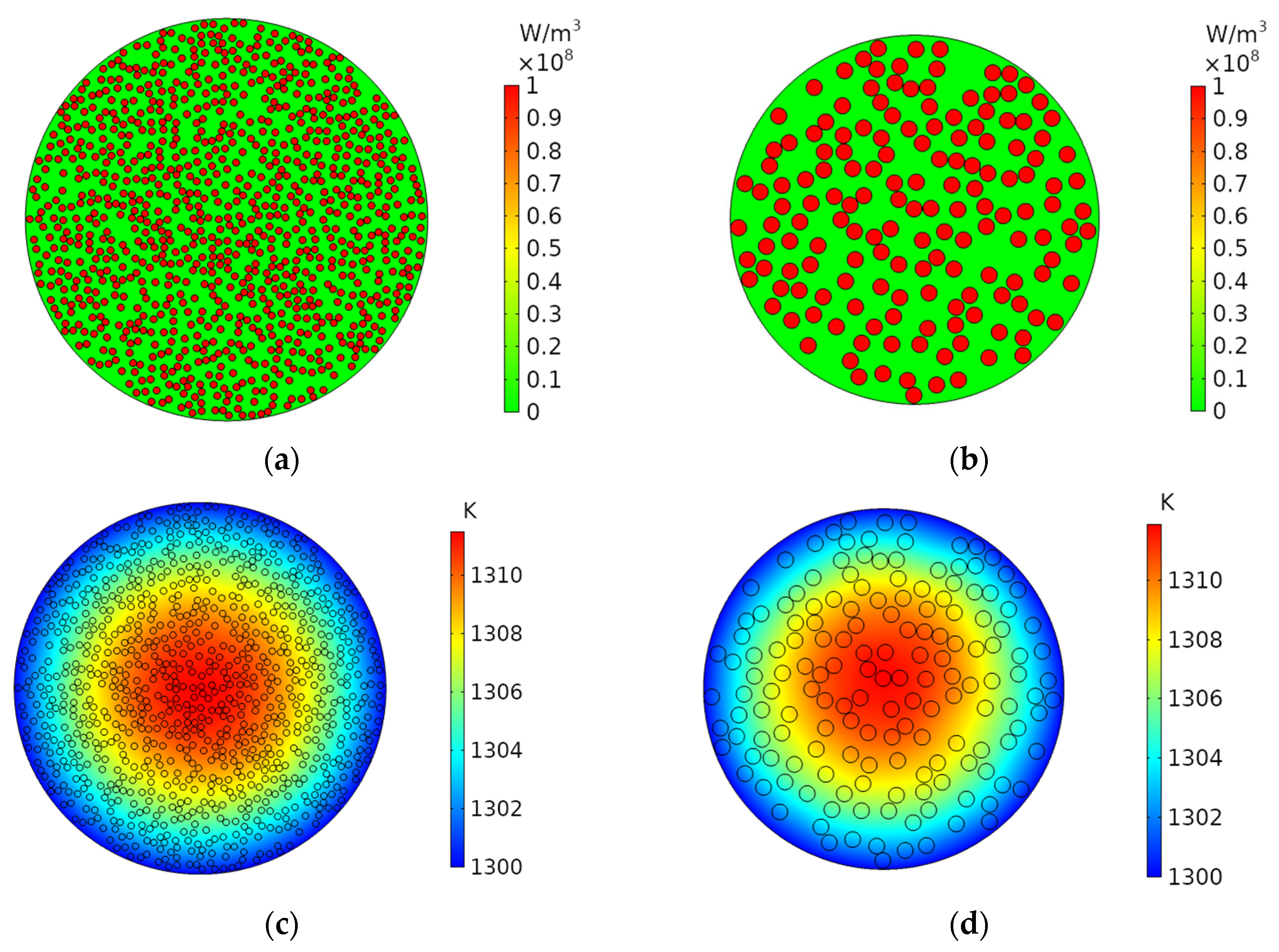
3.1. Typical Results
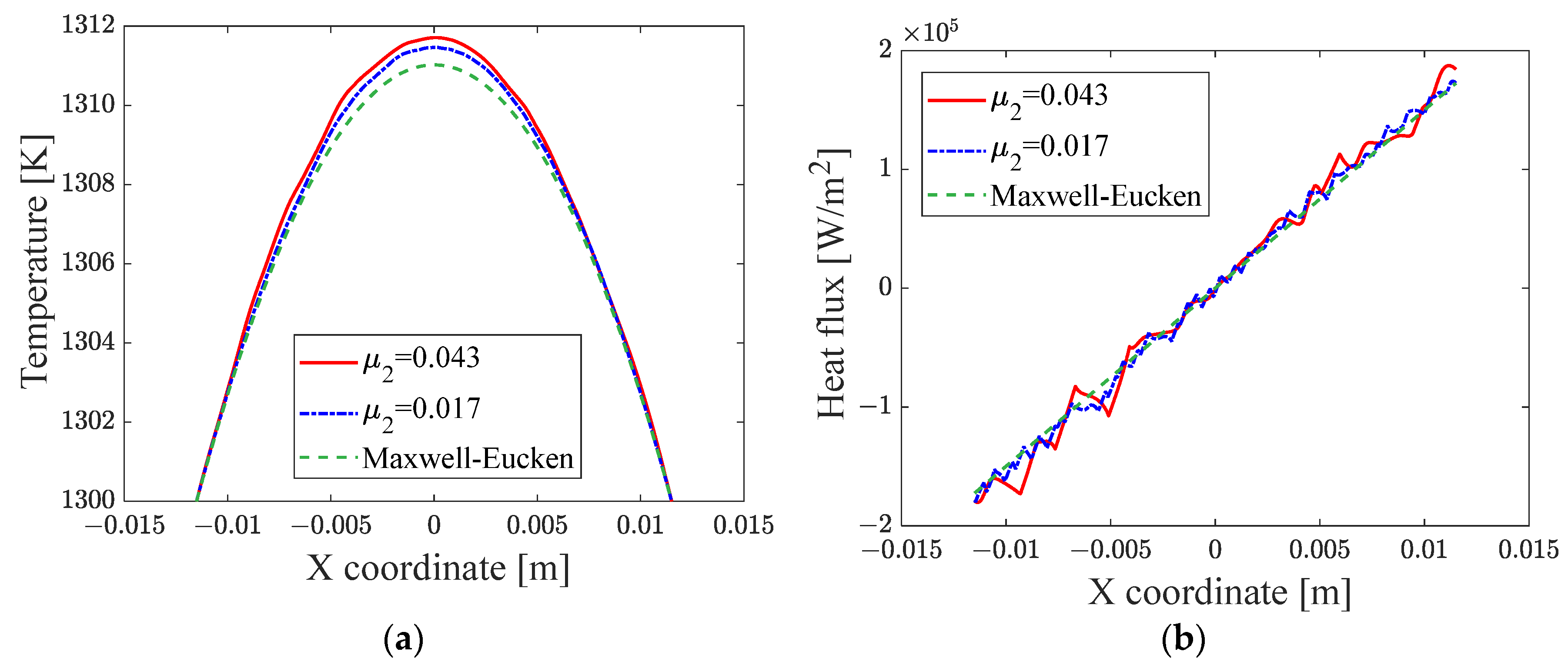
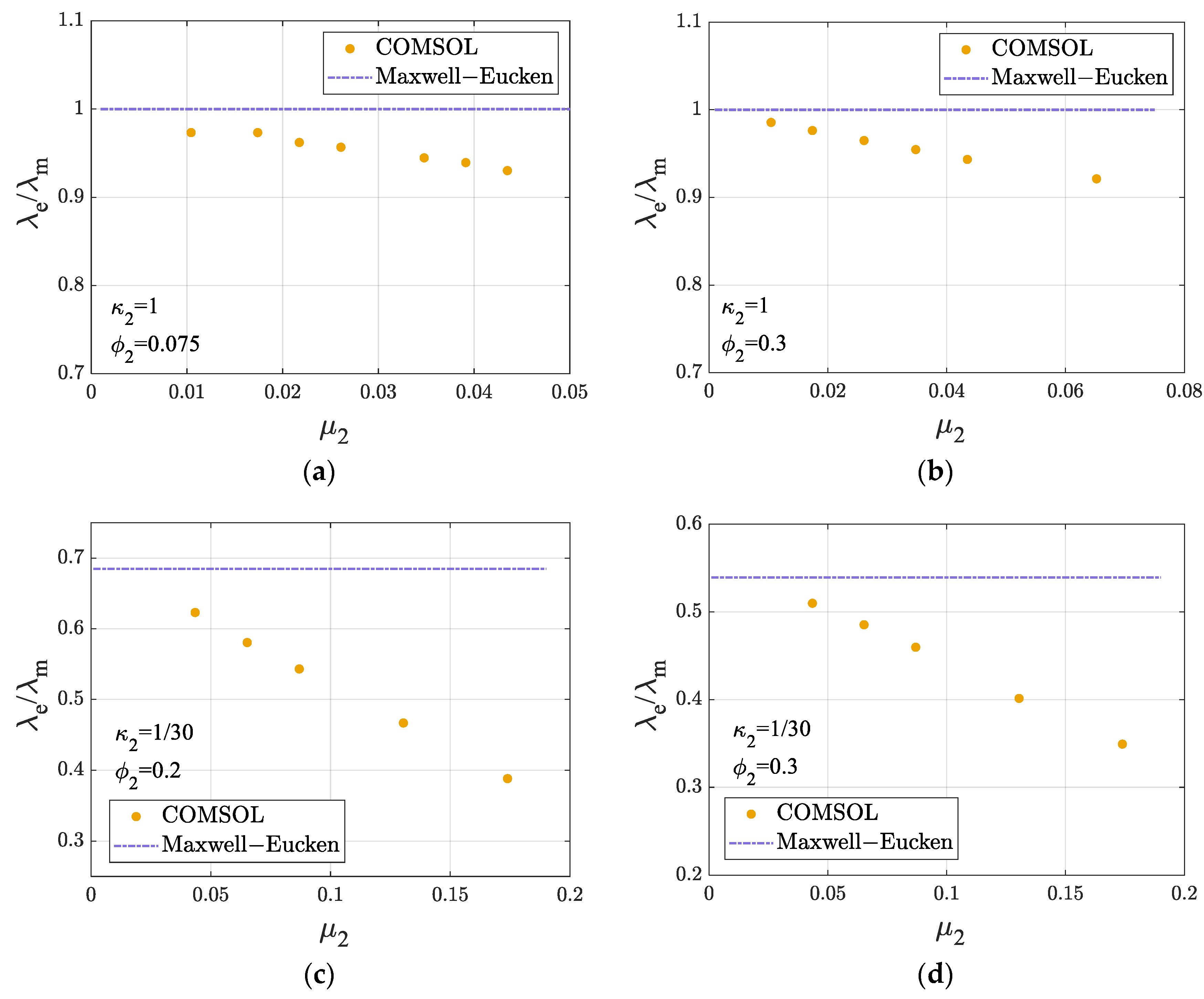
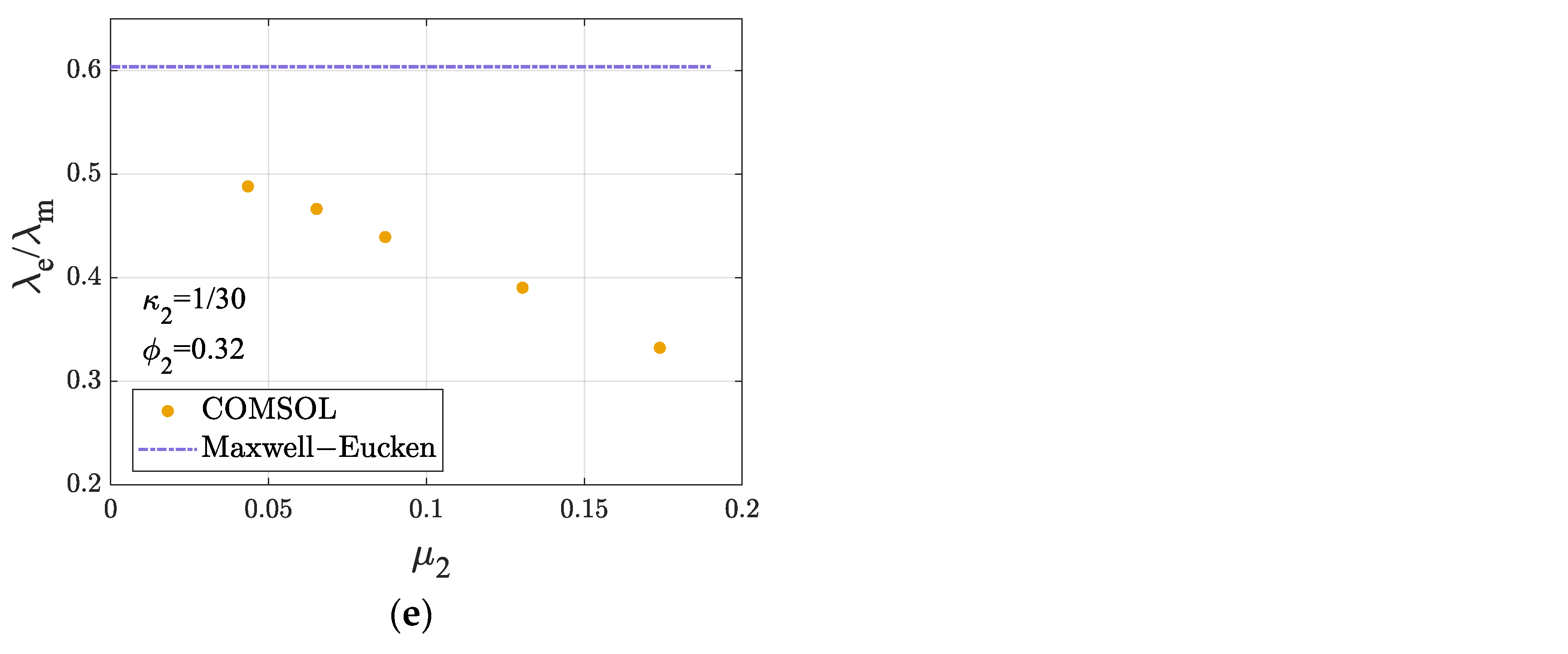
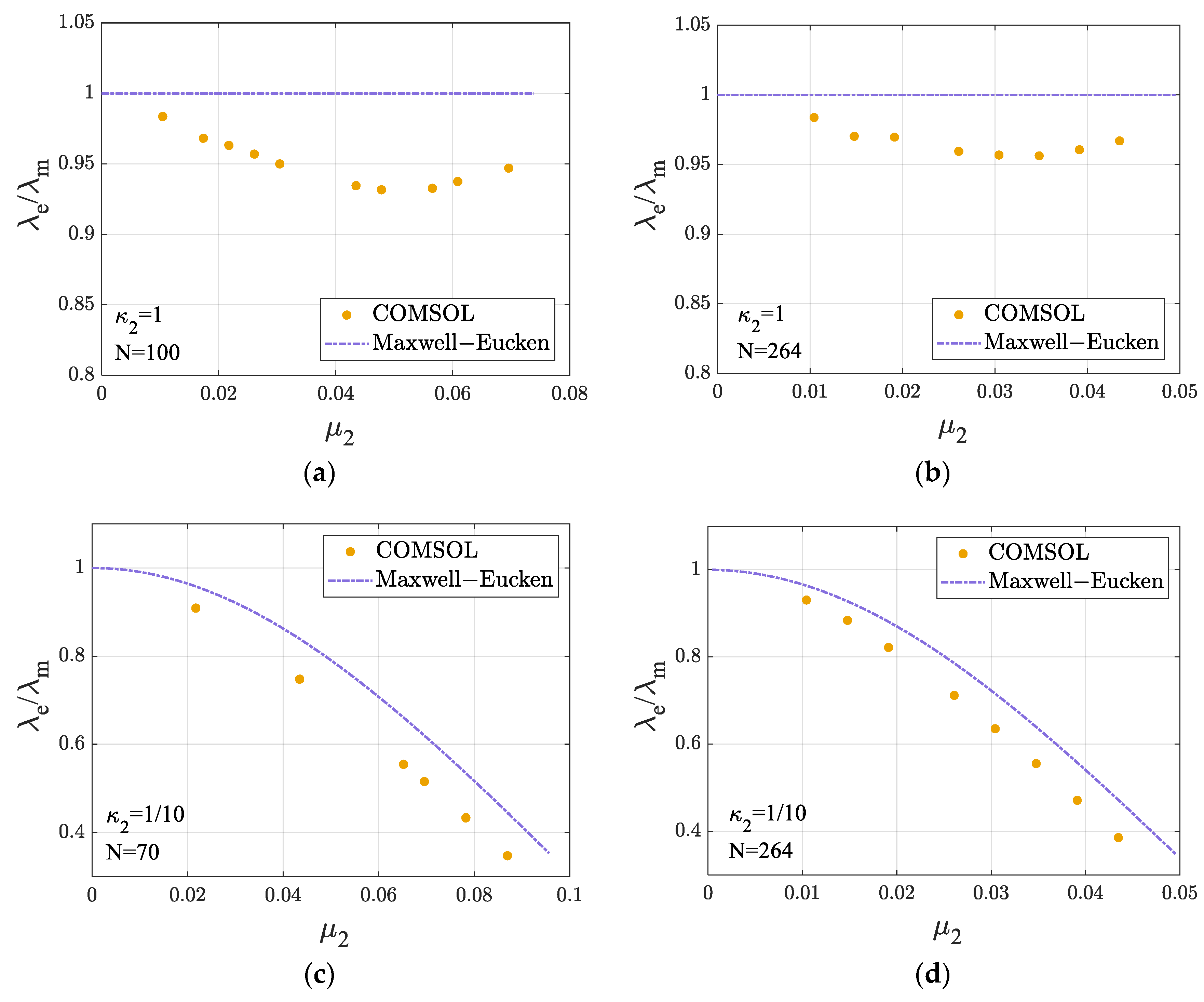
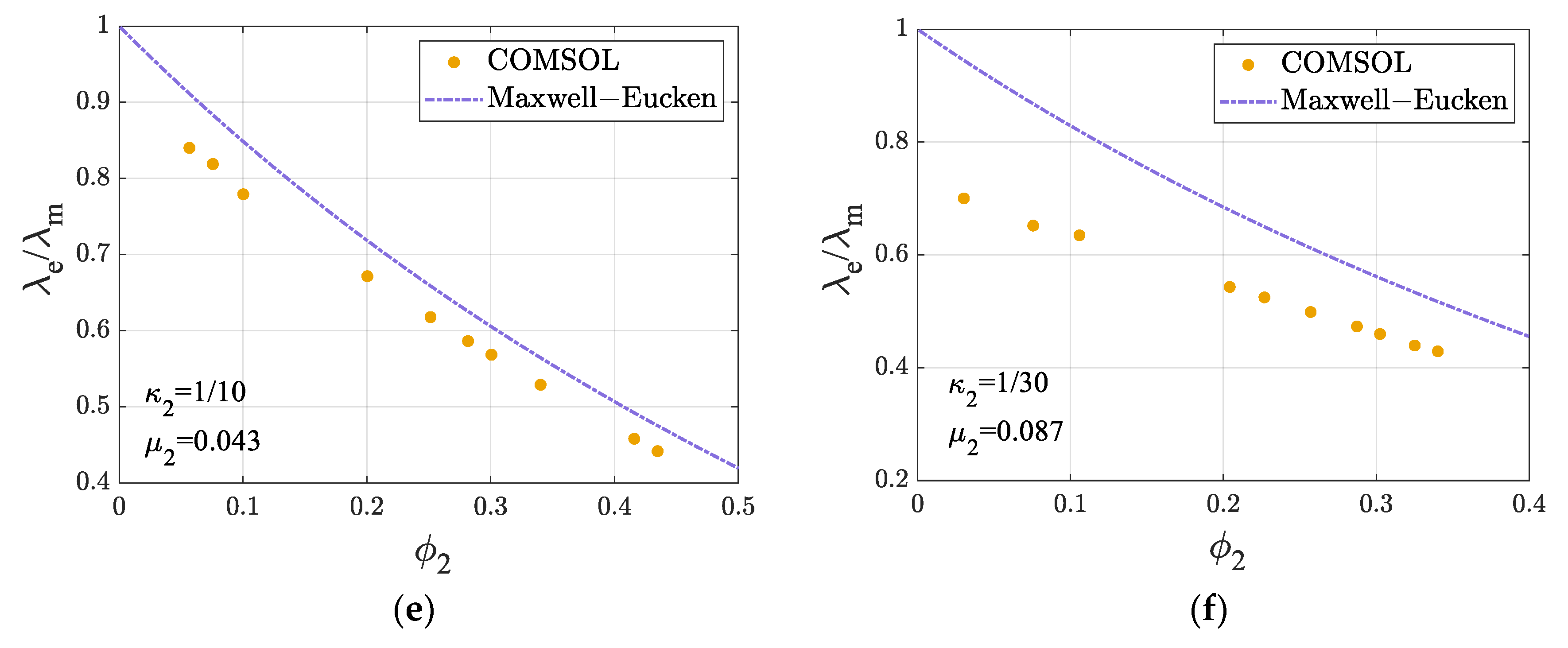
3.2. Influence of Filler Size
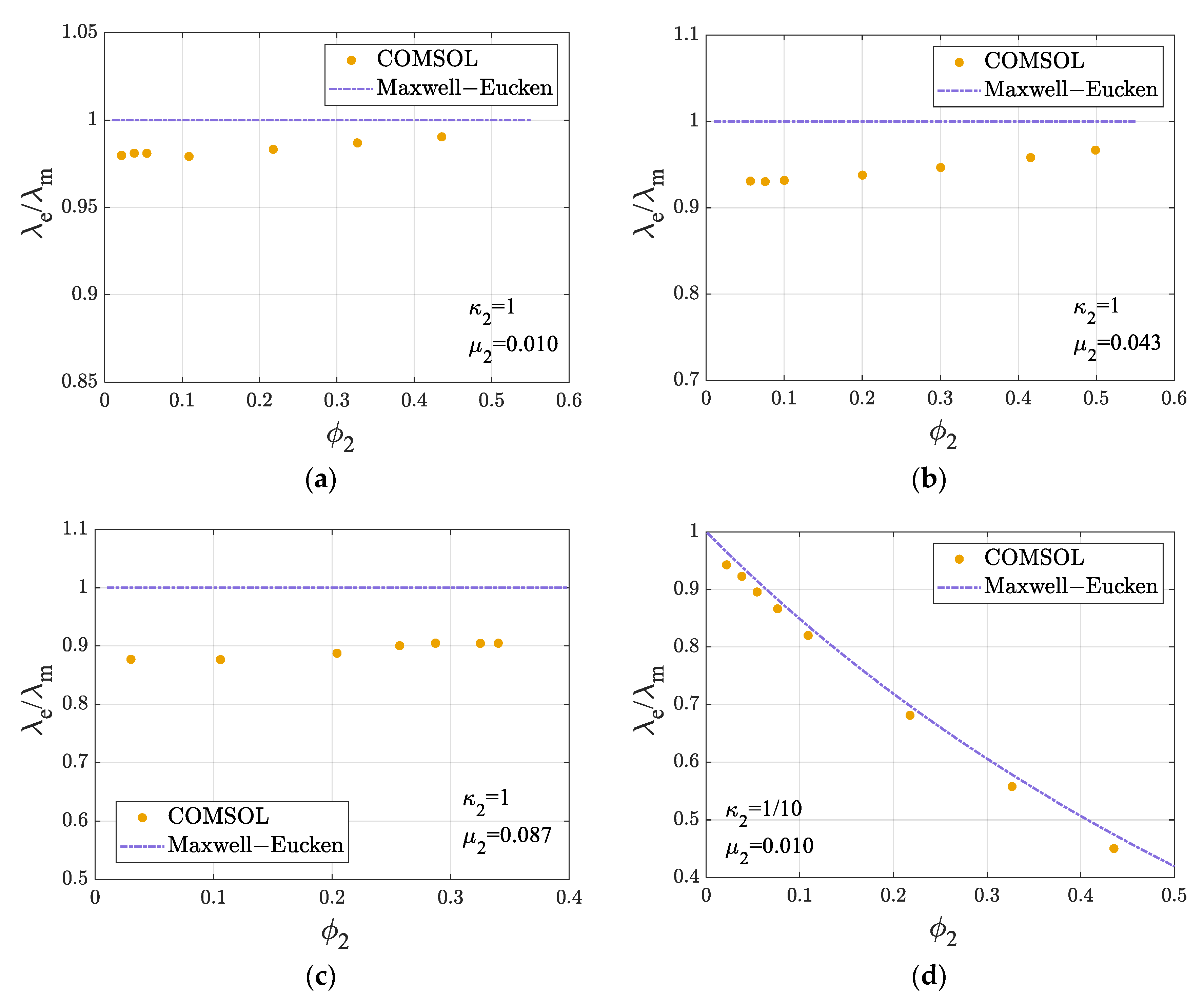
3.3. Influence of Filling Fraction
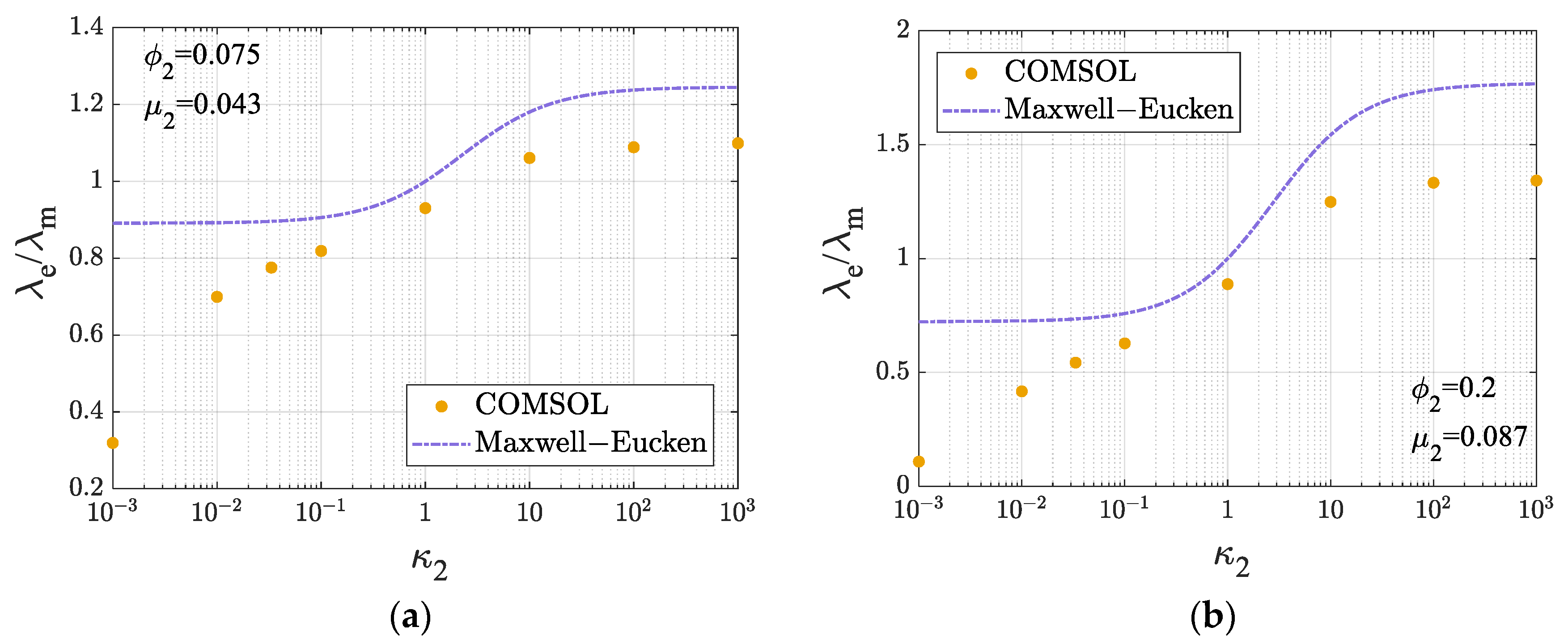
3.4. Influence of Thermal Conductivity
4. Discussion
4.1. Limit as the Size of Internal Heat Sources Approaches Zero
4.2. Individual Effect of Internal Heat Source Filling Fraction
4.3. Asymptotic Behavior of Filler Thermal Conductivity
5. Conclusions
- (1)
- The conventional Maxwell–Eucken model fails to capture the effects of the internal heat source presence and spatial distribution on the ETC of dispersed disks and is therefore not applicable to heat conduction problems involving internal heat sources in such systems.
- (2)
- When the filling fraction of the internal heat sources, i.e., the amount of the dispersed phase, remains constant, the ETC still decreases as the size of the internal heat sources increases. As the size of the internal heat sources approaches zero, the ETC model with internal heat sources converges to the conventional model.
- (3)
- The key trends in the ETC of dispersed disks are consistent with those reflected in the theoretical expression for one-dimensional composite plates. Therefore, in subsequent works, the analytical form of composite plates may serve as a reference for developing an ETC model for dispersed disks. This will also provide a basis for the eventual establishment of an ETC model for particle-dispersed cylinders.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| width of filling plates | |
| width of the composite plate | |
| number of fillers | |
| radius of the large disk | |
| radius of small filling disks | |
| homogenized heat source, W/m3 | |
| heat source of filling plate, W/m3 | |
| heat source of filling disk, W/m3 | |
| average temperature, K | |
| boundary temperature, K | |
| dimensionless thermal conductivity | |
| dimensionless thermal conductivity of composite plate | |
| dimensionless thermal conductivity of dispersed disk | |
| effective thermal conductivity, W/(m·K) | |
| effective thermal conductivity of composite plate, W/(m·K) | |
| thermal conductivity of matrix, W/(m·K) | |
| thermal conductivity of filler phase, W/(m·K) | |
| effective thermal conductivity of composite plate without internal heat sources, W/(m·K) | |
| effective thermal conductivity of dispersed disk without internal heat sources, W/(m·K) | |
| effective thermal conductivity of particle dispersion without internal heat sources, W/(m·K) | |
| dimensionless width of filling plates | |
| dimensionless radius of filling disks | |
| filling fraction | |
| line fraction of filling plates | |
| area fraction of filling disks |
References
- Demkowicz, P.A.; Liu, B.; Hunn, J.D. Coated Particle Fuel: Historical Perspectives and Current Progress. J. Nucl. Mater. 2019, 515, 434–450. [Google Scholar] [CrossRef]
- Brown, N.R.; Ludewig, H.; Aronson, A.; Raitses, G.; Todosow, M. Neutronic Evaluation of a PWR with Fully Ceramic Microencapsulated Fuel. Part II: Nodal Core Calculations and Preliminary Study of Thermal Hydraulic Feedback. Ann. Nucl. Energy 2013, 62, 548–557. [Google Scholar] [CrossRef]
- Progelhof, R.C.; Throne, J.L.; Ruetsch, R.R. Methods for Predicting the Thermal Conductivity of Composite Systems: A Review. Polym. Eng. Sci. 1976, 16, 615–625. [Google Scholar] [CrossRef]
- Pietrak, K.; Wiśniewski, T.S. A Review of Models for Effective Thermal Conductivity of Composite Materials. J. Power Technol. 2015, 95, 14–24. [Google Scholar]
- Miller, J.V. Estimating Thermal Conductivity of Cermet Fuel Materials for Nuclear Reactor Application; NASA: Washington, DC, USA, 1967.
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Cambridge University Press: Cambridge, UK, 1873. [Google Scholar]
- Landauer, R. The Electrical Resistance of Binary Metallic Mixtures. J. Appl. Phys. 1952, 23, 779–784. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. The Effect of Structure on the Conductivity of a Dispersion. J. Colloid Interface Sci. 1983, 94, 90–104. [Google Scholar] [CrossRef]
- Wang, J.; Lu, G.; Ding, M. Parametric Study of Effective Thermal Conductivity for VHTR Fuel Pebbles Based on a Neutronic and Thermal Coupling Method. Ann. Nucl. Energy 2023, 181, 109530. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, J. Preliminary Discussion on the Equivalent Thermal Conductivity Affected by the Inner Heat Source. In Proceedings of the International Topical Meeting on Advances in Thermal Hydraulics, Palaiseau, France, 20–23 October 2020. [Google Scholar]
- Liu, Z.; Ji, Y.; Zhang, H.; Sun, J. Effective Thermal Conductivity of Typical Composite Plate with Inner Heat Source and Temperature Difference. Nucl. Technol. 2022, 208, 1337–1351. [Google Scholar] [CrossRef]
- Belhaouzi, A.; Laaouidi, H.; Zyade, S.; Raji, Y.; Halimi, Y.; Tahiri, M. Exploring the Thermophysical Properties of the Thermal Conductivity of Pigmented Polymer Matrix Composites with Barium Titanate: A Comparative Numerical and Experimental Study. J. Compos. Sci. 2023, 7, 220. [Google Scholar] [CrossRef]
- Panchal, M.; Kang, C.; Ying, A.; Chaudhuri, P. Experimental Measurement and Numerical Modeling of the Effective Thermal Conductivity of Lithium Meta-Titanate Pebble Bed. Fusion Eng. Des. 2018, 127, 34–39. [Google Scholar] [CrossRef]
- Folsom, C.P. Effective Thermal Conductivity of Tri-Isotropic (TRISO) Fuel Compacts. Master’s Thesis, Utah State University, Logan, UT, USA, 2012. [Google Scholar] [CrossRef]
- Gong, J.; Yuan, R.; Song, X.; Wang, Y.; Liu, B.; Liu, M. Numerical Analysis of Effective Thermal Conductivity of FCM with Multilayer TRISO Particle. Nucl. Mater. Energy 2023, 36, 101501. [Google Scholar] [CrossRef]
- Kamalpour, S.; Salehi, A.A.; Khalafi, H.; Mataji-Kojouri, N.; Jahanfarnia, G. The Potential Impact of Fully Ceramic Microencapsulated (FCM) Fuel on Thermal Hydraulic Performance of SMART Reactor. Nucl. Eng. Des. 2018, 339, 39–52. [Google Scholar] [CrossRef]
- Folsom, C.; Xing, C.; Jensen, C.; Ban, H.; Marshall, D.W. Experimental Measurement and Numerical Modeling of the Effective Thermal Conductivity of TRISO Fuel Compacts. J. Nucl. Mater. 2015, 458, 198–205. [Google Scholar] [CrossRef]
- Liu, M.; Lee, Y.; Rao, D.V. Development of Effective Thermal Conductivity Model for Particle-Type Nuclear Fuels Randomly Distributed in a Matrix. J. Nucl. Mater. 2018, 508, 168–180. [Google Scholar] [CrossRef]
- Yu, D.; Wang, F.; Mei, H.; Cheng, X.; Duan, C. An Improved Two-Temperature Method for Computing the Temperature Distributions within a TRISO-Coated Particle Pebble Fuel. Nucl. Eng. Technol. 2025, 57, 103515. [Google Scholar] [CrossRef]
- Liu, M.; Thurgood, J.; Lee, Y.; Rao, D.V. Development of a Two-Regime Heat Conduction Model for TRISO-Based Nuclear Fuels. J. Nucl. Mater. 2019, 519, 255–264. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, B.; Bu, S.; Li, Z.; Chen, D.; Ma, Z.; Zhang, L. A Multi-Annulus Heat Conduction Model for Predicting the Peak Temperature of Nuclear Fuels with Randomly Dispersed TRISO Particles. Prog. Nucl. Energy 2023, 158, 104602. [Google Scholar] [CrossRef]
- Wang, M.; Bu, S.; Zhou, B.; Li, Z.; Chen, D. Multi-Scale Heat Conduction Models with Improved Equivalent Thermal Conductivity of TRISO Fuel Particles for FCM Fuel. Nucl. Eng. Technol. 2023, 55, 1140–1151. [Google Scholar] [CrossRef]
- Liu, Z.; Ji, Y.; Zhang, H.; Sun, J. Numerical Calculations of the Effective Thermal Conductivity of the Dispersion Fuel Sphere with the Internal Heat Sources. In Proceedings of the 2021 28th International Conference on Nuclear Engineering, Online, 4–6 August 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, J. Research on the Equivalent Thermal Conductivity Coefficient of a Composite Plate with Inner Heat Sources. J. Harbin Eng. Univ. 2021, 42, 1832–1836+1842. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.; Sun, J. An Effective Thermal Conductivity Model of Composite Plates with Distributed Inner Heat Sources. J. Tsinghua Univ. Sci. Technol. 2023, 63, 104–113. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Z.; Ji, Y.; Zhang, H.; Sun, J. An Approximate Effective Thermal Conductivity Model in Predicting the Average Temperature of the Fuel Pebble. In Proceedings of the 19th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-19), Online, 6–11 March 2022. [Google Scholar]
- Qiu, T.; Sun, J. The Effective Thermal Conductivity Model of Dispersion Fuel Elements Based on Effective Matrix Approximation. In Proceedings of the 31st International Conference on Nuclear Engineering, Prague, Czech Republic, 4–8 August 2024. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J. Study on the Influence of Internal Heat Source Characteristics and Distribution on Effective Thermal Conductivity of Cylindrical Particle Dispersed Fuel. In Proceedings of the 31st International Conference on Nuclear Engineering, Prague, Czech Republic, 4–8 August 2024. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, version 5.5; Livelink for MATLAB User’s Guide; COMSOL AB: Stockholm, Sweden, 2019.
- Eucken, A. Thermal Conductivity of Ceramics Refractory Materials. Forsch. Geb. Ing. 1932, B-3, 6–21. [Google Scholar]
- Stainsby, R. Investigation of Local Heat Transfer Phenomena in a Prismatic Modular Reactor Core; AMEC NSS Limited: Cheshire, UK, 2009. [Google Scholar]

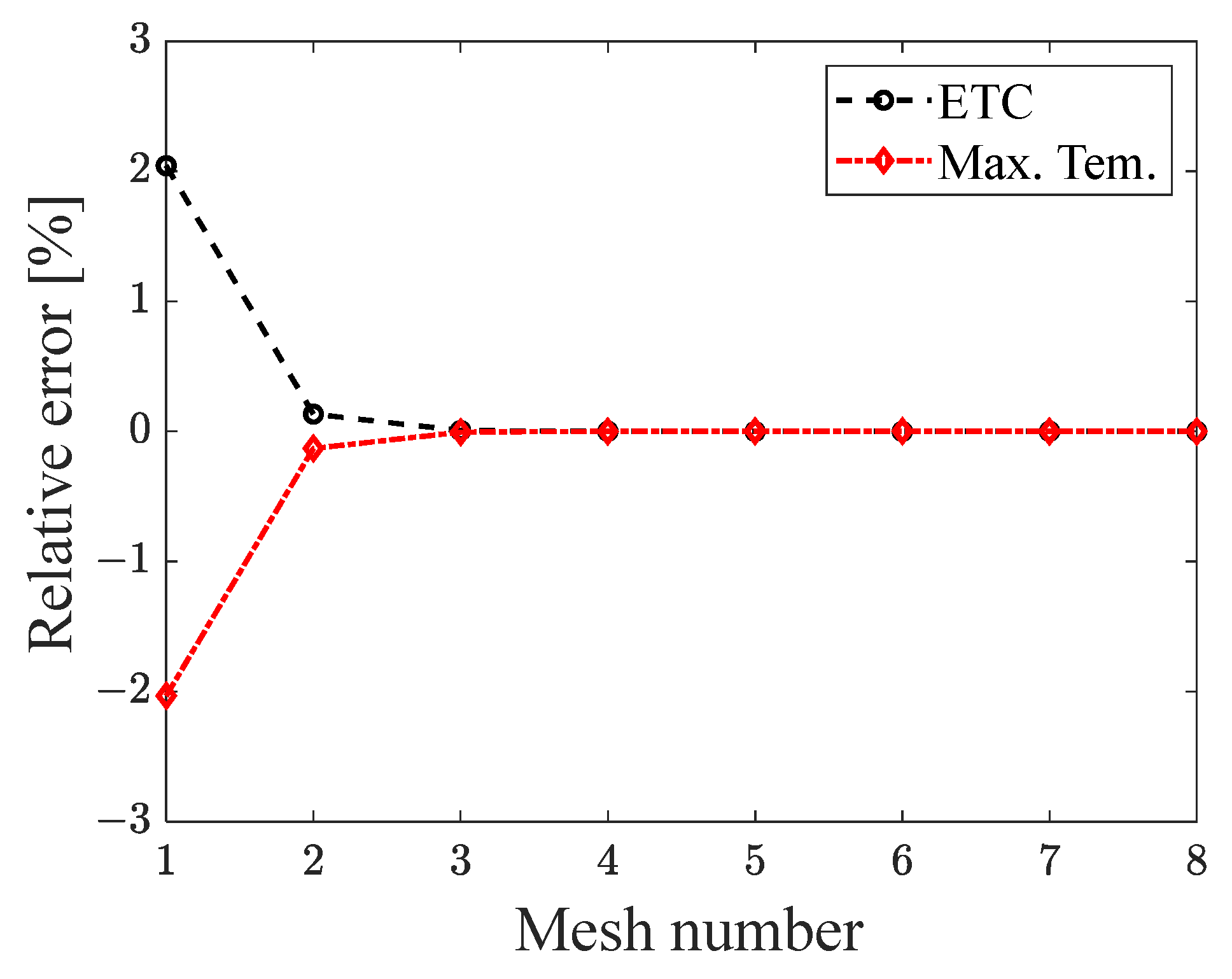

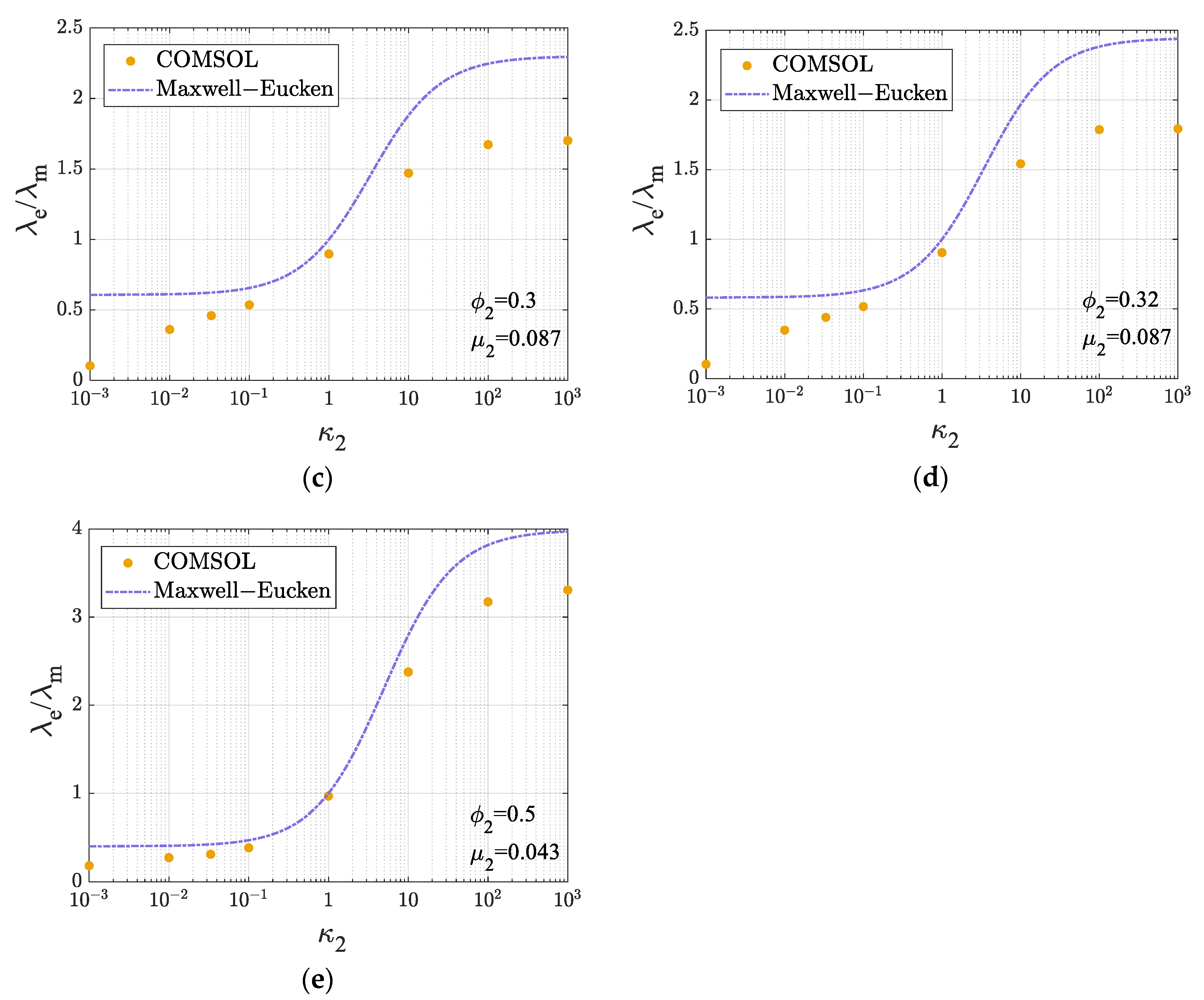
| Mesh Number | Small Disk Mesh Setting | Matrix Mesh Setting | Maximum Element Area [m2] |
|---|---|---|---|
| 1 | Extra coarse | Extra coarse | 6.22 × 10−8 |
| 2 | Coarser | Coarser | 2.97 × 10−8 |
| 3 | Coarse | Coarse | 8.75 × 10−9 |
| 4 | Normal | Normal | 4.90 × 10−9 |
| 5 | Finer | Finer | 3.99 × 10−9 |
| 6 | Extra fine | Extra fine | 3.86 × 10−9 |
| 7 | Extra fine | Extremely fine | 3.64 × 10−9 |
| 8 | Extremely fine | Extremely fine | 1.70 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Qiu, T.; Sun, J. Parametric Study on Effective Thermal Conductivity of Dispersed Disks with Internal Heat Sources. Energies 2025, 18, 4719. https://doi.org/10.3390/en18174719
Liu Y, Qiu T, Sun J. Parametric Study on Effective Thermal Conductivity of Dispersed Disks with Internal Heat Sources. Energies. 2025; 18(17):4719. https://doi.org/10.3390/en18174719
Chicago/Turabian StyleLiu, Yuhao, Tianchen Qiu, and Jun Sun. 2025. "Parametric Study on Effective Thermal Conductivity of Dispersed Disks with Internal Heat Sources" Energies 18, no. 17: 4719. https://doi.org/10.3390/en18174719
APA StyleLiu, Y., Qiu, T., & Sun, J. (2025). Parametric Study on Effective Thermal Conductivity of Dispersed Disks with Internal Heat Sources. Energies, 18(17), 4719. https://doi.org/10.3390/en18174719







