Quasi-Z-Source Inverter-Based Photovoltaic Power System Modeling for Grid Stability Studies

Abstract

Quasi-Z-source inverters (qZSIs) are becoming a powerful power conversion technology in photovoltaic (PV) power systems because they allow energy power conversion in a single stage operation. However, they can cause system resonances and reduce system damping, which may lead to instabilities. These stability problems are well known in grid-connected voltage source converter systems but not in quasi-Z-source inverter (qZSI)-based PV power systems. This paper contributes with Matlab/Simulink and PSCAD/EMTDC models of qZSI-based PV power systems to analyze transient interactions and stability problems. These models consider all power circuits and control blocks of qZSI-based PV power systems and can be used in sensitivity studies on the influence of system parameters on stability. PV power system stability is assessed from the proposed models. The causes of instabilities are analyzed from numerical simulations and possible solutions are proposed.

1. Introduction

Penetration of wind and solar PV energies in grids has been rapidly growing in the last few years [1,2,3,4]. PV power systems have different configurations achieved in a single or two stages [5,6], with the two-stage DC/DC and DC/AC voltage source inverter (VSI) topology being the most common configuration. Nevertheless, single stage topologies with a centralized inverter are gaining ground in a wide range of applications because they are simpler and cheaper than two stage topologies [6,7,8,9,10]. Several impedance-source-network-based power converters with different converter topologies that overcome the drawbacks of traditional converter topologies are reported in research works. A comprehensive review of them, together with their main topologies, modeling, control, and modulation techniques from an engineering application point of view are presented in [8,9]. A complete analytical comparison of impedance-source-network-based power converters related to their passive component count and semiconductor stress, and a comparison between two and multilevel buck–boost inverters based on the already existing impedance-source networks are provided in [10]. Recent solutions based on these networks have been extended to various fields of application such as Z-source inverters and quasi-Z-source inverters (qZSIs) for grid integration into low-voltage energy sources [10]. In particular, introduction of qZSIs in PV power systems improves their efficiency and reliability because they can make both buck or boost DC voltage and energy power conversion in a single-stage operation [11,12,13,14,15,16,17]. The traditional qZSI based on an impedance and semiconductor network coupling the inverter to the dc source is studied in [11,12,13,14]. Four new qZSIs with several improvements and no disadvantages compared to ZSIs are presented and theoretically studied in [15]. In addition, [16,17] examine a new qZSI topology, known as three-level neutral-point-clamped qZSI, which is a combination of the qZSI and the three-level neutral-point-clamped inverter. This new qZSI offers the advantages of both topologies, i.e., buck or boost DC voltage capability, short circuit immunity and high energy density.

PV power systems can cause stability problems in grids because power electronics reduces damping of grid-connected converter systems. Several works characterize dynamic behavior of PV power systems with a two-stage boost DC/DC converter and a DC/AC VSI, and investigate stability [4,18,19]. They conclude that solar irradiance and temperature lead to variations in a PV power system operating point, affecting system stability [18,19] and that control parameters have an influence on it too [4]. Other works provide small-signal models of qZSIs to analyze their dynamics and stability [9,11,12,13,14,20]. The influence of qZSI control on qZSI stability is explored in [11,12,13,14], and qZSI design rules are provided from dynamic models in [11,12]. A broad and worthy study of pole-zero location and impact of parameters on the dynamics of several impedance-source-network-based power converters (including qZSIs)] considering the wide operating ranges of different sources is developed in [9]. A comparative study between various qZSI control schemes is carried out from the small-signal state-space averaged model of qZSIs in [20]. Several works analyze qZSI-based PV power systems to propose dynamic models and assess PV power system stability [21,22,23,24,25]. Most of them focus on the analysis and enhancement of the DC side and the enhancement of AC network impedance performance on the DC side [21,24,25], but the dynamic interaction between the DC and AC side has not been fully studied yet. Only a few works can be found in the literature [22,23], where the effect of the impedance network on qZSI dynamics is analyzed. It is shown that oscillatory instabilities may appear in the modulation ratio triggered by the AC current controller due to the AC network impedance. A design guideline to improve this issue is proposed.

Unlike most published works, which mainly focus on qZSI dynamic behavior, improvement of the DC side of qZSI-based PV power systems and impact of the AC impedance network on qZSI-based PV power system stability, this paper presents a broader study about qZSI-based PV power system stability that provides the following contributions to understand the qZSI-based PV power system dynamics:

• Simulation tools, fully developed for implementation, based on Matlab/Simulink and PSCAD/EMTDC small-signal state-space averaged models of qZSI-based PV power systems which include all their components and controls.
• An exhaustive study about the influence of qZSI-based PV power system parameters on stability.
• Solutions to improve qZSI-based PV power system stability.

These contributions can be a useful tool and a guide on qZSI-based PV power system stability works for designers, engineers and researchers.

2. QZSI-Based PV Power Systems

The circuit and block diagram of qZSI-based PV power systems is illustrated in Figure 1. It consists of a DC bus where an N_p × N_s (number of PV panels in parallel × number of PV panels in series) PV array is connected with a shunt capacitor C_p and a DC cable, characterized with a resistance R_c, to the qZSI, which boosts the output voltage v_dc at the VSI terminals. The maximum power point (MPP) tracking (MPPT) control is used to obtain the maximum power from the PV panel. The PV and current control loops ensure power flow from the PV panel to the AC grid. Moreover, the duty cycle control of the qZSI allows the DC-link peak voltage v_dc,p to be fixed.

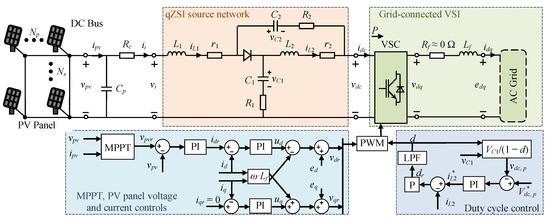
Figure 1. Circuit and block diagram of quasi-Z-source inverter (qZSI)-based photovoltaic (PV) power systems.

The Matlab/Simulink and PSCAD models of the qZSI-based PV power system are presented in the following Sections to assess system stability.

3. Matlab/Simulink Model of the qZSI-Based PV Power System

The Matlab/Simulink small-signal state-space averaged model of the qZSI-based PV power system in Figure 2 is derived. It is used to study the dynamic behavior of the PV power system in order to assess PV system stability and analyzing possible solutions to mitigate instability problems. The dynamic response of the PV power system is obtained by simulations, and the state-space matrix A and eigenvalues λ_i = σ_i ± j·ω_i of the state-space modes of the PV power system can also be obtained from the Matlab/Simulink small-signal state-space averaged model of the qZSI-based PV power system. Moreover, the participation factors of each state-space variable of each mode can be calculated as p_ki = ϕ_ki·ψ_ik, where ϕ_ki and ψ_ik are the elements of the right and left eigenvectors of the state-space matrix A, respectively.

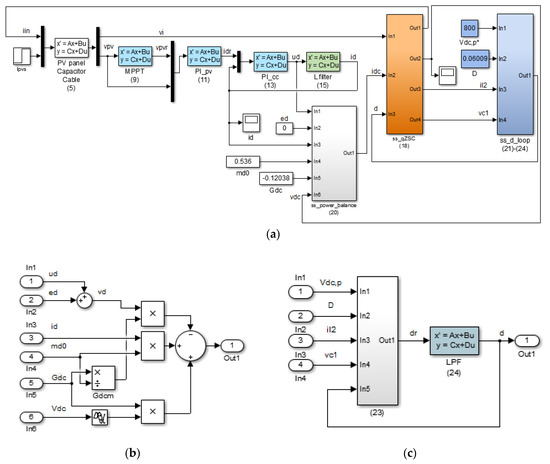
Figure 2. Matlab/Simulink small-signal model of qZSI-based PV power systems (symbol ∆ is omitted for sake of simplicity): (a) General layout; (b) power balance subsystem (20); (c) duty cycle control subsystem.

This Section is divided into Subsections introducing the Matlab/Simulink model of the qZSI-based PV power system subsystems in Figure 2. In order to obtain these subsystem models, the small-signal state-space averaged equations of the circuits in Figure 1 are derived according to the state-space equation form

$$\frac{dx}{dt}=Ax+Bu\hspace{1em}\hspace{1em}y=Cx+Du,$$

(1)

where A, B, C, and D are the state-space, input, output, and feedthrough matrices, x is the state vector, u is the input vector, and y is the output vector.

3.1. PV Installation Modeling

The small-signal state-space model of the PV installation, formed by the PV panel with the MPPT control, the shunt capacitor C_p and the resistance R_c of the cable connecting the PV panel and the qZSI (see Figure 1), is derived.

The equation that relates the output current i_pv and the terminal voltage v_pv in the PV panel is expressed as [2],

$$i_{pv}=N_p\left\{I_{pvL}-I_{pv0}\left\{\exp \left(\frac{v_{pv}/N_s+R_s{i}_{pv}/N_p}{n{V}_T}-1\right)\right\}\right\},$$

(2)

where I_pvL and I_pv0 are the photovoltaic and the saturation currents of the PV cell, R_s is the equivalent series resistance of the PV cell, n is the diode quality factor and V_T = k·T/q is the thermal constant of the PV cell, with k being the Boltzman constant (1.38 × 10⁻²³ J/K), q the Coulomb constant (1.602 × 10⁻¹⁹ C), and T the PV cell temperature in Kelvin. The photovoltaic current I_pvL is proportional to the irradiance level G and is usually referred to as the rated irradiation (i.e., G = 1 Sun = 1000 W/m²). The photovoltaic and saturation currents, I_pvL and I_pv0, also depend on the temperature T, which is 25 °C.

Figure 3a shows the i_pv-v_pv characteristics (2) of a PV panel based on 60 W PV Solarex MSX60 modules [2]. The influence of N_p and N_s on the MPP is also illustrated in Figure 3a for three PV array configurations.

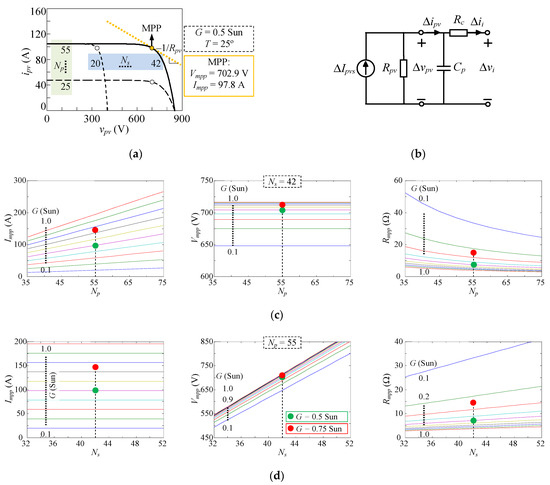
Figure 3. Study of the PV panel (T₁ = 25 °C): (a) i_pv-v_pv characteristics; (b) small-signal equivalent circuit; (c) influence of N_p and G on MPP; (d) influence of N_s and G on MPP.

The small-signal model of the PV panel is obtained from the linearization of i_pv-v_pv characteristics (2) around the MPP (V_pv = V_mpp and I_pv = I_mpp) [5],

$$i_{pv}=I_{pvs}-\frac{1}{R_{pv}}{v}_{pv}\hspace{1em}\hspace{1em}\Rightarrow \hspace{1em}\hspace{1em}\Delta i_{pv}=\Delta I_{pvs}-\frac{1}{R_{pv}}\Delta v_{pv},$$

(3)

where the incremental symbol ∆ identifies the small-signal variables and

$$\begin{array}{l}{I}_{pvs}=I_{pv}+\frac{V_{pv}}{R_{pv}}\hspace{1em}\hspace{1em}{R}_{pv}=-{\frac{d{v}_{pv}}{d{i}_{pv}}|}_{(V_{pv},\hspace{0.17em}{I}_{pv})}=\frac{N_s}{N_p}{R}_{pv\_cell}\\ R_{pv\_cell}=\frac{n{V}_T}{I_{pv0}\exp \left(\frac{V_{pv}/N_s+R_s{I}_{pv}/N_p}{n{V}_T}-1\right)}+R_s.\end{array}$$

(4)

The small-signal circuit of the PV panel (3), shunt capacitor, and cable is shown in Figure 3b and the small-signal state-space model becomes

$$\begin{array}{l}\frac{d}{dt}\left[\Delta v_{pv}\right]=\left[\frac{-1}{C_p{R}_{pv}}\right]\left[\Delta v_{pv}\right]+\left[\begin{array}{cc}\frac{-1}{C_p}& \frac{1}{C_p}\end{array}\right]\left[\begin{array}{c}\Delta i_i\\ \Delta i_{pv}\end{array}\right]\\ \left[\Delta v_i\right]=\left[1\right]\left[\Delta v_{pv}\right]+\left[\begin{array}{cc}-R_c& 0\end{array}\right]\left[\begin{array}{c}\Delta i_i\\ \Delta i_{pv}\end{array}\right].\end{array}$$

(5)

The MPPT control generates the PV panel reference voltage by imposing the maximum value of the instantaneous power from the PV panel, p_pv = i_pv·v_pv. Thus, the MPP can be mathematically characterized as [5]

$${\frac{d{p}_{pv}}{d{v}_{pv}}|}_{\mathrm{MPP}} =\stackrel{{\Sigma }_{mpp}}{\overbrace{{\left[i_{pv}+v_{pv}\frac{d{i}_{pv}}{d{v}_{pv}}\right]}_{\mathrm{MPP}}}} =0\hspace{1em}\hspace{1em}\Rightarrow \hspace{1em}\hspace{1em}{\Sigma }_{mpp}=\frac{i_{pv}}{v_{pv}}+\frac{d{i}_{pv}}{d{v}_{pv}}=0.$$

(6)

According to (6), the sum of the actual conductance and the incremental conductance at the MPP (V_mpp, I_mpp) is equal to zero. The sum Σ_mpp is related to the PV voltage around the MPP by means of the linear I-V characteristics of the PV panel (3) as

$${\Sigma }_{mpp}=-\frac{2}{R_{mpp}}+\frac{I_{mpp}}{v_{pv}}+\frac{V_{mpp}}{R_{mpp}}\frac{1}{v_{pv}},$$

(7)

where R_mpp = V_mpp/I_mpp is the incremental resistance of the linear i_pv-v_pv characteristics of the PV panel at the MPP (3). Considering the previous characterization of the MPP, the PV panel reference voltage is obtained from a PI control as the small-signal relation

$$\begin{array}{l}{v}_{pvr}=\left(k_p^m+\frac{k_i^m}{s}\right){\Sigma }_{mpp}\hspace{1em}\Rightarrow \hspace{1em}\Delta v_{pvr}=\left(k_p^m+\frac{k_i^m}{s}\right)\underset{\Delta {\Sigma }_{mpp}}{\underbrace{k_m\Delta v_{pv}}}\\ \Rightarrow \hspace{1em}\Delta v_{pvr}=k_p^m{k}_m\Delta v_{pv}+k_i^m{k}_m\Delta i_{pvs}\hspace{1em}\hspace{1em}s\Delta i_{pvs}=\Delta v_{pv},\end{array}$$

(8)

where $k_p^m$ and $k_i^m$ are the PI control proportional and integral gains of the MPPT control and k_m = −2/(V_mpp·R_mpp) [5].

According to (8), the small-signal state-space model of the MPPT control is represented by

$$\begin{array}{l}\frac{d}{dt}\left[\Delta i_{pvs}\right]=\left[0\right]\left[\Delta i_{pvs}\right]+\left[1\right]\left[\Delta v_{pv}\right]\\ \left[\Delta v_{pvr}\right]=\left[k_i^m{k}_m\right]\left[\Delta i_{pvs}\right]+\left[k_p^m{k}_m\right]\left[\Delta v_{pv}\right].\end{array}$$

(9)

Figure 3c,d shows the influence of N_p, N_s and G on the MPP of the PV panel (i.e., on I_mpp, V_mpp and R_mpp). The MPP corresponding to the PV array configuration N_p = 55 and N_s = 42 and the operating point T₁ = 25 °C with G = 0.5 Sun and 0.75 Sun labeled with the blue and red dots, respectively. The current I_mpp is affected by N_p and by G, and the increase of both variables leads to the increase of I_mpp. Variations of I_mpp can have a large impact on the performance of the qZSI-PV-based power system, even leading the system to instability in some conditions (see Section 5). The voltage V_mpp is mainly affected by N_s, and the increase of this variable results in the increase of V_mpp. The number of PV panels in series N_s is usually fixed according to the rated voltage of the PV power system, and low variations of V_mpp due to other causes (e.g., the irradiance level G) are controlled by means of the duty cycle control of the qZSI. The incremental resistance R_mpp = V_mpp/I_mpp varies in accordance with the variations of V_mpp and I_mpp.

3.2. PV Panel Voltage Control and Grid-Connected VSI Modeling

The small-signal state-space model of the PV panel voltage control, VSI current control, and grid-connected VSI is presented in Figure 1. The grid d-frame reference current i_dr is generated by the PI-based control of the PV panel voltage. The grid q-frame reference current i_qr is set to zero considering that the VSI operates at unity power factor [6,8]. The grid dq-frame reference voltage v_dqr is provided by the PI-based control of the VSI. The VSI PLL is not considered in the study.

The grid d-reference current generated by the PV panel voltage control is expressed as the small-signal relation

$$\begin{array}{l}{i}_{dr}=-\left(k_p^{pv}+\frac{k_i^{pv}}{s}\right)(v_{pvr}-v_{pv})\hspace{1em}\Rightarrow \\ \Delta i_{dr}=k_i^{pv}\Delta q_{pv}+k_p^{pv}(v_{pv}-v_{pvr})\hspace{1em}\hspace{1em}s\Delta q_{pv}=\Delta v_{pv}-\Delta v_{pvr},\end{array}$$

(10)

where $k_p^{pv}$ and $k_i^{pv}$ are the PI control proportional and integral gains of the PV panel voltage control. According to (10), the small-signal state-space model of the PV panel voltage control is expressed as

$$\begin{array}{l}\frac{d}{dt}\left[\Delta q_{pv}\right]=\left[0\right]\left[\Delta q_{pv}\right]+\left[\begin{array}{cc}1& -1\end{array}\right]\left[\begin{array}{c}\Delta v_{pv}\\ \Delta v_{pvr}\end{array}\right]\\ \left[\Delta i_{dr}\right]=\left[k_i^{pv}\right]\left[\Delta q_{pv}\right]+\left[\begin{array}{cc}{k}_p^{pv}& -k_p^{pv}\end{array}\right]\left[\begin{array}{c}\Delta v_{pv}\\ \Delta v_{pvr}\end{array}\right].\end{array}$$

(11)

The output d-reference voltage generated by the PI compensator of the dq-frame VSC current control is expressed as the small-signal relation

$$\begin{array}{l}{u}_d=\left(k_p^{cc}+\frac{k_i^{cc}}{s}\right)(i_{dr}-i_d)\hspace{1em}\Rightarrow \\ \Delta u_d=k_p^{cc}(\Delta i_{dr}-\Delta i_d)+k_i^{cc}\Delta q_{cc}\hspace{1em}s\Delta q_{cc}=\Delta i_{dr}-\Delta i_d,\end{array}$$

(12)

where $k_p^{cc}$ and $k_i^{cc}$ are the proportional and integral gains of the PI compensator. According to (12), the small-signal state-space model of the PI compensator is represented by

$$\begin{array}{l}\frac{d}{dt}\left[\Delta q_{cc}\right]=\left[0\right]\left[\Delta q_{cc}\right]+\left[\begin{array}{cc}1& -1\end{array}\right]\left[\begin{array}{c}\Delta i_{dr}\\ \Delta i_d\end{array}\right]\\ \left[\Delta u_d\right]=\left[k_i^{cc}\right]\left[\Delta q_{cc}\right]+\left[\begin{array}{cc}{k}_p^{cc}& -k_p^{cc}\end{array}\right]\left[\begin{array}{c}\Delta i_{dr}\\ \Delta i_d\end{array}\right].\end{array}$$

(13)

The small-signal model of the grid-connected VSI is obtained from the d-current dynamics and the grid d-reference voltage v_dr generated by the dq-frame VSI current control as

$$\begin{array}{l}{v}_d=L_{f}s{i}_d-L_f{\omega }_1{i}_q+e_d\\ v_{dr}=u_d-L_f{\omega }_1{i}_q+e_d\end{array}\}\hspace{1em}\hspace{1em}\stackrel{v_d=v_{dr}}{{\displaystyle \Rightarrow }}\hspace{1em}\hspace{1em}s\Delta i_d=\frac{1}{L_f}\Delta u_d,$$

(14)

where L_f is the inductance of the converter filter. According to (14), the small-signal state-space model of the grid-connected VSI is represented by

$$\begin{array}{l}\frac{d}{dt}\left[\Delta i_d\right]=\left[0\right]\left[\Delta i_d\right]+\left[\frac{1}{L_f}\right]\left[\Delta u_d\right]\\ \left[\Delta i_d\right]=\left[1\right]\left[\Delta i_d\right]+\left[0\right]\left[\Delta u_d\right].\end{array}$$

(15)

3.3. qZSI Modeling

This Subsection presents the small-signal state-space averaged model of the qZSI in Figure 1. The qZSI works in two different operational states during one switching cycle T: The shoot-through and the non-shoot-through states (see Figure 4) [11]. The first interval is T₀, where the inverter bridge is equivalent to short circuit. The second interval is T₁, where the inverter is equivalent to a current source, which represents VSI consumption. The shoot-through interval is defined by the duty cycle d = T₀/T and the non-shoot-through interval by T₁/T = 1 − d. The qZSI control of the duty cycle is also plotted in Figure 1. This control allows the adjustment of the dc-link voltage v_dc [11].

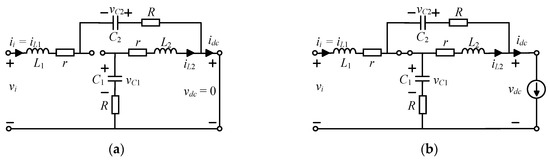
Figure 4. Equivalent circuit of qZSI with continuous current input: (a) Shoot-through state; (b) non-shoot-through state.

3.3.1. Power Circuit Model

The equations during each switching interval of the qZSI can be deduced from the equivalent circuits of the qZSI in Figure 4 [11].

• Shoot-through state: The matrices of the state-space model in this interval are

  $$\begin{array}{cc}\hfill \frac{d}{dt}\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]& =\left[\begin{array}{cccc}-\frac{\left(R+r\right)}{L_1}& 0& 0& \frac{1}{L_1}\\ 0& -\frac{\left(R+r\right)}{L_2}& \frac{1}{L_2}& 0\\ 0& \frac{-1}{C_1}& 0& 0\\ \frac{-1}{C_2}& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L_1}& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\end{array}\right]\hfill \\ \hfill \left[\begin{array}{c}\Delta i_i\\ \Delta v_{dc}\end{array}\right]& =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\end{array}\right].\hfill \end{array}$$

  (16)
• Non-shoot-through state: The matrices of the state-space model in this interval are

  $$\begin{array}{cc}\hfill \frac{d}{dt}\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]& =\left[\begin{array}{cccc}-\frac{\left(R+r\right)}{L_1}& 0& \frac{-1}{L_1}& 0\\ 0& -\frac{\left(R+r\right)}{L_2}& 0& \frac{-1}{L_2}\\ \frac{1}{C_1}& 0& 0& 0\\ 0& \frac{1}{C_2}& 0& 0\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L_1}& \frac{R}{L_1}\\ 0& \frac{R}{L_2}\\ 0& \frac{-1}{C_1}\\ 0& \frac{-1}{C_2}\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\end{array}\right]\hfill \\ \hfill \left[\begin{array}{c}\Delta i_i\\ \Delta v_{dc}\end{array}\right]& =\left[\begin{array}{cccc}1& 0& 0& 0\\ R& R& 1& 1\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{c1}\\ \Delta v_{c2}\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& -2R\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\end{array}\right].\hfill \end{array}$$

  (17)

The small-signal state-space averaged model of the qZSI is finally expressed from (16) and (17) as [11]

$$\begin{array}{cc}\hfill \frac{d}{dt}\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{C1}\\ \Delta v_{C2}\end{array}\right]& =\left[\begin{array}{cccc}-\frac{\left(R+r\right)}{L_1}& 0& \frac{\left(D-1\right)}{L_1}& \frac{D}{L_1}\\ 0& \frac{-\left(R+r\right)}{L_2}& \frac{D}{L_2}& \frac{\left(D-1\right)}{L_2}\\ \frac{1-D}{C_1}& \frac{-D}{C_1}& 0& 0\\ \frac{-D}{C_2}& \frac{1-D}{C_2}& 0& 0\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{C1}\\ \Delta v_{C2}\end{array}\right]+\left[\begin{array}{ccc}\frac{1}{L_1}& \frac{R\left(1-D\right)}{L_1}& \frac{V_1}{L_1}\\ 0& \frac{R\left(1-D\right)}{L_2}& \frac{V_1}{L_2}\\ 0& \frac{D-1}{C_1}& \frac{I_1}{C_1}\\ 0& \frac{D-1}{C_2}& \frac{I_1}{C_2}\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\\ \Delta d\end{array}\right]\hfill \\ \hfill \left[\begin{array}{c}\Delta i_i\\ \Delta v_{dc}\\ \Delta i_{L2}\\ \Delta v_{C1}\end{array}\right]& =\left[\begin{array}{cccc}1& 0& 0& 0\\ \left(1-D\right)R& \left(1-D\right)R& \left(1-D\right)& \left(1-D\right)\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}\Delta i_{L1}\\ \Delta i_{L2}\\ \Delta v_{C1}\\ \Delta v_{C2}\end{array}\right]+\left[\begin{array}{ccc}0& 0& 0\\ 0& -2\left(1-D\right)R& V_2\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}\Delta v_i\\ \Delta i_{dc}\\ \Delta d\end{array}\right],\hfill \end{array}$$

(18)

where D is the steady state duty cycle and V₁ = V_C1 + V_C2 − RI_dc, I₁ = I_dc − I_L1 − I_L2., V₂ = −V₁ + RI₁, with I_L1, I_L2, V_C1, and V_C2 being the steady state values of the state variables.

The qZSI input output current i_dc is obtained from the DC/AC VSI power balance, which, assuming a lossless VSI, can be written as

$$v_{dc}{i}_{dc}=v_d{i}_d+v_q{i}_q.$$

(19)

The power balance (19) is expressed as the following small-signal relation:

$$\begin{array}{l}{V}_{dc}\Delta i_{dc}+I_{dc}\Delta v_{dc}=V_d\Delta i_d+I_d\Delta v_d+V_q\Delta i_q+I_q\Delta v_q\\ \underset{V_d>>V_q}{\overset{E_q=I_q=0}{{\displaystyle \Rightarrow }}}\hspace{1em}\Delta i_{dc}=m_{d0}\Delta i_d-\frac{1}{m_{d0}}{G}_{dc}\Delta v_d+G_{dc}\Delta v_{dc},\end{array}$$

(20)

where m_d0 = V_d/V_dc is the steady-state operation point of the modulation function, G_dc = 1/R_dc = −P/V²_dc, P is the active power flowing through the VSI from the DC to the AC side (see Figure 1), V_d is the steady = state converter voltage, and V_dc and I_dc are the steady-state qZSI output voltage and current, respectively. The Matlab/Simulink model of this small-signal relation of the power balance is presented in Figure 2b.

3.3.2. Duty Cycle Control Model

The duty cycle control of the qSZI-based PV power system in Figure 1 is based on the adjustment of the dc-link peak voltage v_dc,p through a PI-based control of the dc-link voltage reference $V_{dc,\hspace{0.17em}p}^{*}$ together with a P-based control for the inductor-L₂ current. Finally, in order to smooth the duty cycle delivered to the VSI, a low-pass-filter (LPF) tuned to f_c = 25 Hz is used.

The control laws of the dc-link voltage and inductor-L₂ current loops are expressed as the small-signal relation

$$\begin{array}{l}{d}_r=k_p^L\left(k_p^{dc}+\frac{k_i^{dc}}{s}\right)(V_{dc,\hspace{0.17em}p}^{*}-v_{dc,\hspace{0.17em}p})-k_p^L{i}_{L2}\hspace{1em}\Rightarrow \\ \Delta d_r=-k_p^L{k}_i^{dc}\Delta q_{dc}-k_p^L{k}_p^{dc}\Delta v_{dc,\hspace{0.17em}p}-k_p^L\Delta i_{L2}\hspace{1em}s\Delta q_{dc}=\Delta v_{dc,\hspace{0.17em}p},\end{array}$$

(21)

where $k_p^{dc}$ and $k_i^{dc}$ are the proportional and integral gains of the dc-link voltage PI-based control, and $k_p^L$ is the proportional gain of the inductor—L₂ current P-based control. The small-signal averaged expression of the dc-link peak voltage is derived as [10]

$$v_{dc,\hspace{0.17em}p}=\frac{1}{1-d}{v}_{C1}\hspace{1em}\Rightarrow \hspace{1em}\Delta v_{dc,\hspace{0.17em}p}=\frac{1}{1-D}\Delta v_{C1}+\frac{V_{dc,\hspace{0.17em}p}}{1-D}\Delta d.$$

(22)

The small-signal state-space model of the duty cycle d_r is derived from (21) and (22) as

$$\begin{array}{l}\frac{d}{dt}\left[\Delta q_{dc}\right]=\left[0\right]\left[\Delta q_{dc}\right]+\left[\begin{array}{ccc}0& \frac{1}{1-D}& \frac{V_{dc,\hspace{0.17em}p}}{1-D}\end{array}\right]\left[\begin{array}{c}\Delta i_{L2}\\ \Delta v_{C1}\\ \Delta d\end{array}\right]\\ \left[\Delta d_r\right]=\left[-k_p^L{k}_i^{dc}\right]\left[\Delta q_{dc}\right]+\left[\begin{array}{ccc}-k_p^L& -\frac{k_p^L{k}_p^{dc}}{1-D}& -\frac{k_p^L{k}_p^{dc}}{1-D}{V}_{dc,\hspace{0.17em}p}\end{array}\right]\left[\begin{array}{c}\Delta i_{L2}\\ \Delta v_{C1}\\ \Delta d\end{array}\right].\end{array}$$

(23)

The small-signal state-space model of the LPF is represented by

$$\begin{array}{l}\frac{d}{dt}\left[\Delta d\right]=\left[-{\omega }_c\right]\left[\Delta d\right]+\left[{\omega }_c\right]\left[\Delta d_r\right]\\ \left[\Delta d\right]=\left[1\right]\left[\Delta d\right]+\left[0\right]\left[\Delta d_r\right].\end{array}$$

(24)

The Matlab/Simulink model of the duty cycle control is presented in Figure 2c.

4. PSCAD/EMTDC Model

PSCAD implementation of the qZSI-based PV power system is illustrated in Figure 5 according to the power and control systems of the qZSI-based PV power system in Figure 1 and the qZSI-based PV power system modeling in Section 3. The PSCAD model, composed of the power modules of the PV panel, qZSI, VSI, and AC grid, is shown in Figure 5a. Furthermore, Figure 5b presents the three control loops included in the qZSI-based PV power system, i.e., the PV voltage (left-top), current (right-top), and duty cycle (bottom) control loops.

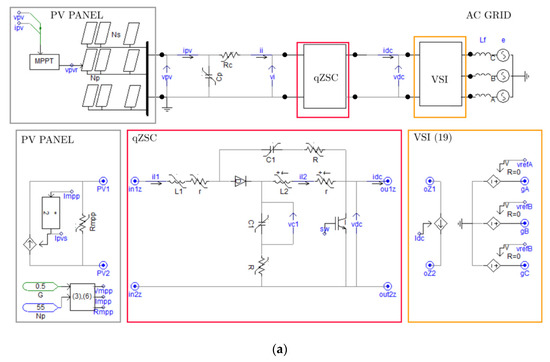
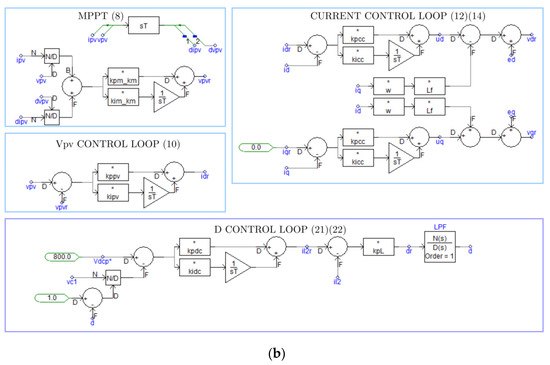
Figure 5. PSCAD/EMTDC model of the qZSI-based PV power system: (a) Power circuit; (b) control circuit.

5. Applications

Simulations with the Matlab/Simulink and PSCAD/EMTDC models of the qZSI-based PV power system in Figure 1 and Table 1 data are shown in Figure 6a. The PV panel supplies a 138 kW 1 kV DC PV power system connected to a strong 400 V AC grid. Note that small-scale (P_pv < 10 kW) PV power systems usually work with DC voltages below 1 kV [7,13,16], but large-scale PV power systems (P_pv > 10 kW) tend to work with DC voltages in the range of 1 kV to 1.5 kV to reduce the initial PV array cost and total cabling required [7,11,19,25]. In the application, the PV panel has 55 arrays connected in parallel, each of which consists of 42 PV Solarex MSX60 modules connected in series. Key data of these modules at 1 Sun are V_oc = 21 V, I_sc = 3.74 A, V_max = 17.1 V, I_max = 3.5 A, P_max = 59.9 W [2]. An irradiance level of 0.5 Sun and MPP voltage and current equal to V_mpp = 16.73 V and I_mpp = 1.77 A, which corresponds to a PV panel voltage, current and active power V_pv = 16.73 × 42 = 702.9 V, I_pvs = 1.77 × 55 = 97.35 A and P_pv = 702.9 × 97.35 = 68.2 kW, respectively, are considered in the studied cases. It must also be noted that traditional IGBTs at the 10 kHz switching frequency f_sw are set in the application, just as in [11,15,20]. It is well known that the use of SiC MOSFETs or Si MOSFETs would allow the switching frequency to be increased up to the 25–65 kHz range to reduce passive component size and improve system efficiency [17,21,25]. According to this, it would be interesting to further develop studies about the influence of switching frequency on dynamic behavior of qZSI-based PV power systems.

Table 1. qZSI-based PV power system parameters.

Circuit and Control	Parameters	Data
PV array	Np × Ns	55 × 42
	G, T	0.5 Sun, 25 °C
PV installation	Rc, Cp	0.0667 Ω, 10 mF
qZSI source network	L1 = L2, r1 = r2	0.3 mH, 0.011 Ω
	C1 = C2, R1 = R2	3 mF, 0.006 Ω
	fsw	10 kHz
VSI	Rf, Lf	≈0 Ω, 0.4 mH
MPPT control	$k_p^m$,$k_i^m$	0.01 Ω, 0.5 Ω/s
PV control	$k_p^{pv}$,$k_i^{pv}$	1.8 Ω−1, 75 Ω−1/s
CC control	$k_p^{cc}$,$k_i^{cc}$	0.424 Ω−1, 150 Ω−1/s
D control	$V_{dc,\hspace{0.17em}p}^{*}$	800 V
	$k_p^{dc}$, $k_i^{dc}$	0.016 V−1, 125 V−1/s
	$k_p^L$	10−4A−1

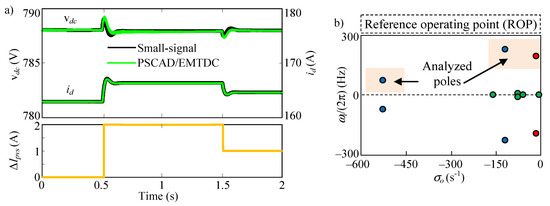
Figure 6. Study of the qZSI-based PV power system with the Matlab/Simulink and PSCAD/EMTDC models: (a) Time domain simulations. (b) Eigenvalues.

The Matlab/Simulink small-signal model of the qZSI-based PV power system model depends on the steady-state stable operation point values (i.e., V_mpp = 702 V, I_mpp = 94.2 A, I_L1 = I_L2 = 94.1 A, V_c1 = 760 V, V_c2 = 63 V and D = 0.06), as obtained from PSCAD/EMTDC time domain simulations.

The dynamic response of the dc-link voltage v_dc and the grid d-frame current i_d is studied when the PV panel current I_pvs is increased by 2 A and subsequently decreased by 1 A at 0.5 s and 1.5 s, respectively. The fair accuracy between the qZSI-based PV power system models is worth noting by comparing the dynamic response of the Matlab/Simulink and PSCAD/EMTDC simulations. It can also be noted that the PV power system is stable at all operating points. As an example, the PV power system eigenvalues of the operating point before 0.5 s, which is called reference operating point (ROP), are shown in Figure 6b. It is observed that the PV power system has no right hand plane (RHP) eigenvalues at the ROP. The same is true for the other two operating points.

The sensitivity of the circuit and control parameters on the qZSI-based PV power system eigenvalues and stability is numerically analyzed from the Matlab/Simulink small-signal state-space averaged model (see results in Table 2). It can be observed that several parameters affect to some extent (i.e., low, medium, or high sensitivity) the locus eigenvalues but not all of them impact on system stability. In order to analyze this issue, Figure 7 shows the locus of the ROP eigenvalues with low, medium, and high sensitivity (labeled in blue and red as in Figure 6b) with respect to the circuit and control qZSI-based PV power system parameters. These parameters are varied according to 10% increments above and below the ROP circuit and control parameter values. The arrows indicate the growing value of the circuit and control parameters. The circuit and control parameters with no impact on the eigenvalues are omitted in Figure 7. It is observed that only the red eigenvalue is related to system instability because it could be shifted to the RHP by circuit and control parameter variations. Thus, only the circuit and control parameters that affect this eigenvalue can impact to some extent (low, medium, or high sensitivity) on system stability (i.e., C_p, R_c, L₁, L₂, C₁, C₂, I_pvs and $V_{dc,\hspace{0.17em}p}^{*}$). The sensitivity level depends on how the red eigenvalue approaches close to the RHP.

Table 2. Sensitivity analysis of the qZSI-based PV power system eigenvalues and stability to circuit and control parameters.

Circuit Parameters				Control Parameters
		Sensitivity				Sensitivity
Circuit	Parameters	Eigenvalues	Stability	Control	Parameters	Eigenvalues	Stability
PV installation	Cp	Low	Low	MPPT	$k_p^m$	Null	Null
	Rc	Medium	Low		$k_i^m$	Null	Null
qZSI source network	L1	Medium	Low	PV	$k_p^{pv}$	Low	Null
	L2	High	High		$k_i^{pv}$	Null	Null
	C1	Medium	Low	CC	$k_p^{cc}$	High	Null
	C2	Medium	Low		$k_i^{cc}$	High	Null
Grid	Lf	Medium	Null	D	$V_{dc,\hspace{0.17em}p}^{*}$	Low	Medium
	ed	Null	Null		$k_p^{dc}$	Null	Null
PV array	Ipvs = 2I·mpp	Medium	High		$k_p^L$	Null	Null
	Rpv = Rmpp	Null	Null

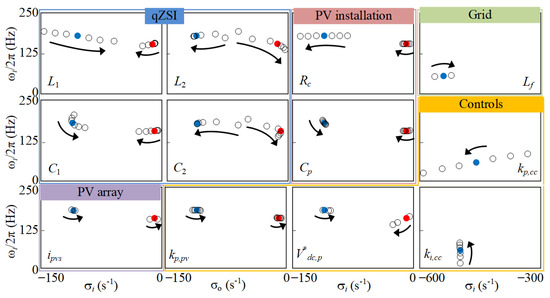
Figure 7. Root locus of the qZSI-based PV power system eigenvalues.

It was numerically verified that only the external circuit parameter I_pvs = 2·I_mpp in Figure 5a can cause system instability. This is so because it is related to the active power P flowing through the VSI (large I_pvs values lead to high P values) and this power affects system stability. The small-signal DC input current and voltage of the VSI, i.e., the qZSI output current and voltage i_dc and v_dc, are related by means of the virtual conductance G_dc = –P/V²_dc (20), which has a negative value for inverter operation of the VSI (i.e., for P > 0). In this situation, the VSI has a non-passive behavior at the DC side, which reduces the damping of qZSI-based PV power systems at resonances, and this can lead to system instability. This external parameter I_pvs increases when the irradiance level G and the number of PV panels in parallel N_p increase (see Figure 3c). Therefore, these factors increase the active power P flowing through the VSI and enlarge the value of G_dc, compromising qZSI-based PV power system stability. It can be observed from Figure 7 that low values of L₂, C₂, $k_p^{pv}$ or high values of L₁, C₁, R_c, C_p can move the system away from the RHP and help make the system more stable. It must also be noted that any factor that reduces the value of G_dc in (20), such as a large steady state qZSI output voltage V_dc, may also improve qZSI-based PV power system stability. For this reason, the increase of $V_{dc,\hspace{0.17em}p}^{*}$ moves the system away from the RHP in Figure 7. Comparison of the above conclusions with the qZSI [9] and qZSI-based PV power system [22], ref. [23] stability studies in the literature shows that:

• The influence of the inductors L₁ and L₂ and the capacitors C₁ and C₂ on qZSI dynamic behavior [9] can be extended to qZSI-based PV power system dynamic behavior: Inductors and capacitors have a high and low impact on the dynamic response, respectively. However, unlike [9], the present study differentiates the value of both inductors and concludes that the increase of L₁ may improve qZSI-based PV power system stability.
• The detailed analysis of the present study shows the impact of the qZSI-based PV power system operating point on instabilities, in particular high and low values of the active power P flowing through the VSI and the steady-state qZSI output voltage V_dc, respectively. The latter is directly related to the negative impact of high values of the duty cycle control in [22,23].
• The impact of the AC network on qZSI-based PV power systems [22,23] is not studied in this paper because a strong AC grid is considered in the application. However, the proposed Matlab/Simulink and PSCAD/EMTDC small-signal state-space averaged models can be used to analyze this concern.

PSCAD/EMTDC simulations are shown in Figure 8 to verify the above conclusions. The dynamic response of the currents i_L1, i_dc, and i_d to G, L₂, $V_{dc,\hspace{0.17em}p}^{*}$ and C₁ variations is plotted. It can be noted that the increase of G from 0.5 Sun to 0.75 Sun causes system instability. On the other hand, the decrease of L₂ from 0.3 mH to 0.225 mH (ΔL₂ = −25 %), the increase of $V_{dc,\hspace{0.17em}p}^{*}$ from 800 V to 960 V (Δ$V_{dc,\hspace{0.17em}p}^{*}$ = +20%), and the increase of C₁ from 3 mF to 3.9 mF (ΔC₁ = +30%) restore system stability after the qZSI-based PV power system becomes unstable due to the step-up of the irradiance level. Although not shown for the sake of space, the influence of the other parameters (i.e., N_p, C₂, $k_p^{pv}$, L₁, R_c and C_p) on stability was also validated.

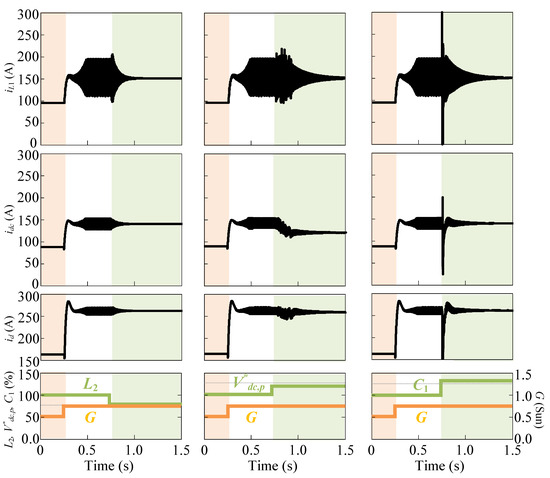
Figure 8. Stability study with PSCAD/EMTDC simulations.

6. Conclusions

This first part of the paper contributes to qZSI-based PV power system stability studies with two simulation tools based on a Matlab/Simulink and a PSCAD model of qZSI-based PV power systems. Both models consider all the main components and controls. They make it possible to analyze system stability based on system eigenvalues and dynamic numerical simulations, respectively. The second part of the paper (Section 5) contributes with the stability study performed from the above models and the discussion about the impact of parameter variations on system stability. Direction on the qZSI-based PV power system stability is provided to designers, engineers, and researchers. The following recommendations and solutions are proposed:

• The operating point is the main factor related to system stability. In particular,

  ○

  The increase of active power flowing through the VSI, which directly depends on the irradiance level and the number of PV panels in parallel, can lead to system stability loss.

  ○

  The dc-link peak voltage also affects system stability. According to this, the increase of the dc-link peak voltage reference may be used to enhance stability because it mitigates the impact of active power flowing through the VSI.

• The qZSI component design is important for upgrading PV power system stability. In particular, low values of L₂, C₂ and high values of L₁, C₁ can help to make the system more stable.
• Other PV power system parameters such as the PV panel shunt capacitor C_p and the DC cable R_c could help to improve stability if they take high values.
• PV installation, qZSI, PV control, and D control parameters have little influence on system stability.

All of the above was verified through time domain simulations with the proposed Matlab/Simulink and PSCAD models, which may become a powerful tool for analyzing other factors related to dynamic interaction between the DC and AC side of qZSI-based PV power systems such as the effect of the AC impedance network on qZSI dynamics.