Abstract
The flow developed on a tidal site can be characterized by combinations of turbulence, shear flows, and waves. Horizontal-axis tidal turbines are therefore subjected to dynamic loadings that may compromise the working life of the rotor and drive train components. To this end, a series of experiments were carried out using a 0.9 m horizontal-axis tidal turbine in a tow tank facility. The experiments included two types of regular waveforms, one of them simulating an extreme wave case, the other simulating a more moderate wave case. The second regular wave was designed to match the peak period and significant wave height of an irregular wave which was also tested. Measurements of torque, thrust, and blade-bending moments were taken during the testing campaign. Speed and torque control strategies were implemented for a range of operational points to investigate the influence that a control mode had in the performance of a tidal stream turbine. The results showed similar average power and thrust values were not affected by the control strategy, nor the influence of either the regular or irregular wave cases. However, it was observed that using torque control resulted in an increase of thrust and blade root bending moment fluctuations per wave period. The increase in fluctuations was in the order of 40% when compared to the speed control cases.
1. Introduction
Achieving commercial and financial viability in the marine energy industry is challenging due to the complex and variant nature of the conditions seen by Horizontal-Axis Tidal Turbines (HATTs). Non-uniformity and unsteadiness occurring in the marine environment in the form of turbulence, sheared flows, surface waves, and tidal cycles mean that tidal turbines are subjected to a wide range of dynamic loading characteristics. The turbine components must be able to withstand the maximum forces induced by the hydrodynamics and be resistant to fatigue damage due to the cyclic nature of these loads. The high variability in the flow characteristics also has implications for optimization of the device in terms of the sizing of components. Fluctuations in power production, resultant from the dynamic tidal resource, pose significant challenges for the power conditioning and control systems. Therefore, it is imperative that the realistic loading characteristics are quantified and the way in which these interact with the turbine system are fully understood.
The potential impacts of wave-current flows on the performance of HATTs have been highlighted by several authors through the use of numerical models. Reference [1] conducted a sensitivity analysis on a Blade Element Momentum Theory (BEMT) model and showed that wave height and spatial non-uniformity in the current are among the most influential parameters on the loading of a turbine rotor. The eccentric thrust loads generated are transmitted through the drivetrain, directly affecting the internal components (e.g., bearings and seals), as later demonstrated in [2]. Reference [3] used computational fluid dynamics techniques (CFD) to investigate the effects of oscillatory motion of waves on HATTs blades. They found that combined wave-current conditions have a substantial influence on the bending moments acting on the turbine, which translates into damaging effects on the drivetrain components. Similarly, Reference [4] employed a CFD model to demonstrate that the maximum thrust force on a tidal stream rotor in wave-current flow increased by approximately 16% compared to that under the relevant current alone case. They also concluded that dynamic stall can occur in some conditions, depending on the turbine position relative to the wave phase.
A handful of experimental studies to support the computational work analyzing the effects of wave-current interactions on small-scale tidal turbine have also been conducted by [5,6,7,8]. A summary of the test parameters used in these investigations is presented in Table 1. Many of these studies analyzed the turbine loads induced by a single waveform (one wave period and wave height combination), and those that included variation in wave height, wave period, and current velocity have limited the tests to only a small range of values. Conditions that would be more consistent with extreme waves have not been included in the studies. In some of the studies the results are also limited to a small portion of the power curve (i.e., small variation in the angular velocity of the rotor) and thus the wave-current effects are not fully visualized. The high blockage ratio present in the study of [5] will have significantly influenced the performance of the turbine, as explained in [9,10], hindering comparison of their results with the other studies.

Table 1.
Summary of experiments undertaken for wave-curreny interactions with three-blade HATTs.
The general consensus from these studies is that the addition of waves to a current does not significantly affect the average value of thrust or torque. However, the torque and thrust fluctuations are substantially increased with the addition of waves, for example [6] found that these were 2–3 times higher than under current alone. The reported size of these fluctuations does vary between the studies, indicating that better quantification of the interaction effects between the different test parameters is necessary to understand how the magnitude of the loading fluctuations changes over a full range of flow conditions.
A further consideration regarding the existing experimental studies is the influence of the facility used. The studies of [7,8] were conducted in tow tanks and consequently without the presence of turbulence. In contrast those of [5,6] were conducted in a flume with a turbulent current; the different turbulence intensities in their test programs are included in Table 1. The facility type will also affect the shape of the waveform, as the turbine is towed into the waves in the tow tank, but the waves travel with the current in the flume tests. The impact of these differences on the turbine loads is not well understood. Direct comparison of the different test campaigns in Table 1 would help elucidate some of these effects, but this is problematic due to the widely different parameter values used in each program.
Further testing programs related to the investigation of waves-current interactions and tidal stream turbines have also been investigated by [11,12,13]. Reference [11] carried out several experiments to investigate the effects of oblique waves in the loading of tidal turbines where it was observed that the presence of in-line waves was more detrimental to the tidal turbine than yawed waves. In a similar context, References [12,13] examined the structural and power variations in a tidal turbine prototype when this was subjected to opposing and focused waves. It was found that peak load and power outputs increased by up to 85% and 200%, respectively, when focused waves were used and were compared to current only conditions. This research also shows the necessity of quantifying the thrust loadings that a tidal turbine will need to withstand under extreme weather conditions.
It is worth mentioning that the prototypes employed by the authors cited in Table 1 and above have been designed to operate under a consistent control mode. According to the literature, the control mechanism used on those investigations was either based on controlling the torque or speed developed by the turbine with most of them operated under speed control. However, correlations between the control method used to achieve the desired operating region and structural loadings produced on the turbines were never discussed. This type of investigation is notably relevant as commercial tidal turbines usually work under a variable-speed controller, in a similar fashion as wind turbines [14].
Recent work published by [15] demonstrated the applicability of using an open-loop control strategy and a constant rotational speed proportional–integral–derivative (PID) feedback loop control on a 1.5 m diameter three-bladed horizontal-axis turbine. Their research showed that an increase in peak performance of almost 14% was achieved when maintaining a constant rotational speed in comparison to an open-loop control strategy. Similarly, Reference [16] explored the use of two reinforcement learning algorithms to control a tidal turbine based on maximum power point tracking. These simulated strategies included a Q-learning and a Neural Fitted Q-iteration, both were assessed in different flow conditions; i.e., current only, turbulence, and two types of waves. The outcomes showed that by using both strategies, the algorithms converged to the optimal power coefficient. However, there is no mention of how each control strategy reflected into the temporal fluctuations of the rotor loading.
To the authors’ knowledge, the latter has only been initially examined by [17]. In that study, two tests were conducted on a small-scale turbine where the equivalent operating point was set with torque and speed control modes. It was observed that the torque-controlled test resulted in a slightly higher average blade force than with the corresponding speed-controlled test. However, this preliminary study only included a single test done in the region of peak power conditions. Therefore, the research presented here aims to expand on that initial work by investigating a wide range of operating conditions and three types of waveforms, including regular and irregular waves.
2. Methodology
The experimental campaign encompassed testing of a small-scale horizontal-axis turbine of 0.9 m rotor diameter at the CNR-INM (formerly INSEAN) towing tank in Rome. The tank dimensions are 9 × 3.5 × 220 , resulting in a blockage ratio of 2.8%. The low blockage characteristics in the facility ensured little influence of this should be seen in any of the tests. The center of the turbine hub was installed at 1.5 below the still water surface on a steel stanchion clamped from above and positioned in the mid-section of the tank as shown in Figure 1.

Figure 1.
Test setup in the CNR-INM wave-tow facility. Horizontal-axis turbine mounted on the tow carriage via stanchion with a set of ultrasonic wave probes on the left.
2.1. Turbine Design Overview
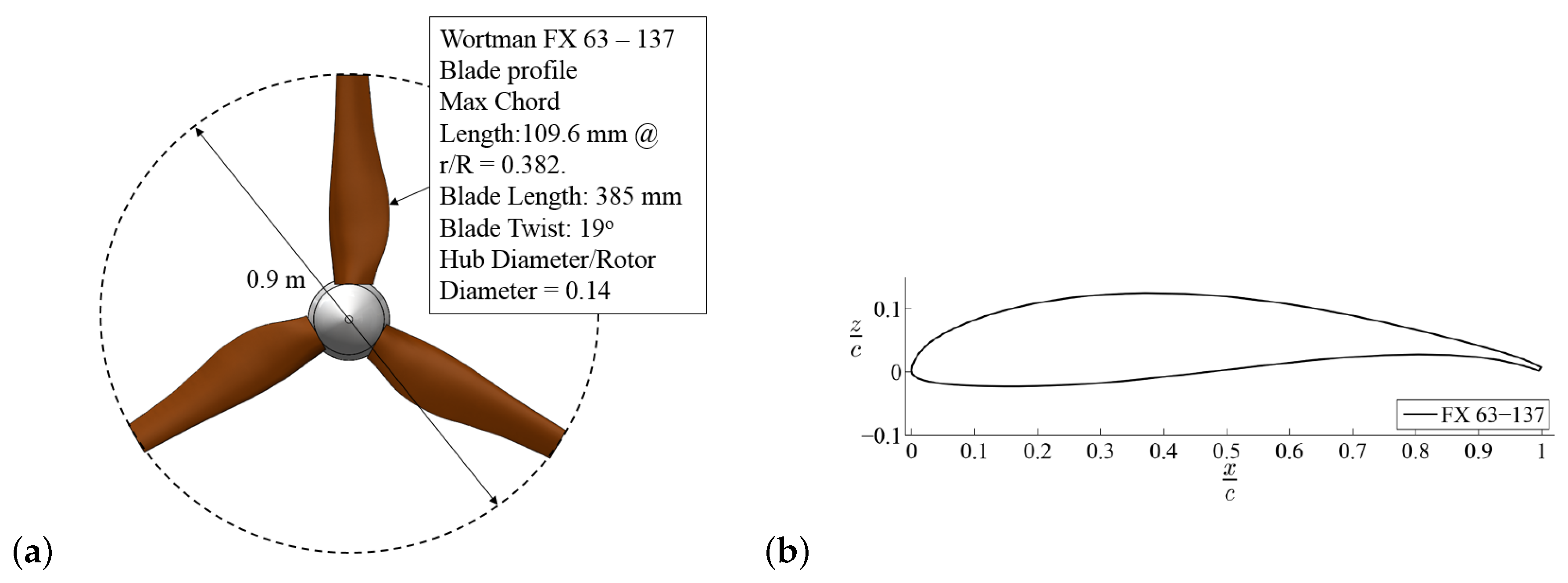
The HATT prototype used was a 3-bladed, direct-drive turbine. The rotor blades are 0.385 in length and were designed using a Wortmann FX 63-137 aerofoil profile. A schematic of the rotor and blade profile can be seen in Figure 2. The pitch angle was set at 8° for all tests. The blade root design was selected to provide a smooth transition to the hub, adequate structural support, and to house the blade root strain gauges. Full details of the turbine design and hub geometry are given in [18,19]. The turbine was equipped with a Bosch Rexroth permanent magnet synchronous machine (PMSM) which was configured to operate in either constant speed or torque mode. Either speed or torque control strategies were applied for all the tests discussed in this paper.
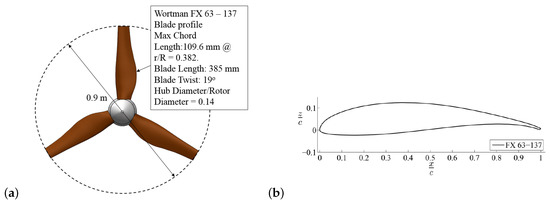
Figure 2.
Rotor schematic for the 0.9 HATT used for the testing (a) and Wortman FX 63-137 profile used to create the turbine blade geometry (b).
To monitor power capture, the induced rotor torque was quantified from the torque generating current (TGC) measured at the motor. The TGC is the quadrature axis current (iq) required by the motor to generate a specified torsional load (). The relationship between the TGC and the torque developed by the motor is related by the, ‘motor torque constant’, which in the case of the PMSM used was specified by the manufacturer as 6.60 −1. Under steady state operation, the motor torque is equal and opposite to the torque developed by the rotor blades () when operating in the tow tank. This can be seen in the ‘swing’ equation for the scale model HATT drive train which is presented in Equation (1).
where, J is the moment of inertia of the turbine drive shaft and rotor in and is the rotational position of the turbine rotor. is the mechanical torque corresponding to the rotor and is the motor torque. In the preceding discussion steady state operation refers to the operation whereby the rotational acceleration of the rotor is approximately zero, i.e., ≃ 0. Under set-point speed control operation, if the turbine rotor produces a large torque during operation, the motor will have to apply a torque in the opposite direction to maintain the specified rotational velocity. Conversely, if the turbine rotor produces a small positive torque then the motor torque will be reduced, again to maintain the zero rotational acceleration objective inherent in speed control operation. Dynamic friction and damping in the drivetrain due to seals and bearing losses was quantified to negate the effects of the lumped dynamic friction and damping factor D in Equation (1). The dynamic friction and damping was obtained by measuring the TGC at several different rotational speeds (rpm) in still water without the blades attached to the hub. The rotor torque was computed as:
The turbine housed an optical encoder for position and rotational velocity measurements. The through-bore encoder was mounted on the drive shaft in close proximity to the PMSM. The encoder is a Heidendain ECN 113. The accuracy of the instrument specified by the manufacturers is ±0.0056°. To monitor the thrust loading on the turbine rotor, an Applied Measurements thrust transducer was fitted on the driveshaft downstream of the rotor hub but upstream of seals and thrust bearings. Calibrations were provided for each direction by the manufacturer. The offset in the calibrations was checked prior to each test run from the recordings made with the turbine and tow carriage stationary. This constant was then taken as the actual offset for the calibration for each test, along with the gradient from the supplied calibrations. Noise in the raw thrust signal was removed prior to analysis by using a consistent gradient filter and maximum and minimum cut off values.
Each blade root was also strain gauged to measure the thrust-wise bending moment applied to the blade. Due to a malfunction of the measuring system in blade 1 only the measurements from the roots of blades 2 and 3 are discussed for the tow-only and regular wave cases.
Data acquisition from all channels (turbine, carriage, flow measurement equipment) were synchronized in terms of their start time using a trigger. Data capture was set at 100 for the flow measurement, carriage, rotor thrust, and blade strain gauge measurements. Data from the motor itself (TGC, rotor speed and rotor position) was sampled at 50 .
2.2. Control Strategy
As discussed, a PMSM was used to provide braking torque (in the torque control case) and to maintain a set-point turbine rotational velocity (in the speed control case). The PMSM was managed by a drive section. The three-phase supply (420 , 50 ) was rectified from AC to DC through a Voltage Source Converter (VSC). An inverter converted the DC bus voltage to a three-phase AC voltage which was connected to the motor. Both the rectifier and inverter were connected via a DC bus integrated with a DC bus capacitor, the voltage at the DC bus was maintained at 750 . The power flow to and from the motor was managed by the VSCs either side of the DC bus—similar to back-to-back setup used for tidal stream and wind turbines adopting a direct-drive PMSM topology. The VSC operated with a switching frequency of 4 kHz. The use of back to-back VSCs and the encoder permitted the use of a servo-based vector-oriented control (VOC) strategy to regulate the turbine’s torque. An additional velocity control loop was also included to set the desired rotational velocity; thus, providing the ability to select the appropriate control strategy; i.e., speed or torque, during the testing campaign. Both control strategies used close-loop control. In the case of the torque control setup the current in the motor phases was measured via a hall effect probe and feedback into the control system to generate a phase current error which is feed through a PID controller. Likewise, in the speed control case the turbine rotational velocity was measured via the encoder and used as feedback into the velocity control loop. Again, the error signal was corrected via a PID controller.
The set-point rotational velocities and applied braking torsion maintained by the motor for each test were selected to undertake testing at a range of tip speed ratio settings (as defined in Section 2.5). The PID controller in both the speed and torque control loops were tuned with guidance from the motor and PLC supplier to achieve critical response by setting appropriate proportional gain values and integral action times.
2.3. Test Program and Procedures
The test program consisted of tow-only, two regular wave-tow, and irregular-wave-tow cases. The tow speed was set equal to 1 m/s for all the cases, and was designed to provide approximately Reynolds independent conditions, (based on chord length at a radial distance of 70% from root to tip). The regular wave-tow cases were divided in two waves types; waves that provided extreme loading conditions to the turbine prototype and here they are referred to as ‘extreme wave-tow’ and characteristic regular waves that corresponded to the significant wave height (HS) and peak wave period (TP) of the irregular wave cases studied here. The second type of regular wave-tow are simply referred to here as ‘regular wave-tow’. The irregular wave cases are referred to as ‘Irregular wave-tow’. The wave height (H) of the regular wave-tow cases was limited by the highest peaks in the irregular wave case not exceeding the maximum possible wave height in the facility (0.45 ). A Jonswap spectrum was used for the irregular waves as a starting point to simulating more realistic wave conditions, with relevance to projects in the North Sea. Table 2 shows a summary of the given test parameters.

Table 2.
Test matrix showing the wave cases and control type used throughout the test campaign. All tests were run at 1.0 m/s.
For each flow condition, tests were run in speed control mode and then in torque control mode, with the set speed and torque values varied between test runs to simulate a range of tip speed ratios for each flow condition. Repeat tests were conducted where time allowed to check for consistency in the measurement systems and estimate uncertainty in the results. Table 3 shows the cases that were repeated throughout the testing campaign for a specific flow condition and control strategy.

Table 3.
Number of tests done for a specific case.
Duration of the Tests
Prior to each test, a recording was taken with stationary blades and carriage, to check initial readings on the instrumentation. To start a test the desired speed or torque set-point was selected and then the carriage was started.
The durations of the tow-only tests were approximately 100 . The repeated tests were recorded for 50 due to time constrains. The regular wave tests were initiated with the carriage positioned halfway along the tank, compromising on test length but maximizing the time before reflections reached the carriage. This resulted in approximately 30 wave forms or 40 of useable data.
For the irregular waves, the test time was maximized to better replicate the Jonswap spectrum, so full carriage runs were completed without mitigating reflections from the beach. Thus, it was possible to capture nearly 120 of data for the irregular wave cases. While not ideal, this was deemed appropriate for preliminary testing in irregular waves to gain insight and start to build knowledge to feed into further testing campaigns during the project where longer test times and reduced reflections will be possible.
2.4. Flow and Wave Measurements
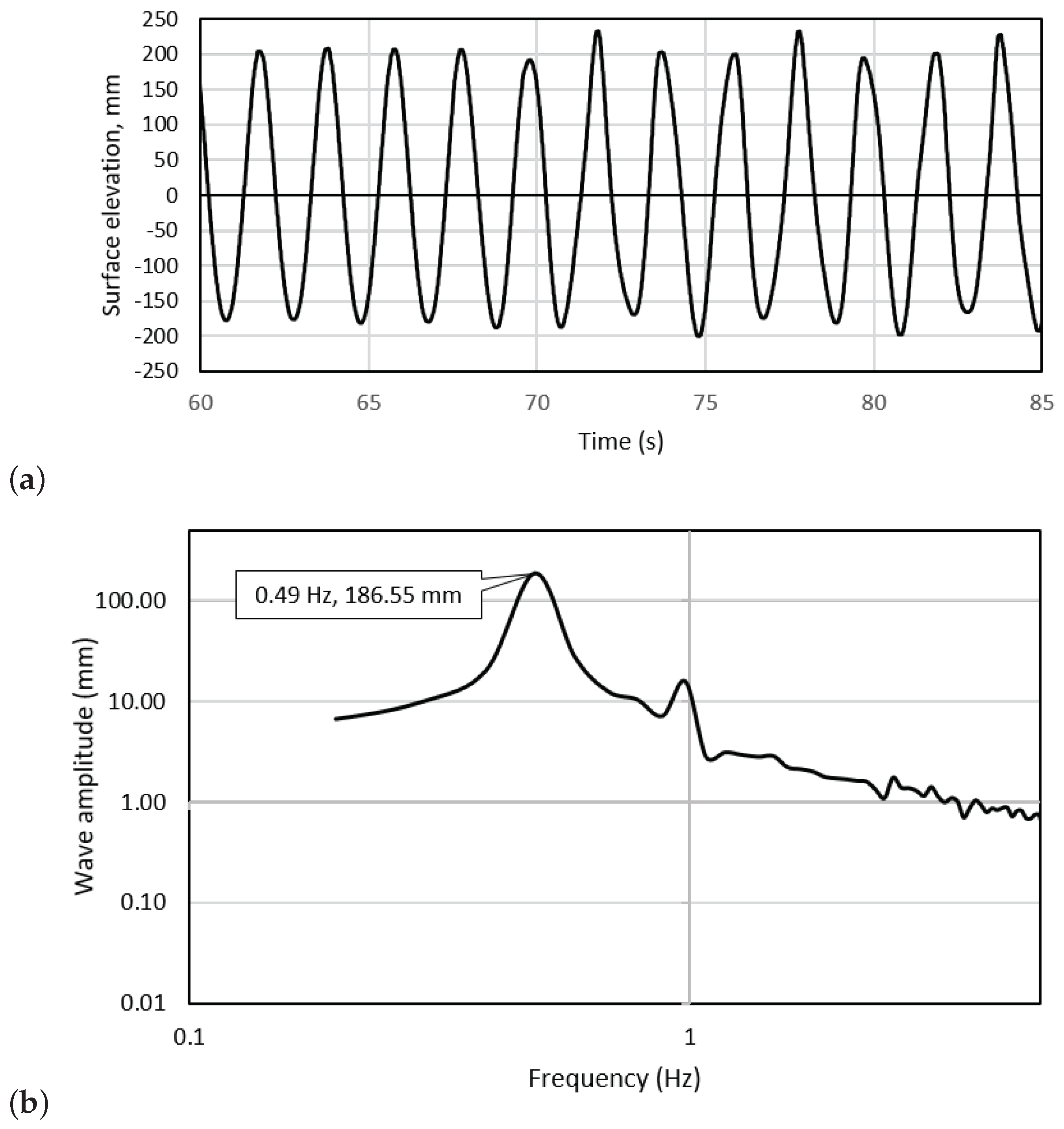
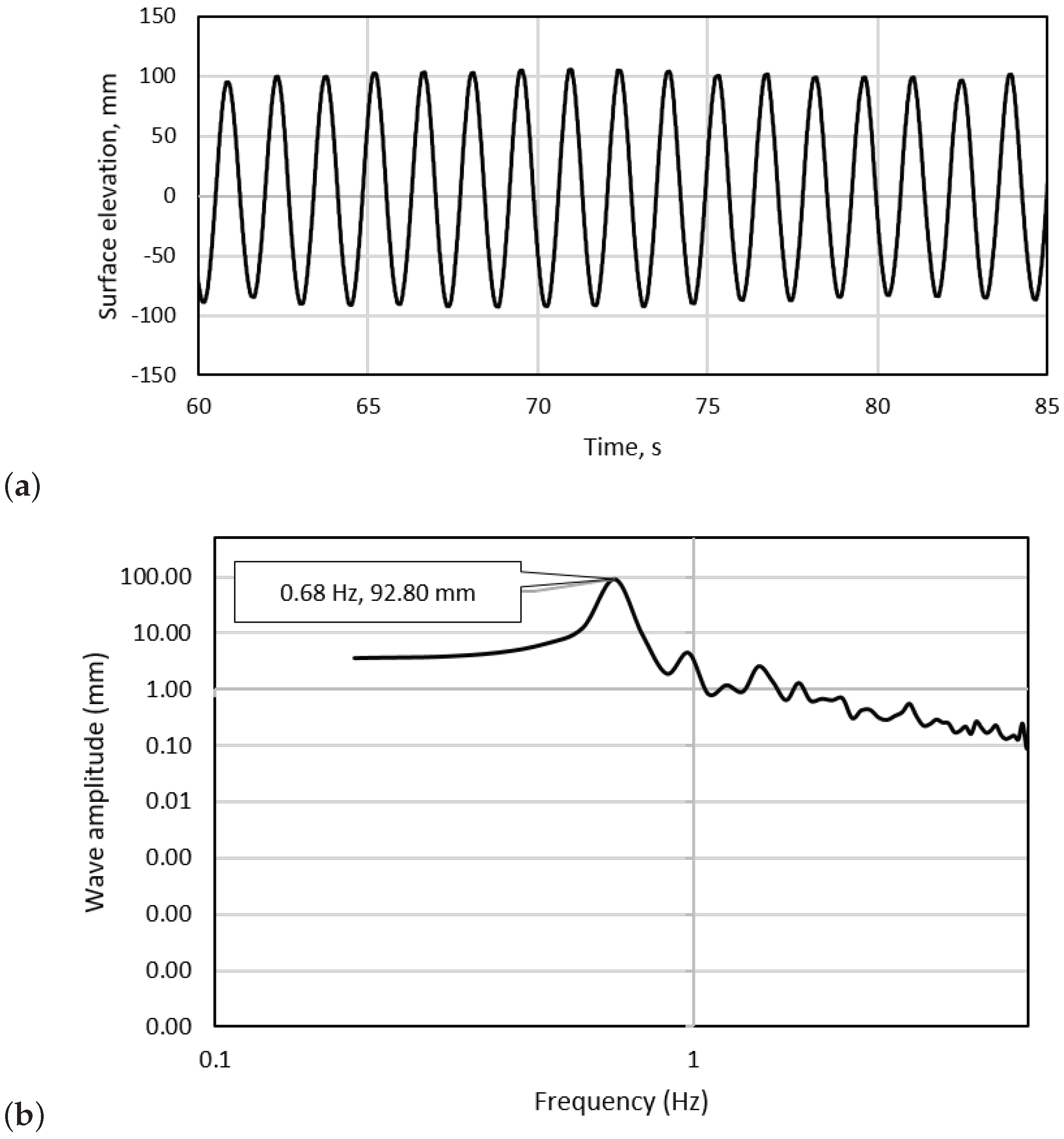
The surface elevation during wave tests was measured primarily by using a capacitance type wave gauge placed in-line with the turbine hub in the cross-stream direction. The distance between the turbine hub and the wave probe was approximately 1.0 . This was calibrated by setting the gauge to a series of known positions in still water. The average wave height recorded across all regular wave-tow tests was 0.19 , with a standard deviation of 0.001 between tests. The average wave period was 1.44 , with a standard deviation of 0.001 between tests. The average wave height recorded across all extreme wave-tow tests was 0.39 m, with a standard deviation of 0.002 between tests. The average wave period was 2 , with a standard deviation of 0.002 between tests. A sample of the wave forms obtained for the regular and extreme waves obtained in two tests can be observed in Figure 3 and Figure 4.
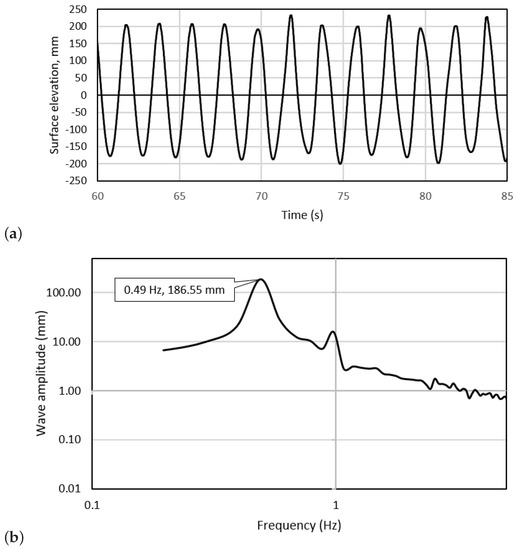
Figure 3.
Surface elevation of one of the Extreme wave-tow cases, demonstrating an average wave height of 0.39 m (a,b) the frequency spectrum of the signal.
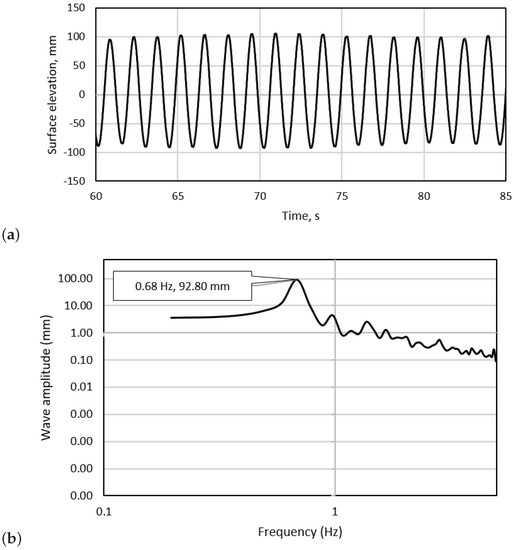
Figure 4.
Surface elevation of one of the Regular wave-tow cases, demonstrating an average wave height of 0.19 m (a,b) the frequency spectrum of the signal.
It can be noticeable in Figure 3a and Figure 4a that the wave heights obtained for each of the regular and extreme tests were consistent. The average wave height across the entire length of the signal for each of the regular wave-tow cases had a deviation of 2.8% of the mean value whereas a slightly higher variability was observed for the extreme wave-tow cases with a variation of nearly 4% of the mean value.
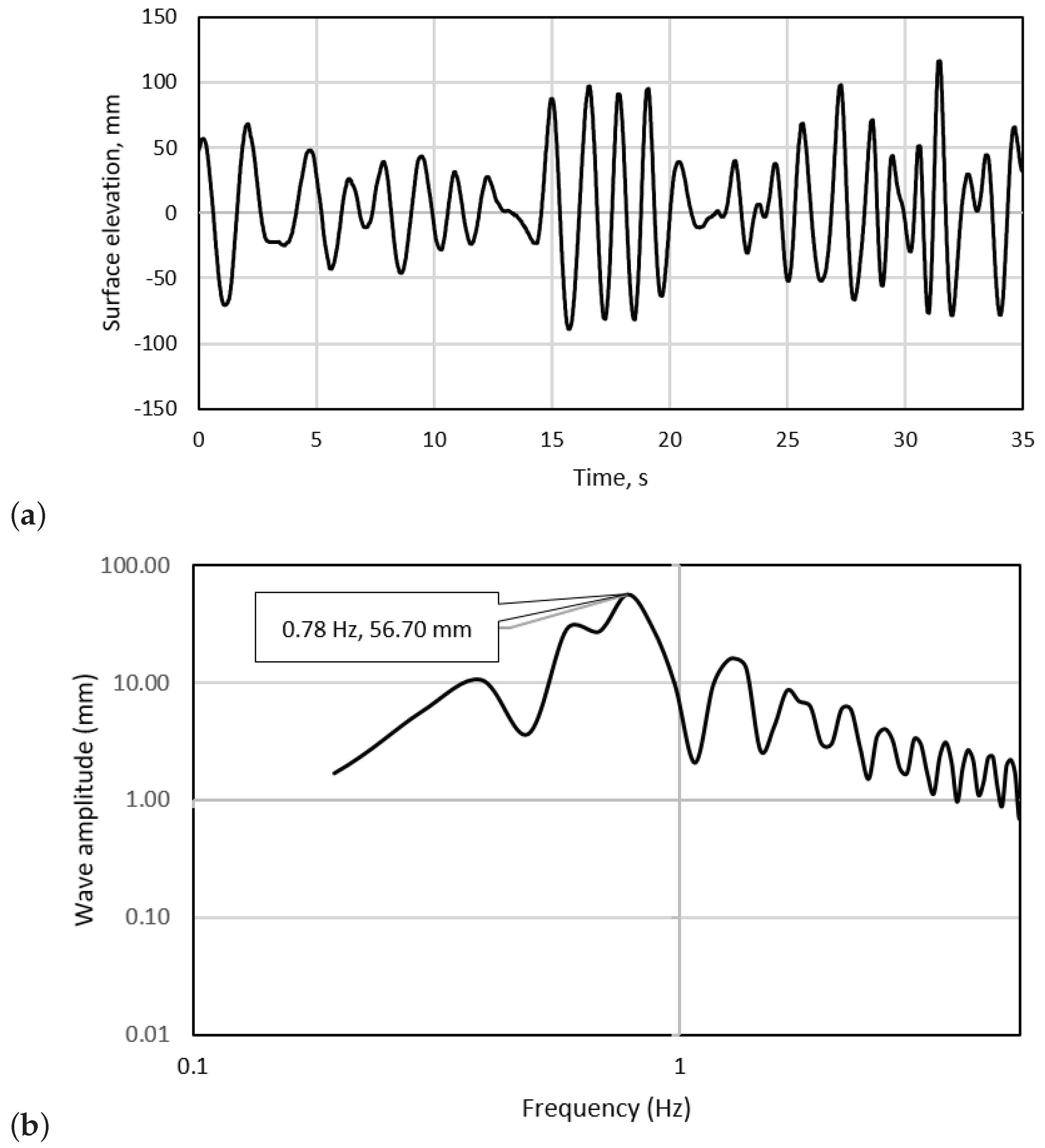
For the irregular wave tests, the records were analyzed in the time domain and the zero up-crossing points were selected to define each wave period. Reasonable agreement between the average wave period and wave height was obtained between repeated test runs. However, variations between the repeated records in terms of the maximum and minimum wave periods were noticeable. The average wave period and wave height are also smaller than the programmed significant wave height and peak period, as it can be seen in Table 4.

Table 4.
Characteristics of the irregular wave tests using the zero up -crossing method.
While the irregular wave forms in this study are somewhat arbitrary in nature, these do still allow the effect of dynamic changes in wave height and period on the turbine loading to be investigated. They will provide a preliminary insight into the possible effects of random wave patterns on the turbine in contrast with regular waveforms. A picture of the surface elevation recorded during the irregular wave tests can be observed in Figure 5.
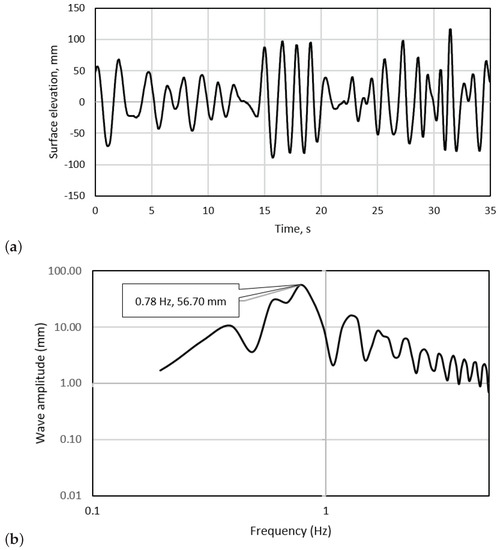
Figure 5.
Water surface elevation time series for the irregular wave case undertaken (a,b) the frequency spectrum of the signal.
The carriage velocity reading will be used to provide an average speed, which should suffice considering that wave-current interaction effects should not be present in a tow tank, resulting in zero mean effect on the ‘current’. When investigating the data in the time domain the wave height measurements will be used to represent the flow conditions.
2.5. Data Processing
The analysis of the data will be described in terms of the following non-dimensional parameters:
where P and T are the average hydrodynamic power and thrust generated by turbine. The power is calculated using the TGC, as previously explained in Section 2.1 multiplied by the turbine angular velocity in rad/s; thus, given a final output in Watts. M is the blade root bending moment. The swept area of the rotor including the central hub is approximately 0.64 m2, deriving it from the turbine radius (r) of 0.45 m. The density of the water was considered in these calculations as 999 kg/m2. Both power () and thrust () coefficients are related in the results section to the tip speed ratio (TSR). This non-dimensional value defines the ratio between the blade tip speed () and the tow velocity (V), as shown in Equation (6). The flow velocity used in these experiments was 1.0 m/s.
The loading fluctuations analysis will be carried out by using maximum and minimum values of the time domain signals. The data processing will also include the frequency domain analysis of the signal.
3. Results and Discussion
The results from the turbine thrust, torque, and blade root bending moment measurements are discussed in this section. Section 3.1 describes the results of power and thrust in terms of non-dimensional parameters, as discussed in Section 2.5. Section 3.1 also includes the average values of the blade root bending moments. Section 3.2 presents the results as average fluctuations per wave period. These mean fluctuations were obtained by calculating the average of the discrete signal periods (peak to peak range). The spectral analysis is presented in Section 3.3 to investigate the relation between the amplitude of the peak frequencies and the control strategies.
3.1. Non-Dimensional Power Curves and Blade-Bending Moments
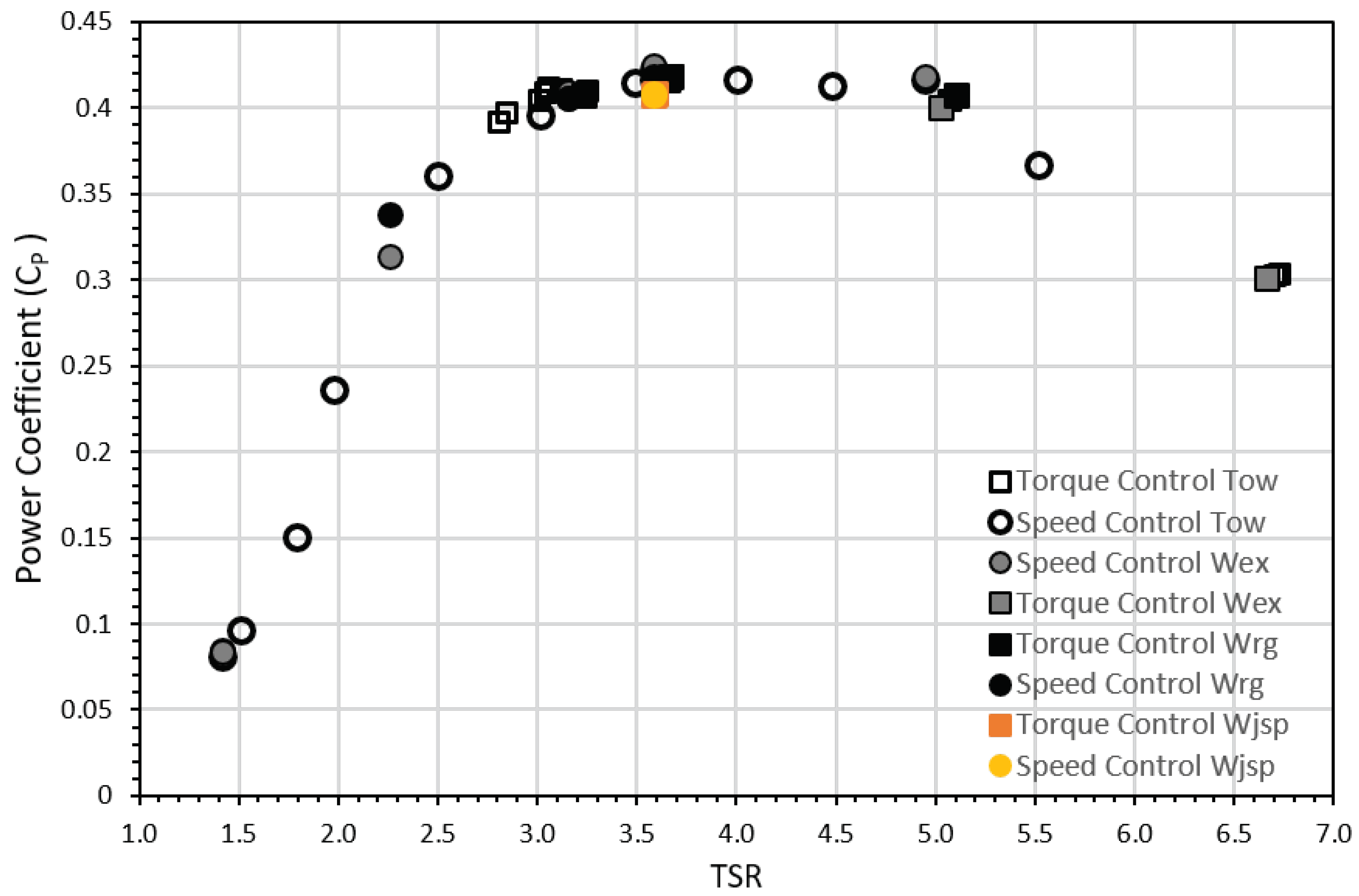
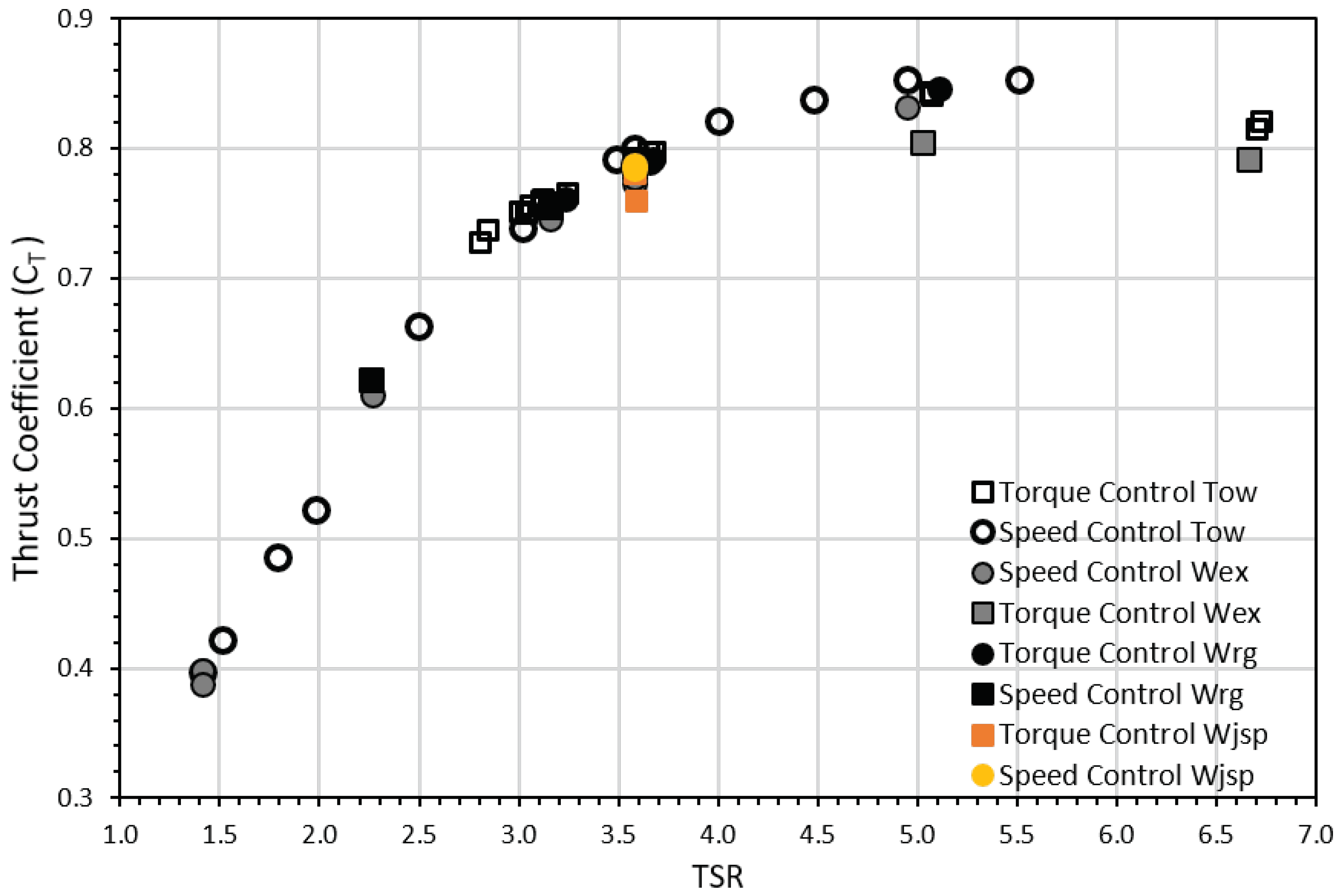
The resultant non-dimensional and performance curves for each of the flow conditions and control strategy described in Table 2 can be seen in Figure 6 and Figure 7. It must be noted that the scatter in both figures is considerably low, especially since the results include repeated tests done for the same operating point. Please note that there is excellent agreement between the repeated values. The standard deviation between three repeated tests was less than 1% of the mean value for each of the power and thrust coefficients for the 18 Nm (TSR ∼ 3) torque control test (tow-only condition). Similarly, two tests were done for a speed control mode at 76 rpm (TSR ∼ 3.6) operating under tow-only conditions, the resultant standard deviation between tests was 1.2% of the mean value for the thrust coefficient and less than 1% for the power coefficient. For the extreme and regular wave-tow tests, the variability between repeated tests was also lower than 1% of the mean value.
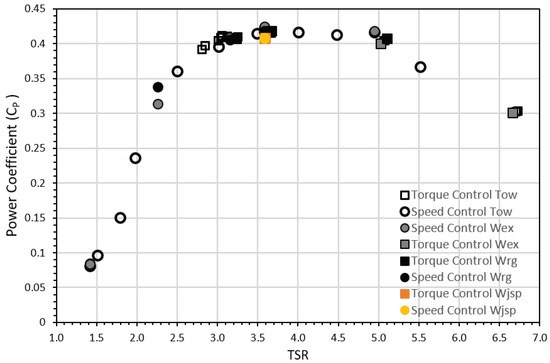
Figure 6.
Power Coefficient ()—Tip speed ratio (TSR) curve including all the test cases for both control strategies.
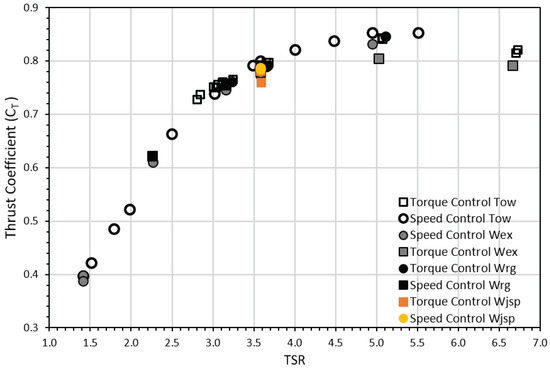
Figure 7.
Thrust coefficient ()—Tip speed ratio (TSR) curve including all the test cases for both control strategies.
The dispersion of the average values between tow-only and wave cases for the same operating point was in the order of 1.3% of the mean value for the thrust coefficient and power coefficient (for a TSR ∼ 3.6). These values also considered torque and speed control cases, demonstrating that mean values were not affected by the control strategy nor the influence of either the regular or irregular wave cases.
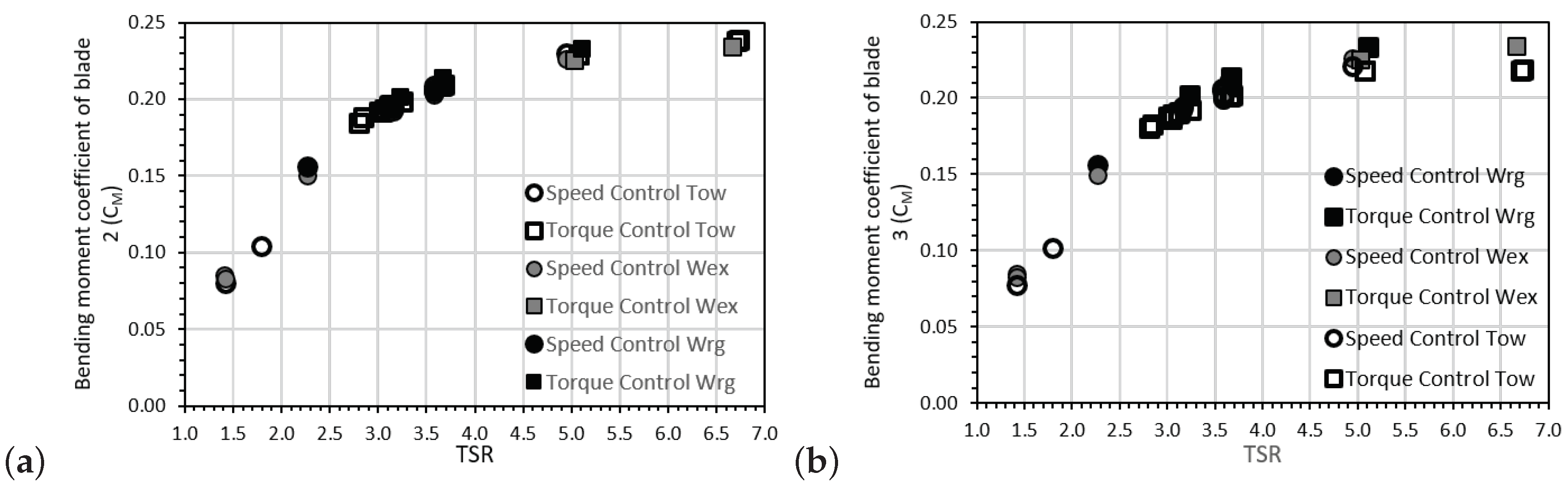
In Figure 8 the mean values of the root bending moment coefficients of blade 2 and blade 3 are given for each of the cases. The blade 2 root bending moment coefficients are about 6% higher than those obtained from the output of blade 3; however, it is clear that they present a similar trend. As the values of blade 2 are constantly greater independently of the rotational speed or of the turbine control mode, it is likely that this increase in bending moment is only due to a slight disparity between the instrumentation and waterproofing methods used for each connection.
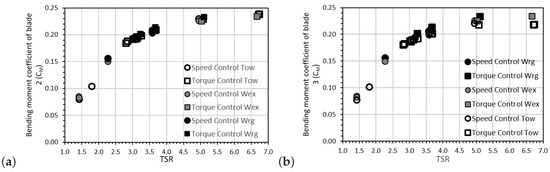
Figure 8.
Average blade root bending moment coefficient () for blade 2 (a) and blade 3 (b) versus tip speed ratio (TSR). Please note that there is not available for the irregular wave-tow tests.
Additional information regarding the repeatability of the tests can be related to the dispersion of the rotational speeds achieved when implementing the speed control mode or the variation of the TGC, when referring to the torque control strategy. The standard deviation in the rotor rotational speed values during speed control mode was found to be less than 0.25 rpm. Similar to the dispersion of and measurements, this is about 1% or less of the mean rotational speed. The standard deviation for the TGC was about 3% of the average values of the torque control mode for all the cases. The calculations for both the rotational speeds and the TGC dispersion values were not altered by the incorporation of waves.
It is noticeable that at a TSR ∼ 5, a relatively large deviation in the mean values for the tow-only and regular wave cases relative to the extreme wave case can be seen when the torque control operation is used. The authors believe this discrepancy is likely to be resultant from the large oscillations in TSR value observed under this test case. The large oscillations in rotational velocity and fluid velocity (due to the wave motion and control strategy) mean a wide range of TSR can be observed for this case. Due to the inherent shape of the curve, which exhibits a relatively small gradient at the maxima region (4.5 < TSR < 5.5) and a relatively steep increase at lower TSR values, this results in a positively skewed data sets leading to a slightly lower mean thrust value.
The main objective of this investigation was to compare the repercussions of using two control strategies in the loading of a HATT. Therefore, an equivalent parameter to reach the same operational point of the turbine was required to be met. For example, to reach a TSR of 3.5 a constant speed of 76 rpm must be met when operating in a speed control mode or a torque of 15 Nm when using a torque control mode. Therefore, when compared torque and rotational speed for a similar case using two control strategies, in this instance 76 rpm and 15 Nm tests, a variation of around 1.9 rpm and 2 Nm between them was achieved.
3.2. Time Average Signal Fluctuations
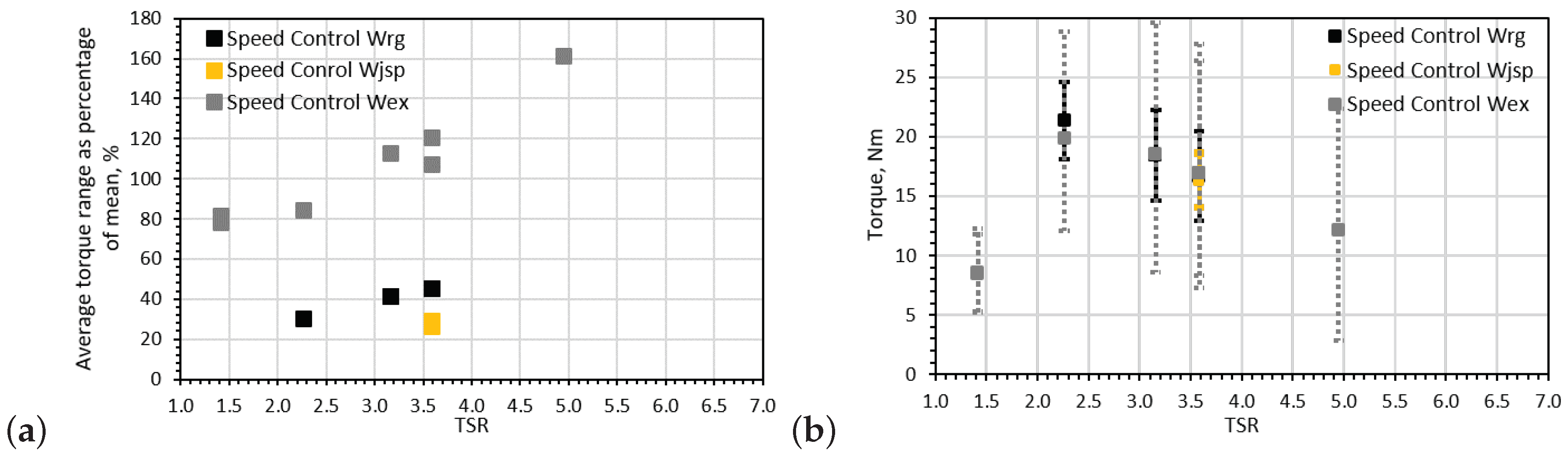
Figure 9a shows the average turbine rotational velocity fluctuation per wave period plotted against TSR for the torque control cases. The average maximum and minimum values of rotational velocity per wave period compared to the TSR are also included in Figure 9b for the same set of cases. The average maxima and minima observed are highlighted by the upper and lower error bars, respectively. The speed control cases have been omitted in Figure 9 as the oscillations in rotational velocity are inherently limited by the control strategy adopted.
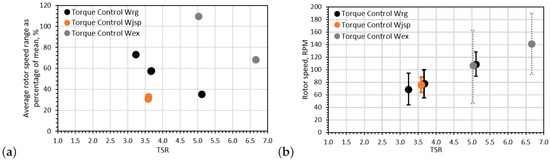
Figure 9.
Average turbine rotational velocity fluctuation per wave period only for torque control cases: (a) the rotational velocity fluctuation range as a percentage of the mean rotational velocity for each case is presented and (b) the average maximum and minimum turbine rotational velocity per wave period are indicated by the extremes of the error bars.
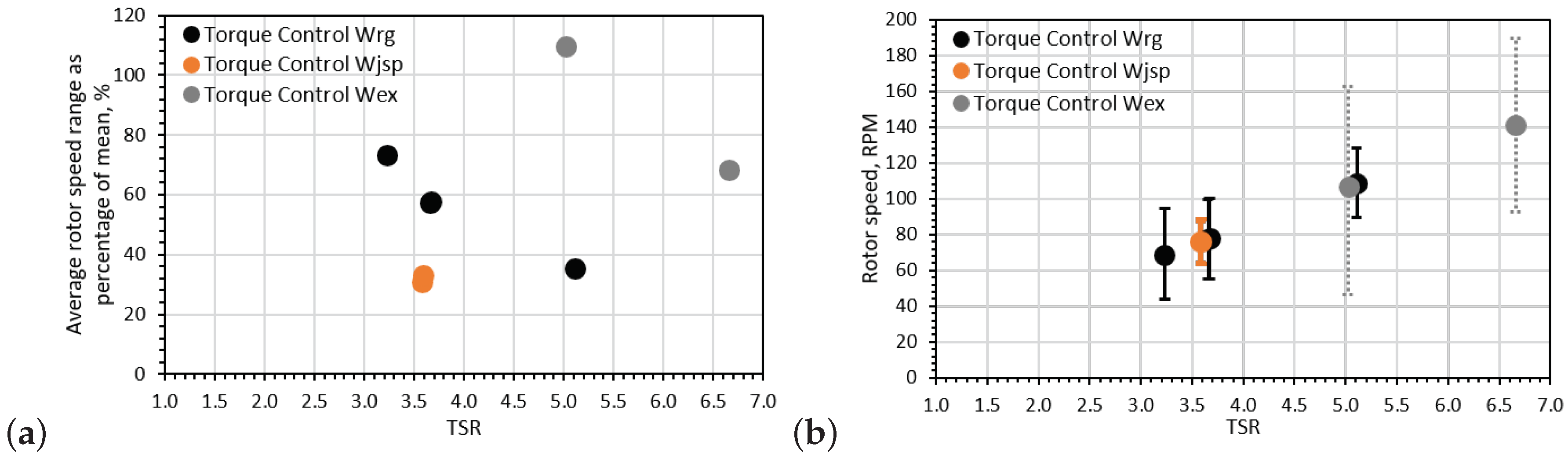
It is clear in Figure 9 that the size of the fluctuations relative to the mean rotational velocity decreases with average rotor speed, but both maximum and minimum speed increase with increased average speed. The fluctuation range is about 57% between the mean value of the rotational speed and the rotational speed range when looking at the regular wave-tow cases. The fluctuations in the two repeated irregular wave cases is ∼34% of the mean speed. A far bigger fluctuation range relative to the mean rotational velocity is observed in the extreme wave-tow case (∼110%) when compared with the regular wave-tow case (∼35%) for the comparable TSR value of 5.1.
In Figure 10 the fluctuations in the torque signals are presented, this time only for the speed-controlled cases. There is a modest increase in the torque fluctuation range with rotational velocity (Figure 10a) with a maximum fluctuation range of about 45% of the mean torque value in regular wave-tow tests. This increase in torque range is more evident for the extreme wave-tow cases with a fluctuating values of between 113% and 120% of the mean torque compared with a 45% fluctuation in the regular-tow case and a 35% fluctuation in the irregular-tow case, again for the comparable TSR of ∼3.6. It should be noted, at the aforementioned TSR, that the extent of fluctuations is relatively scattered for repeated extreme and irregular wave-tow cases, despite repeatability in the mean values observed. The maximum fluctuation in rotor torque was observed at high thrust conditions under the extreme-tow case with fluctuations of ∼160% of the mean value at TSR ∼ 4.9.
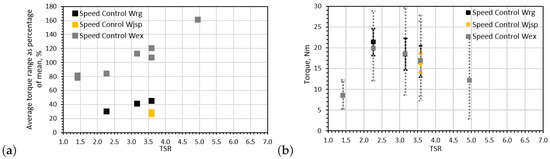
Figure 10.
Average rotor torque fluctuation per wave period only for speed control cases: (a) the torque fluctuation range as a percentage of the mean rotor torque for each case is shown and (b) the average maximum and minimum rotor torque per wave period are indicated by the extremes of the error bars.
The average rotor thrust fluctuations per wave period are plotted in Figure 11 and Figure 12 for the torque and speed control cases, respectively. It is clearly visible that using the torque control mode induces higher thrust fluctuations in the three wave-tow cases. It is visible that there is an opposite trend in the fluctuations occurring in the rotor thrust when using a specific control type. When the speed control mode was used, a linear increase in the variation of the thrust loading was observed in both wave-tow tests whereas a linear decrease in thrust fluctuations is observed when the torque control mode is applied. This contradicts the information reported by [5], who employed a torque control strategy in the experimental campaign and found an increase in the fluctuating thrust coefficient with TSR. However, it is somewhat difficult to compare both results as the fluctuating thrust coefficient shown in [5] was only indicated by a standard deviation value rather than a difference in amplitude between peak values, as it is presented here. Moreover, there are other differences between studies such as waveforms, flow velocities, facility types, and rotor types which will contribute to discrepancies between studies.
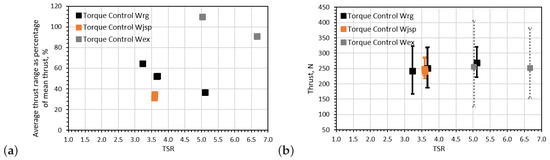
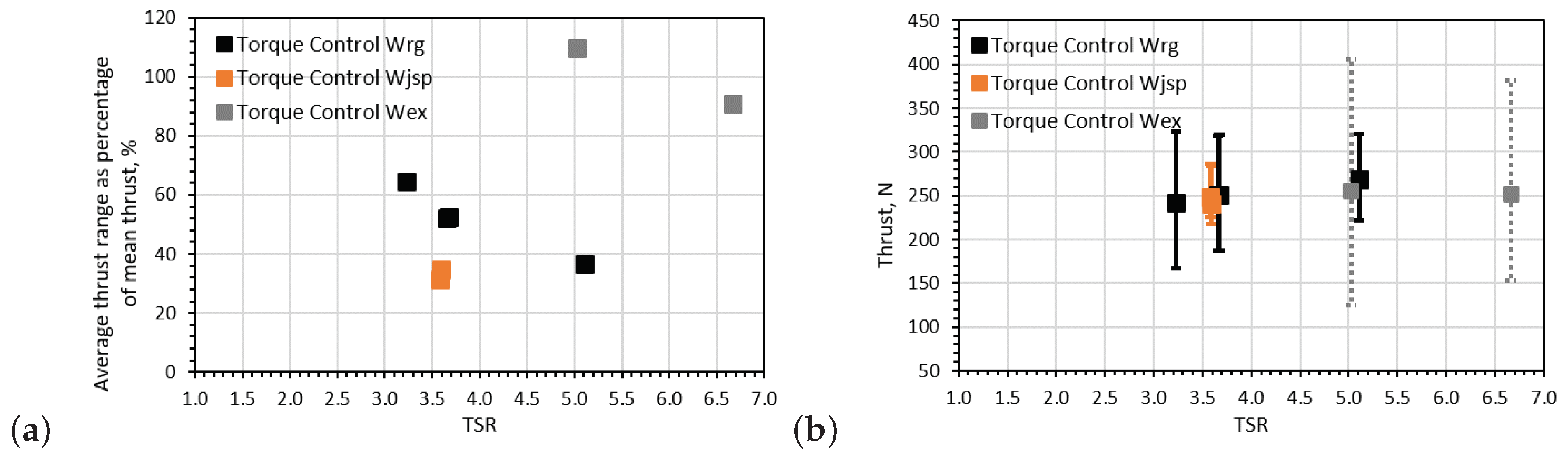
Figure 11.
Average rotor thrust fluctuations per wave period only for torque control cases: (a) the thrust fluctuation range as a percentage of the mean rotor thrust for each case is presented and (b) the average maximum and minimum rotor thrust per wave period are indicated by the extremes of the error bars.
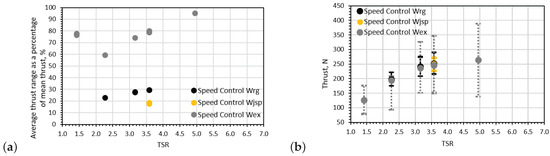
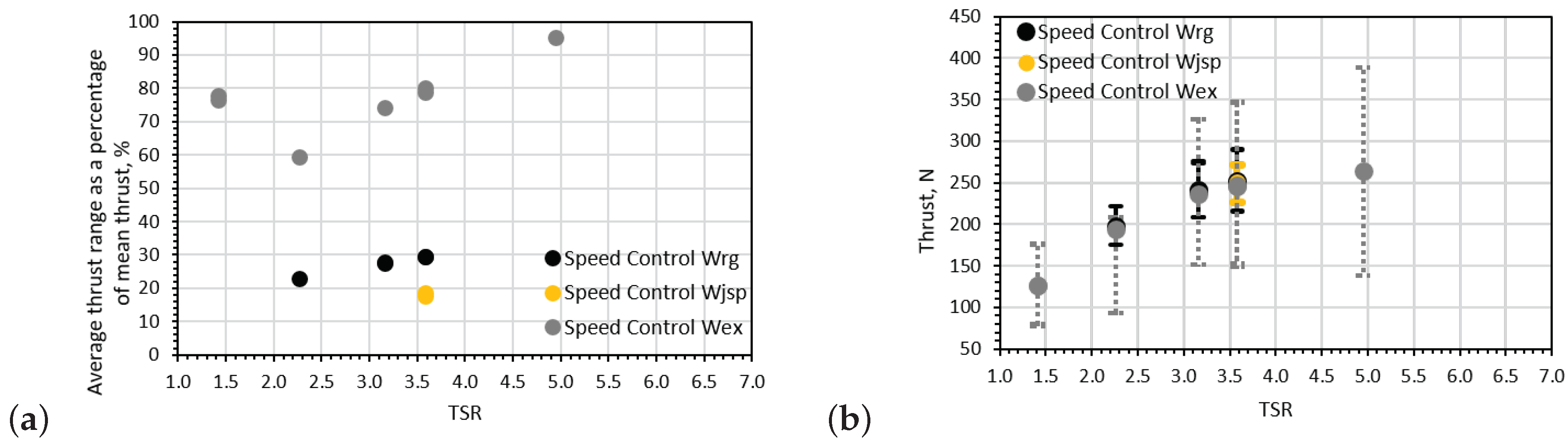
Figure 12.
Average rotor thrust fluctuations per wave period only for speed control cases: (a) the thrust fluctuation range as a percentage of the mean rotor thrust for each case is presented and (b) the average maximum and minimum rotor thrust per wave period are indicated by the extremes of the error bars.
For a similar operating point (TSR ∼ 3.15), the thrust fluctuation of the rotor increased by 57% when applying torque control (∼65% fluctuation relative to the mean value) instead of speed control (∼30% fluctuation relative to the mean value) for the regular wave-tow case. Comparing the effect of control type for the extreme wave-tow case at TSR ∼ 5.0, it can be seen that again an increase in thrust fluctuation was observed when using torque control; that is a 115% average fluctuation observed in the torque control case relative to a 95% fluctuation in the speed control case.
The results would suggest a greater sensitivity of thrust load variations to control strategy at lower TSRs. This phenomenon would appear to arise from the roughly asymptotic nature of the thrust coefficient curve which is specific to the rotor setup tested; as such, the result may be somewhat rotor specific which would also explain differences when comparing the results with other studies. Evidence for this reasoning can be seen in Figure 11b where the maximum thrust per wave period observed for differing TSRs for the regular wave-tow case were approximately constant for the three cases tested. While this reasoning maybe rotor geometry specific, this finding leads to the possible notion of developing rotor designs to mitigate against thrust fluctuations at peak power. Further tests to compare thrust fluctuations in the peak power region for the extreme wave-tow case and the differing control types were not feasible in these experiments due to the turbine stalling at TSRs lower than 5.0. The rotor stalling in the torque control case was due to operating momentarily at TSRs lower than the peak torque TSR for the rotor causing the turbine to stall.
Lastly, there appears to be a correlation between wave height and thrust range, with fluctuation size increasing with average wave height, as the average wave height in the irregular wave time series was lower than that of the regular wave-tow case. However, more experiments are required to fully understand the loading patterns associated with control strategies in random waves.
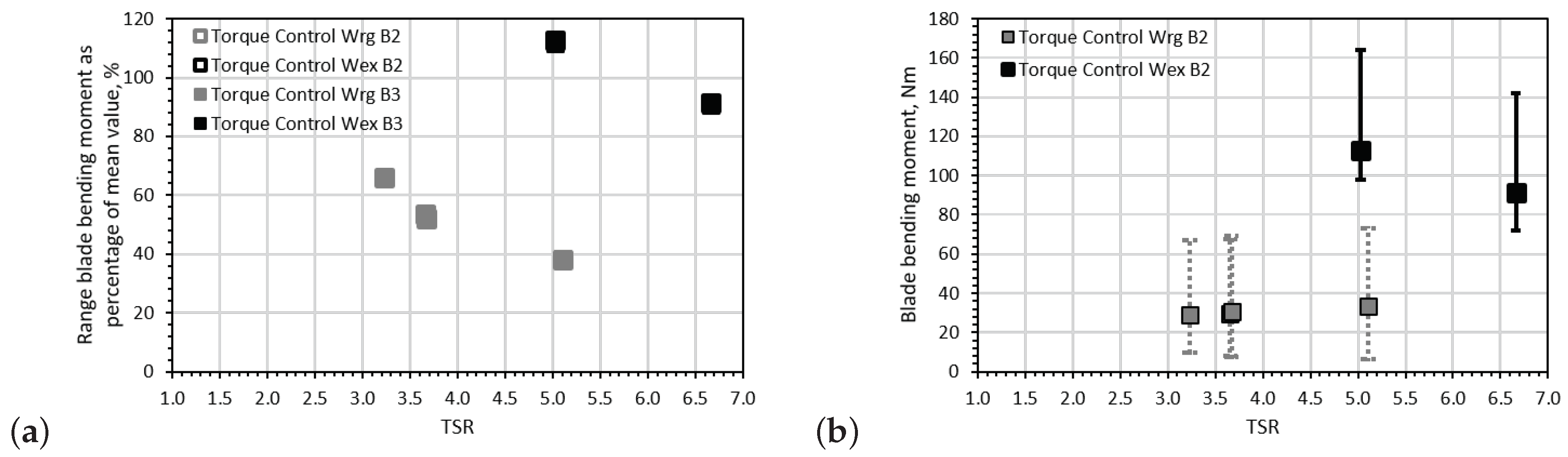
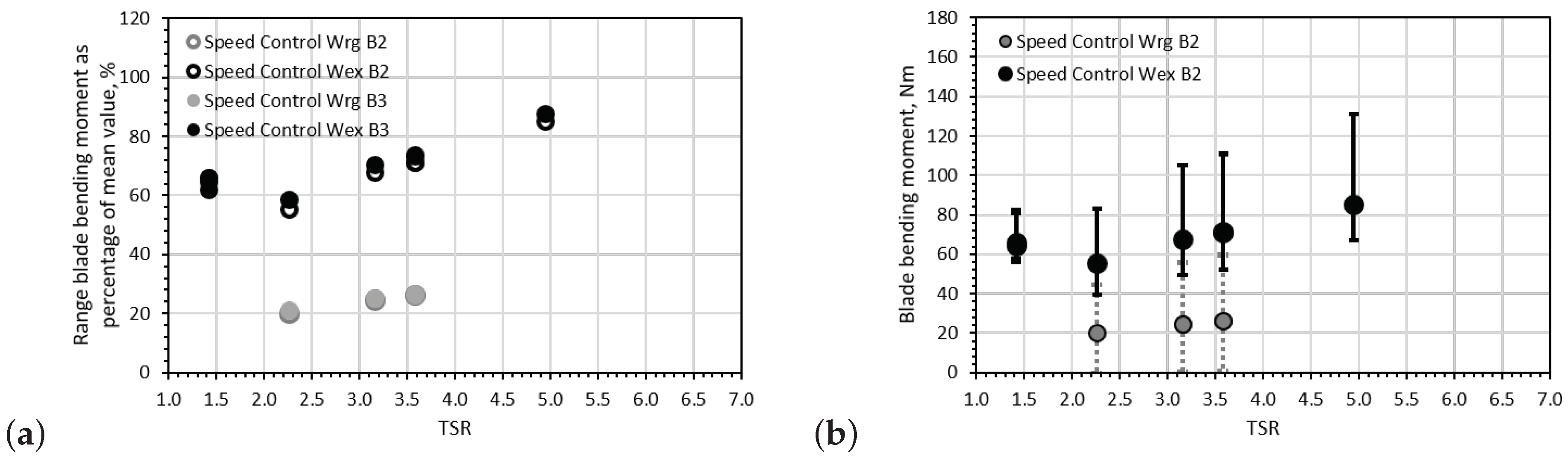
Figure 13 and Figure 14 show the average bending root moment fluctuations per wave period only for torque and speed control cases, respectively. The trend between the average values of the bending moment fluctuations of blade 2 and blade 3 is almost identical. Hence the reason of only using the values of blade 2 to show the maximum and minimum values on Figure 13b and Figure 14b. The pattern of the fluctuations when applying torque or speed control is similar to that presented in Figure 11 and Figure 12 with fluctuation size increasing with TSR in speed control mode but decreasing with TSR in torque control mode.
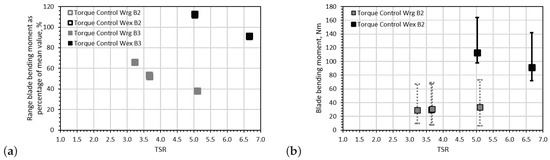
Figure 13.
Average bending root moment fluctuations per wave period only for torque control cases: (a) the bending root moment fluctuation range as a percentage of the mean bending moment for each blade is presented and (b) the average maximum and minimum rotor thrust per wave period are indicated by the extremes of the error bars (only for blade 2).
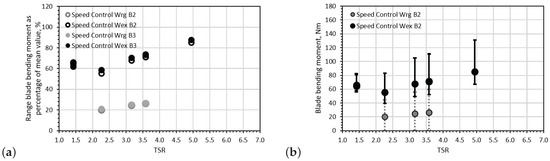
Figure 14.
Average bending root moment fluctuations per wave period only for speed control cases: (a) the bending root moment fluctuation range as a percentage of the mean bending moment for each blade is presented and (b) the average maximum and minimum rotor thrust per wave period are indicated by the extremes of the error bars (only for blade 2).
When comparing the corresponding fluctuations for the same operating region, it was found that the bending moment fluctuation of the blade increased from when applying torque control the torque control mode increases the average bending moment to 53.5% when compared to that obtained in the speed control experiment (26.5%) at TSR = 3.6, in regular wave-tow tests. A small increase of 26% was observed for the only case available for the extreme wave-tow experiment between the torque and speed control. This percentage is substantially lower than that presented by the regular wave-tow cases; however, this was for an operating point of TSR = 5.1 (≃105 rpm). It is interesting that the difference in loading fluctuations between torque and control tests for TSR = 5 are substantially lower than those associated with the regular wave-tow cases, especially since it was depicted in the —TSR curve that the peak power can be achieved between 3.0 < TSR < 5.0. It is clear that additional tests related to torque and control strategies must be performed when a turbine operates under wave and current conditions within this region.
3.3. Frequency Domain Analysis
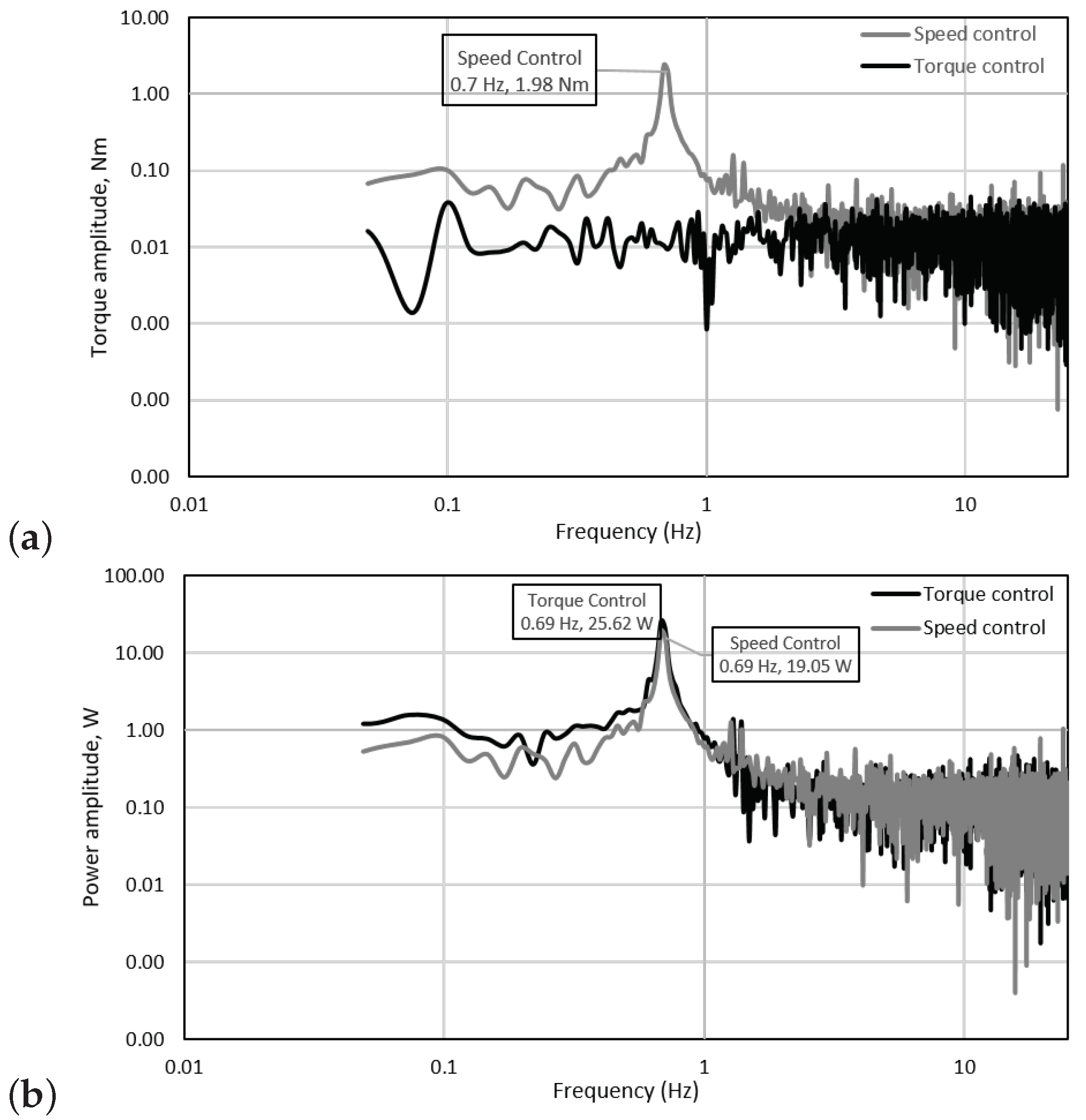
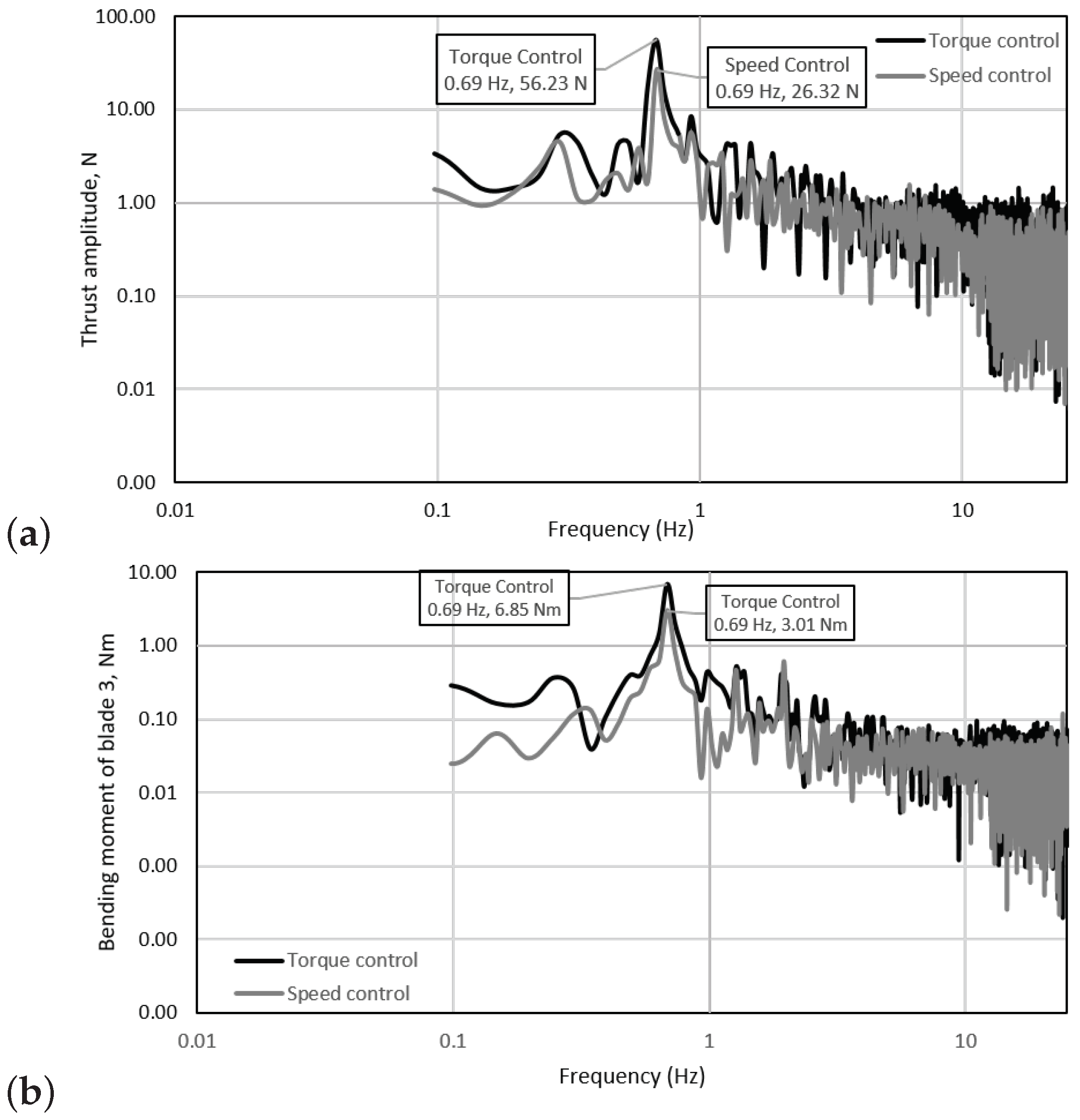
Figure 15 and Figure 16 show the spectral analyses of the torque, power, thrust and root bending moments for toque and speed control conditions for a regular wave-tow case at TSR = 3.6. The dominant frequency observed for most of the plots corresponds to the wave frequency of 0.69 Hz (wave period of 1.44 s). When using speed control, the presence of the wave frequency in the spectrum of the torque signal is evident but unnoticeable when the torque control mode was on. Therefore, it was deemed necessary to include a plot to relate the influence of both torque and speed control strategies in power. It can thus be observed in Figure 15b, that with constant torque the amplitude of the power at the wave frequency is higher. This means that in a scaled-up device, the fluctuating power on the grid will be higher when a turbine is subjected to wave conditions. A similar trend is observed for the spectra of the thrust and blade root bending in Figure 16. However, it is interesting to note that for the extreme wave cases, the power amplitudes are substantially lower than those obtained at constant speed conditions, see Figure 17a. Unfortunately, the experiments related to extreme wave-tow tests were limited, due to the capabilities of the turbine at such extreme conditions. However, in the future it will be contemplated to repeat a similar but more conservative wave-tow condition to confirm the outcomes of this investigation. The results are of relevance as the this means that at this operating point (TSR = 5, = 0.4 and = 0.8) on a larger scale, the drivetrain and rotor will be subjected to smoother mechanical conditions when operating in harsher environments, compared to those achieved at peak conditions (TSR = 3.6, = 0.42 and = 0.78).
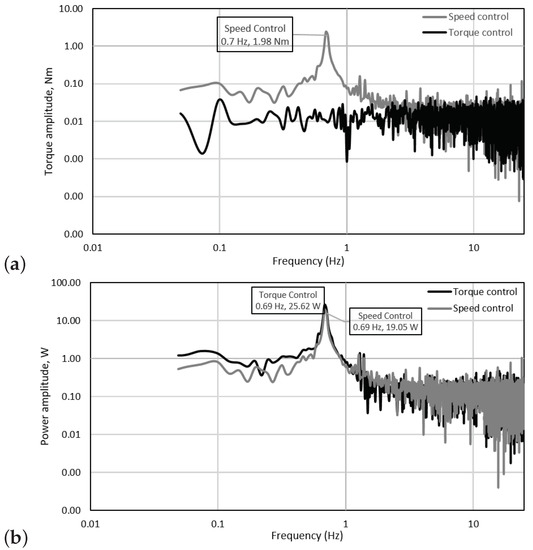
Figure 15.
Frequency domain graphs for a regular wave-tow test at peak power condition of TSR = 3.6, i.e., 76 rpm, 15 Nm for rotor: (a) torque and (b) power.
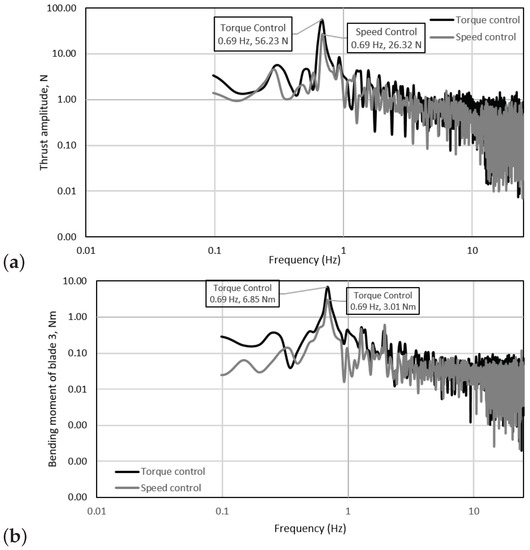
Figure 16.
Frequency domain graphs for a regular wave-tow test at peak power condition of TSR = 3.6, i.e., 76 rpm, 15 Nm for: (a) thrust and (b) root bending moment blade 3.
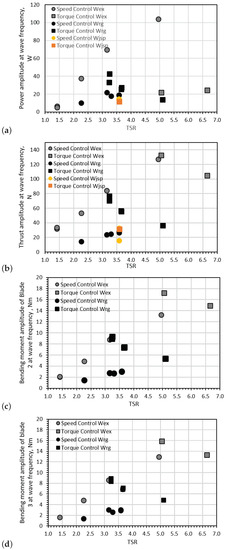
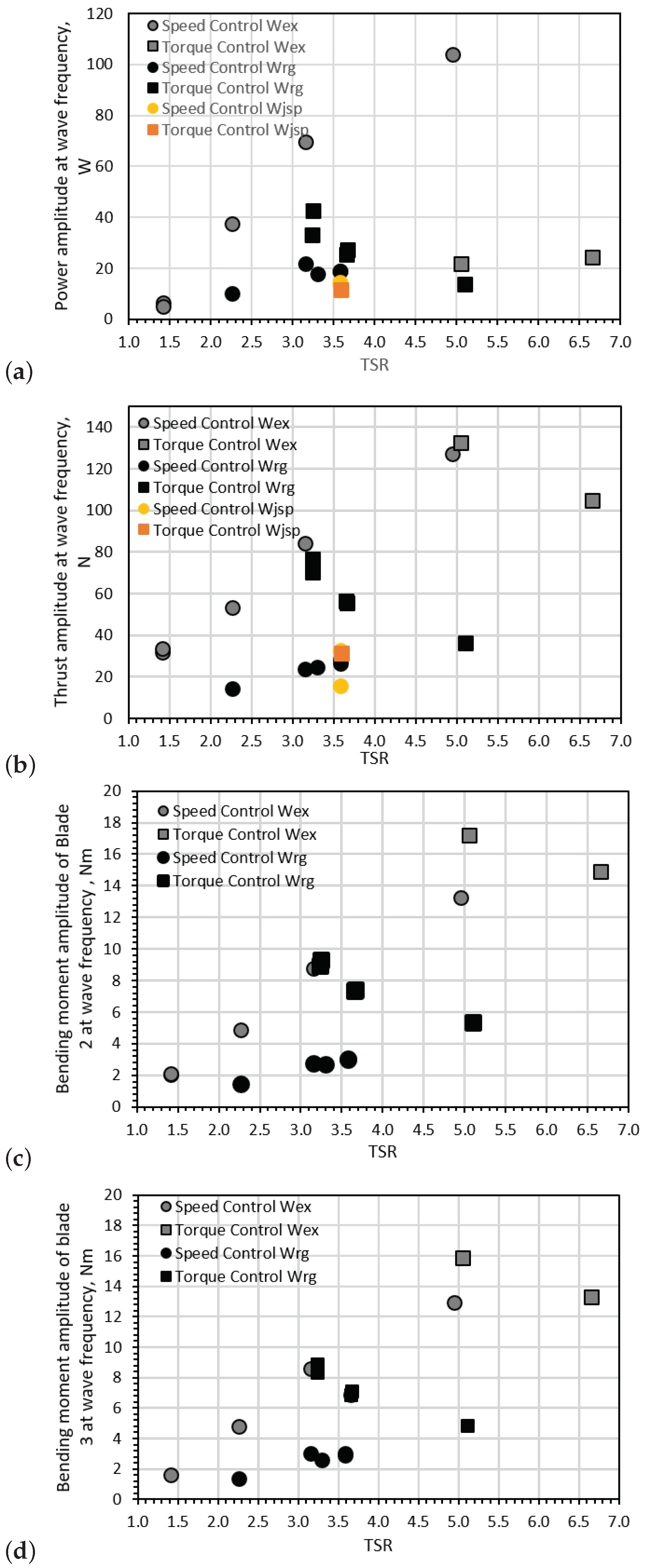
Figure 17.
Amplitudes observed at wave frequencies of: (a) power, (b) rotor thrust, (c) root bending moment blade 2 and (d) root bending moment blade 3.
It is clear that the peak frequencies developed during the torque control tests are higher than those seen in the speed control tests, at least for the regular wave-tow cases shown in Figure 15 and Figure 16. On a smaller scale, the frequencies of the rotational speed are also visible in the power and torque spectra, but the amplitudes are substantially low compared to the magnitude of the wave frequency. The same is depicted in the thrust and bending moment spectra with the addition of the frequency related to the rotational speed in combination with the wave frequency (≃1.96 Hz). Again, the amplitudes of the additional frequencies are considerably lower than those related to the wave frequency. This work is however purely focused on the interaction between in-line waves and currents which may not be fully representative of a tidal site, as demonstrated by [20]; where it was found that between 49–93% of the time the waves propagate with a direction of 20 degrees of tolerance. Therefore, the directionality of waves and currents is of importance and should be incorporated in future experiments to understand the loading on tidal turbines subjected to these conditions.
In Figure 17 the peak amplitudes of corresponding wave frequencies are shown for power, thrust, and root bending moment of blade 2 and 3. For the thrust and root bending moments of blades 2 and 3, the pattern observed is similar to that presented in Figure 13 and Figure 14 where the fluctuation amplitude increases with rotor velocity in speed control mode, but decreases with rotor velocity in torque control mode.
4. Conclusions
The influence that control strategies have on the loading of a three-bladed horizontal -axis HATT was investigated in a wave-tow tank. The turbine was tested under two types of regular wave-tow cases and an irregular wave-tow test. It was found that when looking at average values, the control mode or the type of wave-tow case investigated did not affect the rotor thrust, rotor torque or blade root bending moment measurements when these where compared to tow-only conditions. The thrust and torque fluctuations were substantial under the regular, extreme, and irregular waves cases, with the average peak loads adding up to 30% to the mean value under the conditions tested. However, a greater increase to the mean of nearly 100% was observed when looking at thrust and torque fluctuations developed when the turbine was tested under extreme wave-tow conditions, showing the relation between loading and wave height. For the test cases where the set operational point was reached in both torque and control strategies, it was found that the thrust and root blade-bending moment fluctuations per wave period were in the order of 40% higher when the torque control was applied compare to the thrust control tests. A pattern showing that the thrust and blade root bending moments was observed in both time and frequency domain where the fluctuation or peak amplitude of the thrust or bending moment increased with rotor velocity in speed control mode but decreased with rotor velocity in torque control mode. The power spectra were also studied. It was observed that for the extreme wave-tow cases the amplitude of the wave frequency was substantially lower when using torque control than constant speed. The study shown here highlights the importance for understanding power control, smoothing and integration with the grid, and structural and fatigue design of components such as the blades, driveshaft, generator etc. There is certainly more need to investigate the matter, especially how these effects follow a similar pattern in an environment with wave directionality and turbulence. It is also important to recognize that the experiments undertaken for the irregular wave cases were quite limited. This matter will also be studied in the future in laboratory conditions where longer time series are achievable. Given the fact that the amplitude fluctuations in the power spectra were exceptionally low when applying torque control, further experiments will also be contemplated in the future.
Author Contributions
Conceptualization, M.A. and S.O.-S.; methodology, K.P. and M.A.; software, M.A.; validation, S.O.-S., M.A. and K.P.; formal analysis, S.O.-S., M.A. and K.P.; investigation, I.S.; resources, C.L.; data curation, R.E.; writing–original draft preparation, S.O.-S.; writing–review and editing, S.O.-S. and M.A.; supervision, T.O. and C.J.; project administration, T.O. and C.J.; funding acquisition, M.A., T.O. and C.J.
Funding
This research was funded by EPSRC grant number EP/N020782/1. Facility access was funded by the H2020 MARINET 2 program.
Acknowledgments
This investigation was funded The authors’ would like to thank the staff at CNR-INM for their expertise and support during the testing period.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEMT | Blade Element Momentum Theory |
| CFD | Computational fluid dynamics techniques |
| H | Wave height |
| HATT | Horizontal Axis Tidal Turbine |
| HS | Significant wave height |
| iq | Quadrature axis current |
| PID | Proportional–integral–derivative |
| PMSM | permanent magnet synchronous machine |
| rpm | Revolutions per minute |
| TGC | Torque generating current |
| TP | Peak wave period |
| TSR | Tip Speed Ratio |
| VOC | Vector-oriented control |
| VSC | Voltage Source Converter |
References
- Nevalainen, T.M.; Johnstone, C.M.; Grant, A.D. A sensitivity analysis on tidal stream turbine loads caused by operational, geometric design and inflow parameters. Int. J. Mar. Energy 2016, 16, 51–64. [Google Scholar] [CrossRef]
- Nevalainen, T.; Peter, D.; Johnstone, C. Internal bearing stresses of horizontal axis tidal stream turbines operating in unsteady seas. In Proceedings of the 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016. [Google Scholar]
- Tatum, S.C.; Frost, C.H.; Allmark, M.; O’Doherty, D.M.; Mason-Jones, A.; Prickett, P.W.; Grosvenor, R.I.; Byrne, C.B.; O’Doherty, T. Wave–current interaction effects on tidal stream turbine performance and loading characteristics. Int. J. Mar. Energy 2015, 14, 161–179. [Google Scholar] [CrossRef]
- Holst, M.A.; Dahlhaug, O.G.; Faudot, C. CFD Analysis of Wave-Induced Loads on Tidal Turbine Blades. IEEE J. Ocean. Eng. 2015, 40, 506–521. [Google Scholar] [CrossRef]
- de Jesus Henriques, T.A.; Tedds, S.C.; Botsari, A.; Najafian, G.; Hedges, T.S.; Sutcliffe, C.J.; Owen, I.; Poole, R.J. The effects of wave–current interaction on the performance of a model horizontal axis tidal turbine. Int. J. Mar. Energy 2014, 8, 17–35. [Google Scholar] [CrossRef]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 2013, 59, 1–12. [Google Scholar] [CrossRef]
- Galloway, P.; Myers, L.; Bahaj, A.A. Quantifying wave and yaw effects on a scale tidal stream turbine. Renew. Energy 2014, 63, 297–307. [Google Scholar] [CrossRef]
- Barltrop, N.; Varyani, K.S.; Grant, A.; Clelland, D.; Pham, X. Investigation into wave–current interactions in marine current turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 233–242. [Google Scholar] [CrossRef]
- Consul, C.A.; Willden, R.H.J.; McIntosh, S.C. Blockage effects on the hydrodynamic performance of a marine cross-flow turbine. Philos. Trans. R. Soc. A 2013. [Google Scholar] [CrossRef] [PubMed]
- Ordonez-Sanchez, S.; Ellis, R.; Porter, K.E.; Allmark, M.; O’Doherty, T.; Mason-Jones, A.; Johnstone, C. Numerical Models to Predict the Performance of Tidal Stream Turbines Working under Off-Design Conditions. Ocean Eng. 2018. submitted. [Google Scholar]
- Martinez, R.; Payne, G.S.; Bruce, T. The effects of oblique waves and currents on the loadings and performance of tidal turbines. Ocean Eng. 2018, 164, 55–64. [Google Scholar] [CrossRef]
- Draycott, S.; Payne, G.; Steynor, J.; Nambiar, A.; Sellar, B.; Venugopal, V. An experimental investigation into non-linear wave loading on horizontal axis tidal turbines. J. Fluids Struct. 2019, 84, 199–217. [Google Scholar] [CrossRef]
- Draycott, S.; Nambiar, A.; Sellar, B.; Davey, T.; Venugopal, V. Assessing extreme loads on a tidal turbine using focused wave groups in energetic currents. Renew. Energy 2019, 135, 1013–1024. [Google Scholar] [CrossRef]
- Cooperman, A.; Martinez, M. Load monitoring for active control of wind turbines. Renew. Sustain. Energy Rev. 2015, 41, 189–201. [Google Scholar] [CrossRef]
- Frost, C.; Benson, I.; Jeffcoate, P.; Elsäßer, B.; Whittaker, T. The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments. Energies 2018, 11, 1533. [Google Scholar] [CrossRef]
- Nambiar, A.; Anderlini, E.; Payne, G.S.; Forehand, D.; Kiprakis, A.; Wallace, R. Reinforcement Learning Based Maximum Power Point Tracking Control of Tidal Turbines. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Ordonez-Sanchez, S.; Porter, K.; Frost, C.; Allmark, M.; Johnstone, C.; O’Doherty, T. Effects of Wave-Current Interactions on the Performance of Tidal Stream Turbines. In Proceedings of the 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016. [Google Scholar]
- Allmark, M.; Ellis, R.; Porter, K.; O’Doherty, T.; Johnstone, C. The Development and Testing of a Lab-Scale Tidal Stream Turbine for the Study of Dynamic Device Loading. In Proceedings of the 4th Asian Wave and Tidal Energy Conference, Scottish, UK, 9–13 September 2018. [Google Scholar]
- Ellis, R.; Allmark, M.; O’Doherty, T.; Ordonez-Sanchez, S.; Mason-Jones, A.; Johannesen, K.; Johnstone, C. Design process for a scale horizontal axis tidal turbine blade. In Proceedings of the 4th Asian Wave and Tidal Energy Conference, Scottish, UK, 9–13 September 2018. [Google Scholar]
- Lewis, M.J.; Neill, S.P.; Hashemi, M.R.; Reza, M. Realistic wave conditions and their influence on quantifying the tidal stream energy resource. Appl. Energy 2014, 136, 495–508. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).