Nonlinear Synchronous Control for H-Type Gantry Stage Used in Electric Vehicles Manufacturing
Abstract
:1. Introduction
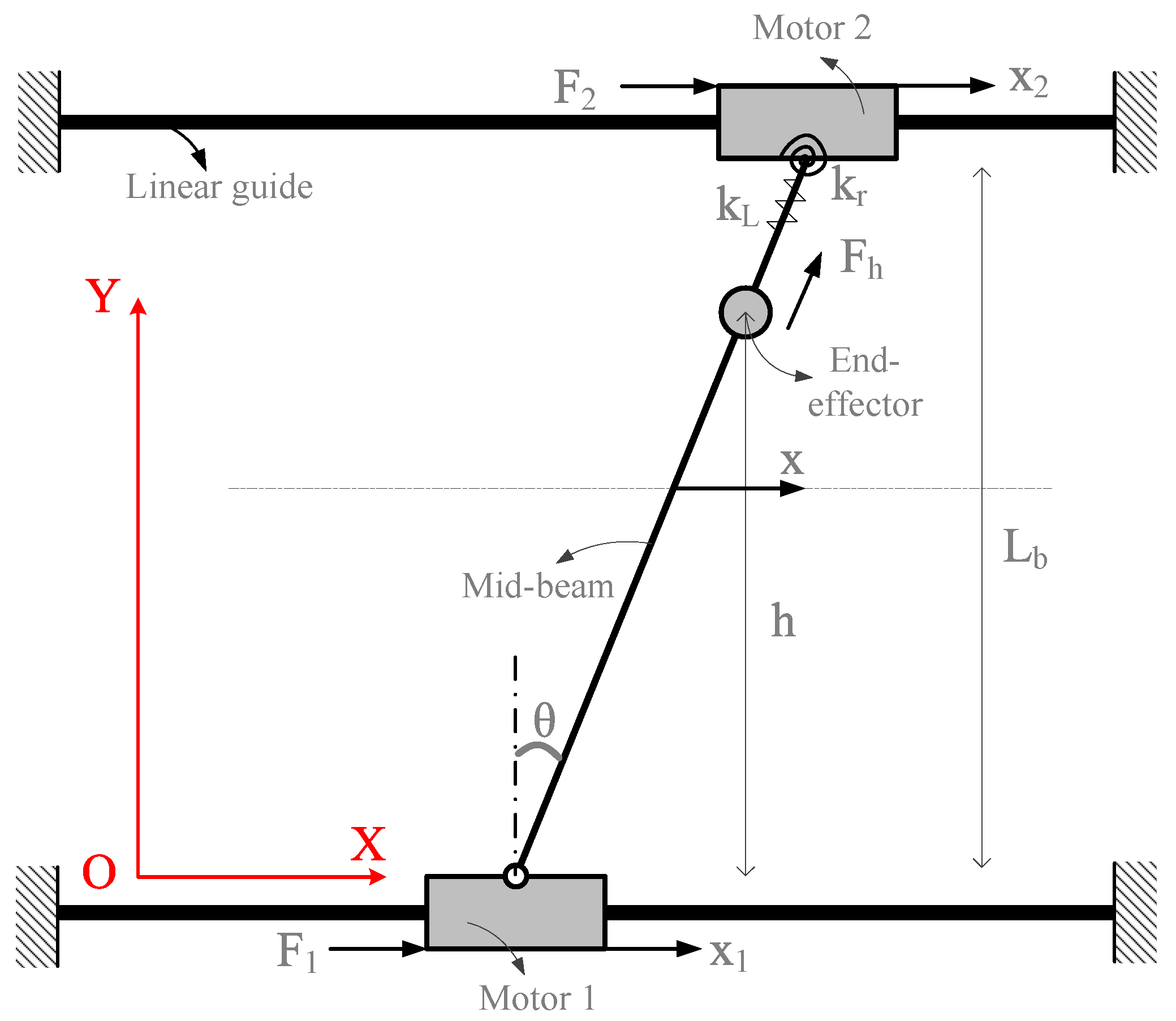
2. Nonlinear Model of HGS
2.1. Dynamic Modeling
- The end-effector moves on the horizontal plane, so that the effects of gravity are ignored.
- The mid-beam is modeled as a rigid body.
- The tensile and rotational deformation of the mid-beam are modeled as a tensile spring with stiffness coefficient and a torsion spring with stiffness coefficient , respectively.
- The end-effector cannot be separated from the mid-beam.
2.2. Friction
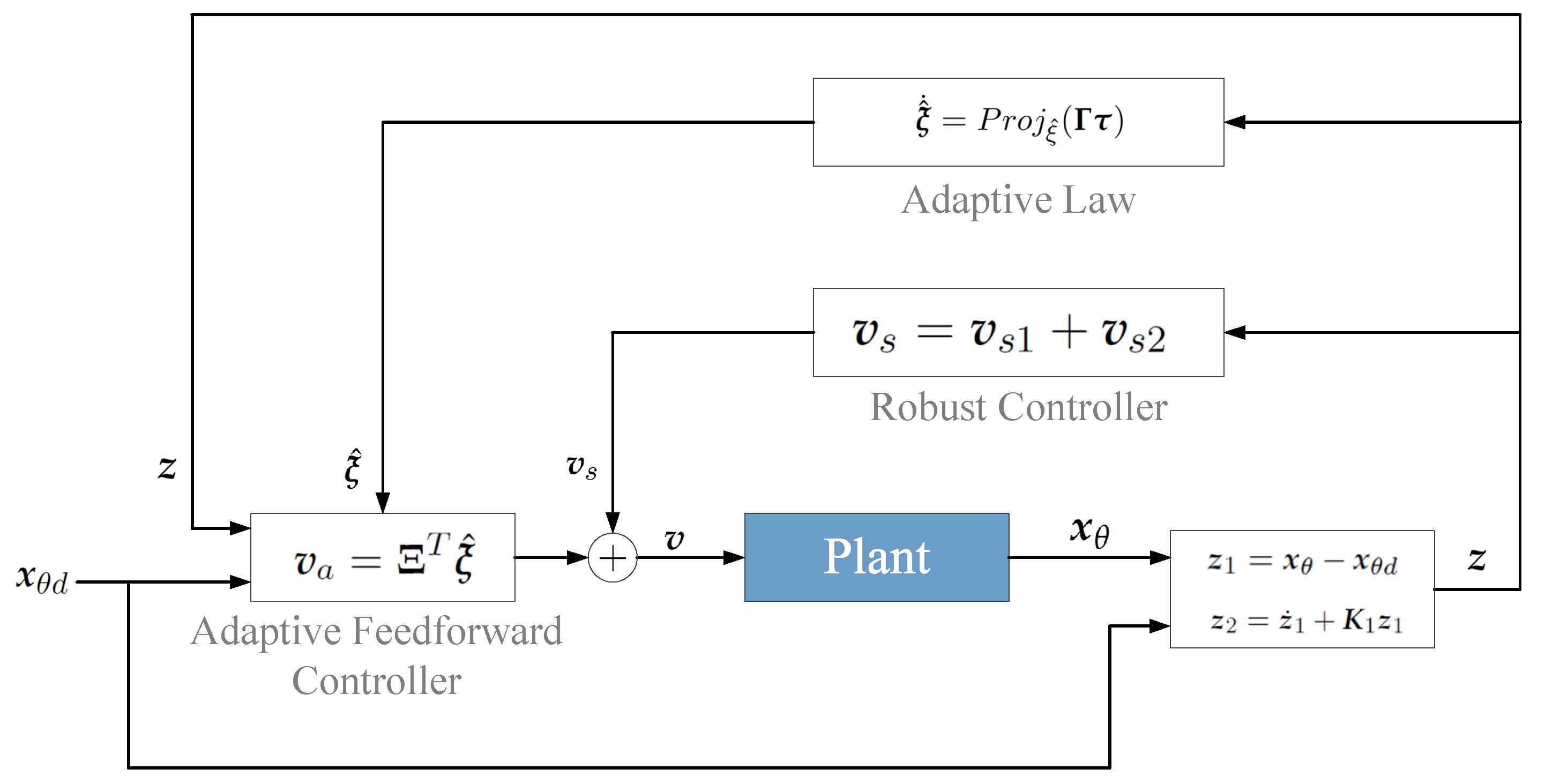
3. Nonlinear Synchronous Controller Design
3.1. Problem Formulation
3.2. Discontinuous Projection
3.3. Controller Design
3.4. Main Results
- (1)
- All system signals are bounded, and the Lyapunov function is bounded by:where , , and are the minimum and maximum eigenvalues of matrix *.
- (2)
- If there is no lumped uncertainty, i.e., , then the asymptotic convergence of system tracking and synchronous error is also achieved, i.e., , as .
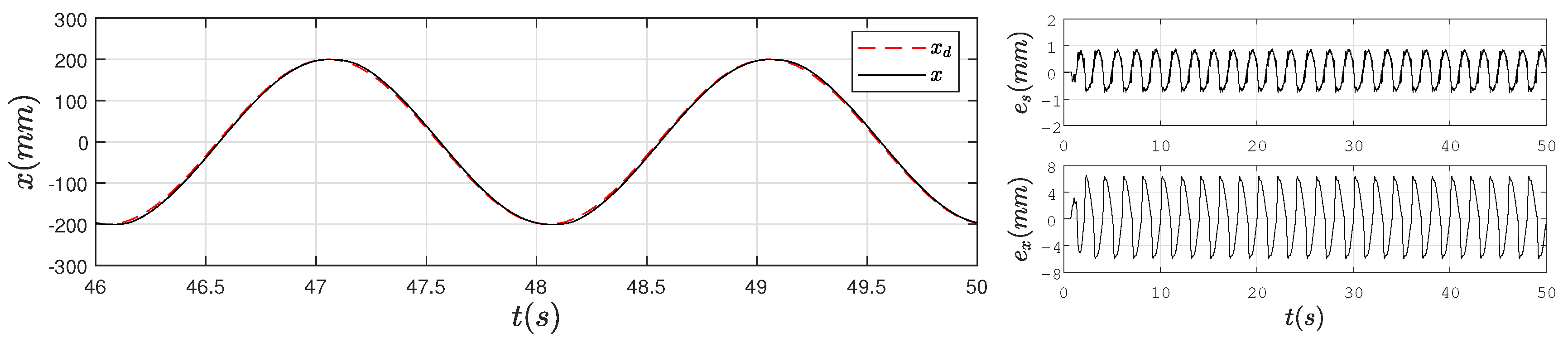
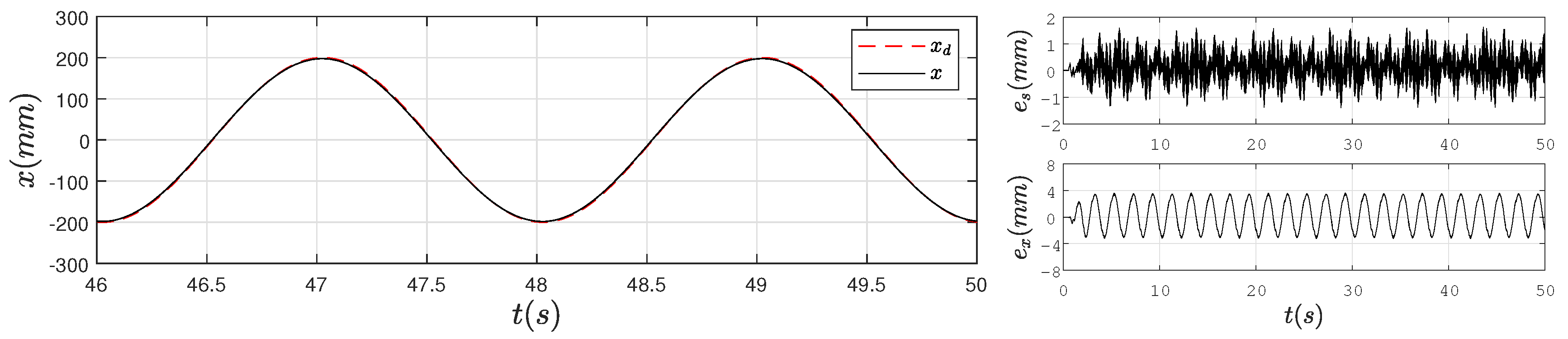
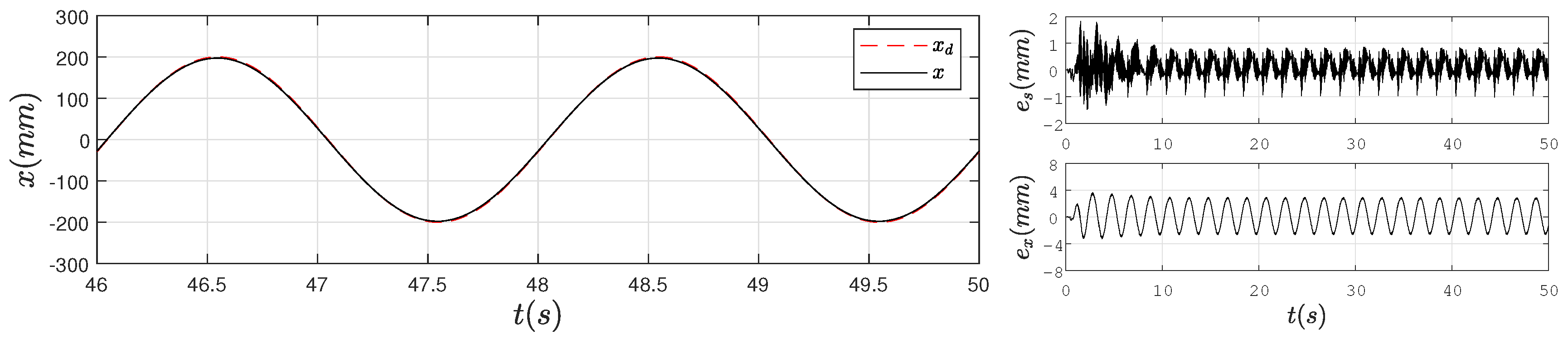
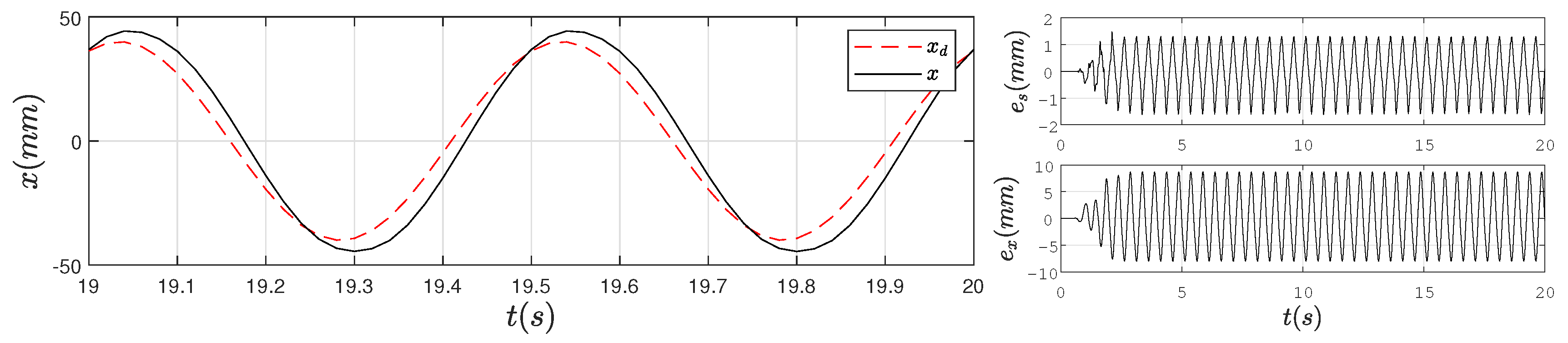
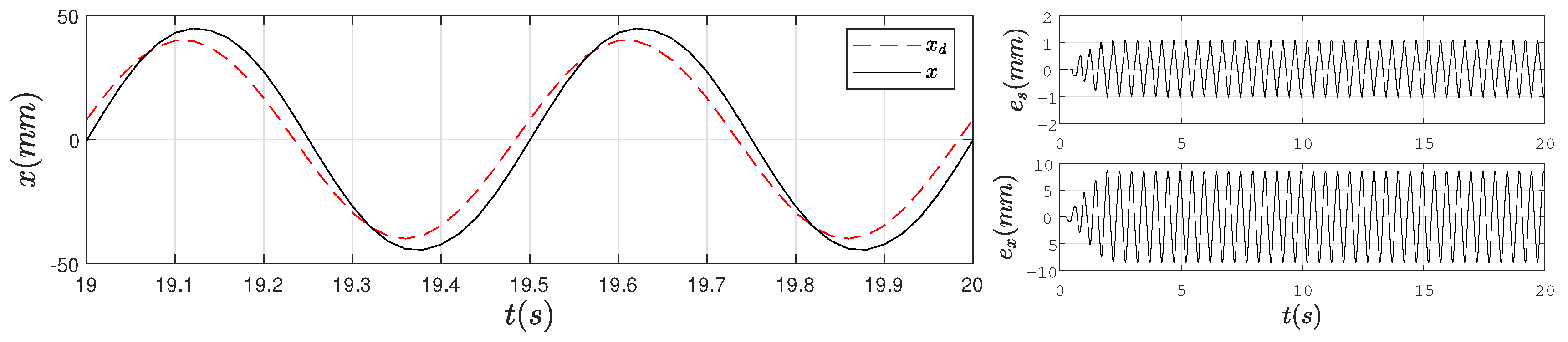
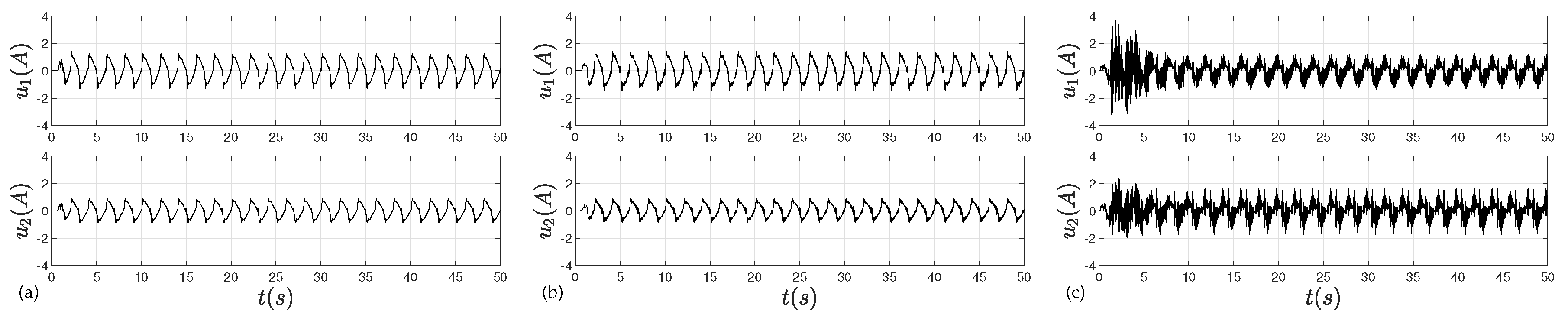
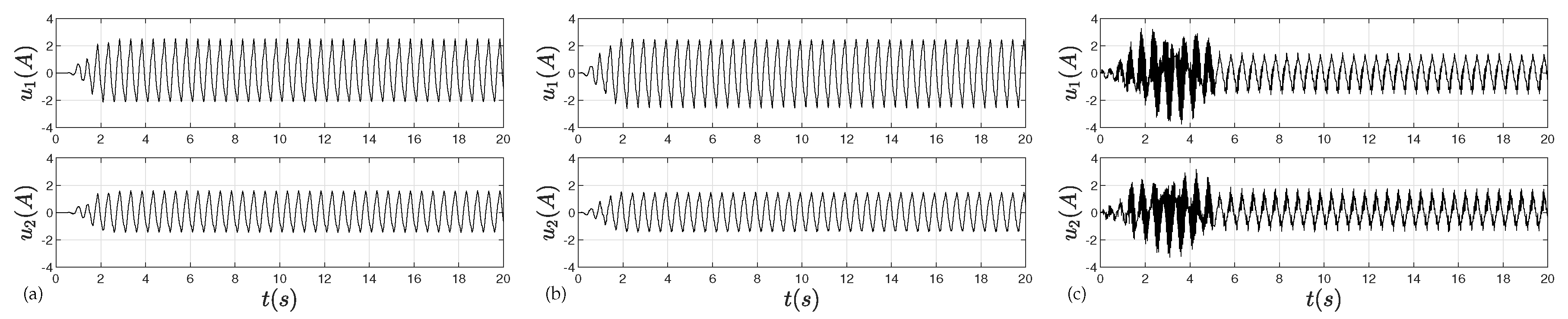
4. Experimental Verification
4.1. Experimental Setup
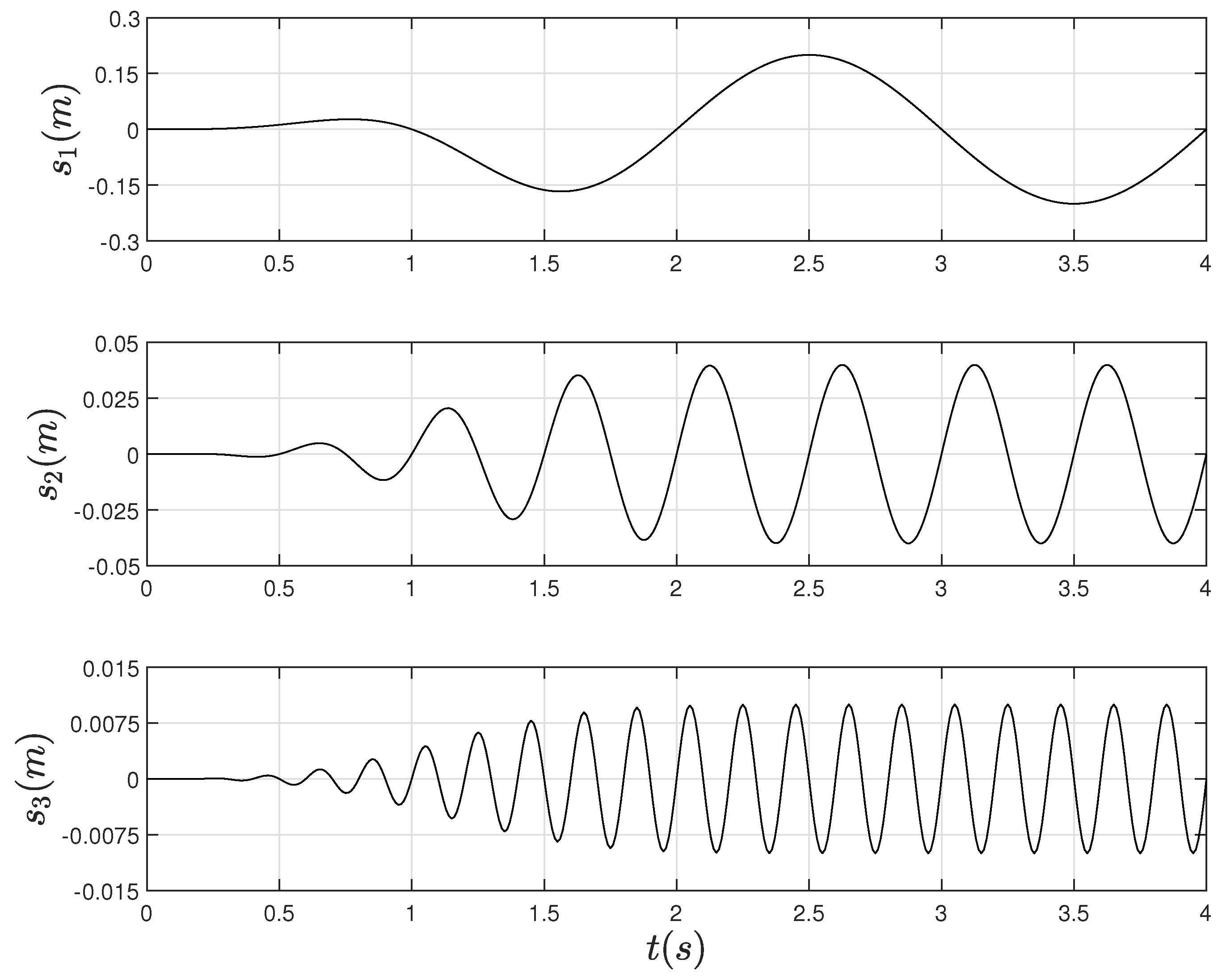
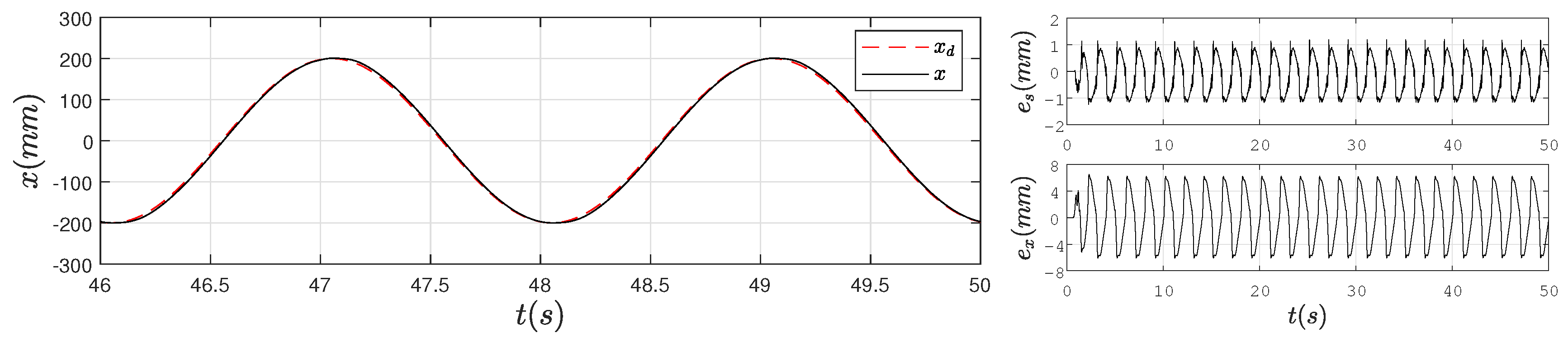
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HGS | H-type gantry stage |
| CCC | Cross-couple control |
| ARSCR | Adaptive robust synchronous control based on the rigid assumed model |
| AC | Adaptive control |
| SMC | Sliding mode control |
Appendix A
Appendix B
References
- Mochizuki, K.; Motai, T. Synchronization of Two Motion Control Axes Under Adaptive Feedforward Control. Adapt. Learn. Control 1990, 114, 196–203. [Google Scholar]
- Koren, Y. Cross-coupled biaxial computer control for manufacturing systems. J. Dyn. Syst. Meas. Control 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Koren, Y.; Lo, C.C. Variable-gain cross-coupling controller for contouring. CIRP Ann. Manuf. Technol. 1991, 40, 371–374. [Google Scholar] [CrossRef]
- Byun, J.H.; Choi, M.S. A method of synchronous control system for dual parallel motion stages. Int. J. Precis. Eng. Manuf. 2012, 13, 883–889. [Google Scholar] [CrossRef]
- Giam, T.S.; Tan, K.K.; Huang, S. Precision coordinated control of multi-axis gantry stages. ISA Trans. 2007, 46, 399. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.S. Modeling and synchronous control of dual mechanically coupled linear servo system. J. Dyn. Syst. Meas. Control 2015, 137, 041009. [Google Scholar] [CrossRef]
- Chen, R.; Jiao, Z.; Yan, L. Dual linear motors synchronous control for horizontal axis of far-field target motion simulators. In Proceedings of the IEEE International Conference on Aircraft Utility Systems, Beijing, China, 10–12 October 2016; pp. 810–813. [Google Scholar]
- Hsieh, M.F.; Yao, W.S.; Chiang, C.R. Modeling and synchronous control of a single-axis stage driven by dual mechanically-coupled parallel ball screws. Int. J. Adv. Manuf. Technol. 2007, 34, 933–943. [Google Scholar] [CrossRef]
- Lin, F.J.; Hsieh, H.J.; Chou, P.H.; Lin, Y.S. Digital signal processor-based cross-coupled synchronous control of dual linear motors via functional link radial basis function network. IET Control Theory Appl. 2011, 5, 552–564. [Google Scholar] [CrossRef]
- Lin, F.J.; Chou, P.H.; Chen, C.S.; Lin, Y.S. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control. IEEE Trans. Ind. Electron. 2011, 59, 1061–1073. [Google Scholar] [CrossRef]
- Chou, P.H.; Chen, C.S.; Lin, F.J. DSP-based synchronous control of dual linear motors via Sugeno type fuzzy neural network compensator. J. Frankl. Inst. 2012, 349, 792–812. [Google Scholar] [CrossRef]
- Lin, F.J.; Chou, P.H.; Chen, C.S.; Lin, Y.S. Three-degree-of-freedom dynamic model-based intelligent nonsingular terminal sliding mode control for a gantry position stage. IEEE Trans. Fuzzy Syst. 2012, 20, 971–985. [Google Scholar] [CrossRef]
- He, H.; Peng, J.; Rui, X.; Hao, F. An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control. Energies 2014, 7, 3748–3763. [Google Scholar] [CrossRef] [Green Version]
- Teo, C.S.; Tan, K.K.; Huang, S.; Lim, S.Y. Dynamic modeling and adaptive control of a multi-axial gantry stage. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics, Waikoloa, HI, USA, 12 October 2005; Volume 4, pp. 3374–3379. [Google Scholar]
- Teo, C.; Tan, K.; Lim, S.; Huang, S.; Tay, E. Dynamic modeling and adaptive control of a H-type gantry stage. Mechatronics 2007, 17, 361–367. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Wang, M.; Sun, W.; Xu, Z. Comparison study on two model-based adaptive algorithms for SOC estimation of lithium-ion batteries in electric vehicles. Energies 2014, 7, 8446–8464. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. A Practical Nonlinear Adaptive Control of Hydraulic Servomechanisms with Periodic-Like Disturbances. IEEE/ASME Trans. Mechatron. 2015, 20, 2752–2760. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Smooth Robust Adaptive Sliding Mode Control of Manipulators with Guaranteed Transient Performance. In Proceedings of the American Control Conference, Baltimore, MD, USA, 29 June–1 July 1994. [Google Scholar]
- Yao, B.; Tomizuka, M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form. Automatica 1997, 33, 893–900. [Google Scholar] [CrossRef]
- Li, X.; Yao, B. Adaptive robust precision motion control of linear motors with negligible electrical dynamics: Theory and experiments. IEEE ASME Trans. Mechatron. 2000, 6, 444–452. [Google Scholar]
- Yao, J.; Deng, W.; Jiao, Z. RISE-Based Adaptive Control of Hydraulic Systems with Asymptotic Tracking. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1524–1531. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, Z.; Gao, H. Saturated Adaptive Robust Control for Active Suspension Systems. IEEE Trans. Ind. Electron. 2013, 60, 3889–3896. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S. A Simultaneous Adaptation Law for a Class of Nonlinearly Parametrized Switched Systems. IEEE Control Syst. Lett. 2019, 3, 487–492. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Roy, S.B.; Kar, I.N. Adaptive–robust control of euler–Lagrange systems with linearly parametrizable uncertainty bound. IEEE Trans. Control Syst. Technol. 2017, 26, 1842–1850. [Google Scholar] [CrossRef]
- Cong, L.; Yao, B.; Zhu, X.; Wang, Q. Adaptive robust synchronous control with dynamic thrust allocation of dual drive gantry stage. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014. [Google Scholar]
- Li, C.; Li, C.; Chen, Z.; Yao, B. Advanced Synchronization Control of a Dual-Linear-Motor-Driven Gantry with Rotational Dynamics. IEEE Trans. Ind. Electron. 2018, 65, 7526–7535. [Google Scholar] [CrossRef]
- Sastry, S.; Bodson, M. Adaptive Control: Stability, Convergence, and Robustness; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]


| Model | Rated Power | Maximum Speed | Continuous Force | Continuous Current |
|---|---|---|---|---|
| Kollmorgen IC44-075 | kW | m/s | 1732 N | A |
| Symbol | Description | Value |
|---|---|---|
| mass of Linear Motor 1 | 32 kg | |
| mass of Linear Motor 2 | 28 kg | |
| mass of the mid-beam | kg | |
| mass of the end-effector | kg | |
| viscous friction coefficient of Motor 1 | N/m/s | |
| viscous friction coefficient of Motor 2 | N/m/s | |
| Coulomb friction coefficient of Motor 1 | 50 N | |
| Coulomb friction coefficient of Motor 2 | N | |
| equivalent stiffness coefficient of the mid-beam | 11,133.4 Nm/rad |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Jiao, Z.; Yan, L.; Shang, Y.; Wu, S. Nonlinear Synchronous Control for H-Type Gantry Stage Used in Electric Vehicles Manufacturing. Energies 2019, 12, 2305. https://doi.org/10.3390/en12122305
Chen R, Jiao Z, Yan L, Shang Y, Wu S. Nonlinear Synchronous Control for H-Type Gantry Stage Used in Electric Vehicles Manufacturing. Energies. 2019; 12(12):2305. https://doi.org/10.3390/en12122305
Chicago/Turabian StyleChen, Ran, Zongxia Jiao, Liang Yan, Yaoxing Shang, and Shuai Wu. 2019. "Nonlinear Synchronous Control for H-Type Gantry Stage Used in Electric Vehicles Manufacturing" Energies 12, no. 12: 2305. https://doi.org/10.3390/en12122305




