Estimating Soil Arsenic Contamination by Integrating Hyperspectral and Geochemical Data with PCA and Optimizing Inversion Models
Highlights
- This study proposed a novel inversion method based on the fusion of geochemical data and PCA-dimensionality-reduced spectral data.
- This study demonstrated the superior performance of the Random Forest model on the fused data.
- This study innovatively integrates direct and precise geochemical data with macroscopic and continuous spectral data. By applying Principal Component Analysis to reduce the dimensionality and noise of the high-dimensional spectral data, core features are effectively extracted, resulting in a fused dataset with more comprehensive information. This method overcomes the limitations of using a single data source and significantly improves the inversion accuracy for mapping the spatial distribution of soil arsenic.
- Among various machine learning models, this study conclusively verifies the exceptional effectiveness of the Random Forest algorithm in processing the multi-source fused data. The model proficiently captures the complex non-linear relationships between arsenic content and multi-source environmental features. Its inherent resistance to overfitting and capability for feature importance assessment provide a reliable tool for high-precision arsenic inversion and pollution mechanism analysis.
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Soil Sampling and Data Preprocessing
2.2.1. Laboratory Analysis
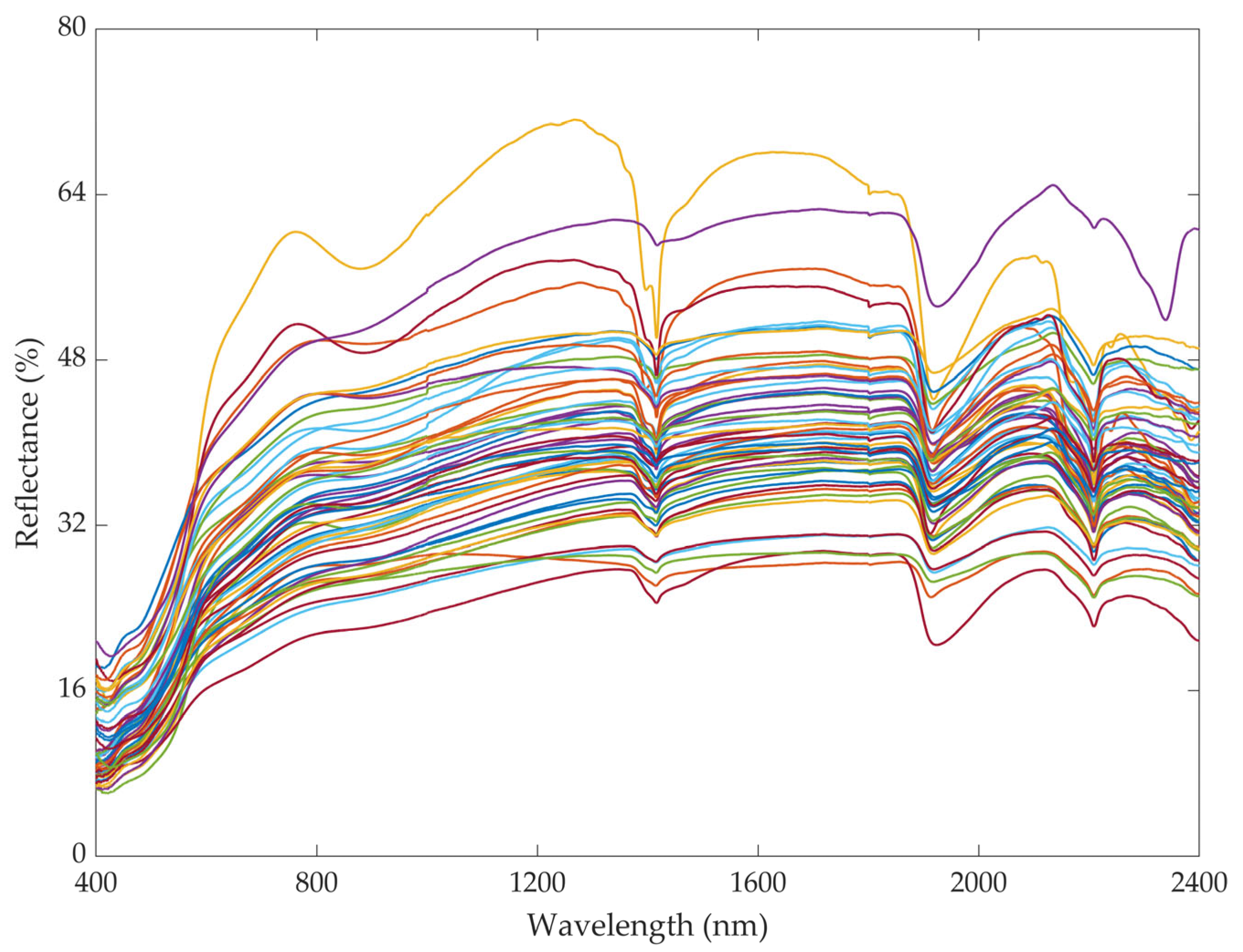
2.2.2. Hyperspectral Data Acquisition
2.3. Model Input Variable Filtering
2.3.1. Principal Component Analysis
2.3.2. Correlation Analysis
2.4. Model Construction and Validation
2.4.1. Modeling Method
2.4.2. Model Validation
2.5. Data Treatment
3. Results
3.1. Arsenic Contamination of Soil
3.2. Statistical Results of Soil Properties
3.3. Filtering of Model Input Variables
3.3.1. Soil Components Associated with Arsenic
3.3.2. Spectral Dimensionality Reduction Using PCA
3.4. Performance of Inversion Models
3.4.1. Modeling of Original Spectral Data
3.4.2. Modeling of Original Spectral Data Combined with Arsenic-Correlated Soil Components
3.4.3. Modeling of the Principal Component by PCA
3.4.4. Hybrid Modeling of Principal Components and Arsenic-Correlated Soil Components
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fatoki, J.O.; Badmus, J.A. Arsenic as an environmental and human health antagonist: A review of its toxicity and disease initiation. J. Hazard. Mater. Adv. 2022, 5, 100052. [Google Scholar] [CrossRef]
- Jomova, K.; Jenisova, Z.; Feszterova, M.; Baros, S.; Liska, J.; Hudecova, D.; Rhodes, C.J.; Valko, M. Arsenic: Toxicity, oxidative stress and human disease. J. Appl. Toxicol. 2011, 31, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Rae, I.D. Arsenic: Its chemistry, its occurrence in the earth and its release into industry and the environment. ChemTexts 2020, 6, 25. [Google Scholar] [CrossRef]
- Tamás, M.; Sharma, S.; Ibstedt, S.; Jacobson, T.; Christen, P. Heavy Metals and Metalloids As a Cause for Protein Misfolding and Aggregation. Biomolecules 2014, 4, 252–267. [Google Scholar] [CrossRef]
- Xu, W.; Jin, Y.; Zeng, G. Introduction of heavy metals contamination in the water and soil: A review on source, toxicity and remediation methods. Green Chem. Lett. Rev. 2024, 17, 2404235. [Google Scholar] [CrossRef]
- Moreno-Jiménez, E.; Manzano, R.; Esteban, E.; Peñalosa, J. The fate of arsenic in soils adjacent to an old mine site (Bustarviejo, Spain): Mobility and transfer to native flora. J. Soils Sediments 2010, 10, 301–312. [Google Scholar] [CrossRef]
- Smith, E.; Naidu, R.; Alston, A.M. Arsenic in the Soil Environment: A Review. Adv. Agron. 1998, 64, 149–195. [Google Scholar]
- Li, W.; Higgins, P. Controlling Local Environmental Performance: An analysis of three national environmental management programs in the context of regional disparities in China. J. Contemp. China 2013, 22, 409–427. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X.; Sun, X.; Sun, Y.; Cen, Y. Predicting nickel concentration in soil using reflectance spectroscopy associated with organic matter and clay minerals. Geoderma 2018, 327, 25–35. [Google Scholar] [CrossRef]
- Ma, C.L.; Zhou, J.M.; Wang, H.Y.; Du, C.W.; Huang, B. Methods for assessment of heavy metal pollution in cropland soils—A case study of Changshu. J. Ecol. Rural. Environ. 2006, 22, 48–53. [Google Scholar]
- Guo, F.; Xu, Z.; Ma, H.; Liu, X.; Gao, L. On Optimizing Hyperspectral Inversion of Soil Copper Content by Kernel Principal Component Analysis. Remote Sens. 2024, 16, 2914. [Google Scholar] [CrossRef]
- Delaney, J.K.; Pezzati, L.; Salimbeni, R.; Zeibel, J.G.; Thoury, M.; Littleton, R.; Morales, K.M.; Palmer, M.; de la Rie, E.R. Visible and infrared reflectance imaging spectroscopy of paintings: Pigment mapping and improved infrared reflectography. In Proceedings of the O3a: Optics for Arts, Architecture, & Archaeology II, Munich, Germany, 14–18 June 2009; p. 739103. [Google Scholar]
- Chen, X.; Warner, T.A.; Campagna, D.J. Integrating visible, near-infrared and short-wave infrared hyperspectral and multispectral thermal imagery for geological mapping at Cuprite, Nevada: A rule-based system. Int. J. Remote Sens. 2010, 31, 1733–1752. [Google Scholar] [CrossRef]
- Bilgili, A.V.; Akbas, F.; Es, H.M.V. Combined use of hyperspectral VNIR reflectance spectroscopy and kriging to predict soil variables spatially. Precis. Agric. 2011, 12, 395–420. [Google Scholar] [CrossRef]
- Morales, G.; Sheppard, J.W.; Logan, R.D.; Shaw, J.A. Hyperspectral Dimensionality Reduction Based on Inter-Band Redundancy Analysis and Greedy Spectral Selection. Remote Sens. 2021, 13, 3649. [Google Scholar] [CrossRef]
- Aishwarya, G.; Kumar, B.L.N.P.; Syamala, D.; Sreya, N.S. Dimensionality Reduction Technique for Hyperspectral Remote Sensing Image Classification. In Proceedings of the 2023 8th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 1–3 June 2023; pp. 1694–1698. [Google Scholar]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Z.; Ma, H.; Liu, X.; Tang, S.; Yang, Z.; Zhang, L.; Liu, F.; Peng, M.; Li, K. Estimating chromium concentration in arable soil based on the optimal principal components by hyperspectral data. Ecol. Indic. 2021, 133, 108400. [Google Scholar] [CrossRef]
- Salem, N.; Hussein, S. Data dimensional reduction and principal components analysis. Procedia Comput. Sci. 2019, 163, 292–299. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Yang, M.; Zhang, Y.; Wang, J.; Marshall, S.; Han, J. Novel Folded-PCA for improved feature extraction and data reduction with hyperspectral imaging and SAR in remote sensing. ISPRS J. Photogramm. Remote Sens. 2014, 93, 112–122. [Google Scholar] [CrossRef]
- Howley, T.; Madden, M.G.; O’Connell, M.-L.; Ryder, A.G. The effect of principal component analysis on machine learning accuracy with high-dimensional spectral data. Knowl.-Based Syst. 2006, 19, 363–370. [Google Scholar] [CrossRef]
- Rodarmel, C.; Shan, J. Principal Component Analysis for Hyperspectral Image Classification. Surv. Land Inf. Sci. 2002, 62, 115–122. [Google Scholar]
- Wallace, J.; Champagne, P.; Hall, G. Multivariate statistical analysis of water chemistry conditions in three wastewater stabilization ponds with algae blooms and pH fluctuations. Water Res. 2016, 96, 155–165. [Google Scholar] [CrossRef]
- Haji Gholizadeh, M.; Melesse, A.M.; Reddi, L. Water quality assessment and apportionment of pollution sources using APCS-MLR and PMF receptor modeling techniques in three major rivers of South Florida. Sci. Total Environ. 2016, 566–567, 1552–1567. [Google Scholar] [CrossRef] [PubMed]
- Rodionova, O.; Kucheryavskiy, S.; Pomerantsev, A. Efficient tools for principal component analysis of complex data—A tutorial. Chemom. Intell. Lab. Syst. 2021, 213, 104304. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, B.; Li, S.; Tian, R.; Zhang, B.; Feng, H.; Tang, Y. A hierarchical residual correction-based hyperspectral inversion method for soil heavy metals considering spatial heterogeneity. J. Hazard. Mater. 2024, 479, 135699. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using soil library hyperspectral reflectance and machine learning to predict soil organic carbon: Assessing potential of airborne and spaceborne optical soil sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- Dwivedi, R.S. Spectral Reflectance of Soils. In Remote Sensing of Soils; Ravi Shankar, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 267–303. [Google Scholar]
- Wan, Y.; Liu, J.; Zhuang, Z.; Wang, Q.; Li, H. Heavy Metals in Agricultural Soils: Sources, Influencing Factors, and Remediation Strategies. Toxics 2024, 12, 63. [Google Scholar] [CrossRef]
- Sharma, V.; Chauhan, R.; Kumar, R. Spectral characteristics of organic soil matter: A comprehensive review. Microchem. J. 2021, 171, 106836. [Google Scholar] [CrossRef]
- Shi, M.; Min, X.; Ke, Y.; Lin, Z.; Yang, Z.; Wang, S.; Peng, N.; Yan, X.; Luo, S.; Wu, J.; et al. Recent progress in understanding the mechanism of heavy metals retention by iron (oxyhydr)oxides. Sci. Total Environ. 2021, 752, 141930. [Google Scholar] [CrossRef]
- Chen, T.; Wen, X.; Zhou, J.; Lu, Z.; Li, X.; Yan, B. A critical review on the migration and transformation processes of heavy metal contamination in lead-zinc tailings of China. Environ. Pollut. 2023, 338, 122667. [Google Scholar] [CrossRef]
- Boisson, J.; Ruttens, A.; Mench, M.; Vangronsveld, J. Evaluation of hydroxyapatite as a metal immobilizing soil additive for the remediation of polluted soils. Part 1. Influence of hydroxyapatite on metal exchangeability in soil, plant growth and plant metal accumulation. Environ. Pollut. 1999, 104, 225–233. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef]
- Tan, K.; Ye, Y.-Y.; Du, P.-J.; Zhang, Q.-Q. Estimation of Heavy Metal Concentrations in Reclaimed Mining Soils Using Reflectance Spectroscopy. Spectrosc. Spectr. Anal. 2014, 34, 3317–3322. [Google Scholar]
- Zhou, W.; Yang, H.; Xie, L.; Li, H.; Yue, T. Hyperspectral inversion of soil heavy metals in Three-River Source Region based on random forest model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, W.; Aihemaitijiang, G.; Zhang, F.; Zhang, J.; Zhang, Y.; Pan, D.; Li, J. Hyperspectral inversion of heavy metal content in farmland soil under conservation tillage of black soils. Sci. Rep. 2025, 15, 354. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Xiao, H.; He, F.; Dai, Z.; Huang, W.; Zhu, B.; Liu, S. Prediction of soil heavy metal content around mine tailings using multiple methods combined with transformed hyperspectral reflectance data. Ore Energy Resour. Geol. 2024, 18, 100072. [Google Scholar] [CrossRef]
- Wang, W.; Liu, K.; Liu, C. Multi-source power data fusion method based on deep learning. In Proceedings of the Second International Conference on Energy, Power, and Electrical Technology (ICEPET 2023), Kuala Lumpur, Malaysia, 10–12 March 2023; pp. 903–908. [Google Scholar]
- Zareapoor, M.; Shamsolmoali, P.; Kumar Jain, D.; Wang, H.; Yang, J. Kernelized support vector machine with deep learning: An efficient approach for extreme multiclass dataset. Pattern Recognit. Lett. 2018, 115, 4–13. [Google Scholar] [CrossRef]
- Almeida, J.S. Predictive non-linear modeling of complex data by artificial neural networks. Curr. Opin. Biotechnol. 2002, 13, 72–76. [Google Scholar] [CrossRef]
- Tealab, A.; Hefny, H.; Badr, A. Forecasting of nonlinear time series using ANN. Future Comput. Inform. J. 2017, 2, 39–47. [Google Scholar] [CrossRef]
- Jiang, N.; Zhou, C.; Lu, S.; Zhang, Z. Effect of Underground Mine Blast Vibrations on Overlaying Open Pit Slopes: A Case Study for Daye Iron Mine in China. Geotech. Geol. Eng. 2018, 36, 1475–1489. [Google Scholar] [CrossRef]
- Du, P.; Xie, Y.; Wang, S.; Zhao, H.; Zhang, Z.; Wu, B.; Li, F. Potential sources of and ecological risks from heavy metals in agricultural soils, Daye City, China. Environ. Sci. Pollut. Res. 2015, 22, 3498–3507. [Google Scholar] [CrossRef]
- Xi, X.; Wang, S.; Yao, L.; Zhang, Y.; Niu, R.; Zhou, Y. Evaluation on geological environment carrying capacity of mining city—A case study in Huangshi City, Hubei Province, China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102410. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.; Jin, B.; Li, Y.; Shi, Z. Assessment of the potential health risks of heavy metals in soils in a coastal industrial region of the Yangtze River Delta. Environ. Sci. Pollut. Res. 2017, 24, 19816–19826. [Google Scholar] [CrossRef]
- Malmir, M.; Tahmasbian, I.; Xu, Z.; Farrar, M.B.; Bai, S.H. Prediction of soil macro- and micro-elements in sieved and ground air-dried soils using laboratory-based hyperspectral imaging technique. Geoderma 2019, 340, 70–80. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X. Estimating soil zinc concentrations using reflectance spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 126–133. [Google Scholar] [CrossRef]
- Cheng, H.; Shen, R.; Chen, Y.; Wan, Q.; Shi, T.; Wang, J.; Wan, Y.; Hong, Y.; Li, X. Estimating heavy metal concentrations in suburban soils with reflectance spectroscopy. Geoderma 2019, 336, 59–67. [Google Scholar] [CrossRef]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral indirect inversion of heavy-metal copper in reclaimed soil of iron ore area. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 222, 117191. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, W.; Cen, Y.; Zhang, L.; Wang, N. Predicting cadmium concentration in soils using laboratory and field reflectance spectroscopy. Sci. Total Environ. 2019, 650, 321–334. [Google Scholar] [CrossRef]
- Raiko, T.; Ilin, A.; Karhunen, J. Principal Component Analysis for Sparse High-Dimensional Data. In Proceedings of the Neural Information Processing, Iconip, Kitakyushu, Japan, 13 November 2007; pp. 566–575. [Google Scholar]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Van Wieringen, W.N.; Peeters, C.F.W. Ridge estimation of inverse covariance matrices from high-dimensional data. Comput. Stat. Data Anal. 2016, 103, 284–303. [Google Scholar] [CrossRef]
- Bolcárová, P.; Kološta, S. Assessment of sustainable development in the EU 27 using aggregated SD index. Ecol. Indic. 2015, 48, 699–705. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Principal component analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Hron, K.; Kynčlová, P.; Garrett, R.G. A new method for correlation analysis of compositional (environmental) data—A worked example. Sci. Total Environ. 2017, 607–608, 965–971. [Google Scholar] [CrossRef] [PubMed]
- Gupta, B. Correlation and Regression. In Interview Questions in Business Analytics; Gupta, B., Ed.; Apress: Berkeley, CA, USA, 2016; pp. 45–55. [Google Scholar]
- Harrington, P.d.B.; Urbas, A.; Tandler, P.J. Two-dimensional correlation analysis. Chemom. Intell. Lab. Syst. 2000, 50, 149–174. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Guebel, D.V.; Torres, N.V. Partial Least-Squares Regression (PLSR). In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.-H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013; pp. 1646–1648. [Google Scholar]
- Cheng, J.-H.; Sun, D.-W. Partial Least Squares Regression (PLSR) Applied to NIR and HSI Spectral Data Modeling to Predict Chemical Properties of Fish Muscle. Food Eng. Rev. 2017, 9, 36–49. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Raj, A.S.; Srinivas, Y.; Oliver, D.H.; Muthuraj, D. A novel and generalized approach in the inversion of geoelectrical resistivity data using Artificial Neural Networks (ANN). J. Earth Syst. Sci. 2014, 123, 395–411. [Google Scholar] [CrossRef]
- Landi, A.; Piaggi, P.; Laurino, M.; Menicucci, D. Artificial Neural Networks for nonlinear regression and classification. In Proceedings of the 2010 10th International Conference on Intelligent Systems Design and Applications, Cairo, Egypt, 29 November–1 December 2010; pp. 115–120. [Google Scholar]
- Demarchi, L.; Canters, F.; Cariou, C.; Licciardi, G.; Chan, J.C.-W. Assessing the performance of two unsupervised dimensionality reduction techniques on hyperspectral APEX data for high resolution urban land-cover mapping. ISPRS J. Photogramm. Remote Sens. 2014, 87, 166–179. [Google Scholar] [CrossRef]
- Lee, K.Y.; Chung, N.; Hwang, S. Application of an artificial neural network (ANN) model for predicting mosquito abundances in urban areas. Ecol. Inform. 2016, 36, 172–180. [Google Scholar] [CrossRef]
- Wang, Q.; Nguyen, T.-T.; Huang, J.Z.; Nguyen, T.T. An efficient random forests algorithm for high dimensional data classification. Adv. Data Anal. Classif. 2018, 12, 953–972. [Google Scholar] [CrossRef]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random forests: From early developments to recent advancements. Syst. Sci. Control Eng. 2014, 2, 602–609. [Google Scholar] [CrossRef]
- Saeys, W.; Mouazen, A.M.; Ramon, H. Potential for Onsite and Online Analysis of Pig Manure using Visible and Near Infrared Reflectance Spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]
- Sawut, R.; Kasim, N.; Abliz, A.; Hu, L.; Yalkun, A.; Maihemuti, B.; Qingdong, S. Possibility of optimized indices for the assessment of heavy metal contents in soil around an open pit coal mine area. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 14–25. [Google Scholar] [CrossRef]
- State Environmental Protection Administration; China National Environmental Monitoring Centre. Background Values of Soil Elements in China; China Environmental Science Press: Beijing, China, 1990. [Google Scholar]
- Maliki, A.A.; Bruce, D.; Owens, G. Spatial distribution of Pb in urban soil from Port Pirie, South Australia. Environ. Technol. Innov. 2015, 4, 123–136. [Google Scholar] [CrossRef]
- Shi, T.; Wang, J.; Chen, Y.; Wu, G. Improving the prediction of arsenic contents in agricultural soils by combining the reflectance spectroscopy of soils and rice plants. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 95–103. [Google Scholar] [CrossRef]
- Wang, J.; Cui, L.; Gao, W.; Shi, T.; Chen, Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar] [CrossRef]
- Ren, H.-Y.; Zhuang, D.-F.; Singh, A.N.; Pan, J.-J.; Qiu, D.-S.; Shi, R.-H. Estimation of As and Cu Contamination in Agricultural Soils Around a Mining Area by Reflectance Spectroscopy: A Case Study. Pedosphere 2009, 19, 719–726. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Ji, J.; Gong, P.; Liao, Q.; Tian, Q.; Ma, H. A Mechanism Study of Reflectance Spectroscopy for Investigating Heavy Metals in Soils. Soil Sci. Soc. Am. J. 2007, 71, 918–926. [Google Scholar] [CrossRef]
- Dragović, R.; Gajić, B.; Dragović, S.; Đorđević, M.; Đorđević, M.; Mihailović, N.; Onjia, A. Assessment of the impact of geographical factors on the spatial distribution of heavy metals in soils around the steel production facility in Smederevo (Serbia). J. Clean. Prod. 2014, 84, 550–562. [Google Scholar] [CrossRef]
- Lee, C.S.-l.; Li, X.; Shi, W.; Cheung, S.C.-n.; Thornton, I. Metal contamination in urban, suburban, and country park soils of Hong Kong: A study based on GIS and multivariate statistics. Sci. Total Environ. 2006, 356, 45–61. [Google Scholar] [CrossRef]





| Elements | Analytical Methods |
|---|---|
| As | Determination of arsenic, antimony, and bismuth by hydride atomic fluorescence spectrometry |
| Cd | Determination of 32 trace elements by plasma mass spectrometry |
| Cr | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| Cu | Determination of 32 trace elements by plasma mass spectrometry |
| Hg | Determination of mercury by cold vapor atomic fluorescence spectrometry |
| Ni | Determination of 32 trace elements by plasma mass spectrometry |
| P | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| Pb | Determination of 32 trace elements by plasma mass spectrometry |
| SiO2 | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| Al2O3 | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| T-Fe2O3 | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| MgO | Determination of 22 elements by plasma optical emission spectrometry |
| CaO | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| Na2O | Determination of 22 elements by plasma optical emission spectrometry |
| K2O | Determination of 34 primary, secondary, and trace elements by X-ray fluorescence spectrometry |
| pH | Determination of pH value of forest soil |
| SOM | Determination of total carbon and organic carbon by high frequency combustion-infrared carbon sulfur meter |
| Arsenic Contamination (mg·kg−1) | Number | Mean | Max | Min | SD | CV |
|---|---|---|---|---|---|---|
| Calibration set | 38 | 23.05 | 57.08 | 2.34 | 13.16 | 1.05 |
| Validation set | 18 | 22.95 | 54.57 | 6.14 | 12.26 | 0.53 |
| Whole dataset | 56 | 23.01 | 57.08 | 2.34 | 12.77 | 0.55 |
| Soil Properties | Mean | Max | Min | SD | CV |
|---|---|---|---|---|---|
| Cd | 0.64 | 2.11 | 0.04 | 0.40 | 0.62 |
| Cr | 65.24 | 116.91 | 10.55 | 25.19 | 0.39 |
| Cu | 89.04 | 320.86 | 21.68 | 64.48 | 0.72 |
| Hg | 0.11 | 0.41 | 0.02 | 0.07 | 0.63 |
| Ni | 24.77 | 47.98 | 5.70 | 10.46 | 0.42 |
| Pb | 65.28 | 592.44 | 17.30 | 75.66 | 1.16 |
| Zn | 135.47 | 401.09 | 47.43 | 65.64 | 0.48 |
| P | 850.30 | 3339.70 | 179.60 | 495.96 | 0.58 |
| S | 261.79 | 549.42 | 54.94 | 114.24 | 0.44 |
| SiO2 | 65.63 | 76.62 | 7.45 | 9.83 | 0.15 |
| Al2O3 | 14.39 | 24.48 | 1.88 | 3.28 | 0.23 |
| T-Fe2O3 | 5.66 | 8.16 | 1.20 | 1.27 | 0.22 |
| MgO | 0.75 | 2.46 | 0.29 | 0.33 | 0.45 |
| CaO | 2.00 | 45.00 | 0.07 | 6.12 | 3.06 |
| Na2O | 0.50 | 2.28 | 0.05 | 0.44 | 0.89 |
| K2O | 1.88 | 2.78 | 0.31 | 0.41 | 0.22 |
| SOM | 38.66 | 75.97 | 6.66 | 18.57 | 0.48 |
| pH | 6.05 | 8.09 | 3.87 | 1.23 | 0.20 |
| Components | Eigenvalue | Variance (%) | Cumulative Contribution Rate (%) |
|---|---|---|---|
| 1 | 1847.74 | 92.34 | 92.34 |
| 2 | 77.84 | 3.89 | 96.23 |
| 3 | 46.67 | 2.33 | 98.56 |
| 4 | 16.54 | 0.83 | 99.39 |
| 5 | 7.48 | 0.37 | 99.76 |
| 6 | 1.52 | 0.08 | 99.84 |
| 7 | 1.11 | 0.06 | 99.90 |
| Sampling Site | Content Range (mg/kg) | Model | R2 | Number of Samples | Authors |
|---|---|---|---|---|---|
| Agricultural regions | 1.91–21.90 | GA-PLSR | 0.56–0.64 | 96 | [76] |
| Agricultural area at mine | 19.33–403.77 | PLSR | 0.58 | 33 | [77] |
| Agricultural area at the Changjiang River Delta | 6.13–13.30 | PLSR | 0.72 | 61 | [78] |
| Agricultural area | 10.25–133.36 | GA-PLSR | 0.42 | 94 | [75] |
| Agricultural regions | 2.34–57.08 | RF | 0.86 | 56 | This study |
| Input Variable | Model | R2 | RMSE | RPD |
|---|---|---|---|---|
| Combination 1 | PLSR | −0.14 | 12.74 | 0.96 |
| ANN | −0.22 | 13.14 | 0.93 | |
| RF | −0.06 | 12.30 | 1.00 | |
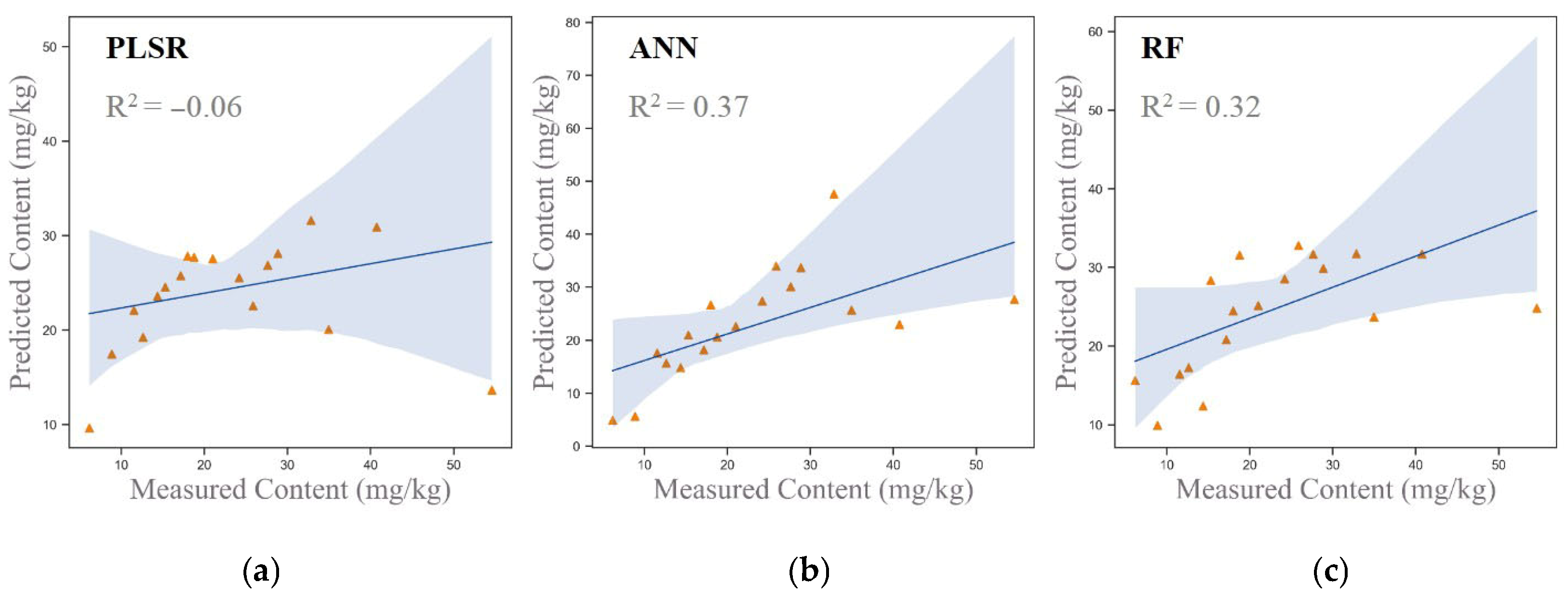
| Combination 2 | PLSR | −0.06 | 12.29 | 1.00 |
| ANN | 0.37 | 9.49 | 1.29 | |
| RF | 0.32 | 9.80 | 1.25 | |
| Combination 3 | PLSR | 0.49 | 8.52 | 1.44 |
| ANN | 0.29 | 10.03 | 1.22 | |
| RF | 0.54 | 8.11 | 1.51 | |
| Combination 4 | PLSR | 0.75 | 5.91 | 2.07 |
| ANN | 0.06 | 11.55 | 1.06 | |
| RF | 0.86 | 4.45 | 2.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Xu, Z.; Ma, H.; Liu, X. Estimating Soil Arsenic Contamination by Integrating Hyperspectral and Geochemical Data with PCA and Optimizing Inversion Models. Sensors 2025, 25, 6857. https://doi.org/10.3390/s25226857
Guo F, Xu Z, Ma H, Liu X. Estimating Soil Arsenic Contamination by Integrating Hyperspectral and Geochemical Data with PCA and Optimizing Inversion Models. Sensors. 2025; 25(22):6857. https://doi.org/10.3390/s25226857
Chicago/Turabian StyleGuo, Fei, Zhen Xu, Honghong Ma, and Xiujin Liu. 2025. "Estimating Soil Arsenic Contamination by Integrating Hyperspectral and Geochemical Data with PCA and Optimizing Inversion Models" Sensors 25, no. 22: 6857. https://doi.org/10.3390/s25226857
APA StyleGuo, F., Xu, Z., Ma, H., & Liu, X. (2025). Estimating Soil Arsenic Contamination by Integrating Hyperspectral and Geochemical Data with PCA and Optimizing Inversion Models. Sensors, 25(22), 6857. https://doi.org/10.3390/s25226857






