Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization
Abstract
:1. Introduction
- (1)
- Additional analyses of different parameter configurations of ACK-MSCKF are performed with more real-world experiments.
- (2)
- Conducting the formulation and implementation of a consistent monocular Ackermann VIO, MAVIO, which not only improves the observability of the VIO scale direction but also resolves the inconsistency problem of ACK-MSCKF for further improving the positioning accuracy.
- (3)
- Introducing the raw GNSS error measurement model, MAVIO-GNSS, which further improves the vehicle positioning accuracy under the long-distance driving state.
- (4)
- The performance of MAVIO and MAVIO-GNSS are comprehensively compared with S-MSCKF and ACK-MSCKF on real-world datasets with twenty rounds, on average, of real-world experiments.
- (5)
- The source code [50] of MAVIO is publicly available to facilitate the reproducibility of related research.
2. The Proposed Approach
2.1. Coordinate Systems and Notations
- (1)
- Inertial Coordinate System of IMU {GI}. The origin of {GI} is the same as that of {I} at the time of VIO initialization. The axes of {GI} are obtained by calculation at the time of VIO initialization, and its z-axis is aligned with Earth’s gravity.
- (2)
- Inertial Coordinate System of Vehicle {GB}. The origin of {GB} is the same as that of {B} at the time of VIO initialization. The axes of {GB} are obtained by calculation at the time of VIO initialization, and its z-axis is aligned with Earth’s gravity.
- (3)
- GNSS Coordinate System {S}. The origin of {S} lies in the center of the GNSS equipment. The x-axis and y-axis point forward and to the right, respectively, following the right-hand rule.
- (4)
- Universal Transverse Mercator Coordinate System {US}. The {US} is a universal global coordinate system. Please refer to [51] for more details.
2.2. The Lever Arm Effect between the Vehicle and IMU Coordinates
2.3. Process Model and Monocular Visual Measurement Model
2.4. Kinematic Error Measurement Model for Vehicle
2.4.1. Measurements of Vehicle Relative Kinematic Error
2.4.2. Measurements of Vehicle Velocity and Angular Rate Error
2.5. Raw GNSS Error Measurement Model
3. Experiments and Results
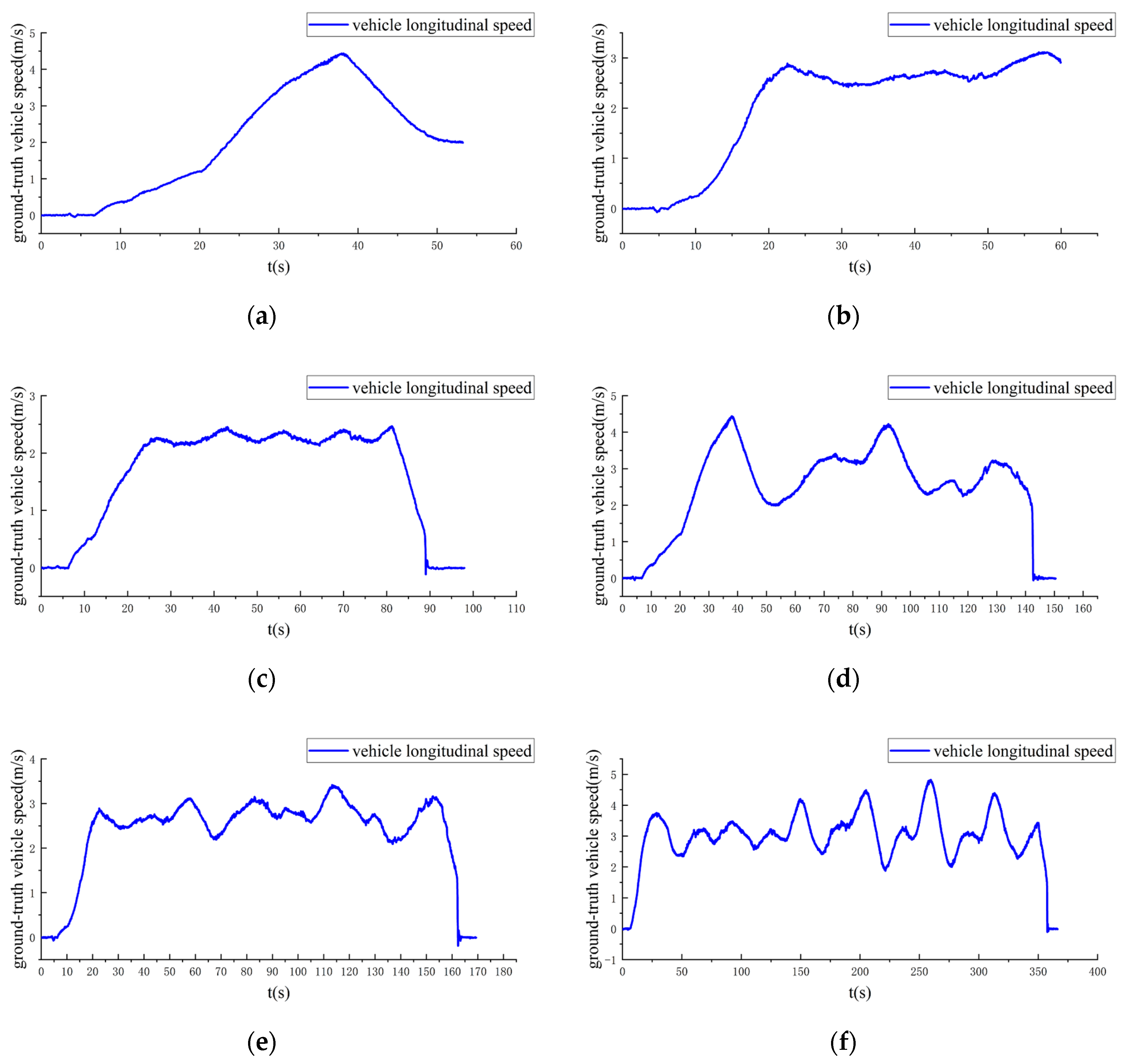
3.1. Experimental Vehicle Platform and Real-World Datasets
3.2. Experimental Results
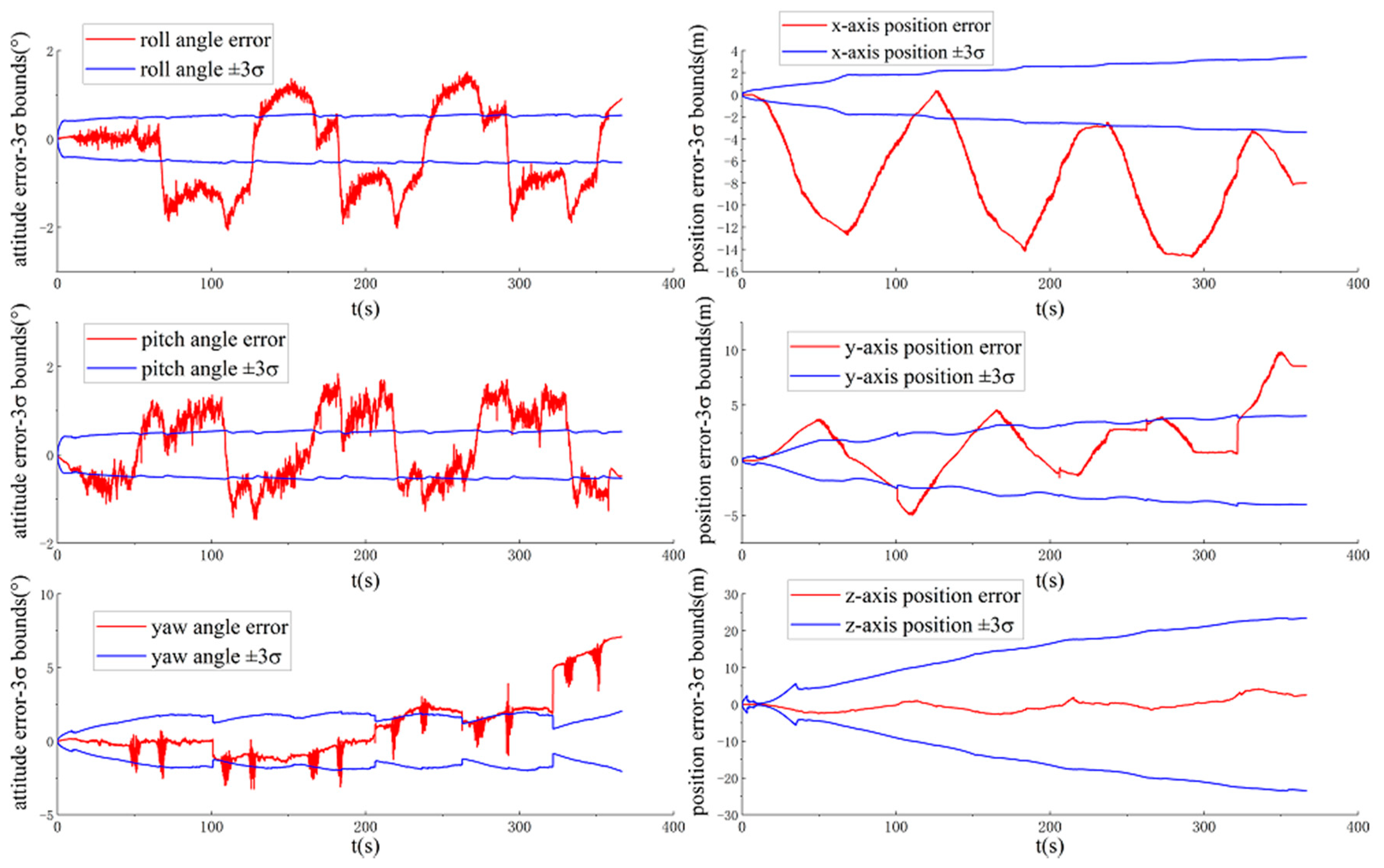
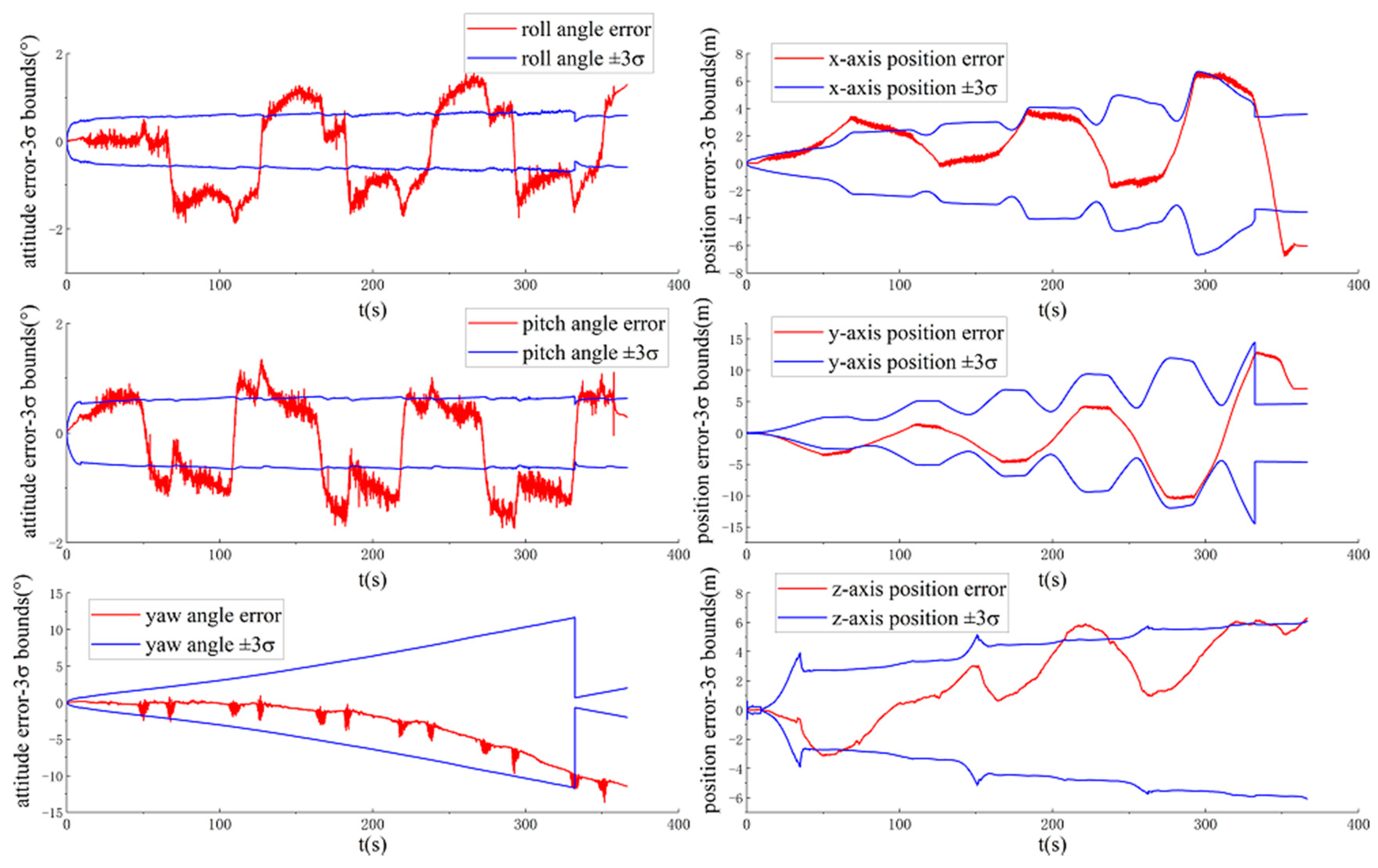
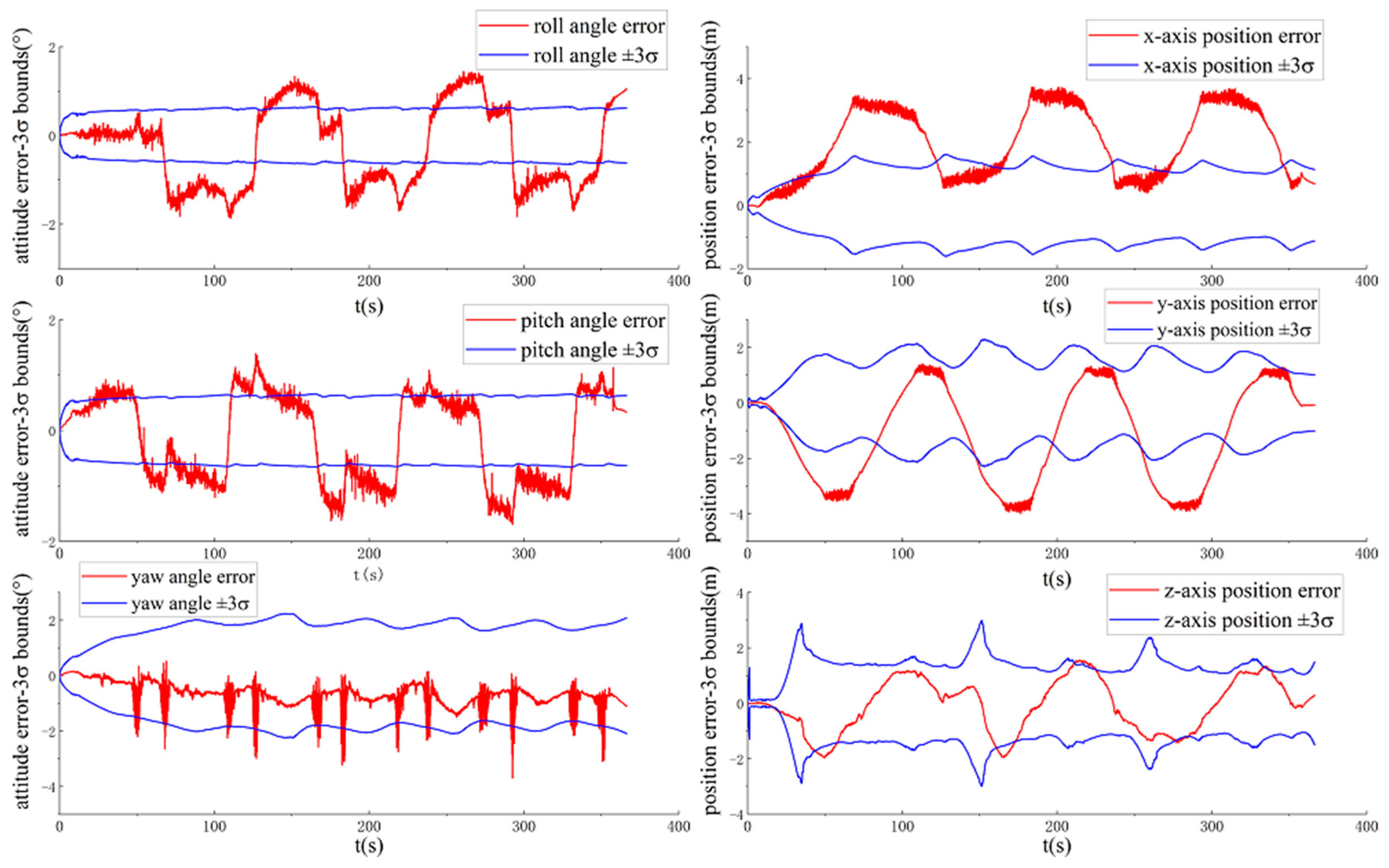
3.2.1. Observability and Consistency Comparison
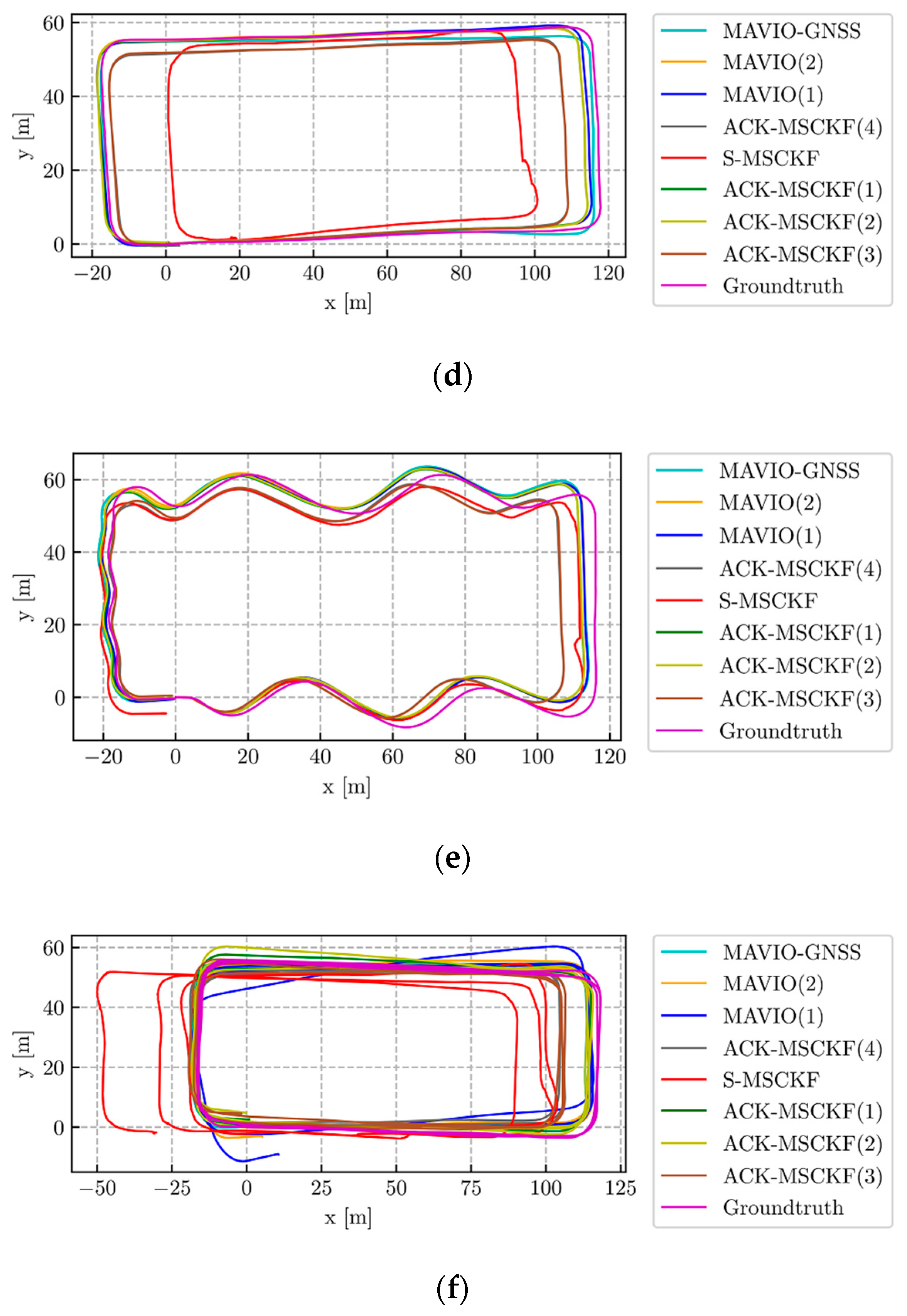
3.2.2. Positioning Accuracy Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Yang, D.; Jiang, K.; Zhao, D.; Yu, C.; Cao, Z.; Xie, S.; Xiao, Z.; Jiao, X.; Wang, S.; Zhang, K. Intelligent and connected vehicles: Current status and future perspectives. Sci. China Technol. 2018, 61, 1446–1471. [Google Scholar] [CrossRef]
- Ma, F.; Wang, J.; Yang, Y.; Wu, L.; Zhu, S.; Gelbal, S.Y.; Aksun-Guvenc, B.; Guvenc, L. Stability Design for the Homogeneous Platoon with Communication Time Delay. Automot. Innov. 2020, 3, 101–110. [Google Scholar] [CrossRef]
- Specht, M.; Specht, C.; Dąbrowski, P.; Czaplewski, K.; Smolarek, L.; Lewicka, O. Road Tests of the Positioning Accuracy of INS/GNSS Systems Based on MEMS Technology for Navigating Railway Vehicles. Energies 2020, 13, 4463. [Google Scholar] [CrossRef]
- Jiang, Q.; Wu, W.; Jiang, M.; Li, Y. A New Filtering and Smoothing Algorithm for Railway Track Surveying Based on Landmark and IMU/Odometer. Sensors 2017, 17, 1438. [Google Scholar] [CrossRef]
- Singh, K.B.; Arat, M.A.; Taheri, S. Literature review and fundamental approaches for vehicle and tire state estimation. Veh. Syst. Dyn. 2018, 57, 1643–1665. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, D.; Wen, F.; Jiang, K. A Unified Multiple-Target Positioning Framework for Intelligent Connected Vehicles. Sensors 2019, 19, 1967. [Google Scholar] [CrossRef] [Green Version]
- Ansari, K. Cooperative Position Prediction: Beyond Vehicle-to-Vehicle Relative Position–ing. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1121–1130. [Google Scholar] [CrossRef]
- Lynen, S.; Achtelik, M.W.; Weiss, S.; Chli, M.; Siegwart, R. A robust and modular multi-sensor fusion approach applied to MAV navigation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems; Institute of Electrical and Electronics Engineers (IEEE), Tokyo, Japan, 3–7 November 2013; pp. 3923–3929. [Google Scholar]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Mourikis, A.I.; Roumeliotis, S.I. A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation. In Proceedings of the Proceedings 2007 ICRA. IEEE International Conference on Robotics and Automation; Institute of Electrical and Electronics Engineers (IEEE), Italy, Roma, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Ramezani, M.; Khoshelham, K. Vehicle Positioning in GNSS-Deprived Urban Areas by Stereo Visual-Inertial Odometry. IEEE Trans. Intell. Veh. 2018, 3, 208–217. [Google Scholar] [CrossRef]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef] [Green Version]
- Huai, Z.; Huang, G. Robocentric Visual-Inertial Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Madrid, Spain, 1–5 October 2018; pp. 6319–6326. [Google Scholar]
- Geneva, P.; Eckenhoff, K.; Huang, G. A Linear-Complexity EKF for Visual-Inertial Navigation with Loop Closures. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Montreal, QC, Canada, 20–24 May 2019; pp. 3535–3541. [Google Scholar]
- Qiu, X.; Zhang, H.; Fu, W.; Zhao, C.; Jin, Y. Monocular Visual-Inertial Odometry with an Unbiased Linear System Model and Robust Feature Tracking Front-End. Sensors 2019, 19, 1941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, X.; Zhang, H.; Fu, W. Lightweight hybrid visual-inertial odometry with closed-form zero velocity update. Chin. J. Aeronaut. 2020. [Google Scholar] [CrossRef]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2014, 34, 314–334. [Google Scholar] [CrossRef] [Green Version]
- Mur-Artal, R.; Tardos, J.D. Visual-Inertial Monocular SLAM With Map Reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Zhao, J.; Guo, Y.; He, W.; Yuan, K. PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features. Sensors 2018, 18, 1159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Chen, M.; Zhang, G.; Bao, H.; Bao, Y. ICE-BA: Incremental, Consistent and Efficient Bundle Adjustment for Visual-Inertial SLAM. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1974–1982. [Google Scholar]
- Von Stumberg, L.; Usenko, V.; Cremers, D. Direct Sparse Visual-Inertial Odometry Using Dynamic Marginalization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Brisbane Convention & Exhibition Centre, Brisbane, Australia, 21–25 May 2018; pp. 2510–2517. [Google Scholar]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A General Optimization-based Framework for Global Pose Estimation with Multiple Sensors. Available online: https://arxiv.org/abs/1901.03642 (accessed on 11 July 2020).
- Qin, T.; Pan, J.; Cao, S.; Shen, S. A General Optimization-based Framework for Local Odometry Estimation with Multiple Sensors. Available online: https://arxiv.org/abs/1901.03638 (accessed on 11 July 2020).
- Usenko, V.; Demmel, N.; Schubert, D.; Stueckler, J.; Cremers, D. Visual-Inertial Mapping With Non-Linear Factor Recovery. IEEE Robot. Autom. Lett. 2020, 5, 422–429. [Google Scholar] [CrossRef] [Green Version]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM. Available online: https://arxiv.org/abs/2007.11898 (accessed on 24 July 2020).
- Scaramuzza, D.; Zhang, Z. Visual-Inertial Odometry of Aerial Robots. Available online: https://arxiv.org/abs/1906.03289 (accessed on 11 July 2020).
- Huang, G. Visual-Inertial Navigation: A Concise Review. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Montreal, QC, Canada, 20–24 May 2019; pp. 9572–9582. [Google Scholar]
- Wu, K.J.; Roumeliotis, S.I. Unobservable Directions of VINS under Special Motions; University of Minnesota: Minneapolis, MN, USA, September 2016; Available online: http://mars.cs.umn.edu/research/VINSodometry.php (accessed on 1 September 2019).
- Wu, K.J.; Guo, C.X.; Georgiou, G.; Roumeliotis, S.I. VINS on wheels. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Singapore, 29 May–3 June 2017; pp. 5155–5162. [Google Scholar]
- Yang, Y.; Geneva, P.; Eckenhoff, K.; Huang, G. Degenerate Motion Analysis for Aided INS With Online Spatial and Temporal Sensor Calibration. IEEE Robot. Autom. Lett. 2019, 4, 2070–2077. [Google Scholar] [CrossRef]
- Wu, K.; Ahmed, A.; Georgiou, G.; Roumeliotis, S. A Square Root Inverse Filter for Efficient Vision-aided Inertial Navigation on Mobile Devices. In Proceedings of the Robotics: Science and Systems XI, Science and Systems Foundation, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Li, D.; Eckenhoff, K.; Wu, K.; Wang, Y.; Xiong, R.; Huang, G. Gyro-aided camera-odometer online calibration and localization. In Proceedings of the 2017 American Control Conference (ACC); Institute of Electrical and Electronics Engineers (IEEE), Seattle, WA, USA, 24–26 May 2017; pp. 3579–3586. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef] [Green Version]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Houseago, C.; Bloesch, M.; Leutenegger, S. KO-Fusion: Dense Visual SLAM with Tightly-Coupled Kinematic and Odometric Tracking. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Montreal, QC, Canada, 20–24 May 2019; pp. 4054–4060. [Google Scholar]
- Zheng, F.; Liu, Y.-H. SE(2)-Constrained Visual Inertial Fusion for Ground Vehicles. IEEE Sensors J. 2018, 18, 9699–9707. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, T.; Pang, F. Tightly-coupled Data Fusion of VINS and Odometer Based on Wheel Slip Estimation. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO); Institute of Electrical and Electronics Engineers (IEEE), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1613–1619. [Google Scholar]
- Quan, M.; Piao, S.; Tan, M.; Huang, S.-S. Tightly-Coupled Monocular Visual-Odometric SLAM Using Wheels and a MEMS Gyroscope. IEEE Access 2019, 7, 97374–97389. [Google Scholar] [CrossRef]
- Liu, J.; Gao, W.; Hu, Z. Visual-Inertial Odometry Tightly Coupled with Wheel Encoder Adopting Robust Initialization and Online Extrinsic Calibration. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Macau, China, 4–8 November 2019; pp. 5391–5397. [Google Scholar]
- Liu, J.; Gao, W.; Hu, Z. Bidirectional Trajectory Computation for Odometer-Aided Visual-Inertial SLAM. Available online: https://arxiv.org/abs/2002.00195 (accessed on 2 February 2020).
- Zhang, M.; Chen, Y.; Li, M. Vision-Aided Localization For Ground Robots. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Macau, China, 4–8 November 2019; pp. 2455–2461. [Google Scholar]
- Ye, W.; Zheng, R.; Zhang, F.; Ouyang, Z.; Liu, Y. Robust and Efficient Vehicles Motion Estimation with Low-Cost Multi-Camera and Odometer-Gyroscope. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Macau, China, 4–8 November 2019; pp. 4490–4496. [Google Scholar]
- Gang, P.; Zezao, L.; Bocheng, C.; Shanliang, C.; Dingxin, H. Robust Tightly-Coupled Pose Estimation Based on Monocular Vision, Inertia and Wheel Speed. Available online: https://arxiv.org/abs/2003.01496 (accessed on 11 July 2020).
- Zuo, X.; Zhang, M.; Chen, Y.; Liu, Y.; Huang, G.; Li, M. Visual-Inertial Localization for Skid-Steering Robots with Kinematic Constraints. Available online: https://arxiv.org/abs/1911.05787 (accessed on 11 July 2020).
- Kang, R.; Xiong, L.; Xu, M.; Zhao, J.; Zhang, P. VINS-Vehicle: A Tightly-Coupled Vehicle Dynamics Extension to Visual-Inertial State Estimator. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC); Institute of Electrical and Electronics Engineers (IEEE), Auckland, New Zealand, 27–30 October 2019; pp. 3593–3600. [Google Scholar]
- Lee, W.; Eckenhoff, K.; Yang, Y.; Geneva, P.; Huang, G. Visual-Inertial-Wheel Odometry with Online Calibration. In Proceedings of the 2020 International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24–30 October 2020. [Google Scholar]
- Ma, F.; Shi, J.; Yang, Y.; Li, J.; Dai, K. ACK-MSCKF: Tightly-Coupled Ackermann Multi-State Constraint Kalman Filter for Autonomous Vehicle Localization. Sensors 2019, 19, 4816. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.; Eckenhoff, K.; Geneva, P.; Huang, G. Intermittent GPS-aided VIO: Online Initialization and Calibration. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA); Institute of Electrical and Electronics Engineers (IEEE), Paris, France, 31 May–31 August 2020; pp. 5724–5731. [Google Scholar]
- MAVIO ROS Package. Available online: https://github.com/qdensh/MAVIO (accessed on 12 August 2020).
- Grafarend, E. The Optimal Universal Transverse Mercator Projection. In International Association of Geodesy Symposia; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1995; Volume 114, p. 51. [Google Scholar]
- Breckenridge, W.G. Quaternions proposed standard conventions. Jet Propuls. Lab. Pasadena, CA, Interoffice Memo. IOM 1999, 343–379. [Google Scholar]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman Filter for 3D Attitude Estimation; University of Minnesota: Minnesota, MN, USA, 2005; Volume 2, p. 2005. [Google Scholar]
- Shi, J. Visual-Inertial Pose Estimation and Observability Analysis with Vehicle Motion Constraints. Ph.D. dissertation, Jilin University, Changchun, China, June 2020. (In Chinese). [Google Scholar]
- Kevin, M.L.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Robot_Localization ROS Package. Available online: https://github.com/cra-ros-pkg/robot_localization (accessed on 1 June 2019).
- Markley, F.L.; Cheng, Y.; Crassidis, J.L.; Oshman, Y. Averaging Quaternions. J. Guid. Control. Dyn. 2007, 30, 1193–1197. [Google Scholar] [CrossRef]
- Zhang, Z.; Scaramuzza, D. A Tutorial on Quantitative Trajectory Evaluation for Visual(-Inertial) Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Institute of Electrical and Electronics Engineers (IEEE), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar]
- AverageVioProc ROS Package. Available online: https://github.com/qdensh/AverageVioProc (accessed on 12 August 2020).
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Consistency Analysis and Improvement of Vision-aided Inertial Navigation. IEEE Trans. Robot. 2013, 30, 158–176. [Google Scholar] [CrossRef] [Green Version]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef] [Green Version]
- Msckf_Vio_GPS Package. Available online: https://github.com/ZhouTangtang/msckf_vio_GPS (accessed on 11 July 2019).
- Kalibr_Allan ROS Package. Available online: https://github.com/rpng/kalibr_allan (accessed on 14 February 2019).
- Hesch, J.A.; Kottas, D.G.; Bowman, S.L.; Roumeliotis, S.I. Observability-Constrained Vision-Aided Inertial Navigation; University of Minnesota: Minneapolis, MN, USA, 2012; Volume 1, p. 6. [Google Scholar]








| ACK-MSCKF | Tunable Parameter Configurations |
|---|---|
| ACK-MSCKF(1) | For Equations (A24) and (A31), |
| ACK-MSCKF(2) | For Equations (A24) and (A31), |
| ACK-MSCKF(3) | Same as Equations (A24) and (A31) |
| ACK-MSCKF(4) | For Equation (A24), |
| MAVIO | Tunable Parameter Configurations |
|---|---|
| MAVIO(1) | Same as Equations (A35) and (A40) |
| MAVIO(2) | For Equation (A35), |
| Dataset | Vehicle Driving State | Travel Duration (s) | Travel Distance (m) | Data Bulk | |||
|---|---|---|---|---|---|---|---|
| Vehicle CAN-Bus | Stereo Images | IMU | Ground Truth | ||||
| VD01 | Straight | 54 | 109 | 8657 | 1615 | 10,808 | 10,818 |
| VD02 | S-shaped | 60 | 122 | 9644 | 1820 | 12,146 | 12,186 |
| VD03 | Circular | 99 | 162 | 15,631 | 2959 | 19,716 | 19,789 |
| VD04 | Straight and Turning | 151 | 371 | 24,171 | 4532 | 30,164 | 30,244 |
| VD05 | S-shaped and Straight and Turning | 170 | 400 | 27,135 | 5102 | 33,933 | 34,025 |
| VD06 | Straight and Turning | 367 | 1085 | 58,463 | 11,014 | 73,169 | 73,386 |
| Methods | VD01 | VD02 | VD03 | VD04 | VD05 | VD06 |
|---|---|---|---|---|---|---|
| MAVIO | 1.29 (a) | 1.29 (a,b) | 1.14 (b) | 1.42 (a) | 1.42 (b) | 1.63 (a) |
| ACK-MSCKF | 1.21 (f) | 1.11 (f) | 0.98 (d,e,f) | 1.31 (f) | 1.21 (f) | 1.46 (f) |
| S-MSCKF | 1.68 | 1.38 | 1.22 | 1.99 | 1.57 | 2.08 |
| Methods | VD01 (m) | VD02 (m) | VD03 (m) | VD04 (m) | VD05 (m) | VD06 (m) |
|---|---|---|---|---|---|---|
| MAVIO | 1.31 (b) | 2.45 (b) | 0.78 (a) | 2.01 (b) | 3.16 (b) | 4.73 (b) |
| MAVIO-GNSS | 1.22 | 2.27 | 0.79 | 1.67 | 3.59 | 3.28 |
| ACK-MSCKF | 1.60 (d) | 2.57 (c) | 0.87 (d) | 2.46 (c,d) | 3.67 (d) | 3.80 (d) |
| S-MSCKF | 9.78 | 2.31 | 2.44 | 14.83 | 4.25 | 21.76 |
| Sub-Trajectory Length (m) | Relative Translation Error (m) | |||
|---|---|---|---|---|
| MAVIO | MAVIO-GNSS | ACK-MSCKF | S-MSCKF | |
| 1 | 0.08 (a, b) | 0.08 | 0.08 (c, d) | 0.22 |
| 5 | 0.23 (b) | 0.21 | 0.26 (c, d) | 0.93 |
| 10 | 0.40 (b) | 0.35 | 0.44 (c, d) | 1.71 |
| 20 | 0.70 (b) | 0.60 | 0.76 (d) | 3.00 |
| 50 | 1.51 (b) | 1.29 | 1.51 (d) | 5.57 |
| 100 | 2.79 (b) | 2.29 | 2.57 (d) | 8.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Shi, J.; Wu, L.; Dai, K.; Zhong, S. Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization. Sensors 2020, 20, 5757. https://doi.org/10.3390/s20205757
Ma F, Shi J, Wu L, Dai K, Zhong S. Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization. Sensors. 2020; 20(20):5757. https://doi.org/10.3390/s20205757
Chicago/Turabian StyleMa, Fangwu, Jinzhu Shi, Liang Wu, Kai Dai, and Shouren Zhong. 2020. "Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization" Sensors 20, no. 20: 5757. https://doi.org/10.3390/s20205757





