Information Decomposition in Bivariate Systems: Theory and Application to Cardiorespiratory Dynamics
Abstract
:1. Introduction
2. Methods
2.1. Information-Theoretic Preliminaries
2.2. Information Dynamics in Bivariate Systems
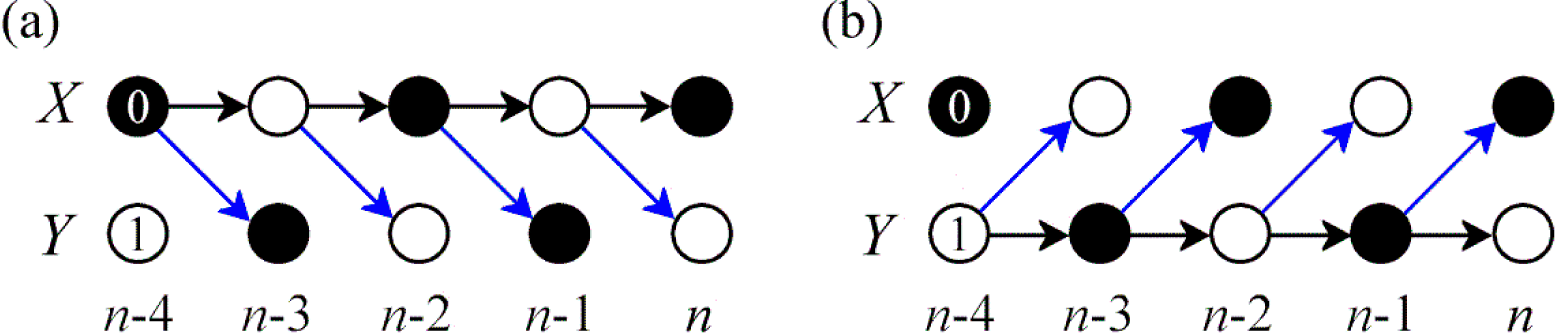
2.3. Properties and Theoretical Interpretation
2.4. Computation of Information Dynamics
3. Simulation Study
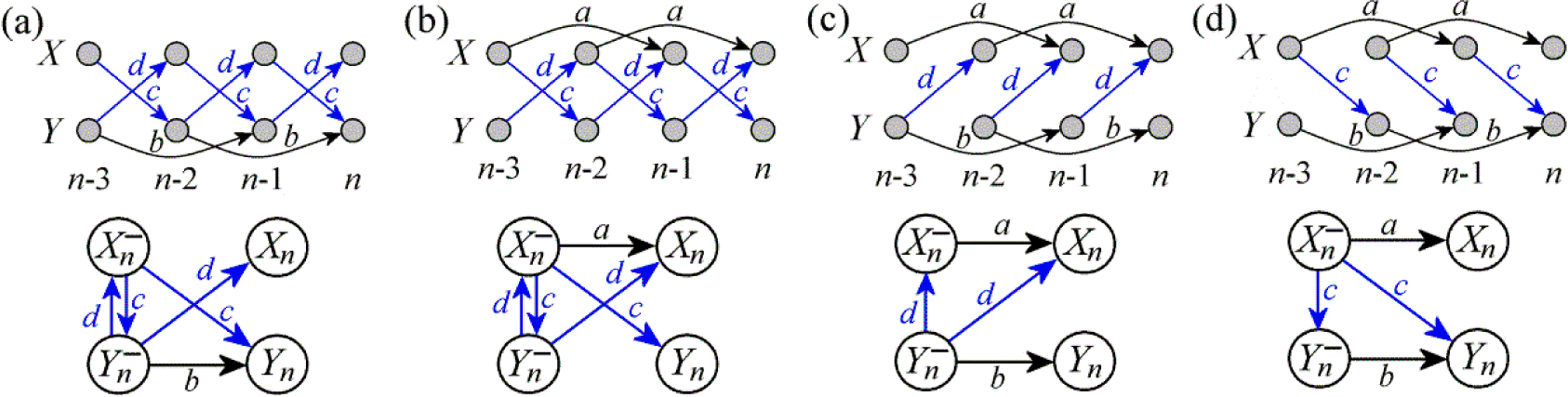
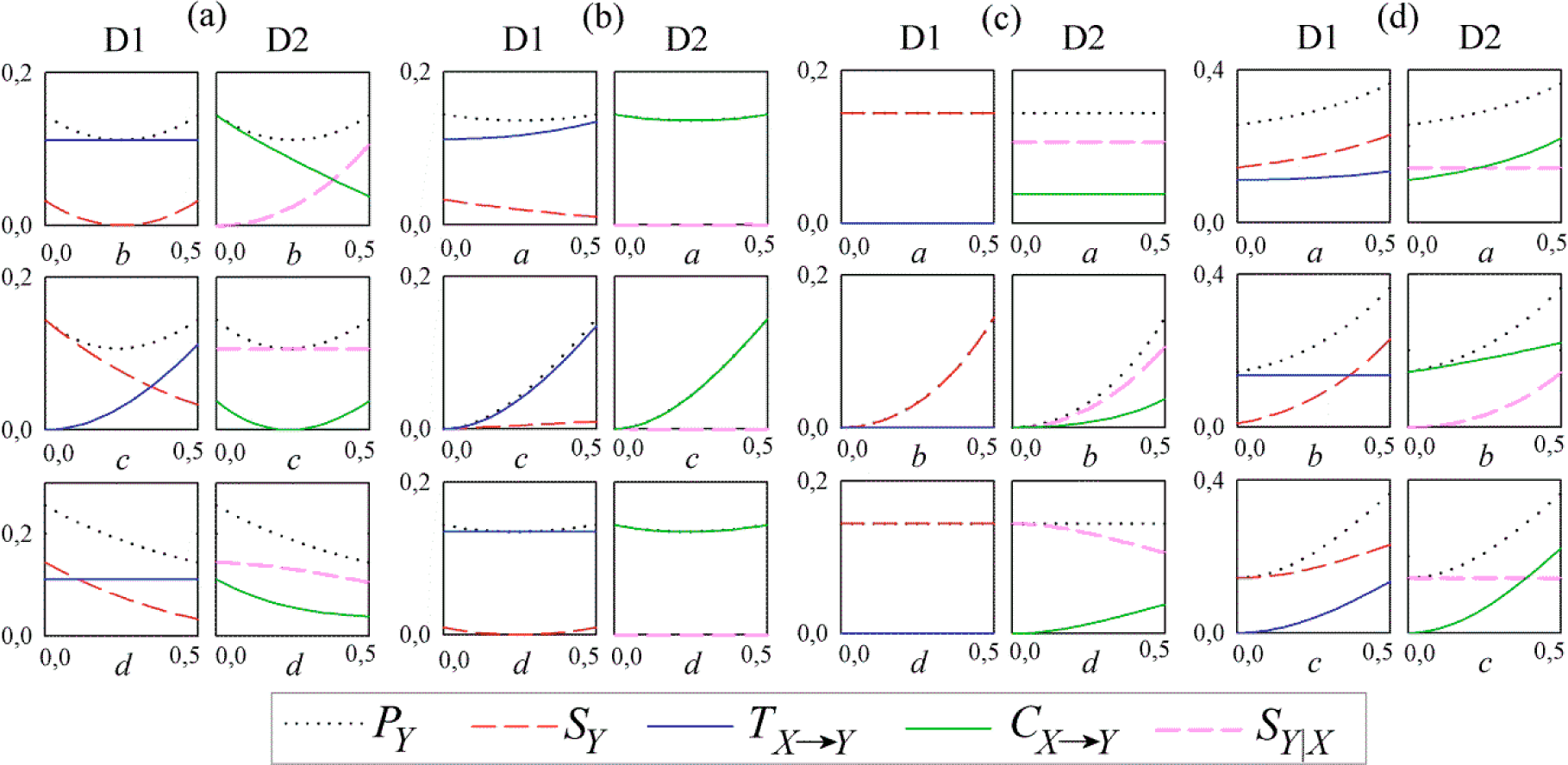
3.1. Linear AR Bivariate Process
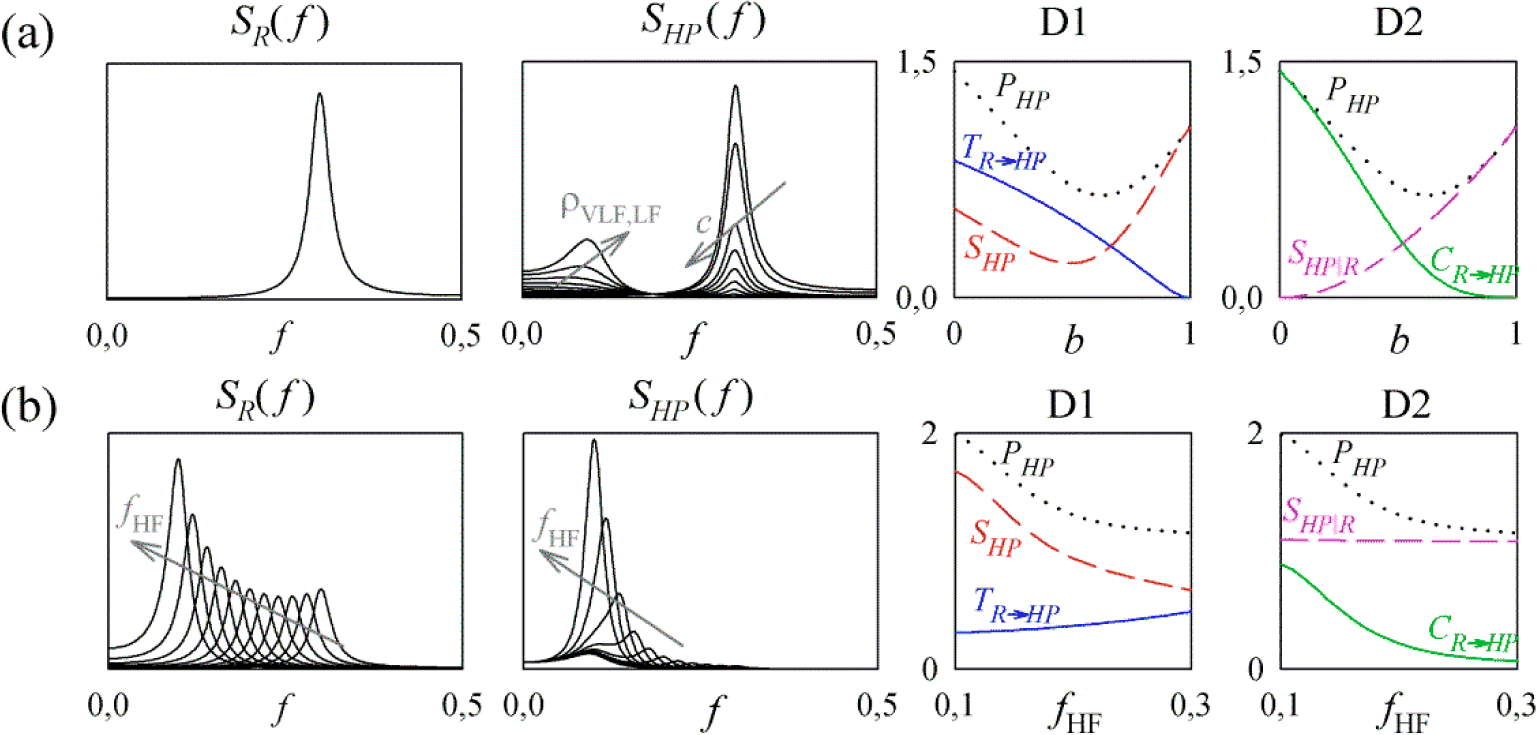
3.2. Simulated Cardiovascular Dynamics
4. Application to Cardiorespiratory Variability
4.1. Experimental Protocols and Data Analysis
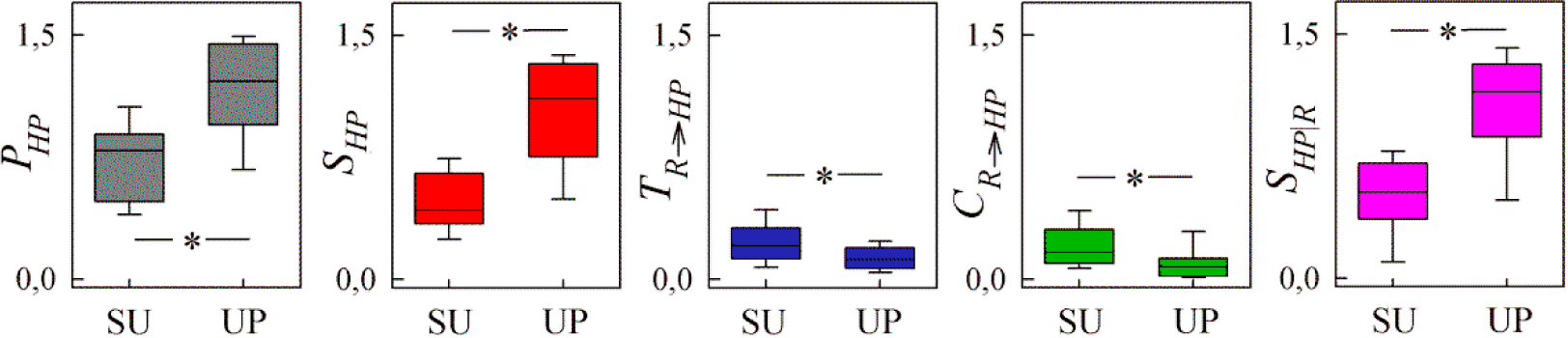
4.2. Results and Discussion
5. Discussion
Author Contributions
Conflicts of Interest
References
- Cohen, M.A.; Taylor, J.A. Short-term cardiovascular oscillations in man: measuring and modelling the physiologies. J. Physiol 2002, 542, 669–683. [Google Scholar]
- Berntson, G.G.; Cacioppo, J.T.; Quigley, K.S. Respiratory Sinus Arrhythmia - Autonomic Origins, Physiological-Mechanisms, and Psychophysiological Implications. Psychophysiology 1993, 30, 183–196. [Google Scholar]
- Valdes-Sosa, P.A.; Roebroeck, A.; Daunizeau, J.; Friston, K. Effective connectivity: Influence, causality and biophysical modeling. Neuroimage 2011, 58, 339–361. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar]
- Porta, A.; Bassani, T.; Bari, V.; Tobaldini, E.; Takahashi, A.C.M.; Catai, A.M.; Montano, N. Model-based assessment of baroreflex and cardiopulmonary couplings during graded head-up tilt. Comp. Biol. Med 2012, 42, 298–305. [Google Scholar]
- Stankovski, T.; Duggento, A.; McClintock, P.V.E.; Stefanovska, A. Inference of Time-Evolving Coupled Dynamical Systems in the Presence of Noise. Phys. Rev. Lett 2012, 109, 024101. [Google Scholar]
- Iatsenko, D.; Bernjak, A.; Stankovski, T.; Shiogai, Y.; Owen-Lynch, P.J.; Clarkson, P.B.M.; McClintock, P.V.E.; Stefanovska, A. Evolution of cardiorespiratory interactions with age. Phil. Trans. Royal Soc. A 2013, 371, 20110622. [Google Scholar]
- Chicharro, D.; Panzeri, S. Algorithms of causal inference for the analysis of effective connectivity among brain regions. Front. Neuroinf 2014, 8. [Google Scholar] [CrossRef]
- Wiener, N. The Theory of Prediction; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Granger, C.W.J. Economic processes involving feedback. Inf. Control 1963, 6, 28–48. [Google Scholar]
- Granger, C.W.J. Testing for causality: A personal viewpoint. J. Econom. Dynam. Control 1980, 2, 329–352. [Google Scholar]
- Porta, A.; Faes, L. Assessing causality in brain dynamics and cardiovascular control. Phil. Trans. Royal Soc. A 2013, 371, 20120517. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Chicharro, D.; Ledberg, A. Framework to study dynamic dependencies in networks of interacting processes. Phys. Rev. E 2012, 86, 041901. [Google Scholar]
- Faes, L.; Porta, A. Conditional entropy-based evaluation of information dynamics in physiological systems. In Directed Information Measures in Neuroscience; Vicente, R., Wibral, M., Lizier, J.T., Eds.; Springer-Verlag: Berlin, Germany, 2014; pp. 61–86. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inform. Sci 2012, 208, 39–54. [Google Scholar]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett 2000, 85, 461–464. [Google Scholar]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wibral, M.; Lizier, J.T.; Vogler, S.; Priesemann, V.; Galuske, R. Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinf 2014, 8, 1. [Google Scholar]
- Faes, L; Nollo, G.; Jurysta, F.; Marinazzo, D. Information dynamics of brain-heart physiological networks during sleep. New J. Phys 2014, 16, 105005. [Google Scholar]
- Faes, L.; Porta, A.; Rossato, G.; Adami, A.; Tonon, D.; Corica, A.; Nollo, G. Investigating the mechanisms of cardiovascular and cerebrovascular regulation in orthostatic syncope through an information decomposition strategy. Auton. Neurosci 2013, 178, 76–82. [Google Scholar]
- Lizier, J.T.; Pritam, S.; Prokopenko, M. Information Dynamics in Small-World Boolean Networks. Artif. Life 2011, 17, 293–314. [Google Scholar]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar]
- Wibral, M.; Vicente, R.; Lindner, M. Transfer entropy in neuroscience. In Directed Information Measures in Neuroscience; Vicente, R., Wibral, M., Lizier, J.T., Eds.; Springer-Verlag: Berlin, Germany, 2014; pp. 3–36. [Google Scholar]
- Chicharro, D.; Ledberg, A. When two become one: The limits of causality analysis of brain dynamics. PLoS One 2012, 7, e32466. [Google Scholar]
- Dahlhaus, R. Graphical interaction models for multivariate time series. Metrika 2000, 51, 157–172. [Google Scholar]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the Curse of Dimensionality in Estimating Multivariate Transfer Entropy. Phys. Rev. Lett 2012, 108, 258701. [Google Scholar]
- Faes, L.; Marinazzo, D.; Montalto, A.; Nollo, G. Lag-specific transfer entropy as a tool to assess cardiovascular and cardiorespiratory information transfer. IEEE Trans. Biomed. Eng 2014, 61, 2556–2568. [Google Scholar]
- Faes, L.; Nollo, G.; Porta, A. Compensated transfer entropy as a tool for reliably estimating information transfer in physiological time series. Entropy 2013, 15, 198–219. [Google Scholar]
- Runge, J.; Heitzig, J.; Marwan, N.; Kurths, J. Quantifying causal coupling strength: A lag-specific measure for multivariate time series related to transfer entropy. Phys. Rev. E 2012, 86, 061121. [Google Scholar]
- Vlachos, I.; Kugiumtzis, D. Nonuniform state-space reconstruction and coupling detection. Phys. Rev. E 2010, 82, 016207. [Google Scholar]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E 2011, 83, 051112. [Google Scholar]
- Porta, A.; Faes, L.; Bari, V.; Marchi, A.; Bassani, T.; Nollo, G.; Perseguini, N.M.; Milan, J.; Minatel, V.; Borghi-Silva, A.; Takahashi, A.C.M.; Catai, A.M. Effect of Age on Complexity and Causality of the Cardiovascular Control: Comparison between Model-Based and Model-Free Approaches. PLoS One 2014, 9, e89463. [Google Scholar]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett 2009, 103, 238701. [Google Scholar]
- Barnett, L.; Seth, A.K. The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. J. Neurosci. Methods 2014, 223, 50–68. [Google Scholar]
- Barrett, A.B.; Barnett, L.; Seth, A.K. Multivariate Granger causality and generalized variance. Phys. Rev. E 2010, 81, 041907. [Google Scholar]
- Faes, L.; Montalto, A.; Nollo, G.; Marinazzo, D. Information decomposition of short-term cardiovascular and cardiorespiratory variability, Proceedings of 2013 Computing in Cardiology Conference (CinC), Zaragoza, Spain, 22–25 September 2013; pp. 113–116.
- Faes, L.; Kugiumtzis, D.; Nollo, G.; Jurysta, F.; Marinazzo, D. Estimating the decomposition of predictive information in multivariate systems. Phys Rev. E 2014. submitted for publication. [Google Scholar]
- Faes, L.; Widjaja, D.; van Huffel, S.; Nollo, G. Investigating cardiac and respiratory determinants of heart rate variability in an information-theoretic framework, Proceedings of 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 6020–6023.
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43–62. [Google Scholar]
- Faes, L.; Nollo, G.; Porta, A. Information domain approach to the investigation of cardio-vascular, cardio-pulmonary, and vasculo-pulmonary causal couplings. Front. Physiol 2011, 2, 1–13. [Google Scholar]
- Porta, A.; Bassani, T.; Bari, V.; Pinna, G.D.; Maestri, R.; Guzzetti, S. Accounting for Respiration is Necessary to Reliably Infer Granger Causality from Cardiovascular Variability Series. IEEE Trans. Biomed. Eng 2012, 59, 832–841. [Google Scholar]
- Task force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J 1996, 17, 354–381.
- Faes, L.; Erla, S.; Nollo, G. Measuring connectivity in linear multivariate processes: definitions, interpretation, and practical analysis. Comp. Math. Methods Med 140513.
- Porta, A.; Guzzetti, S.; Montano, N.; Pagani, M.; Somers, V.; Malliani, A.; Baselli, G.; Cerutti, S. Information domain analysis of cardiovascular variability signals: evaluation of regularity, synchronisation and co-ordination. Med. Biol. Eng. Comput 2000, 38, 180–188. [Google Scholar]
- Porta, A.; Guzzetti, S.; Montano, N.; Furlan, R.; Pagani, M.; Malliani, A.; Cerutti, S. Entropy, entropy rate, and pattern classification as tools to typify complexity in short heart period variability series. IEEE Trans. Biomed. Eng 2001, 48, 1282–1291. [Google Scholar]
- Faes, L.; Nollo, G.; Porta, A. Non-uniform multivariate embedding to assess the information transfer in cardiovascular and cardiorespiratory variability series. Comput. Biol. Med 2012, 42, 290–297. [Google Scholar]
- Van Diest, I.; Vlemincx, E.; Verstappen, K.; Vansteenwegen, D. The Effects of instructed ventilatory patterns on physiological and psychological dimensions of relaxation, Presented at the 17th meeting of the International Society for the Advancement of Respiratory Psychophysiology (ISARP), New York City, NY, USA, 26–27 September 2010.
- Kralemann, B.; Fruhwirth, M.; Pikovsky, A.; Rosenblum, M.; Kenner, T.; Schaefer, J.; Moser, M. In vivo cardiac phase response curve elucidates human respiratory heart rate variability. Nat. Comm 2013, 4. [Google Scholar] [CrossRef]
- Stankovski, T.; Cooke, W.H.; Rudas, L.; Stefanovska, A.; Eckberg, D.L. Time-frequency methods and voluntary ramped-frequency breathing: A powerful combination for exploration of human neurophysiological mechanisms. J. Appl. Physiol 2013, 115, 1806–1821. [Google Scholar]
- Barrett, A.B.; Barnett, L. Granger causality is designed to measure effect, not mechanism. Front. Neurosci 2013, 7, 61–62. [Google Scholar]
- Gigi, S.; Tangirala, A.K. Quantitative analysis of directional strengths in jointly stationary linear multivariate processes. Biol. Cybern 2010, 103, 119–133. [Google Scholar]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci 2011, 30, 45–67. [Google Scholar]
- Kugiumtzis, D. Direct-coupling information measure from nonuniform embedding. Phys. Rev. E 2013, 87, 062918. [Google Scholar]
- Wollstadt, P.; Martinez-Zarzuela, M.; Vicente, R.; Diaz-Pernas, F.J.; Wibral, M. Efficient Transfer Entropy Analysis of Non-Stationary Neural Time Series. PLoS One 2014, 9, e102833. [Google Scholar]
- Labarre, D.; Grivel, E.; Berthoumieu, Y.; Todini, E.; Najim, M. Consistent estimation of autoregressive parameters from noisy observations based on two interacting Kalman filters. Sign. Proc 2006, 86, 2863–2876. [Google Scholar]
- Arnold, M.; Miltner, W.H.; Witte, H.; Bauer, R.; Braun, C. Adaptive AR modeling of nonstationary time series by means of Kalman filtering. IEEE Trans. Biomed. Eng 1998, 45, 553–562. [Google Scholar]
- Baselli, G.; Cerutti, S.; Badilini, F.; Biancardi, L.; Porta, A.; Pagani, M.; Lombardi, F.; Rimoldi, O.; Furlan, R.; Malliani, A. Model for the assessment of heart period and arterial pressure variability interactions and of respiration influences. Med. Biol. Eng. Comput 1994, 32, 143–152. [Google Scholar]
- Fortrat, J.O.; Yamamoto, Y.; Hughson, R.L. Respiratory influences on non-linear dynamics of heart rate variability in humans. Biol. Cybern 1997, 77, 1–10. [Google Scholar]


| Name | Meaning | Symbol | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Prediction Entropy (PE) | Predictive Information | PY | Yn⊥Xn−,Yn− ⇔ PY = 0 | Yn = f (Xn−,Yn−) ⇔ PY = H(Yn) |
| Self Entropy (SE) | Information Storage | SY | Yn⊥Yn− ⇔ SY=0 | Yn = f (Yn−) ⇔ SY = H(Yn) |
| Transfer Entropy (TE) | Information Transfer | TX→Y | Yn⊥Xn−|Yn− ⇒TX→Y = 0 | Yn = f(Xn−,Yn−) ⇔TX→Y = H(Yn|Yn−) |
| Cross Entropy (CE) | Cross Information | CX→Y | Yn⊥Xn−⇔ CX→Y = 0 | Yn=f (Xn−) ⇔ CX→Y = H(Yn) |
| Conditional Self Entropy (cSE) | Internal Information | SY|X | Yn⊥Yn−|Xn −⇒ SY|X = 0 | Yn=f (Xn−,Yn−) ⇔ SY|X = H(Yn|Xn−) |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faes, L.; Porta, A.; Nollo, G. Information Decomposition in Bivariate Systems: Theory and Application to Cardiorespiratory Dynamics. Entropy 2015, 17, 277-303. https://doi.org/10.3390/e17010277
Faes L, Porta A, Nollo G. Information Decomposition in Bivariate Systems: Theory and Application to Cardiorespiratory Dynamics. Entropy. 2015; 17(1):277-303. https://doi.org/10.3390/e17010277
Chicago/Turabian StyleFaes, Luca, Alberto Porta, and Giandomenico Nollo. 2015. "Information Decomposition in Bivariate Systems: Theory and Application to Cardiorespiratory Dynamics" Entropy 17, no. 1: 277-303. https://doi.org/10.3390/e17010277
APA StyleFaes, L., Porta, A., & Nollo, G. (2015). Information Decomposition in Bivariate Systems: Theory and Application to Cardiorespiratory Dynamics. Entropy, 17(1), 277-303. https://doi.org/10.3390/e17010277








