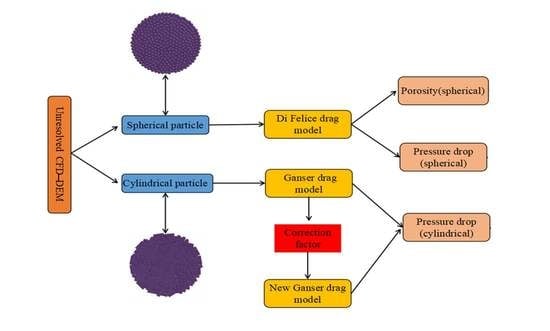
Research on a New Drag Force Model for Cylindrical Particles in Fixed Bed Reactors

Abstract

Fixed bed reactors play an important role in converting solid wastes to high-quality products. The solid wastes, as well as the corresponding catalysts, are often made into cylindrical particles. However, research on the drag force for cylindrical particles is still rarely reported. In this work, the fixed bed porosity was firstly predicted with the unresolved CFD-DEM method and validated against experimental data. Then, the Ergun model, Di Felice model, and Ganser model were evaluated against the reported pressure drop data for both the spherical and cylindrical particles, so that a more solid drag force theory could be selected as a candidate for cylindrical particles. Finally, a new Ganser model was proposed for cylindrical particle drag force prediction based on the reported experimental results and validated by other experimental data. It was found that, for the spherical particle bed, the relative prediction errors of the Di Felice model are approximately 10%, while those of the Ergun model are approximately 15%. For the cylindrical particle bed, the relative prediction errors of the Ganser model are approximately 10%, while those of the Di Felice model are much higher than 10%. With the new Ganser model proposed in this work, the maximum error between the predicted pressure drop and the experimental data can be lowered to approximately 5%. The research is of reference value for drag force model selection when simulating similar FBRs with cylindrical particles.

1. Introduction

Fixed bed reactors (FBRs) can be used for converting solid wastes to high-quality products [1]. Compared with other kinds of reactors, like entrained bed and fluidized bed reactors [2,3], FBRs have the advantages of lower cost and higher feasibility. In terms of bed materials in FBRs, solid waste and the corresponding catalysts are easily made into cylindrical particles [4]. Although FBRs have many advantages, they also suffer from the disadvantage of nonuniform field distribution. It is therefore necessary to deeply study the FBR hydrodynamics so as to mitigate or avoid such a defect. Up to now, many methods have been developed to study the FBR operating property. However, specific reports on the drag force for cylindrical particles in FBR are still rarely seen, hindering the deep understanding of the hydrodynamics in FBR filled with cylindrical particles.

The research methods for FBRs typically include experiments, empirical correlations [5,6,7], and computational fluid dynamics (CFD) simulation [8,9,10,11,12]. Experiments are usually time consuming and cost expensive, while the empirical correlations are usually one- or zero-dimensional and cannot reflect the detailed process in FBRs. In comparison, CFD simulation is very promising because this method can not only predict the detailed physicochemical processes in FBRs but can also be cost effective.

The Eulerian–Eulerian method and the four-way coupling Eulerian–Lagrangian method are usually chosen to simulate dense particle bed in FBRs. For the former method, both the carrier phase and particle phase are considered as fluid, and the particle phase is modeled with the granular kinetic theory [13]. For the latter, the carrier phase is considered as fluid while the particles are tracked in the Lagrangian coordinate with the Discrete Element Method (DEM) [14], known as the CFD-DEM method, which can be further classified into the resolved method [8,15,16] and unresolved method [17,18,19]. Compared with the resolved method, the unresolved method does not require integration along the boundary of particles and works well with coarse mesh. For FBRs with a large number of particles, the unresolved method can be more effective.

For any of the above-mentioned FBR simulation methods, the gas–particle drag model is essential. So far, many models for gas–particle drag force prediction have been developed. The Ergun model [5] is only valid for dense particle flow, while the Wen-Yu [20] model is only valid for dilute particle flow. Gidaspow [21] combined the two models, by using the Ergun equation for bed porosity of less than 0.8 and the Wen-Yu equation for bed porosity greater than 0.8. The Di Felice [22] model determines the drag force as the function of particle Reynolds numbers and porosity and is applicable to the full range of particle Reynolds numbers and porosity. Besides the models originally developed for spherical particles, drag force models for non-spherical particles have also been widely researched. Haider [23] proposed an expression for the drag coefficient of isolated non-spherical particles, which mainly consists of four functions to consider the particle sphericity. Ganser [24] considered the shape and projected area of the particles with the Stokes’ shape factor and Newton’s shape factor and summarized the expression for the drag coefficient of non-spherical particles by dimensionless analysis and similarity criterion. Holzer [25] proposed the expressions for the drag coefficient of non-spherical particles in the full range of Reynolds number based on Ganser’s results. Zhang [26] studied the fluidization behavior of the cylindrical particles with the multi-sphere and bond-sphere models, and the drag force was calculated with the Di Felice model. Gao [27] developed the Super DEM-CFD coupled model for non-spherical particle fluidization and found that the Di Felice-Holzer/Sommerfeld drag force model performed well for particles with different shapes.

It can be seen from the literature review that, although many efforts have made regarding fixed bed simulation, specific research on the drag force model for a cylindrical particle bed in FBRs is still rarely reported. The present study first evaluates both the Ergun model and Di Felice model when predicting the drag force for a packed bed with spherical particles. Then, the Di Felice model and Ganser model are evaluated when predicting the drag force for packed bed with cylindrical particles, and the Ganser model is proved be more advanced. Finally, the Ganser model is further modified so that it can predict the drag force for cylindrical particles more accurately.

2. Mathematical Model and Numerical Solution

The commercial software Fluent and EDEM are coupled by a user defined interface. Fluent calculates the porosity and the fluid dynamics in a given time step. Then, EDEM calculates and transmits the particle position and velocity information to Fluent in the same time step. Finally, the drag force is calculated and transferred to EDEM through the user defined interface to solve the particle motion, and the new drag force is fed back to Fluent through the source term of the momentum equation. The volume averaging method is adopted to obtain the porosity in the governing equations [28]. The unresolved CFD-DEM method mainly includes the governing equations for fluid phase, particles, and the drag force model that calculates the interphase momentum exchange [29,30].

Before the final simulation, three meshes with 3560, 4900, and 6848 cells were tested for the independence analysis. In the independence analysis, the particle diameter was 0.005 m, the porosity was 0.388 and the inlet Reynolds number was 141. The pressure drop values from the three meshes were close, and approximately 850 Pa. In addition, for CFD-DEM simulation, it is required that the mesh should be at least three times the size of the particles. Therefore, the mesh size cannot be too small in the simulation. Then, the mesh with 4900 cells was chosen for the simulation.

2.1. Governing Equations for Fluid Phase

The mass conservation equation is defined as:

$$\frac{\partial ({\epsilon }_{\mathrm{f}}{\rho }_{\mathrm{f}})}{\partial t}+\nabla \cdot ({\epsilon }_{\mathrm{f}}{\rho }_{\mathrm{f}}{\mathit{u}}_{\mathrm{f}})=0$$

(1)

where ɛ_f is the local porosity, ρ_f is the density of the fluid, t is time and u_f is the velocity of fluid. The momentum conservation equation is defined as:

$$\frac{\partial ({\epsilon }_{\mathrm{f}}{\rho }_{\mathrm{f}}{\mathit{u}}_{\mathrm{f}})}{\partial t}+\nabla \cdot ({\epsilon }_{\mathrm{f}}{\rho }_{\mathrm{f}}{\mathit{u}}_{\mathrm{f}}{\mathit{u}}_{\mathrm{f}})=-{\epsilon }_{\mathrm{f}}\nabla p-\nabla \mathsf{\cdot }{\mathit{\tau }}_{\mathrm{f}}+{\epsilon }_{\mathrm{f}}{\rho }_{\mathrm{f}}\mathit{g}-{\displaystyle \sum {\mathit{F}}_{\mathrm{drag}}}$$

(2)

where p is the pressure, g is the gravitational acceleration vector, F_drag is the drag force between phases, which will be discussed later, and τ_f is the viscous stress tensor that can be calculated from Equation (3). The porosity and interphase momentum term are calculated by a coupling routine and communicated to Fluent at each calculation step.

$${\mathit{\tau }}_{\mathrm{f}}=-{\epsilon }_{\mathrm{f}}({\mu }_{\mathrm{f}}+{\mu }_t)(\nabla {\mathit{u}}_{\mathrm{f}}+\nabla {\mathit{u}}_{\mathrm{f}}^{\mathrm{T}})+\frac{2}{3}{\epsilon }_{\mathrm{f}}{\mu }_{\mathrm{f}}\nabla \cdot {\mathit{u}}_{\mathrm{f}}\mathit{\delta }$$

(3)

where δ is the unit tensor with components, μ_f is dynamic viscosity of fluid, μ_t is turbulence viscosity calculated with the k-epsilon equations.

2.2. Governing Equations for Particle Phase

The DEM method is based on the Cundall and Strack theory [31]. The complex behavior of particle–particle collisions is simplified to be a spring–dashpot interaction [32]. The motion of the particle is calculated by Newton’s law of motion. The linear velocity of the particle is given as:

$$m_{\mathrm{p}}\frac{d{\mathit{u}}_{\mathrm{p}}}{dt}=m_{\mathrm{p}}\mathit{g}+{\mathit{F}}_{\mathrm{p}-\mathrm{p}}+{\mathit{F}}_{\mathrm{p}-\mathrm{w}}+{\mathit{F}}_{\mathrm{p}-\mathrm{f}}$$

(4)

where u_p is the linear velocity of particle, m_p is the mass of particle, F_p-p and F_p-w are the particle–particle and particle–wall contact forces. In this work, F_p-f is the particle–fluid interaction force which is defined as Equation (5).

$${\mathit{F}}_{\mathrm{p}-\mathrm{f}}={\mathit{F}}_{\mathrm{drag}}+{\mathit{F}}_{\nabla p}=3\mathsf{\pi }{\mu }_{\mathrm{f}}{d}_{\mathrm{i}}{\mathit{U}}_{\mathrm{r}}-V_{\mathrm{i}}\nabla p$$

(5)

where d_i is the diameter of spherical particle, and V_i is the volume of particle. The first term on the right side of Equation (5) is associated with the fluid kinetic force, which contains the relative velocity U_r = u_f − u_p, referred to as Stokes–Einstein drag force. The second term is the force exerted by the fluid even if it was stationary, referred to as the pressure gradient force. The interaction forces between the fluid and the particles also include the Bassett force, the added-mass force, the Saffman force and Magnus lift force, but they are negligible in the fixed bed reactor where particles move very slowly. The rotation of the particle is defined as:

$${\mathit{I}}_{\mathrm{p}}\frac{d{\mathit{\omega }}_{\mathrm{p}}}{dt}={\displaystyle \sum {\mathit{M}}_{\mathrm{c}}}+{\mathit{M}}_{\mathrm{p}-\mathrm{f}}$$

(6)

where M_c is the contact force and torque acting on the particle, M_p-f is the fluid rotational resistance torque on the particle, I_p is the rotational inertia of particle, and ω_p is the angular velocity of particle.

2.3. Drag Force Model

The drag force on the sphere particle is calculated by:

$${\mathit{F}}_{\mathrm{drag}}=\frac{1}{2}{C}_{\mathrm{d}}{\rho }_{\mathrm{f}}A\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }=\frac{1}{8}{C}_{\mathrm{d}}{\rho }_{\mathrm{f}}\pi d_{\mathrm{i}}^2\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }$$

(7)

where A denotes the projection area of the particle, χ is an empirical value, and C_d denotes the drag coefficient. For different drag models, the expressions of the drag coefficients are different. Di Felice [22] obtained the drag coefficient by fitting the FBR experimental data. The drag force model is valid for both dense and dilute particle flows. In Di Felice, the drag model, χ and C_d are defined as:

$$\chi =3.7-0.65\exp \left[-\frac{{\left(1.5-\log {Re}_{\mathrm{i}}\right)}^2}{2}\right]$$

(8)

$$C_{\mathrm{d}}=(0.63+4.8{R{e}_{\mathrm{i}}}^{0.5}{)}^2$$

(9)

$$R{e}_{\mathrm{i}}=\frac{{\rho }_{\mathrm{f}}{d}_{\mathrm{i}}\left|{\mathit{U}}_{\mathrm{r}}\right|}{{\mu }_{\mathrm{f}}}$$

(10)

where Re_i is the particle Reynolds number. It should be noted that all particles are assumed to be spherical here. For particles of different shapes, the drag coefficient needs to be redefined.

2.4. Porosity Calculation

Besides the drag force model, the local porosity is also contained in the fluid governing equations [32]. Therefore, this parameter can significantly affect the CFD-DEM simulation results. EDEM can calculate the porosity of each computational cell based on the number of particles and particle position. This method does not rely on the correlation of the porosity distribution and can predict the properties of the fluid more accurately.

To overcome the calculation error when the particles are at the boundary of the computational cell, the sub-element method [33] is adopted in this paper. With this method, each particle is divided into N equal parts, and each part has a center point P_i,j. For each particle, if the center of these sub-elements is in the computational cell, the volume of the sub-element will be counted.

3. Results and Discussion

3.1. Packing Porosity with Spherical Particles

The model is first validated against reported FBR experimental data [34]. The experiment is carried out in a FBR filled with spherical particles, the inner diameter of the FBR is 0.1 m, and the effective filling height of the FBR is 0.7 m. The simulated object is shown in Figure 1. For FBR with spherical particles, the mean porosity could be expressed as:

$$\epsilon =1-\frac{2N{d_{\mathrm{i}}}^3}{3D^{2}H}$$

(11)

where N is the number of spherical particles in FBR, d_i is the diameter of the spherical particles, D is the inner diameter of the FBR, and H is the effective filling height (particles accumulation height) of the FBR.

First, the number of particles are calculated according to the experimental mean porosity and Equation (11). Then, the virtual particles of different sizes are dynamically packed in EDEM software to form a dense particle fixed bed. Finally, a coupled CFD-DEM program solves the pressure drop of FBR at different superficial velocity. Air is injected from the bottom of FBR at Reynolds number from 20 to 170.

Table 1. Characteristics of case sphere particle beds.

Case	Particle Shape	Particle Diameter (m)	Particle Number	Simulated Mean Porosity	Experimental Mean Porosity
case (A)	sphere	0.005	51,408	0.388	0.388
case (B)	sphere	0.0035	151,347	0.382	0.382
case (C)	sphere	0.002	784,875	0.402	0.402

lists the characteristics of the simulated particle beds, and the simulated mean porosity agrees well with the experimental data.

Figure 1. Three cases based on experimental study of Park et al. [34]: (a) case (A) d_i = 0.005 m; (b) case (B) d_i = 0.0035 m; and (c) case (C) d_i = 0.002 m.

Figure 1. Three cases based on experimental study of Park et al. [34]: (a) case (A) d_i = 0.005 m; (b) case (B) d_i = 0.0035 m; and (c) case (C) d_i = 0.002 m.

In order to further study the effect of porosity in FBR, the porosity distribution in FBR was first studied. Particles of different sizes were filled into the FBR with an effective height of 0.7 m, and the porosity was then calculated based on the position of the particles in the computational cell. The distributions of average axial porosity for different particle sizes are shown in Figure 2a. The average axial porosity decreases sharply as the height increases, then becomes flat in the middle, and finally increases sharply as the height increases. The average axial porosity at the middle part is mostly between 0.37 and 0.4, and the fluctuation is small. The height of 0 m and 0.7 m correspond to the bottom and top of the particle bed. Because there are no particles below the bottom or above the top, the voids on the horizontal plane of the bottom and top will be very large, so the average axial porosity in these two places is much larger than those in the middle.

Research on the average radial porosity of FBR has always been a hot topic. Figure 2b shows the average radial porosity distribution (ɛ(r)) for different particle sizes. It can be seen that the porosity is larger near the wall and remains basically unchanged when the radius is less than 0.025. The average radial porosity of case (c) is obviously larger than that of the other two groups, mainly because the mean porosity of case (c) is larger than that of the other two groups.

Klerk et al. [35] provided experimental data for different pipe–particle diameter ratios and concluded Equation (12) for the average radial porosity.

$$\epsilon (r)={\epsilon }_{\mathrm{b}}+0.29\exp (-0.6\frac{R-r}{d_{\mathrm{i}}})\left[\cos (2.3\mathsf{\pi }(\frac{R-r}{d_{\mathrm{i}}}-0.16))\right]+0.15\exp (0.9\frac{R-r}{d_{\mathrm{i}}})$$

(12)

where ɛ_b is the average bulk porosity for unconfined packing (Usually the value is 0.36–0.4), r is radial position relative to the FBR center line (the abscissa in Figure 2b), R is the radius of the FBR and d_i is the particle di

Figure 3 shows that the average radial porosity calculated by the empirical formula (Equation (12)) oscillates with the increase of the abscissa. Near the wall of FBR, both the average radial porosity and the oscillation amplitude are big. After about five particle diameters’ length, the oscillation amplitude of the average radial porosity becomes insignificant and closes to 0.36. Because the ratio of the mesh size to the particle diameter is greater than 3, the grid near the wall is sparse, and the predicted average radial porosity near the FBR wall is not accurate. After 4–5 particle diameters’ length, the EDEM prediction result matches the experimental value well.

Figure 3. Comparison of the average radial porosity between simulation and experimental data of Klerk et al. [35].

Figure 3. Comparison of the average radial porosity between simulation and experimental data of Klerk et al. [35].

3.2. Pressure Drop for Packed Bed with Spherical Particles

The porosity and particle diameter play a leading role in the pressure drop of FBR. Therefore, three kinds of spherical particles with different diameters of 0.002, 0.0035 and 0.005 m, are numerically simulated. Figure 4a–c, respectively, show the pressure drop data of the FBRs with three different-sized spherical particles. The simulation results are compared with the corresponding experimental data and the Ergun equation’s prediction. The Ergun equation expressed as Equation (13) is mainly composed of two terms including the turbulent flow term (S₁) and the laminar flow term (S₂).

$$\Delta P=P_0-{(P_0^2-\frac{2000H{G}^2{R}_{g}T(1-\epsilon )}{M_W{d}_{i}g{\epsilon }^3}({\mathrm{S}}_1+{\mathrm{S}}_2\frac{1-\epsilon }{R{e}_{\mathrm{i}}}))}^{0.5}$$

(13)

where P₀ is inlet pressure of FBR, H is the height of FBR, G is the mass flux, R_g is gas constant, T is the temperature, M_W is the molecular weight of gas through FBR, S₁ = 1.75, and S₂ = 150.

The overall change trends of the three cases are the same. As the particle Reynolds number increases, the pressure drop gradually increases. The prediction results from both the Ergun equation and the simulation are slightly lower than the experimental data. Compared to the Ergun equation, the predicted pressure drop is closer to the experimental data.

The maximum relative error between the simulated data and the experimental data is less than 13%. The deviation between simulated data and experimental data is mainly caused by two aspects. First, although EDEM has excellently presented the dynamic packing process of particles in FBR and the mean porosity is in good agreement with the experiment, the established fixed bed model cannot be exactly the same as the experimental one. Second, the particle–wall and particle–particle friction also affects the simulation results, which is not fully reflected in the numerical model. But it must be admitted that the Di Felice drag model is effective for predicting the pressure drop in FBR with spherical particles.

3.3. New Drag Coefficient Model for Cylindrical Particles

Figure 5 sketches a FBR filled with two cylindrical particles of different sizes. The process of simulating the pressure drop characteristics of a FBR filled with cylindrical particles is roughly the same as that of a FBR filled with spherical particles. However, there are two main differences between the two simulations in terms of methodologies on the particle diameter and the mean porosity. For the cylindrical particles, the Di Felice model uses an equivalent diameter proposed by Li and Ma [36] like:

$$d_{\mathrm{eq}}=\phi d_{\mathrm{sd}}$$

(14)

where the Sauter mean diameter (d_sd) [36] and sphericity (φ) [37] are determined by:

$$d_{\mathrm{sd}}=\frac{6V_{\mathrm{p}}}{A_{\mathrm{p}}}$$

(15)

$$\phi =\frac{{\mathsf{\pi }}^{\frac{1}{3}}{(6V_{\mathrm{p}})}^{\frac{2}{3}}}{A_{\mathrm{p}}}$$

(16)

where V_p is the volume of the cylindrical particle and A_p is the surface area of the cylindrical particle. The sphericity is the ratio of the surface area of an ideal sphere with identical volume to the surface area of the cylindrical particle. According to the Di Felice model, the cylindrical particle Reynolds number and the drag force are calculated by:

$$R{e}_{\mathrm{i}}=\frac{{\rho }_{\mathrm{f}}{d}_{\mathrm{eq}}\left|{\mathit{U}}_{\mathrm{r}}\right|}{{\mu }_{\mathrm{f}}}$$

(17)

$${\mathit{F}}_{\mathrm{drag}}=\frac{1}{2}{C}_{\mathrm{d}}{\rho }_{\mathrm{f}}A\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }=\frac{1}{8}{C}_{\mathrm{d}}{\rho }_{\mathrm{f}}\pi d_{\mathrm{eq}}^2\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }$$

(18)

Different from the Di Felice model, the Ganser [24] model calculates the particle Reynolds number based on the equivalent volume particle size and introduces the Stokes’ shape factor and Newton’s shape factor to calculate the drag coefficient. The expressions of the Stokes’ shape factor and Newton’s shape factor are given by dimensionless analysis and similarity criterion, and the drag coefficient is organized as a function of a generalized Reynolds number (Re_iK₁K₂). For cylindrical particles, the Ganser model calculates the particle Reynolds number and drag coefficient with:

$$R{e}_{\mathrm{i}}=\frac{{\rho }_{\mathrm{g}}{d}_{\mathrm{v}}\left|{\mathit{U}}_{\mathrm{r}}\right|}{{\mu }_{\mathrm{g}}}$$

(19)

$$C_d^{\prime }=\frac{24}{R{e}_i{K}_1}\left[1.0+0.1118{\left(R{e}_i{K}_1{K}_2\right)}^{0.6567}\right]+\frac{0.4305K_2}{1+\frac{3305}{R{e}_i{K}_1{K}_2}}$$

(20)

where the Stokes’ shape factor and Newton’s shape factor are calculated by:

$$K_1={(\frac{1}{3}\frac{d_{\mathrm{A}}}{d_{\mathrm{V}}}+\frac{2}{3}{\phi }^{-0.5})}^{-1}-2.25\frac{d_{\mathrm{V}}}{D}$$

(21)

$$K_2={10}^{1.81148{(-\log \phi )}^{0.5743}}$$

(22)

where d_A is the diameter of sphere with equivalent projected area, d_V is the diameter of sphere with equivalent volume. For cylindrical particles, the Ganser model calculates the drag force with:

$${\mathit{F}}_{\mathrm{drag}}=\frac{1}{2}{C_{\mathrm{d}}}^{\prime }{\rho }_{\mathrm{f}}A\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }=\frac{1}{8}{C_{\mathrm{d}}}^{\prime }{\rho }_{\mathrm{f}}\pi d_{\mathrm{A}}^2\left|{\mathit{U}}_{\mathrm{r}}\right|{\mathit{U}}_{\mathrm{r}}{\epsilon }_{\mathrm{f}}^{2-\chi }$$

(23)

For FBR with cylindrical particles, the mean porosity [38] can be expressed as:

$$\epsilon =1-\frac{N{d}^{2}L}{D^{2}H}$$

(24)

where N is the number of cylindrical particles in the particle fixed bed, d and L are the diameter and length of the cylindrical particle, respectively. The characteristics of cylindrical particle the simulation and experiment are listed in

Table 2. Characteristics of cylindrical particle beds.

Case	Particle Shape	Particle Size (m)	Particle Number	Simulated Mean Porosity	Experimental Mean Porosity
case (D)	cylindrical	0.00498d × 0.0139L	12,285	0.395	0.395
case (E)	cylindrical	0.00198d × 0.00495L	220,396	0.389	0.389

[34].

Figure 6a,b show the pressure drop data of the FBRs with two different sized cylindrical particles. The relative errors between the Ganser prediction, the Di Felice prediction, the Wu [39] calculation results and the experimental data are sorted out. It can be seen that the Ganser drag model can give more accurate pressure drop prediction for cylindrical particles than the Di Felice model. The maximum relative error between the simulated Ganser pressure drop and experimental pressure drop does not exceed 13%. This is because the Ganser drag coefficient (C_d′) with shape factors such as Stokes’ shape factor, Newton’s shape factor, and sphericity can calculate the drag force of non-spherical particles better.

To further improve the Ganser model so that it can give more accurate drag force prediction for cylindrical particles, a correction factor K′ is added in the Ganser drag coefficient as shown in Equation (25). The fitting method is used to find the relationship between K′ and the particle Reynolds number. The expression of the cylindrical particle drag coefficient (C_dc′) is:

$$C_{\mathrm{dc}}^{\prime }=K^{\prime }\left[\frac{24}{R{e}_{\mathrm{i}}{K}_1}\left[1.0+0.1118{\left(R{e}_{\mathrm{i}}{K}_1{K}_2\right)}^{0.6567}\right]+\frac{0.4305K_2}{1+\frac{3305}{R{e}_{\mathrm{i}}{K}_1{K}_2}}\right]$$

(25)

The correction factor (K′) can be expressed as follows:

$$K^{\prime }=3.784-96.2R{e}_{\mathrm{i}}+2009{R{e}_{\mathrm{i}}}^2-\frac{0.1446}{{R{e}_{\mathrm{i}}}^{0.5}}$$

(26)

Note that the new Ganser model is built based on cylindrical particles with a diameter of 0.00498 m and a length of 0.0139 m. The experimental pressure drop data for cylindrical particles with diameter of 0.00198 m and length of 0.00495 m are then used to verify the accuracy of this model. It is seen from Figure 7 that the new Ganser model can reduce the relative error to below 10%. The comparison indicates that the correction factor can be proper for cylindrical particles with different sizes. The choice of experimental data may affect the coefficients of the correction factor, but the effects can be small. This has been proved by comparing the predictions of the drag force model from one set of experimental data with another set of experimental data.

4. Conclusions

Accurate prediction of drag force is essential for pressure drop prediction in FBR with spherical or non-spherical particles. In this work, particle porosity prediction with the particle-unresolved CFD-DEM method was firstly validated. Then, the Di Felice model and Ergun model were compared for the drag force prediction of spherical particle bed, and the Di Felice model and Ganser model were compared for drag force prediction of the cylindrical particle bed base. Finally, a new Ganser model was put forward to specifically deal with the drag force between the gas and cylindrical particles. From this work, important conclusions can be drawn as follows:

(1)

The unsolved CFD-DEM model can accurately predict the porosity distribution in FBR;

(2)

For the spherical particle bed, the Di Felice model is more advanced than the Ergun model. The relative prediction errors of the Di Felice model are approximately 10%, while those of the Ergun model are approximately 15%. For the cylindrical particle bed, the Ganser model is more advanced than the Di Felice model. The relative prediction errors of the Ganser model are approximately 10%, while those of the Di Felice model are greater than 10%;

(3)

The new Ganser model can provide more accurate predictions for pressure drop of a packed bed with cylindrical particles. The maximum relative error between the simulated pressure drop and the experimental data is approximately 5%.