RiSSNet: Contrastive Learning Network with a Relaxed Identity Sampling Strategy for Remote Sensing Image Semantic Segmentation
Abstract
:1. Introduction
- (1)
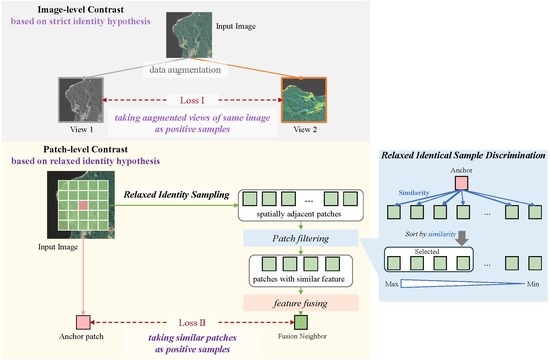
- We proposed a relaxed identity hypothesis as an extension of the strict identity hypothesis currently used to define positive samples for contrastive learning, i.e., to consider similar samples as positive samples instead of considering only augmented views of the same sample. Our proposed relaxed identity hypothesis could fundamentally alleviate the problem of incomplete object recognition due to the over-instantiation of features obtained by contrastive learning.
- (2)
- Following the relaxed identity hypothesis, we proposed a novel contrastive learning method, RiSSNet, which used spatial proximity sampling and visual similarity discrimination strategies to filter out similar samples for the construction of positive sample pairs. With the dual constraints of spatial proximity and visual similarity used to construct positive samples, RiSSNet achieved a more compact feature space through contrastive learning to obtain category-level features instead of instance-level features.
- (3)
- We experimentally verified the effectiveness of the proposed RiSSNet on three representative semantic segmentation datasets, which contributed to a deeper understanding of the relaxation hypothesis.
2. Materials and Methods
2.1. Related Works
2.1.1. Semantic Segmentation of Remote Sensing Images
2.1.2. Semantic Segmentation for Remote Sensing Images Based on Self-Supervised Contrastive Learning
2.1.3. Positive Sampling Strategies
2.2. Method
2.2.1. Overview of RiSSNet
2.2.2. Relaxed Identity Sampling
2.2.3. Relaxed Identical Sample Discrimination
2.2.4. InfoNCE Loss
3. Experiments
3.1. Datasets
3.1.1. Xiangtan
3.1.2. ISPRS Potsdam
3.1.3. GID
3.2. Experiments
- (a)
- Random [28]: a supervised learning method, using the network Deeplab V3+ and only 1% of the fine-tuning data volume for training.
- (b)
- Inpainting [49]: a patch-level generative network that learns by computing the loss of the patched image relative to the original image.
- (c)
- Tile2Vec [45]: a primitive sampling method based on spatial proximity, with samples within the neighborhood treated as positive and samples at a farther distance treated as negative.
- (d)
- SimCLR [9]: a standard strict-identity-constrained network for which positive samples are obtained through the data augmentation of the anchor samples and negative samples are obtained from the rest of the samples in the same batch.
- (e)
- MoCo v2 [11]: a standard strict-identity-constrained network that outperforms SimCLR in several respects, for which positive samples are also obtained by augmenting anchor samples and negative samples are stored in a queue.
- (f)
- Barlow Twins [50]: a self-supervised network with only positive samples, where the positive samples are also augmented by the anchor samples.
- (g)
- FALSE [51]: a self-supervised network that removes false-negative samples from negative samples in contrastive learning.
3.3. Result Analysis
3.3.1. Relaxed Identity Sampling
3.3.2. Relaxed Identical Sample Discrimination
3.3.3. Feature Invariance Augmentation Verification Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ming, D.; Ci, T.; Cai, H.; Li, L.; Qiao, C.; Du, J. Semivariogram-Based Spatial Bandwidth Selection for Remote Sensing Image Segmentation With Mean-Shift Algorithm. IEEE Geosci. Remote Sens. Lett. 2012, 9, 813–817. [Google Scholar] [CrossRef]
- Wang, J.; Qin, Q.; Li, Z.; Ye, X.; Wang, J.; Yang, X.; Qin, X. Deep Hierarchical Representation and Segmentation of High Resolution Remote Sensing Images. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4320–4323. [Google Scholar] [CrossRef]
- Liu, X.; Chi, M.; Zhang, Y.; Qin, Y. Classifying High Resolution Remote Sensing Images by Fine-Tuned VGG Deep Networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7137–7140. [Google Scholar] [CrossRef]
- Ma, W.; Pan, Z.; Guo, J.; Lei, B. Super-Resolution of Remote Sensing Images Based on Transferred Generative Adversarial Network. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1148–1151. [Google Scholar] [CrossRef]
- Misra, I.; van der Maaten, L. Self-Supervised Learning of Pretext-Invariant Representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Favaro, S.J.P. Self-Supervised Feature Learning by Learning to Spot Artifacts. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Caron, M.; Misra, I.; Mairal, J.; Goyal, P.; Bojanowski, P.; Joulin, A. Unsupervised learning of visual features by contrasting cluster assignments. Adv. Neural Inf. Process. Syst. 2020, 33, 9912–9924. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the International Conference on Machine Learning (PMLR), Paris, France, 29 March–1 April 2020; pp. 1597–1607. [Google Scholar]
- Chen, T.; Kornblith, S.; Swersky, K.; Norouzi, M.; Hinton, G.E. Big self-supervised models are strong semi-supervised learners. Adv. Neural Inf. Process. Syst. 2020, 33, 22243–22255. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar]
- Chen, X.; Fan, H.; Girshick, R.; He, K. Improved baselines with momentum contrastive learning. arXiv 2020, arXiv:2003.04297. [Google Scholar]
- Chen, X.; Xie, S.; He, K. An Empirical Study of Training Self-Supervised Vision Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, online, 11–17 October 2021; pp. 9640–9649. [Google Scholar]
- Tao, C.; Qi, J.; Guo, M.; Zhu, Q.; Li, H. Self-supervised remote sensing feature learning: Learning Paradigms, Challenges, and Future Works. arXiv 2022, arXiv:2211.08129. [Google Scholar] [CrossRef]
- Kim, Y.; Park, W.; Roh, M.C.; Shin, J. GroupFace: Learning Latent Groups and Constructing Group-Based Representations for Face Recognition. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5620–5629. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, C.; Poole, B.; Krishnan, D.; Schmid, C.; Isola, P. What makes for good views for contrastive learning? Adv. Neural Inf. Process. Syst. 2020, 33, 6827–6839. [Google Scholar]
- Li, B.; Hou, Y.; Che, W. Data augmentation approaches in natural language processing: A survey. AI Open 2022, 3, 71–90. [Google Scholar] [CrossRef]
- Zhu, J.; Han, X.; Deng, H.; Tao, C.; Zhao, L.; Wang, P.; Lin, T.; Li, H. KST-GCN: A Knowledge-Driven Spatial-Temporal Graph Convolutional Network for Traffic Forecasting. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15055–15065. [Google Scholar] [CrossRef]
- Tao, C.; Qi, J.; Zhang, G.; Zhu, Q.; Lu, W.; Li, H. TOV: The Original Vision Model for Optical Remote Sensing Image Understanding via Self-Supervised Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4916–4930. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Lee, G.S.; Kim, S.H.; Yang, H.J. Self-supervised learning based on spatial awareness for medical image analysis. IEEE Access 2020, 8, 162973–162981. [Google Scholar] [CrossRef]
- Minaee, S.; Cambria, E.; Gao, J. Deep Learning Based Text Classification: A Comprehensive Review. Acm Comput. Surv. 2021, 54, 62. [Google Scholar] [CrossRef]
- Dwibedi, D.; Aytar, Y.; Tompson, J.; Sermanet, P.; Zisserman, A. With a Little Help from My Friends: Nearest-Neighbor Contrastive Learning of Visual Representations. In Proceedings of then 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 9568–9577. [Google Scholar]
- Goyal, P.; Duval, Q.; Seessel, I.; Caron, M.; Misra, I.; Sagun, L.; Joulin, A.; Bojanowski, P. Vision Models Are More Robust And Fair When Pretrained On Uncurated Images Without Supervision. arXiv 2022, arXiv:2202.08360. [Google Scholar]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, Y.; Li, S.; Deng, B.; Cai, W. Self-Supervised Locality Preserving Low-Pass Graph Convolutional Embedding for Large-Scale Hyperspectral Image Clustering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Ding, C.; Zheng, M.; Chen, F.; Zhang, Y.; Zhuang, X.; Fan, E.; Wen, D.; Zhang, L.; Wei, W.; Zhang, Y. Hyperspectral image classification promotion using clustering inspired active learning. Remote Sens. 2022, 14, 596. [Google Scholar] [CrossRef]
- Jia, X.; Xie, Y.; Li, S.; Chen, S.; Zwart, J.; Sadler, J.; Appling, A.; Oliver, S.; Read, J. Physics-Guided Machine Learning from Simulation Data: An Application in Modeling Lake and River Systems. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 270–279. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015. Part III. pp. 234–241. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Wu, Q.; Luo, F.; Wu, P.; Wang, B.; Yang, H.; Wu, Y. Automatic Road Extraction from High-Resolution Remote Sensing Images Using a Method Based on Densely Connected Spatial Feature-Enhanced Pyramid. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3–17. [Google Scholar] [CrossRef]
- Ding, L.; Tang, H.; Bruzzone, L. LANet: Local Attention Embedding to Improve the Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 426–435. [Google Scholar] [CrossRef]
- Wu, Z.; Xiong, Y.; Yu, S.X.; Lin, D. Unsupervised Feature Learning via Non-Parametric Instance Discrimination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3733–3742. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y. CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Liu, J.; Liu, B.; Zhou, H.; Li, H.; Liu, Y. TokenMix: Rethinking Image Mixing for Data Augmentation in Vision Transformers. In Proceedings of the Computer Vision–ECCV 2022, 17th European Conference, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Li, H.; Cao, J.; Zhu, J.; Luo, Q.; He, S.; Wang, X. Augmentation-Free Graph Contrastive Learning of Invariant-Discriminative Representations. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–11. [Google Scholar] [CrossRef]
- Tao, C.; Fu, S.; Qi, J.; Li, H. Thick Cloud Removal in Optical Remote Sensing Images Using a Texture Complexity Guided Self-Paced Learning Method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5619612. [Google Scholar] [CrossRef]
- Peng, X.; Wang, K.; Zhu, Z.; Wang, M.; You, Y. Crafting Better Contrastive Views for Siamese Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16031–16040. [Google Scholar]
- Li, H.; Li, Y.; Zhang, G.; Liu, R.; Huang, H.; Zhu, Q.; Tao, C. Global and local contrastive self-supervised learning for semantic segmentation of HR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Tang, M.; Georgiou, K.; Qi, H.; Champion, C.; Bosch, M. Semantic Segmentation in Aerial Imagery Using Multi-level Contrastive Learning with Local Consistency. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–7 January 2023; pp. 3787–3796. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Yan, Z.; Zhang, Z.; Zhang, Y.; Chen, Y.; Li, H. LaST: Label-Free Self-Distillation Contrastive Learning With Transformer Architecture for Remote Sensing Image Scene Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6512205. [Google Scholar] [CrossRef]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 18661–18673. [Google Scholar]
- Li, H.; Zhang, X.; Xiong, H. Center-wise local image mixture for contrastive representation learning. arXiv 2020, arXiv:2011.02697. [Google Scholar]
- Ayush, K.; Uzkent, B.; Meng, C.; Tanmay, K.; Burke, M.; Lobell, D.; Ermon, S. Geography-Aware Self-Supervised Learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10181–10190. [Google Scholar]
- Jean, N.; Wang, S.; Samar, A.; Azzari, G.; Lobell, D.; Ermon, S. Tile2vec: Unsupervised Representation Learning for Spatially Distributed Data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3967–3974. [Google Scholar]
- Jung, H.; Oh, Y.; Jeong, S.; Lee, C.; Jeon, T. Contrastive self-supervised learning with smoothed representation for remote sensing. IEEE Geosci. Remote Sens. Lett. 2021, 19, 8010105. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The isprs benchmark on urban object classification and 3d building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-3, 293–298. [Google Scholar] [CrossRef] [Green Version]
- Tong, X.Y.; Xia, G.S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef] [Green Version]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Zbontar, J.; Jing, L.; Misra, I.; LeCun, Y.; Deny, S. Barlow Twins: Self-Supervised Learning via Redundancy Reduction. In Proceedings of the International Conference on Machine Learning, online, 18–24 July 2021. [Google Scholar]
- Zhang, Z.; Wang, X.; Mei, X.; Tao, C.; Li, H. FALSE: False Negative Samples Aware Contrastive Learning for Semantic Segmentation of High-Resolution Remote Sensing Image. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6518505. [Google Scholar] [CrossRef]







| Dataset | Resolution | Image Size | Classes | Training | Fine-Tuning | Val |
|---|---|---|---|---|---|---|
| Xiangtan [39] | 2 m | 256 × 256 | 9 | 16051 | 160 | 3815 |
| ISPRS Potsdam [47] | 0.05 m | 256 × 256 | 6 | 16080 | 160 | 4022 |
| GID [48] | 1 m | 256 × 256 | 5 | 98218 | 983 | 10919 |
| Method | Xiangtan | Potsdam | GID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Kappa | OA | mIOU | Kappa | OA | mIOU | Kappa | OA | mIOU | |
| Random [28] | 65.31 | 78.52 | 34.73 | 53.78 | 64.87 | 38.85 | 52.61 | 72.14 | 52.45 |
| Inpainting [49] | 65.40 | 78.45 | 34.93 | 55.74 | 66.28 | 35.45 | 55.94 | 73.82 | 52.48 |
| Tile2Vec [45] | 64.45 | 77.73 | 33.98 | 56.85 | 70.57 | 36.33 | 32.30 | 61.19 | 37.84 |
| SimCLR [9] | 70.08 | 81.12 | 39.17 | 63.40 | 72.02 | 43.63 | 65.18 | 79.40 | 58.63 |
| MoCo v2 [11] | 65.40 | 78.45 | 34.93 | 54.20 | 65.13 | 34.37 | 52.31 | 71.56 | 52.25 |
| Barlow Twins [50] | 67.55 | 79.85 | 36.86 | 58.59 | 68.44 | 39.23 | 54.80 | 72.79 | 54.14 |
| FALSE [51] | 69.41 | 80.99 | 40.27 | 55.96 | 66.31 | 43.15 | 60.98 | 77.52 | 55.25 |
| RiSSNet | 70.16 | 81.21 | 40.25 | 64.81 | 73.08 | 44.96 | 66.10 | 80.21 | 61.41 |
| Selection Method | Xiangtan | Potsdam | GID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Anchor | N_pos | N_neg | Anchor | N_pos | N_neg | Anchor | N_pos | N_neg | |
| Random | 16064 | 41305 | 22951 | 7257 | 39027 | 25101 | 98272 | 308316 | 84772 |
| Our Method | 16064 | 42395 | 21733 | 7257 | 46180 | 18076 | 98272 | 325000 | 68088 |
| Trend | - | ↑1.02 | ↓0.94 | - | ↑1.18 | ↓0.72 | - | ↑1.05 | ↓0.80 |
| Selection Method | Xiangtan | Potsdam | GID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Anchor | N_pos | N_neg | Anchor | N_pos | N_neg | Anchor | N_pos | N_neg | |
| Random | 16000 | 36110 | 27890 | 4000 | 8950 | 7050 | 98240 | 277515 | 115445 |
| Our Method | 16000 | 37919 | 26081 | 4000 | 10279 | 5721 | 98240 | 308359 | 84601 |
| Trend | - | ↑1.05 | ↓0.93 | - | ↑1.14 | ↓0.81 | - | ↑1.11 | ↓0.73 |
| Class | Xiangtan | Potsdam | GID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Ours | Trend | Best | Ours | Trend | Best | Ours | Trend | |
| C_1 | 80.27 | 127.97 | ←→ | 2748 | 1907 | →← | 1723 | 1152 | →← |
| C_2 | 214.63 | 118.27 | →← | 4594 | 3656 | →← | 769 | 237 | →← |
| C_3 | 0 | 0 | - | 3782 | 2372 | →← | 1.75 | 1.77 | →← |
| C_4 | 0 | 0 | - | 1010 | 684 | →← | 22.62 | 18.87 | →← |
| C_5 | 0.78 | 0.28 | →← | 0 | 0 | - | 37.41 | 23.55 | →← |
| C_6 | 7118 | 5000 | →← | 1799 | 1081 | →← | / | / | / |
| C_7 | 0 | 0 | - | 0 | 0 | - | / | / | / |
| C_8 | 0 | 0 | - | / | / | / | / | / | / |
| C_9 | 0 | 0 | - | / | / | / | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jing, W.; Wei, G.; Wu, K.; Su, M.; Liu, L.; Wu, H.; Li, P.; Qi, J. RiSSNet: Contrastive Learning Network with a Relaxed Identity Sampling Strategy for Remote Sensing Image Semantic Segmentation. Remote Sens. 2023, 15, 3427. https://doi.org/10.3390/rs15133427
Li H, Jing W, Wei G, Wu K, Su M, Liu L, Wu H, Li P, Qi J. RiSSNet: Contrastive Learning Network with a Relaxed Identity Sampling Strategy for Remote Sensing Image Semantic Segmentation. Remote Sensing. 2023; 15(13):3427. https://doi.org/10.3390/rs15133427
Chicago/Turabian StyleLi, Haifeng, Wenxuan Jing, Guo Wei, Kai Wu, Mingming Su, Lu Liu, Hao Wu, Penglong Li, and Ji Qi. 2023. "RiSSNet: Contrastive Learning Network with a Relaxed Identity Sampling Strategy for Remote Sensing Image Semantic Segmentation" Remote Sensing 15, no. 13: 3427. https://doi.org/10.3390/rs15133427