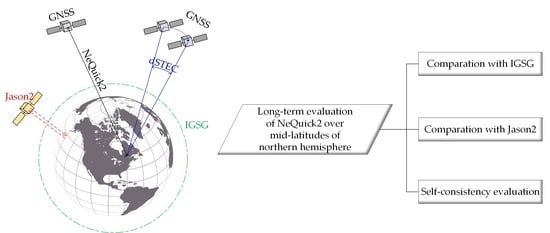
Evaluation of NeQuick2 Model over Mid-Latitudes of Northern Hemisphere
Abstract
:1. Introduction
2. NeQuick2 Model Introduction
3. Models Assessment Methods
3.1. The Final GIM Provided by IGS
3.2. Assessment over the Oceanic Region
3.3. Self-Consistency Evaluation
3.4. Accuracy Index
4. Results and Discussions
4.1. Data Collection
4.2. Validation with IGS Final GIM
4.3. Assessment of NeQuick2 Model over the Ocean
4.4. Self-Consistency Evaluation
5. Conclusions
- (1)
- The comparison with IGSG shows that the maximum deviation can be about 30 TECU on high solar condition days, which mainly appear at the lower latitudes and fluctuates with the sun activities. Moreover, the maximum deviation is about 15 TECU on low solar condition days. In addition, the STD values mainly range from 2 to 6 TECU, with a mean STD value of 2.59 TECU. For different hours, the absolute bias is smaller than two TECU from UTC 0 to 16 o’clock, while the absolute value will be larger than two TECU for UTC 18, 20, and 22 o’clock. In terms of STD values, the values are mainly smaller than three TECU, and there are few differences between hours.
- (2)
- Compared with Jason2, the accuracy of the IGSG and NeQuick2 model over ocean regions shows that the bias of IGSG is more significant than that of the NeQuick2 model. In addition, the difference between IGSG and NeQuick2 model has a periodical variation, which is highly related to the solar condition. The mean STD value is 2.09 TECU for IGSG. and the mean STD value is 3.18 TECU for the NeQuick2 model, which is about 50% worse than IGSG. The maximum STD value would be more significant than four TECU in high solar condition years for the NeQuick2 model, and the corresponding value is about eight TECU for IGSG.
- (3)
- The dSTEC assessment results indicate that the variation in the biases for IGSG is more stable than that of the NeQuick2 model. In addition, the STD value of IGSG is smaller than that of the NeQuick2 model. The mean STD value is 0.86 and 1.52 TECU for IGSG and NeQuick2 model, respectively. The statistical STD values of the IGSG and NeQuick2 model for different ground-based stations indicate that the STD value of IGSG is smaller than 1.50 TECU, and most of them are smaller than one TECU. In terms of the NeQuick2 model, the STD value mainly ranges from 1 to 2 TECU and has a notable variation for different stations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Su, K.; Jin, S. Three Dual-Frequency Precise Point Positioning Models for the Ionospheric Modeling and Satellite Pseudorange Observable-Specific Signal Bias Estimation. Remote Sens. 2021, 13, 5093. [Google Scholar] [CrossRef]
- Scherliess, L.; Schunk, R.W.; Sojka, J.J.; Thompson, D.C. Development of a physics-based reduced state Kalman filter for the ionosphere. Radio Sci. 2004, 39, 1–12. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.; Hairston, M.; et al. Global Assimilation of Ionospheric Measurements (GAIM). Radio Sci. 2004, 39, 1–11. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J. New approaches in global ionospheric determination using ground GPS data. J. Atmos. Sol.-Terr. Phys. 1999, 61, 1237–1247. [Google Scholar] [CrossRef]
- Feltens, J. Development of a new three-dimensional mathematical ionosphere model at European Space Agency/European Space Operations Centre. Space Weather 2007, 5. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Xu, P.; Han, W.; Ge, M.; Shi, C. Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares. Adv. Space Res. 2013, 51, 988–1000. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
- Leitinger, R.; Zhang, M.L.; Radicella, S.M. An improved bottomside for the ionospheric electron density model NeQuick. Ann. Geophys. 2009, 48. [Google Scholar] [CrossRef]
- Nava, B.; Coïsson, P.; Radicella, S. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Zhang, Y.; Mertens, C.J.; Truhlik, V.; Richards, P.; McKinnell, L.-A.; Reinisch, B.W. The International Reference Ionosphere 2012—A model of international collaboration. J. Sp. Weather Space Clim. 2014, 4, A07. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Sp. Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Prol, F.; Hoque, M. Topside Ionosphere and Plasmasphere Modelling Using GNSS Radio Occultation and POD Data. Remote Sens. 2021, 13, 1559. [Google Scholar] [CrossRef]
- Liu, T.; Yu, Z.; Ding, Z.; Nie, W.; Xu, G. Observation of Ionospheric Gravity Waves Introduced by Thunderstorms in Low Latitudes China by GNSS. Remote Sens. 2021, 13, 4131. [Google Scholar] [CrossRef]
- Nina, A. Modelling of the Electron Density and Total Electron Content in the Quiet and Solar X-ray Flare Perturbed Ionospheric D-Region Based on Remote Sensing by VLF/LF Signals. Remote Sens. 2021, 14, 54. [Google Scholar] [CrossRef]
- Feltens, J.; Angling, M.; Jackson-Booth, N.; Jakowski, N.; Hoque, M.; Hernández-Pajares, M.; Aragon-Angel, A.; Orús, R.; Zandbergen, R. Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. 2011, 46, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Gulyaeva, T.L.; Huang, X.; Reinisch, B.W. Plasmaspheric extension of topside electron density profiles. Adv. Sp. Res. 2002, 29, 825–831. [Google Scholar] [CrossRef]
- Bilitza, D.; McKinnell, L.-A.; Reinisch, B.; Fuller-Rowell, T. The international reference ionosphere today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Zakharenkova, I.; Cherniak, I.; Krankowski, A.; Shagimuratov, I. Vertical TEC representation by IRI 2012 and IRI Plas models for European midlatitudes. Adv. Sp. Res. 2014, 55, 2070–2076. [Google Scholar] [CrossRef]
- Adewale, A.; Oyeyemi, E.; Cilliers, P.; McKinnell, L.; Adeloye, A. Low solar activity variability and IRI 2007 predictability of equatorial Africa GPS TEC. Adv. Sp. Res. 2012, 49, 316–326. [Google Scholar] [CrossRef]
- Olawepo, A.; Adeniyi, J.; Oluwadare, E. TEC variations and IRI-2012 performance at equatorial latitudes over Africa during low solar activity. Adv. Sp. Res. 2017, 59, 1800–1809. [Google Scholar] [CrossRef]
- Patel, N.; Karia, S.; Pathak, K. Comparison of GPS-derived TEC with IRI-2012 and IRI-2007 TEC predictions at Surat, a location around the EIA crest in the Indian sector, during the ascending phase of solar cycle 24. Adv. Sp. Res. 2016, 60, 228–237. [Google Scholar] [CrossRef]
- Wan, Q.; Ma, G.; Li, J.; Wang, X.; Fan, J.; Li, Q.; Lu, W. A comparison of GPS-TEC with IRI-TEC at low latitudes in China in 2006. Adv. Sp. Res. 2017, 60, 250–256. [Google Scholar] [CrossRef]
- Adebesin, B.; Ikubanni, S.; Adebiyi, S.; Joshua, B. Multi-station observation of ionospheric disturbance of March 9 2012 and comparison with IRI-model. Adv. Sp. Res. 2013, 52, 604–613. [Google Scholar] [CrossRef]
- Oyeyemi, E.; Adewale, A.; Adeloye, A.; Olugbon, B. An evaluation of the IRI-2007 storm time model at low latitude stations. Adv. Sp. Res. 2013, 52, 1737–1747. [Google Scholar] [CrossRef]
- Sharma, D.; Aggarwal, M.; Bardhan, A. Variability of ionospheric parameters during solar minimum and maximum activity and assessment of IRI model. Adv. Sp. Res. 2017, 60, 435–443. [Google Scholar] [CrossRef]
- Klenzing, J.; Simões, F.; Ivanov, S.; Bilitza, D.; Heelis, R.; Rowland, D. Performance of the IRI-2007 model for equatorial topside ion density in the African sector for low and extremely low solar activity. Adv. Sp. Res. 2013, 52, 1780–1790. [Google Scholar] [CrossRef] [Green Version]
- Jamjareegulgarn, P.; Supnithi, P.; Hozumi, K.; Tsugawa, T. Study of ionospheric topside variations based on NeQuick topside formulation and comparisons with the IRI-2012 model at equatorial latitude station, Chumphon, Thailand. Adv. Sp. Res. 2017, 60, 206–221. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Liu, L.; Wan, W.; Ning, B. Comparison of the observed topside ionospheric and plasmaspheric electron content derived from the COSMIC podTEC measurements with the IRI_Plas model results. Adv. Sp. Res. 2017, 60, 222–227. [Google Scholar] [CrossRef]
- Coisson, P.; Radicella, S.M.; Nava, B.; Leitinger, R. Low and equatorial latitudes topside in NeQuick. J. Atmos. Sol.-Terr. Phys. 2008, 70, 901–906. [Google Scholar] [CrossRef]
- Montenbruck, O.; Rodriguez, B.G. NeQuick-G performance assessment for space applications. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Yuan, Y.; Li, Z.; Li, Y.; Huo, X.; Li, M. An examination of the Galileo NeQuick model: Comparison with GPS and JASON TEC. GPS Solut. 2016, 21, 605–615. [Google Scholar] [CrossRef]
- Migoya-Orué, Y.; Folarin-Olufunmilayo, O.; Radicella, S.; Alazo-Cuartas, K.; Rabiu, A. Evaluation of NeQuick as a model to characterize the Equatorial Ionization Anomaly over Africa using data ingestion. Adv. Sp. Res. 2017, 60, 1732–1738. [Google Scholar] [CrossRef]
- Ahoua, S.M.; Habarulema, J.B.; Obrou, O.K.; Cilliers, P.J.; Zaka, Z.K. Evaluation of the NeQuick model performance under different geomagnetic conditions over South Africa during the ascending phase of the solar cycle (2009–2012). Ann. Geophys. 2018, 36, 1161–1170. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Wang, Z.; An, J.; Liu, J.; Wang, N.; Li, H. Influence of spatial gradients on ionospheric mapping using thin layer models. GPS Solut. 2018, 22, 2. [Google Scholar] [CrossRef]
- Chen, J.; Ren, X.; Zhang, X.; Zhang, J.; Huang, L. Assessment and Validation of Three Ionospheric Models (IRI-2016, NeQuick2, and IGS-GIM) From 2002 to 2018. Sp. Weather 2020, 18, e2019SW002422. [Google Scholar] [CrossRef]
- Liu, A.; Wang, N.; Li, Z.; Wang, Z.; Yuan, H. Assessment of NeQuick and IRI-2016 models during different geomagnetic activities in global scale: Comparison with GPS-TEC, dSTEC, Jason-TEC and GIM. Adv. Sp. Res. 2019, 63, 3978–3992. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I. NeQuick and IRI-Plas model performance on topside electron content representation: Spaceborne GPS measurements. Radio Sci. 2016, 51, 752–766. [Google Scholar] [CrossRef] [Green Version]
- Okoh, D.; Onwuneme, S.; Seemala, G.; Jin, S.; Rabiu, B.; Nava, B.; Uwamahoro, J. Assessment of the NeQuick-2 and IRI-Plas 2017 models using global and long-term GNSS measurements. J. Atmos. Sol.-Terr. Phys. 2018, 170, 1–10. [Google Scholar] [CrossRef]
- Pignalberi, A.; Giannattasio, F.; Truhlik, V.; Coco, I.; Pezzopane, M.; Consolini, G.; De Michelis, P.; Tozzi, R. On the Electron Temperature in the Topside Ionosphere as Seen by Swarm Satellites, Incoherent Scatter Radars, and the International Reference Ionosphere Model. Remote Sens. 2021, 13, 4077. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Wielgosz, P.; Milanowska, B.; Krypiak-Gregorczyk, A.; Jarmołowski, W. Validation of GNSS-derived global ionosphere maps for different solar activity levels: Case studies for years 2014 and 2018. GPS Solutions 2021, 25, 1–15. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Imel, D. Evaluation of the TOPEX/POSEIDON dual-frequency ionosphere correction. J. Geophys. Res. Earth Surf. 1994, 99, 24895–24906. [Google Scholar] [CrossRef]
- Li, M.; Zhang, B.; Yuan, Y.; Zhao, C. Single-frequency precise point positioning (PPP) for retrieving ionospheric TEC from BDS B1 data. GPS Solut. 2018, 23, 18. [Google Scholar] [CrossRef]
- Hu, A.; Li, Z.; Carter, B.; Wu, S.; Wang, X.; Norman, R.; Zhang, K. Helmert-VCE-aided fast-WTLS approach for global ionospheric VTEC modelling using data from GNSS, satellite altimetry and radio occultation. J. Geodesy 2018, 93, 877–888. [Google Scholar] [CrossRef]
- Jee, G.; Schunk, R.W.; Scherliess, L. Analysis of TEC data from the TOPEX/Poseidon mission. J. Geophys. Res. Earth Surf. 2010, 109. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.-B.; Kim, Y.H.; Chung, J.-K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Sp. Phys. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Orus, R.; Cander, L.R.; Hernández-Pajares, M. Testing regional vertical total electron content maps over Europe during the 17–21 January 2005 sudden space weather event. Radio Sci. 2007, 42, 1–12. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X.; Freeshah, M. Performance evaluation of real-time global ionospheric maps provided by different IGS analysis centers. GPS Solut. 2019, 23, 1–17. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Roma-Dollase, D.; Krankowski, A.; García-Rigo, A.; Orús-Pérez, R. Methodology and consistency of slant and vertical assessments for ionospheric electron content models. J. Geod. 2017, 91, 1405–1414. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Ray, S.; Roy, B.; Paul, K.S.; Goswami, S.; Oikonomou, C.; Haralambous, H.; Chandel, B.; Paul, A. Study of the effect of 17–18 March 2015 geomagnetic storm on the Indian longitudes using GPS and C/NOFS. J. Geophys. Res. Sp. Phys. 2017, 122, 2551–2563. [Google Scholar] [CrossRef]













| Layer | |||||
|---|---|---|---|---|---|
| Bottom side | E | ||||
| F1 | |||||
| F2 | |||||
| Topside | \ | ||||
| Year | Proportion of Underestimation (%) | Proportion of Overestimation (%) | Average of Underestimation (TECU) | Average of Overestimation (TECU) |
|---|---|---|---|---|
| 2008 | 15.56 | 84.44 | −0.24 | 1.15 |
| 2009 | 18.08 | 81.92 | −0.64 | 1.17 |
| 2010 | 46.85 | 53.15 | −0.78 | 1.07 |
| 2011 | 35.34 | 64.66 | −1.65 | 3.01 |
| 2012 | 47.67 | 52.33 | −1.91 | 3.07 |
| 2013 | 44.16 | 55.84 | −2.30 | 3.42 |
| 2014 | 44.66 | 55.34 | −2.91 | 5.11 |
| 2015 | 41.64 | 58.36 | −2.49 | 2.58 |
| 2016 | 35.84 | 64.16 | −0.85 | 1.51 |
| 2017 | 13.55 | 86.45 | −0.51 | 1.52 |
| 2018 | 21.36 | 78.64 | −0.60 | 1.18 |
| 2019 | 6.94 | 93.06 | −0.20 | 1.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wei, E.; Xiong, S.; Zhang, T.; Shen, Z. Evaluation of NeQuick2 Model over Mid-Latitudes of Northern Hemisphere. Remote Sens. 2022, 14, 4124. https://doi.org/10.3390/rs14164124
Wang L, Wei E, Xiong S, Zhang T, Shen Z. Evaluation of NeQuick2 Model over Mid-Latitudes of Northern Hemisphere. Remote Sensing. 2022; 14(16):4124. https://doi.org/10.3390/rs14164124
Chicago/Turabian StyleWang, Lingxuan, Erhu Wei, Si Xiong, Tengxu Zhang, and Ziyu Shen. 2022. "Evaluation of NeQuick2 Model over Mid-Latitudes of Northern Hemisphere" Remote Sensing 14, no. 16: 4124. https://doi.org/10.3390/rs14164124