1. Introduction
Real-time precise point positioning (RTPPP) is a technology that uses a real-time service (RTS) product to mitigate different errors in measurements. Compared with real-time kinematic (RTK) technology, RTPPP does not rely on the data from nearby reference stations. RTPPP has thus become a popular solution to obtain precise positions. In its early development, PPP technology was used in the post-processing mode based on precise orbit products from the International GNSS Service (IGS) [
1]. The shortage of real-time precise corrections limited PPP applications in the early stage. RTPPP has become much easier since the official launch of the IGS real-time service (RTS) on 1 April 2013 [
2,
3].
In recent years, RTPPP has become increasingly widely used in land navigation [
4,
5,
6], marine navigation [
7,
8,
9], and airplane navigation [
10]. Now, RTPPP can be performed on smartphones, which will extend RTPPP applications to normal applications in our everyday lives [
5,
6,
11].
RTPPP requires the receiving of the real-time State Space Representation (SSR) product and the RTCM-SSR is its existing internationally standardized format. Currently its main content includes orbit and clock corrections, code and phase bias, and VTEC (Vertical Total Electron Content), in future, it may include STEC (Slant TEC), tropospheric delay and integrity information. Except for RTCM-SSR, there are two other SSR formats, the first is Compact SSR (CSSR) and the other is SPARTN (Safe Position Augmentation for Real-time Navigation) format.
CSSR is a format that transmits compact corrections of satellites that are visible to users in a local region. The corrections include both the conventional SSR corrections and the atmospheric corrections for fast convergence. In typical multi-GNSS PPP service scenario including 69 GNSS satellites, the required date rate of proposed format is about 71% less than that of RTCM-SSR [
12]. The reduction in date rate is achieved mainly by compressing information and using the satellite mask. The SPARTN format is an industry-driven standard for communication of GNSS high accuracy correction data between service providers and end users. It is developed to meet the requirements of safety of life applications, including low bandwidth, accuracy, availability, reliability, and integrity.
Even though the normal data bandwidth of RTS data can be as large as 1 KB/s, the bandwidth is usually not considered because modern wireless networks such as 4G and Wi-Fi can support it easily. For ocean applications, however, these data links are not available. One option for ocean RTPPP is to transmit RTS data via a communication satellite. The cost of this option, however, is much higher than the cost that can be afforded by normal users [
13]. The precise correction service via satellite is also provided by some commercial companies. For example, the annual subscription price of precise satellite correction service from Trimble and Hexagon is more than 1000 USD one year currently. In addition, satellite-based RTPPP will be operational in near future, such as Galileo High Accuracy Service (HAS), and this service is free of charge. This will bring extensive benefits for global precise applications.
The BeiDou short-message service is a wide area service that allows a user to communicate with another user through short messages. Data communication is performed via a geostationary satellite (GEO). In addition, the annual fee for each user is approximately 160 USD, providing a cost-effective way to transmit data from land to ocean. The short-message service has thus become one of the major properties of BeiDou [
14], and it has played an important role in many applications, such as emergency rescue, ocean surveying, and sea transportation. However, the BeiDou short message service has a limited bandwidth [
14,
15]:
These limitations have become a challenge for RTPPP, which requires a high data-rate RTS product in real time. The RTS data can be simplified by the calculation of a range correction for one satellite, which is sum of clock correction and the orbital correction projected into the range domain [
16]. However, this method is not efficient because only one user is supported.
We propose ocean RTPPP based on a new method of broadcasting RTS data via BeiDou short messages. In this paper, the content and format of RTS data are carefully simplified to reduce the required bandwidth. To overcome the limitation on the communication frequency, the satellite position and clock corrections are predicted based on minute-interval RTS orbital and clock corrections. Finally, an experiment is conducted to demonstrate the performance of ocean RTPPP with the BeiDou short-message service.
2. Minimizing the Required Bandwidth of Corrections
The maximum size of each BeiDou short message is 78 bytes, while the RTS data require a much larger data bandwidth. In RTS data, each satellite correction needs three numbers for the orbital correction and one for the satellite clock correction. Other auxiliary data, including the epoch time, satellite name and issue of data (IOD), should also be transmitted. Therefore, the required bandwidth of these data should be reduced so that the corrections can be transmitted efficiently so that RTPPP can be conducted.
The RTS products IGS03 from IGS and CLK91 from Centre National D’Etudes Spatiales (CNES) are used in this study. The orbital corrections of the IGS03 mount point are updated at a 1 min interval, and those of the CLK91 mount point are updated at a 5 s interval. The satellite clock corrections of the IGS03 mount point are updated at a 10 s interval, and those of the CLK91 mount point are updated at a 5 s interval. The RTS product data are collected on 10 days of the year (DOY), i.e., 318, 340, 341, 347, and 351–356 in 2019, and 15 h on average each day. First, these data are analyzed, and then, their characteristics are described. Finally, the method for simplifying the RTS data is presented, and the performance of the new data format is demonstrated.
2.1. Evaluation of the Ranges of Orbital and Clock Corrections
Figure 1 and
Figure 2 show the orbital and clock corrections of GPS, BeiDou, Global Navigation Satellite System (GLONASS), and Galileo.
Table 1 and
Table 2 present their corresponding statistics. The orbital corrections have different ranges: all of the Galileo radial corrections are within 0.512 m; most of the GPS and GLONASS radial corrections are within 1.024 m, and all of them are within 2.048 m; most of the BeiDou radial corrections are within 4.096 m, but some can be as large as more than 20 m.
In terms of along and cross directions, most of the Galileo corrections are within 0.512 m, and all of them are within 2.048 m. Most of the GPS corrections are within 2.048 m, and all of them are within 8.192 m. Most of the GLONASS corrections are within 4.096 m, and all of them are within 8.192 m. Most of the BeiDou corrections are within 8.192 m, and all of them are within 32.768 m.
It can be concluded from
Table 1 and
Table 2 that the radial corrections are smaller than those of the along and cross corrections; additionally, among the four GNSSs, the Galileo orbital corrections are the smallest, and the BeiDou corrections are largest.
Compared with the orbital corrections, the clock corrections are slightly larger. For Galileo, most of the clock corrections are within 0.512 m, and all of them are within 4.096 m. For GPS, most of them are within 1.024 m, and all of them are within 4.098 m. For GLONASS, most of them are within 4.096 m, and all of them are within 8.192 m. For BeiDou, only approximately 85% are within 8.192 m, and some can be as large as more than 15 m.
In summary, the orbital and clock corrections are at the meter level. Assume that the resolution for each bit is 1 mm. For Galileo, most (>90%) radial corrections can require 10 bits. GPS and GLONASS require 11 bits, while BeiDou requires 13 bits. Regarding the along and cross corrections, for Galileo, most can require 10 bits; GPS can require 12 bits; and GLONASS and BeiDou can require 14 bits. With regard to the clock corrections, for Galileo, most can require 10 bits; GPS can require 11 bits; GLONASS can require 13 bits; and BeiDou can require 15 bits.
2.2. Characteristics of Orbital and Clock Corrections
Understanding the characteristics of orbital and clock corrections is important for taking measurements to simplify them effectively. To illustrate the characteristics, the RTS data collected on 23 September 2019, are taken as an example, and only minute-interval orbital and clock corrections are used.
Figure 3 shows the clock corrections (blue) of one GPS satellite (PRN 16).
Figure 4 shows the orbital corrections in the radial, along and cross directions. We see that both the clock and orbital corrections all change smoothly over time and with the same IOD, especially the orbital corrections. Thus, the values after differencing between neighboring epochs will decrease, which will be beneficial for reducing the bandwidth.
Figure 3 is a comparison of the original clock corrections (blue) and their single difference (SD) (red). We see that the maximum values of the original clock corrections are more than 0.8 m, while their SDs are all within 0.2 m.
Figure 5 shows the single difference (left) and double difference (right) between neighboring epochs after removing the effect of IOD change. We see that the SD values are all within 5 cm, and most of the Double Difference (DD) values are within 3 mm. If the SD or DD values of corrections are mainly transmitted, the size of the required bandwidth is reduced significantly, and the RTS corrections of more satellites can be transmitted.
2.3. Steps of Simplification
RTS corrections are generated by computing the errors of satellite orbit and clock, which is generally smooth. Based on this, the proposed overall simplifying scheme is that first, sending the orbit and clock correction of the starting epoch, then sending the difference of orbit and clock corrections of later epochs. The steps of simplification include:
(1) Simplification of the RTS corrections of the first epoch. Having a lower resolution is an efficient way to reduce the bandwidth required. For example, for a correction of 1.256 m, if the resolution is set to 1 mm, 1256 data must be sent and will be encoded as binary data 10,011,101,000, requiring 11 bits; if the resolution is set to 1 cm, 126 data must be sent and will be encoded as 1,111,110, requiring 7 bits. It can be seen that the bandwidth size required can be reduced significantly with the lower resolution. However, by setting a lower resolution, the quantization error can be increased, which should be considered by the user. It is worth noting that the processing of the RTS corrections of the new satellite of the subsequent epoch is the same as that of the first epoch.
(2) Simplification of the RTS corrections of the second epoch. With the corrections of the first epoch, another important simplification method involving transmitting the single difference of the RTS corrections between the neighboring epochs. From the analysis of
Section 2.1, we know that the value ranges can be obviously reduced after differencing between neighboring epochs, and hence, the bandwidth size required is further reduced. Note that when differencing, the used corrections of the first epoch are the sent corrections instead of the original corrections. Therefore, when recovering RTS corrections by accumulating the sent corrections of the first epoch and the sent SD values of the second epoch, the errors introduced in the last step are removed and will not affect the second and subsequent epochs.
(3) Simplification of the RTS corrections of subsequent epochs. For clock corrections, the processing is the same as that of the last step; that is, the SD values between the current and last epochs will be sent. For orbital corrections, the double differences will be obtained and sent, which, from the analysis of
Section 2.1, will be beneficial for saving space due to the BeiDou short messages.
(4) Processing in case of IOD change. When the IOD of the current epoch is different from that of the last epoch, the RTS corrections will change significantly from the last epoch or a jump, and hence, the value ranges will not be obviously reduced by the SD or DD. This is because the RTS corrections of the two neighboring epochs correspond to two different broadcast ephemeris data. To cope with an IOD change, the measures to be taken are first reducing the jump before sending and restoring it when recovering the corrections on the user side. To avoid the jump, the solution is to derive two groups of satellite positions and clock errors of the current epoch with the two sets of broadcast ephemeris data; calculate their differences; and subtract this difference from the SD value of the corrections of the two neighboring epochs before sending or adding this difference when recovering the RTS correction on the user side.
2.4. Value Ranges of Simplified Orbital and Clock Corrections
To test the proposed simplification method of RTS corrections, the RTS data with a 1-min interval-are processed with the simplification procedures in
Section 2.3.
Figure 6 and
Figure 7 show respectively the DD orbital corrections and SD clock corrections without an IOD change. We see that for GPS and Galileo, almost all DD orbital corrections are within 0.1 m; for GLONASS, almost all DD orbital corrections are within 0.2 m; however, for BeiDou, there are many cases at the meter level, which means that the orbital corrections make a sudden change now and then, which may be related to satellite maneuvers. Regarding the SD clock corrections, most of them are within 0.2 m, but for GLONASS and Galileo, there are some cases that are within approximately 0.5 m, and for BeiDou, there are some cases at the meter level.
Table 3 and
Table 4 present the statistics of DD orbital corrections and SD clock corrections without an IOD change. We see that most DD orbital corrections are at the millimeter level and that most SD clock corrections are at the centimeter level. If encoding and sending through BeiDou short messages, for Galileo, GPS, and BeiDou, 90% of DD radial corrections require only 3 bits, and for GLONASS, 90% of DD radial corrections require only 4 bits. Regarding the along and cross corrections, for All GNSSs, 90% of them require only 3 bits. For Galileo, 90% of SD clock corrections require only 5 bits; for BeiDou, 90% of SD clock corrections require only 6 bits; and for GLONASS and GPS, 90% of SD clock corrections require only 7 bits. Compared to the original clock corrections before simplification, the space savings from BeiDou short messages are approximately 50%, and compared to the original orbital corrections before simplification, the savings amount to approximately 70%.
Figure 8 and
Figure 9 show DD orbital corrections and SD clock corrections with an IOD change. We see that the DD orbit corrections of all GNSSs are basically within 0.2 m except for those of BeiDou, which have some values as large as more than 1 m. Regarding the SD clock corrections, most of them are within 0.5 m, but for Galileo and BeiDou, there are some values at the meter level.
Table 5 and
Table 6 present the statistics of DD orbital corrections and SD clock corrections with an IOD change. We see that most of the DD orbital corrections are at the centimeter level and that most SD clock corrections are at the decimeter level. If encoding and sending through BeiDou short messages, for Galileo, more than 90% of DD radial corrections require only 3 bits; for BeiDou, 90% of DD radial corrections require only 4 bits; for GPS, 90% of DD radial corrections require 7 bits; and for GLONASS, 90% of DD radial corrections require 8 bits. Regarding the DD along and cross corrections, for Galileo and BeiDou, more than 90% of them require only 5 bits, while for GPS and GLONASS, more than 90% of them require 8 bits. Regarding the SD clock corrections, for Galileo, more than 90% require only 6 bits; for GPS, more than 90% require 8 bits; for GLONASS, more than 90% require 10 bits; and for Galileo, more than 90% require 12 bits. Compared to the original orbit corrections before simplification, the space savings from BeiDou short messages are approximately 50%, and the BeiDou short message space required by SD clock corrections is also less than that of the original clock corrections.
2.5. Encoding of Simplified RTS Corrections
The bandwidth required can be further reduced with the use of the appropriate encoding scheme. In this study, the proposed encoding scheme includes the following steps:
It is assumed that the maximum and minimum epoch values of some kind of simplified correction (radial, along, cross or clock) are and and that the resolution is . The maximum and minimum integer values are computed as and . Here, the resolution is generally 1 mm. The resolution can be other values, such as 2 mm, for along and cross corrections since they have less effect on RTPPP performance than radial and clock corrections.
Second, calculate , and the bits required is , which satisfies and .
For simplified correction , its binary value to be encoded is .
Finally, the decoded simplified correction value on the user side can be calculated as
Note that resolution and the bits of required space should be sent together with encoded simplified correction values .
2.6. Recovery of Corrections
The epoch-differenced corrections are transmitted to users. It is necessary to recover RTS corrections first before using them.
- (1)
Recovering clock corrections
For the first epoch, the clock corrections can be used directly after decoding; for the subsequent epochs, the clock corrections can be calculated by accumulating the SD clock corrections of previous epochs added to the clock corrections of the first epoch.
- (2)
Recovering orbital corrections
For the first epoch, the orbital corrections can be used directly after decoding; for the second epoch, the orbital corrections are equal to the SD orbital corrections of the second epoch added to the decoded orbital corrections of the first epoch; for subsequent epochs, the orbital corrections can be calculated according to the following formula:
where
is the calculated orbital correction of epoch
and
is the decoded DD orbital correction of epoch
.
2.7. Simplification of RTS Auxiliary Data
RTS auxiliary data mainly include the satellite names, epoch time and IOD for navigation data. In this study, corrections of the satellites that can be observed in a region are transmitted to users. The satellite names are the union of satellites can be observed in a region, which are provided to the service provider through BeiDou short message. These auxiliary data should also be simplified to reduce the length of these data fields. For example, for BeiDou, the length of the IOD data field is 3 bytes, which should also be simplified.
As shown in
Table 7, the satellite name includes two parts. The first part is the system identifier: 0, 1, 2, and 3, representing GPS, GLONASS, Galileo, and BeiDou, respectively. Therefore, the minimum number of bits for the system identifier is 2. The second part is the satellite number, which is renumbered sequentially based on the satellite PRN and which requires 5 bits for GPS, GLONASS and Galileo and 6 bits for BeiDou, as there are more than 32 BeiDou satellites in the sky.
Therefore, a BeiDou satellite name requires 8 bits, and a satellite name for the other three GNSSs requires 7 bits.
As only minute-interval RTS corrections are transmitted to users, the corresponding epoch time can be similar to 00:00:00, 00:01:00, 00:02:00, …, or other forms with regular changes. The time of transmission is very close to the epoch time, and the transmission time delay through the BeiDou short message space is only approximately half a second. It is thus easy to deduce the epoch time according to the receiving time on the user side. In this study, the epoch time of RTS corrections is not contained in the message; thus, the size of the bandwidth required can be further reduced.
IOD information is used to check consistency in the computation and applications of RTS corrections. In other words, it indicates how to match correction data to navigation data. Generally, the time of clock (Toc) can meet the same objective, i.e., if sending the Toc instead of IOD information, the user can also correctly match correction data to navigation data. Since the Toc is easy to simplify, the Toc will be sent instead of IOD information.
The simplification procedures for the Toc include the following steps:
2.8. Reduction of the Required Bit Number
Table 9 shows a comparison of the length of the RTS data field before and after simplification. As seen in
Table 9, before simplification, the length of each RTS data point is 99 bits, i.e., 13 bytes, for GPS, Galileo, or GLONASS; for BeiDou, it is approximately 15 bytes due to the huge value of IOD information. Therefore, the RTS data of at most five satellites can be sent in one short message. After simplification, the length of one satellite RTS data point is approximately 24 bits, i.e., approximately 3 bytes, and therefore, the RTS data of approximately 24 satellites can be sent in one short message. Assuming that 10 satellites can be observed on average for one GNSS, before simplification, two short message devices are needed to send one epoch of RTS data of one GNSS, eight short message devices are needed to send one epoch of RTS data of four GNSSs, and the annual communication fee is approximately 8800 Chinese yuan. After simplification, only two short message devices are needed to send one epoch of RTS data of four GNSSs, and the annual communication fee is 2200 Chinese yuan. Compared to the solution without the simplification, there are savings of 75% on the communication fee when using the simplification solution.
3. Real-Time Precise Ephemeris Forecasting
The precise ephemeris can be obtained at an interval of one minute. Precise satellite positions and the clock errors of the other epochs between two minutes should be forecasted. This section will first introduce how to calculate minute-interval precise ephemeris from minute-interval RTS data, and then will describe how to forecast the precise positions and clock errors of other epochs.
RTS orbital corrections include radial, along and cross components that are related to the satellite position from broadcast ephemeris in a satellite-fixed coordinate system. Thus, before obtaining precise orbital positions, these corrections should be transformed into corrections in the geocentric coordinate. First, the direction unit vector of the satellite to the center of the earth in the radial, along and cross directions can be calculated according to the following formula:
where
and
are vectors of satellite position and velocity from broadcast ephemeris. Then, geocentric corrections can be calculated as follows:
where
,
, and
are RTS corrections in the radial, along and cross directions, respectively. Finally, the minute-interval precise satellite positions are calculated as follows:
and the minute-interval precise clock errors can be calculated according to the following formula:
where
is the clock error from the broadcast ephemeris and
is the RTS clock correction.
In one minute, the change in the satellite position and clock error at time
can be regarded as the following function:
where
is the satellite position or clock error;
is the reference time;
is the coefficient; and
is the order of the polynomial.
The coefficients
in Equation (6) are estimated with the least squares adjustment method to minimize the following equation:
where
is the minute-interval precise satellite position or clock error.
4. Experimental Description and Results
The experiment was conducted in Tangdao Bay, Qingdao City, China, on 23 September 2019, as shown in
Figure 10a. Three GNSS receivers were installed on a boat, as shown in
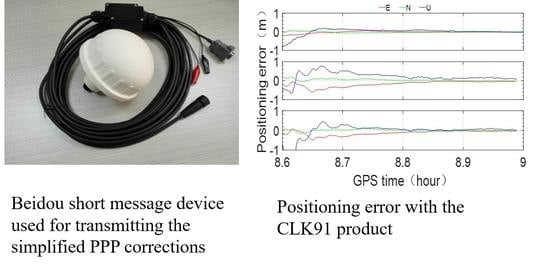
Figure 10b, and only observations of the Trimble ALLOY GNSS receiver with a choke ring antenna were used in this study. In addition, another Trimble ALLOY receiver was set up on the shore at a distance from the shore of no more than 1 km. The short message device used in the experiment was a BDStar Navigation system with model number BDSC-01, as shown in
Figure 11. The observation collection time was from approximately 03:30:00 to 09:00:00 (GPS time), and the sampling interval was 1 s. The RTS data (IGS03 and CLK91) were collected simultaneously; however, an interruption occurred during the collection.
The precise positions of the Trimble ALLOY receiver on the boat were first computed and used to validate the performance of ocean RTPPP. Specifically, the static observations of the receiver on the shore were processed with Bernese 5.2 software, and the PPP positions were obtained with the mm-level RMS. Then, a short baseline was formed between the receiver on the shore and the Trimble ALLOY receiver on the boat, and the precise relative positions were acquired with RTKLib 2.4.2 software. The precise absolute positions of the Trimble ALLOY receiver can be derived by combining the PPP position of the receiver on the shore and the relative position between these two receivers, which will be used to validate the performance of ocean RTPPP with the BeiDou short message service. The observations of the Trimble ALLOY receiver on the boat were post-processed with collected RTS data by simulating RTPPP data processing, including RTS data simplifying, encoding, sending, receiving, and decoding.
To assess the performance of ocean RTPPP with the BeiDou short message service, three scenarios were tested and compared. Scenario A was RTPPP with original RTS data, Scenario B was RTPPP with original RTS data but only minute-interval corrections, and Scenario C was minute-interval simplified corrections received through the BeiDou short message device after encoding, decoding and recovering. The observations of three durations were processed: Duration A: 03:24:00–04:00:00, Duration B: 04:18:00–05:18:00, and Duration C: 08:36:00–09:00:00. The observations of each duration were processed with the IGS03 product (GPS + GLONASS) and CLK91 product (GPS + GLONASS + Galileo + BeiDou).
From
Figure 12,
Figure 13 and
Figure 14, we see that with the IGS03 RTS product, the positioning accuracy of Scenario A can reach sub-meter level instantaneously in the horizontal direction and within one minute in the vertical direction; additionally, the three-dimensional positioning accuracy can reach half a meter level within 10 min and the level of approximately 0.2–0.3 m after approximately 30 min. The positioning performance of Scenario B is obviously less accurate, but the three-dimensional accuracy can reach sub-meter level within 5 min, the level of half a meter within approximately 12 min, and the level of approximately 0.3–0.4 m after approximately 30 min. The numerical results of Scenario C are similar to those of Scenario B, especially in the horizontal direction, except for the first several minutes.
From
Figure 15,
Figure 16 and
Figure 17, we see that with the CLK91 RTS product, the three-dimensional accuracy of Scenario A can reach sub-meter level instantaneously, the level of under half a meter within approximately 2 min and the level of approximately 0.1–0.2 m after approximately 30 min. While the positioning accuracy of Scenario B is obviously less accurate, it can reach sub-meter level instantaneously in the horizontal direction and within 1 min in the vertical direction. The three-dimensional accuracy can reach the level of under half a meter within approximately 10 min and the level of 0.2–0.3 m after approximately 30 min. The positioning performance of Scenario C is very similar to that of Scenario B, especially in the horizontal direction, except for the first several minutes.
5. Conclusions
We present a simplification method for RTS data that enables ocean RTPPP using the BeiDou short message service. The performance of the proposed ocean RTPPP with the BeiDou short message service is investigated. The following conclusions can be drawn:
- (1)
The bandwidth of the simplified RTS data is significantly smaller than that required for the original RTS data;
- (2)
The annual communication fee after RTS data simplification is reduced to one quarter of the original, only approximately 315 USD;
- (3)
Compared with the original RTS data, the accuracy of RTPPP with simplified minute-interval RTS data is lower than that of the original PPP due to the lower rate of RTS clock corrections; and
- (4)
After approximately 30 min, the three-dimensional accuracy of RTPPP with the BeiDou short message service can reach the level of approximately 0.3–0.4 m with GPS + GLONASS and the level of 0.1–0.2 m with GPS + GLONASS + Galileo + BeiDou.
It is possible for a user to miss a short message. As the short message is sent with fixed time interval, it is easy for the user to know that a short message missing in time, and the user can inform the service provider through BeiDou short message as BeiDou short message has two-way communication function. In case of missing message, the user can extrapolate current satellite position and clock correction based on previous messages until the next short message is received. The extrapolated current satellite position and clock correction may not be as precise as that derived from missing message, but the impact on the solution is temporary for only about one minute. The problem of missing message can be solved by installing one more BeiDou short message device at the service provider side, which is used specially for resending the missing message.
In recent years, PPP-RTK has been developed to improve the PPP convergence time, and the phase or code biases should be transmitted from the service provider to the user receiver. These biases vary slowly, and the very limited bandwidth is required for transmission of them. Therefore, the Beidou short message can support the concept of PPP-RTK. Although the BeiDou short message has a longer latency, it is possible to resolve ambiguities, but not as fast as the case with no latency of other corrections.