Causal Analysis of Accuracy Obtained Using High-Resolution Global Forest Change Data to Identify Forest Loss in Small Forest Plots
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Reference Data
2.2.2. Global Forest Cover Change Datasets
2.3. Accuracy Assessment
2.4. Inferences on a Structural Relationship
3. Results
3.1. Descriptions of Forest Loss
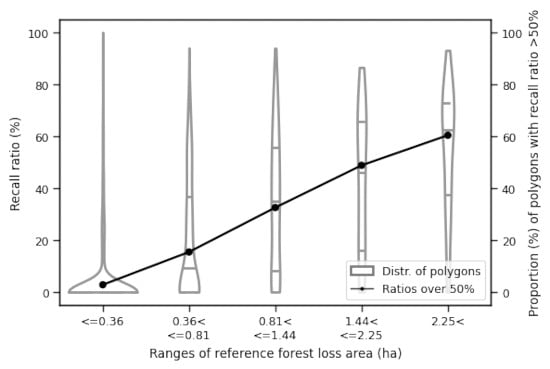
3.2. Recall and Precision Ratios
3.3. Inferences on a Structural Relationship
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chazdon, R.L. Beyond deforestation: Restoring forests and ecosystem services on degraded lands. Science 2008, 320, 1458–1460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fahrig, L. Effects of Habitat Fragmentation on Biodiversity. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 487–515. [Google Scholar] [CrossRef] [Green Version]
- Holl, K.D.; Aide, T.M. When and where to actively restore ecosystems? For. Ecol. Manag. 2011, 261, 1558–1563. [Google Scholar] [CrossRef]
- Harris, N.L.; Goldman, E.; Gabris, C.; Nordling, J.; Minnemeyer, S.; Ansari, S.; Lippmann, M.; Bennett, L.; Raad, M.; Hansen, M.; et al. Using spatial statistics to identify emerging hot spots of forest loss. Environ. Res. Lett. 2017, 12, 024012. [Google Scholar] [CrossRef]
- Alvarenga, L.D.P.; Pôrto, K.C.; de Oliveira, J.R.d.P.M. Habitat loss effects on spatial distribution of non-vascular epiphytes in a Brazilian Atlantic forest. Biodivers. Conserv. 2010, 19, 619–635. [Google Scholar] [CrossRef]
- Lowrance, R.; Todd, R.; Fail, J.; Hendrickson, O.; Leonard, R.; Asmussen, L. Riparian Forests as Nutrient Filters in Agricultural Watersheds. Bioscience 1984, 34, 374–377. [Google Scholar] [CrossRef]
- Gregory, S.V.; Swanson, F.J.; McKee, W.A.; Cummins, K.W. An Ecosystem Perspective of Riparian Zones. Bioscience 1991, 41, 540–551. [Google Scholar] [CrossRef]
- Allan, J.D. Landscapes and Riverscapes: The Influence of Land Use on Stream Ecosystems. Annu. Rev. Ecol. Evol. Syst. 2004, 35, 257–284. [Google Scholar] [CrossRef] [Green Version]
- Blumenthal, S.A.; Chritz, K.L.; Rothman, J.M.; Cerling, T.E. Detecting intraannual dietary variability in wild mountain gorillas by stable isotope analysis of feces. Proc. Natl. Acad. Sci. USA 2012, 109, 21277–21282. [Google Scholar] [CrossRef] [Green Version]
- Zurita, G.A.; Bellocq, M.I. Spatial patterns of bird community similarity: Bird responses to landscape composition and configuration in the Atlantic forest. Landsc. Ecol. 2010, 25, 147–158. [Google Scholar] [CrossRef]
- Yamada, Y. Can a regional-level forest management policy achieve sustainable forest management? For. Policy Econ. 2018, 90, 82–89. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamaura, Y. Decision Support System for Adaptive Regional-Scale Forest Management by Multiple Decision-Makers. Forests 2017, 8, 453. [Google Scholar] [CrossRef] [Green Version]
- Voigt, S.; Kemper, T.; Riedlinger, T.; Kiefl, R.; Scholte, K.; Mehl, H. Satellite image analysis for disaster and crisis-management support. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1520–1528. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B.; Pfaff, E.; Braaten, J.; Nelson, P. Spatial and temporal patterns of forest disturbance and regrowth within the area of the Northwest Forest Plan. Remote Sens. Environ. 2012, 122, 117–133. [Google Scholar] [CrossRef]
- Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Potapov, P.; Hansen, M.C.; Kommareddy, I.; Kommareddy, A.; Turubanova, S.; Pickens, A.; Adusei, B.; Tyukavina, A.; Ying, Q. Landsat Analysis Ready Data for Global Land Cover and Land Cover Change Mapping. Remote Sens. 2020, 12, 426. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; Kommareddy, A.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Brandt, J.S.; Nolte, C.; Agrawal, A. Deforestation and timber production in Congo after implementation of sustainable forest management policy. Land Use Policy 2016, 52, 15–22. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Broadbent, E.N.; Rozendaal, D.M.A.; Bongers, F.; Zambrano, A.M.A.; Aide, T.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.S.; et al. Carbon sequestration potential of second-growth forest regeneration in the Latin American tropics. Sci. Adv. 2016, 2, e1501639. [Google Scholar] [CrossRef] [Green Version]
- Oldekop, J.A.; Sims, K.R.E.; Karna, B.K.; Whittingham, M.J.; Agrawal, A. Reductions in deforestation and poverty from decentralized forest management in Nepal. Nat. Sustain. 2019, 2, 421–428. [Google Scholar] [CrossRef] [Green Version]
- Santika, T.; Wilson, K.A.; Budiharta, S.; Kusworo, A.; Meijaard, E.; Law, E.A.; Friedman, R.; Hutabarat, J.A.; Indrawan, T.P.; St. John, F.A.V.; et al. Heterogeneous impacts of community forestry on forest conservation and poverty alleviation: Evidence from Indonesia. People Nat. 2019, 1, pan3.25. [Google Scholar] [CrossRef]
- Taylor, C.M.; Stutchbury, B.J.M. Effects of breeding versus winter habitat loss and fragmentation on the population dynamics of a migratory songbird. Ecol. Appl. 2016, 26, 424–437. [Google Scholar] [CrossRef] [PubMed]
- Wall, J.; Wittemyer, G.; Klinkenberg, B.; Douglas-Hamilton, I. Novel opportunities for wildlife conservation and research with real-time monitoring. Ecol. Appl. 2014, 24, 593–601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoffels, J.; Hill, J.; Sachtleber, T.; Mader, S.; Buddenbaum, H.; Stern, O.; Langshausen, J.; Dietz, J.; Ontrup, G. Satellite-Based Derivation of High-Resolution Forest Information Layers for Operational Forest Management. Forests 2015, 6, 1982–2013. [Google Scholar] [CrossRef]
- Arjasakusuma, S.; Kamal, M.; Hafizt, M.; Forestriko, H.F. Local-scale accuracy assessment of vegetation cover change maps derived from Global Forest Change data, ClasLite, and supervised classifications: Case study at part of Riau Province, Indonesia. Appl. Geomat. 2018, 10, 205–217. [Google Scholar] [CrossRef]
- Milodowski, D.T.; Mitchard, E.T.A.; Williams, M. Forest loss maps from regional satellite monitoring systematically underestimate deforestation in two rapidly changing parts of the Amazon. Environ. Res. Lett. 2017, 12, 094003. [Google Scholar] [CrossRef] [Green Version]
- Stehman, S.V.; Wickham, J.D. Pixels, blocks of pixels, and polygons: Choosing a spatial unit for thematic accuracy assessment. Remote Sens. Environ. 2011, 115, 3044–3055. [Google Scholar] [CrossRef]
- Linke, J.; Fortin, M.-J.; Courtenay, S.; Cormier, R. High-resolution global maps of 21st-century annual forest loss: Independent accuracy assessment and application in a temperate forest region of Atlantic Canada. Remote Sens. Environ. 2017, 188, 164–176. [Google Scholar] [CrossRef]
- Shimizu, S.; Hoyer, P.O.; Hyvärinen, A.; Kerminen, A. A linear non-gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 2006, 7, 2003–2030. [Google Scholar]
- Shimizu, S. Lingam: Non-Gaussian Methods for Estimating Causal Structures. Behaviormetrika 2014, 41, 65–98. [Google Scholar] [CrossRef]
- Lanka, S.; Shimizu, S.; Inazumi, T.; Sogawa, Y.; Hyvärinen, A.; Kawahara, Y.; Washio, T.; Hoyer, P.O.; Bollen, K. DirectLiNGAM: A direct method for learning a linear non-Gaussian structural equation model. J. Mach. Learn. Res. 2011, 12, 1225–1248. [Google Scholar]
- Sharma, R.; Hara, K.; Tateishi, R. High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach. Land 2017, 6, 50. [Google Scholar] [CrossRef] [Green Version]
- Ota, T.; Mizoue, N.; Yoshida, S. Influence of using texture information in remote sensed data on the accuracy of forest type classification at different levels of spatial resolution. J. For. Res. 2011, 16, 432–437. [Google Scholar] [CrossRef]
- Tanaka, S.; Takahashi, T.; Saito, H.; Awaya, Y.; Iehara, T.; Matsumoto, M.; Sakai, T. Simple Method for Land-Cover Mapping by Combining Multi-Temporal Landsat ETM+ Images and Systematically Sampled Ground Truth Data: A Case Study in Japan. J. For. Plan. 2012, 18, 77–85. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Strahler, A.H.; Boschetti, L.; Foody, G.M.; Friedl, M.A.; Hansen, M.C.; Herold, M.; Mayaux, P.; Morisette, J.T.; Stehman, S.V.; Woodcock, C.E. Global Land Cover Validation: Recommendations for Evaluation and Accuracy Assessment of Global land Cover Maps; EUR 22156 EN–DG; Office for Official Publications of the European Communities: Luxemburg, 2006. [Google Scholar]
- Corbane, C.; Carrion, D.; Broglia, M. Development and implementation of a validation protocol for crisis maps: Reliability and consistency assessment of burnt area maps. Int. J. Digit. Earth 2011, 4, 8–24. [Google Scholar] [CrossRef]
- Baumann, M.; Ozdogan, M.; Wolter, P.T.; Krylov, A.; Vladimirova, N.; Radeloff, V.C. Landsat remote sensing of forest windfall disturbance. Remote Sens. Environ. 2014, 143, 171–179. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. MODIS time-series imagery for forest disturbance detection and quantification of patch size effects. Remote Sens. Environ. 2005, 99, 462–470. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăgu, L. Random forest in remote sensing: A review of applications and future directions. Isprs J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Corcoran, J.; Knight, J.; Gallant, A. Influence of Multi-Source and Multi-Temporal Remotely Sensed and Ancillary Data on the Accuracy of Random Forest Classification of Wetlands in Northern Minnesota. Remote Sens. 2013, 5, 3212–3238. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Vibrans, A.C.; Sannier, C.; Næsset, E.; Hansen, M.C.; Walters, B.F.; Lingner, D.V. Methods for evaluating the utilities of local and global maps for increasing the precision of estimates of subtropical forest area. Can. J. For. Res. 2016, 46, 924–932. [Google Scholar] [CrossRef] [Green Version]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, Y.; Ohkubo, T.; Shimizu, K. Causal Analysis of Accuracy Obtained Using High-Resolution Global Forest Change Data to Identify Forest Loss in Small Forest Plots. Remote Sens. 2020, 12, 2489. https://doi.org/10.3390/rs12152489
Yamada Y, Ohkubo T, Shimizu K. Causal Analysis of Accuracy Obtained Using High-Resolution Global Forest Change Data to Identify Forest Loss in Small Forest Plots. Remote Sensing. 2020; 12(15):2489. https://doi.org/10.3390/rs12152489
Chicago/Turabian StyleYamada, Yusuke, Toshihiro Ohkubo, and Katsuto Shimizu. 2020. "Causal Analysis of Accuracy Obtained Using High-Resolution Global Forest Change Data to Identify Forest Loss in Small Forest Plots" Remote Sensing 12, no. 15: 2489. https://doi.org/10.3390/rs12152489