Assessing Forest/Non-Forest Separability Using Sentinel-1 C-Band Synthetic Aperture Radar

Abstract

Synthetic Aperture Radar has a unique potential for continuous forest mapping as it is not affected by cloud cover. While longer wavelengths, such as L-band, are commonly used for forest applications, in this paper we assess the aptitude of C-band Sentinel-1 data for this purpose, for which there is much interest due to its high temporal resolution (five days) and “free, full, and open” data policy. We tested its ability to distinguish forest from non-forest in six study sites, located in Alaska, Colombia, Finland, Florida, Indonesia, and the UK. Using the time series for a full year significantly increases the classification accuracy compared to a single scene (a mean of $85\%$ compared to $77\%$ across the study sites for the best classifier). Our results show that we can further improve the mean accuracy to $87\%$ when only considering the annual mean and standard deviation of co-polarized (VV) and cross-polarized (VH) backscatter. In this case, separation accuracies of up to $93\%$ (in Finland) are possible, though in the worst case (Alaska), the highest possible accuracy using these variables was $80\%$. The best overall performance was observed when using a Support Vector Machine classifier, outperforming random forest, k-Nearest-Neighbors, and Quadratic Discriminant Analysis. We further show that the small information content we found in the phase data is an artifact of terrain slope orientation and has a negligible impact on classifier performance. We conclude that for the purposes of forest mapping the smaller file size and easier to process GRD products are sufficient, unless the SLC products are used to compute the temporal coherence which was not tested in this study.

1. Introduction

Forests play a major role in our fragile ecosystem. When planted they act as a carbon sink, but when cut down or burnt they act as a carbon source. In light of the universal awareness of the reality and consequences of global climate change, significant international efforts are being undertaken to preserve forests and reforest areas that have experienced large scale deforestation. Examples of these undertakings include the Bonn Challenge, the New York Declaration on Forests, and the Paris Agreement. The first step for prevention of deforestation must be accurate monitoring and mapping of affected areas with as little delay as possible. REDD+ (which stands for “Reducing emissions from deforestation and forest degradation and the role of conservation, sustainable management of forests and enhancement of forest carbon stocks in developing countries”) was adopted by the United Nations Framework Convention on Climate Change (UNFCCC) to reverse deforestation and forest degradation, and hence their contribution to climate change. It requires developing countries to implement Measurement, Reporting and Verification (MRV) systems as part of a National Forest Monitoring System (NFMS). For REDD+ to succeed it is vital that monitoring systems are accurate, scalable, trusted, and comparable. The International Panel on Climate Change (IPCC) defines quality standards for these measurement systems [1], and is specific that remote sensing should be used, but it not specific about the precise technologies and methods that should be used. Similarly, all countries require good maps of their changes in forest areas as part of their reporting on changes in all carbon pools, related to their territory-wide reporting to the UNFCCC on carbon sinks and sources and how these compare to their commitments under the Paris Agreement.

Due to large-scale coverage and regular revisit times, satellite remote sensing is the only viable candidate for large-scale forest cover monitoring systems. Frequent revisits are necessary not only for precise dating of deforestation events, but also because of rapid regrowth, which may make clearings indistinguishable from intact forest within less than two years [2]. Data available from satellite sensors encompass optical imagery (including derivatives such as the Normalized Difference Vegetation Index (NDVI)), Synthetic Aperture Radar (SAR), and LiDAR data, each with different advantages and drawbacks.

Many authors have suggested the use of satellite data for mapping forest area and forest properties for such national monitoring purposes. For example, McRoberts and Tomppo [3] elaborate on the potential of remote sensing data for national forest inventories. They emphasize the low cost of measuring areal quantities such as forest area or volume compared to conventional field sampling, placing a particular focus on k-Nearest-Neighbors (kNN) methods. However, they note limitations in quantifying the uncertainty of forest inventories produced in this way.

Reiche et al. [4] published a commentary in which they note that the majority of REDD+ member countries in the tropics are using Landsat, but no SAR data, for their respective national monitoring systems. That is even though most of these countries are subject to persistent cloud cover throughout the year, resulting in large data gaps for any optical sensor; a problem which demonstrably does not affect SAR sensors at C-band or longer [5]. Scientists have already successfully demonstrated the capabilities of SAR for deforestation monitoring [6,7,8,9]. Reiche et al. attribute this absence of SAR data in national monitoring systems to the comparative ease of processing optical data, the larger historic archives, and the limited availability of free SAR data and SAR processing tools (prior to the launch of Sentinel-1A almost all satellite SAR data were available only on commercial terms). As most global forest maps have been derived from optical imagery—requiring a mosaic over multiple time steps for a cloud-free composite—they have limited temporal repeatability. Two notable exceptions of repeated global forest maps are the maps by Hansen [10] and the Food and Agriculture Organization of the United Nations (FAO) [11], though in practice it is likely that some deforestation is missed or reported late due to cloud cover in these studies too. Moreover, while the Hansen [10] map is continuous cover, the FAO map only samples select distributed boxes [10], meaning it provides useful regional statistics but cannot be used to locate actual deforestation events.

Detecting changes in the forest cover using SAR data requires a statistically significant difference in the pixel measurement of some radar parameter (e.g., backscatter, coherence, interferometric height, or texture) that can be reliably used to distinguish forested and non-forested area. This paper assesses empirically how well forested areas can be distinguished using dual-polarimetric C-band backscatter data, the easiest SAR data to use. At its core this is a classification problem as we are trying to assign a class (forest or non-forest) to each pixel given a series of measurements. As such we begin by discussing a number of papers that have attempted to classify forest and non-forest based on SAR data.

Previous attempts at generating forest maps from SAR data include a global forest map produced from ALOS PALSAR data (L-band SAR) [12]. Shimada et al. note that most existing forest cover maps have either been restricted to less-than-global coverage due to focus on specific forest types or geographic regions or been generated for a single time. While non-forest areas typically yield lower backscatter than forest, deforestation detection is hindered by an initial increase in backscatter following forest clearance because of remaining debris as well as the potential impact of rainfall falling on bare soil. The detection potential was thus found to be greatest once all debris was removed and the area had been converted into agriculture, when a significantly lower backscatter than the original forest cover would be expected. Training and validation data for their forest/non-forest maps were derived from Google Earth imagery, the Degree Confluence Project (DCP), and the FAO Global Forest Resources Assessment (FRA) [11]. The authors used a forest definition of ≥$10\%$ woody vegetation cover throughout. Analysis of forest/non-forest histograms showed that forests followed a normal distribution in ${\gamma }_0$ with the co-polarized backscatter always being larger than the cross-polarized component. The authors found that forest had larger backscatter values but lower variability compared to non-forest areas. They used a very simple manually crafted decision tree as classifier, relying on region-specific HV backscatter thresholds extracted from forest/non-forest histograms. The total forest cover obtained this way was ~$5\%$ less than the FRA and Hansen results. Validation showed an accuracy of $91.25\%$ compared with Google Earth imagery, $94.81\%$ compared with the FRA, and $84.86\%$ compared with the DCP. Discrepancies were attributed to different image acquisition dates, cloud cover impacting the optically-derived maps, confusion of woody vegetation with herbaceous vegetation in the optically-derived maps, as well as the SAR data potentially having too coarse a resolution to detect small patches of low canopy cover forest in a landscape.

In another study, Quegan et al. [13] assess the potential of time series of C-band SAR images for forest biomass mapping. They note that C-band SAR has been less popular for forestry applications because backscatter at this relatively short wavelength saturates at biomass densities of 30–50 Mg ha${}^{-1}$, whereas for P-band, SAR saturation only happens at around 150–200 Mg ha${}^{-1}$, making it capable of assessing variations in a larger range of forest types. Saturation thresholds vary across species due to differences in their dielectric properties, as well as leaf size and orientation. This makes C-band especially ill-suited for detecting forest degradation, i.e., a reduction of biomass while maintaining forest status, as in many parts of the world forests can exceed a biomass density of 500 Mg ha${}^{-1}$. However, for the question at hand here—forest/non-forest discrimination—such a low saturation point should be sufficient.

The main incentive for using multi-temporal SAR data, as opposed to individual time steps alone, is that at individual time steps the backscatter can often look identical for forest and non-forest vegetation types, due to radar speckle and a lack of contrast during some seasons or after rain events. However, when combining multiple scenes the impact of speckle reduces greatly, and the discrimination ability may increase because scenes from times of year with a high contrast between the two classes will be included [13]. Further, Quegan et al. note a relationship between forest stand age and backscatter: the attenuation of the soil contribution increases with growing age, resulting in a reduction of the overall backscatter. Following the initial decrease in backscatter for a growing forest, there is a slower increase leading up to the eventual saturation at the biomass limit. Because denser forest exposes less of the soil, the backscatter is less dependent on soil moisture and roughness and hence was found to exhibit less temporal variability than sparser vegetation or bare soil. Other stable land cover includes grassland and urban areas, but these are stable at lower and higher backscatter values, respectively. As most non-forest areas exhibit greatly varying backscatter values over the year, they occasionally look similar to forest. For these reasons, the authors propose temporal backscatter stability as the most promising feature for forest mapping using C-band SAR data. Quegan et al. identified two types of land cover that would yield classification errors: non-forest areas of low backscatter variability (e.g., built-up areas or grassland), and forest areas of high backscatter variability. The classification accuracies for three test sites in the UK (11 images), Finland (15 images), and Poland (two images) were $90.7\%$, $94.1\%$, and $77.4\%$, respectively. The authors conclude that temporal backscatter stability is in fact the best predictor for forest cover derived from C-band SAR for forest of more than 30 Mg ha${}^{-1}$.

In this paper, we build on these findings by analyzing study sites from a larger range of forest types, using longer time series and the full dual-polarimetric information available in Sentinel-1 Single Look Complex (SLC) data. As opposed to Ground Range Detected (GRD) data, SLC products contain phase information in addition to the backscatter amplitude, which we therefore test to see if it has any useful information content. Given the dual-polarimetric nature of Sentinel-1 data, the only contribution of the phase after preprocessing is the cross-polarized phase difference (detailed in Section 2.2). In contrast to the co-polarized phase difference, which is not available for dual-polarized data, the cross-polarized phase difference is generally regarded as lacking physical importance ([14], p. 297). If this is in fact the case and there is little information in the phase difference alone, then the simpler GRD data should be used due to its simpler processing and smaller file sizes (typically $<1$ GB for GRD and $>4$ GB for SLC), unless more complex features derived from the phase are to be used, for example coherence or interferometric height estimation. Both of these are beyond the scope of this study given our focus on computationally simple and easy to scale methods.

2. Methods

2.1. Study Sites

We have selected six study sites across a broad range of forest biomes: Alaska, Florida, Finland, UK, Indonesia, and Colombia. The locations of the study sites are shown in Figure 1 and in more detail in Figure 2. The reference maps for each study site were constructed from the GlobalForestWatch data set [10] as well as a country-specific land cover map for the corresponding year. It is assumed that both data sets contain inaccuracies for different reasons: The Hansen data set is derived from a Machine Learning approach and hence may not take into account local expert knowledge about differences between biomes. The country specific landcover maps, on the other hand, are released less frequently and only provide a snapshot at a certain time. They, therefore, do not capture land cover change during the study period. For these reasons, only pixels where both data sets agree were used as reference throughout the study.

The UK site is an area in the Kielder Forest Park for the year 2015 and is largely covered by coniferous woodland, grassland, and bog. Reference data for this site were taken from the 2015 land cover map by the UK Centre for Ecology and Hydrology (https://www.ceh.ac.uk/services/land-cover-map-2015).

The site in Florida is part of the Ocala National Forest for the year 2017. This site exhibits diverse land cover including (in order of prevalence) sand pine scrub, coniferous plantations, lacustrine, pasture, sandhills, marshes, and swamps, as well as some urban areas (including transport infrastructure) and water bodies. The land cover reference is taken from the Florida Cooperative Land Cover Map 2017 (https://myfwc.com/research/gis/applications/articles/cooperative-land-cover/).

The Alaskan site is located around Lake Louise for the year 2017 and is mostly covered by spruce, as well as some (low) shrub and freshwater bodies. The corresponding reference data set is the Alaska Vegetation and Wetland Composite 2017 (https://accscatalog.uaa.alaska.edu/dataset/alaska-vegetation-and-wetland-composite).

The Indonesian site is the Indragiri Hilir Regency for the year 2017. The most common land cover classes in this area are shrub-mixed dryland farm, swamp shrub and swamp forest, bare land, various plantations, and mangrove forest. A 2017 land cover map by the Indonesian Ministry of Environment and Forestry is used for reference (http://data.globalforestwatch.org/datasets/land-cover-indonesia).

The Colombian site is located near Solano, Caquetá for the year 2018 and is covered by tall dense forest, rivers, and pasture. The reference map for this site is a national forest inventory data set consolidated by the Colombian Institute of Hydrology, Meteorology and Environmental Studies (IDEAM) (http://smbyc.ideam.gov.co/).

For Finland, a site just north of Lake Oulujärvi was selected for the year 2018. The majority of this site is covered by coniferous forest, with the remaining area made up of water bodies, transitional woodland-shrub, mixed forest, and peat bogs. Reference data were derived from the CORINE Land Cover map 2018 (https://land.copernicus.eu/pan-european/corine-land-cover/clc2018).

Figure 3 shows the Hansen maps as well as country specific reference data for each of the sites. The third row indicates the areas of agreement between the two. The last row shows a sample Sentinel-1 image for the beginning of the respective study period. Note that the Colombian reference data set is the only one that provides a deforestation class, which is why the image labeled “country reference” shows a few red patches for Colombia.

2.2. Data Processing

All data analyzed in this study are Sentinel-1 SLC products. The data were preprocessed with ESA SNAP by applying the following processing steps.

• Apply Orbit File All products were geocoded using Precise Orbit Determination (POD) files with polynomial degree 3.
• Radiometric Calibration The products were radiometrically calibrated to ${\sigma }_0$, preserving complex output [16].
• Debursting In this step, the individual bursts within each subswath were assembled.
• Polarimetric Speckle Filter For speckle reduction, a Refined Lee Filter with window size $7\times 7$ was applied [14,17].
• Terrain Correction The products were processed to $14.07$ m resolution using Range Doppler Terrain Correction with bilinear resampling [18]. This is the native azimuth resolution of Sentinel-1 in Interferometric Wide swath (IW) mode and the resulting resolution of square pixels without multilooking. The terrain correction was done using the Shuttle Radar Topography Mission (SRTM) 1 arc-second Digital Elevation Model (DEM). As the Alaskan site is north of ${60}^{\circ }$N it is not covered by the SRTM and a separate DEM was used, in this case the Alaska 2 Arc-second Digital Elevation Model provided by the United States Geological Survey (USGS). The products were projected to the following map projections: Alaska: EPSG:3338, Colombia: EPSG:3116, Finland: EPSG:3035, Florida: EPSG:3086, Indonesia: EPSG:4326, UK: EPSG:27700.

Because we are working with time series data there is scope for temporal smoothing. Multilooking was therefore not deemed necessary, allowing us to preserve spatial resolution. While the unprocessed SLC data can be represented by a complex scattering vector $\mathit{s}$ containing the amplitude and phase of the co-polarized (VV) and cross-polarized (VH) backscatter

$$\mathit{s}=\left[\begin{array}{c}{S}_{VV}\\ S_{VH}\end{array}\right]=\left[\begin{array}{c}{A}_{VV}{e}^{i{\phi }_{VV}}\\ A_{VH}{e}^{i{\phi }_{VH}}\end{array}\right],$$

(1)

we used the C2 representation of the data, which is the standard output of the preprocessing chain and the basis for any polarimetric applications:

$$C=\mathit{s}{\mathit{s}}^H=\left[\begin{array}{cc}{A}_{VV}^2& A_{VV}{A}_{VH}{e}^{i\Delta \phi }\\ A_{VV}{A}_{VH}{e}^{-i\Delta \phi }& A_{VH}^2\end{array}\right]$$

(2)

where ${(·)}^H$ denotes the Hermitian transpose: ${\left(A^H\right)}_{ij}={\left(A_{ji}\right)}^{*}$, and $\Delta \phi ={\phi }_{VV}-{\phi }_{VH}$.

As a consequence of this representation, the absolute (random) phase is no longer available. As the dependency on the absolute phase has been removed, we cannot reconstruct the scattering vector from the covariance matrix. This leaves three independent variables: $C_{11}$ (the intensity in VV), $C_{22}$ (the intensity in VH), as well as $\Delta \phi$ (the VV-VH phase difference). In the case of fully polarimetric data, the covariance matrix would contain additional terms that include the co-polarized phase difference (VV-HH). While the co-polarized phase difference is related to the number of bounces, and as such is often useful for land cover classification, the cross-polarized phase difference is generally regarded as noise [14]. For the dual-polarized Sentinel-1 data, the HH component and thus the co-polarized phase difference is not available. In this study we compare the ability of these three available variables, individually and together, to distinguish between forest and non-forest. As part of this analysis we test the assertion that the cross-polarized phase difference contains no useful information.

Due to the way the satellites orbit the Earth, roughly half of the data are acquired while the satellite is moving from south to north (this is called ascending orbit) and the other half when it is moving from north to south (descending orbit). This results in different look angles which have a particular impact on the appearance of terrain with topography. This effect can be partially accounted for using a processing step called terrain flattening. However, we do not apply this step as it does not preserve the phase information. Instead, throughout this study, we treat the measurements in both orbits as separate variables. Aggregating over them would artificially increase the variability over pixels affected by topography which would reduce the separation between forest and non-forest distributions.

2.3. Distribution Separability

To assess the separability of forest and non-forest pixels with Sentinel-1 data, we first looked at the distribution of backscatter values within each class. In order to quantify the aptitude of each feature for separating between forest and non-forest, we can compute the Overlap Coefficient (OVL) of the forest and non-forest distributions for each variable. Given two PDF $f\left(x\right)$ and $g\left(x\right)$, the OVL is defined as

$$\mathrm{OVL}(f,g)={\int }_{{\mathbb{R}}^n}min\left(f\left(x\right),g\left(x\right)\right)dx$$

(3)

which can be approximated for the discrete case as

$$\mathrm{OVL}(f,g)=\sum _{i=0}^{N}min\left(f_i,g_i\right)$$

(4)

where $f_i$ and $g_i$ are the values of $f\left(x\right)$ and $g\left(x\right)$ known only at discrete positions $x_i$ for $i=0,\dots ,N$ normalized such that ${\sum }_i{f}_i={\sum }_i{g}_i=1$. An OVL of 1 indicates equality of the distribution, whereas an OVL of 0 means zero overlap and therefore perfect separability.

To see how the theoretical separability holds up in practice, a number of classifiers were trained on the labeled data and their results and scores are compared. The training data comprised a random selection of 10,000 data points per class to discriminate between forest and non-forest. The points were selected at random out of those pixels where both reference data sets are in agreement. All validation was equally performed with respect to the areas of agreement between both references only; areas of disagreement were excluded for both training and validation. There are three available variables: $C_{11}$, $C_{22}$, and $\Delta \phi$. From these variables five different feature sets were generated:

• Each variable measured once in ascending orbit and once in descending orbit (six features in total).
• Each variable measured at every time step (3 × [number of time steps] features in total).
• The mean and standard deviation of each variable, split between ascending and descending orbit

  (a)

  for all three variables (six features in total).

  (b)

  for $C_{11}$ and $C_{22}$ only (four features in total).

  (c)

  for $\Delta \phi$ only (two features in total).

The classifiers tested were k-Nearest-Neighbors (kNN), random forest [19], Quadratic Discriminant Analysis (QDA), and Support Vector Machine (SVM) [20] to cover the most common classifiers in the remote sensing community. QDA is not generally used on a pixel-by-pixel basis as a classifier, but was added as a simple baseline model for comparison. Prior to classification, the features were standardized by subtracting the mean and scaling to unit variance. The scaling is of particular importance for the kNN and to some extent the SVM classifier.

Each classification outcome was rated using the balanced accuracy score as well as Cohen’s Kappa score. The balanced accuracy score is an adaptation of the standard accuracy score which accounts for class imbalances, i.e., the case where the available classes have different numbers of members [21]. It is defined as

$$\mathrm{BACC}=\frac{1}{2}\left(\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}+\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FN}}\right)$$

(5)

with TP, FP, TN, and FN being the number of true positive, false positive, true negative, and false negative observations, respectively.

Cohen’s Kappa is a measure of how much better a classifier performs compared with random guessing [22]. It is defined as

$$\kappa =\frac{p_0-p_e}{1-p_e}$$

(6)

where $p_0$ is the standard accuracy and $p_e$ is the probability of agreement by chance which can be computed as

$$p_e=\frac{1}{N^2}\sum _k{n}_k{n}_k^{\prime }$$

(7)

for N observations and k classes, with $n_k$ being the true number of members of class k and $n_k^{\prime }$ the predicted number of members of class k. A score of 0 indicates no improvement over random guessing. Just like the standard and balanced accuracy scores, the maximum score of 1 is reserved for perfect agreement. The Kappa score allows for negative scores, indicating performance worse than random guessing.

3. Results

3.1. Data Distribution

Figure 4 shows the distribution of the annual mean and standard deviation of backscatter intensity in VV and VH as well as the phase difference $\Delta \phi$ split between ascending and descending orbits for each of the study sites, per class (forest and non-forest). We chose to show the distributions of temporal mean and standard deviation rather than the unaggregated data to yield more pronounced differences between sites and land cover classes as well as mitigate the underlying variability in the backscatter values either due to noise, seasonality, or other effects.

As a general observation, both VV and VH backscatter are larger for forested areas than for non-forested areas, on average. However, the individual distributions appear very different across different study sites. For Alaska, the distributions are nearly identical, whereas for Finland and the UK, the distributions separate very well. An interesting observation can be made about the phase difference. Overall, it seems that there is essentially no information contained in the phase difference when it comes to distinguishing forest from non-forest. The exception is the UK study site in descending orbit, and to some extent Finland, where there is a clear shift between the distributions for the two classes. Less apparent differences are also visible for Alaska and Colombia. Contrary to what has been found by Quegan et al. [13], the histograms of the temporal standard deviation of VV and VH backscatter seem to suggest that forested areas have a larger rather than smaller temporal variability compared to non-forested areas. This is in particular true for regions with pronounced seasonality such as the UK, Alaska, and also Florida, but also holds true to a lesser extent for Colombia and Indonesia. The standard deviation of the phase difference shows no difference between the two classes.

In addition to the univariate distributions, Figure 5 shows two-dimensional Kernel Density Estimation (KDE) plots for pairs of variables. Each subfigure shows the distribution of $C_{11}$ and $C_{22}$ split between forest (in orange) and non-forest (in blue). The first two rows show the annual mean ($\mu$), whereas the last two rows show the standard deviation ($\sigma$), each for ascending and descending orbits. The shade represents the observation density, with darker shades indicating higher density.

These plots highlight the separation of forest and non-forest in a higher-dimensional feature space. Just like for the one-dimensional plots, it is clear that some sites such as Finland separate very well, whereas other sites like Colombia have more ambiguous distributions. Overall, there is a high correlation between $C_{11}$ and $C_{22}$ both in mean and standard deviation. This correlation is apparent from the strongly elongated distributions, especially for the mean in the UK, Finland, and Colombia. The distributions of the standard deviation show a bigger spread and separate less well, in general. In sites with very little seasonality (Colombia and Indonesia), the standard deviation appears very similar between forest and non-forest, indicating that the difference in backscatter variability is largely due to seasonal variations.

There were very few images available for the ascending orbit and the chosen year over the Florida site, so the two subfigures depicting mean and standard deviation for this orbit direction may be misleading and should be ignored.

Figure 6 depicts a more detailed analysis of the bivariate data distributions for the example of the Finnish site. Each subfigure marks one combination of two of the eight features (excluding the phase), where the diagonal subfigures show the corresponding one-dimensional distributions already seen in Figure 4. This plot unveils a strong correlation between all of the variables and as such indicates a possibility of dimensionality reduction. It is also apparent that (at least for this particular site), $C_{11}$ tends to be a slightly better predictor of forest/non-forest than $C_{22}$, and similarly the mean appears more informative than the standard deviation. Non-forest pixels exhibit a stronger correlation between variables, especially between the two orbit directions.

In order to quantify the separability of forest and non-forest for each site,

Table 1. This table shows the overlap coefficients between the forest and non-forest distributions for a variety of different variables including $C_{11}$ (VV backscatter), $C_{22}$ (VH backscatter), and the phase difference $\Delta \phi$, each for ascending and descending orbit, as well as combinations thereof. The three horizontal sections show the results for a single image ($t=0$), as well as the mean ($\mu$) and the standard deviation ($\sigma$). A value close to 0 means low overlap and high separability, whereas a value close to 1 means large overlap and low separability. The table is color coded on a linear scale; with green, yellow, and red corresponding to overlap coefficients of 0, $0.5$, and 1, respectively.

lists the overlap coefficients for each variable and site. The overlaps were derived for the temporal mean and standard deviation, as well as an individual image ($t=0$). In addition, a multidimensional overlap coefficient was computed for each of the groups of features ($t=0$, mean, and standard deviation) and is labeled as “all” in the table. The rows labeled “all (no $\Delta \phi$)” consider only the intensity of VV and VH backscatter, but not the phase. The overlap coefficient for combined mean and standard deviation was not computed due to computational limitations, as a 12-dimensional histogram of even as little as 20 bins per dimension would require around 100 Petabytes of memory.

The values show what was already apparent from the histograms: the separability of forest and non-forest varies to a large extent between different study sites, with the UK and Finnish sites appearing generally the most separable and the Alaskan site the least separable. Moreover, the phase difference shows upwards of $90\%$ overlap in almost all cases except for the UK, indicating little value for telling forested from non-forested areas. For the $t=0$ case, including the phase does slightly reduce the overlap but for the temporal mean and standard deviation no information appears to be gained from the phase for any of the sites. This is highlighted by similar overlap coefficients for all and all (no $\Delta \phi$).

3.2. Classifier Comparison

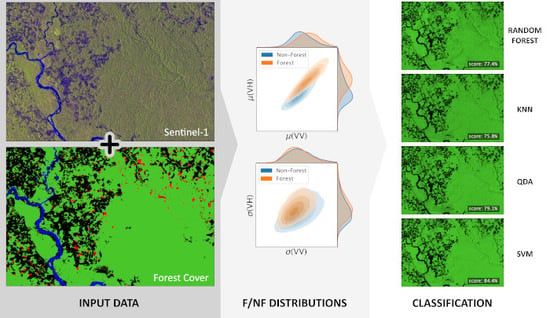
Next, we demonstrate the performance of classification algorithms based on the theoretical class separability. Figure 7 shows the classification outcomes when using the annual mean and standard deviation of all available variables as features (corresponding to case 3(a) in the list of feature sets in Section 2.3). The prediction images are given alongside the reference data, with forest pixels shown in green and non-forest pixels in black.

Random forest and SVM classifiers are favorites among the remote sensing community and indeed they appear to give the best scores overall. The kNN results in particular appear very noisy; this is because kNN is not very robust in the presence of noisy variables like the phase and in fact the results of the kNN classification improve drastically when removing the phase based features.

Table 2. This table summarizes the balanced accuracy scores from Figure 7 and equivalent outcomes from using a single time step or the entire time series. The variables used for classification are VV and VH backscatter as well as the VV-VH phase difference ($\Delta \phi$). The rows differ in whether these variables were considered for a single time step ($t=0$), the entire time series, or the mean and standard deviation ($\mu$ and $\sigma$) of the time series, and whether or not they include the phase difference. The table is color coded on a linear scale; with green, yellow, and red corresponding to accuracy scores of $100\%$, $75\%$, and $50\%$, respectively.

collates the balanced accuracy scores for each of the aforementioned feature sets.

For classification using a single time step, the balanced scores are generally around $65\%$ to $80\%$, varying strongly between sites. For Indonesia, the classification scores are less than $65\%$, whereas in Finland, scores of more than $90\%$ are observed even for a single time step. For most sites, the scores improve drastically when considering the entire time series. That is to be expected as is mitigates variations in backscatter not attributable to land cover, such as topography, seasonality, and random fluctuations. In general, the scores improve to around $75\%$ to $90\%$ when using the full time series as feature vector. There is a further small increase in accuracy when only the mean and standard deviation are used as features. For Florida, some of the scores decrease when the full time series data are used for classification, which could indicate that the reference land cover was collected in the beginning of the year and has subsequently changed, such that the data at $t=0$ may be the best predictor for land cover. In the cases presented here, SVM generally performs best, whereas kNN yields the lowest scores. The exception is Finland, where there is sufficient class separation for the QDA to outperform other classifiers due to its robustness to noise.

Figure 8a shows the balanced accuracy scores for each of the classifiers and study sites. Similarly, Figure 8b shows Cohen’s Kappa scores instead. The three different cases presented here correspond to the last three sections of Table 2.

These plots serve to highlight the poor performance of phase-based features for classifying forest and non-forest: When training the classifiers using the phase exclusively, the balanced accuracy scores are barely above $50\%$ indicating no significant improvement over random guessing. This shows even more clearly in the Kappa scores which are all near $0\%$, with the exception of the UK and Finland where we have already seen a slight separation between forest and non-forest in Figure 4. Even for these two sites, however, there is no improvement when including the phase in addition to $C_{11}$ and $C_{22}$. We can finally conclude that the phase alone contains almost no useful information for discriminating between forest and non-forest as was already apparent from the high overlap coefficient between the phase distributions of the two classes. In most cases, the classification results are equally good or even better when excluding the phase. This is true in particular for kNN, which does not work well in the presence of noise variables (the phase in this case). Only for the simplest model (QDA), and to a lesser extent for random forest and SVM, does the presence of the phase not affect the classifier performance. Overall, including phase information in the feature set may in fact reduce classifier performance.

3.3. UK Phase Anomaly

We now analyze the correlation between phase difference and forest cover that was apparent in the UK study site but not—or to a much lower degree—in the other sites.

Figure 9 shows the spatial distribution of the VV-VH phase difference. There is a clear spatial structure both for the ascending and descending orbit. The pattern suggests a relation between the phase and the topography, specifically the slope orientation of the terrain.

To verify this suspected relation, we computed the correlation between the phase difference as well as various terrain parameters. The platform heading of the satellite is about $-{16}^{\circ }$ for the ascending orbit and $-{163}^{\circ }$ for the descending orbit, relative to north. Figure 10 shows hillshade images generated from a DEM of the study site. The hillshade illumination intensity I is computed from the DEM as a function of the aspect of the terrain slope $\alpha$ and the azimuth angle $\theta$ as

$$I_{\theta }\propto cos\left(\pi -\theta -\alpha \right).$$

(8)

To illustrate the dependence of the observed correlation effect on the azimuth angle, the figure shows one hillshade image for $-{16}^{\circ }$, i.e., the heading angle in the ascending orbit, and another for ${74}^{\circ }$, i.e., for an illumination source displaced by ${90}^{\circ }$. The histograms to the right of the images show the corresponding distributions of the simulated illumination intensity for forest and non-forest for both angles.

The histograms clearly show that there is a correlation effect between forest cover and terrain slope orientation that disappears when the illumination source is rotated by ${90}^{\circ }$. Figure 11 quantifies this correlation and its dependence on the azimuth angle: Figure 11a shows the correlation of the mean VV-VH phase difference in ascending and descending orbit as well as the forest cover with the hillshade image for different azimuth angles $\theta$. The dashed and dotted lines indicate the heading angle and perpendicular directions, respectively. For the ascending orbit, these lines correspond to the special cases shown in Figure 10. Figure 11b shows the correlation with additional terrain parameters such as elevation and slope in matrix form. There is a mild correlation between the hillshade illumination at $-{16}^{\circ }$ and the phase difference of $-0.23$ in the descending orbit, and $0.18$ in the ascending orbit. Combined with the observed relation between forest cover and the hillshade illumination (correlation of $0.1$), this is sufficient to explain the small correlation between forest cover and phase difference in descending orbit of $0.07$. Albeit small, this correlation leads to the shift between forest and non-forest distributions shown in Figure 9a.

As the phase is a geometric phenomenon it is expected to exhibit a dependence on the ground geometry, i.e., the topography. The correlation between hillshade and forest cover is surprising, however. One possible explanation is the difference in solar exposure of north-facing vs. south-facing slopes which could drive differences in vegetation growth. However, this explanation would lead to expect maximum correlation at an azimuth angle of exactly $0^{\circ }$. Instead, the observed correlation appears to correspond to the actual heading angle of the satellite. Other site-specific differences between north- and south-facing slopes are possible. Another explanation could be an intrinsic bias in the reference data. This is unlikely, though, as all reference data have been derived exclusively from optical data and are thus not affected by the same geometric considerations.

We can finally conclude that the apparent correlation between phase difference and forest cover is likely due to a mutual correlation with the terrain slope angle. After accounting for this effect the phase difference shows little prediction power for forest cover.

4. Discussion

The presented results suggest that separation between forest and non-forest is indeed possible using Sentinel-1 C-band data. In general, the separability of these two classes was greatly dependent on the study site. A larger selection of study sites may be required to determine whether this is due to the characteristics of the individual study sites or a feature of the broader climate zones, forest types, and types of forest disturbance found in each site. Overall, forest was characterized by larger backscatter values in both VV and VH, as well as larger annual variation in VV and VH compared to non-forest. This is in contrast to the results by Quegan et al. [13], who found that forest exhibits a lower temporal variability than non-forest. This may be explained by two factors. First, they mainly contrast forest with agriculture, which has a strong annual variability in backscatter due to growth and harvest cycles. Second, the low variability in backscatter was primarily found in older forests, where large biomass values are likely to be above the saturation point for biomass–backscatter relationships, and no backscatter is likely to reach the soil through dense canopies so differences in soil moisture will not change the backscatter observed.

While it was possible to achieve some separation between forest and non-forest even with a single image, using a time series or statistics from a time series was clearly helpful in all cases. Balanced accuracy scores of around $80\%$ to $93\%$ were possible across all study sites when data from multiple scenes were used, but the best accuracy ranged from just $65\%$ up to $91\%$ when a single scene was used. We found no benefit to using the full time series over the simple temporal statistics of mean and standard deviation. In fact, there was a significant increase in classification accuracy when reducing the feature set in this way, due to the notable dimensionality reduction and noise removal.

All classifier scores presented here should not be taken as the best achievable classification results. The goal of this study was not to find the best possible classifier, and as such no efforts were undertaken to optimize any hyperparameters or tune the classifiers. The emphasis was instead on identifying trends in classifier behavior when presented with different sets of features derived from Sentinel-1 SLC data.

Nevertheless, we can make some generalized observations regarding the relative performance of the four classifiers tested. When the classifiers are trained on the full time series, i.e., in the presence of high-dimensional data and high noise, an SVM or random forest classifier was found to give the best result. For a reduced feature set, SVM marginally outperforms random forest, on average.

The performance of the kNN classifier depends greatly on appropriate feature selection. While for the smallest feature set—consisting of annual mean and standard deviation of backscatter alone—this classifier showed similar performance to the other classifiers, adding noisy variables such as the cross-polarized phase difference reduced its mean accuracy from $84.1\%$ to $82.9\%$. In the presence of high-dimensional data such as the full time series, its accuracy was further reduced to $80.5\%$. Given that kNN also does not scale well with large numbers of observations (the algorithm has to search the entire training data for each new data point) we would not recommend using it for forest classification based on these data.

Being the conceptually simplest classifier, QDA is fast and performs well in easy classification problems, i.e., scenarios where the classes show clear separation. This is true in particular of the Finnish study site. As this is not the case for other areas, however, we would not recommend using this classifier in general.

The accuracies achieved here are comparable to the results found in similar studies using diverse sensors. Dostálová et al. [23] use Sentinel-1 GRD data to map forest area over a site in eastern Austria. They achieve a balanced accuracy of $90\%$ compared to validation data obtained from airborne full-waveform laser scanning. Our study complements this result by testing a variety of study sites, as well as quantifying the separation and thus relevance of multiple variables and derived temporal statistics, including phase information. In a global forest/non-forest map generated from L-band ALOS PALSAR data [12], the achieved accuracy was $91.3\%$ compared with Google Earth imagery, $94.8\%$ compared with the FRA, and $84.9\%$ compared with the DCP. Other studies have used optical data, such as Landsat images, to create similar maps. Mayaux et al. [24] assess the accuracy of the Landsat-based Global Land Cover (GLC) 2000 map individually for each land cover class. By combining forest classes and non-forest classes, respectively, the resulting balanced accuracy score for forest/non-forest classification was $91.3\%$. In a European forest/non-forest map also based on Landsat data, Pekkarinen et al. [25] achieve a balanced accuracy of $85.6\%$.

The UK study site exhibited an unexpected shift in phase distributions between forest and non-forest for one particular orbit direction. Our analysis of the topography showed that this shift is driven by the terrain slope orientation. Consequently, while the phase appeared to carry some information, for this site, this is an artifact of the topography and does not make a sufficient case for the inclusion of the phase in these classification efforts. The dependence of forest cover on the terrain is a site specific property that can not be generalized. As this phenomenon is independent of the radar data, the relationship between forest and terrain should be modeled separately rather than using the phase as a proxy for terrain in this way. These results suggest that the phase information of dual-polarized SAR data may be left out of forest monitoring applications unless it is used to derive interferometric quantities, in particular the temporal coherence. Coherence is a measure of the consistency of the phase over time. Because vegetation tends to result in lower temporal coherence [26,27,28,29,30], this could be an additional feature for land cover classification. However, if no interferometric analysis is to be undertaken, we would recommend to work with GRD rather than SLC data for forest monitoring.

There are some limitations to the capacity for forest monitoring using Sentinel-1 data, as highlighted by the poor classification accuracy for single-scene data and the variability of the accuracy across study sites. The need for time series data can be a problem when temporal accuracy is required at sub-annual scale, e.g., for change detection. However, in the absence of time series data some of the added noise can be compensated for with spatial smoothing, at the cost of spatial resolution. Furthermore, the differences between study sites suggest that the accuracy of time series based classification is highest in areas of pronounced seasonality, as witnessed in, e.g., Finland or the UK. Nevertheless, even in areas with low seasonality such as the tropics, accuracies of around $80\%$ to $85\%$ paired with the independence of SAR data from cloud cover make a strong case for its use.

5. Conclusions

In our study of six partially forested areas in Alaska, Colombia, Finland, Florida, Indonesia, and the UK, we looked at the separation between forest and non-forest pixels for different feature sets derived from Sentinel-1 SLC data.

The following are the main conclusions.

(a)

Using an SVM classifier, we were able to achieve balanced accuracy scores up to $93\%$ in Finland, with a mean accuracy of $87\%$ across all study sites.

(b)

Given an annual time series of Sentinel-1 data, it is sufficient to extract the annual mean and standard deviation (separated by orbit) for forest mapping.

(c)

There was little useful information in the cross-polarized phase difference, and no information in its variability. Most classifiers performed equally well or better when excluding the phase difference from the feature set.

(d)

For high-dimensional data, such as unaggregated time series data, we suggest using an SVM or random forest classifier as these appear the most robust to noise. For aggregated statistical data (such as annual mean and variance) our findings suggest that the best results may be achieved with an SVM classifier.

Finally, our goal was to assess the potential of C-band SAR data for forest detection. While longer wavelengths certainly offer better performance, we have observed sufficiently high classification accuracies globally to make a case for the use of Sentinel-1 data in forest monitoring applications. This case is helped by the free and open data policy as well as high revisit frequency, offering a potential for change detection applications.