1. Introduction
Developing devices based on an extracellular matrix (ECM) for either scaffolds for cell culture or surgical biological meshes requires them to have the necessary biomechanical characteristics to sustain the stresses they will be subjected to [
1,
2,
3].
Biological tissues are dynamic structures that serve essential functions within the human body. They are subjected to various mechanical stresses and strains over time, and their mechanical behavior plays a critical role in their physiological functions and response to injuries. Conventionally, mechanical testing has often emphasized the study of rupture behavior, which provides insights into the point at which a material fails under load. While rupture behavior is undoubtedly significant, it offers only a limited perspective on tissue mechanics. A more comprehensive understanding can be achieved by assessing the viscoelastic properties in acellular tissues [
4].
The processes used to obtain biomaterials based on human or animal tissues change their general biological properties, including improving their biocompatibility (especially eliminating the cellular component), although this process may involve matrix degradation and the loss of some structural proteins. All the processes used to obtain ECM-based biomaterials aim to achieve complete decellularization while preserving the structural proteins responsible for the biological and mechanical properties [
5,
6,
7,
8,
9].
Type I collagen is the main component of the extracellular matrix of many tissues. This protein has a deformation at break of between 10 and 20% [
10,
11]. Another important protein in ECM is elastin, which provides its elastic characteristics, or the ability to recover its original shape after applying a defined force without suffering ruptures or permanent deformation. The viscoelastic properties of the extracellular matrix, which includes the vital contributions of both collagen and elastin, are further enhanced by the presence of proteoglycans. The extracellular matrix is a complex network of proteins and carbohydrates that provides structural support to various biological tissues.
Collagen and elastin, as mentioned earlier, offer tensile strength and elasticity to the matrix. However, proteoglycans play a unique role in enhancing the viscoelastic behavior of these tissues. Proteoglycans are large molecules consisting of a core protein and long chains of carbohydrates called glycosaminoglycans. These molecules occupy spaces within the matrix and interact with water [
12].
Proteoglycans have a high affinity for water molecules, and their presence creates a hydrated gel-like environment within the extracellular matrix. This gel structure, along with the collagen and elastin fibers, contributes to the viscoelastic properties of the tissue.
The interaction between proteoglycans and water allows the matrix to resist compressive forces while also providing a mechanism for tissue deformation and recoil over time. This unique combination of properties ensures that biological tissues can withstand mechanical stresses, maintain their shape, and return to their original state, making proteoglycans a crucial component in the dynamic viscoelastic behavior of the extracellular matrix. These properties are essential in various physiological processes, including tissue flexibility, load-bearing, and response to mechanical forces in the body. The combination of all of them is responsible for the viscoelastic behavior observed in many biological tissues [
13,
14].
The variations in the mechanical properties of the different tissues depend on the ratio of their elastic components, such as elastin, and their stiff components, such as fibrillar collagen. For example, the thoracic aorta contains close to 50% of its dry weight in elastin to support the continuous dilation and contraction cycles during systole and diastole at least 60 times per minute throughout the life of an individual, while the tendons are mainly formed by type I collagen since they require greater tensile strength and less elasticity to efficiently transmit the force generated by the muscles to move the limbs [
15,
16,
17,
18,
19,
20,
21].
However, the biomechanical behavior is not only determined by the proportions of ECM components, since the isotropy or anisotropy of these components also determine the global behavior of the tissue. The elastin and collagen in the arteries are arranged circumferentially, forming lamellae, while the collagen in the tendons is aligned longitudinally and parallel to the direction in which muscle traction is exerted [
22].
As ECM is a polymeric material, its response mechanisms to movement or deformation are characterized by the time delay of the response (deformation or stress) concerning the action applied to it (stress or deformation, respectively). The success or failure of the in vivo implantation of a decellularized tissue may depend on its ability to precisely mimic the mechanical response of natural tissue. This not only reproduces the tissue’s stiffness but also its viscoelastic response. Effort has been made to determine the role of the tissue microstructure, its composition, and the packing and ordering of its fibers in the viscoelastic response, and although some models have been proposed to describe it, the problem continues to be a challenge [
23,
24,
25,
26,
27,
28].
In the present study, the viscoelastic response of a decellularized mesh from the porcine esophagus (PEM) prepared by our group [
29] was characterized taking two commercial acellular medical devices derived from porcine small intestine submucosa (SIS) and bovine pericardium (BP) as references.
2. Materials and Methods
2.1. Preparation of Extracellular Matrix from Porcine Esophagus
The protocols used to obtain and process the animal tissue were approved by the Institutional Committee for the Care and Use of Experimental animals (CICUA) of the University of Antioquia, num 101/12 February 2016.
Esophagi were obtained from pigs aged between 12 and 16 weeks destined for human consumption in a local market. Between 20 and 25 cm of the thoracic portion were taken from the esophagi and the mucosa was dissected manually. The mucosa was washed with a sterile saline solution (Corpaul, Col, Antioquia, Colombia) to remove debris, vacuum packed in plastic bags, and frozen for at least 24 h at −20 °C before decellularization. After thawing, the membranes were washed in 250 mL of phosphate-buffered saline (PBS) (Sigma, Burlington, MA, USA) for 3 h. The PBS was then removed and 250 mL of 1% triton X-100 (Sigma) was added for 24 h, washed with 250 mL of PBS for 2 h, a new cycle was repeated with 250 mL of triton X-100 at the same concentration for 24 h, washed again with PBS for 1 h before changing the PBS for sodium dodecyl sulfate SDS (Sigma) at 1% for 24 h, washed again with 250 mL of 1% PBS for one hour, and the PBS was changed again for 1% SDS for another 24 h.
All the above steps were carried out under magnetic stirring at 300 rpm and 4 °C. The matrices were then frozen under vacuum at −20 °C for 24 h, with one group in a single layer (PEMs) and another in two layers perpendicular to each other (PEM-D or Double PEM), and vacuum dried at a temperature of 50° C.
Figure S1 in the Supplementary Material shows the absence of cells in decellularized tissue [
29].
Commercial submucosal matrices from the acellular small intestine (SIS) were acquired, measuring 3 cm × 5 cm (3-Biomat, Bogotá, Colombia), and bovine pericardium (B shows the absence of cells in the decP) measuring 5 cm× 10 cm (Porites, Medellín, Colombia), for comparison with the matrices’ viscoelastic properties.
The thickness of the samples was determined by measuring their cross-section using electron microscopy, and the average thickness of the evaluated samples was as follows: PER 586 µm (SD 52.59); SIS 417 µm (SD 137.8); single PEM 183.5 µm (SD 14.32); and double PEM 250.6 µm (SD 23.19).
2.2. Scanning Electron Microscopy
Longitudinal and transversal decellularized tissue samples were examined by SEM. The longest side of the commercial sample was labeled as longitudinal, while the PEM sample in the cephalocaudal direction of the esophagus was considered to be longitudinal and transversal in the coronal direction.
The samples were fixed with 10% buffered formaldehyde (Merck, Darmstadt, Germany) for 24 h, after which the formaldehyde was removed and 2.5% glutaraldehyde (Merck) was added, left in this solution for 2 h, and dehydrated by a successive series of 30%, 50%, 70%, 90%, 95%, and 99% ethanol. The samples were critical-point dried (Sandri PVT 3D Tousimis, Rockville, MD, USA) at 31 °C and 1072 PSI, fixed on graphite tape, and sputtered with gold (Denton Vacuum Desk IV, Moorestown, NJ, USA.). The samples were evaluated in a scanning electron microscope (Jeol JSM 6490 LV, Peabody, MA, USA) under vacuum to obtain high-resolution images. A secondary electron detector was used to evaluate the samples’ morphology and topography.
2.3. Creep Tests
Tensile creep tests were performed (Seiko Exstar TMA ss6000 dilatometer, Chiba, Japan) with 1 cm × 5 mm specimens of the test areas and variable thickness, according to the sample studied, in triplicate in both the transverse and longitudinal directions and immersed in a thermoregulated distilled water bath at 37 °C. The test samples were mounted between two steel plates secured by screws to prevent slipping (according to the equipment manufacturer’s instruction). The following protocol was used for all the tests: preloading with a load ramp from 0 to 10 mN, at 5 mN per minute, a waiting time of 5 min with a load of 10 mN, a load from 10 to 500 mN at a speed of 100,000 mN per minute, and keeping the load at 500 mN for 60 min, the discharge was performed from 500 to 10 mN and at a speed of 100,000 mN per minute, while deformation was recorded at 10 mN for 15 min. The discharge was evaluated for 90 min in a sample from each group. To analyze the results, compliance was calculated: J(t) = γ (t)/σ, which was represented versus the logarithm of time in seconds (compliance is a function of time, denoted by J(t), the ratio of the deformation or strain (γ) at that time (t), and the applied stress (σ)).
2.4. Rheological Tests between Parallel Plates
The samples’ rheological behavior was studied by a dynamic oscillatory rheometer between 12 mm diameter parallel plates (TA Instruments, DHR 2, New Castle, DE, USA) in a humidified chamber with the lower plate at a constant temperature of 37 °C. First, 12 mm diameter circumferential samples were cut from each matrix and hydrated in distilled water for 15 min before testing. The tests were in triplicate, using an automatic approximation up to a resistance of 0.3 N. A stress sweep test was performed to determine the linear viscoelastic region at a frequency of 1 Hz with a strain of between 0.01 and 15%. The frequency sweep test was performed with a deformation of 0.3% and a frequency range between 0.1 and 20 Hz. The results were analyzed on TA Instruments TRIOS software V3.1.0.3538.
2.5. Dynamic-Mechanical Measurements (DMA) in Tension Mode
Dynamic-mechanical tests (DMA 8000, Perkin Elmer, Waltham, MA, USA) were carried out on 1 cm long × between 5 and 8 mm wide areas and variable thickness in triplicate, and both transverse and longitudinal directions with the samples immersed in a thermoregulated distilled water bath at a constant temperature of 37 °C. A frequency scan was performed between 0.1 Hz and 35 Hz.
2.6. Statistics
All experiments were performed with three biological replicates. The results are given as the mean ± standard deviation (SD). The normality of the different samples was checked using the Shapiro–Wilk normality test with an alpha value of 0.05. For comparisons of two single groups of data, unpaired T-Student tests (p-value = 0.05) were completed. An ordinary one-way ANOVA test (p-value = 0.05) was used for three or more groups to perform multiple comparisons between the column means when the normality test was passed. If the normality test was not passed, then the non-parametric Kruskal–Wallis test was used to compare this non-normal sample with other normal samples (p-value = 0.05) to perform multiple comparisons between the column means. GraphPad Prism 8 software (GraphPad Software, La Jolla, CA, USA) was used for statistical analysis. Differences among the groups are stated as p ≤ 0.05 (*), p ≤ 0.01 (**), p ≤ 0.001 (***), and p ≤ 0.0001 (****) in normal samples, and p ≤ 0.05 (#) in non-normal ones.
4. Discussion
To regenerate tissues by tissue engineering techniques, a three-dimensional support seeded with cells can be implanted at the site of the damage, or alternatively, in cell-free strategies, the implanted support can be expected to be invaded by cells from its neighboring environment. In both cases, the support generates a biomechanical environment in which the material provides the cells with attachment sites, guides the organization of the newly formed extracellular matrix (ECM), and transmits mechanical stress to the cells. These stresses are key factors in determining the cells’ phenotype and therefore their ability to generate functional tissue through mecanotransduction signaling. In experiments carried out on mesenchymal stem cells (MSCs), it was found that the mechanical characteristics of the substrate on which these cells were seeded had an important influence on their differentiation: in very stiff matrices, the MSCs acquired an osteogenic phenotype, while in softer matrices, they could differentiate into chondrocytes or other cells of mesenchymal lineage [
30], so that it is important to understand the mechanical behavior of 3D supports for their use in regenerative medicine [
31,
32,
33,
34,
35]. While traditional mechanical testing often focuses on rupture behavior, this paper argues that evaluating the viscoelastic properties of acellular tissues is of paramount importance. The viscoelastic properties provide a more comprehensive and realistic representation of how these tissues respond to external forces, over rupture behavior alone. This paper discusses the rationale behind this perspective, highlighting its relevance in fields such as biomaterials science, regenerative medicine, and biomechanics.
In the tensile creep tests, it was found that the simple PEM porcine esophageal-derived matrices tested longitudinally had greater rigidity (lower compliance values) than the SIS matrix and much more so than the BP matrix, which is the most deformable, although the double PEM sample showed greater compliance than the monolayer. This effect can be attributed to one layer sliding over another, showing that the inter-layer adhesion of the decellularized matrix is weaker than the structure of the fibers aligned inside each layer, as can be expected, since the two layers are only held together by the physical interaction caused by freezing and drying.
In the case of the PEM matrix, the compliance value is three times greater in the transversal than in the longitudinal direction, while in SIS and BP, it is approximately twice as high. In this direction, the PEM matrix behaves similarly to the SIS, while the BP is once again the most deformable, with much higher compliance values than the others. Interestingly, the double-PEM matrix presents strain values in the transverse direction of the same order as in the longitudinal, showing that the orientation of the fiber bundles in one layer perpendicular to another stiffens the assembly in spite of inter-layer sliding.
It should be noted that the characteristic sigmoid shape is not found in the curves in
Figure 2, as has been reported in other decellularized tissues [
24,
25,
27,
28]. Many viscoelastic or dielectric relaxation processes can be accurately reproduced by the Kohlraush–Williams–Watts Function (KWW) [
36] or the stretched exponential equation. The compliance measured in tension as a function of time D(t) in a creep test KWW equation can be written as follows [
37]:
where
φ(
t) is the relaxation function, which varies between 0 and 1,
DU and
DR are the limit values of
D(
t) at time 0 and infinite time, respectively, (unrelaxed and relaxed compliance, respectively), and
β is a coefficient that varies between 0 and 1, (for
β = 1 it corresponds to the single relaxation time model) and
τ can be called the relaxation time. The shape of this curve for
β = 0.5 is represented in
Figure 2a, with arbitrary values for the rest of the parameters. It can be seen that the relaxation process is extremely wide, which justifies the use of the logarithmic scale on the time axis and also that the relationship between log
D(
t) and log
t is approximately a straight line.
The experimental results in our time interval, which covers around three time decades, show an approximately linear relationship that does not allow any form of extrapolation in order to determine the
DU,
DR,
β parameters or the
τ of Equation (1), although alternative parameters can be equally useful to characterize the viscoelastic response. What the cells seeded in a viscoelastic environment such as these biological matrices can detect is actually the magnitude of the deformation of the matrix to which they adhere, i.e., their rigidity and the speed at which this deformation occurs under the force that the cell or the environment can exert on the tissue. It may thus be sufficient to use the slope of the curve shown in
Figure 2 as a parameter to characterize the viscoelastic response, which we can call the response speed in compliance (r
D). Analyzing the data based on this response speed instead of the relaxation times or relaxation intensities avoids making extrapolations that can lead to huge interpretation errors.
Figure 2c shows that the PEM matrix shows the greatest viscoelasticity even though it is the least deformable. When the load is applied, the tissue is initially stiffer but gradually yields. To our knowledge, it is not known how this more viscoelastic behavior affects cellular responses. It is interesting that the values of r
D are not significantly different in the longitudinal and transversal directions, in spite of significant differences in the value of the compliance.
The recovery after removing the applied load is shown in
Figure 2d, again using the double logarithmic scale. The characteristic initial curvature of the relaxation process can be seen here, although the experimental times do not allow us to venture an extrapolation of the time necessary to reach complete recovery from the initial deformation, as occurred in the loading process. The recoverable deformation of the extracellular matrix depends not only on the elastic characteristics of the organ or tissue from which the ECM is extracted, but also on the methods used to obtain it.
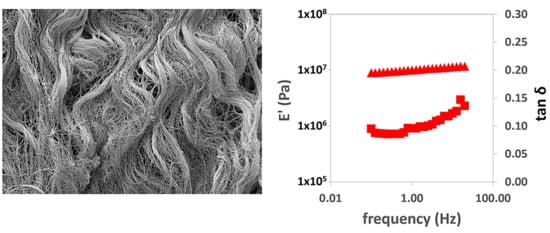
In the dynamic-mechanical tests in tension, the real part of the elastic modulus with frequency can be seen to increase.
Figure 3a,b show this behavior in the longitudinal and transversal direction tests, respectively. As in the creep measurements, it is clear that the viscoelastic relaxation process is much broader than the three decades of frequency available in the equipment used (between 0.1 and 20 Hz). The tan δ values increase with the logarithm of frequency, but they are also far from the characteristic peak of the relaxation process. We used the values of E′ and tan δ measured at a frequency of 1 Hz to compare the stiffness of the different samples (
Figure 3b,c, respectively).
When evaluating the storage modulus (
Figure 3b), differences were found in the properties of the different matrices and in terms of the orientation of the samples at the time of the tests. The simple PEM in the longitudinal direction was found to be more rigid than the other samples evaluated, in line with the results of the creep tests. Also, the measurement in the transverse direction gives a much lower E′ value, in good agreement with the creep tests. The greatest stiffness shown in the creep experiments in the double-PEM matrix in the transverse direction is confirmed, with values close to the measurement of the PEM matrix in the longitudinal direction, probably due to the recruitment of the longitudinal fibers provided by the overlapping fibers. However, this behavior is not found when evaluating the double-PEM sample in the longitudinal direction, since it shows similar behavior to the PEM sample in the transverse direction. No significant differences were found in the SIS and BP samples between the longitudinal and cross-sectional direction measurements. The fact that the sample is subjected to smaller deformations in the dynamic-mechanical experiments than in creep reduces the influence of the orientation of the collagen and elastin fibers on the elastic modulus measured.
The parallel plate rheometer test is a measure of shear strength (see results in
Figure 4). They are qualitatively analogous to those obtained in the tension measurements: a small increase in G′ with frequency, with a linear dependence of log G′ on log f and the curvature of the dependence of tan δ on log f, but far from reaching a maximum. However, all the matrices presented a shear modulus more than two orders of magnitude lower than the Young’s modulus measured in tension. In shear, we measured the deformation produced by some fiber layers sliding over others, and it seems clear that the resistance to this type of stress is weak in this type of tissue, as expected. The value of tan δ, which to a certain extent measures the internal friction in the material, was somewhat higher, but in the same order of magnitude as that measured in tension.
Significant differences were found in terms of shear strength, which depended on the origin of the matrices, while the bilayer double-PEM derived from the porcine esophagus had the highest shear modulus, followed by the SIS and the BP, PEM tissue with lower shear strength.
In this comparative biomechanical characterization assay, it was found that the matrices from the porcine esophagus had greater rigidity than those of porcine intestinal submucosa and bovine pericardium in the evaluation of the longitudinally oriented samples. However, when these were evaluated in the transverse direction, the bovine pericardium was found to be more rigid than the intestinal submucosa and the esophageal matrix in the creep test.
These results can be partially explained by the structure and function of the organs from which matrices were obtained: the esophagus serves a transit function and allows the bolus to pass from mouth to stomach, so that it has to relax transversely by up to three times its size, while it is virtually immobile in the longitudinal direction. The functions of the small intestine are mainly absorptive and propulsive: it distends in all directions despite the fact that in vivo, it has little tolerance to increasing pressure, while by contrast the pericardium is a fibrous membrane with nonelastic properties that limit acute cardiac dilatation. It supports cyclic cardiac distension and contraction at a minimum of 60 times per minute, while resisting the surrounding forces derived from the breathing cycles, which modify the pressure inside the thoracic cavity so that their fibers are intertwined. However, under normal physiological conditions, unlike the esophagus, both the small intestine and the pericardium are subject in vivo to low pressures and also have a more fluid behavior than the esophagus [
38,
39,
40,
41,
42,
43,
44,
45].
The stiffness of the matrices derived from porcine esophagus was found to decrease more than the SIS and pericardium meshes, probably due to the reorganization and redistribution of the forces inside the matrix collagen fibers.
The comprehensive search in various scientific databases for information on the viscoelastic properties of extracellular matrices derived from bovine pericardium, porcine esophagus, and small intestine submucosa has unfortunately yielded results indicating a scarcity of available information in the scientific literature regarding these specific materials.
Most of the published works on the mechanical evaluations on biological matrices have reported on the response measured in tension. The studies by Badylak et al. found that the acellular small intestine submucosa matrices, in a push-through failure load test, had a value of 433.6 +/− 79.5 N, which was higher than that reported by Arnold et al. [
46], who reported a maximum load for this material of 26.65 +/− 7 N. This difference could be attributed to potential variations in the production methods of the different matrices.
In the study published by Chaitin et al. [
47], they demonstrate that the decellularization process preserves the mechanical integrity and extracellular matrix composition of esophageal tissue. In that study, it was observed that native esophageal mucosa exhibited a maximum extension stress between 1.5 and 2.0 MPa at around 450% extension, while the decellularized tissue showed a maximum extension stress between 4.0 MPa and 4.5 MPa at 600% extension. However, there were no significant differences in the elastic modulus, which was 19 +/− 20 and 20 +/− 8 MPa, respectively, which are lower than the values reported in this work both in the longitudinal and transversal direction.
Regarding bovine pericardium, Hülsmann et al. [
48] reported an elastic modulus for native tissue of 27 +/− 6 MPa, and after decellularization, changes in the elastic modulus were observed, depending on the method used, ranging between 10 and 6 MPa. This variation might be attributed to the aldehydes used in the tissue preservation process. It is worth noting that no studies were found that delved deeper into the viscoelastic response of these tissues.
Despite the importance of understanding the viscoelastic properties of ECMs in biomedical and tissue engineering applications, it appears that specific research on these particular tissues has not been extensively documented in the scientific community. This may be due to their relative rarity or a more limited focus compared to other biologically derived materials.
Given the potential significance of such research for medical and engineering applications, there may be a need for further efforts in generating data and studies related to the viscoelastic properties of ECMs derived from bovine pericardium, porcine esophagus, and small intestine submucosa. This gap in the literature could represent an opportunity for future research and scientific contributions that enrich our understanding of these materials and their diverse applications.