Phase Equilibria and Critical Behavior in Nematogenic MBBA—Isooctane Monotectic-Type Mixtures
Abstract
:1. Introduction
2. Results
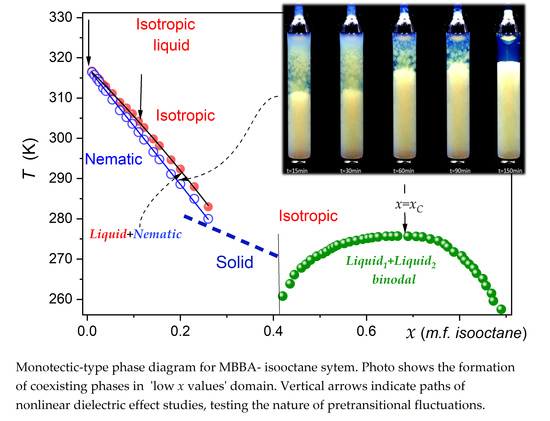
2.1. Phase Diagram
2.2. Liquid-Liquid Binodal
2.3. Critical Opalescence
2.4. NDE Insight into Pretransitional Properties in the Isotropic Liquid Phase
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Wesink, H.H.; Trizac, E. Generalized Onsager theory for strongly anisometric patchy colloids. J. Chem. Phys. 2014, 140, 024901. [Google Scholar] [CrossRef] [Green Version]
- Flory, P.J. Phase equilibria in solutions of rod-like particles. Proc. R. Soc. Lond. A 1956, 34, 73–89. [Google Scholar] [CrossRef]
- Mukhijam, D.M.; Solomon, J. Nematic order in suspensions of colloidal rods by application of a centrifugal field. Soft Matter 2011, 7, 540–545. [Google Scholar] [CrossRef]
- Dierking, I.; Martins, A.; Neto, F. Novel trends in lyotropic liquid crystals. Crystals 2020, 10, 604. [Google Scholar] [CrossRef]
- Jamain, Z.; Azman, A.N.A.; Razali, N.A.; Makmud, M.Z.H. A review on mesophase and physical properties of cyclotriphosphazene derivatives with Schiff base linkage. Crystals 2022, 12, 1174. [Google Scholar] [CrossRef]
- Lekkerkerker, H.N.W.; Vroege, G.J. Liquid crystal phase transitions in suspensions of mineral colloids: New life from old roots. Philos. Trans. R. Soc. A 2013, 371, 20120263. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Smalyukh, I.I. Liquid crystalline cellulose-based nematogels. Sci. Adv. 2017, 3, E1700981. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Maity, S.; Liu, K.; Liu, Q.; Göstl, R.; Portale, G.; Roos, W.H.; Herrmann, A. Nematic DNA thermotropic liquid crystals with photoresponsive mechanical properties. Small 2017, 13, 1701207. [Google Scholar] [CrossRef]
- Tombolato, F.; Ferrarini, A.; Grelet, E. Chiral nematic phase of suspensions of rodlike viruses: Left-handed phase helicity from a right-handed molecular helix. Phys. Rev. Lett. 2006, 96, 258302. [Google Scholar] [CrossRef]
- Beng Saw, T.; Xi, W.; Ladoux, B. Biological tissues as active nematic liquid crystals. Adv. Mater. 2018, 30, 1802579. [Google Scholar] [CrossRef]
- Anisimov, M.A. Critical Phenomena in Liquids and Liquid Crystals; Gordon & Breach Science Publishers: Reading, UK, 1991; ISBN 9782881248061. [Google Scholar]
- Goodby, J.W.; Collings, P.J.; Kato, T.; Tschierske, C.; Gleeson, H.; Raynes, P. Handbook of Liquid Crystals: Vol. 2: Physical Properties and Phase Behavior of Liquid Crystals; Wiley: New York, NY, USA, 2014; ISBN 978-3527327737. [Google Scholar]
- Rzoska, S.J.; Mazur, V.; Drozd-Rzoska, A. Metastable Systems under Pressure; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drozd-Rzoska, A.; Martinez-Garcia, J. A universal description of ultraslow glass dynamics. Nat. Commun. 2013, 4, 1823. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drozd-Rzoska, A. Universal behavior of the apparent fragility in ultraslow glass forming systems. Sci. Rep. 2019, 9, 6816. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New scaling paradigm for dynamics in glass-forming systems. Prog. Mat. Sci. 2023, 101074. Available online: https://arxiv.org/ftp/arxiv/papers/2206/2206.13305.pdf (accessed on 12 December 2022). [CrossRef]
- Drozd-Rzoska, A. Activation volume in superpressed glass-formers. Sci. Rep. 2019, 9, 13787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rzoska, S.J.; Starzonek, S.; Drozd-Rzoska, A. Pretransitional Behavior and Dynamics. In Advances in Colloid Science: Liquid Crystal–Based Nanocolloids; Rahman, M.M., Asiri, A.M., Eds.; Intech: Rijeka, Croatia, 2016; Chapter 12; pp. 265–274. [Google Scholar] [CrossRef] [Green Version]
- Goodby, J.W. The nanoscale engineering of nematic liquid crystals for displays. Liq. Cryst. 2011, 38, 1363–1387. [Google Scholar] [CrossRef]
- Prakash, J.; Kumar, A.; Chauhan, S. Aligning liquid crystal materials through nanoparticles: A review of recent progress. Liquids 2022, 2, 50–71. [Google Scholar] [CrossRef]
- Kronberg, B.; Bassignana, I.; Patterson, D. Phase diagrams of liquid crystal + polymer systems. J. Phys. Chem. 1978, 82, 1714–1719. [Google Scholar] [CrossRef]
- Croucher, M.D.; Patterson, D. Temperature and composition dependences of the heat of mixing of MBBA with hydrocarbon. J. Sol. Chem. 1980, 9, 771–784. [Google Scholar] [CrossRef]
- Martire, E.; Oweimreen, G.A.; Dowell, F. The effect of solute structure on the nematic–isotropic transition in binary mixtures. Inorg. Chim. Acta 1980, 40, X54. [Google Scholar] [CrossRef]
- Oweimreen, G.A. Thermodynamics of solutions of various nonmesomorphic solutes in the nematic and isotropic phases of 7CB. Mol. Cryst. Liq. Cryst. 1981, 68, 257–275. [Google Scholar] [CrossRef]
- Ballauff, M. Phase equilibria in mixtures of thermotropic liquid crystals and flexible polymers. Mol. Cryst. Liq. Cryst. 1986, 136, 175–195. [Google Scholar] [CrossRef]
- Orendi, H.; Ballauff, M. Complete phase diagrams of mixtures of a nematic liquid crystal with n-alkanes. Liq. Cryst. 1989, 6, 497–500. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Zioło, J. The nonlinear dielectric effect applied to study the pretransitional effects in the isotropic phase of the MBBA-benzene solutions. Acta Phys. Pol. A 1990, 78, 915–919. [Google Scholar]
- Orendi, H.; Ballauff, M. Analysis of the phase diagrams of mixtures of a nematic liquid with n-alkanes. Ber. Bunsenges. Phys. Chem. 1992, 96, 96–100. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Zioło, J. Critical properties in the vicinity of the critical consolute point for the 4-methoxybenzylidene-4′butylaniline-isooctane solution. Liq. Cryst. 1992, 11, 9–14. [Google Scholar] [CrossRef]
- Abe, A.; Iizumi, E.; Sasanuma, Y. Phase behavior and ordering characteristics of some chain molecules dissolved in a nematic liquid crystal, 4′-methoxybenzylidene-4-n-butylaniline. Polym. J. 1993, 25, 1087–1098. [Google Scholar] [CrossRef] [Green Version]
- Sasanuma, Y. Conformational and orientational characteristics of chain molecules placed in a nematic field: N-decane and 1,6-dimethoxyhexane dissolved in 4′-methoxybenzylidene-4-n-butylaniline (MBBA). J. Phys. II Fr. 1993, 3, 1759–1778. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. The equivalence of density and field variables for the pretransitional effects in the isotropic phase of nematogens. Phase Transit. 1995, 54, 75–80. [Google Scholar] [CrossRef]
- Matsuyama, A.; Kato, T. Nematic ordering in mixtures of polymers and liquid crystals. J. Chem. Phys. 2000, 11, 1046–1049. [Google Scholar] [CrossRef]
- Jadżyn, J.; Czechowski, G.; Ginovska, M. Pretransitional critical-like behavior of dielectric permittivity in mixtures of mesomorphic and nonmesomorphic compounds. Phys. Rev. E 2005, 71, 052702. [Google Scholar] [CrossRef] [PubMed]
- Denolf, K.; Cordoyiannis, G.; Glorieux, C.; Thoen, J. Effect of nonmesogenic impurities on the liquid crystalline phase transitions of octylcyanobiphenyl. Phys. Rev. E 2007, 76, 051702. [Google Scholar] [CrossRef] [PubMed]
- Ullrich, B.; Ilska, E.; Höhn, N.; Vollmer, D. Long range particle transport in liquid crystal-alkane mixtures. Prog. Colloid Polym. Sci. 2006, 13, 142–146. [Google Scholar] [CrossRef]
- Kundu, S.K.; Okudaira, S.; Kosuge, M.; Shinyashiki, N.; Yagihara, S. Broadband dielectric spectroscopy of a nematic liquid crystal in benzene. J. Chem. Phys. 2008, 129, 164509. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.K.; Okudaira, S.; Kosuge, M. Phase transition and abnormal behavior of a nematic liquid crystal in benzene. J. Phys. Chem. 2009, 113, 11109–11114. [Google Scholar] [CrossRef]
- Serrano, L.A.; Fornerod, M.J.; Yang, Y.; Gaisford, S.; Stellacci, F.; Guldin, S. Phase behaviour and applications of a binary liquid mixture of methanol and a thermotropic liquid crystal. Soft Matter 2018, 14, 4615–4620. [Google Scholar] [CrossRef] [Green Version]
- Reyes, C.G.; Baller, J.; Araki, T.; Lagerwall, J.P.F. Isotropic–isotropic phase separation and spinodal decomposition in liquid crystal–solvent mixtures. Soft Matter 2019, 15, 6044–6054. [Google Scholar] [CrossRef]
- Seregin, V.O.; Pestov, S.M.; Zubairov, R.M. Phase equilibria in 4-pentyloxybenzoic acid-long-chain n-alkane systems. Fine Chem. Technol. 2019, 14, 66–75. [Google Scholar] [CrossRef] [Green Version]
- Sargazi, M.; Linford, M.R.; Kykhaii, M. Liquid crystals in analytical chemistry: A review. Crit. Rev. Anal. Chem. 2019, 49, 243–255. [Google Scholar] [CrossRef]
- Shimada, R.; Urakawa, O.; Inoue, T.; Watanabe, H. Phase equilibrium and dielectric relaxation in mixture of 5CB with dilute dimethyl phthalate: Effect of coupling between orientation and composition fluctuations on molecular dynamics in isotropic one-phase state. Soft Matter 2021, 17, 6259–6272. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F. Liquid Crystals with Nano and Microparticles; World Scientific Publishing: Singapore, 2016. [Google Scholar] [CrossRef] [Green Version]
- Soulé, E.R.; Reven, L.; Rey, A.D. Thermodynamic modelling of phase equilibrium in nanoparticles—Nematic liquid crystals composites. Mol. Cryst. Liq. Cryst. 2012, 553, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Sastry, S.S.; Kumar, L.T.; Vishwam, T.; Murthy, V.R.K.; Lakshminaryana, S.; Tiong, H.S. Dielectric studies on Fe3O4 nanodoped p-n-alkyloKalabmetalxybenzoic acids. Adv. Condens. Matter. Phys. 2014, 2014, 639259. [Google Scholar] [CrossRef] [Green Version]
- Csacha, K.; Juríková, A.; Miškuf, J.; Tomašovičová, N.; Gdovinová, V.; Závišová, V.; Kopčanský, P.; Éber, N.; Fodor-Csorba, K.; Vajda, A. Kinetics of nematic to isotropic phase transition in liquid crystal doped with magnetic nanoparticles. Acta Phys. Pol. A 2017, 131, 949–951. [Google Scholar] [CrossRef]
- Pathaka, G.; Katiyar, R.; Agrahari, K.; Srivastava, A.; Dabrowski, R.; Garbat, K.; Manohar, R. Analysis of birefringence property of three different nematic liquid crystals dispersed with TiO2 nanoparticles. Opto-Electron. Rev. 2018, 26, 11–18. [Google Scholar] [CrossRef]
- Zakutanská, K.; Lacková, V.; Tomašovicová, N.; Burylov, S.; Burylova, N.; Skosar, V.; Juríková, A.; Vojtko, M.; Jadzyn, J.; Kopcanský, P. Nanoparticle’s size, surfactant and concentration effects on stability and isotropc-nematic transition in ferronematic liquid crystal. J. Mol. Liq. 2019, 289, 11125. [Google Scholar] [CrossRef]
- Sung, B.; Chanjoong Kim, H.Y.; Abelmann, L. Inhomogeneous nematic-isotropic phase transition of a thermotropic liquid crystal doped with iron oxide nanoparticles. Phys. Lett. A 2020, 384, 126927. [Google Scholar] [CrossRef]
- Bury, P.; Veveričík, M.; Černobila, F.; Tomašovičová, N.; Zakuanská, K.; Kopčanský, P.; Timko, M.; Jarošová, M. Role of magnetic nanoparticles size and concentration on structural changes and corresponding magneto-optical behavior of nematic liquid crystals. Nanomaterials 2022, 12, 2463. [Google Scholar] [CrossRef]
- Priscilla, P.; Malik, P.; Kumar, A.; Castagna, R.; Singh, G. Recent advances and future perspectives on nanoparticles-controlled alignment of liquid crystals for displays and other photonic devices. Crit. Rev. Solid State Mater. Sci. 2022. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Starzonek, S.; Drozd-Rzoska, A.; Czupryński, K.; Chmiel, K.; Gaura, G.; Michulec, A.; Szczypek, B.; Walas, W. The impact of BaTiO3 nanonoparticles on pretransitional effects in liquid crystalline dodecylcyanobiphenyl. Phys. Rev. E 2016, 93, 534. [Google Scholar] [CrossRef] [Green Version]
- Starzonek, S.; Rzoska, S.J.; Drozd-Rzoska, A.; Czupryński, K.; Kralj, S. Impact of ferroelectric/superparaelectric nanoparticles on phase transitions and dynamics in nematic liquid crystal. Phys. Rev. E 2017, 96, 022705. [Google Scholar] [CrossRef] [Green Version]
- Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.J.; Kralj, S. Nanoparticle-controlled glassy dynamics in nematogen-based nanocolloids. Phys. Rev. E 2019, 99, 052703. [Google Scholar] [CrossRef] [PubMed]
- Češnar, D.; Kyrou, C.; Lelidis, I.; Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.J.; Kutnyak, Z.; Kralj, S. Impact of weak nanoparticle induced disorder on nematic ordering. Crystals 2019, 9, 171. [Google Scholar] [CrossRef] [Green Version]
- Rzoska, S.J.; Starzonek, S.; Łoś, J.; Drozd-Rzoska, A.; Kralj, S. Dynamics and pretransitional effects in C60 fullerene nanoparticles and liquid crystalline dodecylcyanobiphenyl (12CB) hybrid system. Nanomaterials 2020, 10, 2343. [Google Scholar] [CrossRef] [PubMed]
- Łoś, J.; Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S.; Czupryński, K. Fluctuations-driven dielectric properties of liquid crystalline octyloxycyanobiphenyl and its nanocolloids. Soft Matter 2022, 18, 4502–4512. [Google Scholar] [CrossRef]
- Łoś, J.; Drozd-Rzoska, A.; Rzoska, S.J.; Czupryński, K. The impact of ionic contribution to dielectric permittivity in 11CB liquid crystal and its colloids with BaTiO3 nanoparticles. Eur. Phys. J. E 2022, 45, 74. [Google Scholar] [CrossRef]
- Trček, M.; Lavrič, M.; Cordoyiannis, G.; Zalar, B.; Rožič, B.; Kralj, S.; Tzitzios, V.; Nounesis, G.; Kutnjak, Z. Electrocaloric and elastocaloric effects in soft materials. Philos. Trans. R. Soc. A 2016, 374, 20150301. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, A.; Singh, G.; Biradar, A.M. Advances in gold nanoparticle–liquid crystal composites. Nanoscale 2014, 6, 7743–7756. [Google Scholar] [CrossRef]
- Singh, G.; Fisch, M.; Kumar, S. Emissivity and electrooptical properties of semiconducting quantum dots/rods and liquid crystal composites: A review. Rep. Prog. Phys. 2016, 79, 056502. [Google Scholar] [CrossRef]
- Singh, G. Recent advances on cadmium free quantum dots-liquid crystal nanocomposites. Appl. Mater. Today 2020, 21, 100840. [Google Scholar] [CrossRef]
- Varshney, D.; Prakash, J.; Singh, V.P.; Yadav, K.; Singh, G. Probing the impact of bismuth-titanate based nanocomposite on the dielectric and electro-optical features of a nematic liquid crystal material. J. Mol. Liq. 2022, 347, 118389. [Google Scholar] [CrossRef]
- Parveen, A.; Prakash, J.; Singh, G. Impact of strontium titanate nanoparticles on the dielectric, electro-optical and electrical response of a nematic liquid crystal. J. Mol. Liq. 2022, 354, 118907. [Google Scholar] [CrossRef]
- Varshney, D.; Yadav, K.; Prakash, J.; Meena, H.; Singh, G. Tunable dielectric and memory features of ferroelectric layered perovskite Bi4Ti3O12 nanoparticles doped nematic liquid crystal composite. J. Mol. Liq. 2023, 369, 120820. [Google Scholar] [CrossRef]
- Prakash, S.; Singh, Y.S. Carbon nanotube dispersion in nematic liquid crystals: An overview. Prog. Mater. Sci. 2016, 80, 38–76. [Google Scholar] [CrossRef]
- de Gennes, P.G. Phenomenology of short-range order effects in the isotropic phase of nematic materials. Phys. Lett. A 1969, 30, 454–455. [Google Scholar] [CrossRef]
- de Gennes, P.G. Short-range order effects in the isotropic phase of nematic and cholesteric. Mol. Cryst. Liq. Cryst. 1971, 12, 193–214. [Google Scholar] [CrossRef]
- de Gennes, P.G. The Physics of Liquid Crystals; Claredon Press: Oxford, UK, 1974; ISBN 13-9780198512851. [Google Scholar]
- Landau, L.D.; Lifshtz, E.M. Statistical Physics; 1st edition in 1937; Pergamon Press: Tarrytown, NY, USA, 1958; ISBN 9780750633727. (In Russian) [Google Scholar]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979; ISBN 0-8014-1203-X. [Google Scholar]
- de Gennes, P.G.; Badoz, J. Fragile Object: Soft Matter, Hard Science and the Thrill of Discovery; Copernicus: New York, NY, USA, 1996; ISBN 978-1461275282. [Google Scholar]
- Jones, R.A.L. Soft Condensed Matter; Oxford University Press: Oxford, UK, 2002; ISBN 9780198505891. [Google Scholar]
- Stinson, T.W.; Litster, J.D. Pretransitional phenomena in the isotropic phase of a nematic liquid crystal. Phys. Rev. Lett. 1970, 25, 503–508. [Google Scholar] [CrossRef]
- Muta, K.; Takezoe, H.; Kuze, E. Cotton-Mouton effect of alkyl- and alkoxy- cyanobiphenyls in isotropic phase. Jpn. J. Appl. Phys. 1979, 18, 2073. [Google Scholar] [CrossRef]
- Filippini, J.; Poggi, Y. Kerr effect in the isotropic phase of nematic liquid crystals. J. Phys. Lett. 1974, 35, 99–101. [Google Scholar] [CrossRef]
- Bendler, J. Compressibility and thermal expansion anomalies in the isotropic liquid crystal phase. Mol. Cryst. Liq. Cryst. 1977, 38, 19–30. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. Mean-field behaviour of the low frequency non-linear dielectric effect in the isotropic phase of nematic and smectic n-alkylcyanobiphenyls. Liq. Cryst. 1996, 21, 273–277. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Influence of measurement frequency on the pretransitional behavior of the non-linear dielectric effect in the isotropic phase of liquid crystalline materials. Liq. Cryst. 1998, 24, 835–840. [Google Scholar] [CrossRef]
- Rzoska, S.J. Kerr effect and nonlinear dielectric effect on approaching the critical consolute point. Phys. Rev. E 1993, 48, 113–1143. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J.; Degiorgio, V.; Bellini, T.; Piazza, R. Relaxation of the electric birefringence near a critical consolute point. Phys. Rev. E 1994, 49, 3093–3096. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Martinez-Garcia, J.C. Nonlinear dielectric effect in supercritical diethyl ether. J. Chem. Phys. 2014, 141, 094907. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Sánchez, G.; Losada-Pérez, P.; Cerdeiriña, C.A.; Sengers, J.V.; Anisimov, M.A. Asymmetric criticality in weakly compressible liquid mixtures. J. Chem. Phys. 2010, 132, 154502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- 86. Rzoska, S.J.; Drozd-Rzoska, A.; Kalabiński, J. Critical concentration in binary mixtures of limited miscibility. Fluid Phase Equilibria 2021, 540, 112979. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Liquid Crystals; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Palffy-Muhoray, P.; Balzarini, D.A. Refractive index measurements and order parameter determination of the liquid crystal p-ethoxybenzilidene-p-n-butylaniline. Can. J. Phys. 1981, 59, 515–520. [Google Scholar] [CrossRef]
- Jirón, V.; Castellón, E. The experimental average refractive index of liquid crystals and its prediction from the anisotropic indices. Phys. Chem. Chem. Phys. 2022, 24, 7788–7796. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Drozd-Rzoska, A.; Mukherjee, P.K.; Lopez, D.O.; Martinez-Garcia, J.C. Distortions-sensitive analysis of pretransional behavior in n-octyloxycyanobiphenyl (8OCB). J. Phys. Condens. Matter 2013, 25, 245105. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Quasi-tricritical’ and glassy dielectric properties of a nematic liquid crystalline material. Crystals 2020, 10, 297. [Google Scholar] [CrossRef]
- Campbell, F.C. Phase Diagrams: Understanding the Basics; ASM International, Materials Park: Novelty, OH, USA, 2012; ISBN 978-1615038350. [Google Scholar]
- Zhao, J.; Jiang, J. Progress in the solidification of monotectic alloys. Acta Metall. Sin. 2018, 54, 682–700. [Google Scholar] [CrossRef]
- Derimow, N.; Abbaschian, R. Liquid phase separation in high-entropy alloys—A review. Entropy 2018, 20, 890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rai, U.S.; Singh, P.; Singh, N.B. Some thermodynamic aspects of organic eutectic in a monotectic type system. Can. J. Chem. 1987, 65, 2639–2645. [Google Scholar] [CrossRef]
- Rai, U.S.; Rai, R.N. Phase diagram and thermochemical properties of organic eutectic in a monotectic system. Bull. Mater. Sci. 1998, 21, 203–206. [Google Scholar] [CrossRef] [Green Version]
- Rai, U.S.; Pandey, P. Solidification and thermal behaviour of binary organic eutectic and monotectic; succinonitrile–pyrene system. J. Cryst. Growth 2003, 249, 301–308. [Google Scholar] [CrossRef]
- Akbulut, S.; Ocak, Y.; Böyük, U.; Erol, M.; Keşlioğlu, K.; Maraşli, N. Measurement of solid-liquid interfacial energy in the pyrene succinonitrile monotectic system. J. Phys. Condens. Matter 2006, 18, 8503–8512. [Google Scholar] [CrossRef]
- Singh, M.; Rai, R.N.; Rai, U.S. Some physicochemical and thermal studies on organic analog of a nonmetal-nonmetal monotectic alloy; 2-cyanoacetamide–4-chloronitrobenzene system. Am. J. Anal. Chem. 2011, 2, 953–961. [Google Scholar] [CrossRef] [Green Version]
- Abdelkader, H.; Abdallah, O.Y.; Salem, H.; Alani, A.W.G.; Alany, R.G. Eutectic, monotectic and immiscibility systems of nimesulide with water-soluble carriers: Phase equilibria, solid-state characterization and in-vivo/pharmacodynamic evaluation. J. Pharm. Pharmacol. 2014, 66, 1439–1450. [Google Scholar] [CrossRef]
- Huter, C.; Boussinot, G.; Brener, E.A.; Temkin, D.E. Solidification along the interface between demixed liquids in monotectic systems. Phys. Rev. E 2011, 83, 050601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zong, J.; Meng, D. A unified understanding of the cononsolvency of polymers in binary solvent mixtures. Soft Matter 2020, 16, 7789–7796. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Lebedeva, T.N.; Ilyasova, A.N.; Yurov, M.Y.; Golovanov, R.Y.; Artemov, V.V.; Volkov, V.V.; Ezhov, A.A.; Volkov, A.V.; et al. Thermally induced phase separation in semicrystalline polymer solutions: How does the porous structure actually arise? Mater. Today Commun. 2021, 28, 102558. [Google Scholar] [CrossRef]
- Ghebre-Selassies, I.; Martin, C.E.; Zhang, F.; DiNinzio, J. Pharmaceutical Extrusion Technology; CRC Press: Boca-Raton, FL, USA, 2018; ISBN 9780367735081. [Google Scholar]
- Chełkowski, A. Dielectric Physics; PWN-Elsevier: Warsaw, Poland, 1990; ISBN 978-0444997661. [Google Scholar]
- Rzoska, S.J.; Drozd-Rzoska, A.; Starzonek, S. Nonlinear dielectric effect in critical liquids. In Nonlinear Dielectric Spectroscopy: Springer Series Advanced Dielectrics; Richert, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 187–217. ISBN 978-3-319-77574-6. [Google Scholar]
- Gopal, E.S.R. Critical opalescence. Resonance 2000, 4, 37–45. Available online: http://www.chm.bris.ac.uk/webprojects2002/pdavies/Tyndall.html (accessed on 12 December 2022). [CrossRef]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1987; ISBN 978-0195053166. [Google Scholar]
- Kumar, A.; Krishnamurthy, H.R.; Gopal, E.S.R. Equilibrium critical phenomena in binary liquid mixtures. Phys. Rep. 1983, 98, 57–148. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Kalabinski, J. The impact of pressure on low molecular weight near-critical mixtures of limited miscibility. ACS Omega 2020, 5, 20141–20152. [Google Scholar] [CrossRef]
- Kalabiński, J.; Drozd-Rzoska, A.; Rzoska, S.J. New insight into 3-Picoline-Water-Deuterium oxide mixture of limited miscibility with the lower critical consolute temperature. Eur. Phys. J. E 2022, 45, 73. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Szpakiewicz-Szatan, A.; Łoś, J.; Starzonek, S. Supercritical anomalies in liquid ODIC-forming cyclooctanol under the strong electric field. J. Mol. Liq. 2022, 345, 1178491. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Szpakiewicz-Szatan, A.; Łoś, J.; Orzechowski, K. Pretransitional and premelting effects in menthol. Chem. Phys. Lett. 2022, 793, 139461. [Google Scholar] [CrossRef]
- Szpakiewicz-Szatan, A.; Rzoska, S.J.; Drozd-Rzoska, A.; Kalabiński, J. Pretransitional behavior of electrooptic Kerr effect in liquid thymol. Eur. Phys. J. E 2022, 45, 71. [Google Scholar] [CrossRef]
- Beysens, D.; Gbadamassi, M.; Moncef-Bouanz, B. New developments in the study of binary fluids under shear flow. Phys. Rev. A 1983, 28, 2491–2509. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Shear viscosity studies above and below the critical consolute point in a nitrobenzene-decane mixture. Phys. Rev. E 2000, 62, 8071. [Google Scholar] [CrossRef] [PubMed]
- Rowlinson, J.S. Physics of liquids: Are diameters rectilinear? Nature 1986, 319, 362. [Google Scholar] [CrossRef]
- Jüngst, S.; Knuth, B.; Hensel, F. Observation of singular diameters in the coexistence curves of metals. Phys. Rev. Lett. 1985, 55, 2160–2164. [Google Scholar] [CrossRef] [PubMed]
- Reif-Acherman, S. The history of the rectilinear diameter law. Química Nova 2009, 33, 2003–2010. [Google Scholar] [CrossRef] [Green Version]
- Malik, P.; Rzoska, S.J.; Drozd-Rzoska, A.; Jadżyn, J. Critical behavior of dielectric permittivity and electric conductivity in temperature and pressure studies above and below the critical consolute point. J. Chem. Phys. 2003, 118, 9357–9363. [Google Scholar] [CrossRef]
- Cailletet, L.; Mathias, E. Recherches sur les densités de gaz liquéfies et de leurs vapeurs saturées. J. Phys. Theor. Appl. 1886, 5, 549–564. [Google Scholar] [CrossRef]
- Smoluchowski, M. Theorie der opaleszenz von gasen im kritischen zustande, sowie einiger verwandter erscheinungen. Annalen der Physik 1908, 25, 205–226. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Theorie der opaleszenz von homogenen flüssigkeiten und flüs- sigkeitsgemischen in der nähe des kritischen zustandes. Annalen der Physik 1910, 33, 1275–1298. [Google Scholar] [CrossRef] [Green Version]
- Małecki, J.; Zioło, J. Nonlinear dielectric study of pretransitional effects in liquids above the phase transition temperature. Chem. Phys. 1978, 35, 187–192. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Chrapeć, J.; Zioło, J. Nonlinear dielectric effect in a pure and in a nitrobenzene-doped critical solution of perfluoromethylcyclohexane-carbon tetrachloride. J. Phys. Chem. 1988, 92, 2064–2066. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Chrapeć, J.; Zioło, J. Nonlinear dielectric effect in the vicinity of the critical point of binary and doped critical solutions. Physica A 1986, 139, 569–584. [Google Scholar] [CrossRef]
- Chrapeć, J.; Rzoska, S.J. Nonlinear dielectric effect investigation in the immediate vicinity of the critical point. Phys. Lett. A 1989, 139, 343–346. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Rzoska, A.A. Pretransitional behavior of nonlinear dielectric effect for the liquid-solid transition in nitrobenzene. Phys. Rev. E 2016, 93, 06213. [Google Scholar] [CrossRef] [PubMed]
- Chrapeć, J.; Rzoska, S.J.; Zioło, J. Pseudospinodal curve for binary solutions determined from the nonlinear dielectric effect. Chem. Phys. 1987, 111, 155–160. [Google Scholar] [CrossRef]
- Maurel, P.; Price, A.H. Dipole moment of n-(p-methoxybenzylidene)-p-butylaniline. J. Chem. Soc. Faraday Trans. 1973, 2, 1486–1490. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Drozd-Rzoska, A. Dual field nonlinear dielectric spectroscopy in a glass forming EPON 828 epoxy resin. J. Phys. Condens. Matter 2011, 24, 035101. [Google Scholar] [CrossRef]
- Chen, D.; Porada, J.H.; Hooper, J.B.; Klittnick, A.; Shen, Y.; Tuchband, M.R.; Korblova, E.; Bedrov, D.; Walba, D.M.; Glaser, M.A.; et al. Chiral heliconical ground state of nanoscale pitch in a nematic liquid crystal of achiral molecular dimers. Proc. Natl. Acad. Sci. USA 2013, 110, 15931–15936. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Singh, G.; Agra-Kooijman, D.M.; Gao, M.; Bisoyi, H.K.; Xue, C.; Fish, M.R.; Kumar, S.; Li, Q. Room temperature heliconical twist-bend nematic liquid crystal. CrystEngComm 2015, 17, 2778–2782. [Google Scholar] [CrossRef]
- Paterson, D.A.; Xiang, J.; Singh, G.; Walker, R.; Agra-Kooijman, D.M.; Martinez-Felipe, A.; Gao, M.; Storey, J.M.D.; Kumar, S.; Lavrentovich, O.D.; et al. Reversible isothermal twist–bend nematic–nematic phase transition driven by the photoisomerization of an azobenzene-based nonsymmetric liquid crystal dimer. J. Am. Chem. Soc. 2016, 138, 5283–5289. [Google Scholar] [CrossRef]
- Singh, G.; Fu, J.; Agra-Kooijman, D.M.; Song, J.-K.; Vengatesan, M.R.; Srinivasarao, M.; Fisch, M.R.; Kumar, S. X-ray and Raman scattering study of orientational order in nematic and heliconical nematic liquid crystals. Phys. Rev. E 2016, 94, 060701. [Google Scholar] [CrossRef] [Green Version]
- Agra-Kooijman, D.M.; Singh, G.; Fisch, M.R.; Vengatesan, M.R.; Song, J.-K.; Kumar, S. The oblique chiral nematic phase in calamitic bimesogens. Liq. Cryst. 2017, 44, 191–203. [Google Scholar] [CrossRef]
- Chen, X.; Korblova, E.; Dong, D.; Wei, X.; Shao, R.; Radzihovsky, L.; Glaser, M.A.; Maclennan, J.E.; Bedrov, D.; Walba, D.M.; et al. First principles experimental demonstration of ferroelectricity in a thermotropic nematic liquid crystal: Polar domains and striking electro-optics. Proc. Natl. Acad. Sci. USA 2020, 117, 14021–14031. [Google Scholar] [CrossRef] [PubMed]
- Lavrentovich, O.D. Ferroelectric nematic liquid crystal, a century in waiting. Proc. Natl. Acad. Sci. USA 2020, 117, 14629–14631. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Nishikawa, H.; Kougo, J.; Zhou, J.; Dai, S.; Tang, W.; Zhao, X.; Hisai, Y.; Huang, M.; Aya, S. Development of ferroelectric nematic fluids with giant-ε dielectricity and nonlinear optical properties. Sci. Adv. 2021, 7, eabf5047. [Google Scholar] [CrossRef]
- Chen, X.; Korblova, E.; Glaser, M.A.; MacLennan, J.E.; Walba, D.M.; Clark, N.A. Polar in-plane surface orientation of a ferroelectric nematic liquid crystal: Polar monodomains and twisted state electro-optics. Proc. Natl. Acad. Sci. USA 2021, 118, e2104092118. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J.; Drozd-Rzoska, A. Criticality-related fundamental bases for new generations of gas-liquid, liquid-liquid, and liquid (LE) extraction technologies. Eur. Phys. J. E 2022, 45, 67. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp-Smith, A.R.; Veatch, S.L.; Keller, S.L. An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochim. Biophys. Acta 2009, 1788, 53–63. [Google Scholar] [CrossRef] [PubMed]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalabiński, J.; Drozd-Rzoska, A.; Rzoska, S.J. Phase Equilibria and Critical Behavior in Nematogenic MBBA—Isooctane Monotectic-Type Mixtures. Int. J. Mol. Sci. 2023, 24, 2065. https://doi.org/10.3390/ijms24032065
Kalabiński J, Drozd-Rzoska A, Rzoska SJ. Phase Equilibria and Critical Behavior in Nematogenic MBBA—Isooctane Monotectic-Type Mixtures. International Journal of Molecular Sciences. 2023; 24(3):2065. https://doi.org/10.3390/ijms24032065
Chicago/Turabian StyleKalabiński, Jakub, Aleksandra Drozd-Rzoska, and Sylwester J. Rzoska. 2023. "Phase Equilibria and Critical Behavior in Nematogenic MBBA—Isooctane Monotectic-Type Mixtures" International Journal of Molecular Sciences 24, no. 3: 2065. https://doi.org/10.3390/ijms24032065