New Approximation Methods Based on Fuzzy Transform for Solving SODEs: II
Abstract
:1. Introduction
2. Basic Concepts
- 1.
- (positivity and locality)— if and if ;
- 2.
- (continuity)— is continuous on ;
- 3.
- (covering)—for .
- 4.
- for all ;
- 5.
- and for all ;
New Iterative Method
3. New Representations for Basic Functions of FzT
3.1. Generalized Uniform Fuzzy Partitions with the Generalized Normal Case
3.2. Simpler Form of F-Transform Components Based on Generalized Uniform Fuzzy Partitions with the Generalized Normal Case
- Select the generating function K which is assumed to be even, continuous and if .
- Specify the value , where to get the normal generating function K and then compute the value , where .
- If conditions holds, then construct generalized uniform fuzzy partitions of by .
4. New Fuzzy Numerical Methods for Solving SODEs
- Specify the number n of components and compute the step . If we want to obtain as best approximation of f as possible, then n should be large.
- Construct the nodes , where .
- Select the shape of basic functions. This is achieved by selecting the shape of generating function.
- Construct a h-uniform generalized fuzzy partition of by new representations of basic functions are defined by Definition 4.
4.1. Numerical Scheme I: Modified Trapezoidal Rule Based on FzT and NIM for SODEs
4.2. Numerical Scheme II: Modified 2-Step Adams Moulton Method Based on FzT and NIM for SODEs
4.3. Numerical Scheme III: Modified 3-Step Adams Moulton Method Based on FzT and NIM for SODEs
4.4. Error Analysis of Numerical Scheme I for SODEs
5. Applications
- Moreover, comparison of MSE for Examples 2 and 3 shown in Table 6. It is observed that the new fuzzy approximation methods yield more accurate results in comparison with the classical Trapezoidal rule (one step) and classical Adams Moulton method (two and three steps). Hence, the new fuzzy approximation methods provide alternative techniques for solving SODEs with better results.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Algorithms
| INPUT: ; ; endpoints ; integer N; initial condition ; m. |
| Step 1 Set ; ; ; ; ; . |
| Step 2 Define the generalized uniform fuzzy partitions as . |
| Step 3 for to N do Steps 04–15. |
| end. |
| OUTPUT: Approximation X and Y to x and y, respectively at the () values of t. |
| INPUT: ; ; endpoints ; integer N; initial condition ; m. |
| Step 1 Set ; ; ; ; ; . |
| Step 2 Define the generalized uniform fuzzy partitions as . |
| Step 3 Set ; . (In the case of no exact solutions, compute and using Algorithm 1.) |
| Step 4 for to N do Steps 05–18. |
| end. |
| OUTPUT: Approximation X and Y to x and y, respectively at the () values of t. |
| INPUT: ; ; endpoints ; integer N; initial condition ; m. |
| Step 1 Set ; ; ; ; ; . |
| Step 2 Define the generalized uniform fuzzy partitions as . |
| Step 3 Set ; ; ; . (In the case of no exact solutions, compute , , and using Algorithm 1 or 2.) |
| Step 4 for to N do Steps 05–20. |
| end. |
| OUTPUT: Approximation X and Y to x and y, respectively at the () values of t. |
References
- Ahmad, M.Z.; Hasan, M.K.; Baets, B.D. Analytical and numerical solutions of fuzzy differential equations. Inf. Sci. 2013, 236, 156–167. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]
- Sukale, Y.; Daftardar-Gejji, V. New Numerical Methods for Solving Differential Equations. Int. J. Appl. Comput. Math. 2017, 3, 1639–1660. [Google Scholar] [CrossRef]
- Perfilieva, I.; Haldeeva, E. Fuzzy transformation. In Proceedings of the Joint 9th IFSA World Congress and 20th NAFIPS International Conference, Vancouver, BC, Canada, 25–28 July 2001; Volume 4, pp. 1946–1948. [Google Scholar]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Stefanini, L. F-transform with parametric generalized fuzzy partitions. Fuzzy Sets Syst. 2011, 180, 98–120. [Google Scholar] [CrossRef]
- Holčapek, M.; Tichý, T. A smoothing filter based on fuzzy transform. Fuzzy Sets Syst. 2011, 180, 69–97. [Google Scholar] [CrossRef] [Green Version]
- Perfilieva, I.; Daňková, M.; Bede, B. Towards a higher degree F-transform. Fuzzy Sets Syst. 2011, 180, 3–19. [Google Scholar] [CrossRef]
- Bede, B.; Rudas, I.J. Approximation properties of fuzzy transforms. Fuzzy Sets Syst. 2011, 180, 20–40. [Google Scholar] [CrossRef]
- Kokainis, M.; Asmuss, S. Higher Degree F-transforms Based on B-splines of Two Variables. In Information Processing and Management of Uncertainty in Knowledge-Based Systems; Carvalho, J.P., Lesot, M.J., Kaymak, U., Vieira, S., Bouchon-Meunier, B., Yager, R.R., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 648–659. [Google Scholar]
- Hurtik, P.; Perfilieva, I. Image Compression Methodology Based on Fuzzy Transform. In International Joint Conference CISIS’12-ICEUTE’12-SOCO’12 Special Sessions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 525–532. [Google Scholar]
- Patané, G. Fuzzy transform and least-squares approximation: Analogies, differences, and generalizations. Fuzzy Sets Syst. 2011, 180, 41–54. [Google Scholar] [CrossRef]
- Holčapek, M.; Perfilieva, I.; Novák, V.; Kreinovich, V. Necessary and sufficient conditions for generalized uniform fuzzy partitions. Fuzzy Sets Syst. 2015, 277, 97–121. [Google Scholar] [CrossRef] [Green Version]
- Khastan, A. A new representation for inverse fuzzy transform and its application. Soft Comput. 2017, 21, 3503–3512. [Google Scholar] [CrossRef]
- Ziari, S.; Perfilieva, I. On the approximation properties of fuzzy transform. J. Intell. Fuzzy Syst. 2017, 33, 171–180. [Google Scholar] [CrossRef]
- Alkasasbeh, H.A.; Perfilieva, I.; Ahmad, M.Z.; Yahya, Z.R. New fuzzy numerical methods for solving Cauchy problems. Appl. Syst. Innov. 2018, 1, 15. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transform: Application to the Reef growth problem. In Fuzzy Logic in Geology; Demicco, R.V., Klir, G.J., Eds.; Academic Press: Amsterdam, The Netherlands, 2003; Chapter 9; pp. 275–300. [Google Scholar]
- Khastan, A.; Perfilieva, I.; Alijani, Z. A new fuzzy approximation method to Cauchy problems by fuzzy transform. Fuzzy Sets Syst. 2016, 288, 75–95. [Google Scholar] [CrossRef]
- Chen, W.; Shen, Y. Approximate solution for a class of second-order ordinary differential equations by the fuzzy transform. J. Intell. Fuzzy Syst. 2014, 27, 73–82. [Google Scholar]
- Alireza, K.; Zahra, A.; Irina, P. Fuzzy transform to approximate solution of two-point boundary value problems. Math. Meth. Appl. Sci. 2017, 40, 6147–6154. [Google Scholar]
- Holcapek, M.; Valášek, R. Numerical solution of partial differential equations with the help of fuzzy transform technique. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Hodáková, P.; Perfilieva, I. F1-transform of Functions of Two Variables. In EUSFLAT 2013; Atlantis Press: Milan, Italy, 2013; pp. 547–553. [Google Scholar]
- Perfilieva, I.; Hodáková, P.; Hurtík, P. Differentiation by the F-transform and application to edge detection. Fuzzy Sets Syst. 2016, 288, 96–114. [Google Scholar] [CrossRef]
- Ghosh, R.; Chowdhury, S.; Gorain, G.C.; Kar, S. Uniform stabilization of the telegraph equation with a support by fuzzy transform method. QSci. Connect 2014, 2014, 19. [Google Scholar] [CrossRef]
- Ezzati, R.; Mokhtari, F.; Maghasedi, M. Numerical solution of Volterra-Fredholm integral equations with the help of inverse and direct discrete fuzzy transforms and collocation technique. Int. J. Ind. Math. 2012, 4, 221–229. [Google Scholar]
- Zeinali, M.; Alikhani, R.; Shahmorad, S.; Bahrami, F.; Perfilieva, I. On the structural properties of Fm-transform with applications. Fuzzy Sets Syst. 2018, 342, 32–52. [Google Scholar] [CrossRef]
- Baleanu, D.; Agheli, B.; Adabitabar Firozja, M.; Al Qurashi, M.M. A method for solving nonlinear Volterra’s population growth model of noninteger order. Adv. Differ. Equ. 2017, 2017, 368. [Google Scholar] [CrossRef]
- Tomasiello, S. An alternative use of fuzzy transform with application to a class of delay differential equations. Int. J. Comput. Math. 2017, 94, 1719–1726. [Google Scholar] [CrossRef]
- Alijani, Z.; Khastan, A.; Khattri, S.K.; Tomasiello, S. Fuzzy Transform to Approximate Solution of Boundary Value Problems via Optimal Coefficients. In Proceedings of the 2017 International Conference on High Performance Computing Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 466–471. [Google Scholar]
- Tomasiello, S. A First Investigation on the Dynamics of Two Delayed Neurons through Fuzzy Transform Approximation. In Proceedings of the 2017 International Conference on High Performance Computing Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 460–465. [Google Scholar]
- Tomasiello, S.; Gaeta, M.; Loia, V. Quasi–consensus in Second–Order Multi–agent Systems with Sampled Data Through Fuzzy Transform. J. Uncertain Syst. 2016, 10, 243–250. [Google Scholar]
- Noor, M.A.; Noor, K.I.; Mohyud-Din, S.T.; Shabbir, A. An iterative method with cubic convergence for nonlinear equations. Appl. Math. Comput. 2006, 183, 1249–1255. [Google Scholar] [CrossRef]
- Saeed, R.K.; Aziz, K.M. An iterative method with quartic convergence for solving nonlinear equations. Appl. Math. Comput. 2008, 202, 435–440. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Convergence of the New Iterative Method. Int. J. Differ. Equ. 2011, 2011, 10. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Sukale, Y.; Bhalekar, S. A new predictor-corrector method for fractional differential equations. Appl. Math. Comput. 2014, 244, 158–182. [Google Scholar] [CrossRef]
- Alkasasbeh, H.A.; Perfilieva, I.; Ahmad, M.Z.; Yahya, Z.R. New approximation methods based on fuzzy transform for solving SODEs: I. Appl. Syst. Innov. 2018, 1, 29. [Google Scholar]
- Perfilieva, I.; Holčapek, M.; Kreinovich, V. A new reconstruction from the F-transform components. Fuzzy Sets Syst. 2016, 288, 3–25. [Google Scholar] [CrossRef]
- Perfilieva, I. F-Transform. In Handbook of Computational Intelligence; Kacprzyk, J., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Chapter 7; pp. 113–130. [Google Scholar]
- Jahedi, S.; Mehdipour, M.; Rafizadeh, R. Approximation of integrable function based on ø-transform. Soft Comput. 2013, 18, 2015–2022. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 3rd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Bougoffa, L. Solvability of the predator and prey system with variable coefficients and comparison of the results with modified decomposition. Appl. Math. Comput. 2006, 182, 383–387. [Google Scholar] [CrossRef]
- Yusufoğlu, E.; Erbaş, B. He’s variational iteration method applied to the solution of the prey and predator problem with variable coefficients. Phys. Lett. A 2008, 372, 3829–3835. [Google Scholar] [CrossRef]
- González-Parra, G.C.; Arenas, A.J.; Cogollo, M.R. Numerical-analytical solutions of predator-prey models. WSEAS Trans. Biol. Biomed. 2013, 10, 79–87. [Google Scholar]
- Hodakova, P.; Perfilieva, I.; Valasek, R. A new approach to fuzzy boundary value problem. In Uncertainty Modelling in Knowledge Engineering and Decision Making; World Scientific Proceedings Series on Computer Engineering and Information Science; World Scientific: Singapore, 2016; pp. 276–281. [Google Scholar]
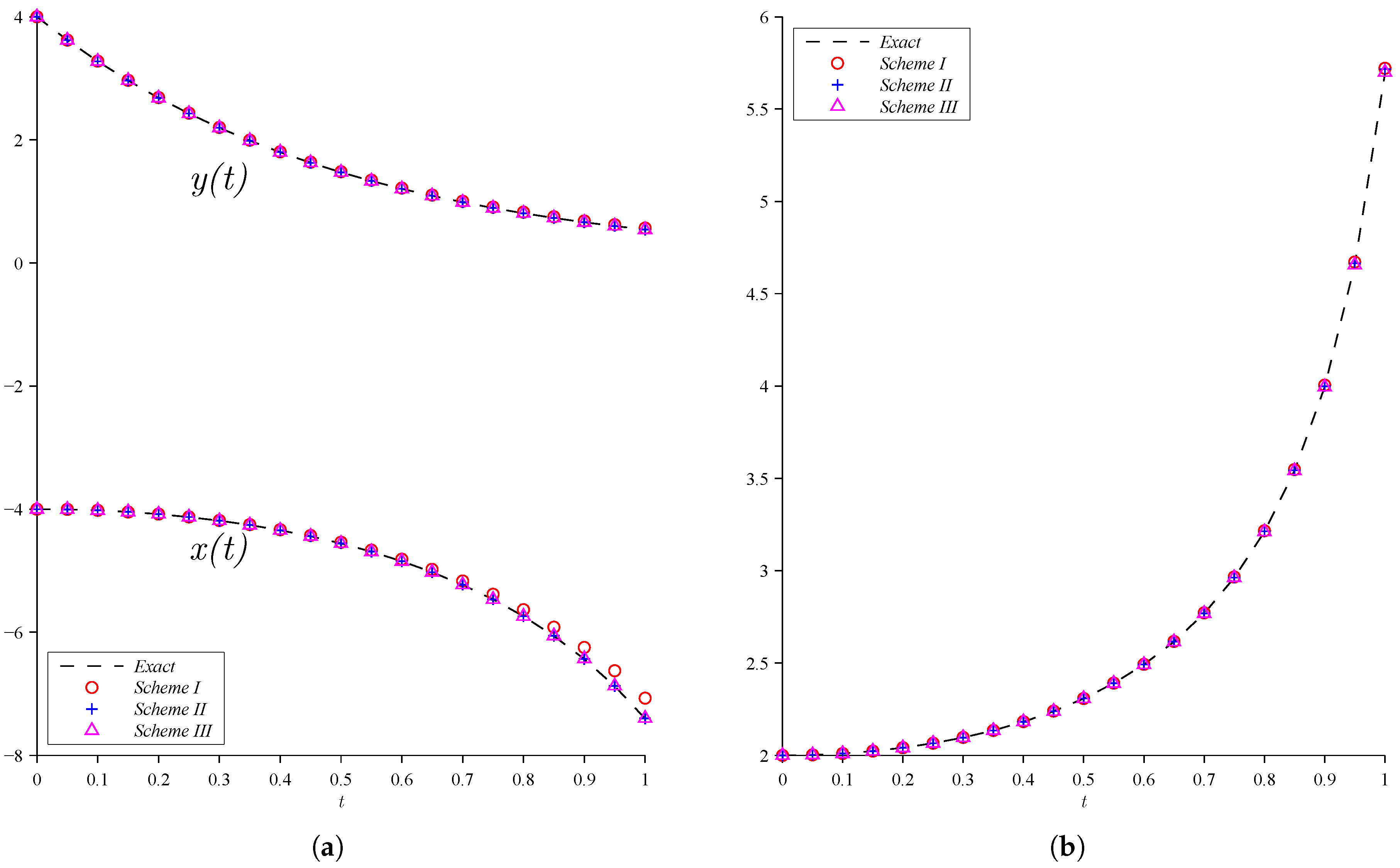
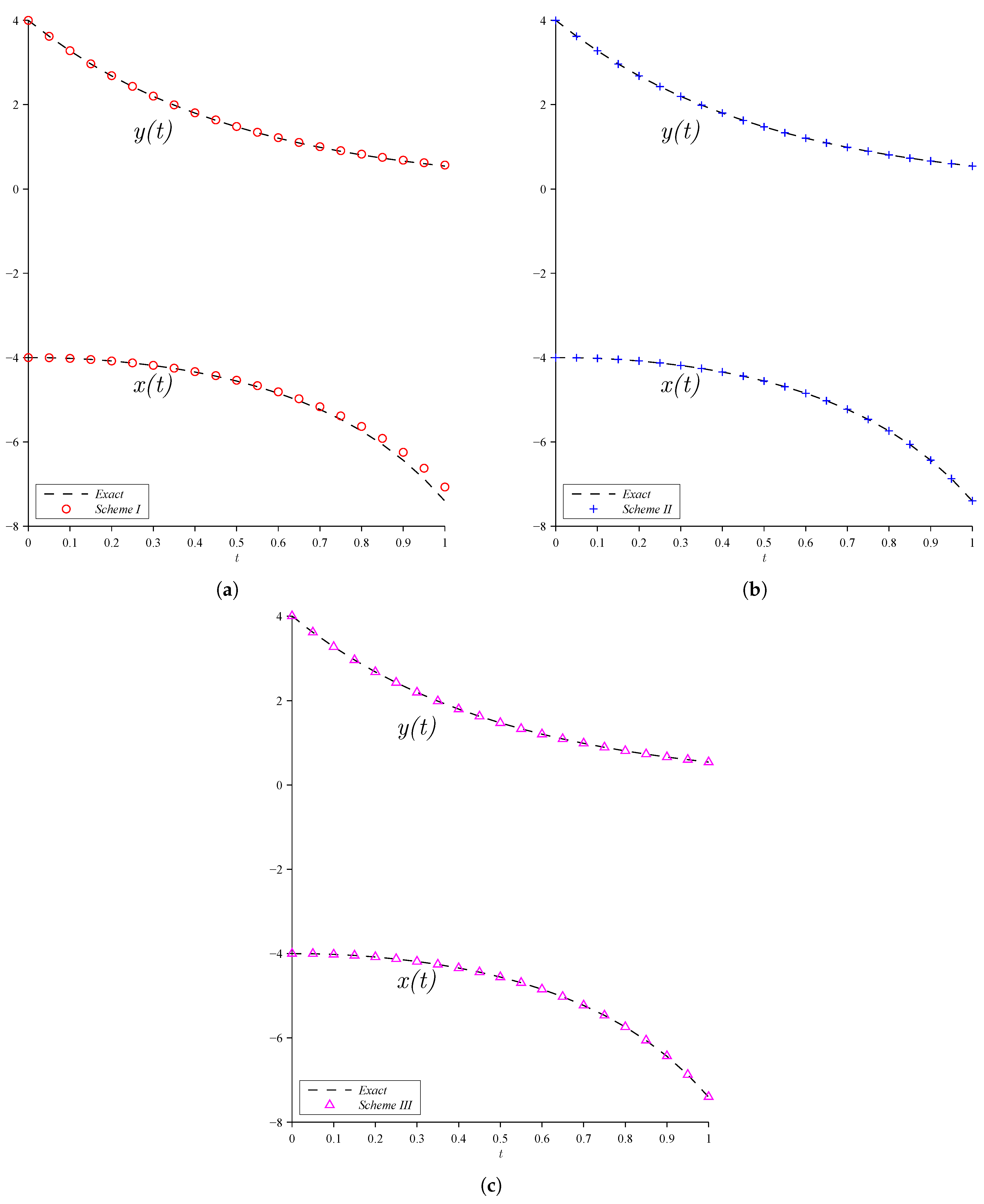
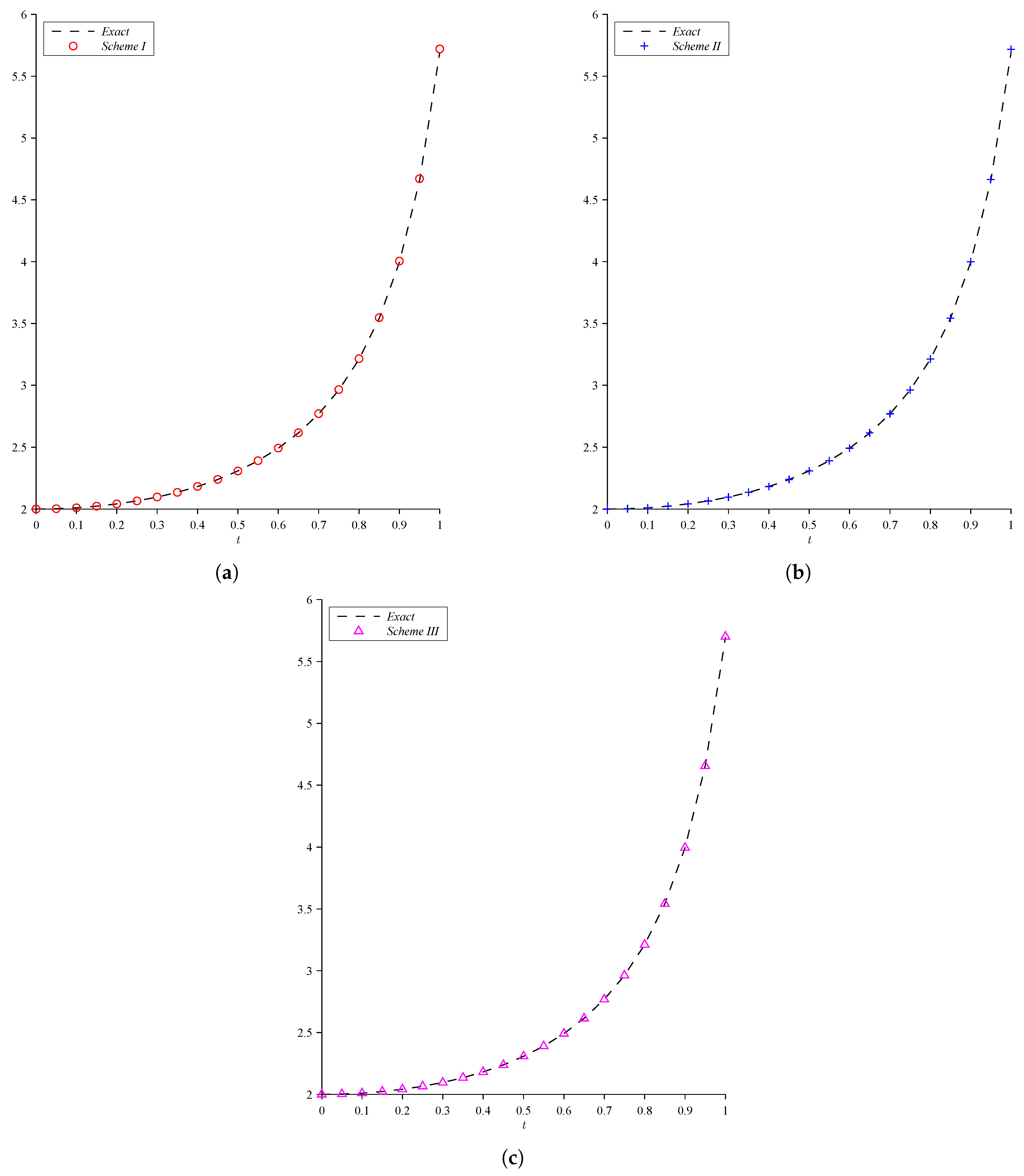
| Solution | Proposed Scheme I | Proposed Scheme II | Proposed Scheme III | Trap | 2-Step Adams | 3-Step Adams | |
|---|---|---|---|---|---|---|---|
| 0.00 | −4.00000 | −4.00000 | −4.00000 | −4.00000 | −4.00000 | −4.00000 | −4.00000 |
| 0.05 | −4.00501 | −4.00506 | −4.00501 | −4.00501 | −4.00714 | −4.00501 | −4.00501 |
| 0.10 | −4.02008 | −4.02059 | −4.02011 | −4.02008 | −4.02627 | −4.02187 | −4.02008 |
| 0.15 | −4.04543 | −4.04589 | −4.04536 | −4.04536 | −4.05752 | −4.04875 | −4.04703 |
| 0.20 | −4.08136 | −4.08128 | −4.08121 | −4.08119 | −4.10134 | −4.08610 | −4.08434 |
| 0.25 | −4.12834 | −4.12721 | −4.12813 | −4.12811 | −4.15850 | −4.13442 | −4.13261 |
| 0.30 | −4.18701 | −4.18423 | −4.18673 | −4.18670 | −4.23015 | −4.19440 | −4.19250 |
| 0.35 | −4.25816 | −4.25304 | −4.25783 | −4.25779 | −4.31783 | −4.26691 | −4.26487 |
| 0.40 | −4.34282 | −4.33453 | −4.34243 | −4.34236 | −4.42361 | −4.35300 | −4.35077 |
| 0.45 | −4.44224 | −4.42976 | −4.44178 | −4.44170 | −4.55014 | −4.45399 | −4.45151 |
| 0.50 | −4.55798 | −4.54001 | −4.55745 | −4.55733 | −4.70086 | −4.57151 | −4.56871 |
| 0.55 | −4.69195 | −4.66686 | −4.69134 | −4.69117 | −4.88023 | −4.70755 | −4.70433 |
| 0.60 | −4.84651 | −4.81220 | −4.84581 | −4.84558 | −5.09399 | −4.86455 | −4.86079 |
| 0.65 | −5.02460 | −4.97833 | −5.02378 | −5.02346 | −5.34964 | −5.04556 | −5.04112 |
| 0.70 | −5.22984 | −5.16805 | −5.22887 | −5.22845 | −5.65700 | −5.25435 | −5.24903 |
| 0.75 | −5.46680 | −5.38480 | −5.46565 | −5.46508 | −6.02912 | −5.49569 | −5.48924 |
| 0.80 | −5.74130 | −5.63286 | −5.73990 | −5.73914 | −6.48349 | −5.77559 | −5.76768 |
| 0.85 | −6.06076 | −5.91759 | −6.05906 | −6.05803 | −7.04390 | −6.10182 | −6.09202 |
| 0.90 | −6.43490 | −6.24582 | −6.43281 | −6.43141 | −7.74310 | −6.48450 | −6.47222 |
| 0.95 | −6.87660 | −6.62636 | −6.87400 | −6.87209 | −8.62699 | −6.93706 | −6.92148 |
| 1.00 | −7.40326 | −7.07221 | −7.40106 | −7.39831 | −9.76103 | −7.47766 | −7.45769 |
| Solution | Proposed Scheme I | Proposed Scheme II | Proposed Scheme III | Trap | 2-Step Adams | 3-Step Adams | |
|---|---|---|---|---|---|---|---|
| 0.00 | 4.00000 | 4.00000 | 4.00000 | 4.00000 | 4.00000 | 4.00000 | 4.00000 |
| 0.05 | 3.61935 | 3.62135 | 3.61935 | 3.61935 | 3.62045 | 3.61935 | 3.61935 |
| 0.10 | 3.27492 | 3.27848 | 3.27485 | 3.27492 | 3.27766 | 3.27601 | 3.27492 |
| 0.15 | 2.96327 | 2.96802 | 2.96314 | 2.96327 | 2.96757 | 2.96496 | 2.96415 |
| 0.20 | 2.68128 | 2.68698 | 2.68112 | 2.68124 | 2.68671 | 2.68326 | 2.68261 |
| 0.25 | 2.42612 | 2.43262 | 2.42595 | 2.42607 | 2.43201 | 2.42819 | 2.42769 |
| 0.30 | 2.19525 | 2.20247 | 2.19508 | 2.19520 | 2.20079 | 2.19724 | 2.19688 |
| 0.35 | 1.98634 | 1.99425 | 1.98619 | 1.98630 | 1.99067 | 1.98815 | 1.98792 |
| 0.40 | 1.79732 | 1.80593 | 1.79718 | 1.79729 | 1.79951 | 1.79888 | 1.79875 |
| 0.45 | 1.62628 | 1.63564 | 1.62616 | 1.62627 | 1.62541 | 1.62754 | 1.62752 |
| 0.50 | 1.47152 | 1.48170 | 1.47143 | 1.47153 | 1.46664 | 1.47245 | 1.47253 |
| 0.55 | 1.33148 | 1.34257 | 1.33142 | 1.33153 | 1.32166 | 1.33207 | 1.33224 |
| 0.60 | 1.20478 | 1.21688 | 1.20474 | 1.20485 | 1.18908 | 1.20500 | 1.20526 |
| 0.65 | 1.09013 | 1.10337 | 1.09012 | 1.09023 | 1.06762 | 1.08998 | 1.09033 |
| 0.70 | 0.98639 | 1.00091 | 0.98641 | 0.98652 | 0.95615 | 0.98587 | 0.98632 |
| 0.75 | 0.89252 | 0.90848 | 0.89257 | 0.89269 | 0.85366 | 0.89163 | 0.89217 |
| 0.80 | 0.80759 | 0.82515 | 0.80766 | 0.80779 | 0.75923 | 0.80632 | 0.80696 |
| 0.85 | 0.73073 | 0.75011 | 0.73084 | 0.73097 | 0.67208 | 0.72910 | 0.72984 |
| 0.90 | 0.66120 | 0.68260 | 0.66133 | 0.66148 | 0.59150 | 0.65919 | 0.66004 |
| 0.95 | 0.59827 | 0.62195 | 0.59844 | 0.59860 | 0.51692 | 0.59590 | 0.59686 |
| 1.00 | 0.54134 | 0.56745 | 0.54145 | 0.54163 | 0.44787 | 0.53860 | 0.53969 |
| Solution | Proposed Scheme I | Proposed Scheme II | Proposed Scheme III | Trap | 2-Step Adams | 3-Step Adams | |
|---|---|---|---|---|---|---|---|
| 0.00 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 |
| 0.05 | 2.00250 | 2.00257 | 2.00250 | 2.00250 | 2.00250 | 2.00250 | 2.00250 |
| 0.10 | 2.01008 | 2.01016 | 2.01007 | 2.01008 | 2.01005 | 2.01006 | 2.01008 |
| 0.15 | 2.02289 | 2.02299 | 2.02289 | 2.02289 | 2.02279 | 2.02285 | 2.02286 |
| 0.20 | 2.04124 | 2.04138 | 2.04124 | 2.04124 | 2.04101 | 2.04117 | 2.04118 |
| 0.25 | 2.06557 | 2.06577 | 2.06558 | 2.06558 | 2.06511 | 2.06546 | 2.06547 |
| 0.30 | 2.09650 | 2.09676 | 2.09652 | 2.09651 | 2.09567 | 2.09633 | 2.09633 |
| 0.35 | 2.13485 | 2.13520 | 2.13488 | 2.13486 | 2.13344 | 2.13459 | 2.13459 |
| 0.40 | 2.18171 | 2.18218 | 2.18176 | 2.18172 | 2.17942 | 2.18132 | 2.18132 |
| 0.45 | 2.23852 | 2.23915 | 2.23860 | 2.23854 | 2.23493 | 2.23795 | 2.23796 |
| 0.50 | 2.30720 | 2.30803 | 2.30731 | 2.30722 | 2.30167 | 2.30637 | 2.30638 |
| 0.55 | 2.39031 | 2.39140 | 2.39047 | 2.39034 | 2.38192 | 2.38910 | 2.38911 |
| 0.60 | 2.49133 | 2.49279 | 2.49157 | 2.49138 | 2.47868 | 2.48956 | 2.48957 |
| 0.65 | 2.61513 | 2.61708 | 2.61549 | 2.61520 | 2.59605 | 2.61251 | 2.61251 |
| 0.70 | 2.76863 | 2.77126 | 2.76917 | 2.76873 | 2.73967 | 2.76465 | 2.76466 |
| 0.75 | 2.96202 | 2.96563 | 2.96288 | 2.96218 | 2.91754 | 2.95585 | 2.95584 |
| 0.80 | 3.21093 | 3.21600 | 3.21235 | 3.21120 | 3.14130 | 3.20103 | 3.20099 |
| 0.85 | 3.54059 | 3.54791 | 3.54308 | 3.54108 | 3.42845 | 3.52398 | 3.52386 |
| 0.90 | 3.99443 | 4.00539 | 3.99914 | 3.99541 | 3.80653 | 3.96482 | 3.96449 |
| 0.95 | 4.65413 | 4.67130 | 4.66407 | 4.65640 | 4.32100 | 4.59671 | 4.59578 |
| 1.00 | 5.69348 | 5.72071 | 5.71719 | 5.69904 | 5.05197 | 5.56751 | 5.56473 |
| Solution | Proposed Scheme I | Proposed Scheme II | Proposed Scheme III | Trap 1 | 2-Step Adams 2 | 3-Step Adams 3 | |
|---|---|---|---|---|---|---|---|
| 0.00 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 | 2.00000 |
| 0.05 | 2.00250 | 2.00257 | 2.00250 | 2.00250 | 2.00250 | 2.00250 | 2.00250 |
| 0.10 | 2.01008 | 2.01016 | 2.01007 | 2.01008 | 2.01005 | 2.01006 | 2.01008 |
| 0.15 | 2.02289 | 2.02299 | 2.02289 | 2.02289 | 2.02279 | 2.02285 | 2.02286 |
| 0.20 | 2.04124 | 2.04138 | 2.04124 | 2.04124 | 2.04101 | 2.04117 | 2.04118 |
| 0.25 | 2.06557 | 2.06577 | 2.06558 | 2.06558 | 2.06511 | 2.06546 | 2.06547 |
| 0.30 | 2.09650 | 2.09676 | 2.09652 | 2.09651 | 2.09567 | 2.09633 | 2.09633 |
| 0.35 | 2.13485 | 2.13520 | 2.13488 | 2.13486 | 2.13344 | 2.13459 | 2.13459 |
| 0.40 | 2.18171 | 2.18218 | 2.18176 | 2.18172 | 2.17942 | 2.18132 | 2.18132 |
| 0.45 | 2.23852 | 2.23915 | 2.23860 | 2.23854 | 2.23493 | 2.23795 | 2.23796 |
| 0.50 | 2.30720 | 2.30803 | 2.30731 | 2.30722 | 2.30167 | 2.30637 | 2.30638 |
| 0.55 | 2.39031 | 2.39140 | 2.39047 | 2.39034 | 2.38192 | 2.38910 | 2.38911 |
| 0.60 | 2.49133 | 2.49279 | 2.49157 | 2.49138 | 2.47868 | 2.48956 | 2.48957 |
| 0.65 | 2.61513 | 2.61708 | 2.61549 | 2.61520 | 2.59605 | 2.61251 | 2.61251 |
| 0.70 | 2.76863 | 2.77126 | 2.76917 | 2.76873 | 2.73967 | 2.76465 | 2.76466 |
| 0.75 | 2.96202 | 2.96563 | 2.96288 | 2.96218 | 2.91754 | 2.95585 | 2.95584 |
| 0.80 | 3.21093 | 3.21600 | 3.21235 | 3.21120 | 3.14130 | 3.20103 | 3.20099 |
| 0.85 | 3.54059 | 3.54791 | 3.54308 | 3.54108 | 3.42845 | 3.52398 | 3.52386 |
| 0.90 | 3.99443 | 4.00539 | 3.99914 | 3.99541 | 3.80653 | 3.96482 | 3.96449 |
| 0.95 | 4.65413 | 4.67130 | 4.66407 | 4.65640 | 4.32100 | 4.59671 | 4.59578 |
| 1.00 | 5.69348 | 5.72071 | 5.71719 | 5.69904 | 5.05197 | 5.56751 | 5.56473 |
| (a) The Values of MSE offor SODEs | |||||||
| Case | Proposed Scheme for | Classical Method for | |||||
| I | II | III | Trapezoidal Rule | 2-Step Adams Moulton | 3-Step Adams Moulton | ||
| Ex.1 | 1.21569 × | 1.21112 × | 3.71739 × | 5.99915 × | 8.37463 × | 4.72086 × | |
| Ex.2 | 6.02153 × | 3.29699 × | 1.77640 × | 2.75574 × | 9.75470 × | 1.01541 × | |
| (b) The Values of MSE of for SODEs | |||||||
| Case | Proposed Scheme for | Classical Method for | |||||
| I | II | III | Trapezoidal Rule | 2-Step Adams Moulton | 3-Step Adams Moulton | ||
| Ex.1 | 1.80417 × | 1.20902 × | 2.08739 × | 1.40165 × | 2.25155 × | 1.09674 × | |
| Ex.2 | 6.02153 × | 3.29699 × | 1.77640 × | 2.75574 × | 9.75470 × | 1.01541 × | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
ALKasasbeh, H.; Perfilieva, I.; Ahmad, M.Z.; Yahya, Z.R. New Approximation Methods Based on Fuzzy Transform for Solving SODEs: II. Appl. Syst. Innov. 2018, 1, 30. https://doi.org/10.3390/asi1030030
ALKasasbeh H, Perfilieva I, Ahmad MZ, Yahya ZR. New Approximation Methods Based on Fuzzy Transform for Solving SODEs: II. Applied System Innovation. 2018; 1(3):30. https://doi.org/10.3390/asi1030030
Chicago/Turabian StyleALKasasbeh, Hussein, Irina Perfilieva, Muhammad Zaini Ahmad, and Zainor Ridzuan Yahya. 2018. "New Approximation Methods Based on Fuzzy Transform for Solving SODEs: II" Applied System Innovation 1, no. 3: 30. https://doi.org/10.3390/asi1030030






