Micromechanical Analysis for Two-Phase Copper-Silver Composites under Large Deformations

Abstract

This study presents a homogenization based on micromechanics approach for a two-phase copper (Cu)-silver (Ag) composite undergoing finite deformations. In this approach, the high-fidelity generalized method of cells (HFGMC) is implemented for the prediction of the effective behavior of two cold-drawn Cu-Ag composites with different drawing strains and to obtain the field (deformation gradient and stress) distributions in the composite. Both metals (Cu or Ag) are rate-dependent crystal plasticity material constituents. HFGMC is applied for studying the deformation behavior of two-phase Cu-Ag composites under uniaxial compression. The micromechanical approach has been verified by comparison with experimental and finite element simulation results. Results in terms of deformation behavior and field distributions are given for two different cold-drawn composites.

1. Introduction

In the last few decades, nonlinear micromechanical models of multiphase composite materials have been the subject of interest for many investigations. The aim of these models is to study the effect of volume fraction and the interphase effects on generating the nonlinear effective response of the composite materials. A detailed review of this class of nonlinear micromechanical methods can be found in [1,2,3], among several others. In addition, the prediction of the local deformation process of periodic alternate multiphase materials requires the detailed description of the spacial description of the soft and hard phases subject to different kinds of loading [4]. Hence, the formation of constitutive equations that govern the large deformations of composite materials, which consist of elasto-viscoplastic phases, is necessary for the modeling and analysis of their deformation behavior. Eutectic Cu-Ag composites form an example of a layered two-phase composite structure that consists of alternate layers of Cu and Ag lamellae inside the grains.

Semi-analytical homogenization such as a generalized method of cells (GMC) has been developed by [1]. This method enables the modeling of complex unit-cell morphologies and is able to study the mechanical response of heterogeneous materials. The generalized method of cells (GMC) is used to predict the thermoelastic behavior of multiphase composites by including the thermal tangent tensor in the constitutive law. The effective tangent and thermal tensors are functions of the mechanical and thermal concentration tensor, respectively. The concentration tensor indicates the relationships between the local and overall behavior. Aboudi [3] also proposed an expanded form of the micromechanical approach to predict the hyperelastic response of viscoelastic multiphase composites. This approach uses viscoelastic, as well as mechanical concentration tensors to form relationships between the local and effective deformation. Moghaddam et al. [5] apply the GMC for determining the elastoplastic behavior by employing the single-crystal plasticity constitutive model. Aboudi proposes a method that can predict the viscoplastic, as well as thermoelastic behavior of multiphase composites. The proposed high fidelity generalized method of cells (HFGMC) includes second order displacement expansion in the multi-cell configuration of the repeating unit-cell (RUC). The HFGMC has been developed in order to predict the local distribution of stresses and strains in a refined manner that previously could not be generated by the GMC [6].

Numerical micromechanical models for two-phase repeating unit-cell (RUC) can be achieved using phenomenological material models at lower length scales, such as finite element, viscoplastic self-consistent and Taylor models [5,7,8]. Another alternative model directly specified for periodic composites is the high fidelity generalized method of cells (HFGMC). HFGMC can be considered as a higher order extension of the generalized method of cells (GMC) [6]. In the HFGMC approach for two-phase composites, the RUC consists of different numbers of subcells. In this approach, the higher order displacement expansion is used in the subcells, utilizing both displacement and stress microvariables to satisfy on an average basis, the equilibrium and continuity (traction and displacement) equations and periodic conditions across the interface between the cells. In Aboudi et al. [3], the HFGMC computational approach has been applied to predict the deformation behavior of various types of multiphase composite materials (elastic, viscoelastic, thermoviscoelastic and electroelastic). In the current work, the HFGMC was enhanced to include crystal plasticity material modeling for two-phase copper-silver composites.

This study presents general formulations for the HFGMC modeling framework implemented with the crystal plasticity material model for two-phase Cu-Ag composites undergoing large deformations. The behavior of composites with elasto-viscoplastic material constituents undergoing large deformations is allowed to deviate far away from equilibrium and is modeled by the HFGMC micromechanical theory. For a given constitutive model, both the micromechanical and macromechanical governing equations based on the homogenization technique for periodic composites are developed, wherein the instantaneous mechanical concentration tensors that relate the local induced deformation in the phase to the current externally-applied deformation gradient are given. Furthermore, the macroscopic constitutive equations of the two-phase composite in terms of its instantaneous stiffness tensors are also provided.

The structure of this paper is outlined as follows. Section 2 deals with the experimental observations for both samples. Section 3 introduces the constitutive equations of a finite elasto-viscoplastic material model based on the isomorphy concept of the elastic laws [9]. Section 4 describes the computational methodology for HFGMC formulation. Section 5 presents results in terms of mechanical behavior, and finally, conclusions are given in Section 6.

Notation: We use the symbolic notation given in the continuum mechanics text book of Bertram [9]. Scalars, vectors, second-order and fourth-order tensors are denoted by a, $\mathbf{a}$, $\mathbf{A}$ and $\mathbb{A}$, respectively. The scalar, dyadic and Rayleigh product are given by ·, ⊗ and $\ast$, respectively, where $\mathbf{a}·\mathbf{b}:=a_i{b}_i$, $\mathbf{a}\otimes \mathbf{b}:=a_i{b}_j{\mathbf{e}}_i\otimes {\mathbf{e}}_j$, $\mathbf{A}*\mathbb{C}:=C_{ijkl}\mathbf{A}{\mathbf{e}}_i\otimes \mathbf{A}{\mathbf{e}}_j\otimes \mathbf{A}{\mathbf{e}}_k\otimes \mathbf{A}{\mathbf{e}}_l$. : denotes the double contraction between tensors, i.e., $\mathbf{A}:\mathbf{B}:=A_{ij}{B}_{ij}$. ${\mathbf{A}}^T$, ${\mathbf{A}}^{-1}$ and $\dot{\mathbf{A}}$ denote the transpose, the inverse and the material time derivative of a second-order tensor $\mathbf{A}$. The linear mapping of a second-order tensor $\mathbf{A}$ by a fourth-order tensor $\mathbb{C}$ is written as $\mathbb{C}\left[\mathbf{A}\right]$.

2. Experimental Methodology

The two cold-drawn Cu-Ag rods having diameters of 12.42 mm ($d_1$) and 6.73 mm ($d_2$) are produced by die casting. The volume fraction of each phase in the polycrystals is given as $v{f}_{Ag}=0.63$, $v{f}_{Cu}=0.37$. Both samples ($d_1$, $d_2$) exhibit a crystallographic texture with different strengths, respectively. X-ray analysis is used to determine the bulk texture of two different cold-drawn Cu-Ag rods. X-ray diffraction (XRD) measurements are performed by using an X-ray tube with a chromium-anode in point focus mode and a 1D detector with secondary $K_{\beta }$ filtering. The measured texture from both samples ($d_1$, $d_2$) has been approximated by 100 grains as a compromise between the precision and computational costs. More details about the initial texture and approximated texture (100 grains) are given in [10,11]. The compression tests are carried out for both cylindrical samples on a universal testing machine. These tests are operated at room temperature for a constant strain rate of ${10}^{-4}$ s${}^{-1}$. The results are reported in terms of true stress ($T_{33}$) and compressive strain ($1-F_{33}$).

3. Constitutive Equations

3.1. Elastic Law

In the present investigation, an elasto-viscoplastic single-crystal constitutive model [9] is considered for the lamellar structure of the Cu and Ag phases. An elasto-viscoplastic material model is applied on the microscale to investigate the material behavior of the aforementioned Cu-Ag polycrystals. Following Lee [12], the deformation gradient $\mathbf{F}$ is multiplicatively decomposed into an elastic part ${\mathbf{F}}_e$ and a plastic part ${\mathbf{F}}_p$:

$$\begin{array}{c}\hfill \mathbf{F}={\mathbf{F}}_e{\mathbf{F}}_p\end{array}$$

(1)

where ${\mathbf{F}}_e$ is the elastic part of the deformation gradient describing elastic stretch and rigid rotation and ${\mathbf{F}}_p$ indicates the plastic contribution from crystallographic slips. The deformation gradient with respect to undistorted state can be defined by:

$$\begin{array}{c}\hfill \tilde{\mathbf{F}}=\mathbf{F}{\mathbf{F}}_p^{-1}\end{array}$$

(2)

From Equation (2), it can be seen that $\tilde{\mathbf{F}}$ and ${\mathbf{F}}_p^{-1}$ correspond to the elastic part and the inverse of the plastic part of the deformation gradient.

For a prescribed macro deformation in terms of Green’s strain tensor ${\tilde{\mathbf{E}}}^G$, the second Piola–Kirchhoff stress tensor ${\tilde{\mathbf{T}}}^{2PK}$ is given by an anisotropic St.Venant–Kirchhoff law:

$$\begin{array}{c}\hfill {\tilde{\mathbf{T}}}^{2PK}=\tilde{\mathbb{K}}\left[{\tilde{\mathbf{E}}}^G\right]\end{array}$$

(3)

with:

$$\begin{array}{c}\hfill {\tilde{\mathbf{E}}}^G=\frac{1}{2}(\tilde{\mathbf{C}}-\mathbf{I}),\tilde{\mathbf{C}}={\tilde{\mathbf{F}}}^T\tilde{\mathbf{F}}\end{array}$$

(4)

In Equation (4), $\tilde{\mathbf{C}}$ denotes Green’s strain tensor with respect to the undistorted placement. $\tilde{\mathbb{K}}$ denotes the fourth-order constant stiffness tetrad for a cubic crystal. The tilde indicates that the $\tilde{\mathbb{K}}$ is formulated with respect to the undistorted placement. The stiffness tetrad is represented by a six by six Voigt matrix, and the components refer to the normalized orthonormal basis ${\mathbf{B}}_{\alpha }$ of symmetric second-order tensors [13,14,15], i.e., ${\tilde{K}}_{\alpha \beta }={\mathbf{B}}_{\alpha }:\tilde{\mathbb{K}}\left[{\mathbf{B}}_{\beta }\right]$:

$$\begin{array}{c}\hfill \tilde{\mathbb{K}}={\tilde{K}}_{\alpha \beta }{\mathbf{B}}_{\alpha }\otimes {\mathbf{B}}_{\beta }=\left[\begin{array}{cccccc}{K}_{1111}& K_{1122}& K_{1122}& 0& 0& 0\\ & K_{1111}& K_{1122}& 0& 0& 0\\ & & K_{1111}& 0& 0& 0\\ & & & 2K_{1212}& 0& 0\\ & sym.& & & 2K_{1212}& 0\\ & & & & & 2K_{1212}\end{array}\right]{\mathbf{B}}_{\alpha }\otimes {\mathbf{B}}_{\beta }\end{array}$$

(5)

$$\begin{array}{c}\hfill {\mathbf{B}}_1={\mathbf{e}}_1\otimes {\mathbf{e}}_1,{\mathbf{B}}_2={\mathbf{e}}_2\otimes {\mathbf{e}}_2,{\mathbf{B}}_3={\mathbf{e}}_3\otimes {\mathbf{e}}_3\end{array}$$

(6)

$$\begin{array}{c}\hfill {\mathbf{B}}_4=\frac{\sqrt{2}}{2}({\mathbf{e}}_2\otimes {\mathbf{e}}_3+{\mathbf{e}}_3\otimes {\mathbf{e}}_2)\end{array}$$

(7)

$$\begin{array}{c}\hfill {\mathbf{B}}_5=\frac{\sqrt{2}}{2}({\mathbf{e}}_1\otimes {\mathbf{e}}_3+{\mathbf{e}}_3\otimes {\mathbf{e}}_1)\end{array}$$

(8)

$$\begin{array}{c}\hfill {\mathbf{B}}_6=\frac{\sqrt{2}}{2}({\mathbf{e}}_1\otimes {\mathbf{e}}_2+{\mathbf{e}}_2\otimes {\mathbf{e}}_1)\end{array}$$

(9)

Copper and silver constituents have a face-centered cubic (fcc) crystal structure. The three independent elastic constants for copper are $K_{1111}=170$ GPa, $K_{1122}=124$ GPa and $K_{1212}=75$ GPa and for silver $K_{1111}=123.99$ GPa, $K_{1122}=93.67$ GPa and $K_{1212}=46.12$ GPa.

3.2. Flow Rule

In general, fcc materials exhibit crystallographic slip in $\left\{111\right\}〈110〉$ slip systems. These 12 primary slip systems are described by the Schmid tensors ${\tilde{\mathbf{S}}}^{\alpha }:={\tilde{\mathbf{d}}}_{\alpha }\otimes {\tilde{\mathbf{n}}}^{\alpha }$, which are given by the slip direction ${\tilde{\mathbf{d}}}_{\alpha }$ and the slip plane normal ${\tilde{\mathbf{n}}}^{\alpha }$. The resolved shear stress ${\tau }^{\alpha }$ in a slip system $\alpha$ can be calculated as:

$$\begin{array}{c}\hfill {\tau }^{\alpha }:=\tilde{\mathbf{C}}{\tilde{\mathbf{T}}}^{2PK}:{\tilde{\mathbf{S}}}^{\alpha }\end{array}$$

(10)

An evolution of the plastic part ${\mathbf{F}}_p$ of $\mathbf{F}$ is given in terms of the shear rate ${\dot{\gamma }}_{\alpha }$ and the Schmid tensors ${\tilde{\mathbf{S}}}^{\alpha }$:

$$\begin{array}{c}\hfill \dot{{\mathbf{F}}_p}{\mathbf{F}}_p^{-1}=\sum _{\alpha }{\dot{\gamma }}^{\alpha }{\tilde{\mathbf{S}}}^{\alpha }\end{array}$$

(11)

The kinetics of dislocation motion have been elaborated by the relationships between the resolved shear stress and the plastic shear rate ${\dot{\gamma }}^{\alpha }$ of the slip system $\alpha$ by using the power law [16]:

$$\begin{array}{c}\hfill {\dot{\gamma }}^{\alpha }={\dot{\gamma }}_0\mathrm{sgn}({\tau }^{\alpha }){|\frac{{\tau }^{\alpha }}{{\tau }_c^{\alpha }(\gamma )}|}^m\end{array}$$

(12)

where ${\dot{\gamma }}_0$ is a constant reference shear rate, and the exponent m determines the strain sensitivity of the material. The initial conditions of the evolution Equation (11) are $\tilde{\mathbf{F}}\left(t=0\right)=\mathbf{Q}\left(t=0\right)\in SO(3)$. The orientation of the crystal is given by a proper orthogonal tensor $\mathbf{Q}\left(t\right):={\mathbf{g}}_i\left(t\right)\otimes {\mathbf{e}}_i$. Here, $\{{\mathbf{e}}_i\}$ is the orthonormal vector base of a fixed Cartesian coordinate system, and $\{{\mathbf{g}}_i\}$ is the orthonormal lattice vector base. The initial resolved shear stress at time $t=0$ is given as ${\tau }_c\left(0\right)={\tau }_{c_0}$.

3.3. Hardening Rule

A simple and very popular ansatz for the two types of hardening (self and latent) is the linear hardening rule [9,17].

$$\begin{array}{c}\hfill {\dot{{\tau }_c}}^{\alpha }=\sum _{\beta }{h}_{\alpha \beta }{\dot{\gamma }}^{\beta },h_{\alpha \beta }=q_{\alpha \beta }\theta \left(\gamma \right)\end{array}$$

(13)

where $\theta (\gamma )=\frac{\mathrm{d}{\tau }_c^{\alpha }}{\mathrm{d}\gamma }$ and $q_{\alpha \beta }$ are the matrix components, which account for self- and latent hardening of the crystal. For the fcc cubic crystal having 12 $\left\{111\right\}〈110〉$ primary slip systems, we consider $q_{\alpha \beta }$ equal to 1.0 for the coplanar slip systems and equal to 0.9 for non-coplanar systems. The critical resolved shear stress of all slip systems as a function of shear $\gamma$ is described by a Voce-type hardening law: [18]

$$\begin{array}{c}\hfill {\tau }_c^{\alpha }={\tau }_{c_0}+({\tau }_s+{\theta }_{\infty }\gamma )(1-exp(-{\theta }_0\gamma /{\tau }_s))\end{array}$$

(14)

with:

$$\begin{array}{c}\hfill \gamma =\int \sum _{\alpha }\left|{\dot{\gamma }}_{\alpha }\right|\mathrm{dt}\end{array}$$

(15)

$\gamma$ is given as an integral over the sum of shear rates of all slip systems. The Voce-type hardening rule contains four hardening parameters, namely the initial resolved shear stress ${\tau }_{c_0}$, a saturation stress ${\tau }_s$, an initial hardening modulus ${\theta }_0$ and a remaining hardening modulus ${\theta }_{\infty }$. The material model has been implemented in the subroutine, in conjunction with HFGMC for homogenization. A Newton–Raphson iteration has been performed using a backward Euler scheme [19].

Since the micromechanical analysis uses the actual stresses, let us apply the following relation that provides the first Piola–Kirchhoff stress tensor ${\mathbf{T}}^{1PK}$ in terms of the second Piola–Kirchhoff stress tensor ${\mathbf{T}}^{2PK}$:

$$\begin{array}{c}\hfill {\mathbf{T}}^{1PK}=\mathbf{F}{\mathbf{T}}^{2PK}\end{array}$$

(16)

Consequently, the following incremental constitutive law of the elasto-viscoplastic material is obtained:

$$\begin{array}{c}\hfill \Delta {\mathbf{T}}^{1PK}=\mathbb{R}:\Delta \mathbf{F}\end{array}$$

(17)

where $\mathbb{R}$ is the fourth-order tangent tensor of the material given by:

$$\begin{array}{c}\hfill R_{mnop}=K_{mrps}{F}_{nr}{F}_{os}+T_{mp}^{2PK}{\delta }_{no}\end{array}$$

(18)

The incremental constitutive Equation (17) of the elasto-viscoplastic material will be used in the micromechanical analysis described in the following to determine the macroscopic finite deformation behavior of two-phase composites composed of Cu/Ag constituents.

4. Computational Methodology

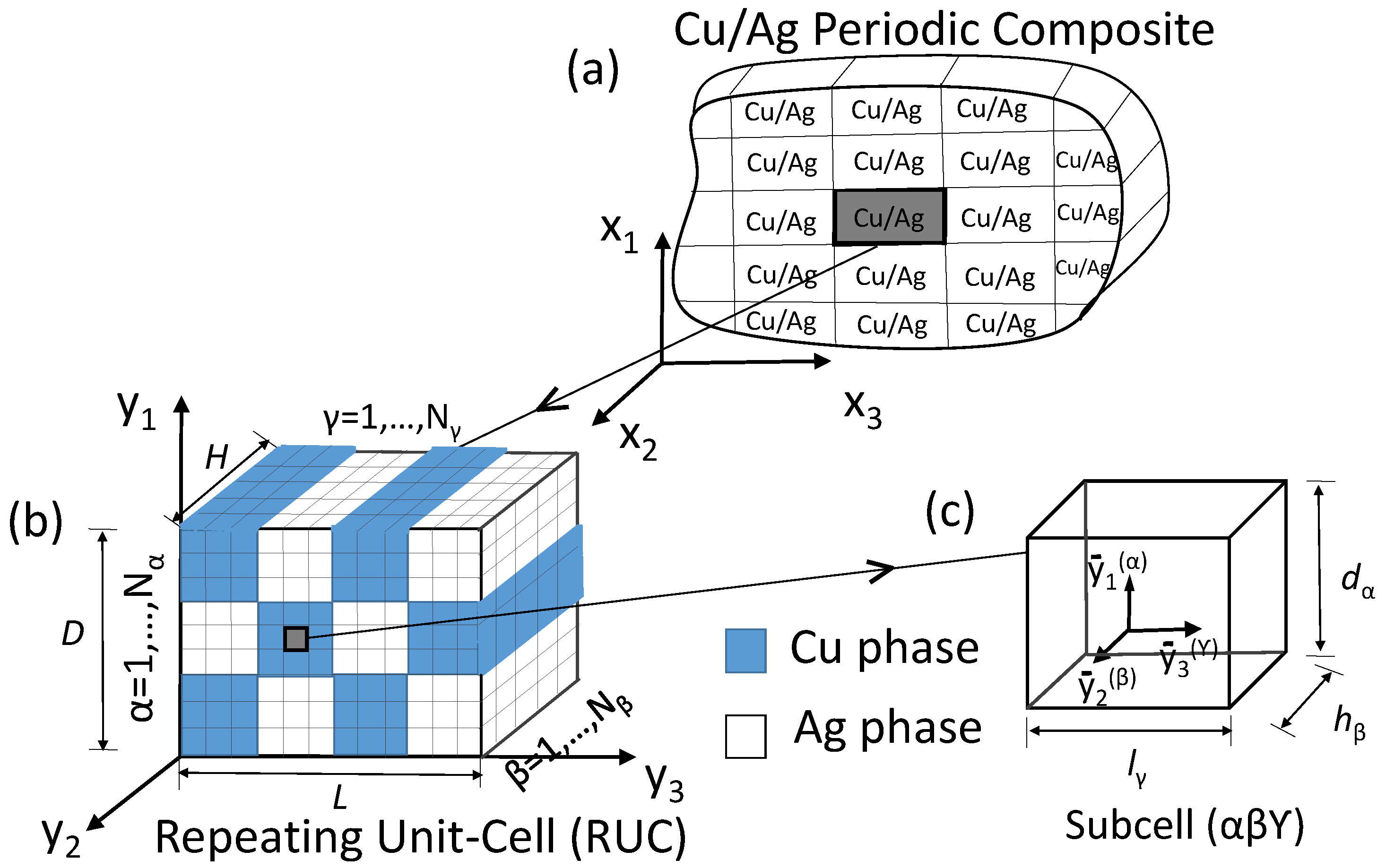
The HFGMC micromechanical modeling theoretical framework with periodic microstructure is shown in Figure 1. The composite with a periodic microstructure is shown in Figure 1a with respect to the initial global coordinates ($x_1$, $x_2$, $x_3$). The repeating unit-cell (RUC) geometry of a two-phase periodic composite is divided into an orthogonal number of subcells, defined with respect to initial local coordinates ($y_1$, $y_2$, $y_3$) (see Figure 1b). The RUC of the two-phase composite is separated into $N_{\alpha }$, $N_{\beta }$ and $N_{\gamma }$ subcells in the $y_1$, $y_2$ and $y_3$ directions, respectively. Each subcell contains a different homogeneous elasto-viscoplastic material. The dimensions of subcell ($\alpha \beta \gamma$) along the 1, 2 and 3 axes are denoted by $d_{\alpha }$, $h_{\beta }$ and $l_{\gamma }$, respectively. In each subcell, a local coordinate system (${\overline{y}}_1^{\alpha }$, ${\overline{y}}_2^{\beta }$, ${\overline{y}}_3^{\gamma }$) is introduced, and the origin is located at the center of the subcell (see Figure 1c).

In the framework of HFGMC micromechanical formulation, the increment of the displacement vector is expanded to second-order as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Delta {\mathbf{w}}^{(\alpha \beta \gamma )}=\Delta \overline{\mathbf{w}}+\Delta {\mathbf{w}}_{(000)}^{(\alpha \beta \gamma )}+{\overline{y}}_1^{(\alpha )}\Delta {\mathbf{w}}_{(100)}^{(\alpha \beta \gamma )}+{\overline{y}}_2^{(\beta )}\Delta {\mathbf{w}}_{(010)}^{(\alpha \beta \gamma )}+{\overline{y}}_3^{(\gamma )}\Delta {\mathbf{w}}_{(001)}^{(\alpha \beta \gamma )}\\ \hfill +\frac{1}{2}(3{\overline{y}}_1^{(\alpha )2}-\frac{d_{\alpha }^2}{4})\Delta {\mathbf{w}}_{(200)}^{(\alpha \beta \gamma )}\\ \hfill +\frac{1}{2}(3{\overline{y}}_2^{(\beta )2}-\frac{h_{\beta }^2}{4})\Delta {\mathbf{w}}_{(020)}^{(\alpha \beta \gamma )}\\ \hfill +\frac{1}{2}(3{\overline{y}}_3^{(\gamma )2}-\frac{l_{\gamma }^2}{4})\Delta {\mathbf{w}}_{(002)}^{(\alpha \beta \gamma )}\end{array}\end{array}$$

(19)

where $\Delta \overline{\mathbf{w}}=[\Delta \overline{\mathbf{F}}·\mathbf{x}]$ consists of the externally-applied mechanical loading, and the unknown coefficients $\Delta {\mathbf{w}}_{(lmn)}^{(\alpha \beta \gamma )}$ are determined, as shown in the following, by implementing the constitutive relations, equilibrium equations together with the interfacial and periodic conditions in the average (integral) sense.

The increments of the components of the deformation gradient tensor are:

$$\begin{array}{c}\hfill \Delta F_{11}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{11}+\Delta w_{1(100)}^{(\alpha \beta \gamma )}+3{\overline{y}}_1^{(\alpha )}\Delta w_{1(200)}^{(\alpha \beta \gamma )}\end{array}$$

(20)

$$\begin{array}{c}\hfill \Delta F_{12}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{12}+\Delta w_{1(010)}^{(\alpha \beta \gamma )}+3{\overline{y}}_2^{(\beta )}\Delta w_{1(020)}^{(\alpha \beta \gamma )}\end{array}$$

(21)

$$\begin{array}{c}\hfill \Delta F_{13}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{13}+\Delta w_{1(001)}^{(\alpha \beta \gamma )}+3{\overline{y}}_3^{(\gamma )}\Delta w_{1(002)}^{(\alpha \beta \gamma )}\end{array}$$

(22)

$$\begin{array}{c}\hfill \Delta F_{21}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{21}+\Delta w_{2(100)}^{(\alpha \beta \gamma )}+3{\overline{y}}_1^{(\alpha )}\Delta w_{2(200)}^{(\alpha \beta \gamma )}\end{array}$$

(23)

$$\begin{array}{c}\hfill \Delta F_{22}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{22}+\Delta w_{2(010)}^{(\alpha \beta \gamma )}+3{\overline{y}}_2^{(\beta )}\Delta w_{2(020)}^{(\alpha \beta \gamma )}\end{array}$$

(24)

$$\begin{array}{c}\hfill \Delta F_{23}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{23}+\Delta w_{2(001)}^{(\alpha \beta \gamma )}+3{\overline{y}}_3^{(\gamma )}\Delta w_{2(002)}^{(\alpha \beta \gamma )}\end{array}$$

(25)

$$\begin{array}{c}\hfill \Delta F_{31}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{31}+\Delta w_{3(100)}^{(\alpha \beta \gamma )}+3{\overline{y}}_1^{(\alpha )}\Delta w_{3(200)}^{(\alpha \beta \gamma )}\end{array}$$

(26)

$$\begin{array}{c}\hfill \Delta F_{32}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{32}+\Delta w_{3(010)}^{(\alpha \beta \gamma )}+3{\overline{y}}_2^{(\beta )}\Delta w_{3(020)}^{(\alpha \beta \gamma )}\end{array}$$

(27)

$$\begin{array}{c}\hfill \Delta F_{33}^{(\alpha \beta \gamma )}=\Delta {\overline{F}}_{33}+\Delta w_{3(001)}^{(\alpha \beta \gamma )}+3{\overline{y}}_3^{(\gamma )}\Delta w_{3(002)}^{(\alpha \beta \gamma )}\end{array}$$

(28)

After lengthy manipulations [3] in which the equilibrium equations in the subcell, interfacial conditions between the subcells and periodicity conditions are imposed in the average sense, the following equation is obtained:

$$\begin{array}{c}\hfill \Delta {\mathbf{F}}^{(\alpha \beta \gamma )}={\mathbb{A}}^{(\alpha \beta \gamma )}:\Delta \overline{\mathbf{F}}\end{array}$$

(29)

where ${\mathbb{A}}^{(\alpha \beta \gamma )}$ is a fourth-order concentration tensor, which relates the local increment of the deformation gradient in the subcell $\Delta {\mathbf{F}}^{(\alpha \beta \gamma )}$ to the externally-applied one $\Delta \overline{\mathbf{F}}$. Consequently, once the increment of the deformation gradient in the subcell has been established, the increment of the first Piola–Kirchhoff stress ($\Delta {{\mathbf{T}}^{1PK}}^{(\alpha \beta \gamma )}$) in the subcell can be readily determined. Thus, Equation (17) can be rewritten as follows:

$$\begin{array}{c}\hfill \Delta {\mathbf{T}}^{1PK(\alpha \beta \gamma )}={\mathbb{R}}^{(\alpha \beta \gamma )}:\Delta {\mathbf{F}}^{(\alpha \beta \gamma )}\end{array}$$

(30)

where ${\mathbb{R}}^{(\alpha \beta \gamma )}$ is the fourth-order tensor of the material within subcell $(\alpha \beta \gamma )$.

In the numerical implementation of HFGMC, the analytical derivation of the HFGMC model [20] is implemented and coupled with the crystal plasticity material model for two-phase Cu-Ag composites. Each subcell contains either Cu or Ag material constituents. Each subcell in the RUC is labeled by the indices ($\alpha \beta \gamma$) with $\alpha =1,\dots ,10$, $\beta =1,\dots ,10$ and $\gamma =1,\dots ,10$. The material parameters for both samples ($d_1$, $d_2$) are listed in

Table 1. Material parameters.

Material	${\dot{\mathit{\gamma }}}_0$ (${\mathit{s}}^{-1}$)	$\mathit{m}(-)$	${\mathit{\tau }}_{{\mathit{c}}_0}$ (MPa)	${\mathit{\tau }}_{\mathit{s}}$ (MPa)	${\mathit{\theta }}_0$ (MPa)	${\mathit{\theta }}_{\mathit{\infty }}$ (MPa)
sample: $d_1$
Cu	0.0001	80	5.5	167.6	7964	9.2
Ag	0.0001	80	5	200.9	4501	20
sample: $d_2$
Cu	0.0001	80	5.5	241.4	14,000	105
Ag	0.0001	80	5	227.6	12,746	50

[11]. The repeating unit-cell (RUC) is subject to uniaxial compression for two different textured Cu-Ag samples ($d_1$, $d_2$) to study the deformation behavior.

5. Numerical Results

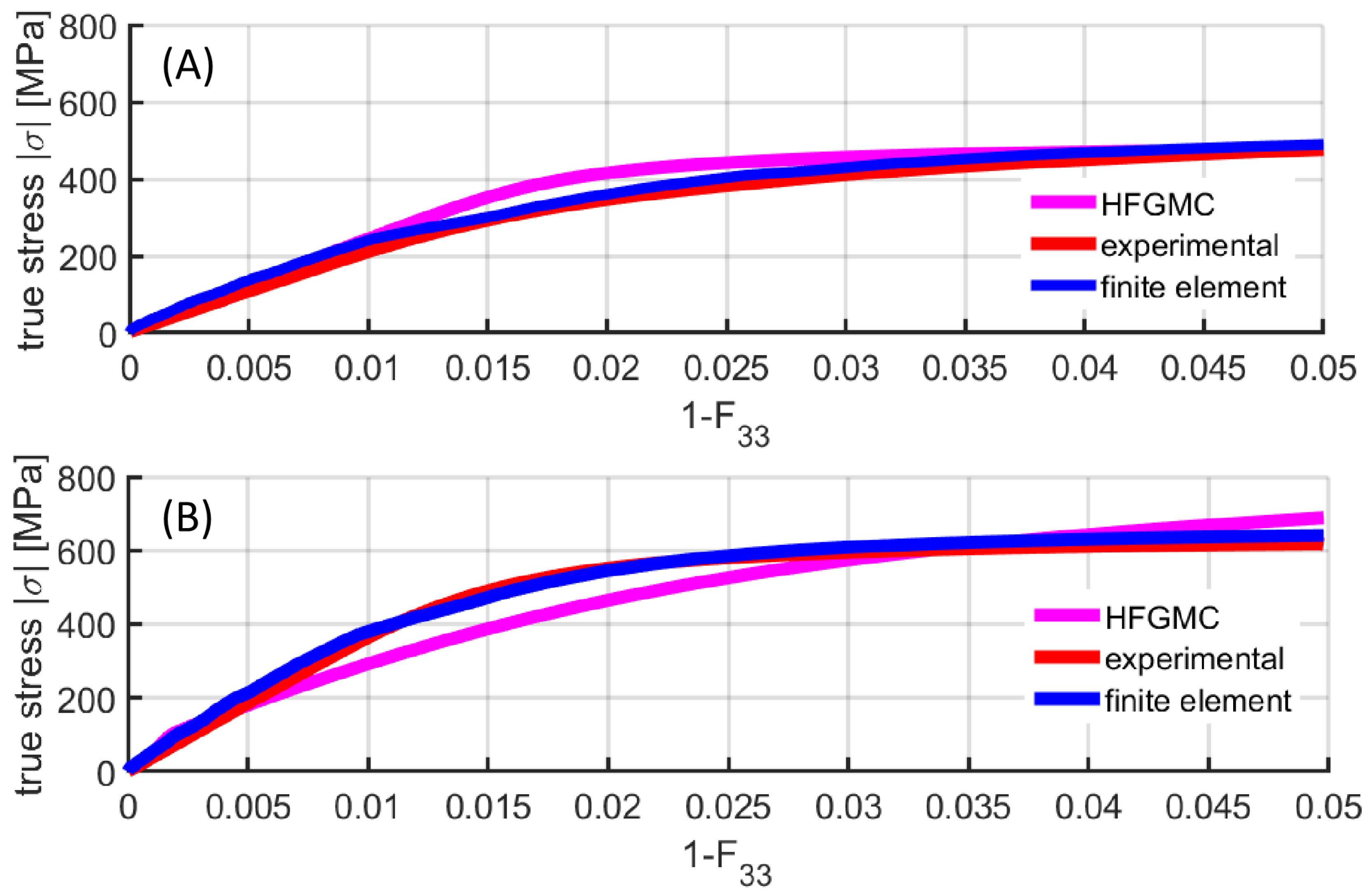
In order to illustrate an application of these constitutive equations, we consider two different textured samples ($d_1$, $d_2$) whose material properties are given in Table 1. Figure 2A,B illustrates the uniaxial mechanical response calibrated from the proposed elasto-viscoplastic HFGMC model compared to the experimental and finite element simulation results under isothermal conditions.

In Figure 2A, the Cauchy stress $T_{33}$ variations with $1-F_{33}$ are caused by the application of uniaxial compression in the Z direction of the large Cu-Ag sample $d_1$. In addition comparisons between the true stresses based on the experimental investigations and finite element simulations [11] of the two-phase Cu-Ag sample $d_1$ are shown. The slight difference in the yield stress predicted by the HFGMC method may be attributed to the fact that in the HFGMC model, the constitutive equations and boundary conditions are implemented in a point-wise manner and in the average sense, respectively. The correspondence of the HFGMC plot to the experimental data and finite element simulated curve is reasonable.

In Figure 2B, the composite mechanical response to uniaxial compression loading of the two-phase Cu-Ag sample $d_2$ is shown by the macroscopic mechanical response ($T_{33}$ vs. $1-F_{33}$). Besides, the comparisons between the experimental and finite simulation results [11] are shown. The HFGMC deformation behavior is in reasonable agreement with the experimental and finite element-simulated curve. However, there is a slight difference in the yield stress and strain hardening in the HFGMC approach. The difference may be due to the heterogeneity in the microstructure and the identified material parameters for sample $d_2$. In addition, the governing equations and boundary conditions are enforced in a point-wise manner and in the average sense, respectively. As seen in Figure 2A,B, the mechanical response are identical in the elastic and elastoplastic region. It can be seen that there is a smooth transition from the elastic to elastoplastic region. The mechanical response however coincides with the corresponding experimental and finite element simulated results. Here, the nonlinearity of the elasto-viscoplastic material is well observed.

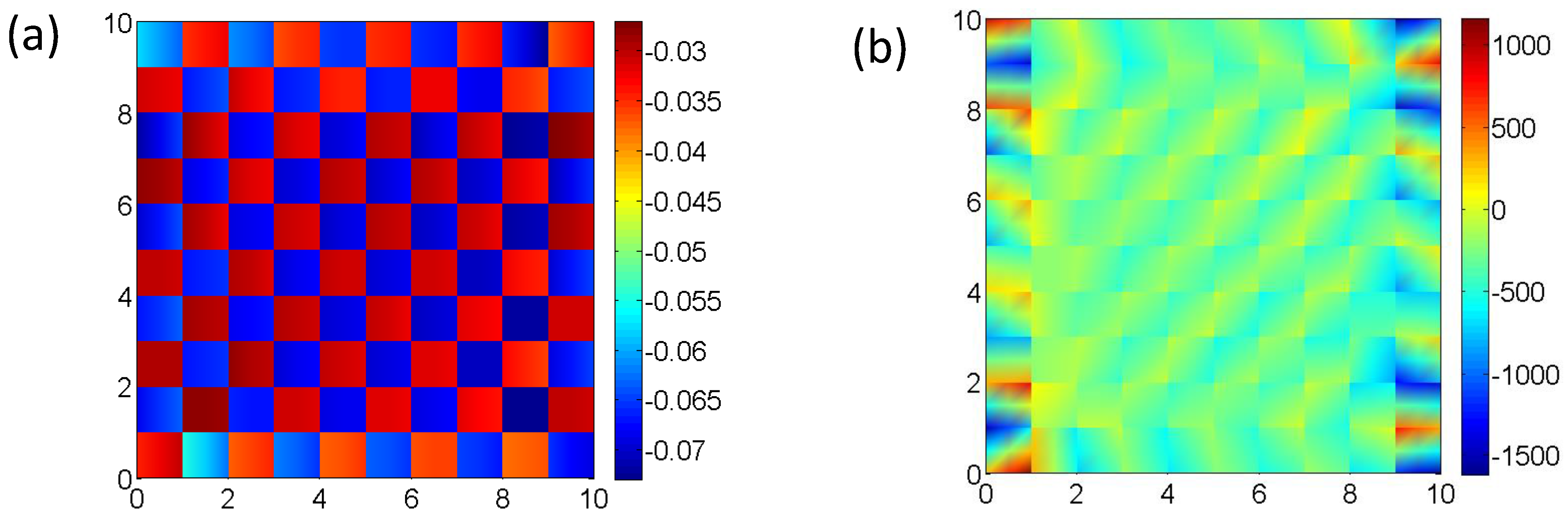
The distribution of the constituents (Cu/Ag), deformation gradient $F_{33}$ and the first Piola–Kirchhoff stress $T_{33}^{1PK}$ for sample $d_1$ is examined in Figure 3. Figure 3a shows the distribution of the material in the plane $y_2$-$y_3$ at $y_1=D/9$, i.e., $(N_{\alpha }=2)$ on the examined cross-section. Here, Cu and Ag constituents with different color contours are shown in the figure (see Figure 3a). Figure 3b,c shows the axial deformation gradient $F_{33}$ and the first Piola–Kirchhoff stress $T_{33}^{1PK}$, respectively. The results show that all subcells are under compression $F_{33}<1$, and the stresses are distributed accordingly for the hard (Cu) and soft (Ag) phase, respectively. The distribution of the $F_{33}$ and $T_{33}^{1PK}$ for the sample $d_2$ in the plane $y_2$-$y_3$ at $y_1=D/9$, i.e., $(N_{\alpha }=2)$, is demonstrated in Figure 4. It can be clearly observed that subcells are under compression $F_{33}<1$ (see Figure 4a). The stress distribution shown in Figure 4b presents that the HFGMC homogenization under a crystal plasticity material modeling predicts the expected distribution at the macroscale.

6. Conclusions

A new elasto-viscoplastic micromechanical formulation for the HFGMC is proposed using elasto-viscoplastic material for Cu and Ag constituents. A HFGMC micromechanical model is employed for the prediction of the mechanical response of two-phase Cu-Ag composites for two different samples ($d_1$, $d_2$) in which each constituent (Cu or Ag) is considered as a rate-dependent elasto-viscoplastic material. The reliability of the micromechanical model prediction is investigated by comparison with the experimental results and finite element simulations, which is valid under a uniaxial compression loading. The stress-strain results for both samples under uniaxial compression show that the effect of plastic deformation behavior is significant.

This HFGMC homogenization model has the advantage of modeling a two-phase periodic composite by discretizing the RUC into quite a few subcells. For example, in the present investigation, 10 × 10 × 10 subcells are sufficient to provide good accuracy. Besides, the running time of the program is quite short (several minutes). In addition, due to the rectangular shape of the subcells, the discretization of the repeating unit-cell is quite simple.

The proposed HFGMC model is shown to be effective for two different Cu-Ag composites calibrated using available experimental data and finite element simulation results. The results of the deformation behavior of the two-phase composites from the proposed HFGMC show the applicability of the proposed model to the wide range of crystalline materials, as well as the multiphase composites.