The Magnetic Phase Transition and Universality Class of h-YMnO3 and h-(Y0.98Eu0.02)MnO3 Under Zero and Applied Pressure
Abstract
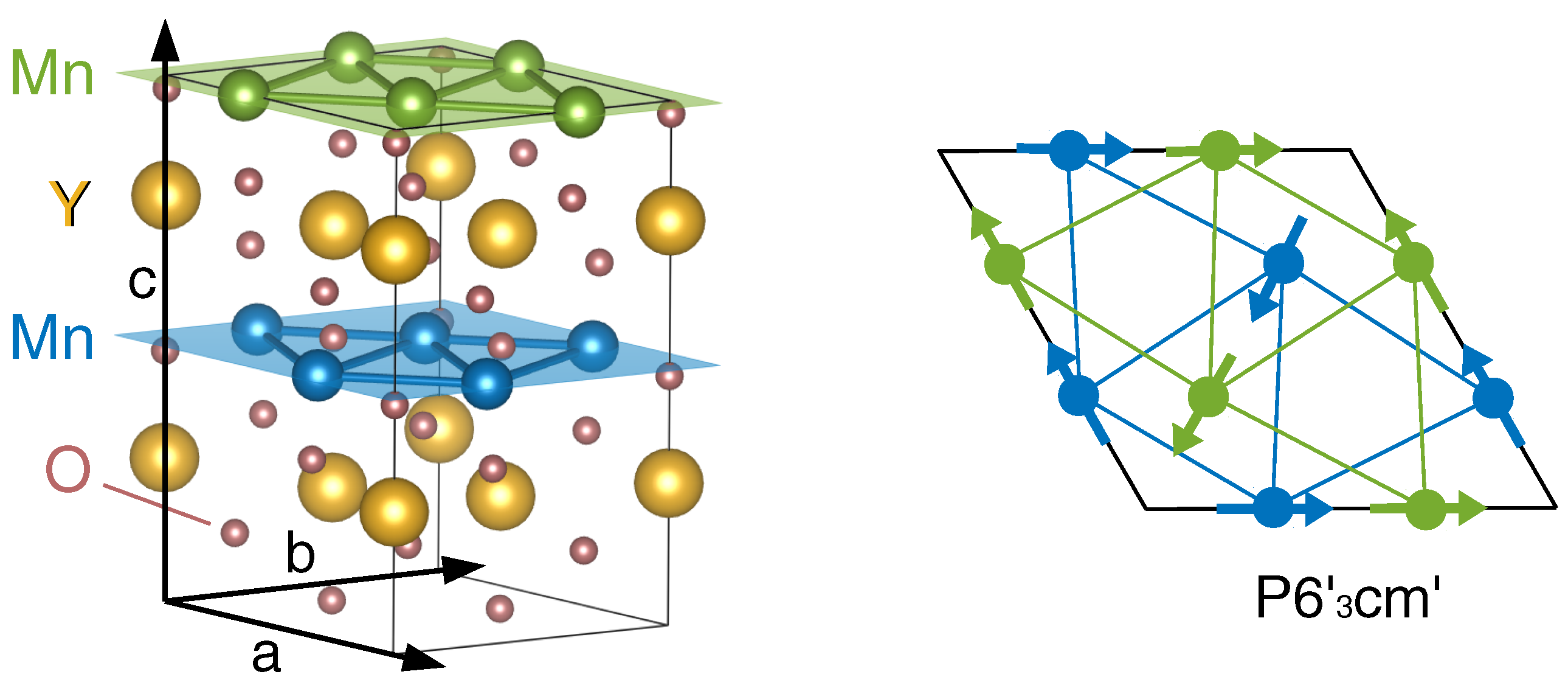
:1. Introduction
2. Experimental Details
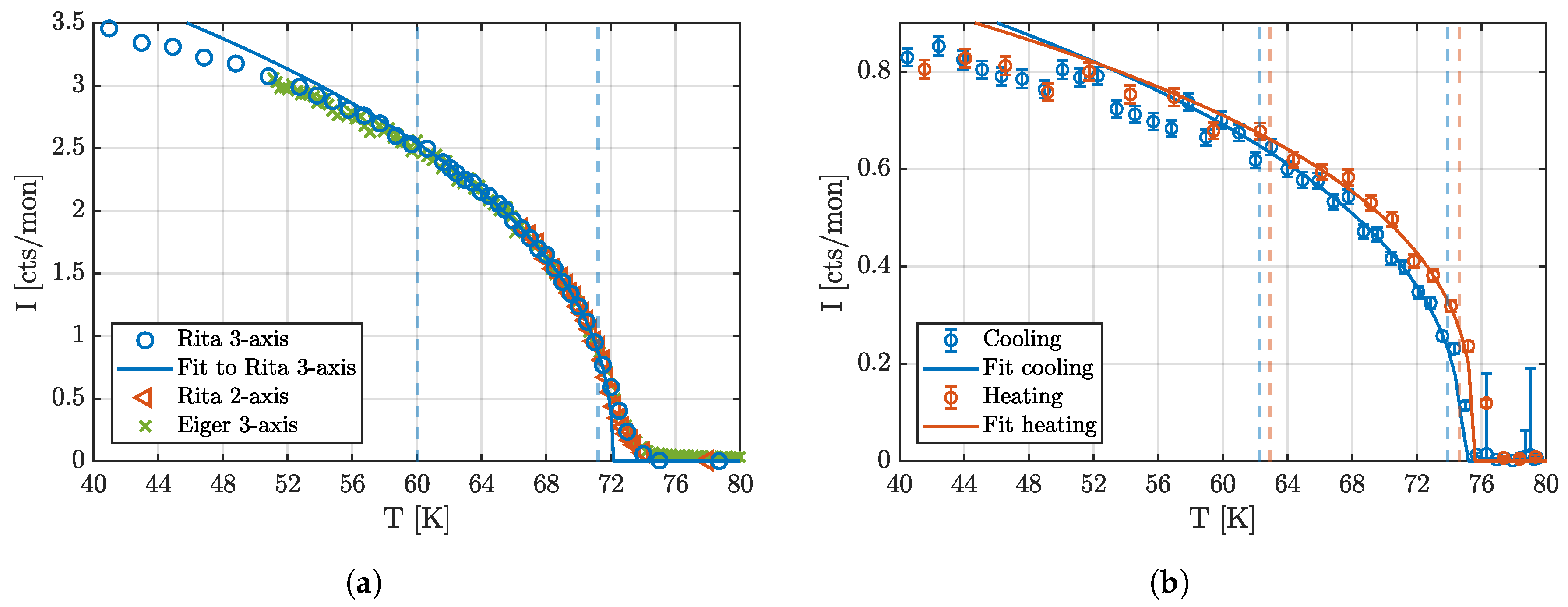
3. Experimental Results: Neutron Diffraction
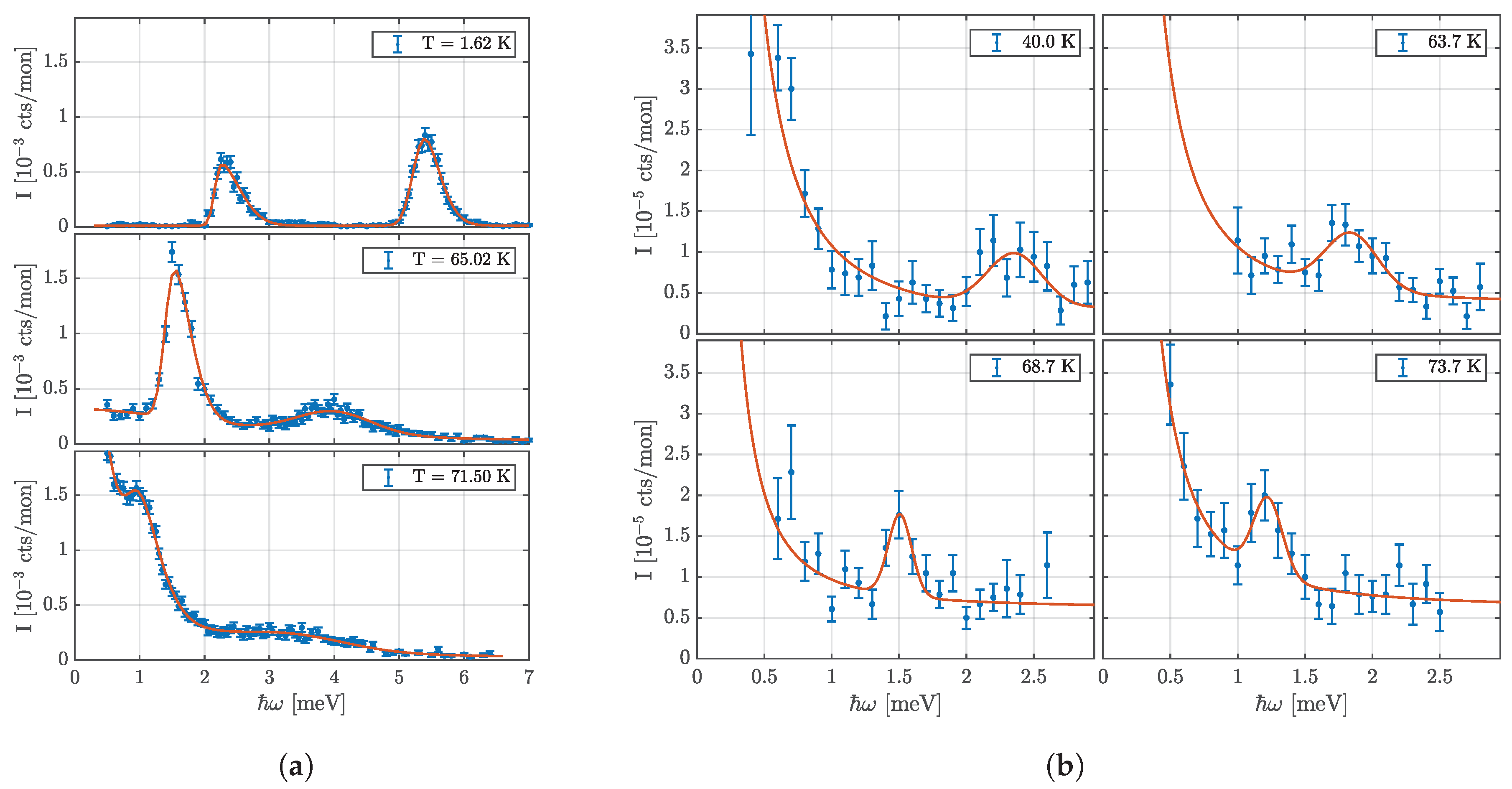
4. Experimental Results: Inelastic Neutron Scattering
5. Discussion
5.1. The Critical Parameters and the Critical Region
5.2. Pressure Effect of the Magnetic Order and Phase Transition
5.3. The Universality Class of h-YMnO
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Diffraction Data Fits





Appendix B. Inelastic Neutron Scattering Data



References
- Hill, N.A. Why Are There so Few Magnetic Ferroelectrics? J. Phys. Chem. B 2000, 104, 6694–6709. [Google Scholar] [CrossRef]
- Lee, S.; Ratcliff, W.; Cheong, S.W.; Kiryukhin, V. Electric field control of the magnetic state in BiFeO3 single crystals. Appl. Phys. Lett. 2008, 92, 192906. [Google Scholar] [CrossRef]
- Catalan, G.; Scott, J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009, 21, 2463. [Google Scholar] [CrossRef]
- Spalding, N.A.; Fiebig, M. The renaissance of Magnetoelectric Multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef] [PubMed]
- Cheong, S.W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Petit, S.; Moussa, F.; Hennion, M.; Pailhès, S.; Pinsard-Gaudart, L.; Ivanov, A. Spin Phonon Coupling in Hexagonal Multiferroic YMnO3. Phys. Rev. Lett. 2007, 99, 266604. [Google Scholar] [CrossRef] [PubMed]
- Sim, H.; Oh, J.; Jeong, J.; Le, M.D.; Park, J.G. Hexagonal RMnO3: A model system for two-dimensional triangular lattice antiferromagnets. Acta Cryst. B 2016, 72, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Pirogov, A.; Kang, M.; Jang, K.H.; Yonemura, M.; Kamiyama, T.; Cheong, S.W.; Gozzo, F.; Shin, N.; Kimura, H.; Noda, Y.; Park, J.G. Giant magneto-elastic coupling in multiferroic hexagonal manganites. Nature 2008, 451, 805–808. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, A.S.; Knight, K.S.; Lightfoot, P. High-temperature phase transitions of hexagonal YMnO3. Phys. Rev. B 2011, 83, 094111. [Google Scholar] [CrossRef]
- Roessli, B.; Gvasaliya, S.N.; Pomjakushina, E.; Conder, K. Spin fluctuations in the stacked-triangular antiferromagnet YMnO3. J. Exp. Theor. Phys. Lett. 2005, 81, 287–291. [Google Scholar] [CrossRef]
- Poirier, M.; Laliberté, F.; Pinsard-Gaudart, L.; Revcolevschi, A. Magnetoelastic coupling in hexagonal multiferroic YMnO3 using ultrasound measurements. Phys. Rev. B 2007, 76, 174426. [Google Scholar] [CrossRef]
- Demmel, F.; Chatterji, T. Persistent spin waves above the Néel temperature in YMnO3. Phys. Rev. B 2007, 76, 212402. [Google Scholar] [CrossRef]
- Lancaster, T.; Blundell, S.J.; Andreica, D.; Janoschek, M.; Roessli, B.; Gvasaliya, S.N.; Conder, K.; Pomjakushina, E.; Brooks, M.L.; Baker, P.J.; et al. Magnetism in Geometrically Frustrated YMnO3 under Hydrostatic Pressure Studied with Muon Spin Relaxation. Phys. Rev. Lett. 2007, 98, 197203. [Google Scholar] [CrossRef] [PubMed]
- Kozlenko, D.P.; Mirebaeu, I.; Park, J.G.; Goncharenko, I.N.; Lee, S.; Park, J.; Savenko, B.N. High-pressure-induced spin liquid phase of multiferroic YMnO3. Phys. Rev. B 2008, 78, 054401. [Google Scholar] [CrossRef]
- Collins, M.F.; Petrenko, O.A. Triangular antiferromagnets. Can. J. Phys. 1997, 75, 605–655. [Google Scholar] [CrossRef]
- Murtazaev, A.K.; Ramazanov, M.K.; Badiev, V.K. Phase Transitions and Critical Properties of the Frustrated Heisenberg Model on a Layer Triangular Lattice with Next-to-Nearest-Neighbor Interactions. J. Exp. Theor. Phys. 2012, 115, 303–308. [Google Scholar] [CrossRef]
- Namdeo, S. Synthesis and Characterization of Novel Perovskite Multiferroics. Ph.D. Thesis, Devi Ahilya University, Indore, India, 2014. [Google Scholar]
- Goian, V.; Kamba, S.; Kadlec, C.; Nuzhnyy, D.; Kuzel, P.; Moreira, J.A.; Almeida, A.; Tavares, P. THz and infrared studies of multiferroic hexagonal Y1−xEuxMnO3 (x = 0–0.2) ceramics. Phase Transit. 2010, 83, 931–941. [Google Scholar] [CrossRef]
- Kozlenko, D.P.; Kichanov, S.E.; Lee, S.; Park, J.G.; Savenko, B.N. Pressure-induced spin fluctuations and spin reorientation in hexagonal manganites. J. Phys. Condens. Matter. 2007, 19, 156228. [Google Scholar] [CrossRef]
- Atou, T.; Chiba, H.; Ohoyama, K.; Yamaguchi, Y.; Syono, Y. Structure Determination of Ferromagnetic Perovskite BiMnO3. J. Solid State Chem. 1999, 145, 639–642. [Google Scholar] [CrossRef]
- Howard, C.J.; Campbell, B.J.; Stokes, H.T.; Carpenter, M.A.; Thomson, R.I. Crystal and magnetic structures of hexagonal YMnO3. Acta Cryst. B 2013, 69, 534–540. [Google Scholar] [CrossRef] [PubMed]
- Fiebig, M.; Fröhlich, D.; Kohn, K.; Leute, S.; Lottermoser, T.; Pavlov, V.V.; Pisarev, R.V. Determination of the Magnetic Symmetry of Hexagonal Manganites by Second Harmonic Generation. Phys. Rev. Lett. 2000, 84, 5620–5623. [Google Scholar] [CrossRef] [PubMed]
- Holm, S.L.; Kreisel, A.; Schäffer, T.K.; Bakke, A.; Bertelsen, M.; Hansen, U.B.; Retuerto, M.; Larsen, J.; Prabhakaran, D.; Deen, P.P.; et al. Magnetic ground state and magnon-phonon interaction in multiferroic h-YMnO3. Phys. Rev. B 2018, 97, 134304. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Skelton, E.F.; Webb, A.W.; Qadri, S.B.; Wolf, S.A.; Lacoe, R.C.; Feldman, J.L.; Elam, W.T.; Carpenter, E.R.; Huang, C.Y. Energy-dispersive X-ray diffraction with synchrotron radiation at cryogenic temperatures. Rev. Sci. Instrum. 1984, 55, 849–855. [Google Scholar] [CrossRef]
- Bahl, C.; Andersen, P.; Klausen, S.; Lefmann, K. The monochromatic imaging mode of a RITA-type neutron spectrometer. Nucl. Instr. Meth. B 2004, 226, 667–681. [Google Scholar] [CrossRef]
- Bahl, C.; Lefmann, K.; Abrahamsen, A.; Rønnow, H.; Saxild, F.; Jensen, T.; Udby, L.; Andersen, N.; Christensen, N.; Jakobsen, H.; et al. Inelastic neutron scattering experiments with the monochromatic imaging mode of the RITA-II spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2006, 246, 452–462. [Google Scholar] [CrossRef]
- Collins, M.F. Magnetic Critical Scattering; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Pailhès, S.; Fabrèges, X.; Régnault, L.P.; Pinsard-Godart, L.; Mirebeau, I.; Moussa, F.; Hennion, M.; Petit, S. Hybrid Goldstone modes in multiferroic YMnO3 studied by polarized inelastic neutron scattering. Phys. Rev. B 2009, 79, 134409. [Google Scholar] [CrossRef]
- Lovesey, S.W. Theory of Neutron Scattering From Condensed Matter; Polarization effects and magnetic scattering; Clarendon Press: Wotton-under-Edge, Gloucestershire, 1984; Volume 2. [Google Scholar]
- Park, J.; Park, J.G.; Jeon, G.S.; Choi, H.Y.; Lee, C.; Jo, W.; Bewley, R.; McEwen, K.A.; Perring, T.G. Magnetic ordering and spin-liquid state of YMnO3. Phys. Rev. B 2003, 68, 104426. [Google Scholar] [CrossRef]
- Kadowaki, H.; Ubukoshi, K.; Hirakawa, K.; Martinez, J.L.; Shirane, G. Experimental study of new type phase transition in triangular lattice antiferromagnet VCl2. J. Phys. Soc. Jpn. 1987, 56, 4027–4039. [Google Scholar] [CrossRef]
- Kawamura, H. Universality of phase transitions of frustrated antiferromagnets. J. Phys. Condens. Matter 1998, 10, 4707. [Google Scholar] [CrossRef]
- Gao, P.; Chen, Z.; Tyson, T.A.; Wu, T.; Ahn, K.H.; Liu, Z.; Tappero, R.; Kim, S.B.; Cheong, S.W. High-pressure structural stability of multiferroic hexagonal RMnO3 (R = Y, Ho, Lu). Phys. Rev. B 2011, 83, 224113. [Google Scholar] [CrossRef]


| Zero Pressure | 1.5 GPa Applied Pressure | |||
|---|---|---|---|---|
| [K] | () | [K] | () | |
| Current work Neutron diffraction, cold TAS | (YMO) (YEMO) | (YMO) (YEMO) | Cooling: Heating: | Cooling: Heating: |
| Current work Neutron inelastic, cold TAS | (YEMO) | (YEMO) | Locked to | |
| Roessli et al. [10] | – | – | ||
| Neutron diffraction, cold TAS | ||||
| Chatterji et al. [12] | – | – | ||
| Neutron diffraction, thermal TAS | ||||
| Kozlenko et al. [14] | 75 | – | Extrapolated: | – |
| Neutron powder diffraction | ||||
| Lancaster et al. [13] | Extrapolated: | – | ||
| SR | ||||
| Poirier et al. [11] | – | – | ||
| Ultrasound | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holm-Dahlin, S.; Janas, S.; Kreisel, A.; Pomjakushina, E.; White, J.S.; Fennell, A.L.; Lefmann, K. The Magnetic Phase Transition and Universality Class of h-YMnO3 and h-(Y0.98Eu0.02)MnO3 Under Zero and Applied Pressure. Quantum Beam Sci. 2018, 2, 16. https://doi.org/10.3390/qubs2030016
Holm-Dahlin S, Janas S, Kreisel A, Pomjakushina E, White JS, Fennell AL, Lefmann K. The Magnetic Phase Transition and Universality Class of h-YMnO3 and h-(Y0.98Eu0.02)MnO3 Under Zero and Applied Pressure. Quantum Beam Science. 2018; 2(3):16. https://doi.org/10.3390/qubs2030016
Chicago/Turabian StyleHolm-Dahlin, Sonja, Sofie Janas, Andreas Kreisel, Ekaterina Pomjakushina, Jonathan S. White, Amy L. Fennell, and Kim Lefmann. 2018. "The Magnetic Phase Transition and Universality Class of h-YMnO3 and h-(Y0.98Eu0.02)MnO3 Under Zero and Applied Pressure" Quantum Beam Science 2, no. 3: 16. https://doi.org/10.3390/qubs2030016






