Analytics of Deep Neural Network-Based Background Subtraction
Abstract
:1. Introduction
2. Related Work
3. Analysis of Background Subtraction Network
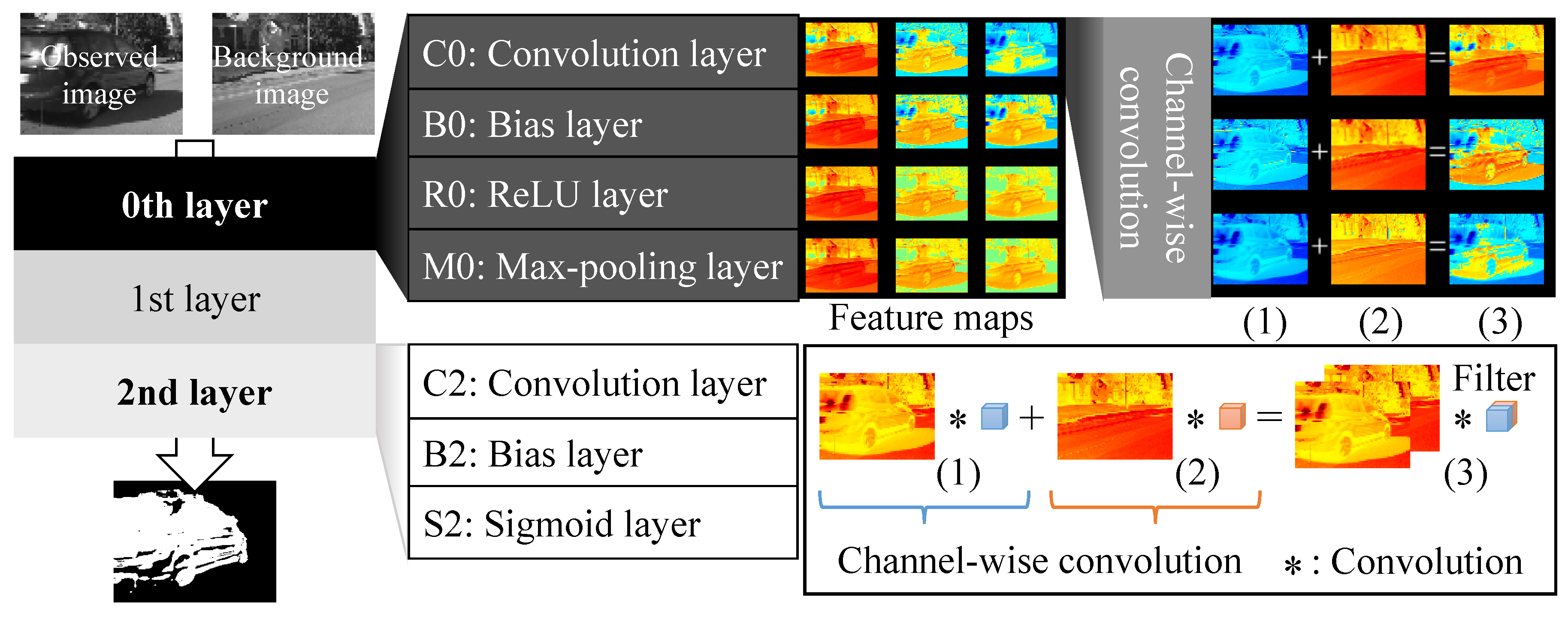
3.1. Network Architecture
3.2. Training Details
3.3. Training Data
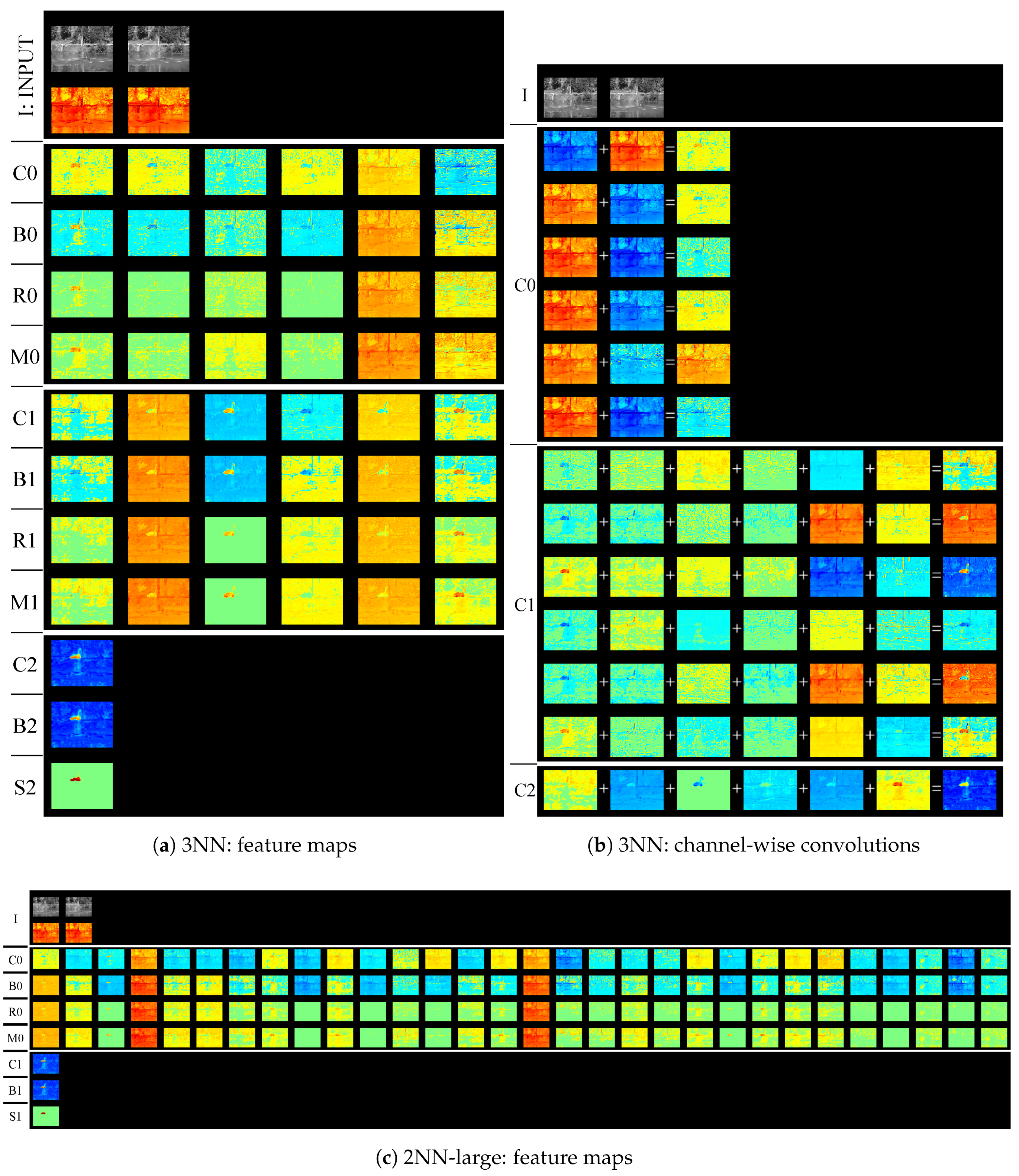
3.4. Background Subtraction Process
4. Experiments
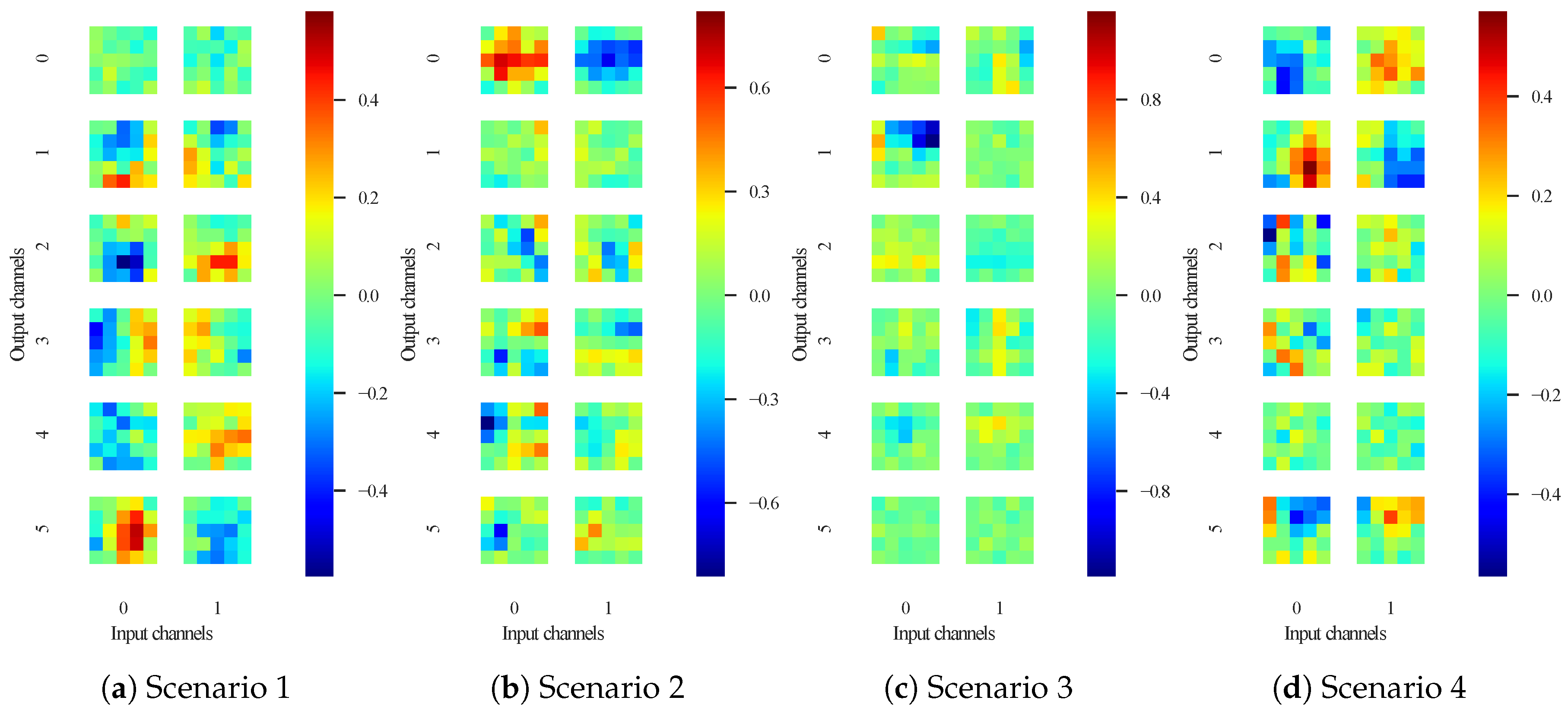
4.1. Experiment 1
- Scenario 1
- The training sequence is the PED sequence. The testing sequence is the HW sequence.
- Scenario 2
- The training sequence is the HW sequence. The testing sequence is the PED sequence.
- Scenario 3
- The training sequence is the HW sequence. The testing sequence is the modified HW sequence.
- Scenario 4
- The training sequence is the PED sequence. The testing sequence is the modified PED sequence.
4.2. Experiment 2
4.3. Experiment 3
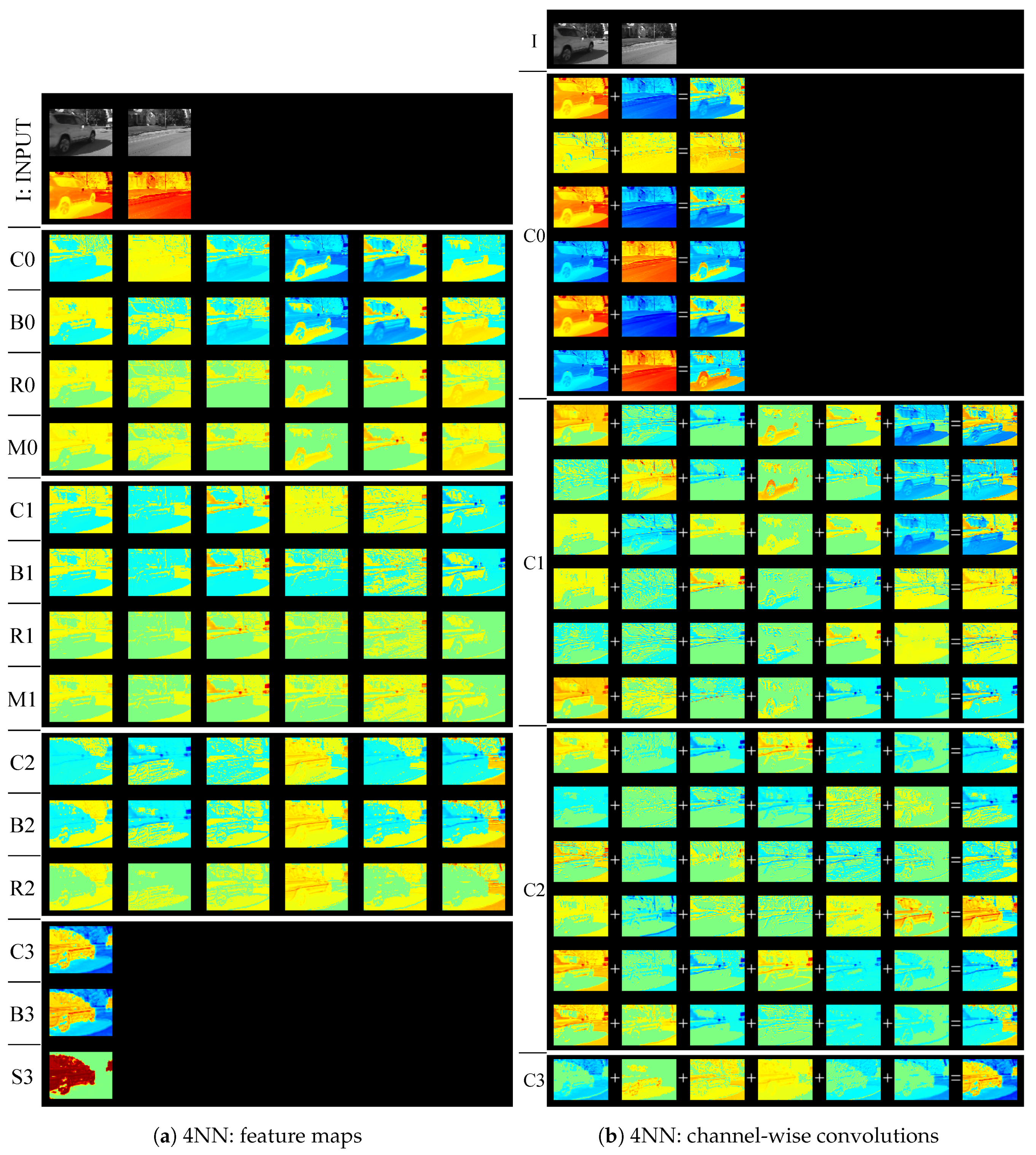
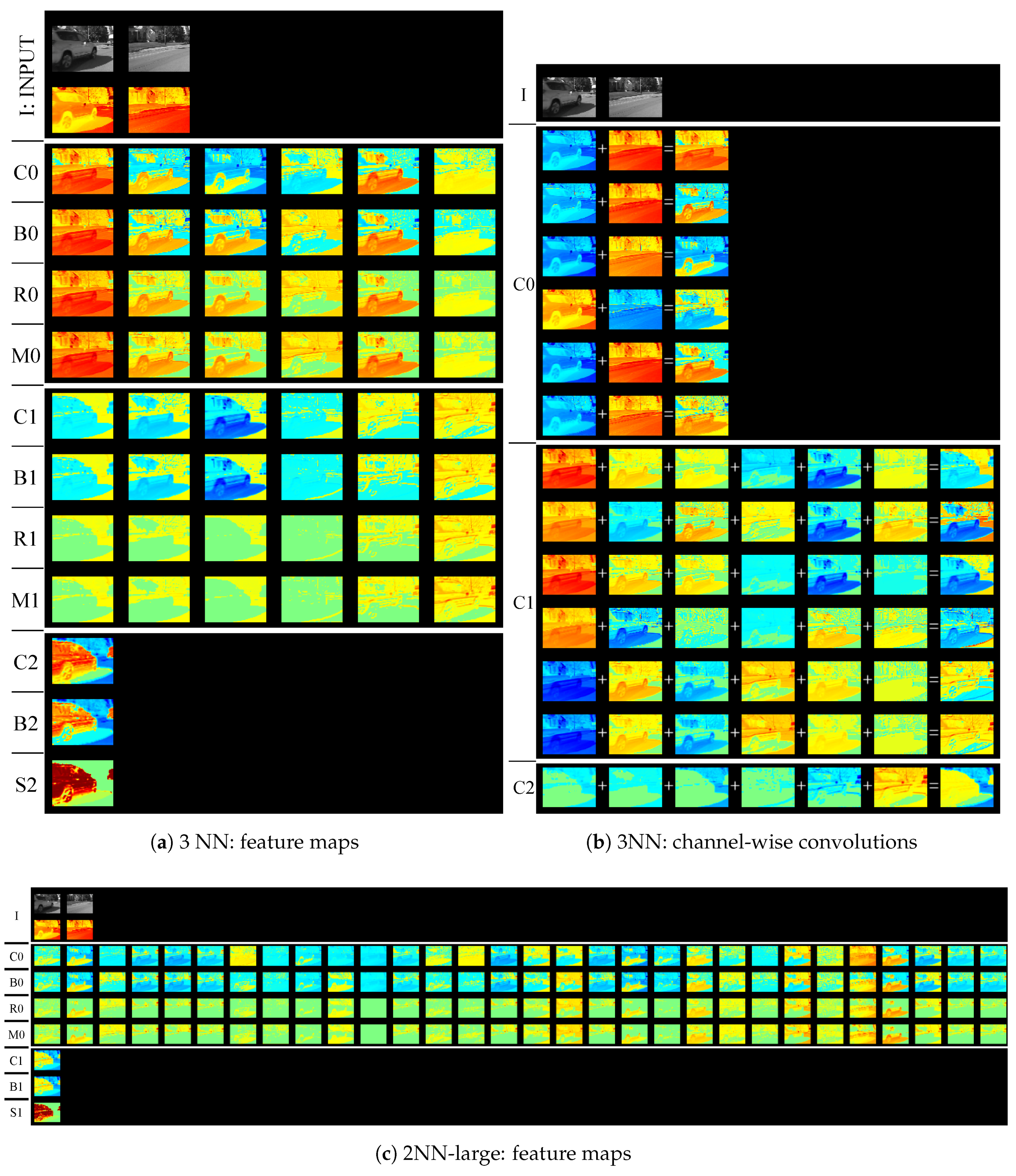
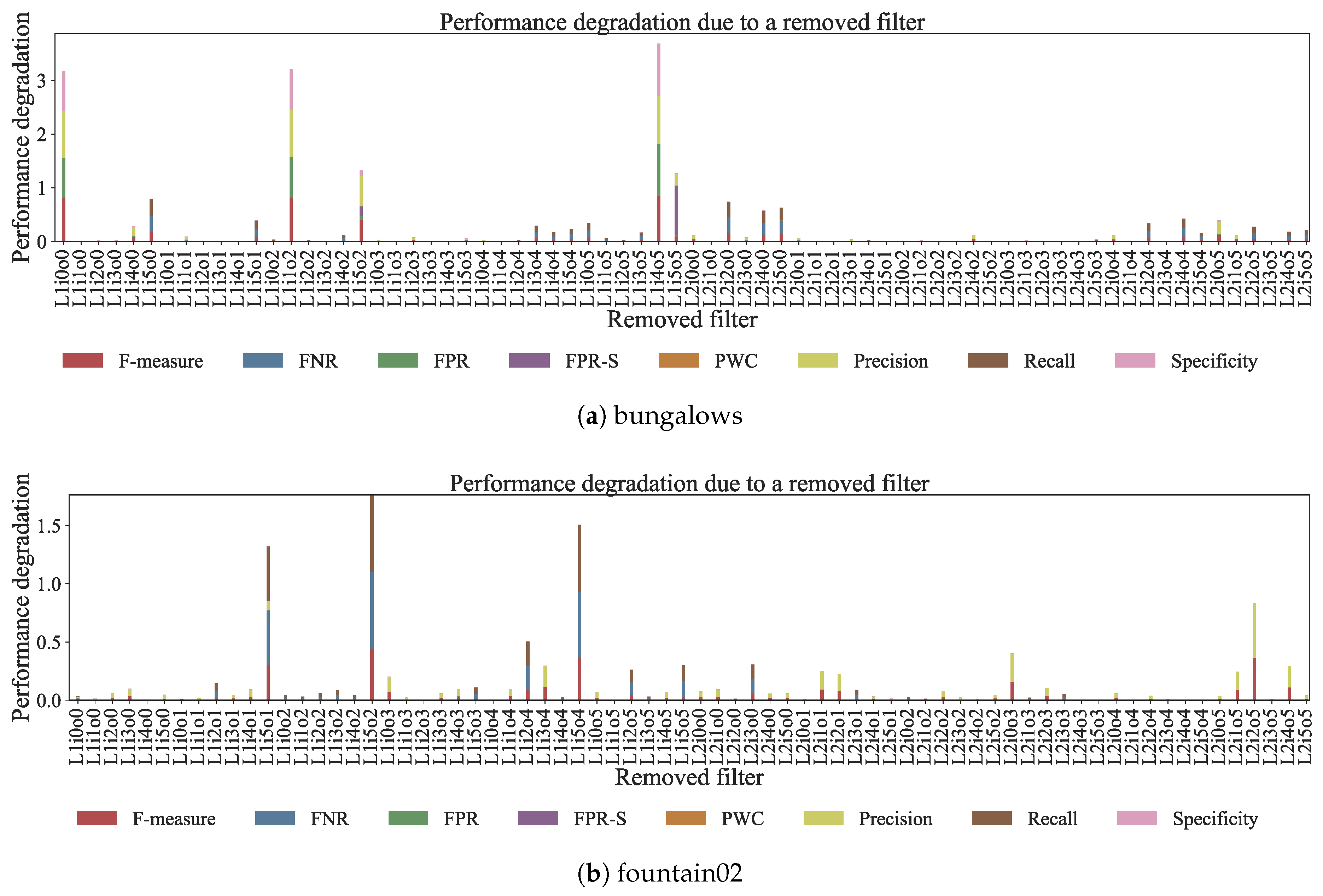
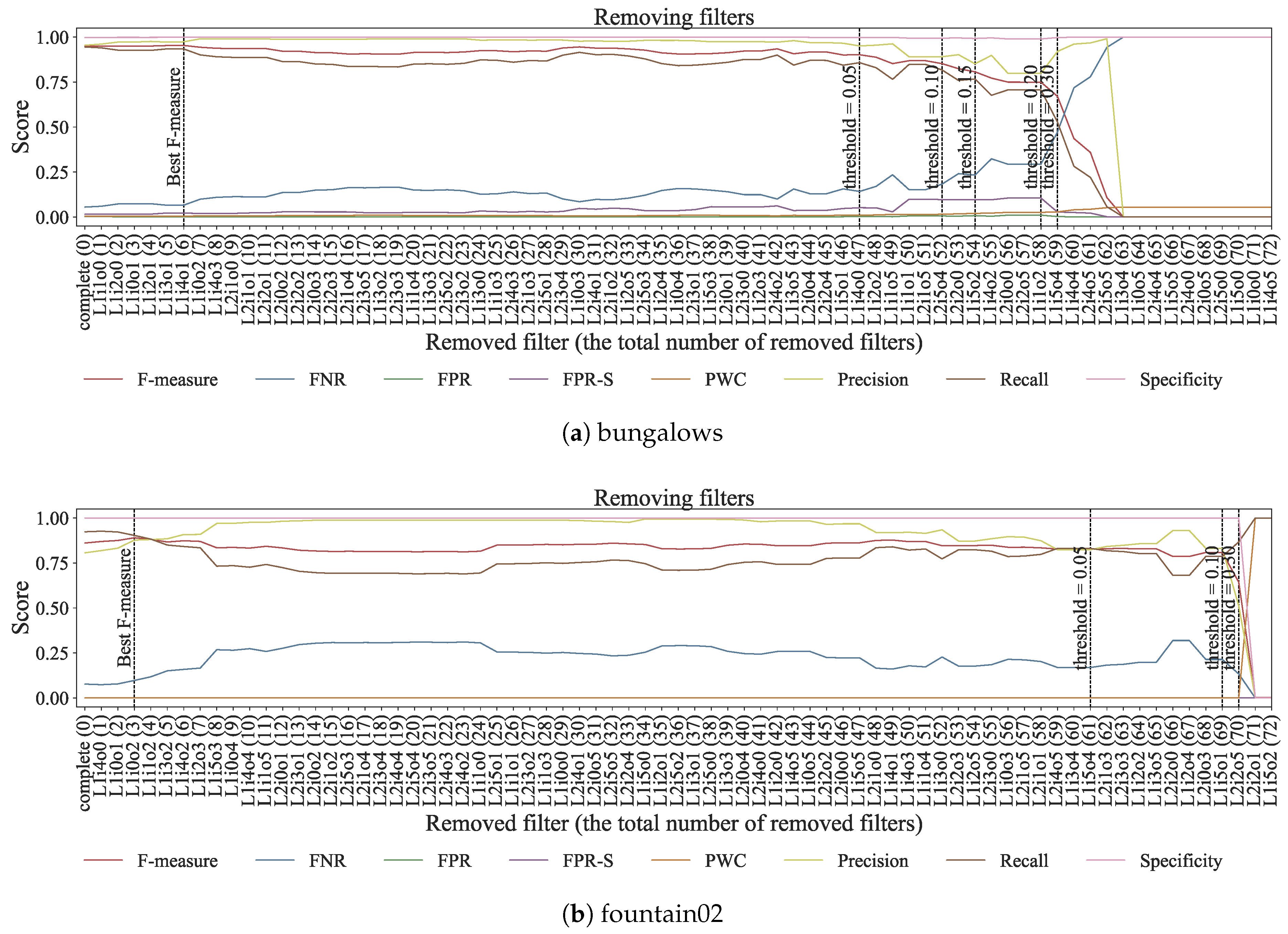
4.4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bouwmans, T. Traditional and recent approaches in background modeling for foreground detection: An overview. Comput. Sci. Rev. 2014, 11, 31–66. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, W.E.L. Adaptive background mixture models for real-time tracking. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 2. [Google Scholar]
- Elgammal, A.; Harwood, D.; Davis, L. Non-parametric model for background subtraction. In Computer Vision-ECCV 2000; Springer: Berlin, Germany, 2000; pp. 751–767. [Google Scholar]
- Heikkilä, M.; Pietikäinen, M.; Heikkilä, J. A texture-based method for detecting moving objects. In Proceedings of the British Machine Vision Conference (BMVC), Kingston, UK, 7–9 September 2004; pp. 1–10. [Google Scholar]
- Yoshinaga, S.; Shimada, A.; Nagahara, H.; Taniguchi, R. Statistical Local Difference Pattern for Background Modeling. IPSJ Trans. Comput. Vis. Appl. 2011, 3, 198–210. [Google Scholar] [CrossRef] [Green Version]
- St-Charles, P.L.; Bilodeau, G.A.; Bergevin, R. Flexible background subtraction with self-balanced local sensitivity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 408–413. [Google Scholar]
- Wang, Y.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An expanded change detection benchmark dataset. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 393–400. [Google Scholar]
- Zhang, Y.; Li, X.; Zhang, Z.; Wu, F.; Zhao, L. Deep learning driven blockwise moving object detection with binary scene modeling. Neurocomputing 2015, 168, 454–463. [Google Scholar] [CrossRef]
- Javad Shafiee, M.; Siva, P.; Fieguth, P.; Wong, A. Embedded motion detection via neural response mixture background modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 19–26. [Google Scholar]
- Braham, M.; Van Droogenbroeck, M. Deep background subtraction with scene-specific convolutional neural networks. In Proceedings of the 2016 International Conference on Systems, Signals and Image Processing (IWSSIP), Bratislava, Slovakia, 23–25 May 2016; pp. 1–4. [Google Scholar]
- Babaee, M.; Dinh, D.T.; Rigoll, G. A deep convolutional neural network for video sequence background subtraction. Pattern Recognit. 2018, 76, 635–649. [Google Scholar] [CrossRef]
- Lim, K.; Jang, W.D.; Kim, C.S. Background subtraction using encoder-decoder structured convolutional neural network. In Proceedings of the 2017 14th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Lecce, Italy, 29 August–1 September 2017; pp. 1–6. [Google Scholar]
- Minematsu, T.; Shimada, A.; Taniguchi, R.-i. Analytics of deep neural network in change detection. In Proceedings of the 2017 14th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Lecce, Italy, 29 August–1 September 2017; pp. 1–6. [Google Scholar]
- Barnich, O.; Van Droogenbroeck, M. ViBe: A powerful random technique to estimate the background in video sequences. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2009), Taipei, Taiwan, 19–24 April 2009; pp. 945–948. [Google Scholar]
- Kim, K.; Chalidabhongse, T.H.; Harwood, D.; Davis, L. Real-time foreground–background segmentation using codebook model. Real-Time Imaging 2005, 11, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Jain, V.; Kimia, B.B.; Mundy, J.L. Background modeling based on subpixel edges. In Proceedings of the IEEE International Conference on Image Processing (ICIP 2007), San Antonio, TX, USA, 16 September–19 October 2007; Volume 6, p. VI-321. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 11. [Google Scholar] [CrossRef]
- Donahue, J.; Jia, Y.; Vinyals, O.; Hoffman, J.; Zhang, N.; Tzeng, E.; Darrell, T. DeCAF: A Deep Convolutional Activation Feature for Generic Visual Recognition. In Proceedings of the 31st International Conference on Machine Learning (ICML 2014), Beijing, China, 21–26 June 2014. [Google Scholar]
- Oliva, A.; Torralba, A. Modeling the shape of the scene: A holistic representation of the spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Braham, M.; Piérard, S.; Van Droogenbroeck, M. Semantic background subtraction. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4552–4556. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Sakkos, D.; Liu, H.; Han, J.; Shao, L. End-to-end video background subtraction with 3d convolutional neural networks. Multimedia Tools Appl. 2017. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 1520–1528. [Google Scholar]
- Wang, Y.; Luo, Z.; Jodoin, P.M. Interactive deep learning method for segmenting moving objects. Pattern Recognit. Lett. 2017, 96, 66–75. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 818–833. [Google Scholar]
- Mahendran, A.; Vedaldi, A. Understanding deep image representations by inverting them. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5188–5196. [Google Scholar]
- Binder, A.; Bach, S.; Montavon, G.; Müller, K.R.; Samek, W. Layer-wise relevance propagation for deep neural network architectures. In Information Science and Applications (ICISA) 2016; Springer: Berlin, Germany, 2016; pp. 913–922. [Google Scholar]
- Chollet, F. Xception: Deep Learning With Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural Networks for Machine Learning Lecture 6a Overview of Mini-Batch Gradient Descent. Available online: https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 14 May 2018).

| Layer | 4NN | 3NN | 2NN | 2NN-large |
|---|---|---|---|---|
| Convolution | ||||
| Max-pooling | ||||
| Convolution | - | - | ||
| Max-pooling | - | - | ||
| Convolution | - | - | - | |
| Convolution |
| Recall | Specificity | FPR | FNR | PWC | Precision | F-Measure | FPR-S | |
|---|---|---|---|---|---|---|---|---|
| bungalows | ||||||||
| 2NN | 0.807 | 0.997 | 0.003 | 0.193 | 1.342 | 0.940 | 0.869 | 0.155 |
| 2NN-large | 0.907 | 0.998 | 0.002 | 0.093 | 0.737 | 0.957 | 0.931 | 0.121 |
| 3NN | 0.916 | 0.998 | 0.002 | 0.084 | 0.650 | 0.964 | 0.939 | 0.094 |
| 4NN | 0.945 | 0.997 | 0.003 | 0.055 | 0.552 | 0.955 | 0.950 | 0.016 |
| cubicle | ||||||||
| 2NN | 0.741 | 0.993 | 0.007 | 0.259 | 1.313 | 0.752 | 0.746 | 0.059 |
| 2NN-large | 0.877 | 0.999 | 0.001 | 0.123 | 0.397 | 0.968 | 0.920 | 0.059 |
| 3NN | 0.880 | 0.999 | 0.001 | 0.120 | 0.411 | 0.959 | 0.918 | 0.026 |
| 4NN | 0.908 | 0.998 | 0.002 | 0.092 | 0.457 | 0.916 | 0.912 | 0.014 |
| peopleInShade | ||||||||
| 2NN | 0.868 | 0.996 | 0.004 | 0.132 | 1.121 | 0.919 | 0.893 | 0.460 |
| 2NN-large | 0.766 | 1.000 | 0.000 | 0.234 | 1.279 | 0.994 | 0.865 | 0.026 |
| 3NN | 0.879 | 0.999 | 0.001 | 0.121 | 0.699 | 0.989 | 0.931 | 0.044 |
| 4NN | 0.886 | 1.000 | 0.000 | 0.114 | 0.650 | 0.992 | 0.936 | 0.033 |
| Recall | Specificity | FPR | FNR | PWC | Precision | F-Measure | FPR-S | |
|---|---|---|---|---|---|---|---|---|
| boats | ||||||||
| 2NN | 0.484 | 1.000 | 0.000 | 0.516 | 0.609 | 0.938 | 0.639 | 0.000 |
| 2NN-large | 0.572 | 1.000 | 0.000 | 0.428 | 0.514 | 0.943 | 0.712 | 0.000 |
| 3NN | 0.550 | 1.000 | 0.000 | 0.450 | 0.534 | 0.949 | 0.696 | 0.000 |
| 4NN | 0.564 | 1.000 | 0.000 | 0.436 | 0.491 | 0.989 | 0.719 | 0.000 |
| fall | ||||||||
| 2NN | 0.877 | 0.998 | 0.002 | 0.123 | 0.449 | 0.932 | 0.904 | 0.869 |
| 2NN-large | 0.908 | 1.000 | 0.000 | 0.092 | 0.262 | 0.982 | 0.943 | 0.711 |
| 3NN | 0.933 | 0.999 | 0.001 | 0.067 | 0.243 | 0.964 | 0.949 | 0.753 |
| 4NN | 0.932 | 1.000 | 0.000 | 0.068 | 0.187 | 0.990 | 0.960 | 0.499 |
| fountain01 | ||||||||
| 2NN | 0.212 | 1.000 | 0.000 | 0.788 | 0.095 | 0.429 | 0.284 | 0.000 |
| 2NN-large | 0.072 | 1.000 | 0.000 | 0.928 | 0.084 | 0.877 | 0.134 | 0.000 |
| 3NN | 0.252 | 1.000 | 0.000 | 0.748 | 0.072 | 0.805 | 0.384 | 0.000 |
| 4NN | 0.030 | 1.000 | 0.000 | 0.970 | 0.088 | 0.578 | 0.057 | 0.000 |
| fountain02 | ||||||||
| 2NN | 0.875 | 0.999 | 0.001 | 0.125 | 0.148 | 0.398 | 0.547 | 0.000 |
| 2NN-large | 0.872 | 1.000 | 0.000 | 0.128 | 0.031 | 0.833 | 0.852 | 0.000 |
| 3NN | 0.789 | 1.000 | 0.000 | 0.211 | 0.026 | 0.953 | 0.863 | 0.000 |
| 4NN | 0.923 | 1.000 | 0.000 | 0.077 | 0.030 | 0.806 | 0.861 | 0.000 |
| Recall | Specificity | FPR | FNR | PWC | Precision | F-measure | FPR-S | |
|---|---|---|---|---|---|---|---|---|
| 2NN | 0.714 | 0.992 | 0.008 | 0.286 | 2.079 | 0.822 | 0.764 | 0.526 |
| 2NN-large | 0.853 | 0.996 | 0.004 | 0.147 | 1.062 | 0.918 | 0.884 | 0.315 |
| 3NN | 0.799 | 0.997 | 0.003 | 0.201 | 1.199 | 0.941 | 0.863 | 0.220 |
| 4NN | 0.879 | 0.995 | 0.005 | 0.121 | 1.099 | 0.893 | 0.883 | 0.138 |
| Performance Degrade | 0↓(Best) | 0.05↓ | 0.1↓ | 0.15↓ | 0.2↓ | 0.25↓ | 0.3↓ |
|---|---|---|---|---|---|---|---|
| bungalows | 0.0833 | 0.6528 | 0.7222 | 0.7500 | 0.8056 | 0.8194 | N/A |
| cubicle | 0.1111 | 0.6528 | 0.7917 | 0.8056 | 0.8194 | 0.8333 | 0.8750 |
| peopleInShade | 0.1111 | 0.6111 | 0.7639 | 0.8333 | 0.8750 | 0.9028 | N/A |
| boats | 0.2639 | 0.4028 | 0.6250 | 0.7917 | 0.8750 | 0.8889 | N/A |
| fall | 0.0417 | 0.5000 | 0.5972 | 0.7222 | 0.7500 | 0.7639 | 0.7778 |
| fountain01 | 0.1667 | 0.5833 | 0.7917 | 0.8056 | N/A | N/A | N/A |
| fountain02 | 0.0417 | 0.8472 | 0.9583 | 0.9722 | N/A | N/A | N/A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minematsu, T.; Shimada, A.; Uchiyama, H.; Taniguchi, R.-i. Analytics of Deep Neural Network-Based Background Subtraction. J. Imaging 2018, 4, 78. https://doi.org/10.3390/jimaging4060078
Minematsu T, Shimada A, Uchiyama H, Taniguchi R-i. Analytics of Deep Neural Network-Based Background Subtraction. Journal of Imaging. 2018; 4(6):78. https://doi.org/10.3390/jimaging4060078
Chicago/Turabian StyleMinematsu, Tsubasa, Atsushi Shimada, Hideaki Uchiyama, and Rin-ichiro Taniguchi. 2018. "Analytics of Deep Neural Network-Based Background Subtraction" Journal of Imaging 4, no. 6: 78. https://doi.org/10.3390/jimaging4060078




