Optimization Based Evaluation of Grating Interferometric Phase Stepping Series and Analysis of Mechanical Setup Instabilities
Abstract
:1. Introduction
2. Methods
2.1. Sinusoid Fitting
2.2. Phase Step Optimization
| Algorithm 1 Least squares optimization of shared abscissa values for simultaneous sinusoid fits to ordinate samples belonging to independent curves j sampled at identical positions . This represents a special case of Algorithm 2 with spatially invariant sampling phases. The relaxation parameter may be chosen <1 if damping of the updates to is desired. For the intermediate argmin operations, see Equations (2)–(5). |
|
| Algorithm 2 Simultaneous least squares optimization of abscissa values and sinusoid fits to ordinate samples belonging to independent curves j sampled at positions with being a slowly varying polynomial with respect to the spatial coordinates and accounting for the expected effects due to translations, magnification and rotations of an interferometer’s gratings. The procedure reduces to Algorithm 1 when considering only the zeroth order term of . |
|
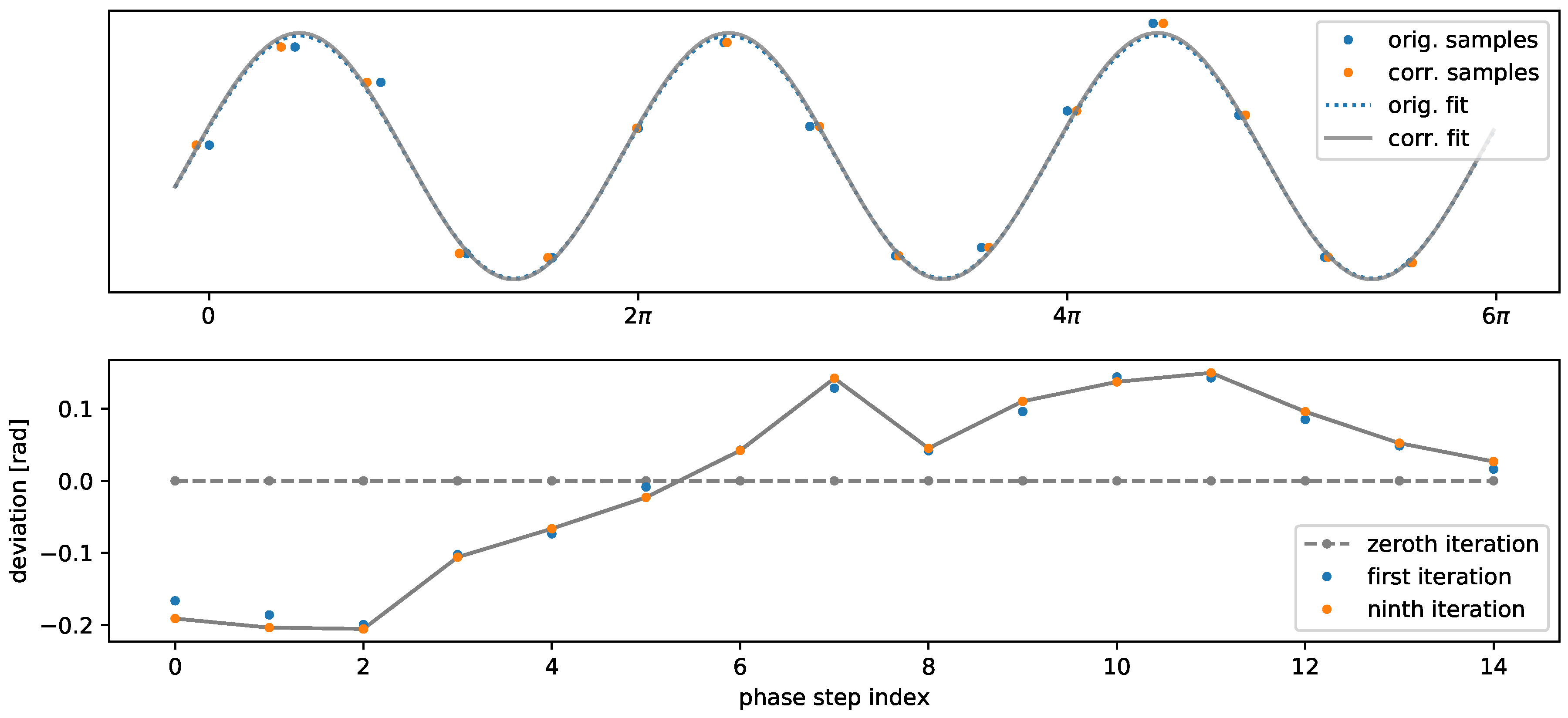
2.2.1. Determination of Individual Phase Deviations
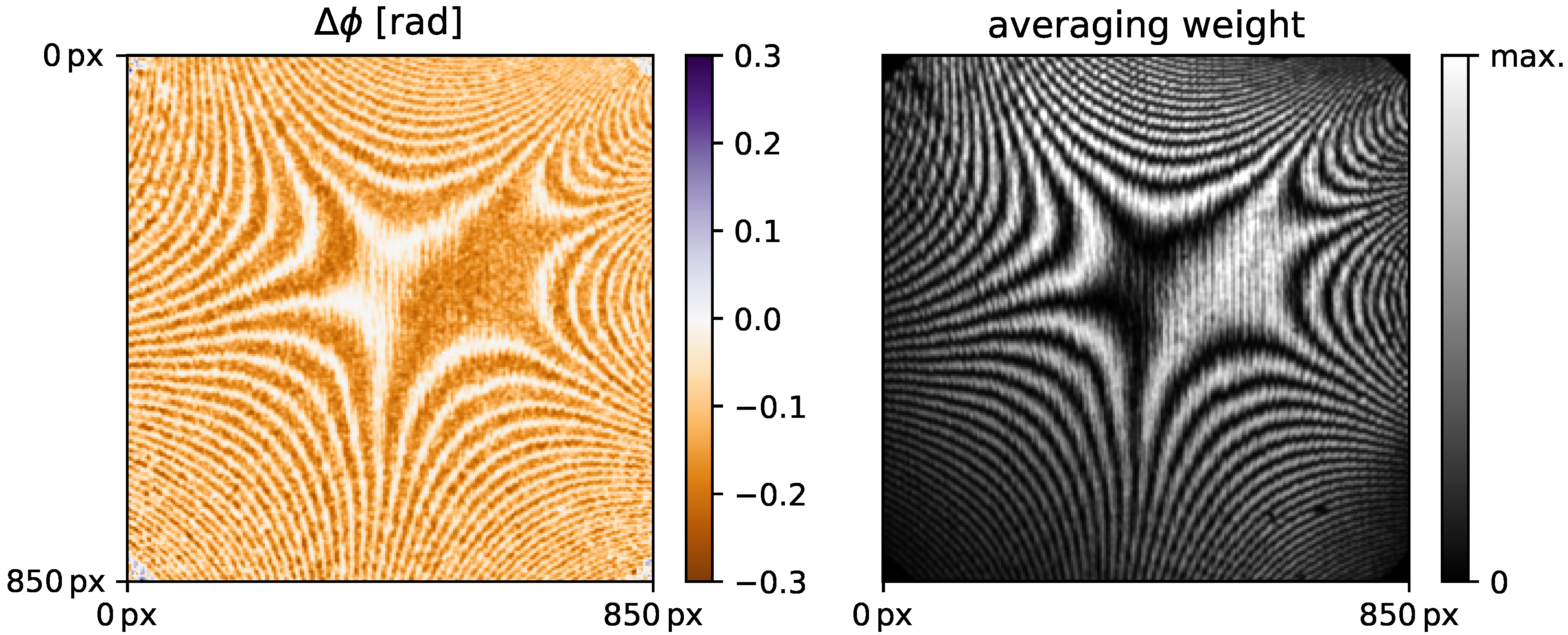
2.2.2. Noise Weighted Average of Phase Deviations
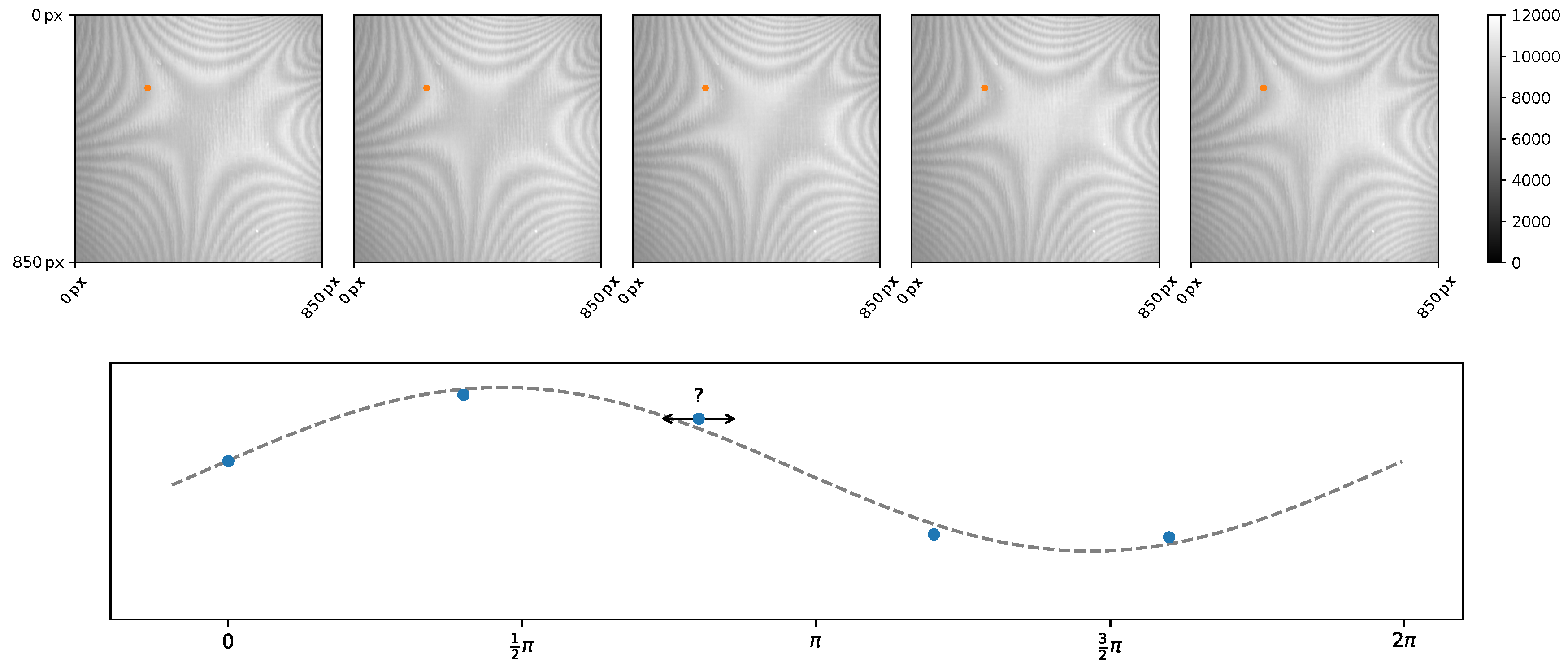
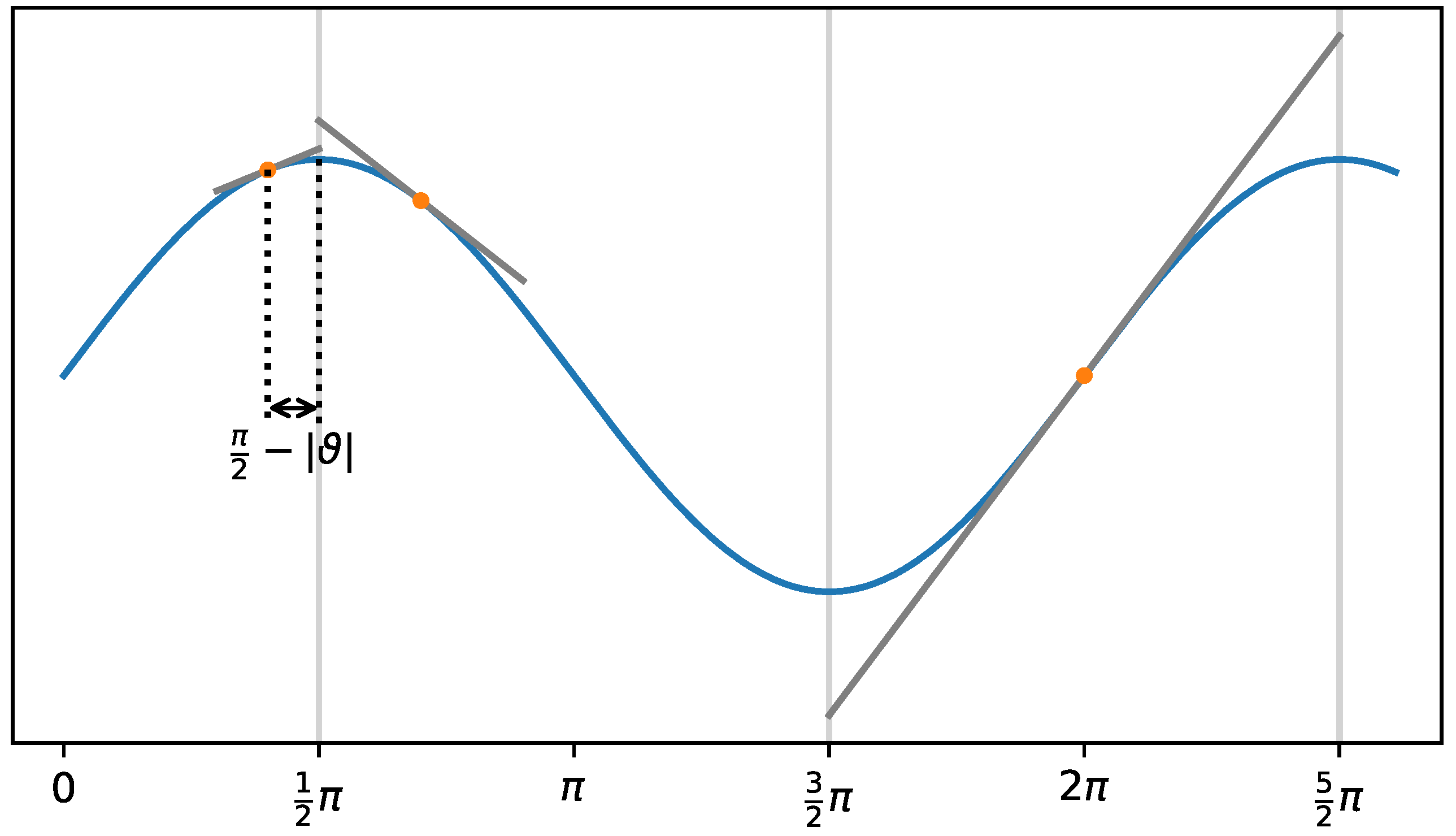
2.2.3. Inhomogeneous Sampling Phase Deviations
2.3. Experimental Setup
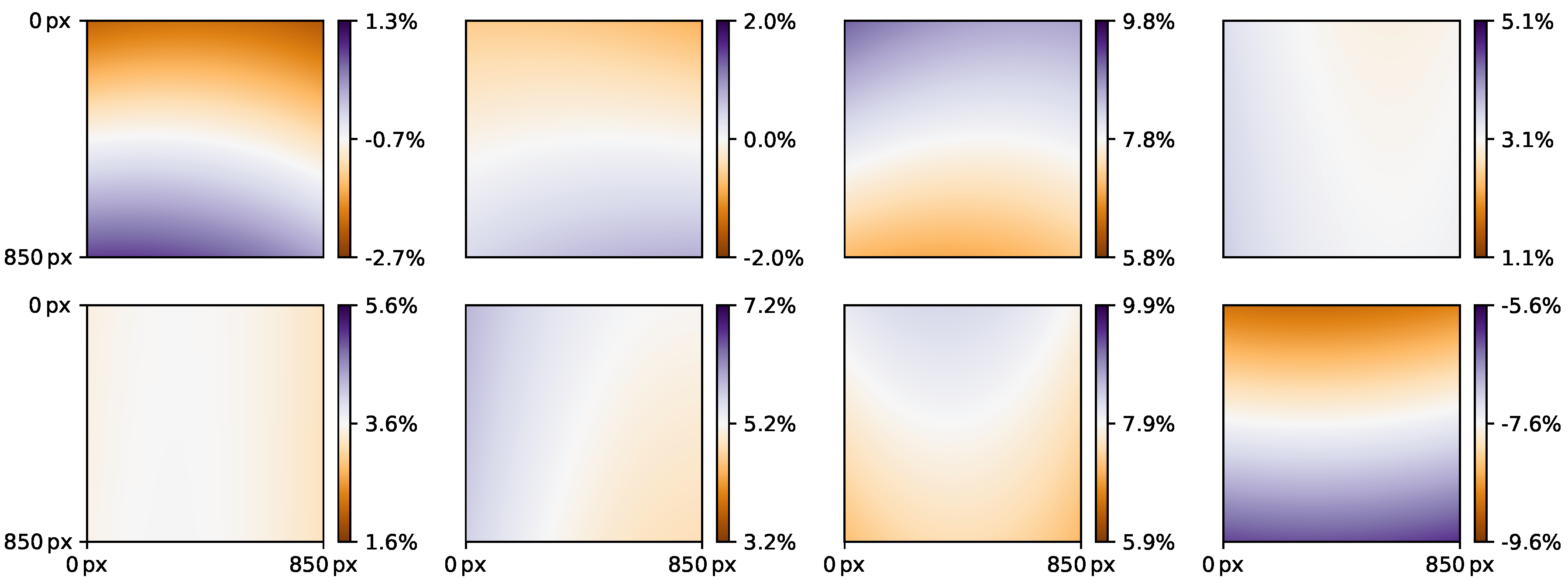
3. Experiment and Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PSC | Phase stepping curve |
| RMSE | Root mean square error |
References
- David, C.; Nöhammer, B.; Solak, H.H.; Ziegler, E. Differential x-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81, 3287–3289. [Google Scholar] [CrossRef]
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of X-Ray Talbot Interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef] [Green Version]
- Revol, V.; Kottler, C.; Kaufmann, R.; Straumann, U.; Urban, C. Noise analysis of grating-based x-ray differential phase contrast imaging. Rev. Sci. Instrum. 2010, 81, 073709. [Google Scholar] [CrossRef] [PubMed]
- Seifert, M.; Kaeppler, S.; Hauke, C.; Horn, F.; Pelzer, G.; Rieger, J.; Michel, T.; Riess, C.; Anton, G. Optimisation of image reconstruction for phase-contrast x-ray Talbot–Lau imaging with regard to mechanical robustness. Phys. Med. Biol. 2016, 61, 6441–6464. [Google Scholar] [CrossRef] [PubMed]
- Vargas, J.; Sorzano, C.O.S.; Estrada, J.C.; Carazo, J.M. Generalization of the Principal Component Analysis algorithm for interferometry. Opt. Commun. 2013, 286, 130–134. [Google Scholar] [CrossRef]
- Kaeppler, S.; Rieger, J.; Pelzer, G.; Horn, F.; Michel, T.; Maier, A.; Anton, G.; Riess, C. Improved reconstruction of phase-stepping data for Talbot-Lau x-ray imaging. J. Med. Imaging 2017, 4, 034005. [Google Scholar] [CrossRef] [PubMed]
- Von Teuffenbach, M.; Noichl, W.; Brendel, B.; Herzen, J.; Pfeiffer, F.; Koehler, T.; Noël, P.B. Grating Position Estimation for Grating-based Computed Tomography. In Proceedings of the Conference on X-ray and Neutron Phase Imaging with Gratings, XNPIG 2017, Zurich, Switzerland, 12–15 September 2017; pp. 169–170. [Google Scholar]
- Ritter, A.; Anton, G.; Weber, T. Simultaneous Maximum-Likelihood Reconstruction of Absorption Coefficient, Reconstruction of Absorption Coefficient, Refractive Index and Dark-Field Scattering Coefficient in X-Ray Talbot-Lau Tomography. PLoS ONE 2016, 11, e0163016. [Google Scholar] [CrossRef] [PubMed]
- Marco, F.D.; Marschner, M.; Birnbacher, L.; Noël, P.; Herzen, J.; Pfeiffer, F. Analysis and correction of bias induced by phase stepping jitter in grating-based X-ray phase-contrast imaging. Opt. Express 2018, 26, 12707–12722. [Google Scholar] [CrossRef] [PubMed]
- Yashiro, W.; Terui, Y.; Kawabata, K.; Momose, A. On the origin of visibility contrast in x-ray Talbot interferometry. Opt. Express 2010, 18, 16890–16901. [Google Scholar] [CrossRef] [PubMed]
- Bech, M.; Bunk, O.; Donath, T.; Feidenhans’l, R.; David, C.; Pfeiffer, F. Quantitative x-ray dark-field computed tomography. Phys. Med. Biol. 2010, 55, 5529–5539. [Google Scholar] [CrossRef] [PubMed]
- Strobl, M. General solution for quantitative dark-field contrast imaging with grating interferometers. Sci. Rep. 2014, 4, 7243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, T.H.; Bech, M.; Bunk, O.; Donath, T.; David, C.; Feidenhans’l, R.; Pfeiffer, F. Directional x-ray dark-field imaging. Phys. Med. Biol. 2010, 55, 3317–3323. [Google Scholar] [CrossRef] [PubMed]
- Revol, V.; Kottler, C.; Kaufmann, R.; Neels, A.; Dommann, A. Orientation-selective X-ray dark field imaging of ordered systems. J. Appl. Phys. 2012, 112, 114903. [Google Scholar] [CrossRef]
- Malecki, A.; Potdevin, G.; Biernath, T.; Eggl, E.; Willer, K.; Lasser, T.; Maisenbacher, J.; Gibmeier, J.; Wanner, A.; Pfeiffer, F. X-ray tensor tomography. Europhys. Lett. 2014, 105, 38002. [Google Scholar] [CrossRef]
- Bayer, F.; Hu, S.; Maier, A.; Weber, T.; Anton, G.; Michel, T.; Riess, C. Reconstruction of scalar and vectorial components in X-ray dark-field tomography. Proc. Natl. Acad. Sci. USA 2014, 111, 12699–12704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogel, J.; Schaff, F.; Fehringer, A.; Jud, C.; Wieczorek, M.; Pfeiffer, F.; Lasser, T. Constrained X-ray tensor tomography reconstruction. Opt. Express 2015, 23, 15134–15151. [Google Scholar] [CrossRef] [PubMed]
- Wieczorek, M.; Schaff, F.; Pfeiffer, F.; Lasser, T. Anisotropic X-ray Dark-Field Tomography: A Continuous Model and its Discretization. Phys. Rev. Lett. 2016, 117, 158101. [Google Scholar] [CrossRef] [PubMed]
- Sharma, Y.; Wieczorek, M.; Schaff, F.; Seyyedi, S.; Prade, F.; Pfeiffer, F. Six dimensional X-ray Tensor Tomography with a compact laboratory setup. Appl. Phys. Lett. 2016, 109, 134102. [Google Scholar] [CrossRef] [Green Version]
- Dittmann, J.; Zabler, S.; Hanke, R. Nested Tomography: Application to Direct Ellipsoid Reconstruction in Anisotropic Darkfield Tomography. In Proceedings of the Conference on X-ray and Neutron Phase Imaging with Gratings, XNPIG 2017, Zurich, Switzerland, 12–15 September 2017; pp. 49–50. [Google Scholar]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dittmann, J.; Balles, A.; Zabler, S. Optimization Based Evaluation of Grating Interferometric Phase Stepping Series and Analysis of Mechanical Setup Instabilities. J. Imaging 2018, 4, 77. https://doi.org/10.3390/jimaging4060077
Dittmann J, Balles A, Zabler S. Optimization Based Evaluation of Grating Interferometric Phase Stepping Series and Analysis of Mechanical Setup Instabilities. Journal of Imaging. 2018; 4(6):77. https://doi.org/10.3390/jimaging4060077
Chicago/Turabian StyleDittmann, Jonas, Andreas Balles, and Simon Zabler. 2018. "Optimization Based Evaluation of Grating Interferometric Phase Stepping Series and Analysis of Mechanical Setup Instabilities" Journal of Imaging 4, no. 6: 77. https://doi.org/10.3390/jimaging4060077





