1. Introduction
Retrieving relevant documents (pages, paragraphs or words) is a critical component in information retrieval solutions associated with digital libraries. The problem has been looked at in two settings: recognition based [
1,
2] like
ocr and recognition free [
3,
4]. Most of the present day digital libraries use Optical Character Recognizers (
ocr) for the recognition of digitized documents and thereafter employ a text based solution for the information retrieval. Though
ocrs have become the de facto preprocessing for the retrieval, they are realized as insufficient for degraded books [
5], incompatible for older print styles [
6], unavailable for specialized scripts [
7] and very hard for handwritten documents [
8]. Even for printed books, commercial
ocrs may provide highly unacceptable results in practice. The best commercial
ocrs can only give word accuracy of 90% on printed books [
4] in modern digital libraries. This means that every 10th word in a book is not searchable. Recall of retrieval systems built on such erroneous text is thus limited. Recognition free approaches have gained interest in recent years. Word spotting [
3] is a promising method for recognition free retrieval. In this method, word images are represented using different features (e.g., Profiles,
sift-bow), and the features are compared with the help of appropriate distance measures (Euclidean, Earth Movers [
9],
dtw [
10]). Word spotting has the advantage that it does not require prior learning due to its appearance-based matching. These techniques have been popularly used in document image retrieval.
Konidaris et al. [
5] retrieve words from a large collection of printed historical documents. A search keyword typed by the user is converted into a synthetic word image which is used as a query image. Word matching is based on computing the
distance metric between the query feature and all the features in the database. Here the features are calculated using the density of the character pixels and the area that is formed from the projections of the upper and lower profile of the word. The ranked results are further improved by relevance feedback. Sankar and Jawahar [
7] have suggested a framework of probabilistic reverse annotation for annotating a large collection of images. Word images were segmented from 500 Telugu books. Matching of the word images is done using the
dtw approach [
11]. Hierarchical agglomerative clustering was used to cluster the word images. Exemplars for the keywords are generated by rendering the word to form a keyword-image. Annotation involved identifying the closest word cluster to each keyword cluster. This involves estimating the probability that each cluster belongs to the keyword. Yalniz and Manmatha [
4] have applied word spotting to scanned English and Telugu books. They are able to handle noise in the document text by the use of
sift features extracted on salient corner points. Rath and Manmatha [
11] used projection profile and word profile features in a
dtw based matching technique.
Recognition free retrieval was attempted in the past for printed as well as handwritten document collections [
4,
7,
12,
13]. Since most of these methods were designed for smaller collections (few handwritten documents as in [
12]), computational time was not a major concern. Methods that extended this to a larger collection [
14,
15,
16] used mostly (approximate) nearest neighbor retrieval. For searching complex objects in large databases,
svms have emerged as the most popular and accurate solution in the recent past [
12]. For linear
svms, both training and testing have become very fast with the introduction of efficient algorithms and excellent implementations [
17]. However, there are two fundamental challenges in using a classifier based solution for word retrieval (i) A classifier needs a good amount of annotated training data (both positive and negative) for training. Obtaining annotated data for every word in every style is practically impossible. (ii) One could train a set of classifiers for a given set of frequent queries. However, they are not applicable for rare queries.
In [
18], Ranjan et al. proposed a one-shot classifier learning scheme (Direct query classifier). The proposed one shot learning scheme enables direct design of a classifier for novel queries, without having any access to the annotated training data, i.e., classifiers are trained for a set of frequent queries, and seamlessly extended for the rare and arbitrary queries, as and when required. The authors hypothesize that word images, even if degraded, can be matched and retrieved effectively with a classifier based solution. A properly trained classifier can yield an accurate ranked list of words since the classifier looks at the word as a whole, and uses a larger context (say multiple examples) for matching. The results of this method are significant since (i) It does not use any language specific post-processing for improving the accuracy. (ii) Even for a language like English, where
ocrs are fairly advanced and engineering solutions were perfected, the classifier based solution is as good, if not superior to the best available commercial
ocrs .
In the direct query classifier (
dqc) scheme [
18], the authors used
dtw distance for indexing the frequent mean vectors. Since the
dtw distance is computationally slow, the authors do not use all the frequent mean vectors for indexing. For comparing two word images,
dtw distance typically takes one second [
3]. This limits the efficiency of
dqc. To overcome this limitation, the authors used Euclidean distance for indexing. The authors use the top 10 (closest in terms of Euclidean distance) frequent mean vectors for indexing. Since the
dtw distance better captures the similarities compared to Euclidean distance for word image retrieval, this restricts the performance of
dqc.
For speed-up,
dtw distance has been previously approximated [
19,
20] using different techniques. In [
20], the authors proposed a fast approximate
dtw distance, in which, the
dtw distance is approximated as a sum of multiple weighted Euclidean distances. For a given set of sequences, there are similarities between the top alignments (least cost alignments) of different pairs of sequences. In [
20], the authors explored these similarities by learning a small set of global principal alignments from the given data, which captures all the possible correlations in the data. These global principal alignments are then used to compute the
dtw distance for the new test sequences. Since these methods [
19,
20] avoid the computation of optimal alignments, these are computationally efficient compared to naive
dtw distance. The fast approximate
dtw distance can be used for efficient indexing in
dqc classifier. However, it gives sub-optimal results. For best results, it needs query specific global principal alignments. In this paper, we introduce query specific
dtw distance, which enables the direct design of global principal alignments for novel queries. Global principal alignments are computed for a set of frequent classes and seamlessly extended for the rare and arbitrary queries, as and when required, without using language specific knowledge. This is a distinct advantage over an
ocr engine, which is difficult to adapt to varied fonts and noisy images and would require language specific knowledge to generate possible hypotheses for out of vocabulary words. Moreover, an
ocr engine can respond to a word image query only by first converting it into text, which is again prone to recognition errors. In [
21,
22], deep learning frameworks are used for word spotting. In [
23], a attribute based learning model
phoc is presented for word spotting. In training phase, each word image is to be given with its transcription. Both word image feature vectors and its transcriptions are used to create the
phoc representation. An
svm is learned for each attribute in this representation. Our approach bears similarity with the
phoc representation based word spotting [
23]. In this sense, both the approaches are designed for handling out-of-vocabulary queries. Our work takes advantage of granular description at ngrams (cut-portion) level. This somewhat resembles the arrangement of characters used in the
phoc encoding. However, training efforts for
phoc are substantial with a large number of classifiers (604 classifiers) being trained and requires complete data for training, which is huge for large datasets. In our work, the amount of training data is restricted to only frequent classes, which is much less compared to
phoc. Further,
phoc requires labels in the form of transcriptions, whereas in our work the labels need not be transcriptions. In addition,
phoc is language dependent [
24] and it is very difficult to apply over different languages. The method proposed in this paper is language independent; it can be applied to any language.
The paper is organized as follows. The next section describes the Direct query classifier (
dqc). Fast approximation of (
dtw) distance is discussed in
Section 3. The query specific
dtw distance is presented in
Section 4. Experimental settings and results are discussed in
Section 5, followed by concluding remarks in
Section 6.
3. Approximating the DTW Distance
In general, DTW distance has quadratic complexity in the length of the sequence. Nagendar et al. [
20] proposed Fast approximate DTW distance (Fast Apprx DTW), which is a linear approximation to the DTW distance. For a pair of given sequences, DTW distance is computed using the optimal alignment from all the possible alignments. This optimal alignment gives a similarity between the given sequences by ignoring local shifts. Computation of optimal alignment is the most expensive operation in finding the DTW distance.
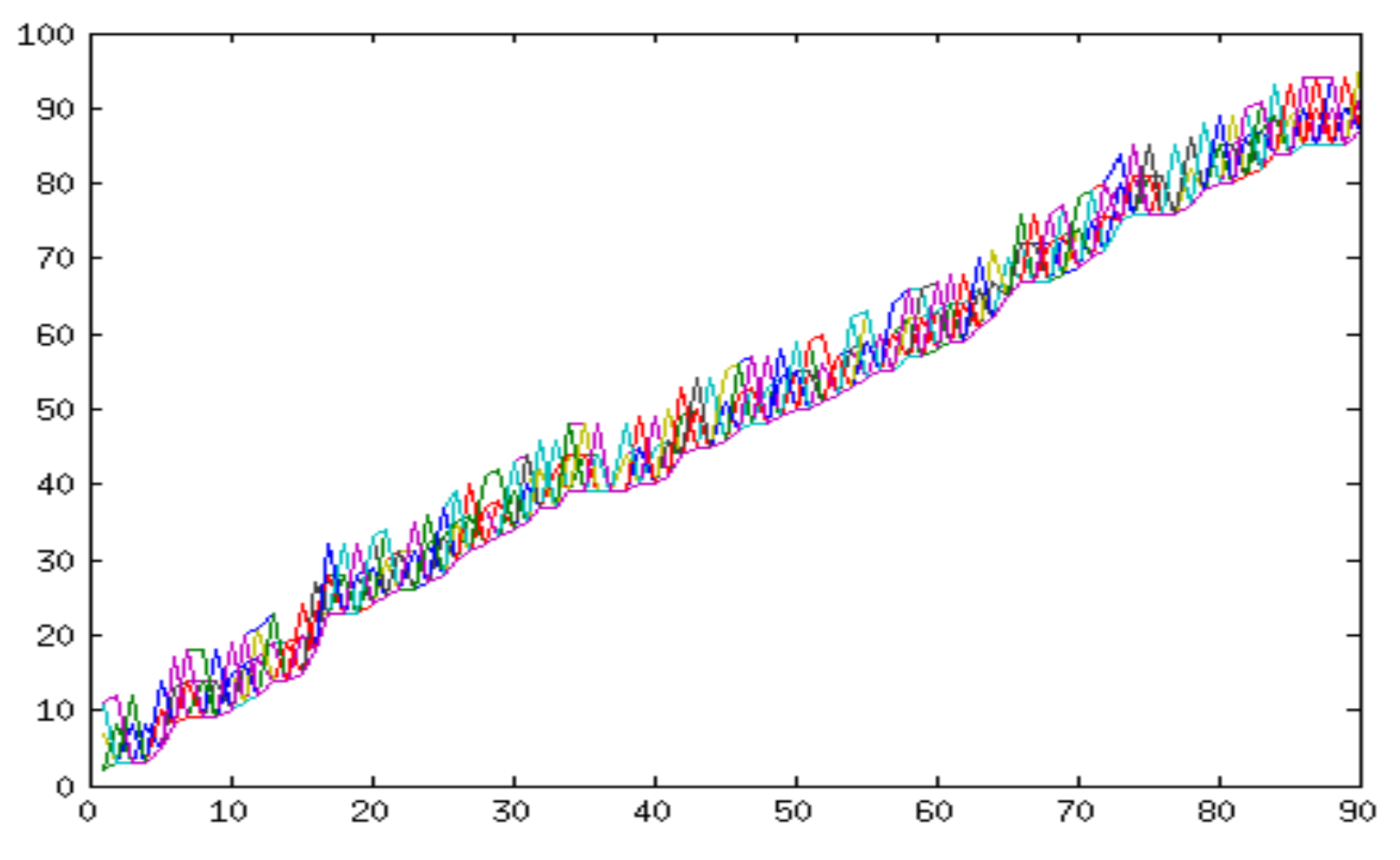
For a given set of sequences, there are similarities between the optimal alignments of different pairs of sequences. For example, if we take two different classes, the top alignments (optimal alignments/least cost alignments) between the samples of class 1 and the samples of class 2 always have some similarity. For a small dataset, the top alignments between few class 1 samples and few class 2 samples are plotted in
Figure 2. It can be observed that the top alignments are in harmony. Based on this idea, we compute a set of global principal alignments from the training data such that the computed global principal alignments should be good enough for approximating the DTW distance between
any new pair of sequences. For new test sequences, instead of finding the optimal alignments, the global principal alignments are used for computing the DTW distance. This avoids the computation of optimal alignments. Now, the DTW distance is approximated as the sum of the Euclidean distances over the global principal alignments.
where
is the set of global principal alignments for the given data
and
is the Euclidean distance between
and
over the alignment
. Notice that the
dtw distance between two samples is the Euclidean distance (ground distance) over the optimal alignment.
To show the performance of Fast Apprx
dtw [
20], we have compared with naive
dtw distance and Euclidean distance for word retrieval problem. Here, these distance measures are used for comparing word image representations. The dataset contains images from three different word classes. The results are given in
Table 1. Nearest neighbor is used for retrieving the similar samples. The performance is measured by mean Average Precision (mAP). From the results, we can observe that Fast Apprx
dtw is comparable to naive
dtw distance and it performs better than Euclidean distance.
4. Query Specific Fast DTW Distance
In Fast approximate
dtw distance [
20] (
Section 3), the global principal alignments are computed from the given data. Here, no class information is used while computing the alignments and also these alignments are query independent, i.e., query information is not used while computing the global principal alignments. In this section, we introduce Query specific
dtw distance, which is computed using query specific (global) principal alignments. The proposed Query specific
dtw distance has been found to give a much better performance when used with the direct query classifier.
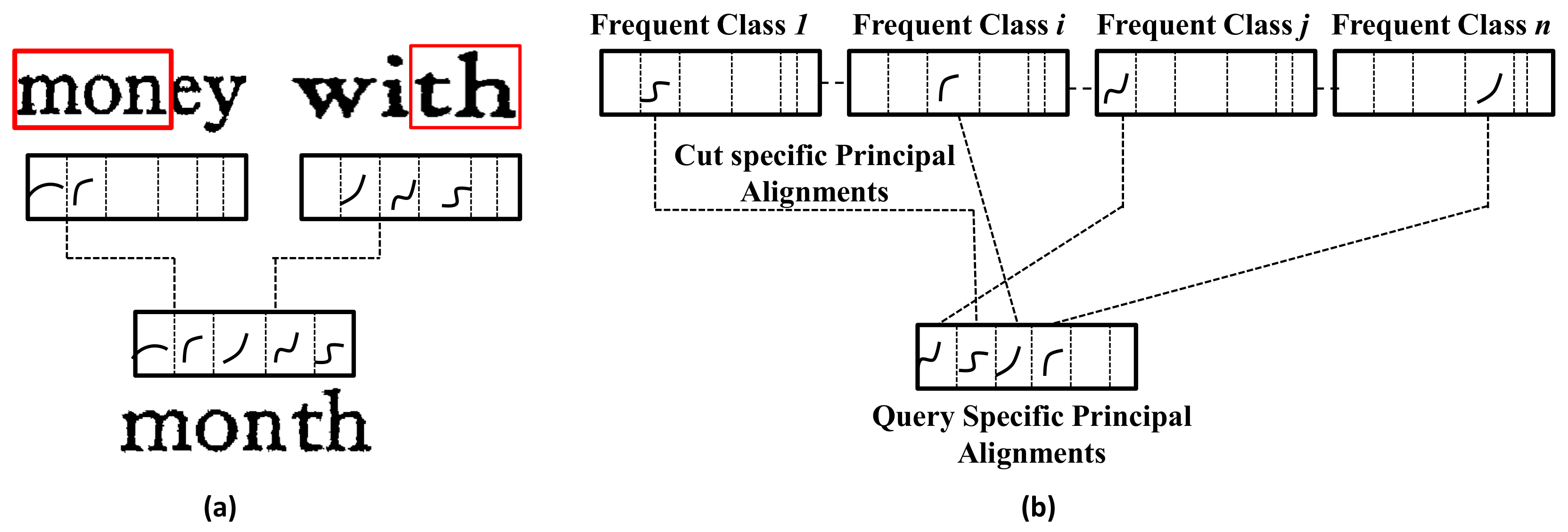
Let be the given data and all the samples are scaled to a fixed size. Let be the most frequent N classes from the data and be their corresponding class means. The matching process using the query specific principal alignments is as follows:
- (i)
Divide each sample from the frequent classes to a fixed number p of equal size portions. Let be the samples (sequences) from the ith class , where is the number of samples in the class . The cut portions for the class means are denoted as , where each cut portion is of length d. Similarly, divide the query into same number p of fixed length portions.
- (ii)
For each class, compute the global principal alignments for each cut portion separately. These are the cut specific principal alignments for the class. For ith class and jth cut portion the cut specific principal alignments are computed from and these are denoted as . These alignments are computed for all the cut portions for each class.
- (iii)
The final step computes the cut specific principal alignments for the given query
as follows. For each cut portion of
, we compute the
dtw distance (Euclidean distance over the cut specific principal alignments) with the corresponding cut portions of all the class means using their corresponding cut specific principal alignments. The distance between the
jth cut portion of
i.e.,
and the
jth cut portion of the
ith class mean i.e.,
is denoted as
For each cut portion of
, we compute the minimum distance mean cut portion over all the class mean vectors. The corresponding cut specific principal alignments of the closest matching mean cut portions are taken as the cut specific principal alignments of the query cut portion. In addition, the corresponding class mean cut portion is taken as the matching cut portion for constructing the query mean. Let the
jth cut portion of the query have the best match with the
jth cut-portion of the class with index
c.
Here the minimum distance is computed over all the frequent classes. We thus have
Here
is the cut specific principal alignments for the
jth cut portion of
. Together, all these query mean cut portions give the query class mean. The query class mean
is given as
. This query class mean
is then used as in Equation (
2) to compute the
lda weight
(query classifier weight). The query specific (QS) DTW distance between the query
and a sample
X from the data is given as
where
p is the number of cut portions.
Figure 3 shows all the processing stages of the nearest neighbor
dqc. To summarize, we generate query specific principal alignments on the fly by selecting and concatenating the global principal alignments corresponding to the smaller
n grams (cut portions). Our strategy is to build cut-specific principal alignments for the most frequent classes; these are the word classes that will be queried more frequently. These cut-specific principal alignments are then used to synthesize the query specific principal alignments (see
Figure 4). The results demonstrate that our strategy gives good performance for queries from both the frequent word classes and rare word classes.
To ensure wider applicability of our approach, we consider that the alignments trained on one dataset may not work well on another dataset. This is mainly due to the print and style variations. For adapting to different styles, we use query expansion (
qe), a popular approach in the information retrieval domain in which the query is reformulated to further improve the retrieval performance. An index is built over the given sample vectors from the database and using approximate nearest neighbor search, the top 10 similar vectors to the given query are computed. These top 10 similar vectors are then averaged to get the new reformulated query. This reformulated query is expected to better capture the variations in the query class. In our experiments, this further improves the retrieval performance. Approximate nearest neighbors are obtained using
flann [
29].
5. Results and Discussions
In this section, we validate the DQC classifier using query specific Fast DTW distance for efficient indexing on multiple word image collections and also demonstrate its quantitative and qualitative performance.
5.1. Data Sets and Evaluation Protocols
In this subsection, we discuss datasets and the experimental settings that we follow in the experiments. Our datasets, given in
Table 2, comprise scanned English books from a digital library collection. We manually created ground truth at word level for the quantitative evaluation of the methods. The first collection (
D1) of words is from a book which is reasonably clean. Second dataset (
D2) is larger in size and is used to demonstrate the performance in case of heterogeneous print styles. Third dataset (
D3) is a noisy book and is used to demonstrate the utility of the performance of our method in degraded collections. We have also given the results over the popular George Washington dataset. For the experiments, we extract profile features [
11] for each of the word images. In this, we divide the image horizontally into two parts and the following features are computed: (i) vertical profile i.e the number of ink pixels in each column (ii) location of lowermost ink pixel, (ii) location of uppermost ink pixel and (iv) number of ink to background transitions. The profile features are calculated on binarized word images obtained using the Otsu thresholding algorithm. The features are normalized to [0, 1], so as to avoid dominance of any specific feature.
To evaluate the quantitative performance, multiple query images were generated. The query images are selected such that they have multiple occurrences in the database and are mostly functional words and do not include the stop words. The performance is measured by mean Average Precision (mAP), which is the mean of the area under the precision-recall curve for all the queries.
5.2. Experimental Settings
For representing word images, we prefer a fixed length sequence representation of the visual content, i.e., each word image is represented as a fixed length sequence of vertical strips. A set of features
,
…,
are extracted, where
∈
is the feature representation of the
ith vertical strip and
L is the number of vertical strips. This can be considered as a single feature vector
of size
. We implement the query specific alignment based solution as discussed in
Section 4. For query expansion based solution, we identify the five most similar samples to the query using approximate nearest neighbor search and compute their mean.
Each dataset contains certain words which are more frequent than others. The number of samples in the frequent word classes are more compared to the rare classes. The retrieval results for frequent queries give better performance because the number of relevant samples available in the dataset is greater. It is worth emphasizing that for the method proposed in this paper (QS DTW), the degradation in the performance for rare queries is much less compared to other methods.
5.3. Results for Frequent Queries
Table 3 compares the retrieval performance of the direct query classifier DQC with the nearest neighbor classifier using different options for distance measures. The performance is shown in terms of mean average precision (mAP) values on three datasets. For the nearest neighbor classifier, we experimented with five distance measures: naive
dtw distance, Fast approximate
dtw distance [
20], query specific
dtw (
qs dtw) distance, Fast
dtw [
30] and Euclidean distance. We see that
dtw performs comparably with
dtw for all the datasets. It performs superior compared to the Fast
dtw, Fast approximate
dtw distance [
20] and performs significantly better compared to Euclidean distance.
For DQC, we experimented with four options for indexing the frequent class mean vectors: subsequence
dtw [
18] (s
dtw), approximate nearest neighbor
nn dqc [
18] (a
nn), Fast
dtw, and
qs dtw. We use the cut-portions obtained from the mean vectors of the most frequent 1000 word classes for (i) computing the cut-specific principal alignments in case of
qs dtw, (ii) computing the closest matching cut-portion (i.e., one with the smallest distance, which can be Euclidean or
dtw) with a cut-portion from the query vector, in case of a
nnor Fast
DTW.
However, since s
dtw has computational complexity
, we restrict the number of frequent words used for indexing to 100. The QS DTW distance improves the performance of the DQC classifier. This is mainly due to the improved alignments involved in the QS DTW distance. The query specific alignments better capture the variations in the query class. Moreover, unlike the case of s
dtw distance, the QS DTW distance has linear complexity and therefore we are able to index all the frequent mean vectors in the DQC classifier. Thus, the proposed method of QS DTW enhances the performance of the DQC classifier [
18].
For frequent queries, the experiments revealed that the QS DTW gets the global principal alignments from the mean vector of the same (query) class. Since the alignments are coming from the query class, it gives minimum distance only for the samples which belong to its own class. Therefore, the retrieved samples largely belong to the query class. The performance is therefore improved compared to s
dtw distance. In contrast, the Fast approximate DTW distance [
20] computes the global principal alignments using all samples in the database, without exploiting any class information. The computed global principal alignments, therefore, include alignments from classes that may be different from the query class. For this reason, it performs inferior to the proposed
dtw distance.
5.4. Results for Rare Queries
The faster indexing offered by the use of QS DTW with DQC allows us to make use of the mean vectors of all the 1000 frequent classes. This gives us a much improved performance of the DQC on rare queries, compared to s
dtw [
18] which uses mean vectors from 100 frequent classes.
Table 4 shows the retrieval performance of DQC with a nearest neighbour classifier using different options for distance measures. The performance is showed in terms of mean average precision (mAP) values on rare queries from three datasets. For the nearest neighbor classifier, we experimented with five distance measures: naive DTW distance, Fast approximate
dtw distance [
20], query specific DTW (QS DTW) distance, Fast
dtw [
30] and Euclidean distance. We see that QS DTW performs comparably with
dtw distance for all the datasets. It performs superior compared to the Fast approximate
dtw distance [
20], Fast
dtw and significantly better compared to Euclidean distance.
For DQC, we observe that QS DTW improves the performance compared to sdtw. This improvement of QS DTW over sdtwis more for rare queries compared to that for frequent queries. This shows that QS DTW can be used for faster indexing for both frequent and rare queries.
For rare queries, the query specific
dtw distance outperforms Fast approximate
dtw [
20] distance. This happens because the Fast approximate
dtw computes the global principal alignments from the database and its performance depends on the number of samples. Also, these alignments are query independent, i.e., they do not use any query information for computing the global principal alignments. For a given query, it needs enough samples from the query class for getting novel global principal alignments. However, in any database, the number of samples for frequent classes dominate the number of samples for rare classes. The global principal alignments for frequent queries are likely to dominate the rare queries. Therefore, the precomputed global principal alignments in Fast approximate
dtw may not capture all the correlations for rare query classes. In the proposed QS DTW distance, the global principal alignments are learned from the
ngrams (cut-portions) of frequent classes. These
n-grams are in abundance and also shared with rare queries, thus there are enough
n-gram samples for learning the cut-specific alignments. The computed query specific alignments for the cut-portions outperform the alignments obtained from Fast approximate
dtw.
It is worth mentioning that FastDTW [
30], which is an approximation method, attempts to compute the DTW distance in an efficient way. It does not consider cut portion similarities, which may be influenced by various printing styles. Hence, these approaches are not applicable in our setting where the dataset can have words printed in varied printing styles, and thus can result in a marked degradation of performance for rare queries. Since query specific DTW finds the approximate DTW distance using cut specific principal alignments, it can exploit properties which cannot be used by other DTW approximation methods.
To summarize, the experiments demonstrate that the proposed query specific DTW performs well for both frequent and rare queries. Since it is learning the alignments from ngrams, it performs comparable to sdtwdistance for rare queries. For some queries, it performed better than the DTW distance.
5.5. Results for Rare Query Expansion
The results for QS DTW enhanced with query expansion (
qe) using five best matching samples are also given in
Table 4. It is observed that QE further improves the performance of our proposed method. To show the effectiveness of query expansion, we have computed the average of the
dtw distance between the given query and all database samples that belonged to the query class. Likewise, we computed the average of the DTW distance for the reformulated query.
Table 5 shows a comparison of the averaged
dtw distance for the given query and the reformulated query using 2, 5, 7, and 10 most similar (to the query) samples from the database. From the results, we can observe that compared to the given query, the reformulated query using five best matching samples gives the lowest averaged
dtw distance to the samples from the query class. This means the reformulated query is a good representative for the given query. However, using nine best matching samples for reformulating the query leads to a higher average of
dtw distances. This means some irrelevant samples to the query are coming in the top similar samples.
5.6. Results on George Washington Dataset
The George Washington (GW) dataset [
31] contains 4894 word images from 1471 word classes. This is one of the popular dataset for word images. We applied our proposed method of DQC using QS DTW for word retrieval on the GW dataset.
Table 6 provides comparative results for seven methods. Experiments are repeated for 100 random queries and the average over these results are reported in the table. We can observe that for the DQC the proposed QS DTW gives better performance than DTW. We can also observe that for the nearest neighbor classifier, QS DTW distance is performing slightly superior to the
dtw distance and Fast approximate
dtw distance. The superiority is because of the principal alignments which are query specific.
5.7. Setting the Hyperparameters
The proposed method has few hyperparameters, like the length of the cut portion and the number of cut specific principal alignments. For tuning these parameters, we randomly choose 100 queries for each dataset and validate the performance over these queries. Queries included in the validation set are not used for reporting the final results.
In
Table 7, we report the effect of varying the cut portion length on retrieval performance. The mAP score is less for smaller cut portion length. In this case, the learned alignments are not capturing the desired correlations. This happens because the occurrence of smaller cut portions is very frequent in the word images. For length more than 30, the mAP is again decreased. This is because the occurrences of larger cut portions are rare. Cut portion lengths in the range of 10 to 20 give better results. In this case, the cut portions are good enough to yield global principal alignments that can distinguish the different word images.
We assessed the effect of varying the number of cut-specific principal alignments on the retrieval performance on the three datasets and the results are given in
Table 8. It is seen that the performance degrades for all the datasets when the number of alignments is chosen as 30. This can be attributed to some redundant alignments getting included in the set of principal alignments. Increasing the number of alignments from 10 to 20 improves performance for dataset D1, but has no effect on the performance for datasets D2 and D3. Therefore, we can conclude that restricting the number of principal alignments in the range 10 to 20 would give good results. In all our experiments, we set the number of cut-specific principal alignments as 10.
5.8. Computation Time
Table 9 gives the computational time complexity for the methods based on
dtw. The main computation involved in the use of QS DTW is that of computing the cut specific principal alignments for the frequent classes.
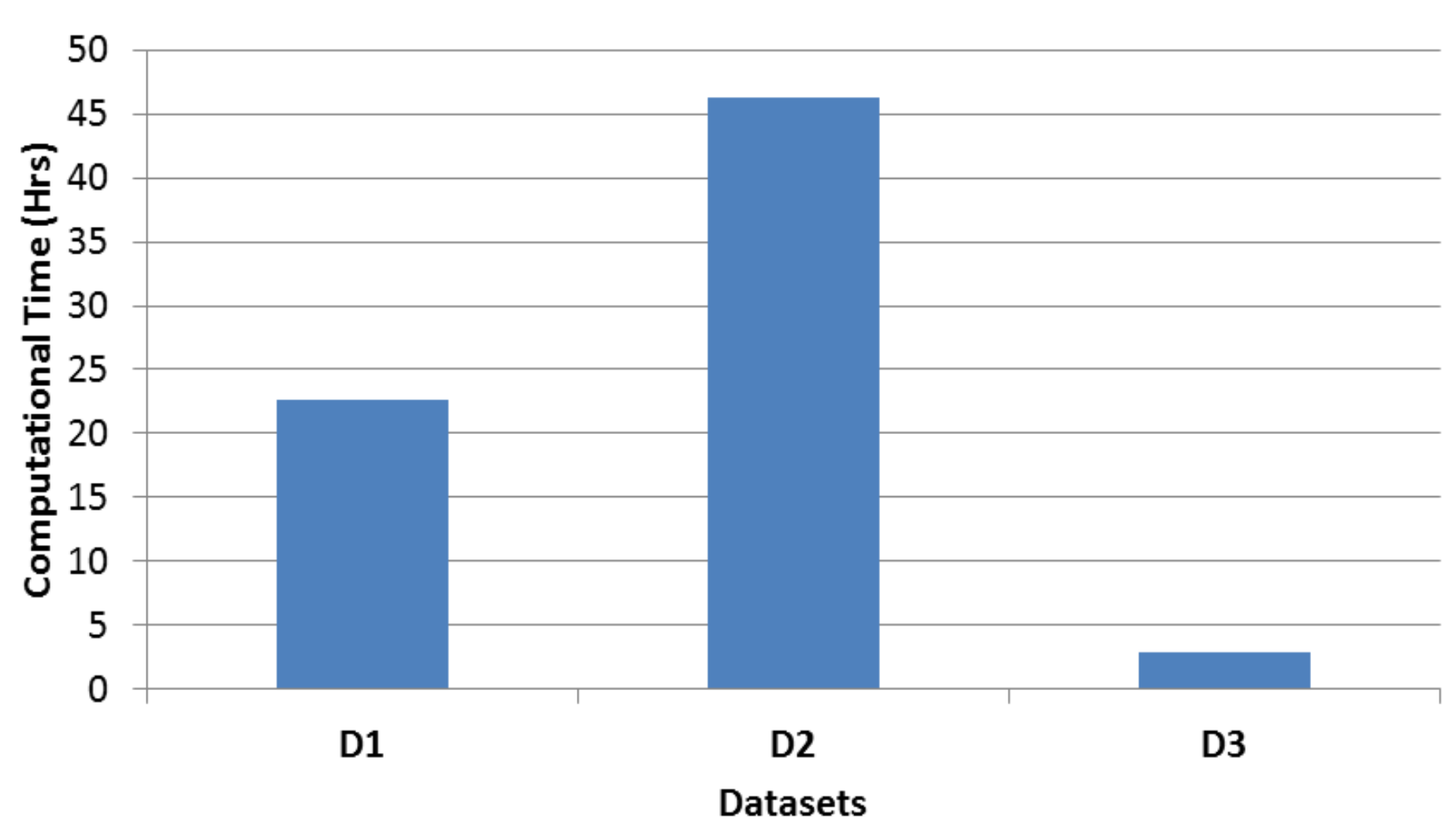
Figure 5 shows the time for computing the cut specific principal alignments for the three datasets. The computation of these cut specific principal alignments can be carried out independently for all the classes. Since we can compute these principal alignments in parallel with each other, the proposed QS DTW scales well with the number of samples compared to Fast Apprx
dtw [
20].
Unlike the case of QS DTW, where the principal alignments are computed for the small cut portions, in Fast Apprx DTW, the principal alignments are computed for the full word image representation. Further, in Fast Apprx DTW, the principal alignments are computed from the entire dataset, unlike the case of QS DTW in which the principal alignments are computed for the individual classes. For these reasons, Fast Apprx DTW is computationally slower compared to the QS DTW.
For a given dataset, computing the cut specific principal alignments for the frequent classes is an offline process. When performing retrieval for a given query, DQC involves computing the query mean by composing together the nearest cut portions from the mean vectors of frequent classes. Further, the query specific principal alignments are not explicitly computed but rather constructed using the cut-specific principal alignments corresponding to the nearest cut portions. Once the query specific principal alignments are obtained, computation of QS DTW involves computing the Euclidean distance (using the query specific principal alignments) with the database images.
For the given two samples
x and
y of length
N, FastDTW [
30] is computed in the following way. First, these two samples are reduced to smaller length (1/8 times) and the naive DTW distance is applied over the reduced length samples to find the optimal warp path. Next, both the optimal path and the reduced length samples from the previous step are projected to higher (two times) resolution. Instead of filling all the entries in the cost matrix in the higher resolution, only the entries around a neighborhood of the projected warp path, governed by a parameter called radius
r, are filled up. This projection step is continued until the original resolution was obtained. The time complexity of FastDTW is
, where
r is the radius. The performance of FastDTW depends on the radius
r. The higher the value of
r, the better the performance is. The time complexity of QSDTW/Fast Apprx DTW is
, where
p is the number of principal alignments. In general,
, for getting the similar performance in both the methods.