Assessment of Geometric Distortion in Six Clinical Scanners Using a 3D-Printed Grid Phantom
Abstract
:1. Introduction
2. Materials and Methods
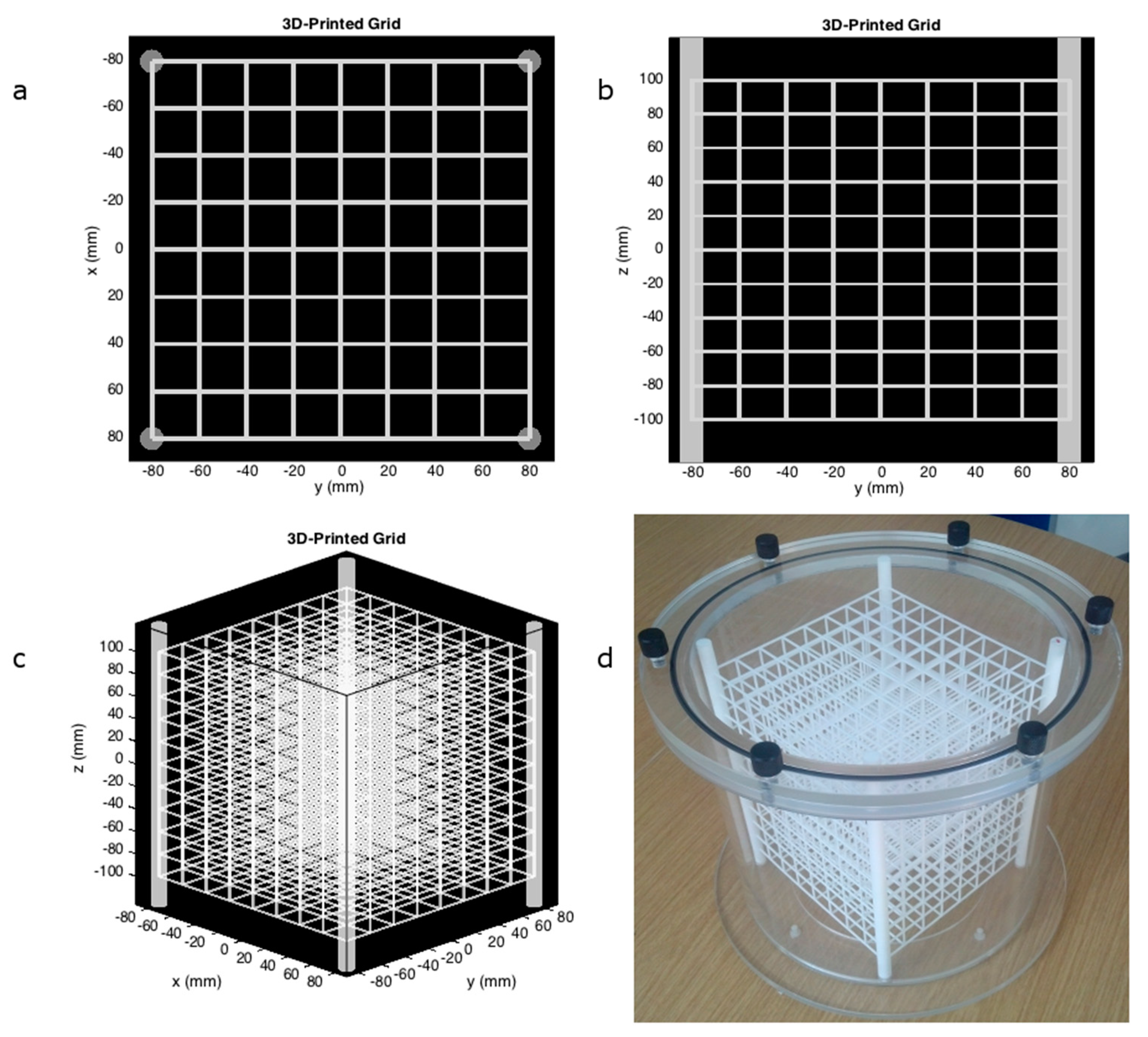
2.1. 3D-Printed Phantom
2.2. Image Acquisition
2.3. Detection of Vertices
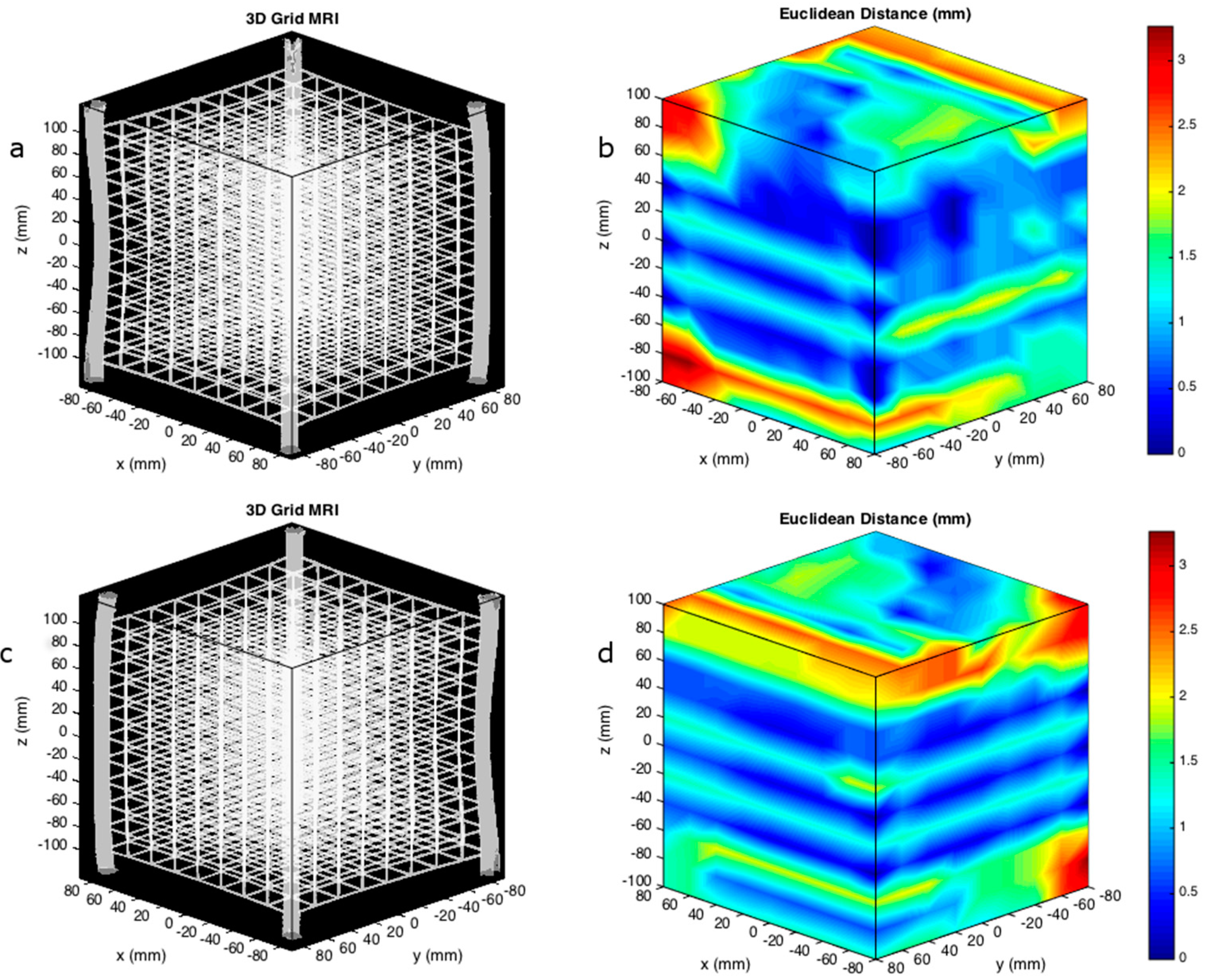
2.4. Detection of the Spatial Distribution of the Vertices
2.5. Error Metric
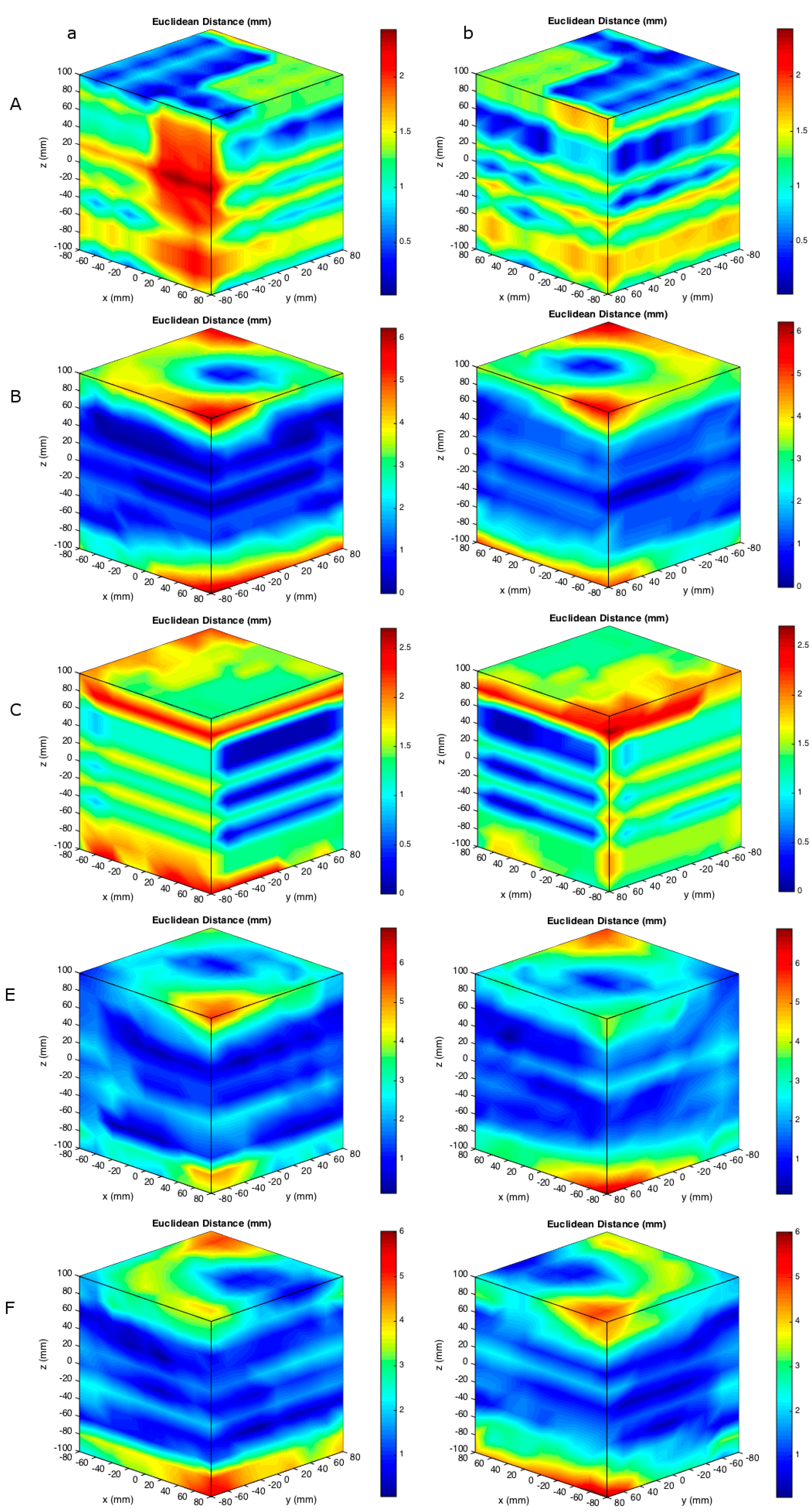
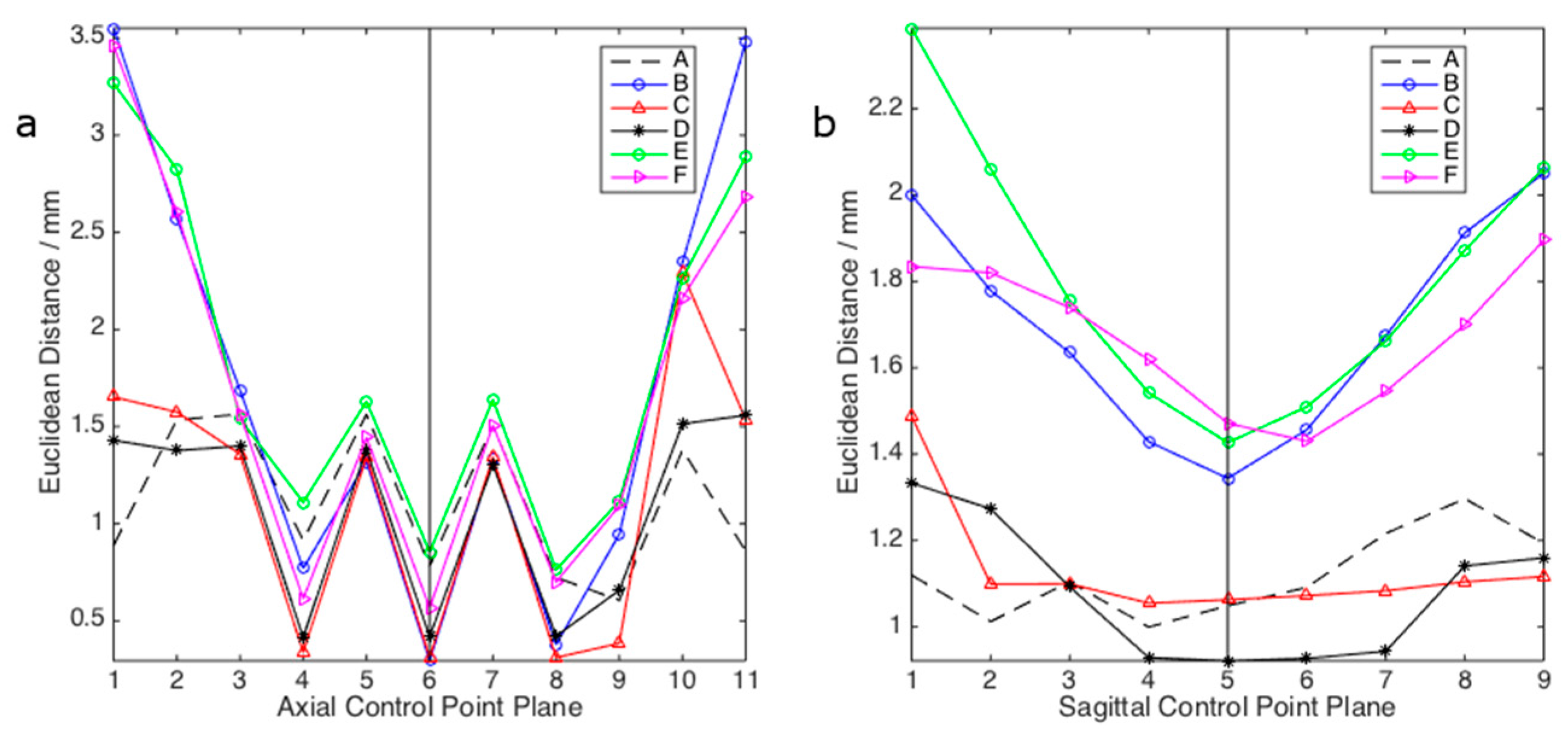
3. Results
4. Discussion
Author Contributions
Conflicts of Interest
References
- Sumanaweera, T.S.; Adler, J.R.; Napel, S.; Glover, G.H. Characterization of spatial distortion in magnetic resonance imaging and its implications for stereotaxic surgery. Neurosurgery 1994, 35, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Doddrell, D.M.; Cowin, G. A novel phantom and method for comprehensive 3-dimensional measurement and correction of geometric distortion in magnetic resonance imaging. Magn. Reson. Imaging 2004, 22, 529–542. [Google Scholar] [CrossRef] [PubMed]
- Price, R.R.; Axel, L.; Morgan, T.; Newman, R.; Perman, W.; Schneiders, N.; Selikson, M.; Wood, M.; Thomas, S.R. Quality assurance methods and phantoms for magnetic resonance imaging—Report of AAPM nuclear magnetic resonance task group no-1. Med. Phys. 1990, 17, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Kawanaka, A.; Takagi, M. Estimation of static magnetic field and gradient fields from NMR image. J. Phys. E Sci. Instrum. 1986, 19, 871–875. [Google Scholar] [CrossRef]
- Mizowaki, T.; Nagata, Y.; Okajima, K.; Kokubo, M.; Negoro, Y.; Araki, N.; Hiraoka, M. Reproducibility of geometric distortion in magnetic resonance imaging based on phantom studies. Radiother. Oncol. 2000, 57, 237–242. [Google Scholar] [CrossRef]
- Walton, L.; Hampshire, A.; Forster, D.M.C.; Kemeny, A.A. A phantom study to assess the accuracy of stereotactic localization, using T1-weighted magnetic resonance imaging with the Leksell stereotactic system. Neurosurgery 1996, 38, 170–176. [Google Scholar] [CrossRef] [PubMed]
- Walton, L.; Hampshire, A.; Forster, D.M.C.; Kemeny, A.A. Stereotactic localization with magnetic resonance imaging: A phantom study to compare the accuracy obtained using two-dimensional and three-dimensional data acquisitions. Neurosurgery 1997, 41, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Apuzzo, M.L.J.; Zee, C.S.; Petrovich, Z. A phantom study of the geometric accuracy of computed tomographic and magnetic resonance imaging stereotactic localization with the Leksell stereotactic system. Neurosurgery 2001, 48, 1092–1098. [Google Scholar] [CrossRef] [PubMed]
- Sumanaweera, T.; Glover, G.; Song, S.; Adler, T.; Napel, S. Quantifying MRI geometric distortion in tissue. Magn. Reson. Med. 1994, 31, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, L.N.; Wachowicz, K.; Thomas, S.D.; Rivest, R.; Fallone, B.G. Characterization, prediction, and correction of geometric distortion in 3 T MR images. Med. Phys. 2007, 34, 388–399. [Google Scholar] [CrossRef] [PubMed]
- Breeuwer, M.; Holden, M.; Zylka, W. Detection and correction of geometric distortion in 3D MR images. Proc. SPIE 2001, 4322. [Google Scholar] [CrossRef]
- Tofts, P.S.; Duboulay, E.P.G.H. Towards quantitative measurements of relaxation-times and other parameters in the brain. Neuroradiology 1990, 32, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Briechle, K.; Hanebeck, U. Template Matching using Fast Normalized Cross Correlation. Proc. SPIE 2011, 4387. [Google Scholar] [CrossRef]
- Crow, F.C. Summed-area Tables for Texture Mapping. SIGGRAPH Comput. Graph. 1984, 18, 207–212. [Google Scholar] [CrossRef]
- Kroon, D.-J. Fast/Robust Template Matching. Matlab File Exchange, 2009. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/24925-fast-robust-template-matching?requestedDomain=www.mathworks.com (accessed on 28 April 2017).
- Doran, S.J.; Charles-Edwards, L.; Reinsberg, S.A.; Leach, M.O. A complete distortion correction for MR images: I. Gradient warp correction. Phys. Med. Biol. 2005, 50, 1343–1361. [Google Scholar] [CrossRef] [PubMed]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1992, 2, 176–201. [Google Scholar] [CrossRef] [PubMed]
- Hillenbrand, D.F.; Lo, K.M.; Punchard, W.F.B.; Reese, T.G.; Starewicz, P.M. High-order MR shimming: A simulation study of the effectiveness of competing methods, using an established susceptibility model of the human head. Appl. Magn. Reson. 2005, 29, 39–64. [Google Scholar] [CrossRef]
- Orth, R.C.; Sinha, P.; Madsen, E.L.; Frank, G.; Korosec, F.R.; Mackie, T.R.; Mehta, M.P. Development of a unique phantom to assess the geometric accuracy of magnetic resonance imaging for stereotactic localization. Neurosurgery 1999, 45, 1423–1429. [Google Scholar] [CrossRef] [PubMed]
- Keller, S.S.; Roberts, N. Measurement of brain volume using MRI: Software, techniques, choices and prerequisites. J. Anthropol. Sci. 2009, 87, 127–151. [Google Scholar] [PubMed]
- Harvey, H.; Orton, M.R.; Morgan, V.A.; Parker, C.; Dearnaley, D.; Fisher, C.; deSouza, N.M. Volumetry of the dominant intraprostatic tumour lesion: intersequence and interobserver differences on multiparametric MRI. Br. J. Radiol. 2017, 90, 20160416. [Google Scholar] [CrossRef] [PubMed]

| System | Vendor | Model | Field (T) | GS (mT/m) | SR (T/m/s) | Homogeneity (ppm) | Diameter (cm) | Length (cm) |
|---|---|---|---|---|---|---|---|---|
| A | Philips | Achieva TX | 3.0 | 40 80 | 200 100 | ≤1.8 1 | 60 | 157 |
| B | Siemens | Verio | 3.0 | 45 | 200 | 4.0 1 | 70 | 173 |
| C | Siemens | Avanto | 1.5 | 33 | 125 | <1.5 (0.8 typical) 2 | 60 | 160 |
| D | Siemens | Prisma | 3.0 | 80 | 200 | 1.1 typical 2 | 60 | 213 |
| E | Siemens | Aera | 1.5 | 45 | 200 | 3.1 1 | 70 | 137 |
| F | Siemens | Aera | 1.5 | 45 | 200 | 3.1 1 | 70 | 137 |
| System | Sequence | TR/TE (ms/ms) | FA (°) | FOV (mm × mm) | In-Plane Resolution (mm × mm) | Slice Width (mm) | Receiver Bandwidth (Hz/pixel) |
|---|---|---|---|---|---|---|---|
| A | 3D FFE | 11/5.2 | 30 | 361 × 361 | 0.71 × 0.71 | 1.25 | 136 |
| B | 3D FLASH | 11/5.0 | 10 | 256 × 256 | 1.0 × 1.0 | 1.0 | 179 |
| C | 3D FLASH | 11/5.2 | 10 | 256 × 256 | 1.0 × 1.0 | 1.0 | 289 |
| D | 3D FLASH | 11/5.0 | 30 | 361 × 361 | 0.71 × 0.71 | 1.25 | 285 |
| E | 3D FLASH | 11/5.0 | 30 | 361 × 361 | 0.71 × 0.71 | 1.25 | 290 |
| F | 3D FLASH | 11/5.0 | 30 | 361 × 361 | 0.71 × 0.71 | 1.25 | 290 |
| System | Mean Error ± Std (mm) |
|---|---|
| A | 1.1 ± 0.47 |
| B | 1.7 ± 1.3 |
| C | 1.1 ± 0.72 |
| D | 1.1 ± 0.65 |
| E | 1.8 ± 1.1 |
| F | 1.7±1.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafar, M.; Jafar, Y.M.; Dean, C.; Miquel, M.E. Assessment of Geometric Distortion in Six Clinical Scanners Using a 3D-Printed Grid Phantom. J. Imaging 2017, 3, 28. https://doi.org/10.3390/jimaging3030028
Jafar M, Jafar YM, Dean C, Miquel ME. Assessment of Geometric Distortion in Six Clinical Scanners Using a 3D-Printed Grid Phantom. Journal of Imaging. 2017; 3(3):28. https://doi.org/10.3390/jimaging3030028
Chicago/Turabian StyleJafar, Maysam, Yassir M. Jafar, Christopher Dean, and Marc E. Miquel. 2017. "Assessment of Geometric Distortion in Six Clinical Scanners Using a 3D-Printed Grid Phantom" Journal of Imaging 3, no. 3: 28. https://doi.org/10.3390/jimaging3030028





