Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids
Abstract
:1. Introduction
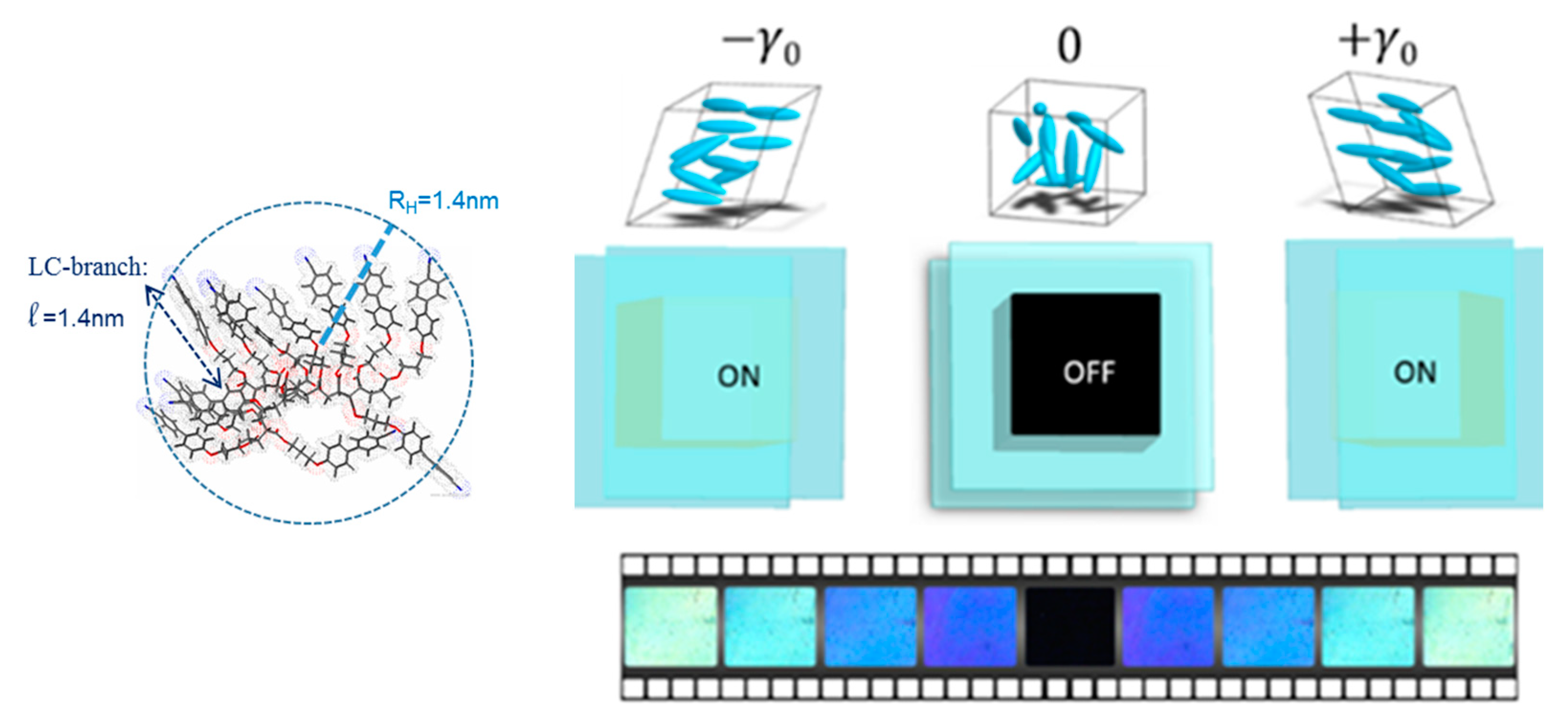
2. Isotropic Phase under a Low-Frequency Mechanical Field: Spectacular Optical Effects
Low-Frequency Optical Response in the Isotropic Phase
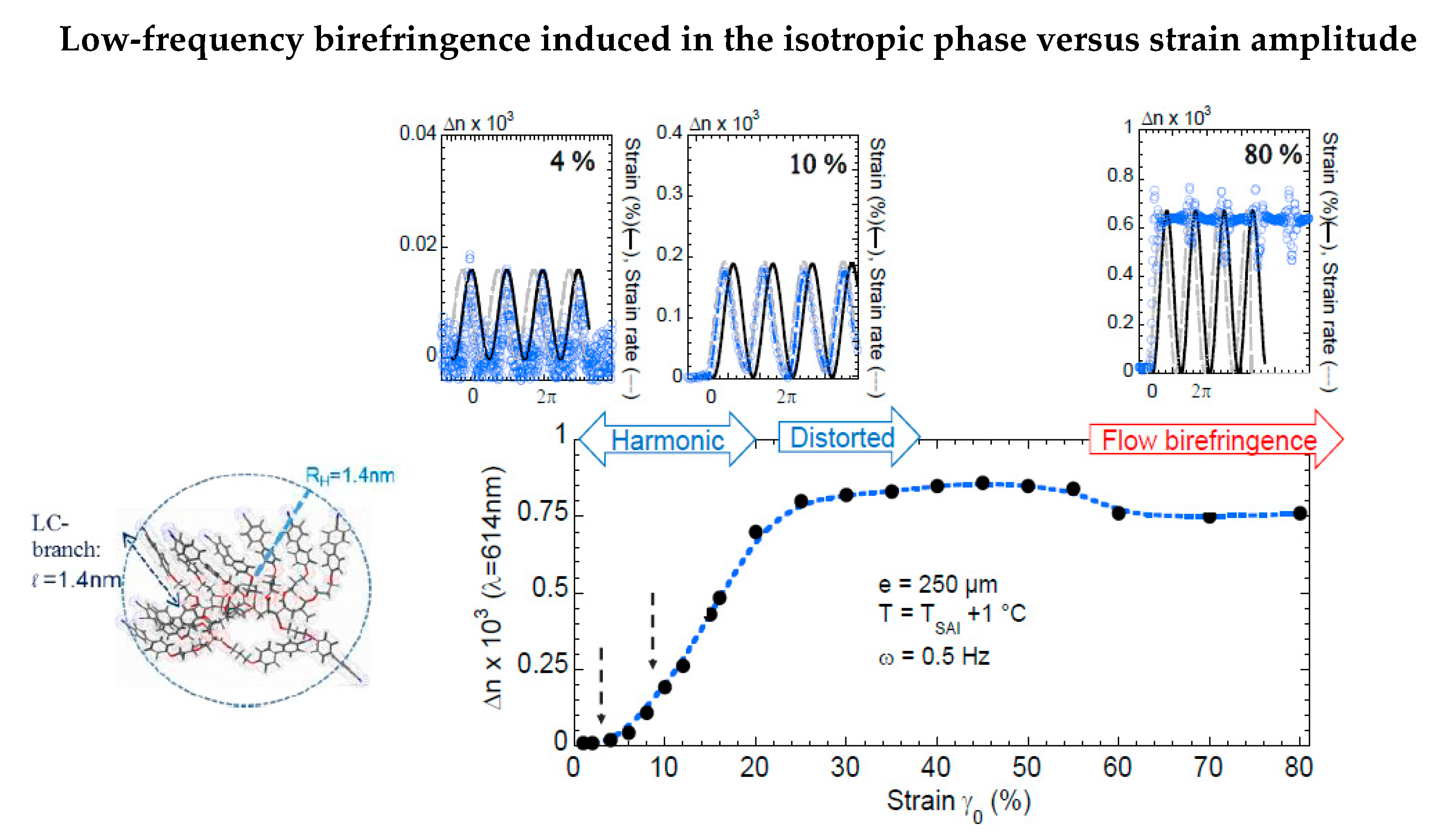
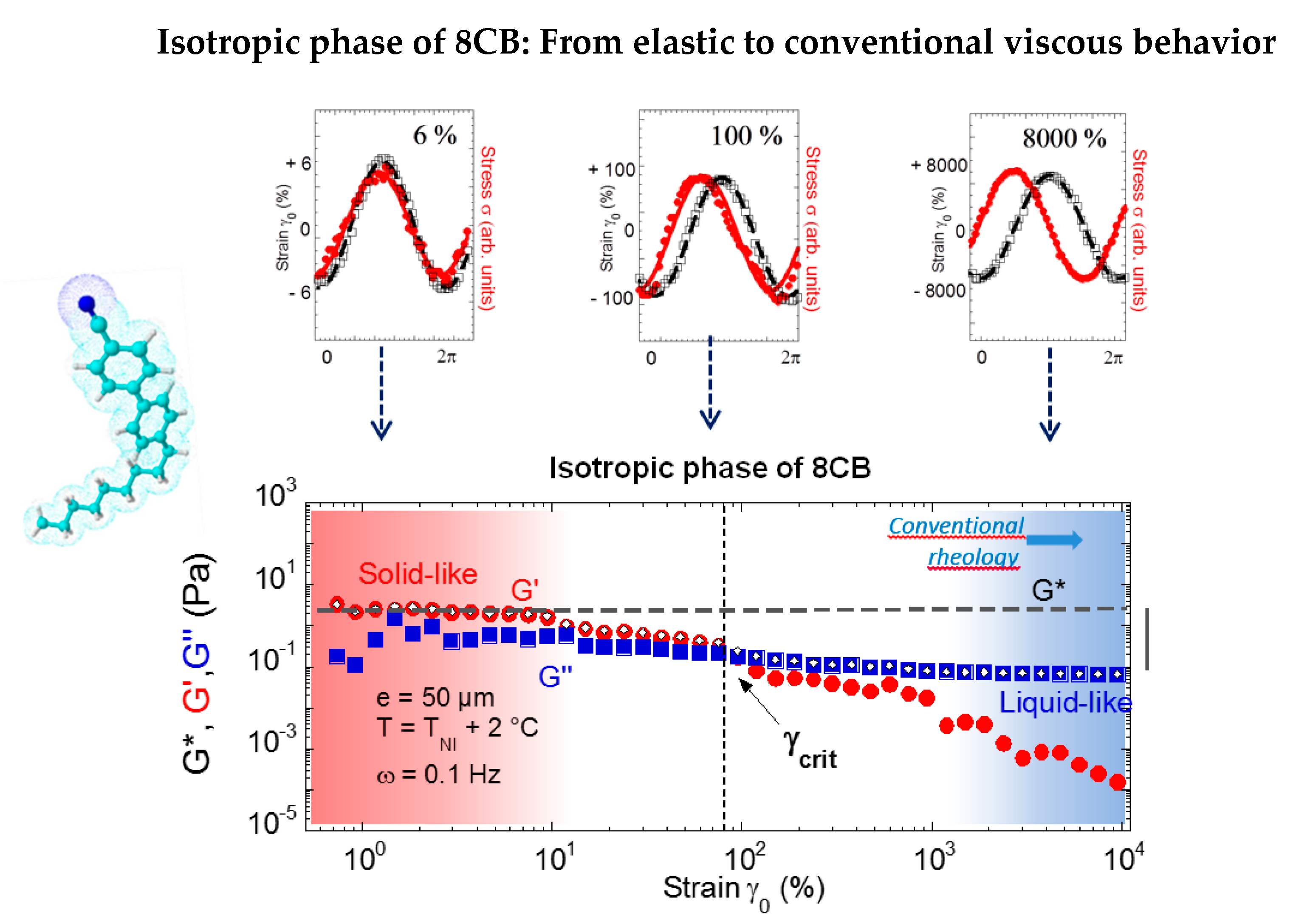
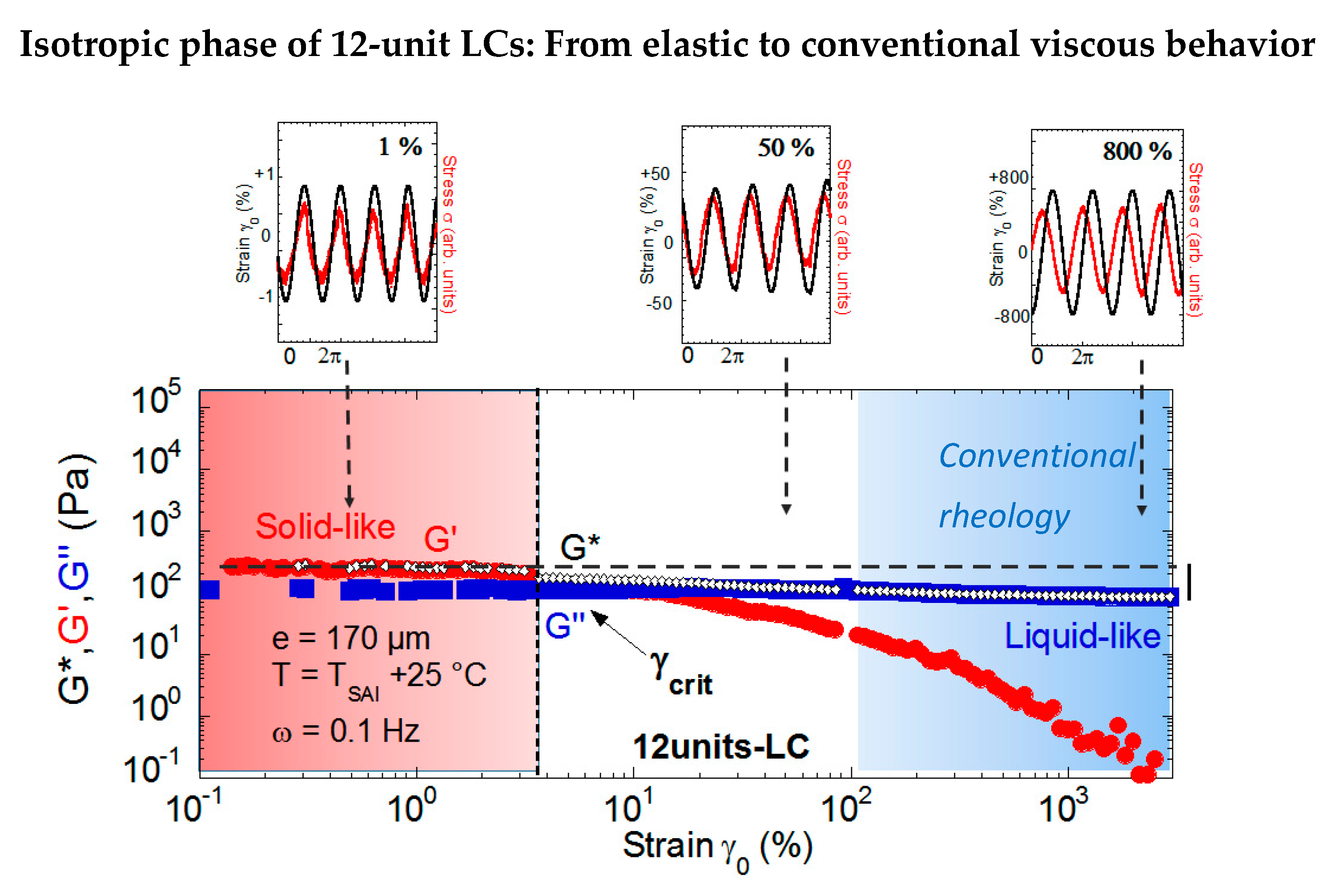
- At the smallest strains (γ0 < 5%), the birefringence is harmonic and in phase with the applied strain.
- In the intermediate regime (5% < γ0 < 25%) the signals are also harmonic but are phase-shifted by π/2 (in phase with the strain rate).
- At larger strains (γ0 > 25%), the signals become distorted, exhibiting higher harmonics. The waves no longer relax between two periods and saturated. The observed, almost continuous signal, as shown for γ0 > 80%, indicates a nearly strain-independent value. The asymptotic behavior at high strain amplitude of the birefringence corresponds to the flow birefringence.
- -
- At a very low strain regime (γ0 < 4%), the birefringent signal is in phase with the applied strain wave (upper left inset).
- -
- For 4% < γ0 < 30%, the optical signal is π/2 phase-shifted in respect to the strain and increases linearly up to 25% strain amplitude (upper medium inset).
- -
- Above 25% strain amplitude, the optical signal does not relax, reaching an asymptotic value corresponding to the flow birefringence.
- -
- The birefringence at very small strain amplitudes (γ0 < γcrit) is in phase with the excitation, indicating an elastic mechanism alternating stretching state and relaxation under oscillatory strain.
- -
- The second regime (γ0 > γcrit), characterized by a π/2 phase-shifted birefringence that increases linearly with the strain, is also harmonic with the excitation. The conservation of the shape of the strain wave (harmonicity) indicates that the strain-induced birefringence is associated to a conservative mechanism (as opposed to a dissipative process). The linearity with the increasing strain amplitude characterizes an elastic process. Finally, the π/2 shift of the phase of the signal indicates a two-step process wherein the first step is achieved in the first elastic regime identified at very low strain rates (γ0 < 4%) close to the transition.
- -
- At higher strain amplitudes, the optical wave is not more harmonic, does not relax between two successive oscillations, and saturates to an asymptotic birefringence value, indicating a dissipative regime. The asymptotical limit of large strains is the steady state shear flow. In this regime, the nearly constant asymptotic value of the birefringence corresponds to the so-called flow birefringence.
3. Introduction to the Viscoelastic Approach: From the Macroscopic to Sub-Millimeter Scale
A Young Discipline
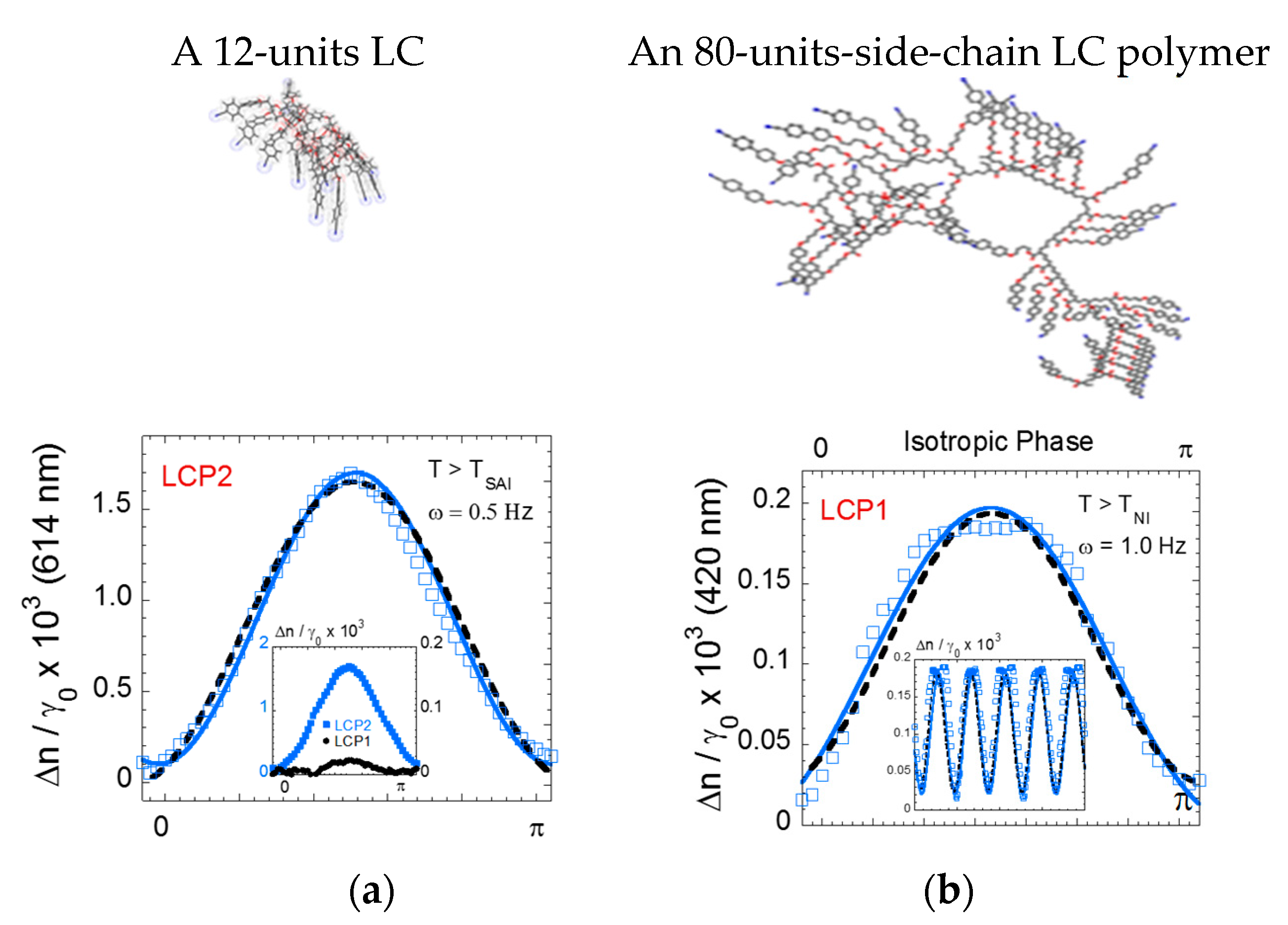
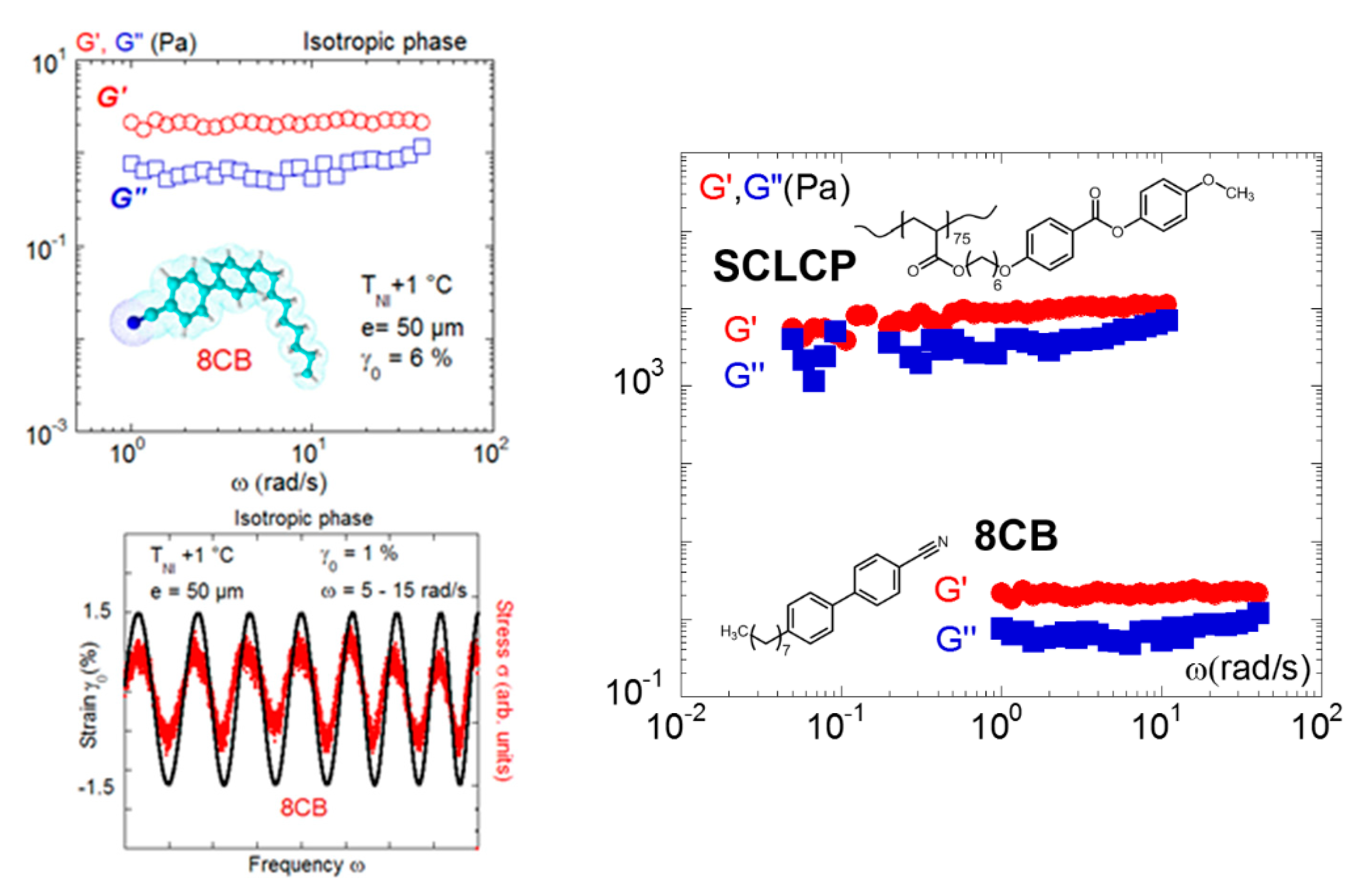
4. The Optical Response of LCs and LCPs in the Isotropic Phase Challenges the Single Molecular Approach
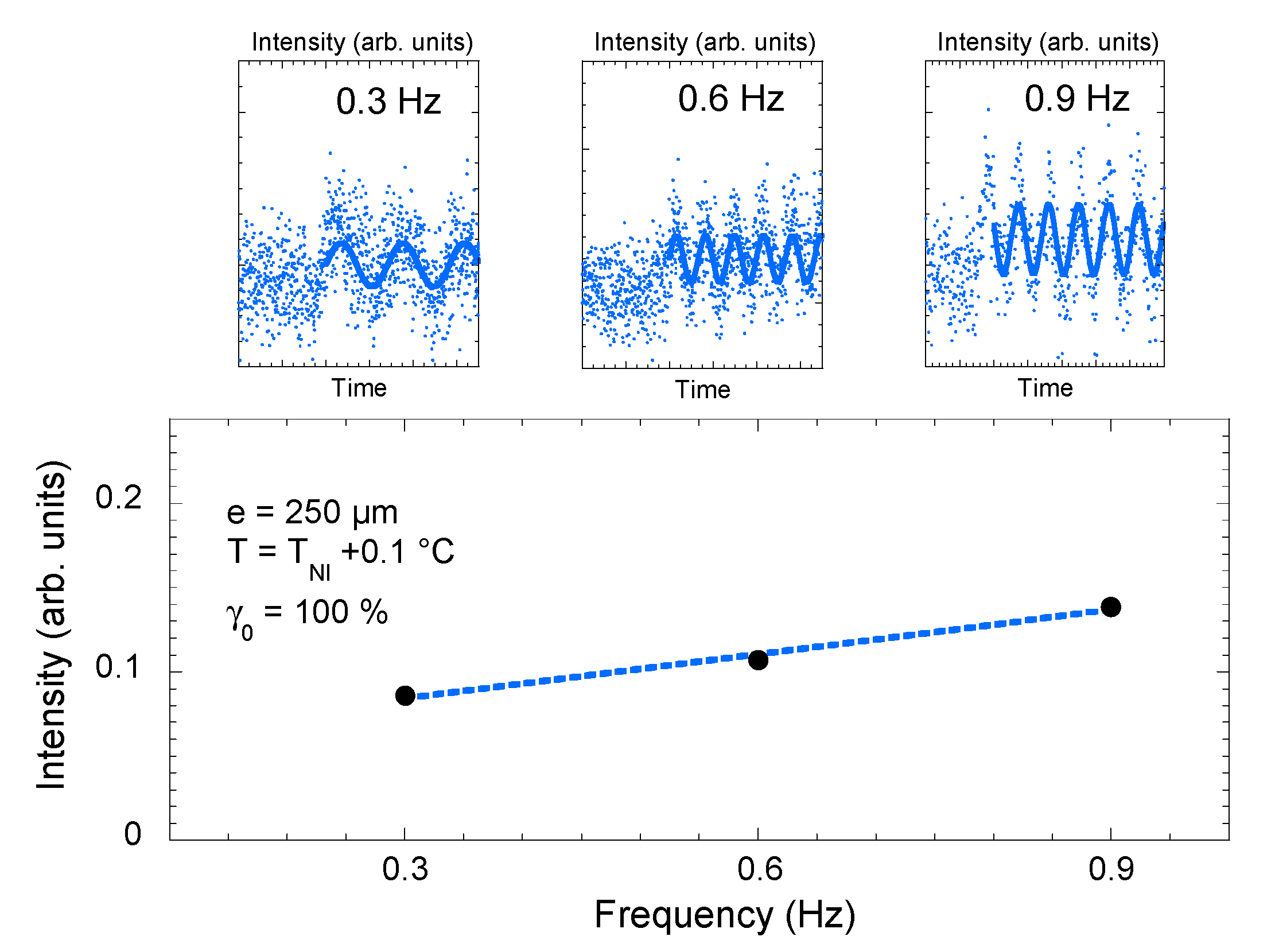
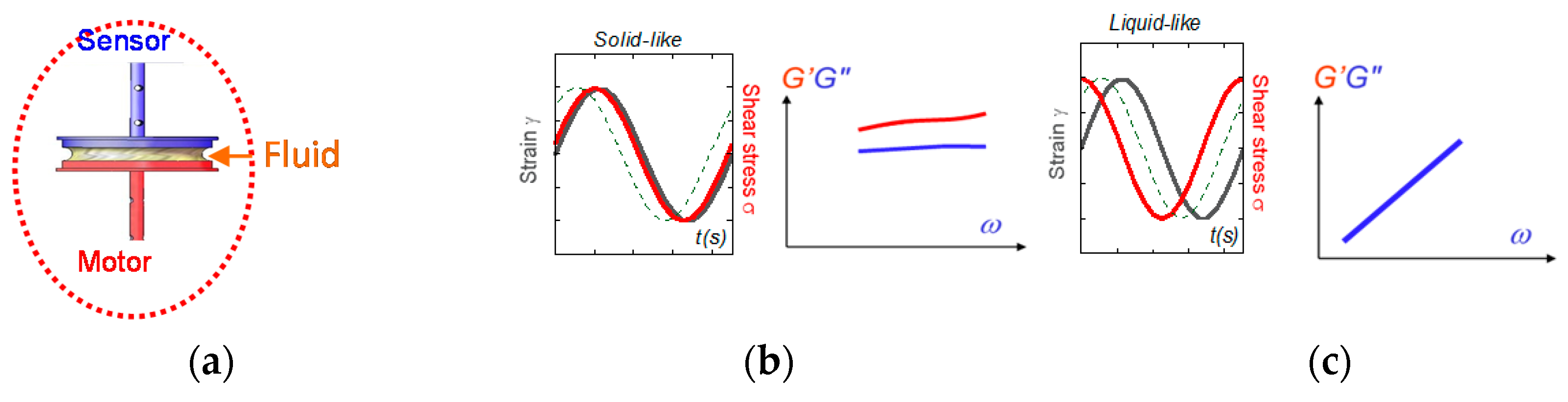
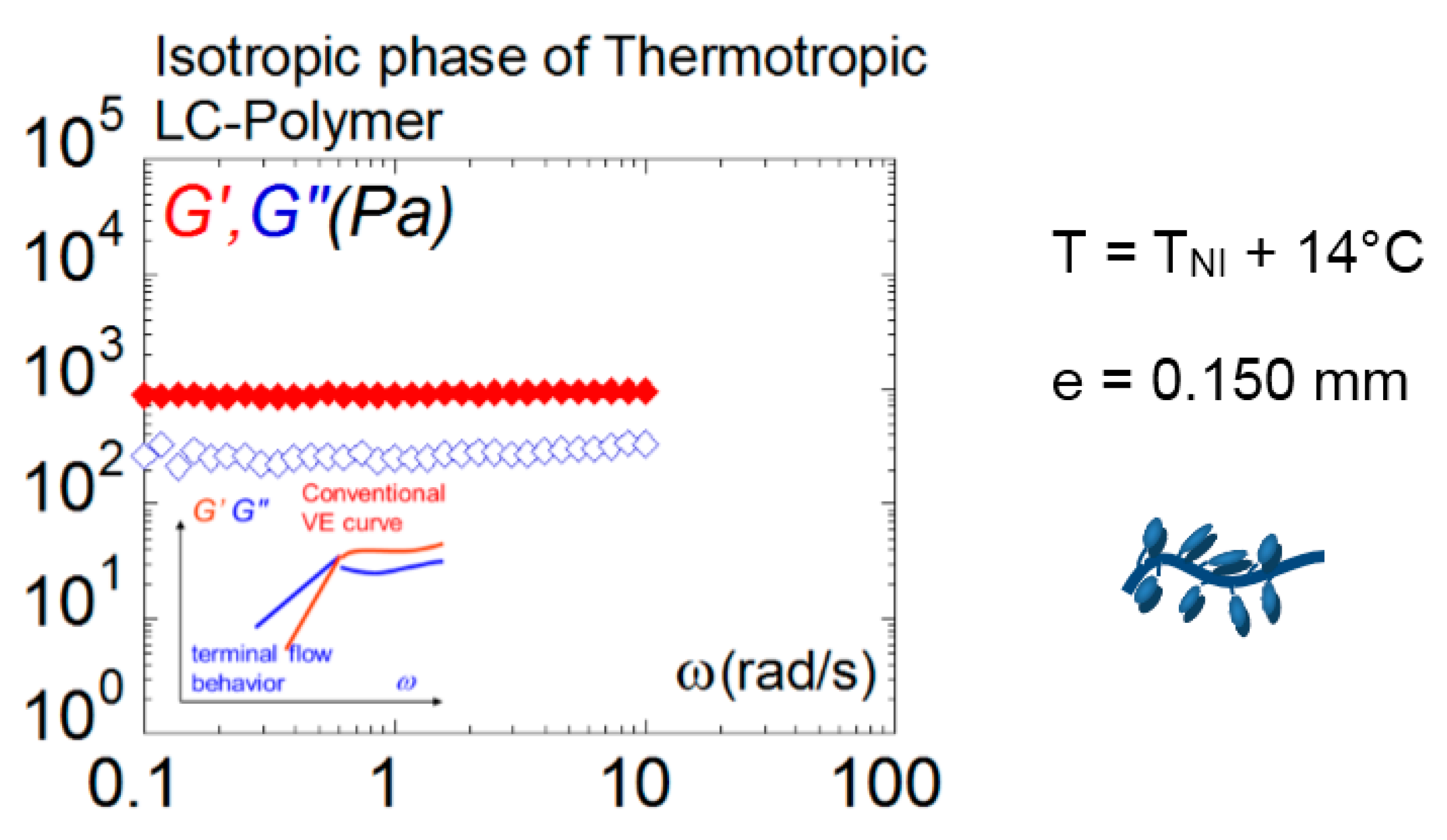
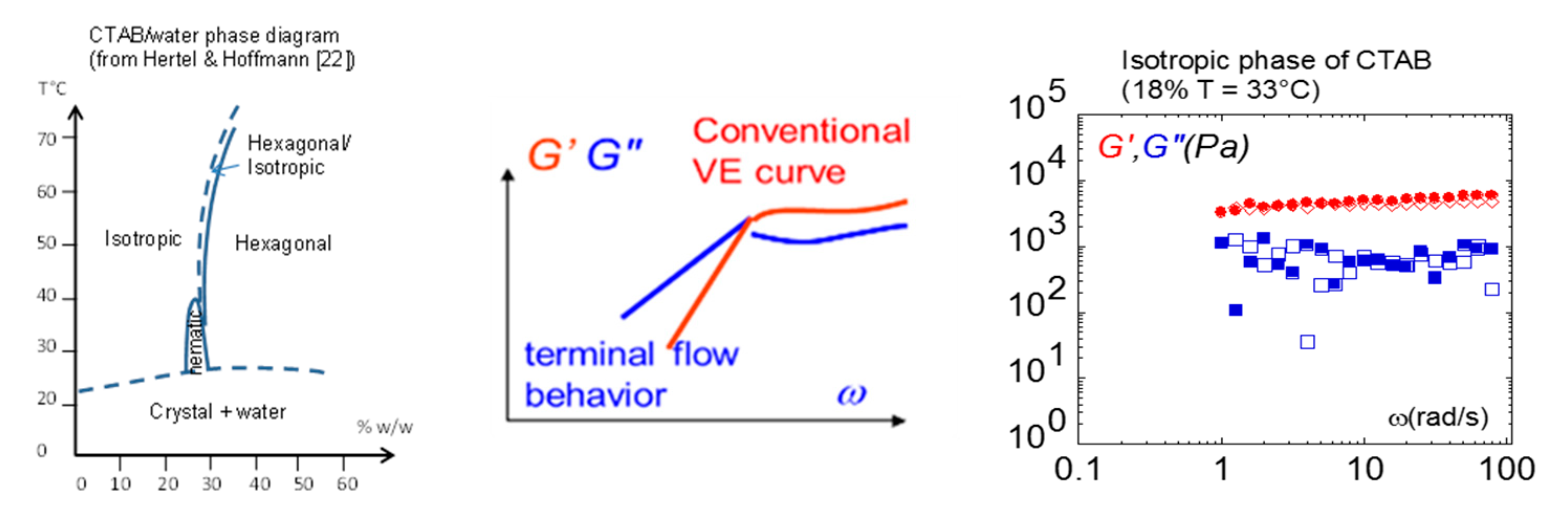
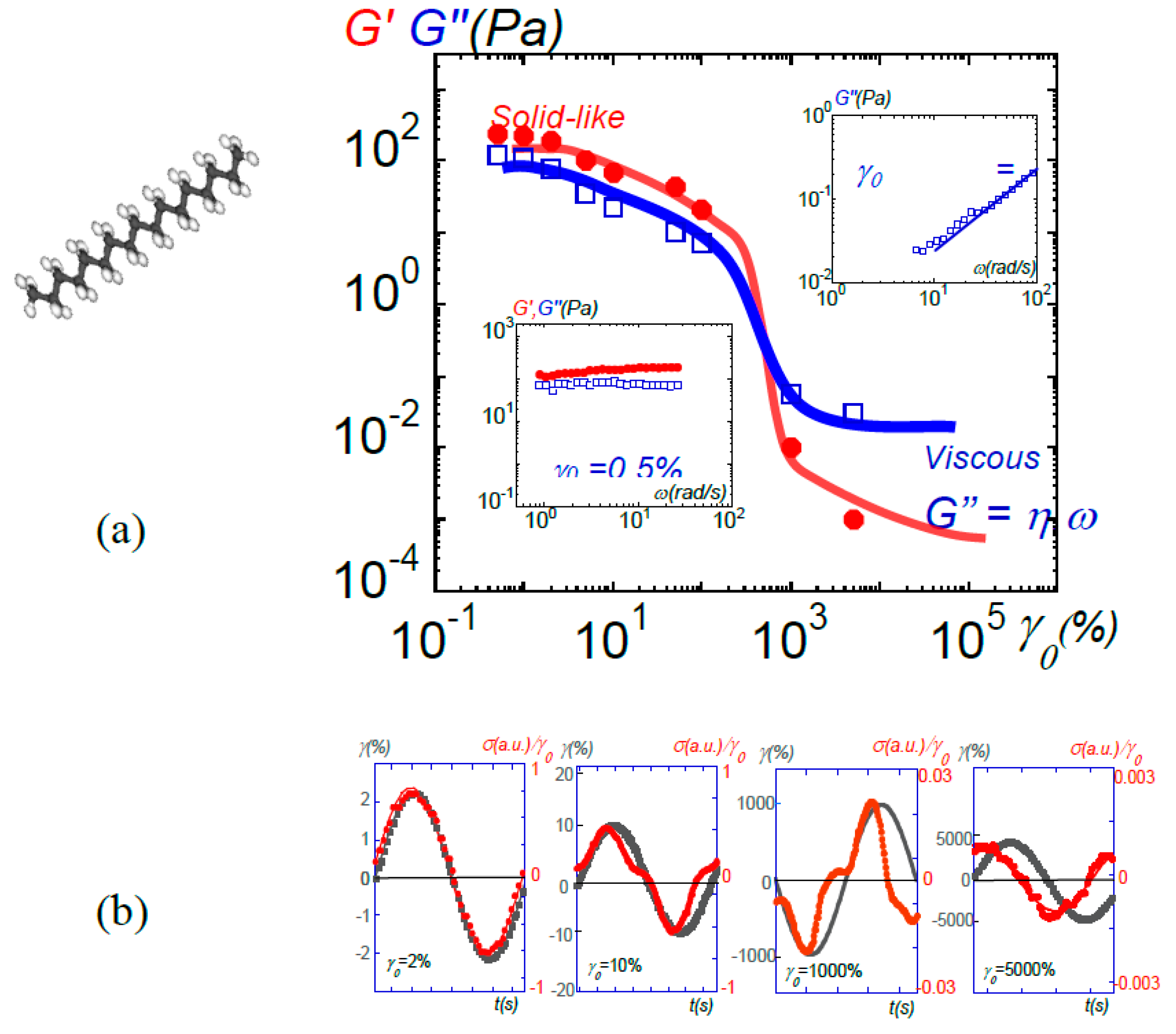
5. Mechanical Response of LC and LCPs in the Isotropic Phase
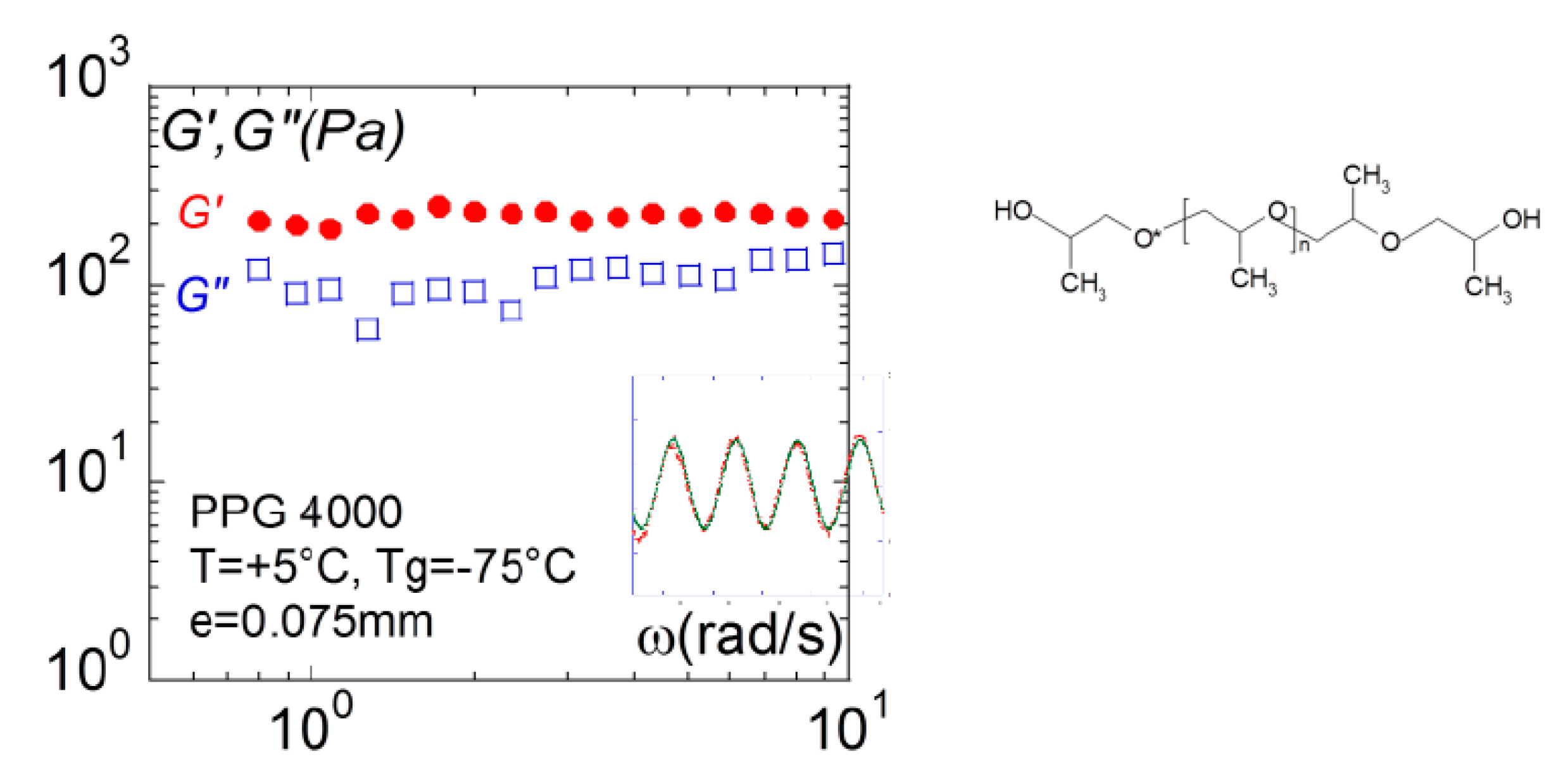
6. Optimizing the Stress Transmission and Accessing Shear Elasticity in Ordinary Fluids
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Denniston, C.; Marenduzzo, D.; Orlandini, E.; Yeomans, J.M. Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Phil. Trans. R. Soc. Lond. A 2004, 362, 1745–1754. [Google Scholar] [CrossRef]
- Marrucci, G. Theoretical aspects of the flow of liquid crystal polymers. In Rheology and Processing of Liquid Crystal Polymers, 1st ed.; Acierno, D., Collyer, A.A., Eds.; Chapman & Hall: London, UK, 1996; pp. 30–48. [Google Scholar]
- Decruppe, J.-P.; Cressely, R.; Makhloufi, R.; Cappelaere, E. Flow birefringence experiments showing a shear-banding structure in a CTAB solution. Colloid Polym. Sci. 1995, 273, 346–351. [Google Scholar] [CrossRef]
- Schmitt, V.; Lequeux, F.; Pousse, A.; Roux, D. Flow behavior and shear induced transition near an isotropic/nematic transition in equilibrium polymers. Langmuir 1994, 10, 955–961. [Google Scholar] [CrossRef]
- Berret, J.F.; Roux, D.C.; Porte, G.; Lindner, P. Shear-Induced Isotropic-to-Nematic Phase Transition in Equilibrium Polymers. Europhys. Lett. 1994, 25, 521. [Google Scholar] [CrossRef]
- See, H.; Doi, M.; Larson, R. The effect of steady flow fields on the isotropic to nematic phase transition in equilibrium polymers. J. Chem. Phys. 1990, 92, 792–800. [Google Scholar] [CrossRef]
- Olmsted, P.D.; Lu, C.-Y.D. Coexistence and phase separation in sheared complex fluids. Phys. Rev. E 1997, 56, 55. [Google Scholar] [CrossRef]
- Pujolle-Robic, C.; Noirez, L. Observation of shear-induced nematic-isotropic transition in side-chain liquid crystal polymers. Nature 2001, 409, 167. [Google Scholar] [CrossRef] [PubMed]
- Pujolle-Robic, C.; Olmsted, P.D.; Noirez, L. Transient and stationary flow behaviour of side chain liquid-crystalline polymers: Evidence of a shear-induced isotropic-to-nematic phase transition. Europhys. Lett. 2002, 59, 364–369. [Google Scholar] [CrossRef] [Green Version]
- Kahl, P.; Noirez, L. From flow birefringence in the isotropic phase to the identification of shear elasticity in liquids. Liquid Cryst. Rev. 2017, 4, 135. [Google Scholar] [CrossRef]
- Bailey, C.; Fodor-Csorba, K.; Verduzco, R.; Gleeson, J.T.; Sprunt, S.; Jakli, A. Large Flow Birefringence of Nematogenic Bent-Core Liquid Crystals. Phys. Rev. Lett. 2009, 103, 237803. [Google Scholar] [CrossRef] [PubMed]
- Hess, S. Flow Alignment and Flow-Induced Phase Transition in Liquid Crystals. Z. Naturforsch. A 1976, 31, 1507–1513. [Google Scholar] [CrossRef]
- Olmsted, P.D.; Goldbart, P.M. Theory of the nonequilibrium phase transition for nematic liquid crystals under shear flow. Phys. Rev. A 1990, 41, 4578. [Google Scholar] [CrossRef] [PubMed]
- Olmsted, P.D.; Goldbart, P.M. Isotropic-nematic transition in shear flow: State selection, coexistence, phase transitions, and critical behavior. Phys. Rev. A 1992, 46, 4966. [Google Scholar] [CrossRef] [PubMed]
- Cates, M.E.; Fielding, S.M. Rheology of giant micelles. Adv. Phys. 2006, 55, 799–879. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, M.L.; Mantegazza, F.; Gallazzi, L.; Zanchetta, G.; Bellini, T. Optical and electro-optical derivation of the pretransitional behavior of orientational and shear viscosities in the isotropic phase of liquid crystals. Phys. Rev. E 2006, 74, 011707. [Google Scholar] [CrossRef] [PubMed]
- Noirez, L. Origin of shear-induced phase transitions in melts of liquid-crystal polymers. Phys. Rev. E 2005, 72, 051701. [Google Scholar] [CrossRef] [PubMed]
- Mendil, H.; Baroni, P.; Noirez, L. Unexpected giant elasticity in side-chain liquid crystal polymer melts: A new approach for the understanding of shear induced phase transitions. Europhys. Lett. 2005, 72, 983. [Google Scholar] [CrossRef]
- Mendil-Jakani, H.; Baroni, P.; Noirez, L. Shear-Induced Isotropic to Nematic Transition of Liquid-Crystal Polymers: Identification of Gap Thickness and Slipping Effects. Langmuir 2009, 25, 5248–5252. [Google Scholar] [CrossRef] [PubMed]
- Farrand, L.D.; Patrick, J.; Marden, S.A. Merck Patent GmbH. EP1690917 B1, 8 October 2008. [Google Scholar]
- Jadzyn, J.; Dabrwoski, R.; Lech, T.; Czechowski, C. Viscosity of the Homologous Series of n-Alkylcyanobiphenyls. J. Chem. Eng. Data 2001, 46, 110–112. [Google Scholar] [CrossRef]
- Kahl, P.; Baroni, P.; Noirez, L. Bringing to Light Hidden Elasticity in the Liquid State Using In-Situ Pretransitional Liquid Crystal Swarms. PLoS ONE 2016, 11, e0147914. [Google Scholar] [CrossRef] [PubMed]
- Rzoska, S.J.; Drozd-Rzoska, A.; Mukherjee, P.K.; Lopez, D.-O.; Martinez-Garcia, J.-C. Distortion-sensitive insight into the pretransitional behavior of 4-n-octyloxy-4’-cyanobiphenyl (8OCB). J. Phys. Condens. Matter 2013, 25, 245105. [Google Scholar] [CrossRef] [PubMed]
- Reys, V.; Dormoy, Y.; Gallani, J.L.; Martinoty, P.; le Barny, P.; Dubois, J.C. Short-Range-Order Effects in the Isotropic Phase of a Side-Chain Polymeric Liquid Crystal. Phys. Rev. Lett. 1988, 61, 2340. [Google Scholar] [CrossRef] [PubMed]
- Kahl, P.; Baroni, P.; Noirez, L. Harmonic strain-optical response revealed in the isotropic (liquid) phase of liquid crystals. Appl. Phys. Lett. 2015, 107, 084101. [Google Scholar] [CrossRef] [Green Version]
- Poynting, J.H.; Thomson, J.J. Properties of Matter; C. Griffin and Co.: London, UK, 1902. [Google Scholar]
- Boltzmann, L. Sitzler Kgl Akad; Wiss: Wien, Austria, 1878; pp. 815–842. [Google Scholar]
- Freeman, S.M.; Weissenberg, K. Some new anisotropic time effects in rheology. Nature 1948, 161, 324. [Google Scholar] [CrossRef] [PubMed]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. J. Chem. Soc. Faraday Trans. II 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; Wiley & Sons: New York, NY, USA, 1970. [Google Scholar]
- Ferry, J.D. Probing Macromolecular Motions through Viscoelasticity. Rubber Chem. Tech. 1981, 54, 72–82. [Google Scholar] [CrossRef]
- Gallani, J.L.; Hilliou, L.; Martinoty, P.; Keller, P. Abnormal Viscoelastic Behavior of Side-Chain Liquid-Crystal Polymers. Phys. Rev. Lett. 1994, 72, 2109–2112. [Google Scholar] [CrossRef] [PubMed]
- Martinoty, P.; Hilliou, L.; Mauzac, M.; Benguigui, L.; Collin, D. Side-Chain Liquid-Crystal Polymers: Gel-like Behavior below Their Gelation Points. Macromolecules 1999, 32, 1746–1752. [Google Scholar] [CrossRef]
- Mendil, H.; Baroni, P.; Noirez, L. Solid-like rheological response of non-entangled polymers in the molten state. Eur. Phys. J. E 2006, 19, 77–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, H.W.; Carson, G.A.; Granick, S. Relaxation time of confined liquids under shear. Phys. Rev. Lett. 1991, 66, 2758–2761. [Google Scholar] [CrossRef] [PubMed]
- Levent Demirel, A.; Granick, S. Origins of solidification when a simple molecular fluid is confined between two plates. J. Am. Chem. Phys. 2001, 115, 1498–1512. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Superlubricity: A paradox about confined fluids resolved. Phys. Rev. Lett. 2004, 93, 096101. [Google Scholar] [CrossRef] [PubMed]
- Kavehpour, H.P.; McKinley, G.H. Tribo-rheometry: From gap-dependent rheology to tribology. Tribol. Lett. 2004, 17, 327–335. [Google Scholar] [CrossRef]
- Badmaev, B.B.; Bazaron, U.B.; Derjaguin, B.V.; Budaev, O.R. Measurement of the shear elasticity of polymethylsiloxane liquids. Phys. B 1983, 122, 241–245. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Bazaron, U.B.; Zandanova, K.T.; Budaev, O.R. The complex shear modulus of polymeric and small-molecule liquids. Polymer 1989, 30, 97–103. [Google Scholar] [CrossRef]
- Collin, D.; Martinoty, P. Dynamic macroscopic heterogeneities in a flexible linear polymer melt. Physica A 2002, 320, 235–248. [Google Scholar] [CrossRef]
- Baroni, P.; Mendil, H.; Noirez, L. Méthode de détermination des propriétés dynamiques d’un matériau fluide ou solide déformable. France Patent n° 0510988, 27 November 2005. [Google Scholar]
- Baroni, P.; Mendil-Jakani, H.; Noirez, L. Innovations pour une mesure complète des propriétés viscoélastiques des fluides. In Techniques de l’Ingénieur, TI Editions ed; Techniques de l’Ingénieur: Paris, France, 2010. [Google Scholar]
- Mendil, H.; Grillo, I.; Baroni, P.; Noirez, L. The frozen state in the liquid phase of side-chain liquid-crystal polymers. Phys. Rev. Lett. 2006, 96, 077801. [Google Scholar] [CrossRef] [PubMed]
- Noirez, L.; Baroni, P.; Cao, H. Identification of Low Frequency Shear elasticity in Liquids n-Heptadecane, Liquid Water and RT-Ionic Liquids [emim][Tf2N]. J. Mol. Liq. 2012, 176, 71–75. [Google Scholar] [CrossRef]
- Wang, S.-Q.; Ravindranath, S.; Wang, Y.; Boukany, P. New theoretical considerations in polymer rheology: Elastic breakdown of chain entanglement network. J. Chem. Phys. 2007, 127, 064903. [Google Scholar] [CrossRef] [PubMed]
- Kahl, P.; Baroni, P.; Noirez, L. Hidden solidlike properties in the isotropic phase of the 8CB liquid crystal. Phys. Rev. E 2013, 88, 050501. [Google Scholar] [CrossRef] [PubMed]
- Noirez, L.; Baroni, P. Identification of a low-frequency elastic behaviour in liquid water. J. Phys. Condens. Matter 2012, 24, 372101. [Google Scholar] [CrossRef] [PubMed]
- Noirez, L. Importance of Interfacial Interactions to Access Shear Elasticity of Liquids and Understand Flow Induced Birefringence from Liquid Crystals to Worm-Like Micellar Solutions. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2017, 72, 10–17. [Google Scholar] [CrossRef]
- Noirez, L.; Mendil-Jakani, H.; Baroni, P. Identification of finite shear-elasticity in the liquid state of molecular (OTP) and polymeric glass formers (PBuA). Philos. Mag. 2011, 91, 1977–1986. [Google Scholar] [CrossRef] [Green Version]
- Noirez, L.; Baroni, P. Revealing the solid-like nature of Glycerol at ambient temperature. J. Mol. Struct. 2010, 972, 16–21. [Google Scholar] [CrossRef]
- Chushkin, Y.; Caronna, C. Madsen A Low-frequency elastic behavior of a supercooled liquid. EPL 2008, 83, 36001. [Google Scholar] [CrossRef]
- Heidenreich, S.; Ilg, P.; Hess, S. Boundary conditions for fluids with internal orientational degrees of freedom: Apparent velocity slip associated with the molecular alignment. Phys. Rev. E 2007, 75, 066302. [Google Scholar] [CrossRef] [PubMed]
- Baroni, P.; Bouchet, P.; Noirez, L. Highlighting a Cooling Regime in Liquids under Submillimeter Flows. J. Phys. Chem. Lett. 2013, 4, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
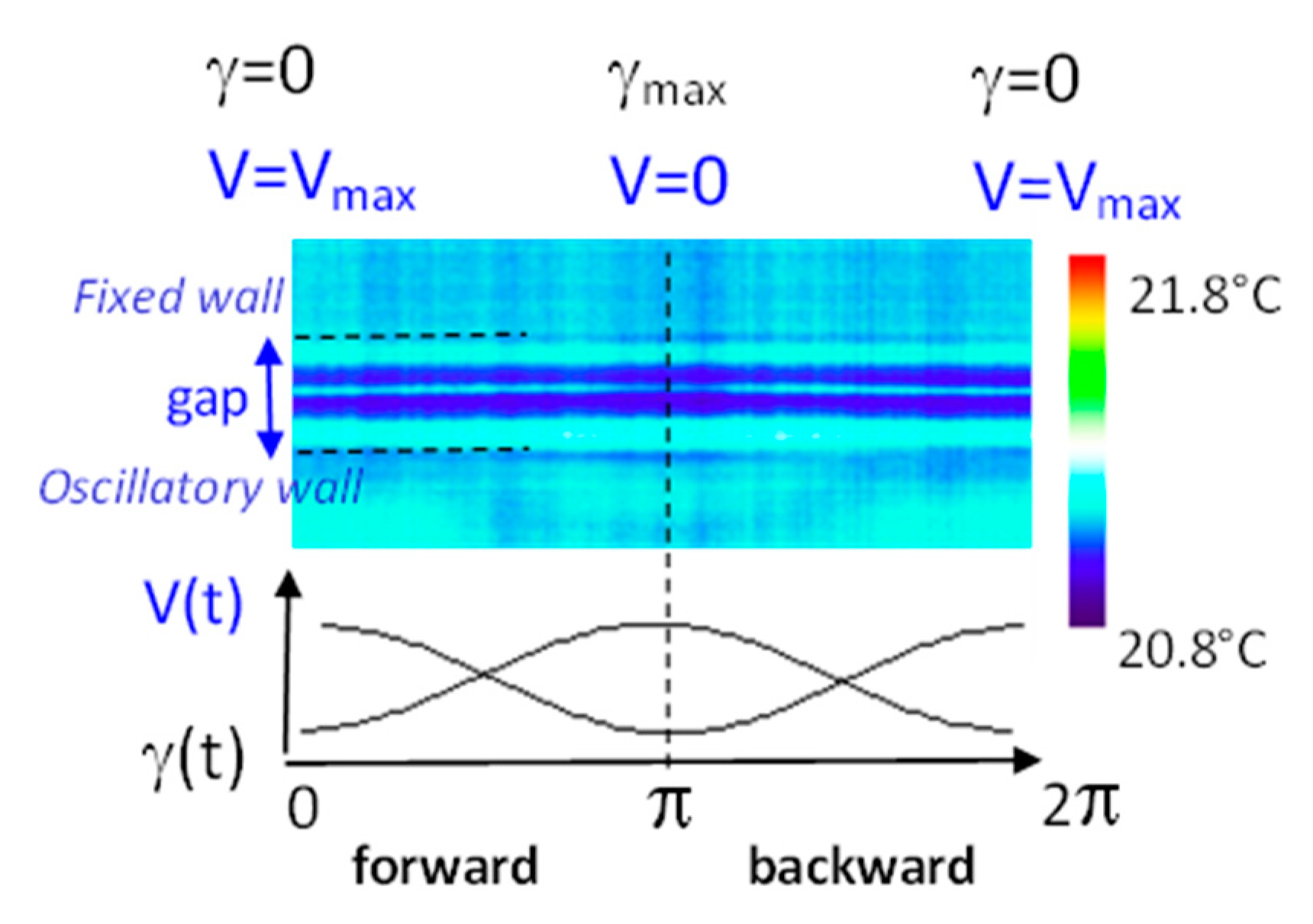
- Noirez, L.; Baroni, P. Identification of thermal shear bands in a low molecular weight polymer melt under oscillatory strain field. Colloid Polym. Sci. 2018, 296, 713–720. [Google Scholar] [CrossRef]
- Adams, J.M.; Fielding, S.M.; Olmsted, P.D. Transient shear banding in entangled polymers: A study using the Rolie-Poly model. J. Rheol. 2011, 55. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.M.; Olmsted, P.D. Nonmonotonic Models are not Necessary to Obtain Shear Banding Phenomena in Entangled Polymer Solutions. Phys. Rev. Lett. 2009, 102, 067801. [Google Scholar] [CrossRef] [PubMed]
- Bolmatov, D.; Zhernenkov, M.; Sharpnack, L.; Agra-Kooijman, D.M.; Kumar, S.; Suvorov, A.; Pindak, R.; Cai, Y.Q.; Cunsolo, A. Emergent Optical Phononic Modes upon Nanoscale Mesogenic Phase Transitions. Nano Lett. 2017, 17, 3870–3876. [Google Scholar] [CrossRef] [PubMed]
- Guenza, M. Cooperative Dynamics in Unentangled Polymer Fluids. Phys. Rev. Lett. 2002, 88, 0259011–0259014. [Google Scholar] [CrossRef] [PubMed]
- Fixman, M. Stress Relaxation in Polymer Melts and Concentrated Solutions. J. Chem. Phys. 1991, 95, 1410–1413. [Google Scholar] [CrossRef]
- Sotta, P.; Deloche, B.; Herz, J.; Lapp, A.; Durand, D.; Rabadeux, J.C. Evidence for short-range orientational couplings between chain segments in strained rubbers: A deuterium magnetic resonance investigation. Macromolecules 1987, 20, 2769–2774. [Google Scholar] [CrossRef]
- Erman, B.; Queslelt, J.-P.; Monnerie, L. Orientation and anisotropy of dangling chains in a deformed network. Polymer 1988, 29, 1823–1826. [Google Scholar] [CrossRef]
- Volino, F. Théorie viscoélastique non-extensive. Annales de Physique 1997, 22, 181–231. [Google Scholar] [CrossRef]
- Pronin, A.A.; Trachenko, K.; Kondrin, M.V.; Lyapin, A.G.; Brazhkin, V.V. Non local dielectric relmaxation in glycerol. Phys. Rev. B 2011, 84, 012201. [Google Scholar] [CrossRef]
- Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Stoupin, S.; Cunsolo, A.; Cai, Y.Q. Thermally triggered phononic gaps in liquids at THz scale. Sci. Rep. 2016, 6, 19469. [Google Scholar] [CrossRef] [PubMed]
- Zaccone, A.; Blundell, J.R.; Terentjev, E.M. Network disorder and nonaffine deformations in marginal solids. Phys. Rev. B 2011, 84, 174119. [Google Scholar] [CrossRef]
- Trachenko, K.; Brazhkin, V.V. Collective modes and thermodynamics of the liquid state. Rep. Prog. Phys. 2016, 79, 016502–016538. [Google Scholar] [CrossRef] [PubMed]
- Trachenko, K.; Brazhkin, V.V. Understanding the problem of glass transition on the basis of elastic waves in a liquid. J. Phys. Condens. Matter 2009, 21, 425104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salili, S.M.; Tamba, M.G.; Sprunt, S.N.; Welch, C.; Mehl, G.H.; Jákli, A.; Gleeson, J.T. Anomalous Increase in Nematic-Isotropic Transition Temperature in Dimer Molecules Induced by a Magnetic Field. Phys. Rev. Lett. 2016, 116, 217801. [Google Scholar] [CrossRef] [PubMed]
- Wiant, D.; Stojadinovic, S.; Neupane, K.; Sharma, S.; Fodor-Csorba, K.; Jákli, A.; Gleeson, J.T.; Sprunt, S. Critical behavior at the isotropic-to-nematic phase transition in a bent-core liquid crystal. Phys. Rev. E 2006, 73, 30703. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noirez, L.; Kahl, P. Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids. Fluids 2018, 3, 43. https://doi.org/10.3390/fluids3020043
Noirez L, Kahl P. Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids. Fluids. 2018; 3(2):43. https://doi.org/10.3390/fluids3020043
Chicago/Turabian StyleNoirez, Laurence, and Philipp Kahl. 2018. "Exploring “Dormant” Opto-Mechanical Properties of the Isotropic Phase of Liquid Crystals and Revealing Hidden Elasticity of (Ordinary) Liquids" Fluids 3, no. 2: 43. https://doi.org/10.3390/fluids3020043




